В данной публикации мы рассмотрим, как комплексное число можно возвести в степень (в т.ч. с помощью формулы Муавра). Теоретический материал сопровождается примерами для лучшего понимания.
-
Возводим комплексное число в степень
- Квадрат числа
- N-ая степень
Возводим комплексное число в степень
Для начала вспомним, что комплексное число имеет общий вид: z = a + bi (алгебраическая форма).
Теперь можем переходить, непосредственно, к решению поставленной задачи.
Квадрат числа
Мы можем представить степень в виде произведения одинаковых множителей, а затем найти их произведение (при этом помним, что i2 = -1).
z2 = (a + bi)2 = (a + bi)(a + bi)
Пример 1:
z = 3 + 5i
z2 = (3 + 5i)2 = (3 + 5i)(3 + 5i) = 9 + 15i + 15i + 25i2 = -16 + 30i
Также можно воспользоваться формулой сокращенного умножения, а именно квадратом суммы:
z2 = (a + bi)2 = a2 + 2 ⋅ a ⋅ bi + (bi)2 = a2 + 2abi – b2
Примечание: Таким же образом, если потребуется, можно получить формулы для квадрата разности, куба суммы/разности и т.д.
N-ая степень
Возвести комплексное число z в натуральную степень n гораздо проще, если оно представлено в тригонометрической форме.
Напомним, в общем виде запись числа выглядит так: z = |z| ⋅ (cos φ + i ⋅ sin φ).
Для возведения в степень можно воспользоваться формулой Муавра (так названа в честь английского математика Абрахама де Муавра):
zn = |z|n ⋅ (cos (nφ) + i ⋅ sin (nφ))
Формула получена путем перемножения комплексных чисел, записанных в тригонометрической форме (перемножаются модули, а аргументы складываются).
Пример 2
Возведем комплексное число z = 2 ⋅ (cos 35° + i ⋅ sin 35°) в восьмую степень.
Решение
z8 = 28 ⋅ (cos (8 ⋅ 35°) + i ⋅ sin (8 ⋅ 35°)) = 256 ⋅ (cos 280° + i sin 280°).
Правила возведения в степень комплексного числа
Содержание:
- Возведение комплексного числа в степень
- Возведение в степень в показательной и тригонометрической форме, формула Муавра
- Примеры решения задач
Возведение комплексного числа в степень
С началом учебы школьникам предстоит, помимо других предметов, осваивать принципы, закономерности, положения и теории математики. Как правило, новую тему начинают с повторения изученного материала, а именно, рассуждают о числах. В начальных классах учащимся передавали знания о натуральных числах. Затем предмет усложнялся, а школьники узнавали о других числовых множествах. Представим их на общей схеме:
Источник: dzen.ru
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Рассмотрим участок, закрашенный синим цветом. Здесь расположены комплексные числа. Разобраться в этом понятии можно путем решения простого уравнения:
(х^{2} + 1 = 0)
Попробуем определить, чему равны корни записанного выражения. В результате получим следующее равенство:
(х^{2} = -1)
Заметим, что при выполнении данного равенства неизвестное нужно возвести во вторую степень и получить при этом отрицательное число. По причине наличия подобных уравнений и необходимости в их решении были введены комплексные числа.
На уроках алгебры ученикам приходится решать множество заданий на разные операции с числами. В большинстве задач и тестов их требуется умножить, поделить или представить в виде какой-либо степени. Реализовывать подобные операции допустимо без учета формата рассматриваемых чисел. В том случае, когда определенное число записано как алгебраическое, то представить его в некой степени, равной n, удобно путем вычисления произведения n идентичных множителей.
Если имеется пара комплексных чисел, к примеру, (z_{1} =a_{1} +b_{1} i и z_{2} =a_{2} +b_{2} i), то для получения в итоге их произведения аналогично комплексного числа нужно учитывать алгебраические законы и условие, что (i^{2} =-1).
Итог умножения пары чисел, являющихся комплексными, например, (z_{1} =r_{1} cdot (cos varphi _{1} +isin varphi _{1} )) и (z_{2} =r_{2} cdot (cos varphi _{2} +isin varphi _{2} )), представляет собой комплексное число, полученное по итогам следующих вычислений: (z_{1} cdot z_{2} =r_{1} cdot r_{2} cdot cos (varphi _{1} +varphi _{2} )+isin (varphi _{1} +varphi _{2} ))
Примечание 1
Интерес представляет история введения в обиход комплексного числа. Изначально мысль о том, что требуется использовать такие числа, зародилась в процессе формализованного поиска ответов на уравнения с неизвестными в третьей степени. При этом в выражении Кардано образовывалось число со знаком минуса, заключенное под знак квадратного корня. Огромное значение для изучения комплексных чисел имеют труды Эйлера, Декарта и Гаусса. К примеру, известный научный деятель в области математики, Эйлер обозначил мнимую единицу за i. Непосредственно понятие комплексного числа было зафиксировано в 1831 году. Автором научного термина является Гаусс.
Возведение в степень в показательной и тригонометрической форме, формула Муавра
В процессе работы с комплексными числами, а именно, их умножении, можно упростить себе задачу, если трансформировать множители в показательную или тригонометрическую форму. В том случае, когда комплексное число имеет вид алгебраического, целесообразно переписать его по-другому, например, выбрать для записи любой из вышеуказанных форматов.
Возвести комплексное число, записанное в показательном виде, в какую-нибудь степень можно с помощью данного соотношения:
Формула 1
(z^k = (re^{ivarphi})^k = r^k e^{ikvarphi}, k in Z)
Если число, являясь комплексным, представлено в тригонометрической форме, то его возводят в степень с помощью следующего выражения:
Формула 2
(z^k = r^k (cos kvarphi + isin kvarphi), k in N)
Формула 3
Формула Муавра гласит, что степень с порядком (n (nin Z_{+})) для некого комплексного числа (z=rcdot (cos varphi +isin varphi )), определяется как комплексное число, равное: (z^{n} =r^{n} cdot (cos nvarphi +isin nvarphi ).)
В действительности формулу Муавра несложно получить путем последовательных преобразований. К примеру, можно самостоятельно умножить рассматриваемое комплексное число (z=rcdot (cos varphi +isin varphi )) на идентичное комплексное число в течение такого количества раз, которое равно n.
Исходя из закономерности Муавра, допустимо сделать вывод о том, что при возведении какого-то комплексного числа в целую степень со знаком плюс, требуется модуль этого числа возвести в заданную степень, а аргумент, принадлежащий рассматриваемому комплексному числу, умножить на степенной показатель.
Не все задания можно решить одним простым действием. Встречаются задачи, где показателем степени, в которую возводят комплексное число, является большим числом. Тогда не нужно тратить время и силы на бесконечные операции умножения этого числа на само себя. Целесообразно упростить решение путем поэтапного выполнения следующего алгоритма:
- записать алгебраическое комплексное число в тригонометрическом формате;
- выполнить возведение в степень полученного числа, руководствуясь соотношением Муавра;
- если это потребуется, выполнить обратное действие и записать полученный результат в алгебраической форме.
Примечание 2
Комплексные числа, а также функции с ними, характеризуются особыми возможностями. С помощью специальных свойств таких чисел можно значительно упростить и повысить качество решений математических, физических и технических задач. К примеру, таким способом обрабатывают сигналы, находят ответы к задачам по теории управления, колебательных движений, электрическом магнетизме. При составлении карт и в гидродинамической предметной области активно применяют трансформации комплексной плоскости. Система, состоящая из комплексных чисел, лежит в основе квантовой механики. Эти знания позволяют сформировать понимание современного физического мира.
Исходя из полученной информации, можно с легкостью решать примеры на представлении комплексных чисел в той или иной степени. При этом не нужно множество раз умножать такое число само на себя. Достаточно внимательно изучить предложенное выражение и применить полученные знания на практике. С другой стороны, имеется несколько способов возведения в степень разных чисел. В качестве примера можно привести бинарное возведение в степень. В таком случае в процессе вычислений используют специальную формулу, сокращающую количество раз, в течение которых требуется выполнить умножение числа само на себя.
Примеры решения задач
В процессе решения примеров с комплексными числами, которые требуется представить в виде той или иной степени, необходимо руководствоваться стандартным алгоритмом действий. Начинать расчеты следует с определения вида уравнения. Поняв, какие действия нужно выполнить, можно вспомнить полезную формулу. Далее остается лишь применить закономерность, либо преобразовать выражение в подходящий формат. Не следует забывать о таком важном условии, как область допустимых значений. Подобная проверка позволит исключить посторонние корни.
Задача 1
Дано комплексное число, которое требуется возвести во вторую степень: (z = sqrt{2}e^{frac{pi}{2}i})
Решение
Воспользуемся уже известной формулой, чтобы представить во второй степени модуль и экспоненту. Запишем поэтапные вычисления согласно стандартному алгоритму и получим искомое значение:
(z^2 = (sqrt{2}e^{frac{pi}{2}i})^2 = 2e^{pi i})
Ответ: (z^2 = 2e^{pi i})
Задача 2
Требуется выполнить возведение комплексного числа z в степень, равную трем, при условии, что комплексное число записано в таком виде: (z = 1+sqrt{3}i)
Решение
Заметим, что формат записи данного числа алгебраический. Исходя из полученных знаний, стоит сначала перевести z в тригонометрическую форму. Таким образом, вычисления получится значительно упростить. Определим, чему равен модуль заданного числа:
(|z| = sqrt{a^2+b^2} = sqrt{1^2 + (sqrt{3})^2} =sqrt{4}=2)
Далее можно приступить к поиску аргумента:
(varphi = frac{b}{a} = arctg frac{sqrt{3}}{1} = frac{pi}{3} )
В итоге получается следующая тригонометрическая запись рассматриваемого комплексного числа:
(z = 2(cos frac{pi}{3} + isin frac{pi}{3}))
Если действовать согласно стандартному алгоритму, то на втором этапе нужно вычислить представленное комплексное число в третьей степени:
(z^3 = 2^3(cos (3 cdot frac{pi}{3})+isin (3 cdot frac{pi}{3})) = 8 (cos pi + isin pi))
В конце расчетов стоит выполнить обратный перевод числа в алгебраический формат. В результате получим:
(z^3 = 8 (-1 + i cdot 0) = -8)
Ответ: (z^3 = -8)
Задача 3
Нужно применить полученные из курса теории знания и возвести комплексное число z в степень n с учетом следующих условий: (z=1+2cdot i n=2..4)
Решение
Вспомним, как умножают комплексные числа, если они записаны в алгебраическом формате. Руководствуясь основным определением, стандартной формулой и подставив исходные данные, получим следующие результаты вычислений:
(z^{2} =(1+2cdot i)cdot (1+2cdot i)=-3+4i)
(z^{3} =z^{2} cdot (1+2cdot i)=-3+4i-6i-8=-11-2i)
(z^{4} =z^{3} cdot (1+2cdot i)=-11-2i-22i+4=-7-24i)
Ответ: (-3+4i , -11-2i, -7-24i.)
Возводить в натуральную степень $n$, если она
достаточно велика, комплексные числа проще всего в
тригонометрической форме, то есть если число
$z=a+b i$ задано в
алгебраической форме, то
его изначально надо записать в тригонометрической.
Пусть число $z=|z|(cos phi+i sin phi)$, тогда умножая его само на себя
$n$ раз (что эквивалентно тому, что мы его
возводим в степень $n$), получим:
$z^{n}=(|z|(cos phi+i sin phi))^{n}=|z|^{n}(cos n phi+i sin n phi)$
Таким образом, модуль степени комплексного числа равен той же степени модуля основания, а
аргумент равен аргументу основания, умноженному на показатель степени.
Если $|z|=1$, то получаем, что
$z^{n}=(cos phi+i sin phi)^{n}=cos n phi+i sin n phi$
Данная формула называется формулой Муавра (Абрахам де Муавр (1667 — 1754) — английский математик).
Пример
Задание. Найти
$z^{20}$, если
$z=frac{1}{2}+frac{sqrt{3}}{2} i$
Решение. Вначале запишем заданное
комплексное число в тригонометрической форме, для этого
вычислим его модуль и аргумент:
$|z|=left|frac{1}{2}+frac{sqrt{3}}{2} iright|=sqrt{left(frac{1}{2}right)^{2}+left(frac{sqrt{3}}{2}right)^{2}}=sqrt{frac{1}{4}+frac{3}{4}}=sqrt{frac{4}{4}}=1$
$arg z=arg left(frac{1}{2}+frac{sqrt{3}}{2} iright)=operatorname{arctg} frac{frac{sqrt{3}}{2}}{frac{1}{2}}=operatorname{arctg} sqrt{3}=frac{pi}{3}$
Тогда
$z=1 cdotleft(cos frac{pi}{3}+i sin frac{pi}{3}right)=cos frac{pi}{3}+i sin frac{pi}{3}$
А отсюда, согласно формуле, имеем:
$z^{20}=left(cos frac{pi}{3}+i sin frac{pi}{3}right)^{20}=cos left(20 cdot frac{pi}{3}right)+i sin left(20 cdot frac{pi}{3}right)=$
$=cos frac{20 pi}{3}+i sin frac{20 pi}{3}=cos frac{21 pi-pi}{3}+i sin frac{21 pi-pi}{3}=$
$=cos left(7 pi-frac{pi}{3}right)+i sin left(7 pi-frac{pi}{3}right)= cos left(pi-frac{pi}{3}right)+i sin left(pi-frac{pi}{3}right)=$
$=-cos frac{pi}{3}+i sin frac{pi}{3}=-frac{1}{2}+i cdot frac{sqrt{3}}{2}=-frac{1}{2}+frac{sqrt{3}}{2} i$
Ответ. $z^{20}=-frac{1}{2}+frac{sqrt{3}}{2} i$
Читать дальше: извлечения корня из комплексного числа.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Возведение комплексных чисел в степень
Начнем
со всем любимого квадрата.
Пример
9
Возвести
в квадрат комплексное число
Здесь
можно пойти двумя путями, первый способ
это переписать степень как произведение
множителей
и
перемножить числа по правилу умножения
многочленов.
Второй
способ состоит в применение известной
школьной формулы сокращенного
умножения
:
Для
комплексного числа легко вывести свою
формулу сокращенного умножения:
.
Аналогичную формулу можно вывести для
квадрата разности, а также для куба
сумма и куба разности. Но эти формулы
более актуальны длязадач
комплексного анализа,
поэтому на данном уроке я воздержусь
от подробных выкладок.
Что
делать, если комплексное число нужно
возвести, скажем, в 5-ую, 10-ую или 100-ую
степень? Ясно, что в алгебраической
форме проделать такой трюк практически
невозможно, действительно, подумайте,
как вы будете решать пример вроде
?
И
здесь на помощь приходит тригонометрическая
форма комплексного числа и, так
называемая, формула
Муавра:
Если комплексное число представлено в
тригонометрической форме
,
то при его возведении в натуральную
степень
справедлива
формула:
Просто
до безобразия.
Пример
10
Дано
комплексное число
,
найти
.
Что
нужно сделать? Сначала нужно представить
данной число в тригонометрической
форме. Внимательные читатели заметили,
что в Примере 8 мы это уже сделали:
Тогда,
по формуле Муавра:
Упаси
боже, не нужно считать на калькуляторе
,
а вот угол в большинстве случае следует
упростить. Как упростить? Образно
говоря, нужно избавиться от лишних
оборотов. Один оборот составляет
радиан
или 360 градусов. Смотрим сколько у нас
оборотов в аргументе
:
оборотов,
в данном случае можно убавить один
оборот:
.
Надеюсь всем понятно, что
и
–
это один и тот же угол.
Таким
образом, окончательный ответ запишется
так:
Любители
стандартов везде и во всём могут
переписать ответ в виде:
(т.е.
убавить еще один оборот и получить
значение аргумента в стандартном виде).
Хотя
–
ни в коем случае не ошибка.
Пример
11
Дано
комплексное число
,
найти
.
Полученный аргумент (угол) упростить,
результат представить в алгебраической
форме.
Это
пример для самостоятельного решения,
полное решение и ответ в конце урока.
Отдельная
разновидность задачи возведения в
степень – это возведение в степень
чисто мнимых чисел.
Пример
12
Возвести
в степень комплексные числа
,
,
Здесь
тоже всё просто, главное, помнить
знаменитое равенство.
Если
мнимая единица возводится в четную
степень, то техника решения такова:
Если
мнимая единица возводится в нечетную
степень, то «отщипываем» одно «и»,
получая четную степень:
Если
есть минус (или любой действительный
коэффициент), то его необходимо
предварительно отделить:
Пример
13
Возвести
в степень комплексные числа
,
Это
пример для самостоятельного решения.
Извлечение корней из комплексных чисел
Наконец-то.
Меня всю дорогу подмывало привести этот
маленький примерчик:
Нельзя
извлечь корень? Если речь идет о
действительных числах, то действительно
нельзя. В комплексных числах извлечь
корень – можно! А точнее, два корня:
Действительно
ли найденные корни являются решением
уравнения
?
Выполним проверку:
Что
и требовалось проверить.
Часто
используется сокращенная запись, оба
корня записывают в одну строчку под
«одной гребёнкой»:
.
Такие
корни также называют сопряженными
комплексными корнями.
Как
извлекать квадратные корни из отрицательных
чисел, думаю, всем понятно:
,
,
,
,
и
т.д. Во всех случаях получается двасопряженных
комплексных корня.
Пример
14
Решить
квадратное уравнение
Вычислим
дискриминант:
Дискриминант
отрицателен, и в действительных числах
уравнение решения не имеет. Но корень
можно извлечь в комплексных числах!
По
известным школьным формулам получаем
два корня:
–
сопряженные комплексные корни
Таким
образом, уравнение
имеет
два сопряженных комплексных корня:
,
Теперь
вы сможете решить любое квадратное
уравнение!
И
вообще, любое уравнение с многочленом
«энной» степени
имеет
ровно
корней,
часть из которых может быть комплексными.
Простой
пример для самостоятельного решения:
Пример
15
Найти
корни уравнения
и
разложить квадратный двучлен на
множители.
Разложение
на множители осуществляется опять же
по стандартной школьной формуле.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Комплексные числа — это расширение поля действительных чисел. Обозначается 


Формально, комплексное число 

(Д2.1)
(Д2.2)
и операцией приравнивания
(Д2.3)
Историческая справка[править]
Термин «комплексное число» впервые использовал французский математик Л. Карно (1753—1823) в 1803 году, но широкое употребление ему придал К. Ф. Гаусс (1777—1855) в 1831 году.
Впервые же мнимые величины, скорее всего, нашли отражение в известном труде Дж. Кардано (1501—1576) «Великое искусство, или об алгебраических правилах» (1545), но он счёл их непригодными для использования в математической практике. Применение мнимых величин для решения кубических уравнений нашли в работах Р. Бомбелли (ок. 1526—1572). Он также разработал базовые правила действий с ними.
Хотя выражения вида 

Геометрическое истолкование комплексных чисел и действий над ними появилось впервые в работе К. Весселя (1745—1818), но зачатки этого представления были сделаны ещё в 1685 году Дж. Валлисом (1616—1703). Современное геометрическое представление, так называемую диаграмму Аргана, предложил в опубликованной в 1806 года работе Ж. Р. Арган (1768—1822), независимо повторивший выводы Весселя.
Символ 
Непротиворечивая модель комплексных чисел была создана в 1837 году У. Р. Гамильтоном (1806—1865). В рамках неё комплексные числа рассматривались как упорядоченные пары действительных чисел. Он же в 1843 году предложил и обобщение комплексных чисел — кватернионы, получив тем самым гиперкомплексные числа. Позже были получены ещё несколько видов гиперкомплексных чисел, например, числа Кэли.
Алгебраическая форма комплексного числа[править]
Арифметическая модель комплексных чисел как пар действительных чисел, предложенная У. Р. Гамильтоном, хотя и непротиворечива, но не удобна в вычислениях, поэтому для манипуляций с ними используют различные их представления.
В рамках гамильтоновского определения действительные числа имеют вид 




Рассмотрим следующее выражение:
(Д2.4)
Применяя формулу (Д2.2), получаем:
(Д2.5)
Следовательно, число 

(Д2.6)
однако и он не безупречен, так как этому уравнению удовлетворяет не только 




Исходя из модели Гамильтона, выведем алгебраическую форму комплексного числа, для этого рассмотрим комплексное число 
(Д2.7)
На основании формулы (Д2.1) можно написать, что
(Д2.8)
Во втором слагаемом сделаем ещё одно преобразование:
(Д2.9)
Воспользовавшись формулой (Д2.2), будем иметь:
(Д2.10)
Теперь, если заменить получившиеся упорядоченные пары их значениями, придём к следующему выражению:
(Д2.11)
Это и есть алгебраическая форма комплексного числа.
Если в формуле (Д2.11) положить 
(Д2.12)
будет называться чисто мнимым числом, или просто мнимым числом.
Условно комплексное число обозначают одной буквой, чаще всего 

Первую проекцию[1] 









В терминах алгебраической формы можно переформулировать определение равенства комплексных чисел (Д2.3):
(Д2.13)
или, если применить условные обозначения:
(Д2.14)
В частности, комплексное число равно нулю, когда его действительная и мнимая части равны нулю:
или
(Д2.15)
Аналогичным путём можно получить алгебраическую форму для комплексно сопряжённого числа: 
Арифметические действия над комплексными числами в алгебраической форме[править]
Алгебраическая форма очень удобна для выполнения арифметических действий, так как в рамках её комплексные числа можно рассматривать как линейные двучлены, роль 


Сложение двух комплексных чисел 

(Д2.16)
Оно непосредственно следует из формулы (Д2.1).
Чтобы получить правило вычитания одного комплексного числа из другого, воспользуемся определением: разностью двух комплексных чисел 


(Д2.17)
Если рассматривать с формальной точки зрения, то следует записать следующее выражение:
(Д2.18)
Теперь в левой части применим формулу суммы комплексных чисел:
(Д2.19)
По определению сравнения двух комплексных пар будем иметь следующую систему:
(Д2.20)
решением которой являются действительные числа 

(Д2.21)
Если применять алгебраическую форму, то вычитание будет более наглядным:
(Д2.22)
Рассмотрим теперь произведение двух комплексных чисел 

(Д2.23)
Деление комплексных чисел, как и деление действительных чисел, является обратной операцией по отношению к произведению. По определению, комплексное число 


(Д2.24)
Найдём произведение в левой части:
(Д2.25)
(Д2.26)
Сравнивая его с числом в правой части, будем иметь систему:
(Д2.27)
Решением будут служить числа:
(Д2.28)
Следовательно, можно записать следующее правило:
(Д2.29)
Выведем теперь правила деления комплексных чисел в алгебраической форме:
(Д2.30)
Домножим числитель и знаменатель дроби на комплексно сопряжённое знаменателя — 
(Д2.31)
В числителе раскроем скобки, а в знаменателе воспользуемся формулой разности квадратов:
(Д2.32)
После упрощений и почленного деления окончательно будем иметь:
(Д2.33)
В частности,
(Д2.34)
и
(Д2.35)
Возведение в целую степень. Прежде чем рассматривать вопрос возведения в степень произвольного комплексного числа 




(Д2.36)
Для 
(Д2.37)
Продолжая умножение, можно получить следующее обобщение:
(Д2.38)
где 
При возведение в степень числа 

(Д2.39)
Теперь, упрощая каждый моном по формулам (Д2.38) и группируя члены, содержащие и не содержащие 

Так как, по определению,
(Д2.40)
то нужно сначала возвести в степень 
Из выше сказанного следует, что при любом целом, отличном от нуля, показателе степени, для комплексного числа общего вида мы получаем другое комплексное число. Если возводить в целую степень чисто мнимое число, то в результате может получиться либо действительное, либо чисто мнимое число.
Вопрос извлечения корней из комплексных чисел мы рассмотрим на примере извлечения квадратного корня. В дальнейшем будет более подробно показано, что извлечение корня для комплексных чисел всегда осуществимо и многозначно.
Итак, по определению, квадратным корнем из комплексного числа 


(Д2.41)
или, раскрывая скобки,
(Д2.42)
Сравнивая действительные и мнимые части комплексных чисел, приходим к системе уравнений:
(Д2.43)
решая которую будем иметь:
(Д2.44)
Выражения 








Замечание. Из выражений (Д2.16) и (Д2.23) становится ясным, почему формулы (Д2.1) и (Д2.2) соответственно имеют такой вид. Возникает законный вопрос, почему нельзя в качестве определения сразу принять, что комплексным числом 










Основные законы действий над комплексными числами[править]
На комплексные числа распространяются все основные законы действия над действительными числами. Они легко выводятся из определения арифметических операций.
(Д2.45)
(Д2.46)
(Д2.47)
(Д2.48)
(Д2.49)
(Д2.50)
(Д2.51)
(Д2.52)
(Д2.53)
(Д2.54)
(Д2.55)
Здесь в общем случае 
Замечание. Как будет показано ниже, при возведении в комплексную степень некоторые формулы (Д2.45)—(Д2.55) могут не выполняться в общем виде.
Комплексно сопряжённое число[править]
Как уже было сказано выше, выбор того, какая упорядоченная пара 








Переход к комплексно сопряжённому удобно рассматривать как унарную (одноместную) операцию, которая изменяет знак у мнимой части комплексного числа 
(Д2.56)
Рассмотрим основные свойства комплексного сопряжения:
Свойство Д2.1. Комплексно сопряжённое от комплексно сопряжённого числа 

(Д2.57)
Это следует из определения операции.
Свойство Д2.2. Сопряжённое к действительному числу 


Это следует из определения действительного числа в рамках модели комплексных чисел и определения комплексного сопряжения.
Свойство Д2.3. Комплексное сопряжение алгебраической суммы равно алгебраической сумме комплексно сопряжённых:
(Д2.58)
Доказательство формулы (Д2.58)
Вывод формулы прост. Если 

(Д2.59)
Тогда комплексно сопряжённое равно
(Д2.60)
С другой стороны, если рассмотреть алгебраическую сумму комплексно сопряжённых 

(Д2.61)
Равенство 
Свойство Д2.4. Комплексное сопряжение произведения равно произведению комплексно сопряжённых:
(Д2.62)
Доказательство формулы (Д2.62)
Свойство Д2.5. Комплексное сопряжение частного равно частному комплексно сопряжённых:
(Д2.65)
Доказательство формулы (Д2.65)
Алгебраическая форма частного комплексных чисел согласно (Д2.33) имеет вид:
(Д2.66)
следовательно, комплексно сопряжённое равно:
(Д2.67)
Частное комплексно сопряжённых:
(Д2.68)
Что и требовалось доказать.
Свойство Д2.7. Вообще, комплексное сопряжение комплексного многочлена равно многочлену от комплексно сопряжённых:
(Д2.69)
где 
Это непосредственно следует из свойств (Д2.3) и (Д2.4).
Свойство Д2.8. Сумма комплексного числа и его сопряжённого есть число действительное, разность — чисто мнимое:
(Д2.70)
На основе этого свойства можно записать:
(Д2.71)
Геометрическая интерпретация комплексного числа[править]
Рассмотрим декартову систему координат на плоскости (рисунок Д2.1), где по оси абсцисс отложена действительная часть 

Таким образом, нахождение сопряжённого значения 
Модуль и аргумент комплексного числа[править]
В связи с векторной интерпретацией можно наглядно ввести понятия модуля и аргумента комплексного числа.
Модулем (абсолютной величиной, амплитудой) 


По теореме Пифагора получаем, что
(Д2.72)
или
(Д2.73)
Причём здесь используется арифметический корень. Непосредственно из (Д2.72) следует, что для вещественных 
Свойства модуля комплексного числа[править]
Свойство Д2.9. Из определения модуля следует, что 


Свойство Д2.10. Для модулей суммы и разности комплексных чисел справедливы следующие неравенства:
(Д2.74)
(Д2.75)
(Д2.76)
(Д2.77)
более того
(Д2.78)
(Д2.79)
Справедливы также обобщённые выражения:
(Д2.80)
(Д2.81)
В (Д2.74)—(Д2.81) равенство достигается только при 
Доказательство свойства Д2.10 отложим до рассмотрения тригонометрической формы комплексного числа, в которой данные формулы легко доказываются.
Свойство Д2.11. Модуль произведения комплексных чисел равен произведению модулей:
(Д2.82)
Доказательство свойства Д2.11
Рассмотрим два выражения:
(Д2.83)
и
(Д2.84)
В формуле (Д2.83) раскроим скобки в подкоренном выражении:
(Д2.85)
Сравнивая (Д2.84) и (Д2.85), убеждаемся в выполнении свойства Д2.11. Что и требовалось доказать.
В частности, верно равенство 


По индукции можно доказать более общее равенство:
(Д2.86)
Откуда можно в частности получить:
(Д2.87)
Свойство Д2.12. Модуль отношения комплексных чисел равен отношению модулей:
(Д2.88)
Доказательство свойства Д2.12
Аналогично предыдущему доказательству рассмотрим два выражения:
(Д2.89)
и
(Д2.90)
В формуле (Д2.89) в подкоренном выражении приведём к общему знаменателю, а потом раскроим скобки в числителе:
(Д2.91)
Сравнивая (Д2.90) и (Д2.91), убеждаемся в выполнении свойства Д2.12. Что и требовалось доказать.
Свойство Д2.13. Для пары комплексных чисел 


Это станет ясно, если рассмотреть выражение 
(Д2.92)
которое совпадает с формулой для расстояния между двумя точками (метрикой) на евклидовой плоскости.
Свойство Д2.14. Модули комплексного числа и его сопряжённого равны:
(Д2.93)
Это легко доказать:
(Д2.94)
Под аргументом 


Однако, из определения следует, что угол задаётся неоднозначно — с точностью до 



![{displaystyle (-pi ,;pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68d42d585d0cc7e452cd100efa4127cc28bedceb)
(Д2.95)
Обычно, когда говорят об аргументе комплексной величины, имеют в виду именно главное значение.
Из определения тригонометрических функций можно получить, что аргумент комплексного числа равен, такому значению 
(Д2.96)
Таким образом, для вычисления (главного значения) аргумента используется следующее выражение:
(Д2.97)
Свойства аргумента комплексного числа[править]
Свойство Д2.15. Аргумент (в общем смысле) произведения комплексных чисел равен сумме аргументов этих чисел:
(Д2.98)
Это свойство (и аналогичные) справедливо и для главных ююзначений, если привести 
![{displaystyle (-pi ,;pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68d42d585d0cc7e452cd100efa4127cc28bedceb)
Методом математической индукции можно также доказать, что
(Д2.99)
Эта формула приводит к такому выражению для натуральной степени комплексного числа:
(Д2.100)
Свойство Д2.16. Аргумент отношения комплексных чисел равен разности аргументов:
(Д2.101)
Здесь предполагает, что 

В частности, справедливо
(Д2.102)
Доказательства этих свойств удобнее вести с использованием показательной формы комплексного числа.
Свойство Д2.17. Аргумент комплексно сопряжённого числа равен противоположному значению аргумента комплексного числа:
(Д2.103)
Это свойство наглядно доказывается из рисунка Д2.2: так как операция комплексного сопряжения соответствует симметричному отражению, относительно оси абсцисс, то угол, который составляет радиус-вектор комплексно сопряжённого будет иметь противоположный знак (если свести его к стандартному полуинтервалу ![{displaystyle (-pi ,;pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68d42d585d0cc7e452cd100efa4127cc28bedceb)
Геометрическая интерпретация арифметических действий с комплексными числами[править]
Изображение комплексных чисел как радиус-векторов на комплексной плоскости позволяет наглядно выполнять основные арифметические операции над комплексными числами. Так сложение и вычитание двух комплексных чисел в геометрическом виде (рисунок Д2.4) сводится к сложению по правилу параллелограмма радиус-векторов этих чисел.
 |
 |
 |
Результатом умножения двух комплексных чисел, согласно (Д2.82) и (Д2.98), является такой радиус-вектор (рисунок Д2.5), у которого модуль равен произведению модулей исходных комплексных чисел, а аргумент — сумме аргументов этих чисел. При делении двух комплексных чисел, согласно (Д2.88) и (Д2.101), нужно построить такой радиус-вектор (рисунок Д2.6), что модуль его будет равен отношению модулей, а аргумент — разности аргументов этих чисел. При этом предполагается, что используется главное значение аргумента результата.
Тригонометрическая форма комплексного числа[править]
Введённые выше модуль и аргумент позволяют записать комплексное число в тригонометрической форме. Для этого выразим из (Д2.96) действительную и мнимую части комплексного числа через тригонометрические функции:
(Д2.104)
где 
Тогда получим такое выражение:
(Д2.105)
которое называется тригонометрической формой комплексного числа.
Такое представление имеет любое комплексное число, кроме 

В таком представление можно просто доказать выражения, связанные с модулем комплексных чисел (см. свойство Д2.10).
Доказательство свойства Д2.10
Докажем формулу (Д2.74). Слева в этом неравенстве стоит такое выражение:
(Д2.106)
Так как 
(Д2.107)
Следует напомнить, что 
Теперь рассмотрим выражение, стоящее с правой стороны неравенства (Д2.74):
(Д2.108)
Сравнивая (Д2.107) и (Д2.108), убеждаемся в справедливости формулы (Д2.74). Что и требовалось доказать.
Из только что приведённого доказательства по индукции выводится и верность формулы (Д2.80).
Для доказательства неравенства (Д2.75) заменим в выражении (Д2.74) 


Чтобы доказать (Д2.76), рассмотрим такое равенство:
(Д2.109)
и применим к нему неравенство (Д2.75). Получим
(Д2.110)
откуда получаем требуемое неравенство 
По аналогии с (Д2.75) доказывается и (Д2.77): заменив в (Д2.76) 

Неравенство (Д2.78) следует из того факта, что в силу коммутативности сложения неравенство (Д2.76) можно записать двумя способами:
(Д2.111)
и
(Д2.112)
Выбрав из двух значений (отличающихся знаком), стоящих в правой части, большее (что эквивалентно, в данном случае, нахождению абсолютного значения), придём к неравенству (Д2.78).
Доказательство неравенства (Д2.79) также основано на замене 
Доказательство обобщённого неравенства (Д2.81) основано на использовании обобщённого неравенств (Д2.80) и (Д2.75):
(Д2.113)
Итак, мы доказали справедливость всех неравенств (Д2.74)—(Д2.81).
Свойство Д2.18. При вычислении целой степени комплексного числа справедлива формула Муавра:
(Д2.114)
Доказательство свойства Д2.18
Формулу Муавра также можно применять для нахождения корней из комплексных чисел.
Свойство Д2.19. Операция извлечения корня 

(Д2.116)
где 
Доказательство свойства Д2.19
По определению корнем 

![{displaystyle {sqrt[{n}]{z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79e0bdaa79edce57d3ddb6be7ca76c938598783b)

(Д2.117)
На основании формулы Муавра равенство (Д2.117) можно записать как
(Д2.118)
где 





Сравнивая модули и аргументы (в общем смысле), получим следующие тождества:
(Д2.119)
(Д2.120)
Так как модули являются положительными действительными числами, то из первого равенства следует, что
(Д2.121)
а из второго получим:
(Д2.122)
С учётом того, что нас интересует только главное значение 



Таким образом, применение формулы Муавра для извлечения корня степени 



Пример Д2.1. Рассмотрим извлечение кубического корня из единицы на множестве комплексных чисел (подробнее см. статью «Корни из единицы»):
Представим 1 в тригонометрической форме:
(Д2.123)
По формуле извлечения корня (Д2.116) получим:
(Д2.123)
или
(Д2.124)
Перейдя к алгебраической форме, имеем:
(Д2.125)
Графически данный результат можно представить в виде равностороннего треугольника, вписанного в единичную окружность (рисунок Д2.7).
Таким образом, формула (Д2.116) позволяет найти все комплексные решения уравнения
(Д2.126)
Показательная форма комплексного числа[править]
Применение формулы Эйлера для определения комплексной экспоненты
(Д2.127)
к тригонометрической форме комплексного числа
(Д2.128)
позволяет получить показательную форму комплексного числа:
(Д2.129)
Такая запись является более компактной по сравнению с тригонометрической, но является ей эквивалентной (при правильном использовании аргумента).
В показательной форме, например, удобно провести доказательства свойств Д2.15 и Д2.16.
Доказательство свойств Д2.15 и Д2.16
Чтобы доказать формулу (Д2.98) представим 

(Д2.130)
Значит
(Д2.131)
тогда
(Д2.132)
Аналогично, можно показать справедливость выражения (Д2.101):
(Д2.133)
а это означает, что
(Д2.134)
Что и требовалось доказать.
Показательная форма комплексного числа удобно позволяет определить показательную и логарифмическую функции комплексного аргумента.
Показательная и логарифмическая функция комплексного аргумента[править]
Показательную форму комплексного числа 
(Д2.135)
поэтому формально логарифм комплексного числа можно определить как
(Д2.136)
Не стоит, однако, забывать, что 
(Д2.137)
которая является многозначной.
Переход от логарифма по основанию 

(Д2.138)
Формулу (Д2.138), а также другие логарифмические тождества для комплексных чисел нужно применять только с учётом их многозначности, в противном случае, это может привести к ошибочному результату.
Экспоненту комплексного числа в алгебраической форме вычисляется по формуле:
(Д2.139)
Для вычисления показательной функции при любом основании служит следующая формула:
(Д2.140)
которую также следует применять, не забывая о многозначности.
Общие замечания[править]
Как уже говорилось выше, при распространении алгебраических тождеств, справедливых для действительных чисел и действительных функций от них, следует проявлять большую осторожность. Так, например, из равенства логарифмов неких выражений ещё не следует равенство самих этих выражений. Тоже самое относится и к вычислению корней из комплексных чисел. Это можно проиллюстрировать на примере следующих математических софизмов:
Пример Д2.2: Рассмотрим такое равенство:
(Д2.141)
которое является явно неверным. Выражение (Д2.141) ошибочно, потому что в нём применяется формула логарифма степени 
Пример Д2.3: Другим известным софизмом является такой:
(Д2.142)
При доказательстве этого «тождества» не учтено, что не только 




Примечания[править]
- ↑ См. статью «Пара».
































































































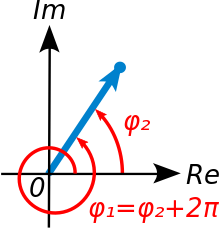






















![{displaystyle {sqrt[{n}]{z}}=z^{1/n}=r^{1/n}left(cos {frac {varphi +2pi k}{n}}+isin {frac {varphi +2pi k}{n}}right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca9bf76f7b906c4c5851c299696203356f59a7a)




![{displaystyle rho ={sqrt[{n}]{r}}=r^{1/n},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e11a666ccdf285deaf7daab0df074c19be264eb)



![{displaystyle {sqrt[{3}]{1}}={sqrt[{3}]{1}}cdot (cos {frac {0+2pi k}{3}}+isin {frac {0+2pi k}{3}})quad (k=0,;1,;2)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0548a67fb4505c6c644412a9f7c573209aec7a7)
![{displaystyle {sqrt[{3}]{1}}=cos {frac {2pi k}{3}}+isin {frac {2pi k}{3}}.quad (k=0,;1,;2)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58808bdaa56e2ddf7b8aaea7dc8752f464664f21)
![{displaystyle {sqrt[{3}]{1}}=left{1;;{frac {-1+i{sqrt {3}}}{2}};;{frac {-1-i{sqrt {3}}}{2}}right}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/287fdea676108ff38fe5cb46eef65c94cecc26ef)
















