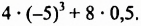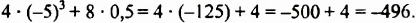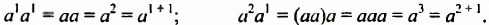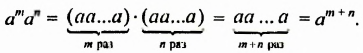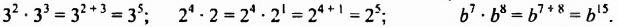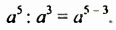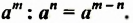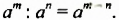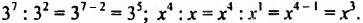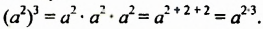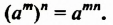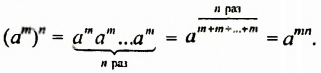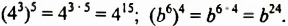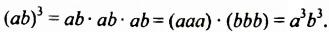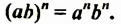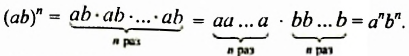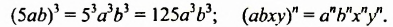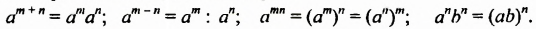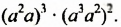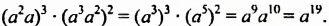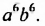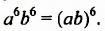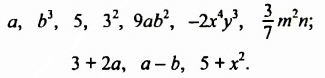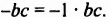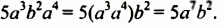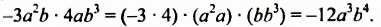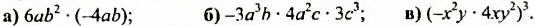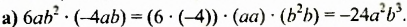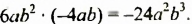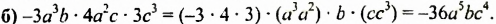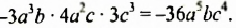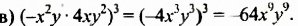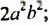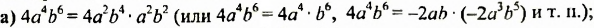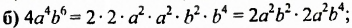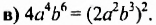Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Возведение в степень одночлена
Поддержать сайт
Запомните!
При возведении в степень одночлена в степень возводится числовой коэффициент и
каждый буквенный множитель.
Рассмотрим пример возведения в куб одночлена: (2a2x)3
Вначале возведем в степень отдельно числовой коэффициент и каждый буквенный множитель.
(2a2x)3 = 23(a2)3 x3
При возведении в степень буквенных множителей используем правило
возведения степень в степень.
Напоминаем, что при возведении степени в степень показатели степеней перемножаются.
23(a2)3 x3 =
23 a2 · 3 x3 = 8a6x3
Запишем итоговое решение.
(2a2x)3 = 23(a2)3 x3 =
23a2 · 3x3 = 8a6x3
Примеры возведения в степень одночленов
- (3а)3 = 33a3 = 27a3
- (−2b)2 = (−2)2b2 = 4b2
( x2m4)3 =()3 (x2)3 (m4)3 =
x2 · 3 m4 · 3 =
x6m12
(в данном примере используем правило
возведения в степень дроби)- (−ab2)2 = (−1)2a2 b2 · 2
= 1a2 b4 = a2 b4 - (−3px)3 =
(−3)3 p3 x3 =
−27p3 x3
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Алгоритм умножения одночленов
- Определить коэффициент результирующего одночлена: перемножить все коэффициенты умножаемых одночленов.
- Используя свойства степеней и перемножая, найти общую степень для каждой из переменных.
В результате умножения одночленов получается одночлен.
Например: $ (frac{2}{3} a^2 b) cdot (3ab^5 )$
Шаг 1. Коэффициент многочлена $ frac{2}{3} cdot 3 = 2 $
Шаг 2. Степени переменных: $ a^{2+1} = a^3, b^{1+5} = b^6 $
Получаем: $(frac{2}{3} a^2 b) cdot (3ab^5 ) = frac{2}{3} cdot 3cdot a^{2+1} cdot b^{1+5} = 2a^3 b^6$
Алгоритм возведения одночлена в степень
Возвести в степень каждый множитель одночлена и перемножить полученные результаты.
В результате возведения одночлена в степень получается одночлен.
Например: $ (frac{2}{3} a^2 b^5)^3 $
Степень каждого сомножителя: $ left(-frac{2}{5}right)^3 = frac{2^3}{5^3} = frac{8}{125}, (a^2 )^3 = a^6,(b^5 )^3 = b^15 $
Получаем: $ (frac{2}{3} a^2 b^5)^3 = left(-frac{2}{5}right)^3 cdot (a^2 )^3 cdot (b^5 )^3 = frac{8}{125} a^6 b^{15} $
Примеры
Пример 1. Выполните умножение одночленов:
а) $ (-3a^2 xy^5 )cdot( frac{1}{9} ax^4 y^2 ) = -3 cdot frac{1}{9} cdot a^{2+1} cdot x^{1+4} cdot y^{5+2} = -frac{1}{3} a^3 x^5 y^7 $
б) $ (7az)cdot(- frac{1}{4} a^2 xy) cdot (16xz^4 ) = -7cdot frac{1}{4} cdot 16 cdot a^{1+2}cdot x^{1+1}cdot z^{1+4} = -28a^3 x^2 z^5 $
Пример 2. Найдите куб одночленов:
а) $ (3a^5 by^2 )^3 = 3^3cdot(a^5 )^3cdot b^3cdot(y^2 )^3 = 27a^{15} b^3 y^6 $
б) $ left(-frac{1}{2}xy^2 z^7right)^3 = left(-frac{1}{2}right)^3cdot x^3cdot(y^2 )^3cdot(z^7 )^3 = -frac{1}{8} x^3 y^6 z^{21} $
Пример 3. Упростите выражение:
а) $ 3x^5 cdot left(frac{1}{24}x^2 y^3right)^2 cdot (-64y)=- frac{3cdot64}{24} cdot x^{5+4} cdot y^{6+1} = -frac{3cdot8^2}{3cdot8} x^9 y^7 = -8x^9 y^7 $
б) $ (-2ab)^3cdot underbrace{0,125}_{=1/8text{}} a^2 c = -2^3cdot frac{1}{8} cdot a^{3+2} b^3 c = -a^5 b^3 c $
в) $ left(1frac{2}{3}bz^7right)^5 cdot left(-frac{3}{5}azright)^4 = left(frac{5}{3}right)^5 cdot left(-frac{3}{5}right)^4 cdot a^4 b^5 z^{5cdot7+4} = frac{5}{3} a^4 b^5 z^{39} $
г) $ (-0,5m^2 n^5 )^2 cdot 12mn^3 = left(-frac{1}{2}right)^2 cdot 12 cdot m^{4+1} cdot n^{10+3} = 3m^5 n^{13} $
Пример 4*. При каком значении n верно равенство:
а) $ left(frac{1}{6}xyright)^n cdot 72x = 2x^3 y^2 $
Запишем уравнения для коэффициентов и степеней переменных слева и справа:
$$ {left{ begin{array}{c} left(frac{1}{6}right)^n cdot 72 = 2 \ x^{n+1} = x^3 \ y^n = y^2 end{array} right.} $$
Получаем n = 2. Проверяем:
$$ left(frac{1}{6}xyright)^2 cdot 72x = left(frac{1}{6}right)^2 cdot 72 cdot x^{2+1} cdot y^2 = 2x^3 y^2 $$
Ответ: n=2
б) $ (-1 frac{1}{3} a^2 b)^n cdot 0,75b^3 = 1 frac{1}{3} a^4 b^5 $
Запишем уравнения для коэффициентов и степеней переменных слева и справа:
$$ {left{ begin{array}{c} left(-1frac{1}{3}right)^n cdot 0,75 = 1frac{1}{3} \ a^{2n} = a^4 \ b^{n+3} = b^5 end{array} right.} $$
Получаем n = 2. Проверяем:
$$ left(-1frac{1}{3}a^2bright)^2 cdot 0,75b^3 = left(-frac{4}{3}right)^2 cdot left(frac{3}{4}right) cdot a^4 cdot b^{2+3} = frac{4}{3}a^4b^5 = 1frac{1}{3}a^4b^5 $$
Ответ: n = 2
Содержание:
Одночлены
Степень с натуральным показателем
Напомним, что произведение двух или трех одинаковых множителей, каждый из которых равен
Квадрат числа 5 называют еще второй степенью этого числа, а куб — третьей степенью.
Соответственно произведение 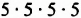
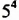
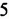
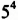
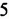
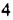
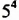
Определение:
Степенью числа 
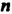
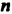



Степень с основанием 
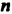
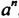

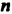
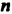

Итак, по определению
Выясним знак степени с натуральным показателем.
тогда
— любая натуральная степень числа 0 равна 0.
, тогда
— любая натуральная степень положительного числа есть положительное число.
тогда
. Степень отрицательного числа с четным показателем является положительным числом, поскольку произведение четного количества отрицательных чисел положительно. Степень отрицательного числа с нечетным показателем является отрицательным числом, поскольку произведение нечетного количества отрицательных чисел отрицательно.
Возводить числа в степень с натуральным показателем можно с помощью микрокалькулятора. Вычислить, например, значение 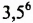
или по более удобной схеме:
Получим значение степени: 1838,265625.
Возведение в степень — действие третьей ступени. Напомним, что если выражение без скобок содержит действия разных ступеней, то сначала выполняют действия высшей ступени, а потом — низшей. Так, чтобы найти значение выражения 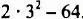
Примеры выполнения заданий:
Пример №110
Вычислить
Решение:
Выполняя вычисления, можно:
а) записывать каждое действие в отдельности:
б) записывать вычисления в строчку:
Ответ. 496.
Свойства степени с натуральным показателем
Умножение степеней с одинаковыми основаниями
Рассмотрим произведения двух степеней с основанием 
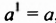
Следовательно, 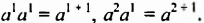
Свойство 1. Для любого числа 

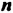
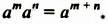
Из свойства 1, которое еще называют основным свойством степени, следует правило умножения степеней:
Чтобы умножить степени с одинаковыми основаниями, нужно основание оставить прежним, а показатели степеней сложить.
Например:
Правило умножения степеней распространяется на произведение трех и более степеней. Например:
Деление степеней с одинаковыми основаниями
Рассмотрим равенство 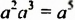
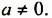
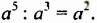
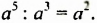
В этом примере частное степеней с одинаковыми основаниями равно степени с тем же основанием и показателем, который равен разности показателя степени делимого и показателя степени делителя. Сформулируем и докажем соответствующее свойство в общем случае.
Свойство 2. Для любого числа 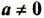
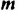
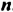
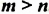
Доказательство. Поскольку 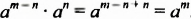
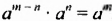
Из доказанного свойства следует правило деления степеней:
Чтобы разделить степени с одинаковыми основаниями, нужно основание оставить прежним, а из показателя степени делимого вычесть показатель степени делителя.
Например:
Возведение степени в степень
! Возведем степень 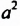
Итак, 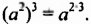
Свойство 3. Для любого числа 
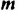
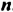
Доказательство.
Из свойства 3 следует правило возведения степени в степень:
Чтобы возвести степень в степень, нужно основание оставить прежним, а показатели степеней перемножить.
Например:
Возведение произведения в степень
Возведем произведение 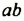
Итак, 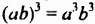
Свойство 4. Для любых чисел 
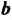
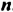
Доказательство.
Имеем такое правило:
Чтобы возвести в степень произведение, нужно возвести в эту степень каждый множитель и результаты перемножить.
Это правило распространяется на произведение трех и более множителей. Например:
Примечание. Доказанные тождества 
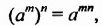
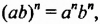
- Заказать решение задач по высшей математике
Примеры выполнения заданий:
Пример №111
Упростить выражение
Решение:
Пример №112
Вычислить:
Пример №113
Представить 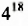
Решение:
Пример №114
Представить в виде степени произведение
Решение:
Одночлен и его стандартный вид
Рассмотрим две группы выражений:
Какова особенность выражений первой группы? Чем они отличаются от выражений второй группы?
Выражения первой группы — это переменные, числа, их степени и произведения. Такие выражения называют одночленами. В общем виде одночлен — это произведение чисел, переменных и их степеней.
Выражения второй группы не являются одночленами, поскольку содержат действия сложения или вычитания.
Рассмотрим одночлен 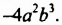
Одночленом стандартного вида называют такой одночлен, который содержит только один числовой множитель, находящийся на первом месте, ч степени разных переменных.
Числовой множитель одночлена стандартного вида называют коэффициентом одночлена. Коэффициент одночлена 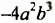
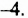
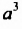
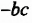

Одночлен 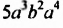
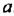
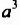
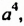
Умножение одночленов
Перемножим одночлены 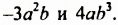
-3а2Ь • 4aby = (-3 • 4) • (а2а) • (ЬЬг) = -12аъЬ
Итак, произведением одночленов -Ъа2Ь и 4аЬъ является одночлен -12а3Ь*. Вообще, произведением любых одночленов является одночлен.
Возведение одночлена в степень
Возведем одночлен -5а2Ь в куб. Используя свойства степени, получим:
Итак, кубом одночлена 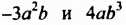
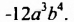
Степень одночлена
В одночлене 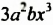
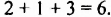
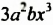
Степенью одночлена называют сумму показателей степеней всех переменных, которые в него входят. Если одночленом является число, отличное от нуля, то считают, что степень такого одночлена равна нулю.
Например: 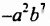
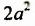
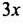
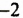
Примеры выполнения заданий:
Пример №115
Записать выражение в виде одночлена стандартного вида:
Сокращенная запись:
Сокращенная запись:
Пример №116
Представить одночлен 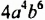
а) произведения двух одночленов стандартного вида;
б) произведения двух одночленов, одним из которых является
в) квадрата одночлена стандартного вида.
Решение:
Интересно знать
Понятие степени с натуральным показателем возникло в античные времена в связи с вычислением площадей и объемов. Толкование степеней 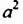
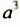
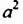
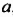
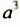
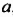
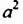
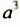
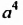
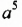
Только в XVII в. французский математик Рене Декарт (1596-1650) дал геометрическое толкование произведения любого числа множителей после чего и произведение 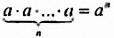
Декарт же ввел и современное обозначение степени с натуральным показателем в виде
- Многочлены
- Формулы сокращенного умножения
- Разложение многочленов на множители
- Системы линейных уравнений с двумя переменными
- Делимость натуральных чисел
- Выражения и уравнения
- Линейное уравнение с одной переменной
- Целые выражения
Что такое одночлены в математике? Зачем они нужны? Мы рассмотрим с вами определение одночлена, стандартный вид одночлена и дадим определение степени одночлена.
Определение
Одночлен – это выражение, которой представляет собой произведение числа, переменной или переменных и степеней переменных. Например, ,
,
,
– примеры одночленов.
Выражения или
– не являются одночленами, так как представляют сумму и частное, а не произведение.
Стандартный вид одночлена
Стандартный вид одночлена – это произведение числа и переменных в различной степени. Согласно этому число можно считать одночленом, так как оно может быть представлено в виде произведения числа на переменную в нулевой степени: . Например,
– одночлен стандартного вида.
Примеры стандартного вида одночлена:
,
,
,
,
,
.
Степень одночлена
Степенью одночлена называется сумма показателей степеней переменных. Например, одночлен – это одночлен второй степени, а
– одночлен седьмой степени.
Степень одночлена – равна единица, а степень одночлена
– нулю.
Подобные одночлены
Подобными одночленами называют одночлены, которые отличаются только числовым коэффициентом, а также те одночлены, которые равны между собой.
Примеры подобных одночленов: и
,
и
,
и
.
Приведение к одночлену стандартного вида
Задание 1
Приведите к одночлену стандартного вида произведение .
Решение: перемножим сначала числа , теперь переменные x
, теперь переменные
:
.
Стандартный вид многочлена:
Ответ: .
Задание 2
Приведите к одночлену стандартного вида выражение .
Решение: Перемножим числовые коэффициенты выражения , затем перемножим степени переменной x
. Получим стандартный вид одночлена:
Ответ: .
Задание 3
Приведите сумму подобных одночленов к одночлену стандартного вида:
Решение: Просто сложим все одночлены, ориентируясь на числовую часть: , а переменные просто припишем, получаем стандартный вид одночлена:
.
Ответ:
Возведите одночлен в степень
Задание 1
Возведите одночлен в квадрат.
Решение: .
Ответ:
Задание 2
Возведите одночлен в куб.
Решение: .
Ответ:
Задание 3
Какова степень одночлена .
Решение:
Для того чтобы определить степень одночлена, нужно:
- представить одночлен в стандартном виде,
- сложить показатели степеней переменных одночлена.
Сначала надо представить одночлен в стандартном виде, для этого выполним возведение в степень: , посчитаем сумму показателей степеней
, получается степень одночлена 10.
Ответ: 10




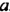
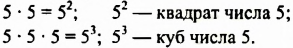
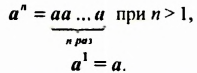
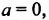 тогда
тогда 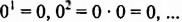 — любая натуральная степень числа 0 равна 0.
— любая натуральная степень числа 0 равна 0.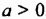 , тогда
, тогда 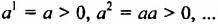 — любая натуральная степень положительного числа есть положительное число.
— любая натуральная степень положительного числа есть положительное число.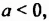 тогда
тогда  . Степень отрицательного числа с четным показателем является положительным числом, поскольку произведение четного количества отрицательных чисел положительно. Степень отрицательного числа с нечетным показателем является отрицательным числом, поскольку произведение нечетного количества отрицательных чисел отрицательно.
. Степень отрицательного числа с четным показателем является положительным числом, поскольку произведение четного количества отрицательных чисел положительно. Степень отрицательного числа с нечетным показателем является отрицательным числом, поскольку произведение нечетного количества отрицательных чисел отрицательно.