Как найти кубики в параллелепипеде

Представление о том, что такое прямоугольный параллелепипед, все имеют еще с детства, когда играли в кубики, держали в руках такие предметы, как коробка из-под сока или из- под конфет, видели аквариум такой формы. В жизни мы постоянно сталкиваемся с предметами, которые представляют собой прямоугольный параллелепипед (рисунок 1).

Определение

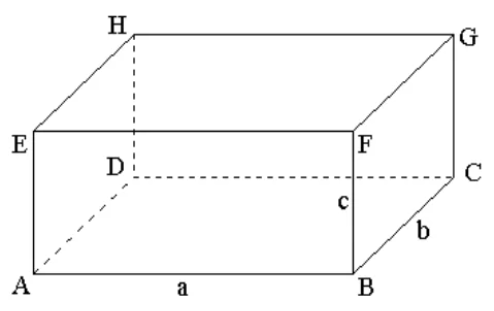
Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками. Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Основания параллелепипеда – это его верхняя и нижняя грани.

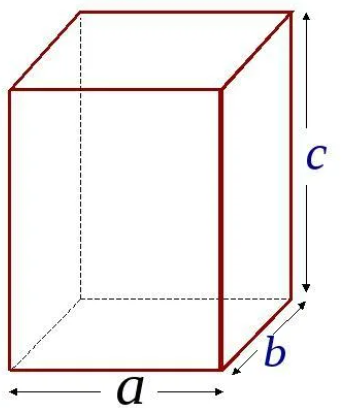
Так, на рисунке 2 показан прямоугольный параллелепипед ABCDEFGH. Он имеет 6 граней, основаниями являются грани ABCD и EFGH.

У параллелепипеда есть вершины, их 8. Они обозначены заглавными латинскими буквами. Также у прямоугольного параллелепипеда есть 12 ребер – это стороны граней: AB, BC, CD, AD, EF, FG, HG, EH, AE, BF, CG, HD.

Противоположные (не имеющие общих вершин) грани прямоугольного параллелепипеда равны.

Длина, ширина, высота

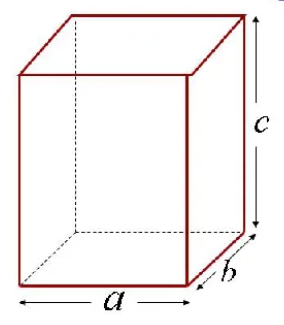
Прямоугольный параллелепипед имеет три измерения – длину (а), ширину (b) и высоту (c) – рисунок 3. Зная эти измерения, можно найти не только площадь каждой грани, но и площадь всей поверхности прямоугольного параллелепипеда.

Так как каждая грань параллелепипеда – это прямоугольник, то для нахождения площади любой грани надо умножить длину и ширину этих граней, т.е S=ab, S=bc, S=ac.

Для нахождения площади поверхности прямоугольного параллелепипеда надо сложить площади всех граней, то есть S поверхности = ab+bc+ac+ab+bc+ac. Так как противоположные грани равны, то их площади тоже равны, значит S поверхности = 2ab+2bc+2ac. Это действие можно записать короче, вынося 2 за скобки, как общий множитель, то есть S поверхности = 2(ab+bc+ac). Таким образом, нахождение площади поверхности становится более быстрым.

Куб

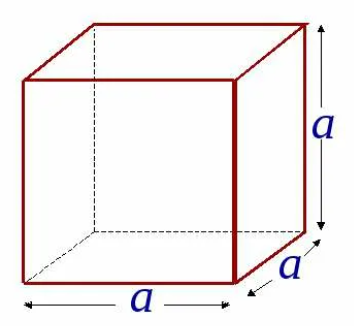
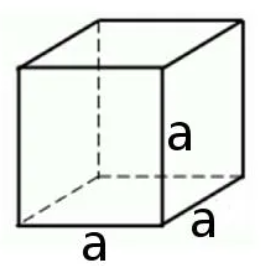
Прямоугольный параллелепипед, у которого все измерения равны, называется кубом. Поверхность куба состоит из шести равных квадратов (рисунок 4).

Для нахождения площади одной грани достаточно найти площадь квадрата по формуле S=a². Тогда для нахождения площади поверхности куба надо эту площадь умножить на 6, так как шесть равных граней у куба: S=6a²

Объем прямоугольного параллелепипеда

С понятием объема люди встречаются в повседневной жизни ежедневно. Мы наливаем воду в чайник, в ванну, другие жидкости в разные ёмкости – это всё измеряется в определенных единицах и является объемом. Наши шкафы, холодильники и другие подобные предметы – имеют объемы, так как мы их заполняем определенными вещами. На рисунке 5 показаны предметы, которые мы используем и которые имеют определенный объем.

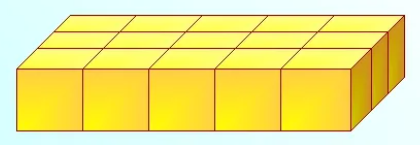
Рассмотрим объемные геометрические фигуры. Так, например, прямоугольный параллелепипед. Рассмотрим рисунок 6, где показано, что параллелепипед состоит из нескольких одинаковых кубиков. Значит, объем данного параллелепипеда равен сумме объемов его кубиков.

 

За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.

Объем куба с ребром 1 мм называют кубическим миллиметром и записывают 1 мм³; с ребром 1 см – кубическим сантиметром (см³) и так далее. Измерить объем фигуры – значит подсчитать, сколько единичных кубов в ней помещается. Если объем маленького кубика на рисунке 3 принять за единицу, то объем нашего прямоугольного параллелепипеда будет равен 15 кубическим единицам.

Формула объема прямоугольного параллелепипеда

Чтобы найти объем прямоугольного параллелепипеда, надо перемножить три его измерения – длину, ширину и высоту. То есть V=abc (рисунок 4). Зная, что произведение длины и ширины – это есть площадь основания, получим, что V=(ab)h=Sh, где h – высота прямоугольного параллелепипеда. Таким образом, мы получили еще одну формулу для нахождения объема параллелепипеда.

Объем куба

Поскольку у куба все ребра равны (рисунок 7), то его объем вычисляется по формуле:

V=a³

Пирамида

Прямоугольный параллелепипед является одним из видов многогранников. Также одним из видов многогранника является пирамида, образ которой также известен нам из жизни – из истории и других источников (рисунок 9).

Поверхность пирамиды состоит из боковых граней – треугольников, которые имеют общую вершину, а в её основании могут быть различные многоугольники – треугольник, четырехугольник, пятиугольник и т.д. (рисунок 10).

Таким образом, пирамиды можно классифицировать по количеству сторон основания (треугольная, четырехугольная, пятиугольная и т.д.). Если пирамида треугольная (рисунок 11), то её основанием может служить любая грань.

Даниил Романович | Просмотров: 1.1k

Представим себе такую историю…

– Паша, а ты когда-нибудь собирал кубик Рубика? – спросил Саша.

– Конечно! И не один раз, – ответил Паша. –
Кстати, кубик Рубика отличная игрушка-головоломка,
которая развивает логическое мышление.

– Да, мне тоже он очень нравится! – продолжил
Саша. – Я вот сегодня собрал кубик Рубика за 15 минут.
Пока собирал, задумался, а сколько всего маленьких кубиков в нём?

– И в правду, – задумался Паша, – и сколько
же их там?

– Не знаю! – ответил Саша. – Сколько ни
пытался их пересчитать, всё сбивался. В общем, так и не получилось у меня их
сосчитать.

– А давай спросим у Электроши!
– предложил Паша. – Он точно знает, как их посчитать.

– Ребята, прежде чем я вам расскажу о
прямоугольном параллелепипеде, давайте немного разомнёмся и выполним устные
задания, – предложил Электроша.

– Давайте сверимся! Посмотрите, что у вас
должно было получиться!

– А теперь вернёмся к вашему вопросу, –
продолжил Электроша. – Только сначала ответьте мне на
вопрос: какую форму имеет кубик Рубика?

– Кубик Рубика
имеет форму прямоугольного параллелепипеда, а точнее – форму куба, – ответили
мальчишки.

– Молодцы! – похвалил ребят Электроша. – Важным свойством любого геометрического тела
является его вместимость, то есть объём фигуры. Величина объёма
даёт нам представление о том, какую часть пространства занимает интересующий
нас объект.

Кстати, с такой величиной, как объём, мы
очень часто встречаемся в нашей жизни. Может, вы сможете привести примеры,
когда мы интересуемся объёмом? – спросил у ребят Электроша.

– Например, объём коробки с соком, объём
бассейна, объём школьного кабинета, – начал Саша.

– Ещё нам нужно знать объём топливного бака
машины, показатели потребления газа или воды на счётчиках, – продолжил Паша.

– Хорошие примеры! – похвалил ребят Электроша. – А как вы думаете, что нужно знать для того,
чтобы измерить объём? – спросил у ребят Электроша.

– Наверное, нужно знать единицу измерения
объёмов, – предположили мальчишки.

– Правильно! – подтвердил Электроша.
– Напомню, что для измерения отрезков мы вводили единичный отрезок, для
измерения углов – единичный угол, а для измерения площадей фигур – единичный
квадрат.

Для измерения объёмов также вводятся единицы
измерения. За единицу измерения объёма выбирают куб, ребро которого равно
единичному отрезку. Такой куб называют единичным.

Например, объём куба с ребром 1 миллиметр
называют кубическим миллиметром. Пишут так: .

Объём куба с ребром 1 сантиметр называют кубическим
сантиметром. Пишут так: .

Объём куба с ребром 1 дециметр называют кубическим
дециметром. Пишут так: .

Всем хорошо известна и такая единица объёма,
как 1 литр. Пишут так  дм³   л. Это другое название кубического
дециметра.

Объём куба с ребром 1 метр называют кубическим
метром. Пишут так: .

Объём куба с ребром 1 километр называют кубическим
километром. Пишут так: .

Легко заметить, что название единицы объёма
получается из названия единицы длины присоединением прилагательного
«кубический».

– Как вы думаете, что значит измерить объём
фигуры? – спросил у ребят Электроша.

– Измерить
объём фигуры – значит подсчитать, сколько единичных кубов в ней
помещается, –
сказали мальчишки.

– Молодцы! – похвалил ребят Электроша. – Проще всего измерить объём прямоугольного
параллелепипеда. Чем мы сейчас и займёмся.

– Посмотрите: на листке бумаги изображён
прямоугольный параллелепипед со следующими измерениями: длина 5 сантиметров,
ширина 2 сантиметра и высота 3 сантиметра. Давайте посчитаем, сколько единичных
кубов может в нём поместиться.

– Начнём укладывать кубики на дно
прямоугольного параллелепипеда, – предложили мальчишки. – Итак, сначала положим
на дно ряд единичных кубиков со стороной 1 сантиметр вдоль длинной стены.
Видим: поместилось 5 таких кубиков. Затем вдоль этих кубиков уложим ещё 1 ряд.
Тоже получим ещё пять кубиков.

– Хорошо! – сказал Электроша.
– Тогда сколько всего кубиков у вас поместилось на дне прямоугольного
параллелепипеда?

– На дне параллелепипеда помещается слой из единичных кубиков, то есть слой из 10 кубов.

– Молодцы! – похвалил ребят Электроша. – А чтобы заполнить
весь прямоугольный параллелепипед, сколько в него нужно вложить таких слоёв?

– Так как высота нашего параллелепипеда 3 сантиметра,
то в него вместится 3 слоя кубиков, в каждом из которых будет по 10 кубиков.
Тогда получается, что весь прямоугольный параллелепипед можно заполнить 30 кубиками.

– Всё правильно! – согласился Электроша. – Мы получили, что всего в нашем параллелепипеде
помещается единичных кубов. Поэтому объём нашего параллелепипеда равен  (см³).

– Электроша,
получается, что три измерения прямоугольного параллелепипеда позволяют
посчитать, сколько всего кубиков в нём поместится? – спросил Паша.

– Да, – ответил Электроша.
– Запомните! Объём прямоугольного параллелепипеда равен произведению
трёх его измерений.

Формулу для вычисления объёма прямоугольного
параллелепипеда в буквенном виде можно записать следующим образом: , где   – объём, , и – измерения прямоугольного параллелепипеда.
При вычислениях обязательно нужно обращать внимание, чтобы все измерения
прямоугольного параллелепипеда были выражены в одинаковых единицах.

– А теперь давайте решим одну задачку, –
предложил Электроша. – Определите объём блока бумаги,
если длина одного листа 20 миллиметров, ширина – 15 миллиметров, а всего в
блоке помещается 500 таких листов (считать толщину листа равной 1 миллиметру).

– Сначала вычислим площадь одного листа, –
сказал Паша, – она будет равна  (мм²).

– А потом площадь этого листа умножим на
количество листов, помещающихся в блоке, – продолжил Саша, – то есть  (мм³).

– Молодцы! – похвалил ребят Электроша. – Обратите внимание: блок бумаги имеет форму
прямоугольного параллелепипеда. Значит, мы с вами сейчас нашли объём
параллелепипеда, но с помощью другой формулы. Запомните! Объём
прямоугольного параллелепипеда равен произведению площади основания на высоту.

В буквенном виде эту формулу записывают так: , где – площадь основания прямоугольного
параллелепипеда,   – его высота.

– А теперь давайте всё же вернёмся к вашему
первоначальному вопросу, – продолжил Электроша. – Вы
хотели выяснить, сколько кубиков содержится в кубике Рубика.
Мы с вами уже определили, что эта замечательная игрушка имеет форму прямоугольного
параллелепипеда, а если быть точнее, то форму куба. Может, вы уже сможете
посчитать количество маленьких кубиков, из которых состоит кубик Рубика?

– Так, – начал рассуждать Саша, – длина
нашего кубика Рубика состоит из 3 маленьких кубиков, точно
такие же ширина и высота. Значит, в нашем кубике Рубика
помещается  маленьких кубиков.

– Всё правильно! – сказал Электроша.
– Изначально кубик Рубика состоял из 27 связных между
собой разноцветных кубиков, но затем его конструкция упростилась до набора из 26
маленьких кубиков, а вместо внутреннего кубика разместился хитроумный
скрепляющий механизм. Кстати, а вы знаете кем, как и когда была придумана эта
замечательная игрушка? – спросил Электроша.

– Не знаем, – ответили мальчишки.

– Скажу вам только, что знаменитый кубик Рубика придумал венгерский преподаватель архитектуры Эрно Рубик в 1974 году.

А вот уже историю его создания и
усовершенствования вы можете изучить на досуге.

– А теперь смотрите, мы с вами определили,
что наш кубик Рубика имеет форму куба. Поскольку у
куба все рёбра равны, то его объём вычисляют по формуле:  , где  – длина ребра куба. Именно поэтому третью
степень числа называют кубом числа.

А теперь, ребята, давайте посмотрим, как вы
всё поняли, и выполним несколько заданий.

Задание первое: объём класса 96 кубических
метров. Найдите высоту стены, если площадь пола 32 квадратных метра.

Решение: класс имеет форму прямоугольного
параллелепипеда. Нам известна площадь пола, то есть площадь основания
прямоугольного параллелепипеда. Значит, можем воспользоваться формулой для
вычисления объёма прямоугольного параллелепипеда через площадь основания и
высоту: . Выразим из этой формулы высоту: . И подставим в получившуюся формулу объём класса и площадь пола:  (м). Получаем, что высота стены равна 3 метрам.

Следующее задание: длина аквариума 80 сантиметров,
ширина 45 сантиметров, высота 65 сантиметров. Сколько литров воды нужно налить,
чтобы уровень воды был ниже верхнего края аквариума на 5 сантиметров?

Решение: высота нашего аквариума 65
сантиметров, а воду нужно налить так, чтобы её уровень был ниже верхнего края
аквариума на 5 сантиметров. Значит, от высоты аквариума отнимем 5 сантиметров: . Получим, что высота уровня воды равна 60 сантиметрам. Воспользуемся
формулой для вычисления объёма прямоугольного параллелепипеда:
. Получим, что в аквариум нужно налить  (см³). Переведём в литры. Мы знаем, что  л  дм³ , а значит, равен  см³ . Тогда получаем, что в
аквариум нужно налить  см³  л.

Задания

Версия для печати и копирования в MS Word

Решение:

Вначале разобьем наш параллелепипед на кубики 2 на 2.

Очевидно, что три грани могут быть окрашены только у боковых кубиков, а таковых будет всего 4 с одного торца и четыре с другого торца параллелепипеда. То есть, всего 8 кубиков.

Теперь посчитаем кубики с одной окрашенной гранью. Очевидно, что такие кубики должны лежать только в центре фигуры. Таким образом получаем 10 кубиков.

Правда, вопрос немного с подвохом.

Если имеется в виду — сколько кубиков только с одной окрашенной гранью, то ответ — 10 кубиков.

Если имеется в виду — сколько всего кубиков с одной окрашенной гранью, то очевидно, что это все кубики в количестве 36 штук, ибо одна грань у всех у них будет окрашена.