Математики разрезают фигуры в поисках частей уравнений
Время на прочтение
8 мин
Количество просмотров 4.7K
Новая работа над задачей о «равносоставленности» объясняет, когда имеется возможность разрезать одну фигуру и собрать из неё другую
Если у вас есть две плоские фигуры из бумаги и ножницы, можете ли вы разрезать одну фигуру и переставить кусочки так, чтобы получить другую? Если можете, тогда две эти фигуры «ножнично конгруэнтны» [равносоставлены].
Однако математиков интересует, можно ли обнаружить такое взаимоотношение у фигур, не используя ножницы? Иначе говоря, есть ли у этих фигур такие характеристики, которые можно было бы измерить заранее и определить, конгруэнтны ли они?
Для двумерных фигур ответ прост. Нужно просто измерить их площади; если они совпадают, то фигуры ножнично конгруэнтны.
Но для фигур в высших измерениях – к примеру, для трёхмерного мяча или одиннадцатимерного пончика, который невозможно себе представить – вопрос разрезания и пересборки в другом виде становится гораздо сложнее. И несмотря на века попыток, математики не могли определить характеристик, подтверждающих равносоставленность для большинства фигур высшей размерности.
Однако этой осенью два математика совершили наиболее значимый прорыв в решении этой задачи за несколько десятилетий. В работе, представленной в Чикагском университете 6 октября, Джонатан Кэмпбел из университета Дьюка и Инна Захаревич из Корнеллского университета совершили значимый шаг по направлению к доказательству ножничной конгруэнтности для форм любых размерностей.
Но не только. Как и большинство важных задач математики, равносоставленность – это кроличья нора: скромное заявление, затягивающее математиков в глубокую нору сложной математики. В попытках понять ножничную конгруэнтность, Кэмпбелл и Захаревич, возможно, показали новый способ рассуждать о совершенно другой области этой науки: об алгебраических уравнениях.
Первый разрез
Равносоставленность может показаться простой задачей. Более 2000 лет назад Евклид догадался, что две двумерные фигуры одной площади можно переставлять из одной в другую. Разумно предположить, что фигуры высших измерений одинакового объёма можно переделывать аналогично.
Но в 1900-м году Давид Гильберт предположил, что эта задача на самом деле не так проста.
В том году, выступая на международном математическом конгрессе в Париже, он определил 23 открытых задачи, которые, по его мнению, будут направлять математическую мысль в ближайшее столетие. Третья из них касалась ножничной конгруэнтности [равносоставленность равновеликих многогранников]. Гильберт предположил, что не все трёхмерные фигуры одного объёма конгруэнтны – и бросил математикам вызов, предложив найти пару фигур, доказывающих это.
Через год после речи ученик Гильберта, Макс Ден, так и сделал. Такой срок показался математикам подозрительным. «Некоторые считают, что Гильберт включил эту задачу в список только потому, что её уже решил его ученик», — сказала Захаревич.
Был ли это заговор или нет, результат Дена перевернул представление математиков о равносоставленности. Он доказал, что тетраэдр единичного объёма не является равносоставленным кубу того же объёма. Неважно, как вы разрежете первый, вы никогда не сможете собрать из кусочков второй.
Кроме демонстрации того, что равенства объёмов недостаточно для определения равносоставленности, Ден предложил новый способ измерения фигур. Он доказал, что любые трёхмерные фигуры, равносоставленные друг другу, должны иметь одинаковый объём, а также совпадать по новой мере.
Ден сконцентрировался на внутренних углах между двумя гранями трёхмерной фигуры. К примеру, внутри куба все грани встречаются под прямыми углами. Но в более сложных формах углы бывают разными и имеют разную важность. Углы между более длинными рёбрами больше влияют на форму фигуры, чем углы между более короткими рёбрами, поэтому Ден присвоил углам веса на основе длин формирующих их рёбер. Он скомбинировал эту информацию в сложную формулу, выдававшую в итоге единственное число – «инвариант Дена» – для заданной фигуры.
Математики хотят знать, когда фигуру можно разрезать и собрать из неё другую.
Двумерные фигуры равносоставлены, если у них одинаковая площадь.
Трёхмерные фигуры равносоставлены, если у них одинаковые объём и инвариант Дена.
Куб и тетраэдр не равносоставлены – у них одинаковый объём, но разный инвариант Дена.
Фигуры можно резать на кусочки, а графики уравнений – на подграфики. Математики ищут аналог инварианта Дена, который показывает, что два уравнения состоят из одинаковых кусочков.
Ден доказал, что любые трёхмерные фигуры, равносоставленные друг другу, должны иметь одинаковый объём и инвариант Дена. Но он не смог ответить на более сложный вопрос: если у трёхмерных фигур одинаковый объём и инвариант Дена, значит ли это, что они обязательно равносоставлены? Жан-Пьер Сидлер, наконец, доказал это в 1965. Через три года Бьёрг Джессен показал, что эти же две характеристики определяют равносоставленность в четырёх измерениях.
Результаты Сидлера и Джессена были серьёзными шагами вперёд, но математики – народ жадный: достаточно ли объёма и инварианта Дена для определения равносоставленности фигур во всех измерениях? Достаточно ли этих измерений в других геометрических пространствах, кроме Евклидового – в сферической геометрии (представьте себе широту и долготу на поверхности Земли) или седловидной вселенной гиперболической геометрии?
В конце XX века математик Александр Борисович Гончаров предложил подход, который, по его мнению, мог решить всю задачу раз и навсегда – и при этом связать равносоставленность с совершенно другой областью математики.
Странные связи
Математика полна неожиданных связей. Захаревич говорит, что заниматься математикой – это как наткнуться на нечто странное в природе, и попытаться понять, почему оно такое.
«Если вы встретите в лесу кольцо из грибов, и не будете знать, как грибы растут, вы задумаетесь, откуда им известно, как расти кругом? – сказала она. – Причина же в том, что грибы имеют грибницу, растущую под землёй».
В 1996 году Гончаров сформулировал набор гипотез, говорящих о существовании математической структуры, также скрытой под поверхностью. Если эта структура существует, она сможет объяснить, почему некоторые математические явления – включая равносоставленность – работают именно так.
Одна из гипотез утверждает, что объёма фигуры и её инварианта Дена достаточно для определения равносоставленности фигур любой размерности и в любом пространстве.
«Гончаров сказал, что те же принципы, что применяются в трёх измерениях, применимы во всех», — сказал Чарльз Вейбель из университета Рутгерса.
Но Гончаров, ныне работающий в Йельском университете, также предсказал, что эта скрытая структура объяснит гораздо больше этого. Он сказал, что равносоставленность – это концепция более универсальная, и что она применима не только к разрезанию геометрических фигур, но и к разрезанию форм, порождаемых решениями алгебраических уравнений – к примеру, графика уравнения x2 + y2 + z2 = 1. А информация, необходимая для классификации по равносоставленности, отражает информацию, необходимую для классификации алгебраических уравнений – такую, при которой уравнения одного класса будут составлены из одинаковых кусочков.
Связь была шокирующей, будто бы принцип, подходящий для систематизации животных каким-то образом позволял бы вам систематизировать ещё и химические элементы. Многие математики считают эту идею настолько же странной, насколько она кажется на первый взгляд.
«Это совершенно загадочно. На первый взгляд, эти вещи вообще не должны быть связаны», — сказал Кэмпбелл.
Разрезая уравнения
Чтобы понять, как могут быть аналогичными геометрические фигуры и алгебраические уравнения, сначала полезно будет понять, как можно разбить решения уравнений на части. Для этого давайте вернёмся к нашему предыдущему примеру и нарисуем график уравнения x2 + y2 + z2 = 1.
Это будет сфера. Однако эта поверхность является не только набором решений этого уравнения: это также набор множества более мелких графиков, или подграфиков, решений других уравнений. К примеру, на поверхности сферы можно нарисовать окружность на манер земного экватора. Это один подграфик, представляющий решения алгебраического уравнения x2 + y2 = 1. Или можно изолировать единственную точку на северном полюсе сферы, соответствующую уравнению z = 1. Изучая различные подграфики, которые можно нарисовать в рамках более крупного графика – нечто вроде его составных частей – вы можете узнать какие-то свойства более крупного графика.
Более 50 лет математики разрабатывали теорию подграфиков алгебраических уравнений. Как обычная материя состоит из атомов, так и, по мнению математиков, алгебраические уравнения состоят из фундаментальных частей под названием «мотивы». Термин происходит от французского слова motif, обозначающего базовые элементы мелодии.
Инна Захаревич из Корнеллского университета
«Мотивы – это фундаментальные составные части. Они расскажут обо всём, из чего состоят алгебраические уравнения, как мелодия, состоит из различных составных частей», — сказала Захаревич. Сфера, к примеру, состоит из окружностей, точек и плоскостей. Каждая из них состоит из составных частей (проявляющихся в результате математических действий над ними), и так далее, всё ниже и ниже, пока мы не придём к мотивам, предполагаемому фундаменту алгебраических уравнений.
Математикам нужно классифицировать алгебраические уравнения по их мотивам, чтобы получить полную и систематическую картину уравнений, принадлежащих к важнейшим математическим объектам. Это сложная и незаконченная задача. Но в 1996 году Гончаров предположил, что сортировка фигур по равносоставленности и сортировка алгебраических уравнений по мотивам являются двумя сторонами одной задачи – то есть, классификация одной даст вам принцип, по которому можно классифицировать и другую.
Он предположил, что эта связь имеет в основе аналог инварианта Дена. Только вместо того, чтобы появляться из простейших геометрических подсчётов, этот аналог должен возникнуть из похожего расчёта мотивов алгебраических уравнений («мотивное копроизведение»).
«Идея в том, что задача инварианта Дена параллельна другой задаче, связанной с мотивами», — сказал Вейбель.
Но чтобы обнаружить такую связь, математикам сначала нужно доказать, что инвариант Дена действительно сортирует фигуры по равносоставленным группам. Сам Ден показал, что любые равносоставленные трёхмерные фигуры имеют равные объёмы и инвариант Дена. Однако Ден, и все остальные после него, не опровергли возможность того, что существуют некие фигуры высших измерений одинакового объёма и с одинаковым инвариантом Дена, не являющиеся при этом равносоставленными. В своей новой работе Кэмпбелл и Захаревич попытались навсегда закрыть эту возможность.
Два по цене одного
В июне 2018 года Кэмпбелл и Захаревич три недели работали вместе в Институте передовых исследований в Принстоне, Нью-Джерси. Они давно интересовались равносоставленностью, но Захаревич считала, что гипотезы Гончарова были слишком сложными, чтобы с ними можно было разобраться за такое короткое время. А Кэмпбелл всё равно хотел попытаться, и Захаревич не пришлось долго уговаривать.
«Джонатан сказал: ’У нас есть три недели, давай попробуем подступиться к этому и посмотрим, что у нас получилось, к концу первой’», — сказала Захаревич. Через две недели они разработали многие ключевые идеи, лежащие в основе их новой работы.
В работе они проводят контринтуитивный мысленный эксперимент. Чтобы понять его представьте, что у вас есть гостиница со множеством комнат. Вам нужно расположить все равносоставленные друг с другом фигуры в одной комнате. Нам неизвестно, как определять, что фигуры являются равносоставленными – в этом и есть корень проблемы. Однако для нашего мысленного эксперимента давайте представим, что это возможно. Или, как говорит Захаревич, «Мы притворимся, что существует некая всезнающая личность, которой известно, равносоставлены две фигуры или нет».
Рассортировав фигуры по комнатам, мы проверим, что у всех фигур в одной комнате одинаковый объём и одинаковый инвариант Дена. Также важно проверить, что все фигуры одинакового объёма и с одинаковым инвариантом Дена оказались в нужной комнате – что в баре гостиницы не ошиваются отбившиеся от коллектива фигуры. Цель мысленного эксперимента доказать наличие идеального взаимно однозначного соответствия между группами равносоставленных фигур и группами фигур, имеющих одинаковый объём и одинаковый инвариант Дена. Существование такого соответствия докажет, что для определения равносоставленности фигур вам действительно будет достаточно только объёма и инварианта Дена.
Гончаров предсказал существование такого соответствия, и Кэмпбелл с Захаревич доказали его наличие – при выполнении одного условия. Соответствие существует, если верен ещё один недоказанный результат, связанный с гипотезами Бейлинсона.
Две гипотезы Гончарова – классификация равносоставленных фигур по объёму и инварианту Дена, а также классификация алгебраических уравнений по аналогу инварианта Дена – не доказываются работой Кэмпбелла и Захаревич полностью. Однако их работа всё же обеспечивает математиков более чётким представлением о том, как доказать их все: если у вас получится доказать гипотезы Бейлинсона, тогда, благодаря работе Кэмпбелла и Захаревич, вы бесплатно получите в придачу и равносоставленность.
«Их работа действительно переосмысливает эту задачу, — сказал Вейбель. – Когда вы связываете таким образом две гипотезы, это проливает свет на структуру изучаемого объекта».
Кэмпбелл и Захаревич сейчас работают ещё с одним математиком, Даниилом Руденко из Чикагского университета, пытаясь определить связь между разрезанием фигур и разбором на части уравнений, предложенным Гончаровом. Руденко до этого уже несколько продвинулся в этом направлении. Теперь, совместно с Кэмпбеллом и Захаревич, он надеется продвинуться гораздо дальше.
«Думаю, у нас есть все шансы достичь значительного прогресса. Может быть, таким способом даже получится доказать гипотезы Гончарова», — сказал Руденко.
Как находить и читать фигуры на графике?
Время прочтения ≈ 10 минут
Для того, чтобы научиться читать и находить графические фигуры в трейдинге, необходимо узнать какие фигуры технического анализа существуют. Фигурами называют модели, образованные множеством свечей, выстроенных определенным образом. Данные модели могут быть как разворотными, так и указывать на продолжение предшествующего тренда. С помощью фигур технического анализа мы можем прогнозировать дальнейшее движение цены и заключать сделки по направлению движения для извлечения прибыли.
Содержание статьи:
- Как распознать фигуры на графике?
- Как легче строить фигуры в трейдинге
Как распознавать фигуры на графике?
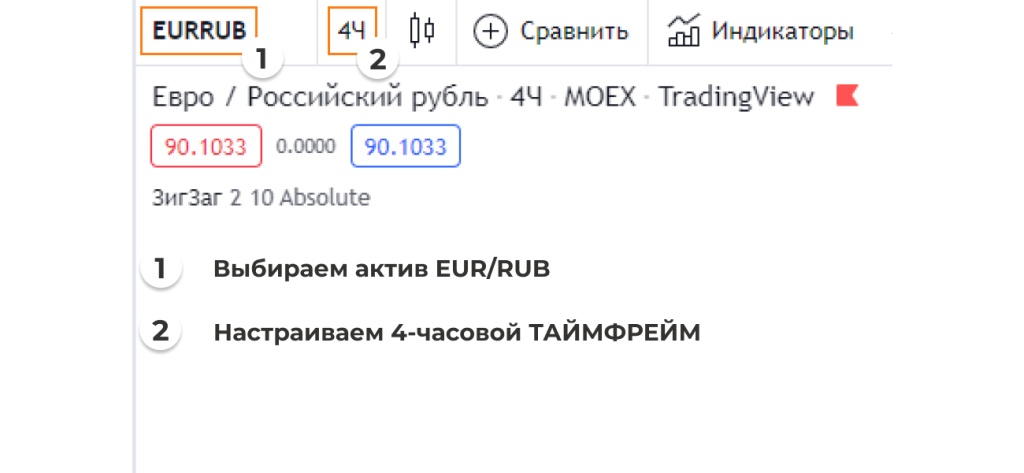
- Открываем график и выбираем актив. В нашем случае мы воспользовались ресурсом tradingview.com и выбрали валютную пару EUR/RUB.
- Выбираем 4-х часовой таймфрейм. Фигуры технического анализа лучше отрабатывают на старших таймфреймах.
- Увеличиваем график, чтобы каждая свеча была хорошо видна и нам ничего не мешало для объективного восприятия картинки.
-
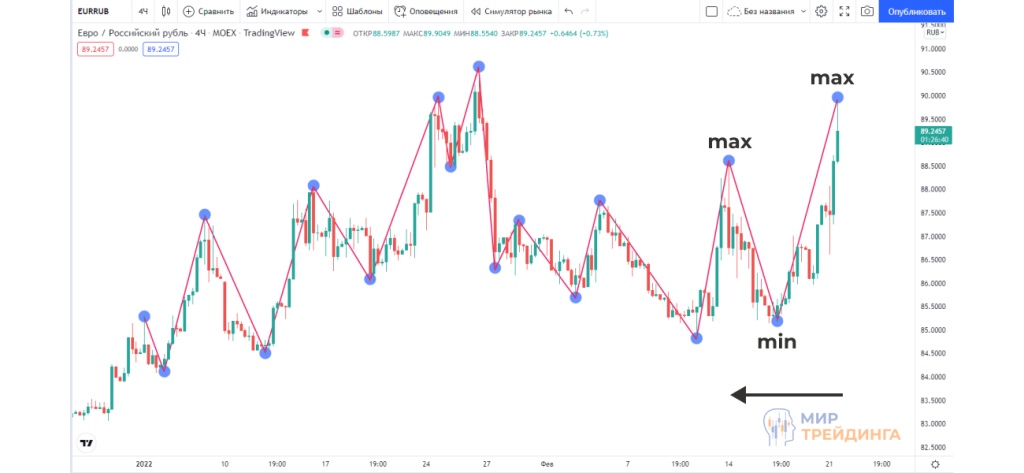
Отмечаем последовательно минимумы и максимумы цены на крайнем отрезке графика и соединяем отметки.
- Смотрим, какая фигура образовывается или уже сформировалась в итоге.
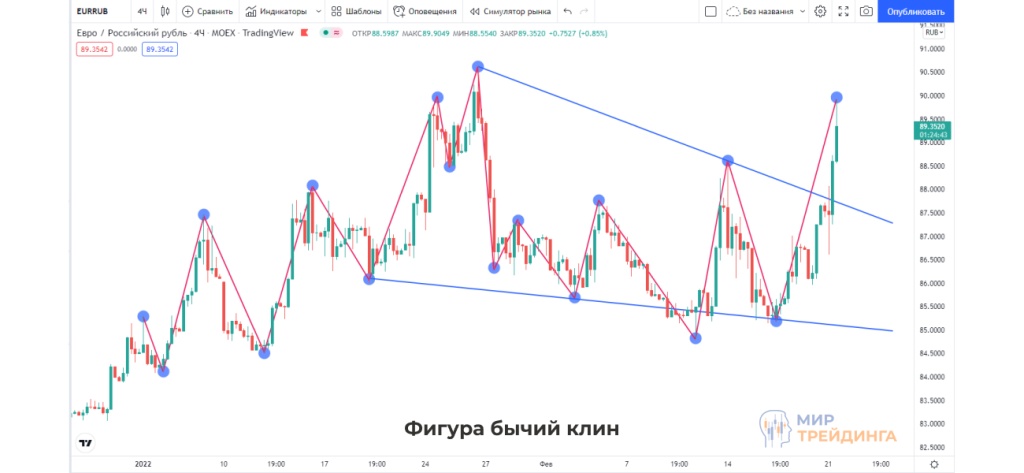
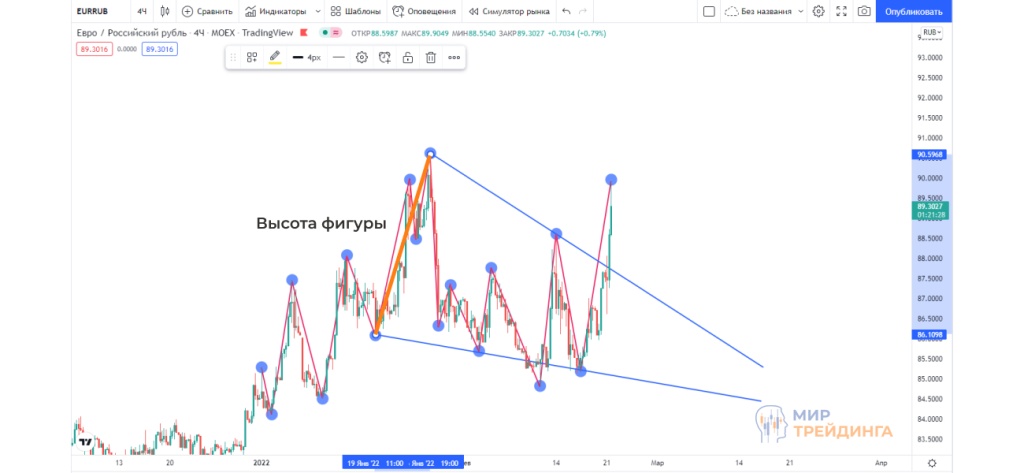
- Соединив минимумы нижней трендовой линией и максимумы верхней трендовой, мы понимаем, что на графике сформировалась фигура бычий клин. Обычно она пробивается наверх.
- Чтобы определить уровень цены, до которого дойдет график при отработке фигуры, нам необходимо отложить высоту фигуры вверх от места пробития клина.
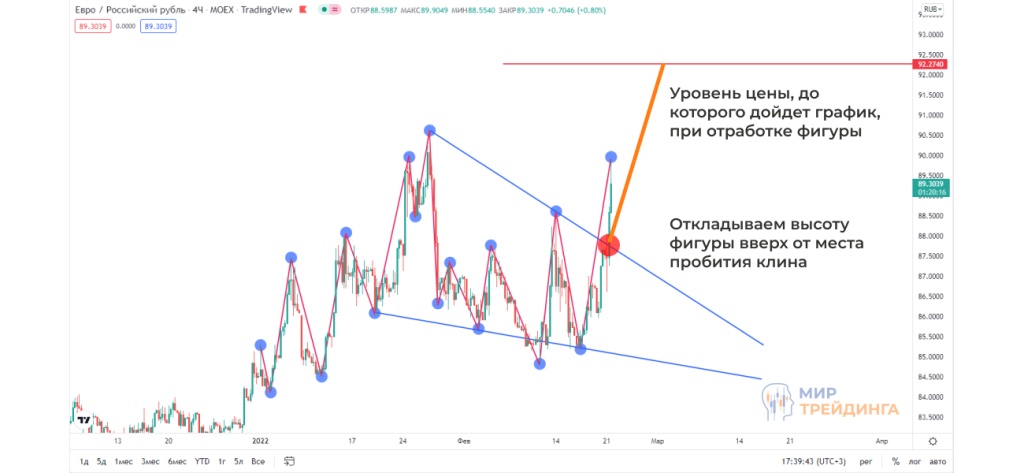
Как легче строить фигуры в трейдинге
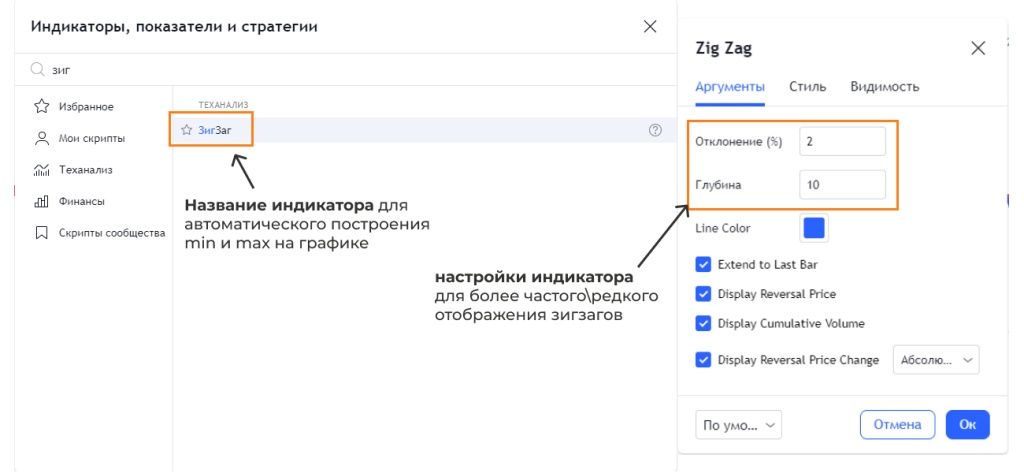
Для упрощения построений минимумов и максимумов и отрезков между ними можно использовать индикатор Зиг-Заг.
- Вводим название индикатора в поиск. Добавляем его на график.
- С помощью настроек отклонения и глубины мы можем варьировать частоту зигзагов.
Научившись находить фигуры на графике, вы сможете определить дальнейшее движение цены и открывать сделки в правильном направлении. Однако даже выучив назубок все формации на графике, торговать в прибыль будет сложно. Нужна проработанная торговая система. В нее входят многие пункты. Изучить и перенять прибыльную стратегию можно на курсе “Снайпер для начинающих”. Небольшой курс поможет вам понять основную теорию и быстро перейти к практике. Чтобы получить доступ к бесплатным материалам, оставьте заявку ниже под кнопкой.
ОСТАВЬ ЗАЯВКУ И ПРОЙДИ
КУРС «СНАЙПЕР ДЛЯ НАЧИНАЮЩИХ»
СОВЕРШЕННО БЕСПЛАТНО
ПОЛУЧИТЬ
Технологическая карта урока математики
в 1 классе.
Тема: Части фигур.
ФИО
Шуралева
Нина Владимировна, учитель начальных классов МБОУ «СОШ №39» «Центр
физико-математического развития» г. Рязани.
Предмет
Математика
Класс
Общеобразовательный,
1в
Тема
урока
Части
фигур
Цели
Актуализировать
представления учащихся о разбиении фигур на части и составлении целой фигуры
из частей.
Задачи
Образовательные:
На основе работы с раздаточным материалом устанавливают
взаимосвязи между частями фигур и целой фигурой.
Фиксируют взаимосвязи между целым и частями с помощью символов.
Тренируют навыки счета в пределах 9.
Воспитательные: показывают толерантное
отношение к чужому мнению, приходят на помощь однокласснику.
Развивающие: определяют тему и цели
урока, показывают умение работать в паре.
Основные понятия
Фигура, часть, целое
Ресурсы:
— основные
— дополнительные
Учебник Петерсон Л.Г. «Математика 1 класс»
Презентация
Этап
урока
Деятельность
учителя
Деятельность
учащихся
Планируемые
результаты
1. Организационный
момент.
Вот звонок нам дал сигнал Поработать
час настал. Так что время не теряем И работать
начинаем. -Посмотрите, все ли приготовлено у вас к уроку?
— Покажите своё настроение.
Улыбнитесь друг другу — Подарите и мне свои улыбки. Спасибо.
— Ваши улыбки располагают к приятному
общению, создают хорошее настроение. — Сегодня у нас
гости, улыбнитесь и им.
Проверяют готовность к уроку, эмоционально настраиваются на
работу.
Показывают карточки.
Коммуникативные:
планирование
учебного сотрудничества с учителем и сверстниками.
Личностные:
желание и стремление хорошо учиться.
2. Актуализация
знаний.
Логическая
задача.
Плитку
шоколада разделили на 9 частей. Света съела 3 части, Вася-2 части. Какая часть
шоколада осталась: большая или меньшая?
Показывает
слайд 2.
Организует
повторение на понятия «часть», «целое».
-Назовите
целое и части в числовых равенствах.
-Как
найти целое? Как найти часть?
-Какую
фигуру разбили на части?
-Какие
геометрические фигуры вы знаете?
Слайд 3.
— Можно ли составлять равенства для геометрической фигуры,
также как мы составляли его для числового отрезка?
— Проверим наши предположения и попробуем составить равенства
с геометрическими фигурами.
Меньшая,
так как съели 5 частей, а осталось 4 части.
Открывают
тетради по математике.
Составляют
числовые равенства по рисунку, записывают их в тетрадь.
Ответы
детей.
Проверяют
ответы на доске.
Обводят
целое.
Тетради
закрывают.
Ответы
детей.
Озвучивают
свои предположения.
Познавательные: учатся
логически мыслить; извлекать нужную информацию из рисунка; ориентируются в
собственной системе знаний.
Коммуникативные:
слушают,
дополняют, рассуждают.
Коммуникативные: умение
работать в паре; слышать и слушать товарища по парте; прислушиваться к чужому
мнению.
Познавательные: проявлять логику и
смекалку, выдвигать предположения.
Регулятивные: контролировать действия
партнёра; сохранять учебную задачу и осуществлять контроль.
4.Самоопределение
к деятельности.
3.Проблема.
Организует исследовательскую работу детей в парах по составлению
и разбиению фигур.
Повторяет с детьми технику безопасности с ножницами.
Слайд 4.
Просит
из двух треугольников составить один треугольник.
Из
скольких частей состоит фигура?
Показывает
слайд 5 с правильным ответом.
Слайд 6.
Просит
составить из 4 маленьких треугольников два одинаковых квадрата
Показывает
слайд 7 с правильным ответом.
-Что мы
делали сейчас?
Организует работу по работе с кругом. Меняя расположение частей
просит составить «бабочку», «затем змейку».
1.
Сверяют свои ответы с эталоном на доске. Слайд 8.
2.
Слайд 9.
3.
4.
5.
6.
Слайд 10, 11.
7.
На основании полученных исследований просит сделать вывод. Для
этого надо выбрать ответы на вопросы на доске и сформулировать вывод.
8.
«Что мы делали?» (составляли, вычисляли, измеряли) «Каким
способом?» (перемещая части, раскладывая фигуры, перечисляя элементы)
Вернёмся к первой фигуре. Слайд 12.
Попробуем сделать к ней такие же записи, какие выполняли к
числовому отрезку.
Слайд 13.
Игра «Пазл».
-Как найти целую фигуру?
9.
Игра «Пазл».
-Как найти часть фигуры?
Слайд 14.
Отгадайте
ребус.
Проблема: Что может связать понятия: целая фигура, части
фигур, сумма, разность.
Предположите, о чём сегодня ещё узнаем
на уроке?
Помогает в формулировке выводов.
Исследуют фигуры, делят их на части. Составляют из частей разные
фигуры. Наблюдают.
Работа в
парах.
На
столах лежат голубые квадраты. Они поделены по диагонали пополам.
Разрезают
квадрат по диагонали.
Составляют
один большой треугольник.
Фигура
целая состоит из двух частей.
Разрезают
квадрат по двум диагоналям, получают 4 маленьких треугольника.
Из 4
треугольников составляют два квадрата.
-Из
целых фигур получали части, из частей составляли новые фигуры.
Работа в парах.
Один ученик разрезает круг оранжевого цвета на 4 одинаковые
части, другой -фиолетовый. Меняются двумя частями круга с товарищем по парте.
Составляют фигуры по заданию учителя.
Формулируют вывод: составляли фигуры перемещая части фигур.
Открывают
тетради по математике, записывают равенства.
У доски
2 ученика.
Проверяют
с образцом на доске.
Работают
в паре.
Из слов
составляют предложение. «Чтобы найти целую фигуру, надо сложить её части».
«Чтобы
найти часть фигуры, нужно вычесть из целого часть».
Отгадывают
ребус.
Ответы
детей: сумма, разность.
Из
частей фигуры мы научились составлять новые фигуры. А теперь узнаем, как
связаны слова: «сумма», «разность», «части фигур», «целая фигура».
Познавательные:
осуществлять
синтез как составление целого из частей.
Коммуникативные:
осуществлять
работу в паре.
Регулятивные:
сохраняют учебную задачу и осуществляют контроль; контролируют
действия партнёра; выбирают действия в
соответствии с поставленной задачей и условиями её реализации.
Коммуникативные: находят правильное решение
задачи, аргументируют его.
Личностные: помогают друг другу в
составлении фигур.
Личностные: приходят на помощь товарищу в случае затруднения выполнения работы.
Регулятивные: планируют и выполняют работу по намеченному
плану; принимают и сохраняют учебную задачу при выполнении задания.
Познавательные: используют знаково-символичные
информационные средства для решения учебной задачи.
Познавательные: учатся логически мыслить;
проявлять смекалку.
Познавательные:
выдвигать предположения; формулировать выводы.
Коммуникативные: сотрудничают с учителем и
сверстниками.
Регулятивные: сравнивают свои действия и
результат с эталоном с целью обнаружения и исправления ошибок.
4.Первичное закрепление.
Работа
по учебнику.
№3 стр.
26.
Учит способу фиксирования данного разбиения в виде символов
-Какая
геометрическая фигура изображена под цифрой 1?
-Как её
назвали?
-Назовите
целое и части.
-Прочитайте
и объясните первое равенство.
-Что
запишем во второй строке?
-Посмотрите
на третью строку. Чему равна разность? Докажите.
-Что
запишем в четвёртой строке?
2) Самостоятельно составьте буквенные равенства по кругу.
Выполните
второе задание самостоятельно.
-Как вы думаете можно составлять равенства, опираясь на
геометрические фигуры?
Действуют ли здесь правила нахождения целого и части?
-Чему равна целая фигура?
— Как найти часть фигуры?
Работают в группе. Выполняют задание на закрепление полученных
знаний.
-Квадрат.
Буквой
«к»-целое; «а», «б»-части.
Читают,
объясняют.
Сложили
две части и получили целое «к».
-Части
поменяли местами.
-Из
целого «к» вычесть часть «а»- получим вторую часть «б».
-Из
целого «к» вычли часть «б» и получили часть «а».
Сравнивают
с образцом на слайде.
2 человека у доски.
Работают самостоятельно. Проверяют по
слайду компьютера с комментированием.
Можно.
Да.
Целая фигура равна сумме частей.
Чтобы найти часть фигуры нужно из целой фигуры вычесть другую
часть.
Регулятивные: контролировать действия в процессе выполнения задания; сравнивать
способ действия и его результат с заданным эталоном с целью обнаружения
отклонений и отличий от эталона.
Коммуникативные: умение с достаточной
полнотой и точностью выражать свои мысли в соответствии с задачами и
условиями коммуникации.
Регулятивные: контролировать
действия в процессе выполнения задания.
Коммуникативные:
слушают, дополняют, рассуждают.
Познавательные:
формулируют
вывод.
№6
стр.27
Составление буквенных равенств по треугольнику.
Фронтальная работа с комментированием.
-Что
представляет собой целая фигура?
-Из
скольких частей состоит большой треугольник? Назовите эти части.
Как
найти целое? Части?
-Вставьте
пропущенные буквы.
Подведем итог:
Из чего состоит целая фигура?
Как найти часть фигуры?
Один ученик объясняет пропущенные буквы, остальные слушают,
записывают.
А — это целое, значит получаем б +в +г +д.
Из целого а вычитаем часть б, остается в +г + д.
В окошечко вставляем а, так как вычитать можно только из
целого, а вычитая в, остается б+г+д.
Чтобы остались части б д, нужно из целого а вычесть в и г.
Целая
фигура состоит из суммы её частей.
Часть
фигуры равна разности и другой части.
Регулятивные: контролировать способ действия и его результат с заданным
эталоном с целью обнаружения отклонений и отличий от эталона; вносить
необходимые дополнения и коррективы в способ действия в случае расхождения с
эталоном.
Коммуникативные:
сотрудничать с учителем и сверстниками.
Познавательные: учатся
формулировать вывод.
3. Физкультминутка.
Песенка
про жирафа
Поют и
выполняют движения под музыку.
4. Повторение
изученного материала.
Стр.27
№8
Игра «Аквариум»
-Что такое аквариум?
— А из чего состоят рыбки, которые живут в аквариуме учебника?
— Что вы запишите в овалах?
— Какие выражения знаете?
— Составьте выражения.
Взаимопроверка учебников-тетрадей.
— А какое число живет в этом аквариуме?
Расскажите про него всё, что знаете.
Ответы детей:
Аквариум-это
искусственный водоём или стеклянная ёмкость с водой для содержания рыб,
водных животных и растений.
-Из желтых и зеленых
треугольников.
-Выражения.
-Сумму чисел; разность чисел.
Один ученик составляет выражения на доске.
Проверяют друг у друга выполнение задания и сверяют с ответами
на доске.
Число 9.
Рассказывают
про число 9.
Коммуникативные:
слушать одноклассников; оформлять свои мысли в
устной форме и излагать их в соответствии с задачами и условиями
коммуникации.
Регулятивные: контролировать действия партнёра;
анализировать
работу, оценивать результат действия. Контролировать своё поведение.
Коммуникативные:
слушать
собеседника, не перебивать; дополнять ответ.
5. Рефлексия.
Оцените
свои достижения на уроке.
-У кого
сегодня всё получилось?
-Кому
было что-то непонятно?
-Покажите,
с каким настроением вы заканчиваете урок?
Ответы
детей.
Показывают
карточки.
Регулятивные:
контролируют
своё поведение.
6. Подведение
итогов урока.
Что мы
делали на уроке?
Чему
научились?
Какое
задание понравилось выполнять?
Ответы
детей.
Задание у головоломок очень простое: нужно на картинке среди рябящих в глазах мелких деталей отыскать ещё более мелкую деталь. Художник будет пытаться всячески вас обмануть, пририсовывая ненужные линии, но не поддавайтесь. Все ответы будут в конце материала, но раньше времени чур не подглядывать!
Найдите маленького цыплёнка на этой пасхальной пасторали.
Эти котейки специально подняли хвосты, чтобы спрятать среди них кролика.
В этом море мороженого плавает одинокий чупа-чупс. Где?
А здесь нужно отыскать семь отличий. Их правда семь, приглядитесь.
Среди этих слонят спряталось сердечко. Сможете отыскать?
Эти панды — фанаты футбола — буквально запинали несчастный мяч. Но, чтобы спасти беднягу, придётся сперва его найти.
Здесь есть не только подарочные пакеты, но и открытка. Угадайте где?
Всего у одного тигра на этой картинке нет близнеца. У какого?
Среди снежинок притаился снеговик. Он маленький, так что придётся потрудиться!
А эта головоломка — самая сложная! Сможете отыскать среди конфет волшебную палочку?
Здесь вам нужна звезда. Видите её?
Итак! Мы уверены, что вы нашли все нужные детали, но для успокоения души вот вам ответы:
Головоломка на визуальные навыки: только 1% людей может решить её за 10 секунд
Сначала найдём длину стороны вырезанного квадрата. Сторона прямоугольника, где вырезали квадрат, противолежит стороне в 15 см, значит, и эта сторона была равна 15 см. После вырезания квадрата на этой стороне осталось два отрезка длиной 5 см и 7 см. Значит, мы можем найти отрезок, вырезанный из этой стороны.
15-5-7=3 (см) — это и будет сторона квадрата. Значит, боковые стороны в месте вырезания тоже по 3 см.
Сторона прямоугольника, противолежащая стороне в 6 см, тоже равна 6 см.
Остаётся только сложить все отрезки по периметру.
6+5+3+3+3+7+6+15=48 (см) — периметр фигуры.
Ответ: периметр получившейся фигуры равен 48 см.