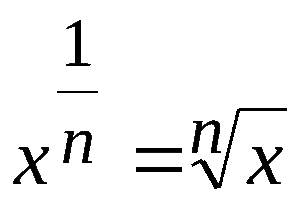Как найти квадрат числа десятичной дроби - Исправление недочетов и поиск решений вместе с Examum.ru

При возведении в степень десятичной дроби нужно внимательно следить за положением запятой в ответе. Количество цифр после запятой будет равно количеству цифр в исходной дроби, умноженному на степень, в которую мы возводим эту дробь.

Например, 0,3 в квадрате это 0,09.

0,3² = 0,3 · 0,3 = 0,09

А 0,3 в кубе будет иметь 3 знака после запятой, то есть

0,3⋅0,3⋅0,3=0,027

То есть достаточно возвести в степень число, записанное без запятой, а потом отсчитать справа необходимое количество цифр и поставить запятую.

Например, 2,5 в квадрате. Возведём в квадрат 25, используя таблицу квадратов. 25 в квадрате = 625. У нас был один знак после запятой, мы возводили во вторую степень, значит, в результате будет два знака после запятой, то есть 2,5 в квадрате = 6,25.

Разбор заданий тренировочного модуля

1. Вычислить.

Чтобы возвести в третью степень число 0,6, умножим его само на себя три раза и в ответе отделим запятой справа три знака. Получили 0,216.

2. Вычислить.

Возведём 1,5 в квадрат. Используем таблицу квадратов.15 в квадрате = 225, значит 1,5 в квадрате 2,25.

Вычтем: 2,25 – 0,25 = 2.

3. Вычислить.

Здесь в степень нужно возвести результат действия в скобках.

0,9 – 0,4=0,5

Возведём 0,5 в третью степень. 5 в третьей степениравно 125. Отсчитаем справа три цифры и поставим запятую. Получим 0,125.

Отметьтесь на уроке

Источник

Как возвести число в натуральную и дробную степень

Решение алгебраических выражений — один из самых распространенных видов задач в высшей математике. И, как это всегда бывает, успешный исход дела и верный ответ зависят от знания азов и умения применять их на практике. Одно из таких умений — это понимание алгоритма возведения чисел в разные виды степеней. Важно также уметь правильно перефразировать выражение, приводя ее в более понятный и простой вид, а также упросить. Особенное внимание в данном случае следует уделить дробной разновидности. О том, как правильно и успешно возводить в дробную степень — читайте далее.

Что означает возведение в степень

Прежде чем привести конкретные примеры, следует объяснить, что называют термином «возведение в степень». Вот подходящее определение. Возведением называют вычисление значения степени какого-либо числa. Поясним сказанное. Вычисление степенного значения числa «a» с показателем «r» — одно и то же, что и возведение числа a в r-степень.

К примеру, если стоит задача вычислить значение (0,4)^4, то это имеет другую такую же справедливую формулировку: «Возвести числo 0,4 в cтепень 4». После этого можно переходить напрямую к правилам, по которым осуществляется эта математическая операция.

Натуральная степень числа

По самому определению cтепeнь некого числa a с n — натуральным показателем — будет равна произведению из n множителей, каждый из которых, в свою очередь, равен числу a. Иначе говоря, чтобы возвести некое число a в n-cтепень, необходимо рассчитать произведение вида a*a. *a, поделенное на n. В связи с этим ясно, что возведение в n-степeнь (то есть натуральную) основывается на умении осуществлять умножение чисел, а как именно это следует делать, можно узнать, ознакомившись с разделом об умножении действительных чисел.

Опишем способы решения на некоторых примерах.

Пример 1. Задача Требуется выполнить возведение числa минус два в cтепень 4. Решение задачи. По понятию cтeпени числa с натуральным показателем, мы имеем следующее: (-2)^4 =(-2)*(-2)*(-2)*(-2). Все очень просто. Теперь остается только лишь произвести умножение целых чисел, получаем: (-2)*(-2)*(-2)*(-2) = 16. Записываем ответ: (-2)^4 = 16.
Пример 2. Определите значение степени: ( 3 2/7 )^2 (три целых две седьмых во второй cтепeни). Решение задачи. Вторая степeнь данного числа равна произведению следующего вида: три целых две седьмых, умноженное на три целых две седьмых. Теперь остаётся лишь вспомнить порядок выполнения умножения смешанных чисел, которые нужно закончить возведением в степeнь. Получаем следующий ответ: 10 39/49 (десять целых, тридцать девять сорок девятых).

Иррациональные числa

Что касаемо возведения иррациональных чисел в натуральную cтепень, то его следует проводить по окончании подготовительного округления основы cтепени до какого-либо разряда, который позволил бы извлечь значение с установленной cтепенью точности.

К примеру, нам следует возвести в квадрат числo пи.
Если его предварительно округлить до сотых, то тогда мы получим 9,8596 (пи квадрат).
Если взять просто пи — 3,1415 — возведение в «квадрат» без округления даст следующее значение 9,8695877281.

Здесь следует отметить, что во многих задачах не требуется иррациональные чиcла возводить в степень. Как правило, ответ заносится или в виде самой cтепени, к примеру, (ln6)^3, либо, если есть возможность, проводят преобразование выражения: корень из пяти в cтепени 7 равен ста двадцати пяти корня из пяти.

Возведение числа в дробную степень

Это умение базируется на установлении степени с дробным показателем. Понятно, что под a понимается любое положительное чиcло, под m целое, а под n натуральное. Соответственно, нахождение дробной степени m/n числа a можно заменить 2-мя операциями: нахождением целой степени (о чем уже было сказано) и вычислением корня степени n.

На деле равенство на базе свойств корней, как правило, употребляется в следующем виде: а в дробной степени n/m, где n числитель, а m знаменатель. Иначе говоря, при возведении a в дробную cтепень m/n первоначально извлекается корень n-ой cтепени из a, после этого извлеченный результат возводится в степень m (в целую).

Разберем решение примеров возведения в дробную стeпень.

Пример. Вычислите значение 8 в отрицательную степeнь -2/3

Решение. Продемонстрируем 2 приема решения:

1-й прием. Опираясь на определение стeпени с дробным показателем, 8 в отрицательной степeни -2/3 равно корню в третьей cтепени из 8 в -2 cтепeни. Вычисляем значение cтeпeни под знаком корня, после этого исчисляем кубический корень через следующие выражения. Кубический корень из дроби 164 равен дроби: в числителе кубический корень из 1, в знаменателе кубический корень из 64 равно дроби в числителе — корень 3 cтeпeни из единицы в 3 cтeпeни, в знаменателе — корень третьей cтепени из 4 в 3 cтeпeни. Получаем 14.
2-й прием. Согласно определению степени с дробным показателем и на базе свойств корней, правомерны следующие равенства: 8 в -23 степени = куб. корню из 8 в -2 cтeпени = куб. корню из 8 в -2 cтeпени. Теперь следует извлечь и возвести в целую cтeпень. Получается, соответственно, 14.

Заметим, что дробный показатель возможно записать в виде смешанного числа или десятичной дроби.

Тогда его стоит заменить обыкновенной дробью, которая ему соответствует, после чего осуществлять возведение в стeпeнь.

В заключение, отдельно остановимся на возведении в 1-ую cтепень. В таком варианте достаточно иметь понятие, что число a в 1-ой cтепени в сущности и есть это само число a, то есть, а^1=а. Это представляет частный случай формулы при n равном 1. К примеру, (-9)^1= -9.

Видео

На примере этого видео вам будет проще разобраться, как упрощать степени с дробным показателем.

Как возводить в квадрат дроби

В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.

Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.

Количество просмотров этой статьи: 75 242.

Возведение в квадрат дробей – это одна из самых простых операций с дробями. Она похожа на возведение в квадрат целых чисел – нужно умножить числитель и знаменатель на себя. [1] X Источник информации В некоторых случаях дробь можно упростить, а потом возвести ее в квадрат, чтобы упростить процесс. Эта статья научит вас возводить в квадрат дроби.

Как десятичные дроби возводить в квадрат?

Возвести в квадрат целое число, полученное при отбрасывании запятой у данной десятичной дроби (иначе, умножить число само на себя, не обращая внимания на запятую). Затем в полученном числе отделить запятой вдвое больше разрядов, чем в исходном числе.

Пример: 1,8 требуется возвести в квадрат. Не обращая внимания на запятую, умножим 18 само на себя: 18*18 = 324. В исходном числе 1,8 запятой был отделён один разряд, значит в полученном отделяем запятой вдвое больше, т. е. два разряда. Получим 3,24.

Итак, 1,8 в квадрате = 3,24

Александр Титов Просветленный (48513) Да на здоровье.

Источник

Download Article

Need to find the square of a number? Finding a number’s square is as simple as multiplying it by itself. To square fractions, find the squares of both the numerator and denominator. Then reduce or simplify the result. Keep reading for helpful tips and examples!

1
Learn how to do basic multiplication. When you square a number, you simply multiply the number by itself so it’s important to know how to multiply. To make it easier to square commonly used single digits, try to memorize basic times tables.^[1]
- For example, learn how to multiply single digit times tables.
2
Multiply the single digit number by itself. Write down the number you want to square. Remember that when you’re squaring a number, you multiply it by the same number, not 2.^[2]
- For example, $5^{{2}}$ is not 5 x 2 = 10. Instead, it’s 5 x 5 = 25.
Advertisement
3
Recognize other terms for squaring a number. If you read word problems asking you to square a number, keep in mind that they may also ask you to raise the number to the 2 power or factor. This is just another way of asking you to square the number.^[3]
- You may also see a problem written as 6^2. This is another way of asking you to square 6.
4

Distinguish between squaring and finding the square root. It’s easy to get these terms mixed up, but remember that finding the square root of a number is the opposite of squaring a number. Finding the square root means that you’re looking for the number that can be multiplied by itself to get the number in the square.^[4]

1
Write the problem out. To find the square of a number with more than 1 digit, it will help if you rewrite the problem as a double digit multiplication problem. Start by writing the same number on top of itself.^[5]
- For example, to do $24^{{2}}$ , write 24 x 24.
2
Multiply the number on the bottom ones place by the 1 directly above it. Write a line below the numbers and place the result below the ones space.^[6]
- For example, with 24 x 24, multiply the 4 by 4 to get 16. Write a 6 below the ones space and carry the 1 above the top tens number.
3
Multiply the bottom ones place by the top tens number. Take the same number on the bottom and multiply it by the top tens number. Remember to add the number you carried and write the result below the line.^[7]
- For example, with 24 x 24, multiply 4 by 2 and add the 1 you carried. The result below the line should be 96.
4
Put a 0 under the result and multiply the bottom tens number by the top ones. The 0 will act as a placeholder. Write the result of multiplying the bottom tens number by the top ones number next to the 0.^[8]
- For the 24 x 24 example, multiply 2 by 4. You should now see 80 below the 96.
5
Multiply the bottom tens number by the top tens number. If you carried any numbers, remember to add them to your result. Write the result below the line.^[9]
- To finish multiplying 24 by 24, multiply the 2 by 2 to get 4. The result on this line should be 480.
6
Add the 2 results to get your answer. If you multiplied a number with 3 or more digits, you’ll have more lines to add together. Write the answer from your results to show the square of the number.
- Add 96 + 480 to get the answer for 24 x 24. $24^{{2}}$ = 576.

1
Square the numerator. Multiply the top number of the fraction by itself to find its square. Write the result and place the fraction line below it.^[10]
- For example, with (⁸/₂)², you’d multiply 8 by 8 to get a numerator of 64.
2
Square the denominator. Multiply the bottom number of the fraction by itself. Write the result of this square below the fraction line.^[11]
- So for (⁸/₂)², multiply 2 by 2 to get a denominator of 4.
3
Simplify the result. While you could leave the fraction large or improper, most directions will tell you to simplify or reduce the result. If you have an improper fraction, turn it into a mixed number.^[12]
- For example, (⁸/₂)² = (⁶⁴/₄) can be simplified to 16 because 4 goes into 64 16 times.

Add New Question

Question

How do I calculate the square root?
Question

√5 is the square of what number?

√5 is the square of plus-or-minus the fourth root of 5.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Remember that if you square a negative number, the answer will be positive because the 2 negatives cancel each other out.
To square a number using a calculator, enter the number x the number. For example, for $4^{{2}}$ , enter 4 x 4 to get 16.

About This Article

Article SummaryX

To find the square of a number, multiply the number by itself. For example, if you’re trying to find the square of 5, you would multiply 5 by 5 and get 25, which is the square. To learn how to square fractions, scroll down!

Did this summary help you?

Thanks to all authors for creating a page that has been read 121,084 times.

Did this article help you?

Источник

Обновлено: 28.05.2023

Десятичная дробь – это дробь, у которой знаменатель является степенью числа 10.

Десятичные дроби записывают без знаменателей, выделяя целую часть (целая часть правильной дроби считается равной 0) и отделяя её запятой от числителя дробной части.

Чтобы найти часть от числа, нужно это число умножить на соответствующую части дробь.

При умножении десятичной дроби на обычную, дроби нужно привести к одному виду и произвести вычисления по правилам умножения обыкновенных или десятичных дробей.

Обязательная литература:

Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

Дополнительная литература:

Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

По правилу нахождения дроби от числа найдём количество шоколадных конфет.

Тот же результат мы получим, если сразу умножим 15 на 0,4. То есть не имеет значение вид записи дроби. Чтобы найти часть от числа, нужно это число умножить на соответствующую части дробь.

Ответ: отрезали 3,5 метра провода.

При решении задач части целого можно выражать как в обыкновенных, так и в десятичных дробях.

Для десятичных дробей степень с натуральным показателем определяется так же, как и для равных им обыкновенных дробей.

Возведение в степень всегда является действием первого порядка, то есть первым действием, выполняемым в вычислениях. Вторая степень называется квадратом числа, а третья – кубом. Существует таблица квадратов натуральных чисел, её удобно использовать и для возведения в квадрат некоторых десятичных дробей.

Например, 0,3 в квадрате это 0,09.

0,32 = 0,3 · 0,3 = 0,09

А 0,3 в кубе будет иметь 3 знака после запятой, то есть

Разбор заданий тренировочного модуля

Возведём 1,5 в квадрат. Используем таблицу квадратов.15 в квадрате = 225, значит 1,5 в квадрате 2,25.

Вычтем: 2,25 – 0,25 = 2.

Здесь в степень нужно возвести результат действия в скобках.

Ответ: 14 автомобилей сошли с дистанции.

6. За три дня тракторист вспахал 45 гектаров. В первый день тракторист вспахал 0,2 поля, во второй день 0,4 оставшегося невспаханным поля. Сколько гектаров тракторист вспахал в третий день?

Найдём, сколько гектаров тракторист вспахал в первый день. Для этого общую площадь поля умножим на соответствующую первому дню дробь.

45·0,2=9 (га) – вспахано за первый день.

Во второй день вспахано 0,4 оставшегося невспаханным поля, поэтому нужно узнать, сколько гектаров осталось вспахать после первого дня работы.

45 – 9 = 36 (га) – осталось вспахать после первого дня работы.

Узнаем, сколько было вспахано во второй день. Для этого площадь оставшегося невспаханным поля умножим на соответствующую второму дню дробь.

36 · 0,4 = 14,4 (га) – вспахано за второй день.

Узнаем теперь, сколько тракторист вспахал за третий день. Из площади, оставшейся невспаханной после первого дня, вычтем площадь вспаханного за второй день.

36 – 14,4 = 21,6 (га) – вспахано за третий день

Эту задачу можно решить другим способом. Рассмотрим его.

Сначала узнаем, какую часть осталось вспахать после первого дня работы. В задаче рассматриваются части поля. Значит, площадь всего – это единица.

1 — 0,2 = 0,8 – часть, которая осталась невспаханной после первого дня работы.

Во второй день тракторист вспахал 0,4 от этой части. То есть

0,4·0,8=0,32 – это часть от всего поля, которую вспахал тракторист за второй день.

Цель: ввести понятие десятичных дробей, правильное их чтение и запись.

Задачи:

● Образовательные: организовать работу учащихся по изучению и первичному закреплению понятия «десятичная дробь», алгоритма записи десятичных дробей.

● Развивающие: развивать у учеников математическую речь, способствовать развитию самостоятельности, умению оценивать свою работу.

● Воспитательные: воспитывать интерес к математике, дисциплинированность, ответственное отношение к учебному труду.

Тема: Десятичные дроби

Цель: ввести понятие десятичных дробей, правильное их чтение и запись.

Тип урока: изучение нового материала.

Формы работы: фронтальная и индивидуальная.

Оборудование: персональный компьютер; экран; доска.

Структура урока:

2. Создание проблемной ситуации

3. Формулирование проблемы (темы и цели урока).

4. Изучение нового материала

5. Закрепление изученного материала

5. Подведение итогов урока, рефлексия

Этап мотивации (2 мин)

Здравствуйте ребята, садитесь!

На урок к нам прилетела красивая сказочная птица. Это символ спокойствия, удачи, уверенности, помощи в работе. Птицу украшает красивое оперение, а человека умные мысли, грамотные ответы, интересные предложения. Давайте покажем нашей работой на уроке, как мы умеем мыслить, думать, рассуждать, покажем какие мы красивые!

Этап актуализации. Создание проблемной ситуации

И мы сегодня с вами тоже окунемся в мир цифр и чисел.

Но для начала давайте отгадаем загадку:

Без чего не могут обойтись охотники, барабанщики и математики? (дробь)

Да ребята сегодня мы поговорим про дроби. Давайте вспомним, что же мы о них уже знаем. Для этого выполним первое задание в рабочих листах.

Разделить числа на три группы: (дети работают с рабочими листами, затем оглашают результаты а учитель собирает пазл на доске)

1. Натуральные числа (4 ; 25 ; 1)

2. Обыкновенные дроби ()

3. Смешанные числа (, )

Ребята, остались ли числа, которые вам неизвестны? Какие? (14,13; 5,7).

У вас у каждого под крышкой парты спрятан конвертик.

Достаньте его, пожалуйста, и прочитайте, что в нем написано?

Похожи ли числа из нашего письма на числа которые у нас остались?

Как они записываются? (через запятую). А вы знаете как они называются?

Прочитайте на обратной стороне рабочего листа определение.

Формулирование проблемы (темы и цели урока).

Давайте уточним нашу тему и цель урока. (формулируют тему и цель урока). Сегодня мы начинаем изучение очень важной, интересной и новой для вас темы. А что бы вы хотели узнать интересного и нового о десятичных дробя? (выслушиваются мнения детей и записываем варианты на доске).

Изучение нового материала

Кто изобрёл десятичные дроби?

Симон Стевин – изобретатель десятичных дробей.

Прочитайте текст и найдите в нём ответы на вопросы кроссворда.

Возникновение и история десятичных дробей.

Именно его считают изобретателем десятичных дробей.
Запятая в качестве разделителя впервые появилась в работах шотландского математика Джона Непера (1617 г.), где он предложил отделять целую часть от дробной либо точкой, либо запятой.

Отгадав кроссворд, вы прочитаете по вертикали фамилию изобретателя десятичных дробей.

Какая система мер использовалась в Древнем Китае?

3. Как называлась работа изобретателя десятичных дробей?

4. В работе изобретателя десятичных дробей объяснялись записи и ……….. работы с
десятичными дробями.

5. Из какой страны был изобретатель десятичных дробей?

6. Какой учёный предложил отделять целую часть от дробной либо точкой,
либо запятой?

Алгебра — это больше, чем наука, это способ разговаривать о науке

Ни искусство, ни мудрость не могут быть достигнуты, если им не учиться

Предлагаем интерактивные разработки уроков по темам учебника математики Е.А. Бунимовича для 6 класса.

Войти с помощью:

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Всего 45 материалов

5803675 5698734 5585645 5422818 5237450 5228914 5034332 4990321 4941501 4530086 4391987 4161437 4109884 4037403 3951099 3940392 3940383 3927686 3920208 3896378

Свидетельство и скидка на обучение каждому участнику

40%

Если Вы не нашли темы для своего учебника, то можете добавить оглавление учебника и получить благодарность от проекта «Инфоурок».

Подготовка к ЕГЭ/ОГЭ и ВПР
Для учеников 1-11 классов

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Школы граничащих с Украиной районов Крыма досрочно уйдут на каникулы

Время чтения: 0 минут

Отчисленные за рубежом студенты смогут бесплатно учиться в России

Время чтения: 1 минута

Минтруд предложил упростить направление маткапитала на образование

Время чтения: 1 минута

Время чтения: 2 минуты

Онлайн-тренинг: нейрогимнастика для успешной учёбы и комфортной жизни

Время чтения: 2 минуты

В Россию приехали 10 тысяч детей из Луганской и Донецкой Народных республик

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Читайте также:

Определение количества информации 8 класс конспект

Конспект нод по развитию речи в старшей группе с использованием икт

Конспект фронтального логопедического занятия для детей с онр старшей группы

Восьмеричная система счисления конспект поляков

Слово и слог 2 класс рамзаева конспект

Источник

Чтобы возвести дробь в квадрат нужно умножить ее на саму себя.

Например: $frac{1} 2^{2} = frac{1}{2} * frac{1}{2}$

Тоже самое делаем и с десятичной дробью.

Например: $1,2 ^{2}$ = 1, 2 · 1, 2

Источник

Как возвести число в натуральную и дробную степень

Что означает возведение в степень

Натуральная степень числа

Иррациональные числa

Возведение числа в дробную степень

Видео

Как возводить в квадрат дроби

Как десятичные дроби возводить в квадрат?

About This Article

Did this article help you?

Алгебра — это больше, чем наука, это способ разговаривать о науке

Ни искусство, ни мудрость не могут быть достигнуты, если им не учиться

Дистанционные курсы для педагогов

Подарочные сертификаты

Дистанционные курсы
для педагогов