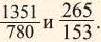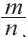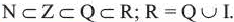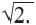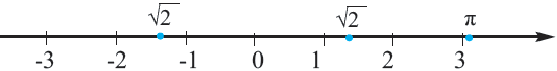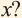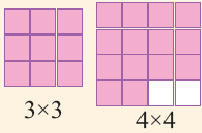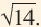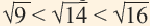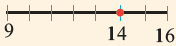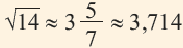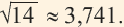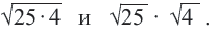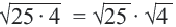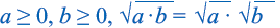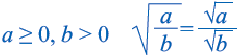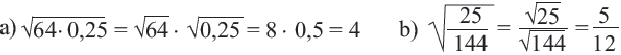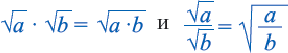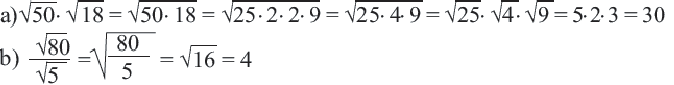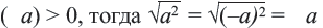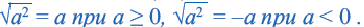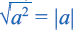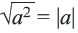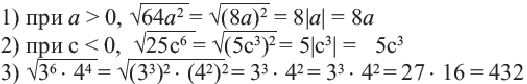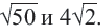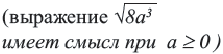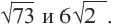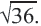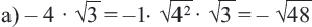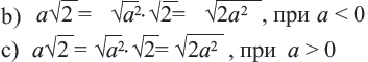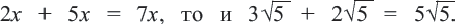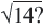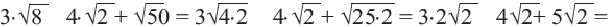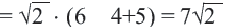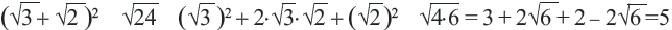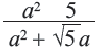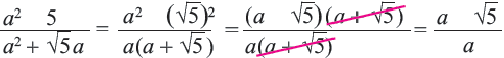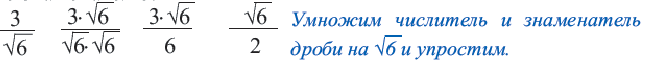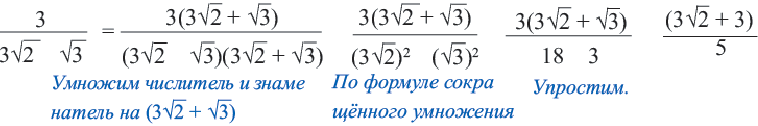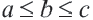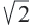Иррациональное число не так страшно, как кажется; это просто число, которое не может быть выражено в виде простой дроби или, иначе говоря, иррациональное число — это бесконечная десятичная дробь, которая продолжает бесконечное число знаков после запятой. Вы можете выполнять большинство операций с иррациональными числами так же, как и с рациональными числами, но когда дело доходит до получения квадратных корней, вам придется научиться приближать значение.
Что такое иррациональное число?
Так что же такое иррациональное число? Возможно, вы уже знакомы с двумя очень известными иррациональными числами: π или «pi», которое почти всегда сокращается до 3.14, но фактически продолжается бесконечно справа от десятичной точки; и «е», то есть число Эйлера, которое обычно сокращается до 2.71828, но также продолжается бесконечно справа от десятичной точки.
Но существует гораздо больше иррациональных чисел, и вот простой способ определить некоторые из них: если число под знаком квадратного корня не является идеальным квадратом, то этот квадратный корень является иррациональным числом.
Это очень большой глоток, так что вот пример, чтобы прояснить это. Также полезно помнить, что идеальный квадрат — это число, квадратный корень которого является целым числом:
√8 иррациональное число? Если вы запомнили свои идеальные квадраты или нашли время для их поиска, вы будете знать, что √4 = 2 и √9 = 3. Поскольку √8 находится между этими двумя числами, но между 2 и 3 нет целых чисел чтобы быть его корнем, √8 иррационально.
Взятие квадратного корня иррационального числа
Когда дело доходит до вычисления квадратного корня иррационального числа, у вас есть два варианта. Либо вставьте иррациональное число в калькулятор, либо в онлайн-калькулятор с квадратными корнями (см. Ресурсы), и в этом случае калькулятор выдаст вам приблизительное значение — или вы можете использовать четырехэтапный процесс, чтобы оценить его самостоятельно.
Пример 1: Оцените значение иррационального числа √8.
-
Найти начальное значение
-
Разделите на свою оценку
-
Вычислить среднее
-
Повторите шаги 2 и 3 по мере необходимости
Найдите идеальные квадраты, которые были бы по обе стороны от √8 на числовой линии. В этом случае √4 = 2 и √9 = 3. Выберите тот, который ближе всего к вашему целевому номеру. Поскольку 8 намного ближе к 9, чем к 4, выберите √9 = 3.
Затем разделите число, корень которого вы хотите — 8 — на вашу оценку. Продолжая пример, у вас есть:
8 ÷ 3 = 2, 67
Теперь найдите среднее значение результата из шага 2 с делителем из шага 2. Здесь это означает усреднение 3 и 2, 67. Сначала сложите два числа вместе, а затем разделите на два:
3 + 2.67 = 5.6667 (это фактически повторяющийся десятичный 5.6666666666, но для краткости он был округлен до четырех десятичных знаков.)
5, 6667 ÷ 2 = 2, 83335
Результат шага 3 все еще не точен, но он становится ближе. При необходимости повторите шаги 2 и 3, используя каждый раз результат шага 3 в качестве нового делителя на шаге 2.
Чтобы продолжить пример, вы должны разделить 8 на результат шага 3 (2.83335), который дает вам:
8 ÷ 2.83335 = 2.8235 (опять же, ради краткости округляем до четырех знаков после запятой).
Затем вы бы усреднили результат вашего деления с делителем, который дает вам:
2, 83335 + 2, 8235 = 5, 65685
5, 65685 ÷ 2 = 2, 828425
Вы можете продолжить этот процесс, повторяя шаги 2 и 3 по мере необходимости, пока ответ не будет настолько точным, насколько это необходимо.
Как насчет иррациональных квадратных корней?
Иногда вместо того, чтобы найти квадратный корень иррационального числа, вам нужно иметь дело с иррациональными числами, которые выражены в форме квадратного корня — один из самых известных, о которых вы узнаете, — √2.
С √2 мало что можно сделать, кроме приблизительного значения, как описано выше. Но если вы получите большее иррациональное число в форме квадратного корня, вы можете иногда использовать тот факт, что √cd = √c × √d, чтобы переписать ответ в более простой форме.
Рассмотрим иррациональный квадратный корень √32. Хотя у него нет основного корня (то есть неотрицательного целочисленного корня), вы можете выделить его во что-то со знакомым основным корнем:
√32 = √16 × √2
Вы по-прежнему мало что можете сделать с √2, но √16 = 4, поэтому вы можете сделать еще один шаг и записать это как √32 = 4√2. Хотя вы не исключили полностью знак радикала, вы упростили это иррациональное число, сохранив при этом его точное значение.
An irrational number isn’t as scary as it sounds; it’s just a number that can’t be expressed as a simple fraction or, to put it another way, an irrational number is a never-ending decimal that continues an infinite number of places past the decimal point. You can perform most operations on irrational numbers just as you’d do with rational numbers, but when it comes to taking square roots, you’re going to have to learn to approximate the value.
What’s an Irrational Number?
So what is an irrational number, anyway? You may already be familiar with two very famous irrational numbers: π or «pi,» which is almost always abbreviated as 3.14 but in fact continues infinitely to the right of the decimal point; and «e,» a.k.a. Euler’s number, which is usually abbreviated as 2.71828 but also continues infinitely to the right of the decimal point.
But there are a lot more irrational numbers out there, and here’s an easy way to spot some of them: If the number beneath a square root sign is not a perfect square, then that square root is an irrational number.
That’s an awfully big mouthful, so here’s an example to make it clear. It also helps to remember that a perfect square is a number whose square root is an integer:
Is √8 an irrational number? If you’ve memorized your perfect squares or take the time to look them up, you’ll know that
sqrt{4} = 2 text{ and } sqrt{9} = 3
Since √8 is in between those two numbers, but there’s no integer between 2 and 3 to be its root, √8 is irrational.
Taking the Square Root of an Irrational Number
When it comes to calculating the square root of an irrational number, you have two choices. Either put the irrational number into a calculator or an online square root calculator (see Resources), in which case the calculator will return an approximate value for you – or you can use a four-step process to estimate the value yourself.
Example 1: Estimate the value of the irrational number √8.
Find the perfect squares that would be to either side of √8 on the number-line. In this case, √4 = 2 and √9 = 3. Choose the one that’s closest to your target number. Since 8 is much closer to 9 than to 4, choose
sqrt{9} = 3
Next, divide the number whose root you want – 8 – by your estimate. Continuing the example, you have:
frac{8}{3} = 2.67
Now, find the average of the result from Step 2 with the divisor from Step 2. Here, that means averaging 3 and 2.67. First add the two numbers together, and then divide by two:
3 + 2.67 = 5.6667
(This is actually the repeating decimal 5.6666666666, but it has been rounded to four decimal places for the sake of brevity.)
frac{5.6667}{2} = 2.83335
The result from Step 3 still isn’t exact, but it’s getting closer. Repeat Steps 2 and 3 as needed, using the result from Step 3 as the new divisor in Step 2 every time.
To continue the example, you would divide 8 by the result from Step 3 (2.83335), which gives you:
frac{8}{2.83335} = 2.8235
(Again, rounding to four decimal places for the sake of brevity.)
You would then average the result of your division with the divisor, which gives you:
2.83335 + 2.8235 = 5.65685 \ ,\ frac{5.65685}{2} = 2.828425
You can continue this process, repeating Steps 2 and 3 as needed, until the answer is as exact as you need it to be.
What About Irrational Square Roots?
Sometimes instead of finding the square root of an irrational number, you need to deal with irrational numbers that are expressed in square root form – one of the most famous you’ll learn about is √2.
There’s not a lot you can do with √2, aside from approximating its value as described above. But if you get a larger irrational number in square root form, you can sometimes use the fact that
sqrt{cd} = sqrt{c} × sqrt{d}
to rewrite the answer in a simpler form.
Consider the irrational square root √32. Although it doesn’t have a principal root (that is, a non-negative, integer root), you can factor it into something with a familiar principal root:
sqrt{32} = sqrt{16} × sqrt{2}
You still can’t do much with √2, but √16 = 4, so you can take this a step further and write it as
sqrt{32} = 4sqrt{2}
While you haven’t eliminated the radical sign entirely, you’ve simplified this irrational number while also preserving its exact value.
Содержание:
Иррациональные числа
Практическая работа 1. Великий греческий математик, физик, астроном и изобретатель Архимед хотел найти рациональное число, квадрат которого равен 3. С этой целью он выбрал числа
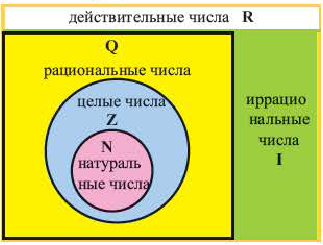
Классификация чисел
Любое рациональное число можно записать в виде дроби
Каждую конечную десятичную дробь можно записать в виде бесконечной десятичной периодической дроби с цифрой 0 в периоде. Но есть такие числа, которые невозможно представить в виде десятичной периодической дроби. Бесконечная десятичная непериодическая дробь выражает число, которое не является рациональным. Такие числа называются иррациональными числами. Иррациональное число невозможно представить в виде 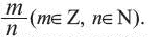
a) 0,1010010001… (количество нулей после каждой единицы увеличивается на один);
b) 0,123456789101112… (в дробной части записана последовательность натуральных чисел);
c) 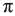
Если 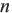
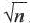
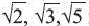
Практическая работа.
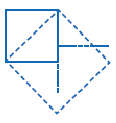
1) Начертите квадрат со стороной равной единичному отрезку и проведите диагональ данного квадрата. На диагонали квадрата постройте новый квадрат. Убедитесь, что площадь полученного квадрата в два раза больше площади единичного квадрата. Покажите, что сторона полученного квадрата равна соответственно
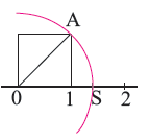
2) Повторите работу по алгоритму, представленному ниже. На координатной оси постройте квадрат, сторона которого равна единичному отрезку. Начертите окружность с центром в точке нуль, радиусом равным диагонали квадрата и отметьте точку пересечения с числовой осью. Объясните связь между соответствующим данной точке числом и длиной диагонали квадрата.
Числовая ось, рациональные, иррациональные числа
Каждой точке на числовой оси соответствует единственное число (рациональное или иррациональное) и каждому числу, на числовой оси соответствует единственная точка. Опираясь на это числа можно сравнивать. Число, соответствующее точке, которая расположена правее, больше числа, соответствующему точке, расположенной левее.
Практическая работа.
1) При помощи калькулятора вычислите значения 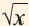
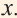
2) На координатной плоскости отметьте точки из таблицы, с соответствующими координатами, и соедините их плавной линией.
3) Может ли 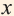
4) Как изменяются соответствующие значения 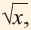
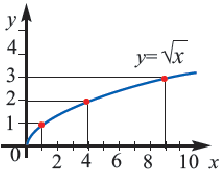
Функция y=√x и её график
Функция 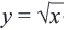
В таблице, которую вы заполнили, показаны некоторые значения аргументов 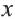
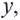
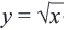
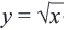
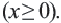
График функции 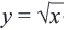
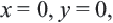
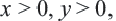
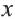
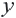
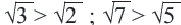
Приближенное значение квадратного корня
Практическая работа.
Какова наибольшая длина стороны квадрата, составленного из 14 одинаковых единичных квадратов? Как вы нашли результат? Между какими последовательными натуральными числами, являющимися точными квадратами, расположено число 14?
Приближённое значение квадратного корня можно найти при помощи калькулятора, но существуют и другие методы. Вычислить приближённое значение квадратного корня можно при помощи числовой оси и чисел, являющихся точными квадратами. Например, найдём при помощи данного метода,
Число 14 расположено между числами 9 и 16. Квадратные корни этих чисел соответственно равны 3 и 4. Целая часть квадратного корня из 14 равна 3. Найдём приближённое значение дробной части:
На числовой прямой от 14 до 9-ти 5 единиц, от 9-ти до 16 — 7 единиц.
Дробная часть числа 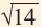
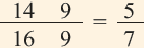
Полученное приближённое значение
Значение, найденное при помощи калькулятора
Квадратный корень из произведения и частного
Исследование: Найдите значение выражений
Верно ли равенство?
Проверьте, что соответствующее равенство верно для любых двух неотрицательных чисел.
Квадратный корень из произведения и частного
При
Корень из произведения неотрицательных множителей равен произведению корней из этих же множителей. Это свойство верно и для более двух множителей
Аналогичным образом можно показать, что при
Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.
Пример:
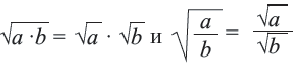
Пример:
Квадратный корень степени
Из того, что арифметический квадратный корень не может принимать отрицательных значений, следует что равенство 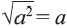
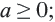
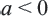
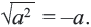
Действительно, при , 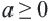
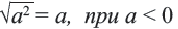
Таким образом,
Приняв во внимание, что абсолютное значение числа всегда положительное или равно нулю) и объединив два равенства, приведённых выше получим следующее
Для извлечения корня чётной степени подкоренное выражение надо записать в виде квадрата идентичного выражения, а затем применить тождество
Пример:
Преобразование выражений, содержащих квадратные корни
Вынесение множителя из-под знака корни
Пример 1. Сравним числа
При решении мы заменили 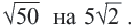
- Заказать решение задач по высшей математике
Пример 2. 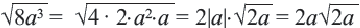
Внесение множителя под знак корня
Пример 3. Сравним числа
Заменим число 6 на
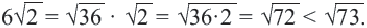
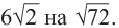
Пример 4.
Сложение и вычитание корней, имеющих одинаковое подкоренное выражение вида 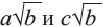
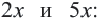
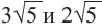
Пример:
Чему равна длина двух досок, если длина одной доски равна
Пример:
Пример:
Пример:
Сократите дробь.
Освобождение знаменателя от иррациональности
Сумма, разность, произведение (кроме умножения на «0» ) и отношение рационального и иррационального чисел является иррациональным числом. А вот сумма, разность, произведение и отношение двух иррациональных чисел может быть рациональным числом.
Пример:
а) При 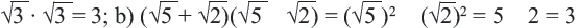
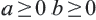
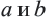
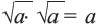
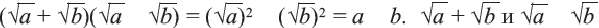
Пример:
Определение вида треугольника по длинам его сторон
Пусть 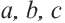
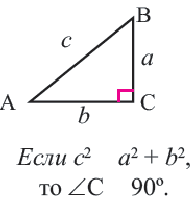
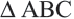
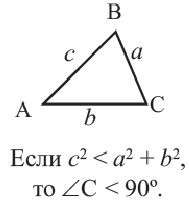
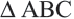
Особые прямоугольные треугольники
Теорема 1. В равнобедренном прямоугольном треугольнике гипотенузы больше любого из катетов в 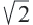
Отношение сторон: 1 : 1 :
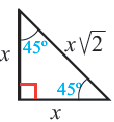
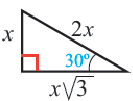
Теорема 2. В прямоугольном треугольнике с острым углом 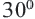
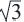
Отношение сторон: 1 : 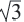
- Действительные числа
- Решение уравнений высших степеней
- Системы неравенств
- Квадратные неравенства
- Уравнения и неравенства содержащие знак модуля
- Уравнение
- Метод математической индукции
- Система координат в пространстве
Иррациональное число не так страшно, как кажется; это просто число, которое нельзя выразить простой дробью или, иначе говоря, иррациональное число — это бесконечное десятичное число, продолжающееся бесконечное количество разрядов после десятичная точка. Вы можете выполнять большинство операций с иррациональными числами так же, как с рациональными числами, но когда дело доходит до извлечения квадратного корня, вам придется научиться приближать значение.
Что такое иррациональное число?
Так что же такое иррациональное число? Возможно, вы уже знакомы с двумя очень известными иррациональными числами: π или «пи», которое почти всегда сокращается до 3,14, но на самом деле продолжается до бесконечности справа от десятичной точки; и «е», также известное как число Эйлера, которое обычно сокращается до 2,71828, но также продолжается до бесконечности вправо от десятичной точки.
Но существует гораздо больше иррациональных чисел, и вот простой способ определить некоторые из них: если число под знаком квадратного корня не является полным квадратом, тогда этот квадратный корень является иррациональным номер.
Это ужасно громоздко, так что вот пример, чтобы прояснить это. Также полезно помнить, что полный квадрат — это число, квадратный корень которого является целым числом:
√8 — иррациональное число?Если вы запомнили свои идеальные квадраты или потратили время на их поиск, вы поймете, что
sqrt {4} = 2 text {и} sqrt {9} = 3
Поскольку √8 находится между этими двумя числами, но нет целого числа от 2 до 3, которое могло бы быть его корнем, √8 иррационально.
Извлечение квадратного корня из иррационального числа
Когда дело доходит до вычисления квадратного корня из иррационального числа, у вас есть два варианта. Либо поместите иррациональное число в калькулятор, либо в онлайн-калькулятор квадратного корня (см. Ресурсы), и в этом случае калькулятор вернет вам приблизительное значение — или вы можете использовать четырехэтапный процесс, чтобы оценить значение сам.
Пример 1:Оцените значение иррационального числа √8.
Найдите идеальные квадраты, которые будут по обе стороны от √8 на числовой прямой. В этом случае √4 = 2 и √9 = 3. Выберите тот, который ближе всего к вашему целевому числу. Поскольку 8 гораздо ближе к 9, чем к 4, выберите
sqrt {9} = 3
Затем разделите число, корень которого вы хотите — 8 — на вашу оценку. Продолжая пример, у вас есть:
frac {8} {3} = 2,67
Теперь найдите среднее значение результата из шага 2 с делителем из шага 2. Здесь это означает усреднение 3 и 2,67. Сначала сложите два числа, а затем разделите на два:
3 + 2.67 = 5.6667
(На самом деле это повторяющееся десятичное число 5,6666666666, но для краткости оно было округлено до четырех знаков после запятой.)
frac {5.6667} {2} = 2,83335
Результат шага 3 все еще неточный, но приближается. При необходимости повторите шаги 2 и 3, каждый раз используя результат из шага 3 в качестве нового делителя на шаге 2.
Чтобы продолжить пример, вы должны разделить 8 на результат шага 3 (2,83335), что даст вам:
frac {8} {2,83335} = 2,8235
(Снова округляем до четырех знаков после запятой для краткости.)
Затем вы усредните результат своего деления с делителем, который даст вам:
2,83335 + 2,8235 = 5,65685 \ , \ frac {5,65685} {2} = 2,828425
Вы можете продолжить этот процесс, повторяя шаги 2 и 3 по мере необходимости, пока ответ не будет настолько точным, насколько вам нужно.
А как насчет иррациональных квадратных корней?
Иногда вместо того, чтобы найти квадратный корень из иррационального числа, вам нужно иметь дело с иррациональными числами, которые выражаются в форме квадратного корня — одно из самых известных, о которых вы узнаете, — это √2.
С √2 мало что можно сделать, кроме как приблизить его значение, как описано выше. Но если вы получаете большее иррациональное число в форме квадратного корня, вы можете иногда использовать тот факт, что
sqrt {cd} = sqrt {c} × sqrt {d}
переписать ответ в более простой форме.
Рассмотрим иррациональный квадратный корень √32. Хотя у него нет основного корня (то есть неотрицательного целочисленного корня), вы можете разделить его на что-то со знакомым основным корнем:
sqrt {32} = sqrt {16} × sqrt {2}
Вы по-прежнему мало что можете сделать с √2, но √16 = 4, поэтому вы можете пойти дальше и записать его как
sqrt {32} = 4 sqrt {2}
Хотя вы не исключили полностью знак радикала, вы упростили это иррациональное число, сохранив при этом его точное значение.