Как найти квадрат растояния

22 января 2014

Это первый урок из серии видеоуроков, посвященных задачам B13. Перед нами стандартная задача, которую часто дают на пробниках и контрольных работах. Однако решать ее мы будем весьма нестандартным методом.:)

Задача B13. Дан многогранник, изображенный на рисунке. Все двугранные углы прямые. Найдите, насколько расстояние между вершинами
A
и C2 отличается от квадрата расстояния между вершинами
E
и G1. В ответ запишите положительное число.

Для решения любых таких задач нам потребуется обобщенная теорема Пифагора. Давайте отмотаем время назад и вспомним, что такое обычная теорема Пифагора. У нас есть прямоугольный треугольник с катетами
a
,
b
и гипотенузой
c
:

В этом случае квадрат гипотенузы равен сумме квадратов катетов:

c

² =
a

² +
b

²

Теорема Пифагора в пространстве

Но все это рассматривается лишь на плоскости, потому что треугольник — это плоская фигура. Однако та же самая формула работает и в пространстве.

Теорема Пифагора в пространстве. Рассмотрим прямоугольный параллелепипед, или, просто говоря, кирпич. Такой параллелепипед однозначно задается своими сторонами
a
,
b
и
c
. Кроме того, у него есть главная диагональ. Эта диагональ соединяет наиболее удаленные точки параллелепипеда. Разумеется, если параллелепипед прямоугольный, то таких диагоналей сразу несколько, при этом все они будут равны и будут считаться по одной и той же формуле.

Диагональ обозначим буквой
l
. В этом случае можно записать формулу:

l

² =
a

² +
b

² +
c

²

Как связана теорема Пифагора и расстояния между точками в пространстве

Возможно, кто-то сейчас спросит: а какое отношение диагональ, тем более, в параллелепипеде имеет к нашему прямоугольному треугольнику со сторонами
a
,
b
и
c
? Отношение, на самом деле, самое прямое. Давайте достроим наш треугольник до прямоугольника, и получим, что гипотенуза
c
является диагональю на прямоугольнике.

Таким образом, перед нами, по сути, аналог теоремы Пифагора для трехмерного пространства. Давайте немножко перепишем ее:

Внимательные ученики наверняка заметят, что эта формула очень похожа на формулу расстояния в трехмерном пространстве между точками
a
и
b
. Разумеется, при условии, что точка
A
лежала бы в начале координат, а точка
B
имела координаты, равные длинам сторон нашего параллелепипеда:

A
= (0; 0; 0);

B
= (
a
,
b
,
c
).

Однако ничего удивительного в этом нет, потому что длина диагонали
l
— это как раз и есть расстояние между наиболее удаленными точками параллелепипеда.

Метод обхода точек

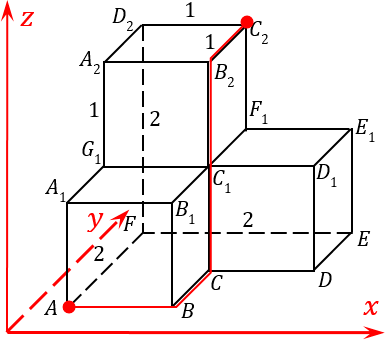
Но хватит теории, давайте перейдем непосредственно к нашей задаче. Итак, в первую очередь нужно найти расстояние от точки
A
до точки
C

₂. И вот для того, чтобы найти это расстояние, сейчас мы воспользуемся замечательным приемом, который называется обход точек.

Метод обхода точек заключается в следующем:

1. Построим систему координат с осями, параллельными ребрам нашего многогранника. Назовем эти оси x, y и z.
2. А теперь давайте поставим ручку в нашу точку A и попытаемся каким-то образом, двигаясь по ребрам, добраться до точки C
   ₂.

Нахождение диагонали методом обхода точек

Разумеется, последовательность осей может быть любой, решение и ответ от этого не изменится. И двигаться из одной точки в другую тоже можно по-разному. Например, можно идти к точке
B
, затем к точке
C
, затем вверх до точки
B

₂ и, наконец, двигаться вдаль — и мы попадем в точку
C

₂:

Давайте разметим, полученный нами путь:

1. Из точки A в точку B мы двигались вдоль оси x в положительном направлении. Запишем: 1x;
2. От точки B в точку C мы двигались вдоль оси игрек опять же по положительному направлению, то есть вглубь. Так и запишем 1y;
3. Затем мы шагнули на два шага вверх из точки C в точку B
   ₂. так и напишем: 2z;
4. Еще один шаг из точки B
   ₂ в точку C
   ₂ вдоль y, т. е. вглубь нашего рисунка. Запишем: 1y.

А теперь, когда мы отметили каждое звено нашей ломанной, соединяющие точки
A
и
C

₂, выпишем, сколько шагов мы получили вдоль каждой координатной оси с учетом знаков:

1. x: 1;
2. y: 1 + 1 = 2;
3. z: 2.

Теперь возвращается к нашей обобщенной теореме Пифагора и замечаем, что оси
x
,
y
и
z
— это, по сути,
a
,
b
и
c
, т. е. длины сторон параллелепипеда. Следовательно, мы можем посчитать длину диагонали этого параллелепипеда:

Вот и все! Мы получили расстояние от точки
A
до
C

₂, согласно рисунку нашего многогранника.

Диагональ параллелепипеда не зависит от маршрута обхода

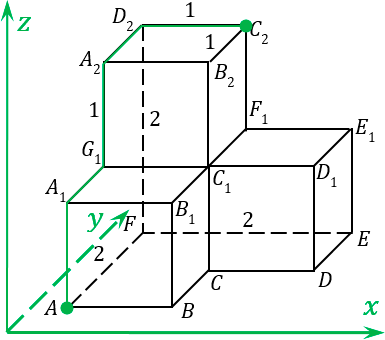
Однако внимательные ученики спросят: а что будет, если мы пойдем по другому пути? Ведь от точки
A
до точки
C

₂ можно идти и другим путем: сначала вверх до точки
A
₁, затем вглубь до точки
G

₁, затем вверх до точки
A

₂, затем снова в глубину до точки
D

₂, и, наконец вправо до точки
C

₂:

Получили совсем другой маршрут, и возникает логичный вопрос: не будет длина на этом маршруте иметь совсем другое значение координат
x
,
y
и
z
, и, соответственно, другое значение
l
? Давайте проверим.

Размечаем наш второй маршрут:

1. из точки A в точку A
   ₁ мы попадаем, смещением оси z на единичку: 1z;
2. из точки A
   ₁ в точку G
   ₁ мы попадаем, смещением по y на единичку: 1y;
3. из точки G
   ₁ в точку A
   ₂ — смещение по z: 1z;
4. из точки A
   ₂ в точку D
   ₂ — смещение по y: 1y;
5. от D
   ₂ до C
   ₂ — смещение вправо, т.е. в положительную сторону по x: 1x.

Выписываем полученные смещения:

1. x: 1
2. y: 1 + 1 = 2
3. z: 1 + 1 = 2

Итого выражение для диагонали
l
получилось в точности тем же самым:

Таким образом, мы убедились, что итоговое значение величины
l
, т. е. расстояние между точками
A
и
C

₂ не зависит от того, каким маршрутом мы будем идти из одной точки в другую. Следовательно, при решении реальных задач вы вправе выбрать любой маршрут, который будет удобен именно вам. И вообще, тот факт, что расстояние между двумя точками не зависит от того, как это расстояние мерить, на самом деле вполне логичен. Мы же занимаемся математикой, а не гаданием на кофейной гуще. Поэтому, по какому бы пути мы не пошли, ответ получится одним и тем же.

Расстояние между двумя точками в пространстве не зависит от того, как мы это расстояние считаем. Если все расчеты выполнены правильно, ответ получится одним и тем же.

Вычисление квадрата расстояния методом обхода точек

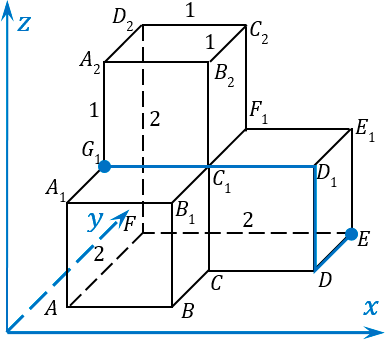
Возвращаемся к нашему заданию и переходим ко второй его части. Нужно найти расстояние между точкой
E
и точкой
G

₁. Опять предлагаю воспользоваться методом обхода точек. Начнем путь от точки
E
, будем двигаться к точке
D
, потом из точки
D
в точку
D

₁, и потом от
D

₁ напрямую в точку
G

₁:

Размечаем нашу ломанную:

1. из точки E в точку D мы попадаем смещением по оси y на единицу в сторону, противоположную положительному направлению оси: -1y;
2. затем мы поднимаемся вверх на одну единицу по оси z, т. е. этот отрезок ломанной обозначаем как 1z;
3. потом мы смещаемся влево из точки D
   ₁ в точку G
   ₁ на две единицы вдоль оси x и получаем -2x.

Давайте запишем, что у нас получилось:

1. x: -2
2. y: -1
3. z: 1

По каждой из осей зафиксировано лишь одно смещение, ничего складывать, как в предыдущих случаях, не надо. Просто находим длину отрезка, соединяющего точки
E
и
G

₁. Давайте назовем этот отрезок
l

₂. Его длина равна:

Окончательное решение задачи B13

Вспоминаем, что от нас требуется найти в условии задачи. А от нас требуется квадрат расстояния между этими вершинами. Следовательно, нам нужна величина:

l

₂
² = 6

При произведении в квадрат корень исчезает.

Внимательно читайте условие задачи. Недостаточно просто найти длину отрезка или значение переменной — нужно предъявить именно ту величину, которую у нас спрашивают.

Осталось найти ту самую разницу, которую от нас требуют найти в условии задачи. Назовем ее ∆:

∆ = 6 − 3 = 3

Вот мы и нашли ответ — он равен 3.

Ключевой прием — обход точек

Еще раз — ключевая идея решения всей этой задачи. Она состоит в том, чтобы прямо на рисунке начертить путь из одной искомой точки в другую и посмотреть: вдоль каких координатных осей выполняется смещение и насколько. Затем мы выписываем эти смещения и считаем общее расстояние по обобщенной теореме Пифагора.

При этом возникает замечательный эффект: итоговое расстояние, которое мы считаем, не зависит от того, какой маршрут обхода мы выберем. В любом случае, как бы мы ни шли из одной точки в другую, расстояние получится одним и тем же. Разумеется, при условии, что все вычисления будут выполнены верно.

Аналогичным образом мы считаем второе расстояние. Пусть вас совершенно не смущает, что тут получаются отрицательные координаты, потому что при возведении в квадрат минусы сжигаются. Наконец, остается сосчитать ту самую разницу, которую требуется найти в условии задачи. Тут вообще все очень просто, и никаких дополнительных пояснений не требуется.

Краткая сводка по задачам B13

Итак, мы решили задачу B13 мы будем методом обхода точек. Давайте еще раз посмотрим, из каких шагов состояло наше решение:

1. Добавить к рисунку оси координат, параллельные ребрам многогранника;
2. Начертить «траекторию движения» от одной точки до другой, двигаясь исключительно по ребрам исходного многогранника;
3. Выяснить, вдоль какой оси происходит смещение на каждом отрезке полученной ломаной, и посчитать общее смещение;
4. Найти итоговое расстояние по обобщенной теореме Пифагора: l
   ² = a
   ² + b
   ² + c
   ², где a, b, c — суммарные смещения вдоль каждой из осей.

Но что будет, если выбрать другой маршрут? Не случится ли так, что при этом возникнут другие суммарные смещения и, следовательно, другое расстояние? Спешу вас обрадовать: суммарные смещения и расстояние между точками не зависит от выбранного маршрута. Мы убедились в этом лично, когда рассмотрели альтернативный маршрут обхода.

В общем, чертите путь так, как вам удобно — ответ всегда будет одним и тем же. В этом и состоит прелесть метода обхода точек.

Смотрите также:

1. Обход точек в стереометрии — 2
2. Разбор задачи 8 из ЕГЭ на площадь полной поверхности призмы/параллелепипеда.
3. Решение ЕГЭ-2011: вариант 1, часть B
4. Метод коэффициентов, часть 1
5. Задача B5: площадь сектора
6. Решение задач на движение по воде

В данной статье хочу рассказать вам об определённом типе задач по стереометрии, одну из которых, возможно, предстоит решить именно вам на ЕГЭ по математике. Это задачи на решение составных многогранников:

Обычно требуется найти расстояние (или квадрат расстояния) между двумя точками; какой-либо угол, либо значение одной из тригонометрических функций обозначенного в условии угла.

Для решения  необходимо знать совсем не много теории: теорему Пифагора; определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике; значения углов тригонометрических функций.

Рассмотрим задачи:

Найдите расстояние между вершинами А и С₂  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Результат умножьте на  корень из шести  и запишите ответ.

Соединим точки  А и С₂   и рассмотрим  прямоугольный треугольник АА₂С₂:

По теореме Пифагора:

Ответ: 6

Найдите угол САD₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

Соединим точки C, А, D₂:

Рассмотрим треугольник CАD₂:  AC = CD₂ = AD₂, так как являются диагоналями квадратов со сторонами равными 8. Следовательно, треугольник CАD₂ – равносторонний, то есть все его  углы равны 60°.

Таким образом, угол CАD₂ = 60°.

Ответ: 60

Найдите квадрат расстояния между вершинами В₂ и D₃ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Соединим точки B₂, B₃ и D₃. Рассмотрим прямоугольный треугольник B₂B₃D₃:

По теореме Пифагора:

Ответ: 12

Найдите тангенс угла АBB₃ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Соединим точки В и B₃, из точки B₃ опустим перпендикуляр на ребро АВ, точку пересечения обозначим как К. Рассмотрим прямоугольный треугольник КВB₃:

Ответ: 2

Найдите квадрат расстояния между вершинами D и C₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Соединим точки В  и C₂, а так же C₂  и С:

Рассмотрим прямоугольный треугольник СВС₂.  По теореме Пифагора:

Ответ: 46

245376. Найдите квадрат расстояния между вершинами В₂ и D₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Посмотреть решение

245380. Найдите тангенс угла AВB₃ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Посмотреть решение

245382. Найдите квадрат расстояния между вершинами D и C₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Посмотреть решение

При решении подобных заданий главное – это «увидеть» треугольник, в который входит искомый элемент (отрезок, угол) и построить этот треугольник.  А далее уже использовать указанную в начале статьи теорию.

Есть ещё задачи с параллелепипедами:

245359   245360   245361   245362   245363

Процесс решения в них сводится к решению прямоугольного треугольника: нужно найти расстояние между вершинами (квадрат расстояния), либо заданный угол.

Мы продолжим рассматривать задачи по стереометрии? не пропустите! На этом всё. Как видите, ничего сложного. Успеха вам!

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

А вы в школе разве математику не проходили?? ? О_о

Квадрат — когда одинаковые числа умножаются друг на друга. А если это зависимость? Тогда это выглядит вот так.

y

0 х

Такую зависимость выводят, а не понимают.

Если, к примеру, у вас в первом доме один человека ходит в школу, а во втором доме в квадрат больше его номера, а в третьем в квадрат больше, тогда это зависимость. Т. е. это само по себе просто существует, но просто кто-то посчитал это. И кто-то сделал вывод о квадратичной зависимости. А если бы у вас в первом доме ходил один человек в школу, а во втором доме два человека, а в третьем три — тогда это была бы линейная зависимость. Но она просто определяется путём подсчёта. Это вовсе не зависит от того кто какую кашу или хлеб ест. Просто в каждом следующем доме детей больше, а где-то взрослых или пожилых людей. Но, кто-то сообразил, что можно номера домов и количество учащихся в школе детей составить в некую вымышленную зависимость. Т. е. она взята просто так. Но, кто-то, именно, сообразил придумать вот такую зависимость, которая ни от чего в общем-то не зависит. Просто кто-то был наблюдательным и умел считать. И только.

И записывается линейная зависимость как x = у, а квадратичная зависимость x = y².

Для примера с домами и детьми учащимися в школе:
х — номер дома;
y — количество учащихся в школе.

И если номер дома 1, тогда:
при линейной зависимости 1 соответствует 1;
при квадратичной зависимости 1 соответствует 1²

А если номер дома 2, тогда:
при линейной зависимости 2 соответствует 4;
при квадратичной зависимости 2 соответствует 2² = 4.

А если номер дома 3, тогда:
при линейной зависимости 3 соответствует 3;
при квадратичной зависимости 3 соответствует 3² = 9.

Только учти, что х = у² это — та самая зависимость (или функция) , где знак равенства не просто так сам по себе знак равно, а именно имеет смысл само по себе такого вида математическое выражение. А оттого и называется зависимостью, т. е. функцией. Если в нём заменить буквы на числа, то само выражение окажется бессмысленным. Т. е. от чего начали, к тому и вернулись. Сама же зависимость была придуманна просто так. Просто кто-то увидал её, и так её описал.

О квадратных уравнениях в правильном порядке

Как вам преподавали квадратные уравнения в школе? Это был 7-8 класс, примерно. Вероятнее всего, вам рассказали что есть формулы корней через дискриминант, что направление ветвей зависит от старшего коэффициента. Через пару занятий дали теорему Виета. Счастливчикам еще рассказали про метод переброски. И на этом решили отпустить.

Вы довольны такой базой? Вам не рассказали ни геометрический смысл, ни как это получить.

Спустя некоторое время обдумывания сей несправедливости, я решил написать эту статью и тем самым закрыть гештальт о фрагментарности знаний.

Вы не найдете здесь ничего нового по факту, но, возможно, это даст посмотреть на такое простое понятие с другой стороны.

Начнем с конца

Когда я перечислял темы, касающиеся квадратных уравнений, я делал это примерно в том же порядке, в котором изучают их в школе. Но такой порядок не оправдан с точки зрения обучения, и вот почему:

• Дискриминант дается просто как данность (за редким исключением, когда показывают вывод этих формул через приведение к полному квадрату)

• Мощнейшая по своей сути теорема Виета дается в конце и только как эвристический способ решения

Гораздо проще начать с теоремы Виета.

Рассмотрим квадратный трехчлен

В силу основной теоремы алгебры (примем её как данность, так как её действительно тяжело доказать), мы знаем, что у этого уравнения должно быть два корня. Допустим, что это некоторые числа . Тогда можно переписать изначальное уравнение как выражение его корней:

Оба эти уравнения эквиваленты, так как они оба зануляются в (первое по определению , второе по построению).

Раскрывая скобки, мы получим следующее:

Откуда приравняв соответствующие коэффициенты с имеющимися, получим знаменитую систему:

Мы только что доказали теорему Виета на случай квадратного трехчлена. Это потрясающий результат: мы начинаем получать некоторую информацию о корнях, которые, как мы предположили, существуют. И этот результат мы будем использовать далее.

Геометрия параболы

Вершина

Здесь можно было бы рассказать весь первый курс алгебры университета: о фокусах, директрисах, о конических сечениях, первой и второй производной…

Но раз мы ограничились школьной программой (7-8 класс, если быть точным), то и рассуждения у нас будут простые.

Самая, на мой субъективный взгляд, интересная точка параболы – это её вершина. Она уникальным образом задает положение параболе и дает понимание о том, как устроены корни.

Но формулу для нее мы не знаем, до первых понятий о производной нам еще 3 года в среднем. Будем выкручиваться.

Парабола – симметричная фигура. До того момента, как мы сдвинули ее относительно оси , ось служит для нее осью симметрии. Когда же мы начинаем ее сдвигать, становится видно, что она продолжает быть симметричной, но уже относительно оси, проходящей через вершину.

Тогда от вершины в обе стороны до корней равные расстояния, а это значит, что вершина параболы лежит ровно между корнями. Тогда координата вершины это среднее между ее корнями

Пока что мы не знаем наши корни. Но благодаря теореме Виета мы знаем, чему равна сумма корней!

Потрясающий результат, который нам пригодится далее.

Ещё немного про корни

Мы знаем, что корни, графически, это те точки, в которых кривая пересекает ось . Очень полезное знание, учитывая, что смотря на параболу, исключительно визуально, мы понимаем что у нас может быть 3 случая:

1. Корней нет, при этом

   1. Либо значение в вершине больше нуля и старший коэффициент больше нуля

   2. Либо значение в вершине меньше нуля и старший коэффициент меньше нуля

2. Корень один, но кратности 2 (не забываем основную теорему алгебры), и значение в вершине равно нулю

3. Корня два

Второй случай тривиален, до третьего мы еще дойдем. Интересно математически взглянуть на первый. Найдем значение квадратного трехчлена в вершине:

И теперь все же рассмотрим первый случай: парабола висит над осью ветвями вверх.

Домножим первое неравенство на . Учитывая, что , знак неравенства сменится на противоположный:

Это условие, при котором корней нет.

Рассмотрим вкратце противоположный случай: парабола висит под осью ветвями вниз.

Какая-то магия. Получается, что это условие инвариантно относительно положения параболы. Но тем оно лучше.

На данном этапе прошу заметить, что это только условие отсутствия действительных корней. Да, это похоже на дискриминант, но давайте представим, что вы этого не знаете.

Понятие дискриминанта

Мы уже многое поняли о корнях: в какой они связи с коэффициентами, когда они не существуют, каким образом они лежат относительно вершины. Все это безумно полезно, но это все до сих пор не способ найти значения алгебраически.

Давайте будем отталкиваться от того, что мы уже знаем: от вершины. Если бы мы каким-то образом знали расстояние между корнями, то могли бы однозначно найти и сами корни.

Таки что мешает нам это сделать? Но как настоящие математики, давайте находить квадрат расстояния между корнями. Не теряя общности, будем считать, что – больший корень. Тогда

Пока что выглядит не очень, но на что-то это очень сильно похоже. Не видите? Давайте выделим полный квадрат, но по сумме, а не по разности: добавим , но чтобы все осталось в точности так же, это же и вычтем.

Все еще не видите? Воспользуемся снова теоремой Виета:

Мы получили квадрат расстояния между корнями с учетом растяжения коэффициентом .

Так мы теперь можем найти корни! Вершина параболы да половину расстояния между корнями в обе стороны:

Или, немного преобразовав

Квадрат расстояния между корнями квадратного трехчлена и есть дискриминант.

В общем случае, дискриминант — более сложное понятие, связанное с кратными корнями. Но для квадратного уравнения в 7 классе этого достаточно.

Теперь, если рассуждать о дискриминанте как о расстоянии, становится логично и понятно, почему если он равен нулю, то корень всего один; а если отрицательный, то действительных корней вообще нет.

Заключение

Заметьте, что единственное, что мы предположили, что корня два и они существуют. Единственное, что приняли на веру, это основную теорему алгебры. До всего остального мы дошли исключительно умозрительными заключениями и простейшей алгеброй.

Как по мне, это именно то, как должны преподавать эту тему в школе.