Гость:
Решение. {a+b+c=48 {a^2+b^2+c^2=800 {a+b+c=48 {2c^2=800 c=20 {a+b=28 a=28-b {a^2+b^2=400 b^2-28b+192=0 b1=16 b2=12 a1=12 a2=16 (a-b)^2=(16-12)^2=16 Как вас много-то! Скучаете в каникулы-то.
Гость:
ответ 16
Гость:
Обозначим катеты как «а» и «b», гипотенузу как «с», тогда: из 2-го условия: a^2+b^2+c^2=2c^2=800; c^2=400; c=20 из 1-го условия: a+b+20=48; a+b=28 Отсюда система: {a+b=28; a=28-b {a^2+b^2=400 (28-b)^2+b^2=400 784-56b+b^2+b^2=400 b^2-28b+192=0 Из урав-ия следует, что один катет=16, другой=12 Квадрат разности катетов=(16-12)^2=16
Гость:
Я не так поняла условие.. . Я не так поняла условие.. . По условию, a^2+b^2+c^2=800 или 2с^2=800, c^2=400, с=20. а+b+с=48 илb a+b=28 Тогда (a+b)^2=28^2; a^2+b^2+2ab=784; c^2+2ab=784, 2ab=784-400=384. Найти: (a-b)^2=a^2+b^2-2ab=400-384=16
Гость:
Вот так: a^2+b^2=(a+b)^2-2ab = 800 = 48^2-2ab; -2ab = 800 — 48^2; (a-b)^2 = (a^2+b^2)-2ab = 800+800-48^2 Виноват) Я почему то решил, что речь идет о сумме катетов) ) Значит мое решение относится только к катетам. Прошу не принимать во внимание ((
Стороны прямоугольного треугольника
Стороны фигур
Треугольник, у которого один угол прямой, называется прямоугольным. Сторона, расположенная напротив прямого угла, является гипотенузой, она самая длинная в прямоугольном треугольнике. Остальные две его стороны, образующие прямой угол — катеты. Зная величину обоих катетов, можно вычислить размер гипотенузы по теореме Пифагора:
c2 = a2+b2 ,
где a, b — катеты, с — гипотенуза прямоугольного треугольника.
Отсюда, длина гипотенузы равна корню квадратному из суммы квадратов катетов:
Калькулятор расчета длины стороны прямоугольного треугольника зная катеты
Калькулятор расчета длины стороны прямоугольного треугольника зная катет и гипотенузу
Если известна величина катета и гипотенузы и необходимо найти длину второго катета, преобразуем представленную выше формулу. В результате получаем: квадрат искомого катета будет равен квадрату гипотенузы минус квадрат другого катета. Отсюда, длина катета равна корню квадратному из разности квадрата гипотенузы и квадрата другого катета:
После того, как найдены все стороны треугольника, находим его периметр, как сумму двух катетов и гипотенузы. Площадь треугольника равняется половине произведения катетов.
Теорема Пифагора является основополагающим звеном в Евклидовой геометрии, на котором базируются большая часть всех вытекающих из теоремы Пифагора следствий и других теорем. Выведенная еще в VI веке до нашей эры, теорема связывает стороны прямоугольного треугольника простым уравнением, и имеет множество доказательств, одно из которых объединяет в себе как алгебру, так и геометрию.
Согласно теореме Пифагора, в прямоугольном треугольнике есть катеты a и b – это стороны прилегающие к прямому углу, и сумма их квадратов дает квадрат гипотенузы – третьей стороны треугольника, лежащей напротив прямого угла.
Доказать это можно, построив четыре прямоугольных треугольника так, чтобы на длинном катете каждого из них был расположен короткий катет следующего треугольника, при этом вершины углов совпадают.
Как видно из рисунка, общая фигура представляет собой квадрат со стороной c, являющей одновременно гипотенузой данных треугольников, а площадь этой фигуры равна c2, согласно формуле площади квадрата. Помимо того, что этот квадрат включает в себя четыре прямоугольных треугольника площадью 
, в центре его находится еще один, маленький квадрат. Сторона маленького квадрата равна разности катетов, следовательно, его площадь будет равна квадрату этой разности.
(a-b)2=a2-2ab+b2
Представим площадь большого квадрата в виде суммы площадей маленького квадрата и четырех треугольников по принципу суперпозиции.
Таким образом, площадь квадрата одновременно равна гипотенузе во второй степени и сумме катетов во вторых степенях, что и требовалось доказать.
a2+b2=c2
Теорема Пифагора является основополагающим звеном в Евклидовой геометрии, на котором базируются большая часть всех вытекающих из теоремы Пифагора следствий и других теорем. Выведенная еще в VI веке до нашей эры, теорема связывает стороны прямоугольного треугольника простым уравнением, и имеет множество доказательств, одно из которых объединяет в себе как алгебру, так и геометрию.
Согласно теореме Пифагора, в прямоугольном треугольнике есть катеты a и b – это стороны прилегающие к прямому углу, и сумма их квадратов дает квадрат гипотенузы – третьей стороны треугольника, лежащей напротив прямого угла.
Доказать это можно, построив четыре прямоугольных треугольника так, чтобы на длинном катете каждого из них был расположен короткий катет следующего треугольника, при этом вершины углов совпадают.
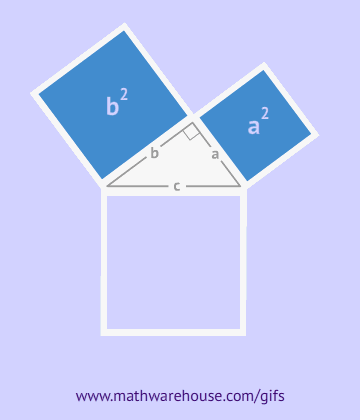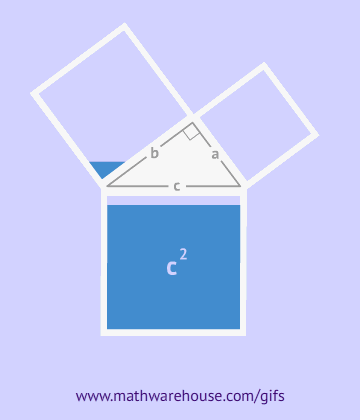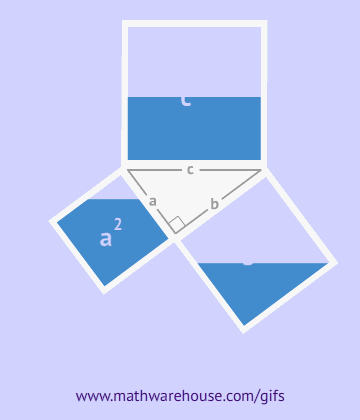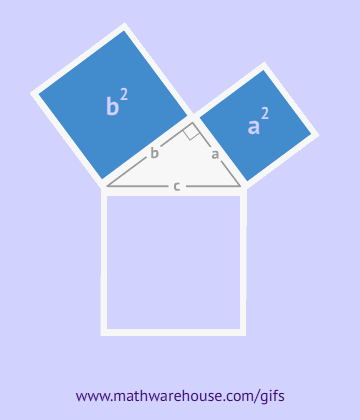
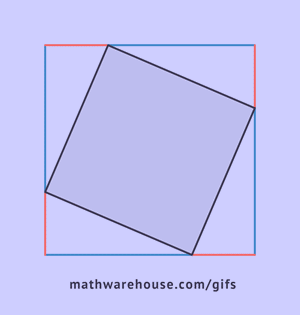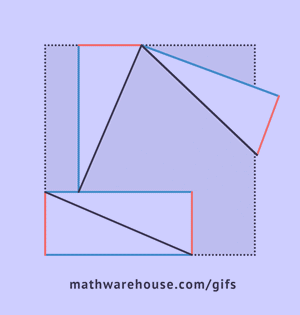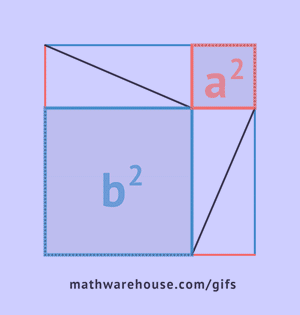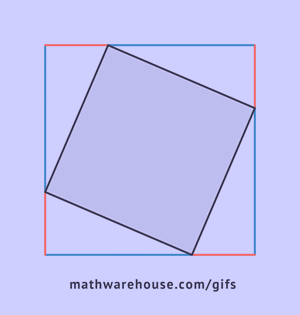
Как видно из рисунка, общая фигура представляет собой квадрат со стороной c, являющей одновременно гипотенузой данных треугольников, а площадь этой фигуры равна c2, согласно формуле площади квадрата. Помимо того, что этот квадрат включает в себя четыре прямоугольных треугольника площадью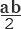 
, в центре его находится еще один, маленький квадрат. Сторона маленького квадрата равна разности катетов, следовательно, его площадь будет равна квадрату этой разности. (a-b)2=a2-2ab+b2
Представим площадь большого квадрата в виде суммы площадей маленького квадрата и четырех треугольников по принципу суперпозиции.
Таким образом, площадь квадрата одновременно равна гипотенузе во второй степени и сумме катетов во вторых степенях, что и требовалось доказать. a2+b2=c2
Рассмотрим формулы, связанные с прямоугольным треугольником.
Сторона, лежащая против прямого угла, называется гипотенузой, две другие стороны — катеты.
1. Соотношения сторон в прямоугольном треугольнике:
2. Любимая теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
3. Если из вершины прямого угла проведена высота (CH), которая делит гипотенузу на отрезки, называемые проекциями катетов на гипотенузу (AH — проекция катета AC, BH — проекция катета CB), имеют место быть формулы:
Квадрат высоты равен произведению проекций катетов на гипотенузу;
Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.
Отсюда вытекает формула:
Все три треугольника окажутся подобными:
Радиусы вписанной и описанной окружностей.
Заметим, что центр описанной окружности всегда лежит на середине гипотенузы, поэтому если провести из вершины прямого угла медиану, она будет равна половине гипотенузы.
Площадь можно вычислить следующими способами:
