Как найти квадрат суммы формула - Исправление недочетов и поиск решений вместе с Examum.ru

Алгебра

7 класс

Урок № 26

Квадрат суммы

Перечень рассматриваемых вопросов:

Алгебраические выражения.
Многочлен.
Формула квадрата суммы.
Разложение многочлена на множители.

Тезаурус:

Формула квадрата суммы:

(а + b)² = а² + 2аb + b²

Квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.

Основная литература:

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

Дополнительная литература:

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Формула квадрата суммы:

(а + b)² = а² + 2аb + b².

Квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа, т. к. а и b можно считать произвольными числами.

Исходя из определения степени, левая часть формулы квадрата суммы – это произведение двух одинаковых многочленов. Применим правило умножения многочлена на многочлен и получим выражение, которое будет совпадать с правой частью формулы квадрата суммы.

(a + b)² = (a + b)(a + b) = a² + ab + ab + b² = a² + 2ab + b².

Будем применять формулу квадрата суммы, при выполнении различных заданий.

Например, преобразуем выражение в многочлен стандартного вида.

(2а + 3с)² = (2а)² + 2·2а·3с + (3с)²= 4а²+ 12ас + 9с².

Эту формулу можно применить для упрощения вычислений.

Например, вычислим 42²= (40 + 2)²= 40²+2·40·2 + 2² = 1600 +160 + 4 = 1764.

Ответ:1764.

Стоит отметить, что если формулу квадрата суммы читать справа налево, то говорят, что представленный многочлен можно разложить на множители, притом на два одинаковых.

а² + 2аb + b² = (а + b)² – разложение на множители.

Представим многочлен в виде квадрата суммы:

25а²+ 10ас + с².

Решение:

25а²+ 10ас + с²= (5а)²+ 2 · 5ас + (с)²= (5а + с) ².

Докажем, что при любом значении с, многочлен 9с²+30с + 25 принимает положительные значения.

Доказательство.

Для доказательства воспользуемся формулой квадрата суммы. Представим многочлен 9с²+ 30с + 25 в виде квадрата суммы.

9с²+ 30с + 25 = (3с + 5)²

Квадрат любого числа всегда принимает положительное значение, поэтому при любом значении с, многочлен 9с²+30с + 25 принимает положительные значения.

Что и требовалось доказать.

Разбор заданий тренировочного модуля.

1. Преобразуйте трёхчлен в квадрат двучлена:

6ас + а²+ 9с².

Решение.

Для начала, переставим первое и второе слагаемое местами. Далее обратим внимание на первое и последнее слагаемое многочлена. Первое слагаемое это квадрат а, третье слагаемое ‑ квадрат выражения 3с. Так как второе слагаемое равно удвоенному произведению выражения 3с и а, то этот трёхчлен можно представить в виде квадрата суммы 3с и а.

6ас + а²+ 9с²= а² +6ас + 9с²= а² + 2 · 3ас + (3с)²= (а + 3с)²

Ответ: (а + 3с)².

2. Представьте выражение в виде многочлена:

с(с + 8х)².

Решение.

Воспользуемся формулой квадрата суммы и правилом умножения одночлена на многочлен.

с(с + 8х)²= с(с² + 2 · 8хс + (8х)²) = с(с² + 16хс + 64х)²= с³ + 16с²х + 6 4х².

Ответ: с³ + 16с²х + 64х².

Источник

Квадрат суммы

Определение.

Квадрат суммы двух выражений равен квадрату первого, плюс удвоенное произведение первого и второго, плюс квадрат второго:

(a + b)² = a² + 2ab + b²

Вывод формулы квадрата суммы

Для доказательства справедливости формулы квадрата суммы достаточно перемножить выражения раскрыв скобки:

(a + b)² = (a + b)·(a + b) = a² + ab + ba + b² = a² + 2ab + b²

Применение формулы квадрата суммы

Формулу квадрата суммы удобно использовать:

для раскрытия скобок
для упрощения выражений
для вычисления квадратов больших чисел, не используя калькулятор или умножение в столбик

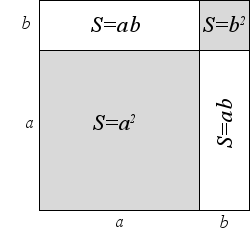
Геометрическая интерпретация

Формулу квадрата суммы двух положительных чисел a и b можно изобразить геометрически

Рассмотрим квадрат со стороной (a + b), его площадь равна (a + b)².

В противоположных углах рассматриваемого квадрата построим квадраты со сторонами a и b.

Тогда большой начальный квадрат, будет разделен на четыре части: два квадрата с площадями a² и b², а также два прямоугольника с площадями равными ab. Тогда получаем, что

(a + b)² = (a + b)·(a + b) = a² + b² + ab+ ab = a² + 2ab + b²

Примеры задач на применение формулы квадрата суммы

Пример 1.

Раскрыть скобки (x + 3)².

Решение:

(x + 3)² = x² + 2·3·x + 3² = x² + 6x + 9

Пример 2.

Раскрыть скобки (2x + 3y²)².

Решение:

(2x + 3y²)² = (2x)² + 2·(2x)·(3y²) + (3y²)² = 4x² + 12xy² + 9y⁴

Пример 3.

Упростить выражение

9x² + 6x + 1(3x + 1)

Решение:

Можно заметить, что выражение в числителе — это разложенный квадрат суммы

9x² + 6x + 1(3x + 1) = (3x + 1)²(3x + 1) = 3x + 1

Заметим, что с помощью формулы квадрата суммы легко находить квадраты больших чисел, не используя калькулятор или умножение в столбик.

Пример 4.

Вычислить 71².

Решение:

71² = (70 + 1)² = 70² + 2·70·1 + 1² = 4900 + 140 + 1 = 5041

Источник

В данной публикации мы рассмотрим одну из формул сокращенного умножения, а именно, квадрат суммы. Также разберем примеры решения задач для закрепления изложенного материала.

Формула квадрата суммы
Доказательство формулы
- Арифметическое
- Геометрическое
Примеры задач

Формула квадрата суммы

Квадрат суммы слагаемых a и b равняется квадрату a плюс удвоенное произведение a и b плюс квадрат b.

(a + b)² = a² + 2ab + b²

Выражение может быть представлено и в обратном порядке:

a² + 2ab + b² = (a + b)²

Доказательство формулы

Арифметическое

Представим формулу в виде произведения двух одинаковых скобок (другими словами, умножим выражение на само себя):
(a+b)(a+b).

Теперь раскроем скобки согласно арифметическим правилам и получаем:
(a+b)(a+b) = a² + ab + ba + b² = a² + 2ab + b².

Геометрическое

Для того, чтобы доказать формулу геометрически, изобразим квадрат, который поделен с помощью двух отрезков на четыре части таким образом, что получились:

два квадрата с разной длиной стороны (a или b);
2 прямоугольника с одинаковой длиной (a) и шириной (b).

Площадь большого квадрата равна (a + b)² и, одновременно, сумме площадей фигур, из которых состоит:

S_кв. = (a + b)² = a² + ab + ab + b² = a² + 2ab + b².

Примеры задач

Задание
Чему равен квадрат суммы (2x + 4y³)²?

Решение
Воспользуемся формулой сокращенного умножения:
(2x + 4y³)² = (2x)² + 2 ⋅ 2x ⋅ 4y³ + (4y³)² = 4x² + 16xy³ + 16y⁶

Примечание:
Формулу можно использовать для быстрых расчетов в уме, например:

63² = (60 + 3)² = 60² + 2 ⋅ 60 ⋅ 3 + 3² = 3600 + 360 + 9 = 3969.
94² = (90 + 4)² = 90² + 2 ⋅ 90 ⋅ 4 + 4² = 8100 + 720 + 16 = 8836.

Источник

Формула квадрата суммы
Формула квадрата разности
Примеры

Формула квадрата суммы

Возведем в квадрат сумму (a+b):

$$ (a+b)^2 = (a+b)(a+b) = a(a+b)+b(a+b) = a^2+ab+ab+b^2 = a^2+2ab+b^2 $$

Мы получили формулу квадрата суммы двух выражений:

$$(a+b)^2 = a^2+2ab+b^2$$

Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого и второго выражения, плюс квадрат второго выражения.

Формула помогает нам избавиться от лишней работы: не перемножать скобки каждый раз и не приводить постоянно подобные, получая из четырёх слагаемых три.

Вместо a и b в формуле могут быть любые одночлены (и даже многочлены), которые нужно подставить. Поэтому в правиле и говорится о «выражениях», а не просто о «переменных». Например:

$$ (5x^2+7y)^2 = (5x^2 )^2+2cdot5x^2cdot7y+(7y)^2 = 25x^2+70x^2 y+49y^2 $$

Геометрическое объяснение

Рассмотрим квадрат со стороной (a+b). Он состоит из двух квадратов и двух прямоугольников. Для площади можем записать: $$ S = (a+b)^2 = a^2+b^2+2ab $$
Откуда $$ (a+b)^2 = a^2+2ab+b^2 $$
И формула квадрата суммы замечательно подтверждается геометрическими соображениями.

Формула квадрата разности

Теперь возведём в квадрат разность:

$$ (a-b)^2 = (a-b)(a-b) = a(a-b)-b(a-b) = a^2-ab-ab+b^2 = a^2-2ab+b^2 $$

Мы получили формулу квадрата разности двух выражений:

$$ (a-b)^2 = a^2-2ab+b^2$$

Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого и второго выражения, плюс квадрат второго выражения.

Геометрическое объяснение

Рассмотрим квадрат со стороной a, в один из углов которого вписан квадрат поменьше со стороной $b lt a$.
Для его площади можем записать: $$a^2 = (a-b)^2+b^2+2(a-b)b$$ Откуда $$(a-b)^2 = a^2-b^2-2(a-b)b = $$ $$a^2-b^2-2ab+2b^2 = a^2-2ab+b^2 $$
И формула квадрата разности также подтверждается геометрией.

Внимание!

Не забывайте о втором слагаемом в формулах квадрата двучленов!

Не путайте знаки «+» и «-» перед слагаемыми!

Неправильно: $(a+b)^2$ ≠ $a^2+b^2 или (a-b)^2 $≠$ a^2-b^2$

Правильно: $(a+b)^2 = a^2+$ 2ab $+b^2 и (a-b)^2 = a^2$ -2ab+$ b^2$

Примеры

Пример 1. Найдите квадрат суммы:

а) $(x+y)^2 = x^2+2xy+y^2$

б) $(3+t)^2 = 3^2+2cdot3t+t^2 = 9+6t+t^2$

в) $(3a+4b)^2 = (3a)^2+2cdot3acdot4b+(4b)^2 = 9a^2+24ab+16b^2$

г) $(4k^2 m+5n)^2 = (4k^2 m)^2+2cdot4k^2 mcdot5n+(5n)^2 = 16k^4 m^2+40k^2 mn+25n^2$

Пример 2. Найдите квадрат разности:

а) $(m-n)^2 = m^2-2mn+n^2$

б) $(x-5)^2 = x^2-2xcdot5+5^2 = x^2-10x+25$

в) $(7y-9z)^2 = (7y)^2-2cdot7ycdot9z+(9z)^2 = 49y^2-126yz+81z^2$

г) $(3km^2-8n^2 )^2 = (3km^2 )^2-2cdot3km^2cdot8n^2+(8n^2 )^2 = 9k^2 m^4-48km^2 n^2+64n^4$

Пример 3. Выполните действия:

а) $(10m-1)^2+20m = (10m)^2-2cdot10mcdot1+1+20m =$

$= 100m^2-20m+1+20m = 100m^2+1 $

б) $36k^2-(1-6k)^2 = 36k^2-(1-2cdot6k+(6k)^2 ) = 36k^2-1+12k-36k^2 = 12k-1 $

в) $4(x-1)-(2x+1)^2 = 4x-4-((2x)^2+2cdot2x+1) = 4x-4-4x^2-4x-1 = -4x^2-5$

г) $ frac{1}{3} (3y+4)^2-8y = frac{1}{3} ((3y)^2+2cdot3ycdot4+4^2 )-8y = frac{1}{3} (9y^2+24y+16)-8y =$

$=3y^2+8y+frac{16}{3}-8y=3y^2+5 frac{1}{3}$

Пример 4. Решите уравнение:

а) $(7-x)^2-(x+8)^2 = 45$

$49-14x+x^2-(x^2+16x+64) = 45 $

49-14x-16x-64 = 45

-30x = 45-49+64

-30x = 60

x = -2

б) $(2x-15)^2-x(4x+3) = 153$

$(2x)^2-2cdot2xcdot15+15^2-4x^2-12x = 153 $

-60x+225-12x = 153

-72x = 153-225

-72x = -72

x = 1

Источник

Чтобы сумму возвести в квадрат, можно к сумме квадратов первого и второго выражений прибавить удвоенное их произведение:

a+b2=a2+2ab+b2

Так как:

a+b2=a+b⋅a+b=a⋅a+a⋅b+b⋅a+b⋅b==a2+ab+ba+b2=a2+2ab+b2.

Пример:

представить квадрат в виде многочлена:

6z+92

Применим формулу квадрата суммы:

6z+92=6z2+2⋅6z⋅9+92=36z2+108z+81

Можно раскрыть квадрат как произведение одинаковых многочленов, но вычисления будут более трудоёмкими:

6z+92=6z+9⋅6z+9=6z⋅6z+6z⋅9+9⋅6z+9⋅9==36z2+54z+54z+81=36z2+108z+81.

Источник