Как найти квадрат суммы одночленов - Исправление недочетов и поиск решений вместе с Examum.ru

Квадрат суммы

Квадрат суммы двух чисел можно искать как произведение двух множителей. Но удобнее один раз вывести формулу и в дальнейшем сумму возводить в квадрат уже с помощью этой формулы.

Формула квадрата суммы двух чисел — одна из формул сокращенного умножения, которые называются так потому, что позволяют сократить вычисления.

Квадрат суммы двух одночленов называют квадратом двучлена.

$[{(a + b)^2} = (a + b)(a + b) = ]$

$[ = {a^2} + ab + ab + {b^2} = {a^2} + 2ab + {b^2}]$

Таким образом, формула квадрата суммы двух чисел —

$[{(a + b)^2} = {a^2} + 2ab + {b^2}]$

Найти квадрат суммы выражений:

$[1){(x + 5)^2};]$

$[2){(3x + 7y)^2};]$

$[3){(2{x^3} + 5{x^7})^2};]$

$[4){(10a + b{c^5})^2}.]$

Решение:

$[1){(x + 5)^2} = ]$

Первое слагаемое — x, второе — 5. Значит, a=x, b=5. Применяем формулу квадрата суммы:

$[ = {x^2} + 2 cdot x cdot 5 + {5^2} = {x^2} + 10x + 25.]$

$[2){(3x + 7y)^2} = ]$

Все, что стоит до знака «+» — это a, все после «+» — b. В данном случае a=3x, b=7y.

На начальном этапе обучения может помочь работе с формулой квадрата двучлена рисунок.

Если выражение, стоящее до знака «+», заключить в квадрат, а выражение после «+» — в круг, то схематически формулу квадрата суммы можно представить так:

Рисунок позволяет наглядно показать, что стоит на месте a и b в каждом конкретном случае.

Применив эту схему к нашему примеру, получим

В традиционной записи возведение в квадрат суммы записывают так:

$[{(3x + 7y)^2} = {(3x)^2} + 2 cdot 3x cdot 7y + {(7y)^2} = ]$

$[ = 9{x^2} + 42xy + 49{y^2};]$

Важно помнить — при возведении в квадрат произведения или степени их обязательно записывать в скобках!

При возведении в квадрат используем свойства степеней.

$[3){(2{x^3} + 5{x^7})^2} = ]$

$[ = {(2{x^3})^2} + 2 cdot 2{x^3} cdot 5{x^7} + {(5{x^7})^2} = ]$

$[ = 4{x^6} + 20{x^{10}} + 25{x^{14}};]$

$[4){(10a + b{c^5})^2} = {(10a)^2} + 2 cdot 10a cdot b{c^5} + {(b{c^5})^2} = ]$

$[ = 100{a^2} + 20ab{c^5} + {b^2}{c^{10}}.]$

Источник

Алгебра

7 класс

Урок № 26

Квадрат суммы

Перечень рассматриваемых вопросов:

Алгебраические выражения.
Многочлен.
Формула квадрата суммы.
Разложение многочлена на множители.

Тезаурус:

Формула квадрата суммы:

(а + b)² = а² + 2аb + b²

Квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.

Основная литература:

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

Дополнительная литература:

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Формула квадрата суммы:

(а + b)² = а² + 2аb + b².

Квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа, т. к. а и b можно считать произвольными числами.

Исходя из определения степени, левая часть формулы квадрата суммы – это произведение двух одинаковых многочленов. Применим правило умножения многочлена на многочлен и получим выражение, которое будет совпадать с правой частью формулы квадрата суммы.

(a + b)² = (a + b)(a + b) = a² + ab + ab + b² = a² + 2ab + b².

Будем применять формулу квадрата суммы, при выполнении различных заданий.

Например, преобразуем выражение в многочлен стандартного вида.

(2а + 3с)² = (2а)² + 2·2а·3с + (3с)²= 4а²+ 12ас + 9с².

Эту формулу можно применить для упрощения вычислений.

Например, вычислим 42²= (40 + 2)²= 40²+2·40·2 + 2² = 1600 +160 + 4 = 1764.

Ответ:1764.

Стоит отметить, что если формулу квадрата суммы читать справа налево, то говорят, что представленный многочлен можно разложить на множители, притом на два одинаковых.

а² + 2аb + b² = (а + b)² – разложение на множители.

Представим многочлен в виде квадрата суммы:

25а²+ 10ас + с².

Решение:

25а²+ 10ас + с²= (5а)²+ 2 · 5ас + (с)²= (5а + с) ².

Докажем, что при любом значении с, многочлен 9с²+30с + 25 принимает положительные значения.

Доказательство.

Для доказательства воспользуемся формулой квадрата суммы. Представим многочлен 9с²+ 30с + 25 в виде квадрата суммы.

9с²+ 30с + 25 = (3с + 5)²

Квадрат любого числа всегда принимает положительное значение, поэтому при любом значении с, многочлен 9с²+30с + 25 принимает положительные значения.

Что и требовалось доказать.

Разбор заданий тренировочного модуля.

1. Преобразуйте трёхчлен в квадрат двучлена:

6ас + а²+ 9с².

Решение.

Для начала, переставим первое и второе слагаемое местами. Далее обратим внимание на первое и последнее слагаемое многочлена. Первое слагаемое это квадрат а, третье слагаемое ‑ квадрат выражения 3с. Так как второе слагаемое равно удвоенному произведению выражения 3с и а, то этот трёхчлен можно представить в виде квадрата суммы 3с и а.

6ас + а²+ 9с²= а² +6ас + 9с²= а² + 2 · 3ас + (3с)²= (а + 3с)²

Ответ: (а + 3с)².

2. Представьте выражение в виде многочлена:

с(с + 8х)².

Решение.

Воспользуемся формулой квадрата суммы и правилом умножения одночлена на многочлен.

с(с + 8х)²= с(с² + 2 · 8хс + (8х)²) = с(с² + 16хс + 64х)²= с³ + 16с²х + 6 4х².

Ответ: с³ + 16с²х + 64х².

Источник

Формула квадрата суммы
Формула квадрата разности
Примеры

Формула квадрата суммы

Возведем в квадрат сумму (a+b):

$$ (a+b)^2 = (a+b)(a+b) = a(a+b)+b(a+b) = a^2+ab+ab+b^2 = a^2+2ab+b^2 $$

Мы получили формулу квадрата суммы двух выражений:

$$(a+b)^2 = a^2+2ab+b^2$$

Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого и второго выражения, плюс квадрат второго выражения.

Формула помогает нам избавиться от лишней работы: не перемножать скобки каждый раз и не приводить постоянно подобные, получая из четырёх слагаемых три.

Вместо a и b в формуле могут быть любые одночлены (и даже многочлены), которые нужно подставить. Поэтому в правиле и говорится о «выражениях», а не просто о «переменных». Например:

$$ (5x^2+7y)^2 = (5x^2 )^2+2cdot5x^2cdot7y+(7y)^2 = 25x^2+70x^2 y+49y^2 $$

Геометрическое объяснение

Рассмотрим квадрат со стороной (a+b). Он состоит из двух квадратов и двух прямоугольников. Для площади можем записать: $$ S = (a+b)^2 = a^2+b^2+2ab $$
Откуда $$ (a+b)^2 = a^2+2ab+b^2 $$
И формула квадрата суммы замечательно подтверждается геометрическими соображениями.

Формула квадрата разности

Теперь возведём в квадрат разность:

$$ (a-b)^2 = (a-b)(a-b) = a(a-b)-b(a-b) = a^2-ab-ab+b^2 = a^2-2ab+b^2 $$

Мы получили формулу квадрата разности двух выражений:

$$ (a-b)^2 = a^2-2ab+b^2$$

Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого и второго выражения, плюс квадрат второго выражения.

Геометрическое объяснение

Рассмотрим квадрат со стороной a, в один из углов которого вписан квадрат поменьше со стороной $b lt a$.
Для его площади можем записать: $$a^2 = (a-b)^2+b^2+2(a-b)b$$ Откуда $$(a-b)^2 = a^2-b^2-2(a-b)b = $$ $$a^2-b^2-2ab+2b^2 = a^2-2ab+b^2 $$
И формула квадрата разности также подтверждается геометрией.

Внимание!

Не забывайте о втором слагаемом в формулах квадрата двучленов!

Не путайте знаки «+» и «-» перед слагаемыми!

Неправильно: $(a+b)^2$ ≠ $a^2+b^2 или (a-b)^2 $≠$ a^2-b^2$

Правильно: $(a+b)^2 = a^2+$ 2ab $+b^2 и (a-b)^2 = a^2$ -2ab+$ b^2$

Примеры

Пример 1. Найдите квадрат суммы:

а) $(x+y)^2 = x^2+2xy+y^2$

б) $(3+t)^2 = 3^2+2cdot3t+t^2 = 9+6t+t^2$

в) $(3a+4b)^2 = (3a)^2+2cdot3acdot4b+(4b)^2 = 9a^2+24ab+16b^2$

г) $(4k^2 m+5n)^2 = (4k^2 m)^2+2cdot4k^2 mcdot5n+(5n)^2 = 16k^4 m^2+40k^2 mn+25n^2$

Пример 2. Найдите квадрат разности:

а) $(m-n)^2 = m^2-2mn+n^2$

б) $(x-5)^2 = x^2-2xcdot5+5^2 = x^2-10x+25$

в) $(7y-9z)^2 = (7y)^2-2cdot7ycdot9z+(9z)^2 = 49y^2-126yz+81z^2$

г) $(3km^2-8n^2 )^2 = (3km^2 )^2-2cdot3km^2cdot8n^2+(8n^2 )^2 = 9k^2 m^4-48km^2 n^2+64n^4$

Пример 3. Выполните действия:

а) $(10m-1)^2+20m = (10m)^2-2cdot10mcdot1+1+20m =$

$= 100m^2-20m+1+20m = 100m^2+1 $

б) $36k^2-(1-6k)^2 = 36k^2-(1-2cdot6k+(6k)^2 ) = 36k^2-1+12k-36k^2 = 12k-1 $

в) $4(x-1)-(2x+1)^2 = 4x-4-((2x)^2+2cdot2x+1) = 4x-4-4x^2-4x-1 = -4x^2-5$

г) $ frac{1}{3} (3y+4)^2-8y = frac{1}{3} ((3y)^2+2cdot3ycdot4+4^2 )-8y = frac{1}{3} (9y^2+24y+16)-8y =$

$=3y^2+8y+frac{16}{3}-8y=3y^2+5 frac{1}{3}$

Пример 4. Решите уравнение:

а) $(7-x)^2-(x+8)^2 = 45$

$49-14x+x^2-(x^2+16x+64) = 45 $

49-14x-16x-64 = 45

-30x = 45-49+64

-30x = 60

x = -2

б) $(2x-15)^2-x(4x+3) = 153$

$(2x)^2-2cdot2xcdot15+15^2-4x^2-12x = 153 $

-60x+225-12x = 153

-72x = 153-225

-72x = -72

x = 1

Источник

Ирина Алексеевна Антоненко

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Бином Ньютона

Одними из основных формул сокращенного умножения является формулы квадрата суммы и квадрата разности двух одночленов.

Данные формулы можно вывести с помощью Бинома Ньютона.

Формула бинома Ньютона для натуральных чисел имеет следующий вид:

Здесь $C^0_n, C^1_n,dots ,C^{n-1}_n,C^n_n$ — коэффициенты Бинома Ньютона.

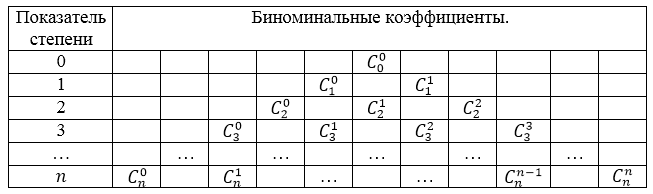
Коэффициенты разложения Бинома Ньютона можно находить с помощью треугольника Паскаля.

Треугольник Паскаля имеет следующую структуру (рис. 1).

Рисунок 1. Структура треугольника Паскаля

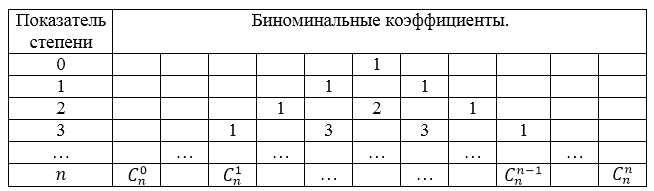
Значения коэффициентов треугольника паскаля приведены в следующей таблице (рис. 2):

Рисунок 2. Коэффициенты треугольника Паскаля

Формула квадрата суммы

Выведем с использованием формулы Бинома Ньютона формулу квадрата суммы ${(a+b)}^2$. Из формулы Бинома Ньютона получаем:

Используя таблицу 2, получим:

Таким образом, квадрат суммы двух выражений равен сумме квадрата первого выражения с удвоенным произведением первого выражения на второе и квадратом второго выражения:

Пример 1: возвести в квадрат $(2x+3y)$

Используя формулу квадрата суммы, получим:

Замечание

!!! Здесь стоит обратить особое внимание, что формулу надо применяя к одночленам, входящим в сумму, целиком. Типичной ошибкой в данном случае бывает то, что зачастую в квадрат возводят только часть одночлена (к примеру, возводят не $2x$ целиком, а только $x$, что является ошибкой!!!)

«Квадрат суммы и квадрат разности» 👇

Формула квадрата разности

Найдем теперь формулу разности суммы. Для этого вначале представим выражение в следующем виде:

Воспользуемся формулой Бинома Ньютона:

Используя таблицу 2, получим:

Таким образом, квадрат разности двух выражений равен сумме квадрата первого выражения с квадратом второго выражения без удвоенного произведения первого выражения на второе:

Примеры задач на использование формул квадрата суммы и разности

Пример 1

Выполнить возведение в квадрат:

а) ${(-9a+4b)}^2$

б) ${(-8a-5b)}^2$

в) ${(x^2-7)}^2$

Решение:

а) ${(-9a+4b)}^2$

Поменяем одночлены, стоящие в скобке, местами:

[{(-9a+4b)}^2={(4b-9a)}^2]

Воспользуемся формулой квадрата разности:

[{(4b-9a)}^2={(4b)}^2-2cdot 4bcdot 9a+{(9a)}^2={16b}^2-72ab+{81a}^2]

б) ${(-8a-5b)}^2$

Так как квадрат всегда положительное число, то получим:

[{(-8a-5b)}^2={(8a+5b)}^2]

Воспользуемся формулой квадрата суммы:

[{(8a+5b)}^2={(8a)}^2+2cdot 5bcdot 8a+{(5b)}^2={64a}^2+80ab+{25b}^2]

в) ${(x^2-7)}^2$

Воспользуемся формулой квадрата разности:

[{(x^2-7)}^2={(x^2)}^2-2cdot x^2cdot 7+7^2=x^4-14x^2+49]

Пример 2

Представить в виде квадрата:

а) $4a^2+12a+9$

б) $x^2-20xy^2+100y^4$

Решение:

а) $4a^2+12a+9$

Воспользуемся формулой квадрата суммы:

[4a^2+12a+9={(2a)}^2+2cdot 2acdot 3+3^2=(2a+3)^2]

б) $x^2-20xy^2+100y^4$

Воспользуемся формулой квадрата разности:

[x^2-20xy^2+100y^4=x^2-2cdot xcdot 10y^2+{(10y)}^2=(x-10y)^2]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Цели: формирование знаний о формулах
сокращённого умножения и их применении; развитие
умений сравнивать, сопоставлять, обобщать,
выявлять закономерности; показ тесной связи
математики с другими науками.

ХОД УРОКА

1. Беседа – подготовка к восприятию
нового материала

Вступительное слово учителя. На
протяжении нескольких последующих уроков мы с
вами будем говорить о формулах сокращённого
умножения. Как вы понимаете, что такое формулы,
для чего они нужны и где вы с ними уже
встречались. Приведите примеры формул и докажите
вышесказанное вами.
Подводя итоги сказанного вами, можно
сформулировать следующее определение.
Формула – это равенство, содержащее некоторое
утверждение, записанное с помощью
математических символов.
Чтобы работать с формулой, что нужно о ней знать,
уметь делать?

Гимн формуле

Формулы всюду – в космосе, в небе,
К Северу, в Африку с ними плыви.
Даже в кино есть такое названье,
Как в алгебре, помните?
«Формула любви».

В физике, химии-формулы,
Нам их не сосчитать.
Алгебра нам поможет
Формулы изучать!

Надо уметь составить!
Надо уметь доказать!
Надо её использовать,
Ну а короче, – знать!

И.Кушнир, Л.Финкельштейн [1, с.30]

– А как вы думаете, что такое формулы
сокращённого умножения и для чего они нужны?
– Попробуйте сами сформулировать цели и задачи
сегодняшнего урока. Чему мы будем учиться?

2. Устная работа

Как прочитать выражение

Выражение чтоб прочитать,
Надо действия в нём сосчитать.
Ты последнее нам называй,
А потом выраженье читай!

В.Чучуков [1, с.29]

А как прочитать выражение? Скажите прозой,
своими словами как вы понимаете, что написано в
этом стихотворении.

Задание 1.(Приложение
1, слайд 2) Прочитайте выражение:

ab, 2ab, a² + b², (x + y)², x² – y²,
(m – k)², 3cd.

Выражения можно читать, а можно и …записывать.
Выполняя оба эти действия, мы занимаемся
переводом с математического языка на русский и
наоборот. То есть, играем в переводчиков.
Поиграем ещё.

Задание 2. Запишите в виде выражения
(два ученика пишут на обороте доски, остальные в
своих тетрадях):

а) сумму 3n и a
б) квадрат а
в) квадрат 3n
г) удвоенную разность 3n и а
д) удвоенное произведение 3n и а
е) квадрат суммы а и 3n
ж) сумму квадратов а и 3n
з) квадрат разности а и 3n
и) разность квадратов а и 3n.

Проверяем ваши записи. (Приложение
1, слайд 3) Если есть ошибки,
постарайтесь сами объяснить их причину и больше
не допускать их. Кто справился без ошибок? Значит,
вы молодцы. На слайде №3 по щелчку мыши
появляется слово «Молодцы!».

3. Переход к изучению нового материала

Задание 3.(Приложение
1, слайд 4) Выполните последовательно
указанные задания. (Задания, записанные слева,
предлагается выполнить ученику на доске,
объясняя правило умножения одночленов. Задания,
записанные справа, учащиеся выполняют
самостоятельно.)

1) Запишите на математическом языке:

Квадрат суммы чисел m и
n.
Квадрат суммы чисел p и q.

2) Преобразуйте полученное выражение, используя
определение степени. Выполните умножение и
приведите подобные слагаемые.

3) Запишите итог предыдущего задания:

(m + n)²
=
(p + q)² =

Не выполняя промежуточных действий,
представьте выражение (a + b)² в виде
многочлена стандартного вида. Один ученик
записывает её на доске: (a + b)² = a² + 2ab + b².

Задание 4.(Приложение
1, слайд 5) Выполните последовательно
указанные задания. (Задание может быть выполнено
самостоятельно, либо по аналогии с заданием 3).

1) Запишите на математическом языке:

Квадрат разности чисел m и
n.
Квадрат разности чисел p и q.

3) Запишите итог предыдущего задания:

(m – n)²
=
(p – q)² =

Не выполняя промежуточных действий,
представьте выражение (a – b)² в виде
многочлена стандартного вида.

После короткой паузы на слайде №6
демонстрируются обе формулы.

(a + b)² = a² + 2ab + b²
(a – b)² = a² – 2ab + b²

Найдите общее и отличие в этих формулах. Обе эти
формула можно объединить в одну. По щелчку мыши
появляется на том же слайде общая формула: (a ± b)²
= a² ± 2ab + b².

4. Объяснение нового материала

– Прочитайте левую часть полученного
равенства. Прочитайте правую часть полученного
равенства. (Приложение 1,
слайд 7, а затем 8).
– Можно ли назвать это равенство формулой? А
формулой сокращённого умножения и почему? Как бы
вы назвали эту формулу? По щелчку мыши на том же
слайде появляется её верное название.
Попробуйте её прочитать. Сравните свою
формулировку с текстом в учебнике. Читаем вслух,
а на слайде №7 и №8 последовательно
появляется текст по щелчку мыши.

Задание 5. Соедините стрелками
предложения с соответствующими слагаемыми по
образцу (Приложение 1,
слайды №№9-11).

Проиллюстрируем полученные формулы, используя
геометрию. Найдём площади квадратов со сторонами
(a + b) и (a – b).
Появляется слайд №12, а за ним и №13. Правая часть
формул на них появляется по щелчку мыши.

5. Первичное осмысление нового материала

Следующее задание учащиеся выполняют на
листочках.

Задание 6. Заполните пропуски:

а) (а – ____)² =______… _______ + 81;
б) (_____+8)² = с² + _____…_______;
в) (______…_______)² = 25m² – ________ + 16p²;
г) (______…5х)² = 4р² + _______…_______.

Дополнительные задания для тех, кто
справился быстрее других:

1) Придумайте свой аналогичный пример.
2) Придумайте такой пример, чтобы пропущенные
символы невозможно было вставить. Как называются
такие задания? (Некорректные).

Задание 7. Преобразуйте квадрат
двучлена в многочлен стандартного вида:

(a – b)² =
(b – a)² =
(a + b)² =
(– a + b)² =
(– a + b)² =

Запишите, квадраты каких двучленов равны и
объясните почему?

6. Закрепление изученного материала

Задания из задачника [2]: №6аб, №7аб, №14а, №15а,
№18аб, №19аб.

Задание 8. (Задание исследовательского
характера для самостоятельной работы). Вычислите
по вариантам: 352 и 652; 552 и 752. Поменяйтесь
тетрадями с соседом. Что вы заметили? Попробуйте
сформулировать правило возведения в квадрат
числа, оканчивающегося цифрой 5. Чтобы…, надо
число его десятков умножить на число, большее его
на 1 и к полученному произведению приписать 25.

7. Итог урока

1. Каким общим названием объединены
формулы, с которыми вы сегодня познакомились?
2. Запишите по памяти и сформулируйте формулы
квадрата суммы и квадрата разности.
3. Учитель читает стихотворение с помощью
учащихся, которые заканчивают строку подходящей
рифмой. В это время на слайде №14 постепенно
появляется формула (a + b)² = a² + 2ab + b²

О формуле (а + b)²

Думаем, что очень будет кстати
Нам поговорить об a плюс b в квадрате.
Потому что, скажем вам открыто,
Эта формула особо знаменита.

Её учили столько лет назад,
Что знал её ещё наш петикантроп-брат.
Итак, начнём учить, ребята.
Всё начинается с квадрата.

Чтоб дело быстро шло –
В квадрат возводим первое число,
И здесь, конечно, будет кстати,
Сказать, что записали а в квадрате. Щелчок
мыши.

Не только чтоб продлить стихотворенье,
Прибавим к а произведенье
Трёх чисел: 2 и букв а,b, Щелчок мыши.
Да, тех, которые сидели на трубе.

А эти в алгебре, ни на какой трубе.
Зовут удвоенным произведением аb.
И лишь тогда получим результат,
Когда прибавится ещё один квадрат.

И третий раз всё будет кстати –
Прибавим просто bв квадрате. Щелчок мыши.
И в заключении три слова:
Наша формула готова!
(а + b)² = а² + 2аb + b².

И.Кушнир, Л.Финкельштейн [1, с.33]

8. Домашнее задание на слайде №14
появляется по щелчку мыши:

§28, выучить формулы [3]
№13, №14б, №15б, №18вг. [2]

Список литературы:

1. Математика в стихах. Задачи, сказки,
рифмованные правила. 5-11 классы.
Автор-составитель О.В.Панишева.– Волгоград:
Учитель, 2009. с.29, 30,33.
2. Алгебра, 7. Часть 2. Задачник. Под редакцией
А.Г.Мордковича. – Москва: Мнемозина, 2014. с.127.
3. Алгебра, 7. Часть 2. Учебник. Под редакцией
А.Г.Мордковича. – Москва: Мнемозина, 2014. с.113-115.

Источник