Rafail
[136K]
8 лет назад
Специальной формулы не существует. Иногда можно воспользоваться формулой квадрата суммы или квадрата разности. Например 206^2=(200+6)^2=200^2+2*200*6+6^2=40000+2400+36=42436,
197^2=(200-3)^2=200^2-2*200*3+3^2=40000-1200+9=38809.
Ну а в общем случае воспользуйтесь формулой квадрата суммы трех чисел:
(а+b+c)^2=a^2+b^2+c^2+2*(a*b+a*c+b*c).
Например 362^2=300^2+60^2+2^2+2*(300*60+300*2+60*2)=
=90000+3600+4+2*(18000+600+120)=93604+37440=131044
автор вопроса выбрал этот ответ лучшим
комментировать
в избранное
ссылка
отблагодарить

В этом уроке разобраны методики и алгоритмы, позволяющие научиться этому навыку.
Квадрат суммы и квадрат разности
Одним из самых простых способов возведения двузначных чисел в квадрат является методика, основанная на использовании формул квадрата суммы и квадрата разности:
Для использования этого метода необходимо разложить двузначное число на сумму числа кратного 10 и числа меньше 10. Например:
- 372 = (30+7)2 = 302 + 2*30*7 + 72 = 900+420+49 = 1 369
- 942 = (90+4)2 = 902 + 2*90*4 + 42 = 8100+720+16 = 8 836
Практически все методики возведения в квадрат (которые описаны ниже) основываются на формулах квадрата суммы и квадрата разности. Эти формулы позволили выделить ряд алгоритмов упрощающих возведение в квадрат в некоторых частных случаях.
Квадрат близкий к известному квадрату
Если число, возводимое в квадрат, находится близко к числу, квадрат которого мы знаем, можно использовать одну из четырех методик для упрощенного счета в уме:
На 1 больше:
Методика: к квадрату числа на единицу меньше прибавляем само число и число на единицу меньше.
- 312 = 302 + 31 + 30 = 961
- 162 = 152 + 15 + 16 = 225 + 31 = 256
На 1 меньше:
Методика: из квадрата числа на единицу больше вычитаем само число и число на единицу больше.
- 192 = 202 – 19 – 20 = 400 – 39 = 361
- 242 = 252 – 24 – 25 = 625 – 25 – 24 = 576
На 2 больше
Методика: к квадрату числа на 2 меньше прибавляем удвоенную сумму самого числа и числа на 2 меньше.
- 222 = 202 + 2*(20+22) = 400 + 84 = 484
- 272 = 252 + 2*(25+27) = 625 + 104 = 729
На 2 меньше
Методика: из квадрата числа на 2 больше вычитаем удвоенную сумму самого числа и числа на 2 больше.
- 482 = 502 – 2*(50+48) = 2500 – 196 = 2 304
- 982 = 1002 – 2*(100+98) = 10 000 – 396 = 9 604
Все эти методики можно легко доказать, выведя алгоритмы из формул квадрата суммы и квадрата разности (о которых сказано выше).
Квадрат чисел, заканчивающихся на 5
Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу приписываем 25.
- 152 = (1*(1+1)) 25 = 225
- 252 = (2*(2+1)) 25 = 625
- 852 = (8*(8+1)) 25 = 7 225
Это верно и для более сложных примеров:
- 1552 = (15*(15+1)) 25 = (15*16)25 = 24 025
Квадрат чисел близких к 50
Посмотрите работу алгоритма на примерах:
- 442 = (25-6)*100 + 62 = 1900 + 36 = 1936
- 532 = (25+3)*100 + 32 = 2800 + 9 = 2809
Квадрат трехзначных чисел
Возведение в квадрат трехзначных чисел может быть осуществлено при помощи одной из формул сокращенного умножения:
Нельзя сказать, что этот способ является удобным для устного счета, но в особо сложных случаях его можно взять на вооружение:
4362 = (400+30+6)2= 4002 + 302 + 62 + 2*400*30 + 2*400*6 + 2*30*6 = 160 000 + 900 + 36 + 24 000 + 4 800 + 360 = 190 096
Тренировка
Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.
Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.
|
0 / 0 / 0 Регистрация: 20.11.2015 Сообщений: 65 |
|
|
1 |
|
Квадрат трехзначного числа оканчивается тремя цифрами, равными этому числу20.11.2015, 20:09. Показов 10773. Ответов 2
Задача :»Квадрат трехзначного числа оканчивается тремя цифрами, равными этому числу. Найдите и выведите все такие числа.»
0 |
|
vint-81 охотник 1011 / 535 / 650 Регистрация: 29.09.2014 Сообщений: 1,083 |
||||
|
20.11.2015, 20:38 |
2 |
|||
|
Решение
1 |
|
ФедосеевПавел Модератор 8316 / 4215 / 1602 Регистрация: 01.02.2015 Сообщений: 13,118 Записей в блоге: 4 |
||||
|
20.11.2015, 20:51 |
3 |
|||
|
Или
Добавлено через 45 секунд
2 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
20.11.2015, 20:51 |
|
Помогаю со студенческими работами здесь Квадрат трехзначного числа оканчивается тремя цифрами, которое как раз составляют это число. Напишите программу поиска этих чисел Напишите программу поиска трехзначных чисел, таких, что сумма трех цифр на которые оканчивается квадрат этого числа, равняется этому числу. [КуМир] Программа поиска трехзначных чисел, квадрат которых оканчивается тремя цифрами, составляющих исходное ч
Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 3 |
{(АС5)2} Возведение в квадрат трехзначных чисел, оканчивающихся на цифру 5.
Мы уже знаем, что (АС5)2 можно найти как (АС)*-(АС + 1) * 100 + 25. При нахождении квадрата трехзначных чисел по этому правилу требуется перемножение двузначных чисел, что может оказаться затруднительно. Для такого случая приводим формулу, еще более упрощающую процесс вычислений:
(АС5)2 = (А * 10 + С5:5) * А * 1000 + (С5)2,
где С — число десятков, а А — цифры слева от него.
Пример:
4252 = (4*10 + 25:5)*4*1000+252 =45*4*1000 + 625 = 180625;
1452 = (10 + 45:5)*1*1000 + 452 = 19*1000 + 2025 = 21025.
Обоснование:
(a*100+b*10+5)2=[a*10+(b*10+5):5]*а*1000 + (b*10 + 5)2 = (а*100)2 + + (Ь*10 + 5)*(а*100)*2 + (Ь*10 + 5)2 = (а*100 + Ь*10 + 5)2.

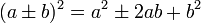
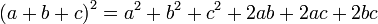

 Сообщение было отмечено Pascal1234 как решение
Сообщение было отмечено Pascal1234 как решение