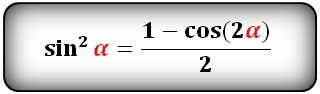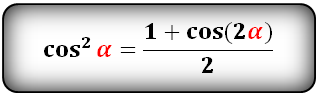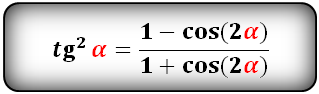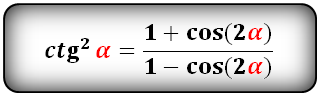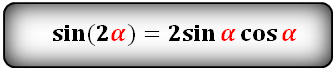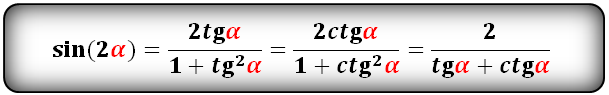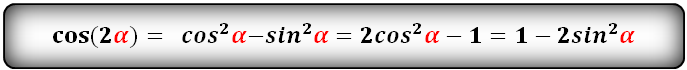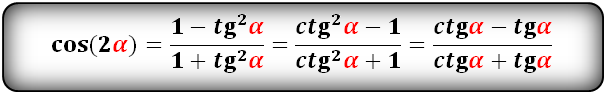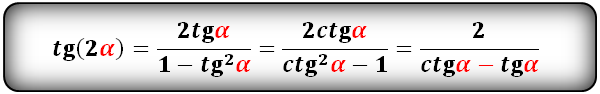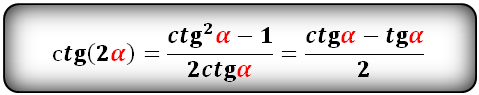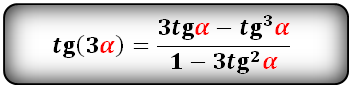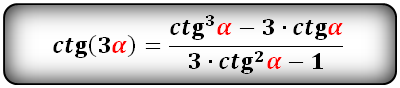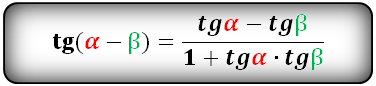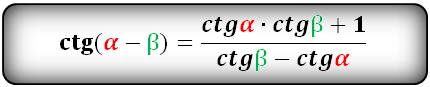Как найти квадрат тригонометрической функции

to continue to Google Sites

Not your computer? Use Guest mode to sign in privately. Learn more

Источник
Формулы квадратов тригонометрических функций

$$sin^2x= frac{1-cos2x}{2}$$

$$cos^2x= frac{1+cos2x}{2}$$

$$tg^2x= frac{1-cos2x}{1+cos2x}$$

$$ctg^2x= frac{1+cos2x}{1-cos2x}$$

$$sin^2 frac{x}{2}= frac{1-cosx}{2}$$

$$cos^2 frac{x}{2}= frac{1+cosx}{2}$$

$$tg^2 frac{x}{2}= frac{1-cosx}{1+cosx}$$

$$ctg^2 frac{x}{2}= frac{1+cosx}{1-cosx}$$

Источник

п.1. Решение простейших тригонометрических уравнений

Про аркфункции (обратные тригонометрические функции) и их свойства – см. §9-11 данного справочника.
Обобщим результаты решения простейших уравнений, полученные в этих параграфах.

Уравнение ОДЗ Решение
$$ sinx=a $$ $$ -1leq aleq 1 $$ begin{gather*} x=(-1)^k arcsin a+pi kLeftrightarrow\ Leftrightarrow left[ begin{array} {l l} x_1=arcsin a+2pi k\ x_2=pi-arcsin a+2pi k end{array} right. end{gather*}
$$ cosx=a $$ $$ -1leq aleq 1 $$ begin{gather*} x=pm arccos a+2pi k end{gather*}
$$ tgx=a $$ $$ ainmathbb{R} $$ begin{gather*} x=arctga+pi k end{gather*}
$$ ctgx=a $$ $$ ainmathbb{R} $$ begin{gather*} x=arcctga+pi kLeftrightarrow\ Leftrightarrow x=arctgfrac1a+pi k end{gather*}

Частные случаи, для которых запись результата отличается от общей формулы:

a=0 a=-1 a=1
$$ sinx=a $$ $$ x=pi k $$ $$ -fracpi2+2pi k $$ $$ fracpi2+2pi k $$
$$ cosx=a $$ $$ x=fracpi2+pi k $$ begin{gather*} pi+2pi k end{gather*} begin{gather*} 2pi k end{gather*}

Например:

п.2. Решение уравнений с квадратом тригонометрической функции

К простейшим также можно отнести уравнения вида:

Уравнение ОДЗ Решение
$$ sin^2x=a $$ $$ 0leq aleq 1 $$ begin{gather*} x=pm arcsinsqrt{a}+pi k end{gather*}
$$ cos^2x=a $$ $$ 0leq aleq 1 $$ begin{gather*} x=pm arccossqrt{a}+pi k end{gather*}
$$ tg^2x=a $$ $$ ageq 0 $$ begin{gather*} x=pm arctgsqrt{a}+pi k end{gather*}
$$ ctg^2x=a $$ $$ ageq 0 $$ begin{gather*} x=pm arcctgsqrt{a}+pi k end{gather*}

Например:

п.3. Различные формы записи решений

Как известно, в тригонометрии все функции связаны между собой базовыми отношениями (см. §12 данного справочника). Если нам известна одна из функций, мы можем без труда найти все остальные. Преобразования в уравнениях приводят к тому, что решение может быть записано через любую из этих функций.
Кроме того, понижение степени или универсальная подстановка (см. §15 данного справочника) приводят к увеличению или уменьшению исходного угла в 2 раза, и ответ может оказаться очень непохожим на решения, полученные другими способами для того же уравнения.

Например:

Различные формы записи решений Решим уравнение (sin^2x=0,64)
Для квадрата синуса решение имеет вид: begin{gather*} x=pm arcsinsqrt{0,64}+pi k=\ =pm arcsin0,8+pi k end{gather*} На числовой окружности этому решению соответствуют 4 базовых точки, которые можно представить по-разному: begin{gather*} x=pm arcsin0,8+pi k=\ =pm arccos0,6+pi k=\ =pm arctgfrac43+pi k end{gather*}

Если решать уравнение с помощью формулы понижения степени, получаем: begin{gather*} sin^2x=frac{1-cos2x}{2}=0,64Rightarrow 1-cos2x=1,28Rightarrow cos2x=-0,28Rightarrow\ Rightarrow 2x=pm arccos(-0,28)+2pi kRightarrow x=pmfrac12 arccos(-0,28)+pi k end{gather*} Если же решать уравнение с помощью универсальной подстановки: begin{gather*} sin^2x=left(frac{2tgfrac{x}{2}}{1+tg^2frac{x}{2}}right)^2=0,64Rightarrowfrac{2tgfrac{x}{2}}{1+tg^2frac{x}{2}}=pm 0,8Rightarrow 1+tg^2frac{x}{2}=pm 2,5tgfrac{x}{2}Rightarrow\ left[ begin{array}{l l} tg^2frac{x}{2}+2,5tgfrac{x}{2}+1=0\ tg^2frac{x}{2}-2,5tgfrac{x}{2}+1=0 end{array} right. Rightarrow left[ begin{array}{l l} left(tgfrac{x}{2}+2right)left(tgfrac{x}{2}+frac12right)=0\ left(tgfrac{x}{2}-2right)left(tgfrac{x}{2}-frac12right)=0 end{array} right. Rightarrow left[ begin{array}{l l} tgfrac{x}{2}=pm 2\ tgfrac{x}{2}=pmfrac12 end{array} right. Rightarrow\ Rightarrow left[ begin{array}{l l} x=pm arctg2+2pi k\ x=pm 2arctgfrac12+2pi k end{array} right. end{gather*} Таким образом, решая одно и то же уравнение, мы получаем очень разные по виду ответы. Однако, при проверке, все полученные множества решений совпадают.

Внимание!
При решении тригонометрических уравнений разными способами полученные ответы могут значительно отличаться по виду, но при этом они описывают одно и то же множество решений, т.е. являются равносильными.

п.4. Примеры

Пример 1. Решите уравнение обычным способом и с помощью универсальной подстановки. Сравните полученные ответы и множества решений. Сделайте вывод.
a) (sin x=frac{sqrt{3}}{2})

Пример 1a Обычный способ: begin{gather*} x=(-1)^k arcsinfrac{sqrt{3}}{2}+pi k=(-1)^kfracpi3 +pi k Leftrightarrow\ Leftrightarrow left[ begin{array}{l l} x=fracpi3+2pi k\ x=frac{2pi}{3}+2pi k end{array} right. end{gather*} 2 базовых точки на числовой окружности.

Универсальная подстановка: begin{gather*} sinx=frac{2tgfrac{x}{2}}{1+tg^2frac{x}{2}}Rightarrow 1+tg^2frac{x}{2}=frac{2tgfrac{x}{2}}{sqrt{3}/2}Rightarrow tg^2frac{x}{2}-frac{4}{sqrt{3}}tgfrac{x}{2}+1=0\ D=left(-frac{4}{sqrt{3}}right)^2-4=frac{16}{3}-4=frac43, tgfrac{x}{2}=frac{frac{4}{sqrt{3}}pmfrac{2}{sqrt{3}}}{2}Rightarrow left[ begin{array}{l l} tgfrac{x}{2}=frac{1}{sqrt{3}}\ tgfrac{x}{2}=sqrt{3} end{array} right. \ left[ begin{array}{l l} frac{x}{2}=fracpi6+pi k\ frac{x}{2}=fracpi3+pi k end{array} right. Rightarrow left[ begin{array}{l l} x=fracpi3+2pi k\ x=frac{2pi}{3}+2pi k end{array} right. Leftrightarrow x=(-1)^kfracpi3+pi k end{gather*} Ответы и множества решений совпадают.
Ответ: ((-1)^kfracpi3+pi k)

б) (cos2x=frac12)

Пример 1б Обычный способ: begin{gather*} 2x=pm arccosfrac12+2pi kRightarrow\ x=pmfrac12left(arccosfrac12+2pi kright)=\ =pmfrac12cdotfracpi3+pi k=pmfracpi6+pi k end{gather*} 4 базовых точки на числовой окружности.

Универсальная подстановка: begin{gather*} cos2x=frac{1-tg^2x}{1+tg^2x}=frac12Rightarrow 2(1-tg^2x)=1+tg^2xRightarrow 3tg^2x=1Rightarrow tgx=pmfrac{1}{sqrt{3}}\ x=pmfracpi6+pi k end{gather*} Ответы и множества решений совпадают.
Ответ: (pmfracpi6+pi k)

в) (sinleft(frac{x}{2}+fracpi3right)=1)
Обычный способ: begin{gather*} frac{x}{2}+fracpi3=fracpi2+2pi kRightarrow frac{x}{2}=fracpi2-fracpi3+2pi k=fracpi6+2pi kRightarrow x=fracpi 3+4pi k end{gather*} Одна базовая точка на числовой окружности с периодом (4pi).
Универсальная подстановка: begin{gather*} sinleft(frac{x}{2}+fracpi3right)=frac{2tgfrac{frac{x}{2}+fracpi3}{2}}{1+tg^2frac{frac{x}{2}+fracpi3}{2}}=1Rightarrow tg^2left(frac{x}{4}+fracpi6right)-2tgleft(frac{x}{4}+fracpi6right)-2tgleft(frac{x}{4}+fracpi6right)+1=0Rightarrow\ left(tgleft(frac{x}{4}+fracpi6right)-1right)^2=0Rightarrow tgleft(frac{x}{4}+fracpi6right)=1Rightarrow frac{x}{4}+fracpi6=frac{pi}{4}+pi kRightarrow\ Rightarrow frac{x}{4}=fracpi4-fracpi6+pi kRightarrow frac{x}{4}=frac{pi}{12}+pi kRightarrow x=fracpi3+4pi k end{gather*} Ответы и множества решений совпадают.
Ответ: (fracpi3+4pi k)

г*) (tgleft(3x+fracpi3right)=0)
Обычный способ: begin{gather*} 3x+fracpi3=arctg0+pi k=pi kRightarrow 3x=-fracpi3+pi kRightarrow x=-fracpi9+frac{pi k}{3} end{gather*} Универсальная подстановка: begin{gather*} tgleft(3x+fracpi3right)=frac{2tgfrac{3x+fracpi3}{2}}{1-tg^2frac{3x+fracpi3}{2}}=0Rightarrow tgfrac{3x+fracpi3}{2}=0Rightarrowfrac{3x+fracpi3}{2}=pi kRightarrow\ Rightarrow 3x+fracpi3=2pi k=3x=-fracpi3+2pi kRightarrow=-fracpi9+frac{2pi}{3} end{gather*} При использовании универсальной подстановки потеряна половина корней (период увеличился в 2 раза). Это связано с тем, что мы отбросили еще одно решение: (tgfrac{3x+fracpi3}{2}rightarrowinfty) — значение тангенса у асимптот. Действительно, в этом случае дробь стремится к 0, что удовлетворяет уравнению. Получаем: begin{gather*} frac{3x+fracpi3}{2}=fracpi2+pi kRightarrow 3x+fracpi3=pi+2pi kRightarrow 3x=frac{2pi}{3}+2pi kRightarrow x=frac{2pi}{9}+frac{2pi k}{3} end{gather*} Таким образом, мы получили два семейства решений: begin{gather*} left[ begin{array}{l l} x=-fracpi9+frac{2pi k}{3}\ x=frac{2pi}{9}+frac{2pi}{3} end{array} right. end{gather*} Представим последовательности решений в градусах, подставляя возрастающие значения (k): begin{gather*} left[ begin{array}{l l} x=-20^{circ}+120^{circ}k=left{…,-20^{circ},100^{circ},220^{circ},…right}\ x=40^{circ}+120^{circ}k=left{…,40^{circ},160^{circ},280^{circ},..right} end{array} right. end{gather*} Теперь представим полученное обычным способом решение в градусах: $$ x=-fracpi9+frac{pi k}{3}=-20^{circ}+60^{circ}k=left{…,-20^{circ},40^{circ},100^{circ},160^{circ},220^{circ},280^{circ},…right} $$ Получаем, что: begin{gather*} left[ begin{array}{l l} x=-fracpi9+frac{2pi k}{3}\ x=frac{2pi}{9}+frac{2pi}{3} end{array} right. Leftrightarrow x=-fracpi9+frac{pi k}{3} end{gather*} Ответы и множества решений после учета значений у асимптот совпадают.
Ответ: (-fracpi9+frac{pi k}{3})

Вывод: при использовании универсальной подстановки нужно быть аккуратным и помнить о возможности потерять корни. Семейство бесконечных решений для тангенса (frac{x}{2}=fracpi2+pi k), т.е. (x=pi+2pi k) нужно проверять как возможное решение для исходного уравнения отдельно.

Внимание!

При использовании универсальной подстановки можно потерять часть корней исходного тригонометрического уравнения.
Поэтому вместе с универсальной подстановкой проверяется также дополнительное возможное решение для бесконечного тангенса половинного угла: (x=pi+2pi k). begin{gather*} f(sin(x), cos(x),…)=0Leftrightarrow\ left[ begin{array}{l l} fleft(tgleft(frac{x}{2}right)right)=0\ (?) x=pi+2pi k end{array} right. end{gather*} где слева – исходное уравнение, а справа – универсальная подстановка и дополнительное возможное (не обязательное) семейство решений.

Пример 2.Решите уравнение обычным способом и с помощью формул понижения степени. Сравните полученные ответы и множества решений. Сделайте вывод.
a) (sin^2x=frac34)

Пример 2a Обычный способ: begin{gather*} x=pm arcsinsqrt{frac34}+pi k=pm arcsinfrac{sqrt{3}}{2}+pi k=pmfracpi3+pi k end{gather*}

Формулы понижения степени: begin{gather*} sin^2x=frac{1-cos2x}{2}=frac34Rightarrow 1-cos2x=frac32Rightarrow cos2x=-frac12Rightarrow\ Rightarrow 2x=pm arccosleft(-frac12right)+2pi k=pmfrac{2pi}{3}+2pi kRightarrow x=pmfracpi3+pi k end{gather*} Ответы и множества решений совпадают.
Ответ: (pmfracpi3+pi k)

б) (cos^2 2x=1)

Пример 2б Обычный способ: begin{gather*} 2x=pm arccossqrt{1}+pi k=pm 0+pi k=pi kRightarrow x=frac{pi k}{2} end{gather*} Формулы понижения степени: begin{gather*} cos^2 2x=frac{1+cos4x}{2}=1Rightarrow 1+cos4x=2Rightarrow\ cos4x=1Rightarrow 4x=0+2pi k=2pi kRightarrow x=frac{pi k}{2} end{gather*}

Ответы и множества решений совпадают.
Ответ: (frac{pi k}{2})

в) (sin^2left(frac{x}{2}+fracpi3right)=frac14)

Пример 2в Обычный способ: begin{gather*} frac{x}{2}+fracpi3=pm arcsinsqrt{frac14}+pi k=pm arcsinfrac12+pi=pmfracpi6+pi k\ frac{x}{2}=-fracpi3pmfracpi6+pi k= left[ begin{array}{l l} fracpi2+pi k\ -fracpi6+pi k end{array} right. Rightarrow x= left[ begin{array}{l l} -pi+2pi k\ -fracpi3+2pi k end{array} right. end{gather*}

Формулы понижения степени: begin{gather*} sin^2left(frac{x}{2}+fracpi3right)=frac{1-cosleft(2left(frac{x}{2}+fracpi3right)right)}{2}=frac14Rightarrow 1-cosleft(x+frac{2pi}{3}right)=frac12Rightarrow\ Rightarrow cosleft(x+frac{2pi}{3}right)=frac12Rightarrow x+frac{2pi}{3}=pm arccosleft(frac12right)+2pi kRightarrow\ Rightarrow x=-frac{2pi}{3}pmfracpi3+2pi k= left[ begin{array}{l l} -pi+2pi k\ -fracpi3+2pi k end{array} right. end{gather*} Ответы и множества решений совпадают.
Ответ: (-pi+2pi k, -fracpi3+2pi k)

г) (tg^2left(x+fracpi4right)=1)

Пример 2г Обычный способ: begin{gather*} x+fracpi4=pm arctgsqrt{1}+pi k=pmfracpi4+pi kRightarrow\ Rightarrow x=-fracpi4pmfracpi4+pi k= left[ begin{array}{l l} -fracpi2+pi k\ pi k end{array} right. end{gather*}

Формулы понижения степени: begin{gather*} cos^2left(x+fracpi4right)=frac{1}{1+underbrace{tg^2left(x+fracpi4right)}_{=1}}=frac12\ cos^2left(x+fracpi4right)=frac{1+cosleft(2left(x+fracpi4right)right)}{2}=frac12 Rightarrow cosleft(2x+fracpi2right)=0Rightarrow\ Rightarrow -sin2x=0Rightarrow sin2x=0 Rightarrow 2x=pi kRightarrow x=frac{pi k}{2} end{gather*} Из чертежа видно, что begin{gather*} left[ begin{array}{l l} -fracpi2+pi k\ pi k end{array} right. Leftrightarrow x=frac{pi k}{2} end{gather*} Оба решения соответствуют 4 базовым точкам на числовой окружности через каждые 90°. Множества решений совпадают. Ответы не совпадают, но являются равнозначными.
Ответ: (frac{pi k}{2})
Вывод: формулы понижения степени не расширяют и не урезают множество корней исходного уравнения. Полученные ответы либо совпадают, либо нет, но всегда являются равнозначными.

Источник

Ниже представлены таблицы с формулами степеней (квадрат, куб, в 4-ой степени) прямых и обратных тригонометрических функций: синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).

Содержание
скрыть

  • Формулы квадратов

  • Формулы кубов

  • Формулы функций в 4-ой степени

Формулы квадратов
Степень Формула
Синус в квадрате Степени тригонометрических функций
Степени тригонометрических функций
Косинус в квадрате Степени тригонометрических функций
Степени тригонометрических функций
Тангенс в квадрате Степени тригонометрических функций
Котангенс в квадрате Степени тригонометрических функций

microexcel.ru

Формулы кубов
Степень Формула
Синус в кубе Степени тригонометрических функций
Косинус в кубе Степени тригонометрических функций
Тангенс в кубе Степени тригонометрических функций
Котангенс в кубе Степени тригонометрических функций

microexcel.ru
Степень Формула
Синус в 4-ой степени Степени тригонометрических функций
Косинус в 4-ой степени Степени тригонометрических функций
Тангенс в 4-ой степени Степени тригонометрических функций
Котангенс в 4-ой степени Степени тригонометрических функций

microexcel.ru

Источник

Уравнения разложения тригонометрических функций:квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.

Квадрат синуса

Квадрат косинуса

Квадрат тангенса

Квадрат синуса

Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)

sin(2α)- через sin и cos:

все тригонометрические формулы

sin(2α)- через tg и ctg:

все тригонометрические формулы

cos(2α)- через sin и cos:

все тригонометрические формулы

cos(2α)- через tg и ctg:

все тригонометрические формулы

tg(2α) и сtg(2α):

все тригонометрические формулы

все тригонометрические формулы

Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):

все тригонометрические формулы

все тригонометрические формулы

все тригонометрические формулы

все тригонометрические формулы

Тригонометрические формулы преобразования разности аргументов

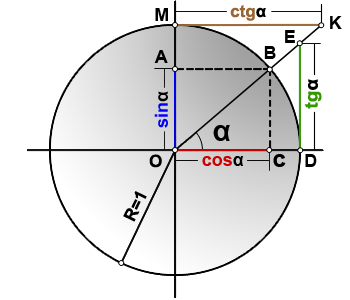
все тригонометрические формулы

все тригонометрические формулы

все тригонометрические формулы

все тригонометрические формулы

все тригонометрические формулы

sin(α)=OA

cos(α)=OC

tg(α)=DE

ctg(α)=MK

R=OB=1

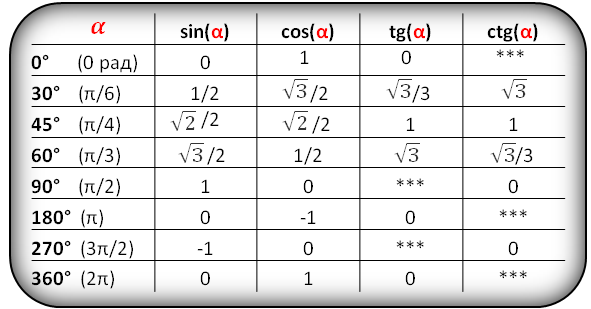
Значения функций для некоторых углов, α

все тригонометрические формулы

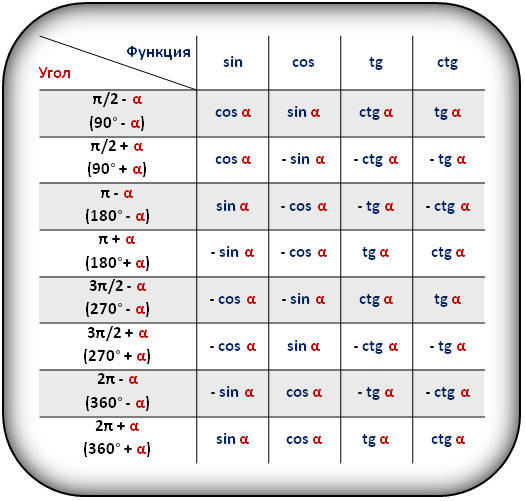
В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).

формулы приведения для тригонометрических функций

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти свой потерянный телефон через интернет
  • Как составить конспект по русскому языку пример
  • Барселона как найти работу
  • Как найти линию заданную пересечением плоскостей
  • Как найти ip адрес через cmd