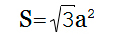Древнегреческий корень τετρά — четыре — прочно вошёл в нашу жизнь. Это и школьная тетрадь, и игрушка «Тетрис»,
и геометрическое тело «тетраэдр». Правильный тетраэдр, τετράεδρον, — это пирамида с четырьмя вершинами, шестью
рёбрами и четырьмя одинаковыми гранями — правильными треугольниками. Вторая часть слова — εδρον — и означает
«основание», «грань».
Если правильный тетраэдр разрезать плоскостью, проходящей через середины четырёх его рёбер, то в сечении получится квадрат!
И этот квадрат разделит тетраэдр на две одинаковые половинки. А граница этого квадрата будет
геодезической на правильном тетраэдре — резиночка, так натянутая, не будет съезжать.
Площадь поверхности тетраэдра
Площадь поверхности тел
Тетраэдром является геометрическая фигура, представляющая собой простейший многогранник с четырьмя гранями. Любая грань тетраэдра является треугольником. Кроме 4-х граней у тетраэдра имеется шесть ребер и четыре вершины. В правильном тетраэдре все ребра равны. Расчет S тетраэдра необходим при решении разных проектировочных задач, т.к. он является важным конструктивным элементом в сложных строительных и других конструкциях. Площадь поверхности тетраэдра несложно вычислить с помощью онлайн калькулятора, подставив исходные данные в приведенную ниже формулу:
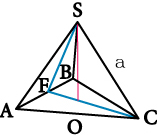
a — величина ребра тетраэдра.
Площадь тетраэдра рассчитывается как корень квадратный из произведения квадрата длины ребра на 3.
Расчет площади поверхности тетраэдра
Содержание
§
Вспомогательная страница к разделу
☞
ОПРЕДЕЛИТЕЛЬ
Геометрические приложения определителя
Уравнения кривых и поверхностей
Уравнение прямой, проходящей через точки плоскости с координатами $ (x_{1},y_1) $ и $ (x_{2},y_2) $:
$$
left|
begin{array}{lll}
x & y & 1 \
x_1 & y_1 & 1 \
x_2 & y_2 & 1
end{array}
right|=0 qquad iff qquad
left|
begin{array}{ll}
x-x_1 & y-y_1 \
x_2-x_1 & y_2-y_1
end{array}
right|=0 .
$$
Уравнение окружности, проходящей через точки плоскости с координатами $ (x_{1},y_1) , (x_2,y_2) $ и $ (x_{3},y_3) $ (окружности, описанной вокруг треугольника):
$$
left|
begin{array}{llll}
x^2+y^2 & x & y & 1 \
x_1^2+y_1^2 & x_1 & y_1 & 1 \
x_2^2+y_2^2 & x_2 & y_2& 1 \
x_3^2+y_3^2 & x_3 & y_3& 1
end{array}
right|=0 .
$$
При условии, что все три точки коллинеарны (лежат на одной прямой; см.
☞
ЗДЕСЬ ):
$$
left|
begin{array}{lll}
x_1 & y_1 & 1 \
x_2 & y_2 & 1 \
x_3 & y_3 & 1
end{array}
right|=0
$$
окружность вырождается в прямую
$$
left|
begin{array}{clll}
0 & x & y & 1 \
x_1^2+y_1^2 & x_1 & y_1 & 1 \
x_2^2+y_2^2 & x_2 & y_2& 1 \
x_3^2+y_3^2 & x_3 & y_3& 1
end{array}
right|=0 .
$$
Координаты центра окружности, проходящей через точки $ (x_{1},y_1) , (x_2,y_2) $ и $ (x_{3},y_3) $:
$$
x_C=frac{left|
begin{array}{lll}
x_1^2+y_1^2 & y_1 & 1 \
x_2^2+y_2^2 & y_2& 1 \
x_3^2+y_3^2 & y_3& 1
end{array}
right|}
{2left|
begin{array}{lll}
x_1 & y_1 & 1 \
x_2 & y_2 & 1 \
x_3 & y_3 & 1
end{array}
right|},quad
y_C=-frac{left|
begin{array}{lll}
x_1^2+y_1^2 & x_1 & 1 \
x_2^2+y_2^2 & x_2& 1 \
x_3^2+y_3^2 & x_3& 1
end{array}
right|}
{2left|
begin{array}{lll}
x_1 & y_1 & 1 \
x_2 & y_2 & 1 \
x_3 & y_3 & 1
end{array}
right|} .
$$
Т
Теорема [Птолемей]. Точки
$$ P_1=(x_{1},y_1) , P_2=(x_2,y_2), P_3 =(x_{3},y_3), P_4=(x_{4},y_4) $$
лежат на одной окружности или на одной прямой тогда и только тогда, когда выполнено равенство
$$
left|
begin{array}{cccc}
0 & |P_1P_2|^2 & |P_1P_3|^2 & |P_1P_4|^2 \
|P_1P_2|^2 & 0 & |P_2P_3|^2 & |P_2P_4|^2 \
|P_1P_3|^2 & |P_2P_3|^2 & 0 & |P_3P_4|^2 \
|P_1P_4|^2 & |P_2P_4|^2 & |P_3P_4|^2 & 0
end{array}
right|=0 .
$$
Здесь $ |P_jP_k|^2=(x_j-x_k)^2+(y_j-y_k)^2 $.
Доказательство, альтернативная геометрическая формулировка, а также пространственный аналог теоремы
☞
ЗДЕСЬ.
Уравнение плоскости, проходящей через точки пространства с координатами $ (x_{1},y_1,z_1) $, $ (x_{2},y_2,z_2) $ и $ (x_{3},y_3,z_3) $:
$$
left|
begin{array}{llll}
x & y & z & 1 \
x_1 & y_1 & z_1 & 1 \
x_2 & y_2 & z_2 & 1 \
x_3 & y_3 & z_3 & 1
end{array}
right|=0 .
$$
Уравнение сферы, проходящей через точки $ (x_{1},y_1,z_1) $, $ (x_{2},y_2,z_2) $, $ (x_{3},y_3,z_3) $ и $ (x_{4},y_4,z_4) $:
$$
left|
begin{array}{cllll}
x^2+y^2+z^2 & x & y & z & 1 \
x_1^2+y_1^2+z_1^2 & x_1 & y_1 & z_1 & 1 \
x_2^2+y_2^2+z_2^2 & x_2 & y_2 & z_2 & 1 \
x_3^2+y_3^2+z_3^2 & x_3 & y_3 & z_3 & 1 \
x_4^2+y_4^2+z_4^2 & x_4 & y_4 & z_4 & 1
end{array}
right|=0 .
$$
При условии, что все четыре точки компланарны (лежат в одной плоскости; см.
☞
ЗДЕСЬ ):
$$
left|
begin{array}{llll}
x_1 & y_1 & z_1 & 1 \
x_2 & y_2 & z_2 & 1 \
x_3 & y_3 & z_3 & 1 \
x_4 & y_4 & z_4 & 1
end{array}
right|=0
$$
сфера вырождается в плоскость. Координаты центра сферы:
$$
x_C=frac{left|
begin{array}{clll}
x_1^2+y_1^2+z_1^2 & y_1 & z_1 & 1 \
x_2^2+y_2^2+z_2^2 & y_2 & z_2 & 1 \
x_3^2+y_3^2+z_3^2 & y_3 & z_3 & 1 \
x_4^2+y_4^2+z_4^2 & y_4 & z_4 & 1
end{array}
right|}{2,left|
begin{array}{llll}
x_1 & y_1 & z_1 & 1 \
x_2 & y_2 & z_2 & 1 \
x_3 & y_3 & z_3 & 1 \
x_4 & y_4 & z_4 & 1
end{array}
right|},
y_C=-frac{left|
begin{array}{clll}
x_1^2+y_1^2+z_1^2 & x_1 & z_1 & 1 \
x_2^2+y_2^2+z_2^2 & x_2 & z_2 & 1 \
x_3^2+y_3^2+z_3^2 & x_3 & z_3 & 1 \
x_4^2+y_4^2+z_4^2 & x_4 & z_4 & 1
end{array}
right|}{2,left|
begin{array}{llll}
x_1 & y_1 & z_1 & 1 \
x_2 & y_2 & z_2 & 1 \
x_3 & y_3 & z_3 & 1 \
x_4 & y_4 & z_4 & 1
end{array}
right|},
z_C=frac{left|
begin{array}{clll}
x_1^2+y_1^2+z_1^2 & x_1 & y_1 & 1 \
x_2^2+y_2^2+z_2^2 & x_2 & y_2 & 1 \
x_3^2+y_3^2+z_3^2 & x_3 & y_3 & 1 \
x_4^2+y_4^2+z_4^2 & x_4 & y_4 & 1
end{array}
right|}{2,left|
begin{array}{llll}
x_1 & y_1 & z_1 & 1 \
x_2 & y_2 & z_2 & 1 \
x_3 & y_3 & z_3 & 1 \
x_4 & y_4 & z_4 & 1
end{array}
right|}
$$
§
Сформулированные выше геометрические задачи являются частными случаями общей задачи об
☞
ИНТЕРПОЛЯЦИИ.
Площади
Площадь треугольника с вершинами $ P_1=(x_{1},y_1) , P_2=(x_{2},y_2) $ и $ P_3=(x_{3},y_3) $ равна абсолютной величине (модулю) выражения
$$
frac{1}{2}
left|
begin{array}{lll}
1 & x_1 & y_1 \
1 & x_2 & y_2 \
1 & x_3 & y_3
end{array}
right| .
$$
Доказательство
☞
ЗДЕСЬ.
Квадрат площади треугольника $ P_{1}P_2P_3 $ выражается через квадраты длин его сторон по формуле
$$
S^2=-frac{1}{16}
left|
begin{array}{cccc}
0 & |P_1P_2|^2 & |P_1P_3|^2 & 1 \
|P_1P_2|^2 & 0 & |P_2P_3|^2 & 1 \
|P_1P_3|^2 & |P_2P_3|^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right| ,
$$
которая в развернутом виде
$$
=frac{1}{16}left(|P_1P_2|+|P_1P_3|+|P_2P_3| right)left(|P_1P_2|+|P_1P_3|-|P_2P_3| right)left(|P_1P_2|-|P_1P_3|+|P_2P_3| right)
left(-|P_1P_2|+|P_1P_3|+|P_2P_3| right)
$$
представляет собой формулу Герона.
Площадь треугольника с вершинами $ P_1=(x_{1},y_1,z_1) , P_2=(x_{2},y_2,z_2) $ и $ P_3=(x_{3},y_3,z_3) $ в $ mathbb R^{3} $ равна
$$
frac{1}{2} sqrt{ left|
begin{array}{lll}
1 & x_1 & y_1 \
1 & x_2 & y_2 \
1 & x_3 & y_3
end{array}
right|^2
+
left|
begin{array}{lll}
1 & x_1 & z_1 \
1 & x_2 & z_2 \
1 & x_3 & z_3
end{array}
right|^2+
left|
begin{array}{lll}
1 & y_1 & z_1 \
1 & y_2 & z_2 \
1 & y_3 & z_3
end{array}
right|^2
} .
$$
Выражение под радикалом можно преобразовать к виду
$$
detleft[left(
begin{array}{lll}
x_2-x_1 & y_2-y_1 &z_2- z_1 \
x_3-x_1 & y_3-y_1 & z_3- z_1
end{array}
right)cdot left(
begin{array}{ll}
x_2-x_1 & x_3-x_1 \
y_2-y_1 & y_3-y_1 \
z_2-z_1 & z_3-z_1
end{array}
right)right]
$$
с помощью теоремы Бине-Коши. Таким образом, площадь треугольника также равна
$$
frac{1}{2} sqrt{ left|
begin{array}{cc}
langle P_2P_1,P_2P_1 rangle & langle P_2P_1,P_3P_1 rangle \
langle P_2P_1,P_3P_1 rangle & langle P_3P_1,P_3P_1 rangle
end{array}
right|} ,
$$
где скобками $ langle , rangle $ обозначено скалярное произведение.
Площадь четырехугольника с вершинами $ P_1=(x_{1},y_1) , P_2=(x_{2},y_2), P_3=(x_{3},y_3), P_4=(x_4,y_4) $ равна абсолютной величине (модулю) выражения
$$
frac{1}{2}
left| begin{array}{cc}
x_1-x_3 & y_1-y_3 \
x_2-x_4 & y_2-y_4
end{array}
right| =frac{1}{2} left[(x_1-x_3)(y_2-y_4)-(x_2-x_4)(y_1-y_3)right]
$$
при условии, что стороны не пересекаются.
Площадь $ n_{} $-угольника $ P_{0}P_1dots P_{n-1} P_0 $ с вершинами $ P_0 = (x_{0},y_0) ,dots,
P_{n-1} = (x_{n-1},y_{n-1}) $ равна
абсолютной величине (модулю) выражения
$$
frac{1}{2} sum_{k=1}^{n-2}
left|
begin{array}{lll}
1 & x_0 & y_0 \
1 & x_k & y_k \
1 & x_{k+1} & y_{k+1}
end{array}
right|
$$
при условии, что стороны не пересекаются.
П
Пример. Найти площадь пятиугольника, изображенного на рисунке.
Решение. Имеем: $ P_{0} =(1,2),P_1= (3,4),P_2=(4,1), P_3=(6,5) , P_4=(2,6) $.
$$
S=frac{1}{2}Bigg(
left| begin{array}{ccc}
1& 1 & 2 \
1& 3 & 4 \
1& 4 & 1
end{array}
right| +
left| begin{array}{ccc}
1& 1 & 2 \
1& 4 & 1 \
1& 6 & 5
end{array}
right|
+
left| begin{array}{ccc}
1& 1 & 2 \
1& 6 & 5 \
1 & 2 & 6
end{array}
right|
Bigg) =
$$
$$
=frac{1}{2}(-8+14+17)=frac{23}{2} .
$$
Геометрический смысл суммирования будет более понятен, если перенумеровать точки, сделав стартовой $ P_{1} $: слагаемые в сумме
$$
frac{1}{2}Bigg(
left| begin{array}{ccc}
1& 3 & 4 \
1& 4 & 1 \
1& 6 & 5
end{array}
right| + left| begin{array}{ccc}
1& 3 & 4 \
1& 6 & 5 \
1& 2 & 6
end{array}
right| +
left| begin{array}{ccc}
1& 3 & 4 \
1& 2 & 6 \
1 & 1 & 2
end{array}
right| Bigg) = frac{1}{2}(10+7+6)
$$
теперь отвечают за площади треугольников, на которые разбит пятиугольник точечными линиями.
♦
Площадь параллелограмма в $ {mathbb R}^{2} $ с вершинами $ (0,0), (x_{1},y_1) , (x_2,y_2), (x_1+x_2,y_1+y_2) $ равна абсолютной величине (модулю) определителя
$$
left|
begin{array}{ll}
x_1 & y_1 \
x_2 & y_2 \
end{array}
right| .
$$
П
Пример. Для $ x_{1} =3,y_1=1,x_2=1,y_2=2 $
имеем: $ S_{}=3cdot 2 — 1 cdot 1 = 5 $.
Площадь параллелограмма в $ {mathbb R}^{3} $ с вершинами $ (0,0,0), (x_{1},y_1,z_1) , (x_2,y_2,z_2), (x_1+x_2,y_1+y_2,z_1+z_2) $ равна
$$
sqrt{detleft[left(
begin{array}{lll}
x_1 & y_1 & z_1 \
x_2 & y_2 & z_2 \
end{array}
right)cdot left(
begin{array}{ll}
x_1 & x_2 \
y_1 & y_2 \
z_1 & z_2
end{array}
right)right]
}=sqrt{left|
begin{array}{cc}
x_1^2+y_1^2 + z_1^2 & x_1x_2+y_1y_2+z_1z_2 \
x_1x_2+y_1y_2+z_1z_2 & x_2^2+y_2^2 + z_2^2 \
end{array}
right|
} .
$$
Если применить к определителю произведения матриц теорему Бине-Коши, то получим следующее равенство
$$
detleft[left(
begin{array}{lll}
x_1 & y_1 & z_1 \
x_2 & y_2 & z_2 \
end{array}
right)cdot left(
begin{array}{ll}
x_1 & x_2 \
y_1 & y_2 \
z_1 & z_2
end{array}
right)right]=
left|
begin{array}{ll}
x_1 & y_1 \
x_2 & y_2 \
end{array}
right|^2+left|
begin{array}{ll}
x_1 & z_1 \
x_2 & z_2 \
end{array}
right|^2
+
left|
begin{array}{ll}
y_1 & z_1 \
y_2 & z_2 \
end{array}
right|^2 ,
$$
которое интерпретируется следующим образом: квадрат площади параллелограмма в $ mathbb R^{3} $ равен сумме квадратов площадей его проекций на координатные плоскости. Можно считать этот результат обобщением теоремы Пифагора.
Объемы
тетраэдра
Объем тетраэдра в $ mathbb R^{3} $ с вершинами $ P_1= (x_{1},y_1,z_1) ,P_2=(x_2,y_2,z_2) , P_3=(x_3,y_3,z_3) , P_4=(x_4,y_4,z_4) $ равен абсолютной величине (модулю) выражения
$$
frac{1}{6}
left|
begin{array}{llll}
1 & x_1 & y_1 & z_1 \
1 & x_2 & y_2 & z_2 \
1 & x_3 & y_3 & z_3 \
1 & x_4 & y_4 & z_4
end{array}
right| .
$$
Формула Тартальи (Кэли-Менгера) для квадрата объема тетраэдра через длины его ребер:
$$
V^2=frac{1}{288}
left|
begin{array}{ccccc}
0 & |P_1P_2|^2 & |P_1P_3|^2 & |P_1P_4|^2 & 1 \
|P_1P_2|^2 & 0 & |P_2P_3|^2 & |P_2P_4|^2 & 1 \
|P_1P_3|^2 & |P_2P_3|^2 & 0 & |P_3P_4|^2 & 1 \
|P_1P_4|^2 & |P_2P_4|^2 & |P_3P_4|^2 & 0 & 1 \
1 & 1 & 1 & 1 & 0
end{array}
right| .
$$
Доказательство
☞
ЗДЕСЬ.
Интересно было бы посмотреть, как эта формула выглядела в оригинале у Тартальи, если аппарат определителей был придуман лет на 250 позже…
=>
Если точки $ P_1,P_2,P_3,P_4 $ компланарны, т.е. тетраэдр вырождается в плоский четырехугольник, то формула Тартальи дает связь между сторонами четырехугольника и его диагоналями:
$$
left|
begin{array}{ccccc}
0 & |P_1P_2|^2 & |P_1P_3|^2 & |P_1P_4|^2 & 1 \
|P_1P_2|^2 & 0 & |P_2P_3|^2 & |P_2P_4|^2 & 1 \
|P_1P_3|^2 & |P_2P_3|^2 & 0 & |P_3P_4|^2 & 1 \
|P_1P_4|^2 & |P_2P_4|^2 & |P_3P_4|^2 & 0 & 1 \
1 & 1 & 1 & 1 & 0
end{array}
right|=0 , .
$$
Применение тождества Сильвестра дает (в обозначениях рисунка):
$$
left|
begin{array}{cccc}
0 & |P_2P_3|^2 & d_2^2 & 1 \
|P_2P_3|^2 & 0 & |P_3P_4|^2 & 1 \
d_2^2 & |P_3P_4|^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right| cdot
left|
begin{array}{cccc}
0 & |P_1P_2|^2 & |P_1P_4|^2 & 1 \
|P_1P_2|^2 & 0 & d_2^2 & 1 \
|P_1P_4|^2 & d_2^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right|
=
$$
$$
=
left|
begin{array}{cccc}
|P_1P_2|^2 & 0 & d_2^2 & 1 \
d_1^2 & |P_2P_3|^2 & |P_3P_4|^2 & 1 \
|P_1P_4|^2 & d_2^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right|^2 , .
$$
Откуда получаем формулу
$$
2, d_1^2 d_2^2=(|P_1P_2|^2+|P_2P_3|^2+|P_3P_4|^2+|P_1P_4|^2-d_2^2) d_2^2+
$$
$$
+(|P_3P_4|^2-|P_2P_3|^2)(|P_1P_2|^2-|P_1P_4|^2)+
$$
$$
+left{
left|
begin{array}{cccc}
0 & |P_2P_3|^2 & d_2^2 & 1 \
|P_2P_3|^2 & 0 & |P_3P_4|^2 & 1 \
d_2^2 & |P_3P_4|^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right| cdot
left|
begin{array}{cccc}
0 & |P_1P_2|^2 & |P_1P_4|^2 & 1 \
|P_1P_2|^2 & 0 & d_2^2 & 1 \
|P_1P_4|^2 & d_2^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right|right}^{1/2} , ,
$$
позволяющую определить длину диагонали $ d_1 $ четырехугольника $ P_1P_2P_3P_4 $ через длину его второй диагонали и длины сторон.
Из формулы Герона далее следует:
$$
2,d_1^2 d_2^2=(|P_1P_2|^2+|P_2P_3|^2+|P_3P_4|^2+|P_1P_4|^2-d_2^2) d_2^2+
$$
$$
+ (|P_2P_3|^2-|P_3P_4|^2)(|P_1P_2|^2-|P_1P_4|^2)+
$$
$$
+16, S_{triangle P_1P_2P_3} S_{triangle P_1P_3P_4} , .
$$
Объем симплекса в $ mathbb R_{}^{n} $ с вершинами в
$$ P_1=(x_{11},x_{12},dots,x_{1n}) ,P_2=(x_{21},x_{22},dots,x_{2n}) , dots ,P_n=(x_{n1},x_{n2},dots,x_{nn}),P_{n+1}=(x_{n+1,1},x_{n+1,2},dots,x_{n+1,n}) , $$
т.е. тела, заданного уравнениями
$$
left{ X=sum_{j=1}^{n+1} alpha_j P_j big| , alpha_1ge 0,dots alpha_{n+1} ge 0, sum_{j=1}^{n+1} alpha_j =1 right}
$$
равен абсолютной величине (модулю) выражения
$$
frac{1}{n!}left| begin{array}{cllll}
1 & x_{11}& x_{12} &dots & x_{1n} \
1 & x_{21}& x_{22} & dots & x_{2n} \
vdots & & & & vdots \
1 & x_{n1}& x_{n2}& dots & x_{nn} \
1 & x_{n+1,1} & x_{n+1,2} & dots & x_{n+1,n}
end{array}
right| .
$$
Формула Кэли-Менгера для квадрата объема симплекса через длины его ребер:
$$
V^2=frac{(-1)^{n-1}}{2^n(n!)^2}
left|
begin{array}{cccccc}
0 & |P_1P_2|^2 & |P_1P_3|^2 & dots & |P_1P_{n+1}|^2 & 1 \
|P_1P_2|^2 & 0 & |P_2P_3|^2 & dots & |P_2P_{n+1}|^2 & 1 \
|P_1P_3|^2 & |P_2P_3|^2 & 0 & dots & |P_3P_{n+1}|^2 & 1 \
dots & & & & & dots \
|P_1P_{n+1}|^2 & |P_2P_{n+1}|^2 & |P_3P_{n+1}|^2 & dots & 0 & 1 \
1 & 1 & 1 & dots & 1 & 0
end{array}
right| .
$$
В частном случае: объем пирамиды
$$
left{ X=(x_1,dots,x_n) in mathbb R^n Big|
sum_{j=1}^nfrac{x_j}{a_j} le 1, x_1 ge 0,dots, x_n ge 0 right} quad npu quad a_1>0,dots,a_n>0
$$
равен
$$
frac{1}{n!}prod_{j=1}^n a_j .
$$
параллелепипеда
Объем $ n_{} $-мерного параллелепипеда в $ {mathbb R}^{n} $, построенного на вершинах
$$ (0,0,dots,0), (x_{11},x_{12},dots,x_{1n}) ,(x_{21},x_{22},dots,x_{2n}) , dots ,(x_{n1},x_{n2},dots,x_{nn}), $$
равен абсолютной величине (модулю) определителя
$$
left| begin{array}{cccc}
x_{11}& x_{12} &dots & x_{1n} \
x_{21}& x_{22} & dots & x_{2n} \
dots & & & dots \
x_{n1}& x_{n2}& dots & x_{nn}
end{array}
right| .
$$
Доказательство
☞
ЗДЕСЬ.
Объем $ m_{} $-мерного параллелепипеда в $ {mathbb R}^{n} $, построенного на вершинах
$$ (0,0,dots,0), (x_{11},x_{12},dots,x_{1n}) ,(x_{21},x_{22},dots,x_{2n}) , dots , (x_{m1},x_{m2},dots,x_{mn}), $$
равен
$$
sqrt{det(Xcdot X^{top}}) npu X=
left( begin{array}{cccc}
x_{11}& x_{12} &dots & x_{1n} \
x_{21}& x_{22} & dots & x_{2n} \
dots & & & dots \
x_{m1}& x_{m2}& dots & x_{mn}
end{array}
right) .
$$
Здесь $ {}^{top} $ означает транспонирование.
Объем $ n_{} $-мерного параллелепипеда, ограниченного плоскостями
$$
a_{j1}x_1+a_{j2}x_2+dots+a_{jn}x_n= pm h_j npu j in {1,dots, n }
$$
равен
$$
frac{2^n displaystyle prod_{j=1}^n h_j}{det[a_{jk}]_{j,k=1}^n} .
$$
эллипсоида
Объем $ n_{} $-мерного эллипсоида, ограниченного поверхностью
$$
(x_1,x_2,dots ,x_n)left( begin{array}{cccc}
a_{11} & a_{12} & dots & a_{1n} \
a_{12} & a_{22} & dots & a_{2n} \
dots & & & dots \
a_{1n} & a_{2n} & dots & a_{nn}
end{array}
right)
left(
begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right) =1
$$
(квадратичная форма, стоящая в левой части, положительно определена) равен
$$
frac{pi^{n/2}}{Gamma(frac{n}{2}+1)} frac{1}{sqrt{det [a_{jk}]_{j,k=1}^n}} .
$$
Здесь $ Gamma_{} $ обозначает гамма-функцию, при вычислениях значений которой в последней формуле достаточно пользоваться следующими ее свойствами:
$$Gamma left(frac{1}{2}right)=sqrt{pi}, Gamma(1)=Gamma(2)=1, Gamma(x+1)=xGamma(x) npu forall x >0, Gamma(n+1)=n! npu forall n in {mathbb N} . $$
П
Пример. Площадь, ограниченная эллипсом
$$ a_{11}x_{1}^2+2a_{12}x_1x_2 + a_{22}x_2^2=1 , ,$$
вычисляется по формуле
$$ frac{pi}{sqrt{a_{11}a_{22}-a_{12}^2}} . $$
Объем фигуры, ограниченной эллипсоидом
$$
(x_1,x_2,x_3)left( begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{12} & a_{22} & a_{23} \
a_{13} & a_{23} & a_{33}
end{array}
right)
left(
begin{array}{c}
x_1 \ x_2 \ x_3
end{array}
right) =1
$$
равен
$$
frac{4}{3} frac{pi}{sqrt{left| begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{12} & a_{22} & a_{23} \
a_{13} & a_{23} & a_{33}
end{array}
right|
}} .
$$
Объем фигуры, ограниченной четырехмерным эллипсоидом (в записи, аналогичной предыдущей) –
$$ frac{pi^2}{2sqrt{det(A)}} . $$
Классификация алгебраических кривых и поверхностей
Источники
[1]. Uspensky J.V. Theory of Equations. New York. McGraw-Hill. 1948