Почему скалярное произведение векторов называется именно скалярным и что представляет собой? Чем оно отличается от результатов других операций над векторами? Что такое скаляр? Скаляр — это число.
И скалярное произведение векторов — это тоже число. Этим оно и отличается от уже рассмотренной суммы векторов, и от векторного произведения векторов, которое ещё предстоит рассмотреть.
Скалярное произведение векторов: теория и решения задач
В отличие от скалярного произведения, сумма векторов — это вектор, и векторное произведение — тоже вектор.
Определение 1. Скалярным произведением векторов называется число (скаляр), равное произведению длин (модулей) этих векторов на косинус угла между ними. Формула скалярного произведения векторов согласно определению 1. Можно встретить и другое название этой операции: внутреннее произведение.
Скалярное произведение вектора на себя называется скалярным квадратом. На этом уроке будем решать распространённые задачи не только на непосредственное вычисление скалярного произведения, но и на выяснение ортогональности (перпендикулярности) векторов, вида угла (тупой, острый, прямой) между векторами, вычисление скалярного произведения векторов, которые даны в координатах, вычисление длин диагоналей параллелограма, построенного на вектора.
Но все по порядку. Перед каждым видом задач будем обращать внимание на то, что на этот счёт гласит теория. По ходу урока вам пригодится онлайн-калькулятор для проверки решения задач на скалярное произведение векторов.
Если в задаче и длины векторов, и угол между ними преподнесены «на блюдечке с голубой каёмочкой», то условие задачи и её решение выглядят так:
Пример 1. Даны векторы . Найти скалярное произведение векторов , если их длины и угол между ними представлены следующими значениями:
Решение:
Справедливо и другое определение, полностью равносильное определению 1.
Определение 2. Скалярным произведением векторов называется число (скаляр), равное произведению длины одного их этих векторов на проекцию другого вектора на ось, определяемую первым из указанных векторов. Формула согласно определению 2:
- (2)
- или
- (3)
Задачу с применением этой формулы решим после следующего важного теоретического пункта.
Определение скалярного произведения векторов через координаты
То же самое число можно получить, если перемножаемые векторы заданы своими координатами.
Определение 3. Скалярное произведение векторов — это число, равное сумме попарных произведений их соответствующих координат.
На плоскости
Если два вектора и на плоскости определены своими двумя декартовыми прямоугольными координатами и, то скалярное произведение этих векторов равно сумме попарных произведений их соответствующих координат:
Пример 2. Найти численную величину проекции вектора на ось, параллельную вектору. Решение. Находим скалярное произведение векторов, складывая попарные произведения их координат:
Теперь нам требуется приравнять полученное скалярное произведение произведению длины вектора на проекцию вектора на ось, параллельную вектору (в соответствии с формулой ). Находим длину вектора как квадратный корень из суммы квадратов его координат:
Составляем уравнение и решаем его:
Ответ. Искомая численная величина равна минус 8.
В пространстве
Если два вектора и в пространстве определены своими тремя декартовыми прямоугольными координатами
и
то скалярное произведение этих векторов также равно сумме попарных произведений их соответствующих координат, только координат уже три.
Задача на нахождение скалярного произведения рассмотренным способом — после разбора свойств скалярного произведения. Потому что в задаче потребуется определить, какой угол образуют перемножаемые векторы.
Свойства скалярного произведения векторов
- переместительное свойство: от перемены местами перемножаемых векторов величина их скалярного произведения не меняется).
- сочетательное относительно числового множителя свойство: скалярное произведение вектора, умноженного на некоторый множитель, и другого вектора, равно скалярному произведению этих векторов, умноженному на тот же множитель).
- распределительное относительно суммы векторов свойство: скалярное произведение суммы двух векторов на третий вектор равно сумме скалярных произведений первого вектора на третий вектор и второго вектора на третий вектор).
- скалярный квадрат вектора больше нуля), если — ненулевой вектор, и , если — нулевой вектор.
В определениях изучаемой операции мы уже касались понятия угла между двумя векторами. Пора уточнить это понятие. На рисунке выше видны два вектора, которые приведены к общему началу. И первое, на что нужно обратить внимание: между этими векторами существуют два угла — φ1 и φ2.
Какой из этих углов фигурирует в определениях и свойствах скалярного произведения векторов? Сумма рассмотренных углов равна 2π и поэтому косинусы этих углов равны. В определение скалярного произведения входит только косинус угла, а не значение его выражения.
Но в свойствах рассматривается только один угол. И это тот из двух углов, который не превосходит π, то есть 180 градусов. На рисунке этот угол обозначен как φ1:
- Два вектора называют ортогональными и угол между этими векторами — прямой (90 градусов или π/2), если скалярное произведение этих векторов равно нулю. Ортогональностью в векторной алгебре называется перпендикулярность двух векторов.
- Два ненулевых вектора составляют острый угол (от 0 до 90 градусов, или, что тоже самое — меньше π/2) тогда и только тогда, когда их скалярное произведение положительно.
- Два ненулевых вектора составляют тупой угол (от 90 до 180 градусов, или, что то же самое — больше π/2) тогда и только тогда, когда их скалярное произведение отрицательно.
Источник: https://function-x.ru/vectors_scalar.html
Система координат
С чего было бы логично начать обсуждение метода координат? Наверное, с понятия системы координат. Вспомни, когда ты с нею впервые столкнулся.
Мне кажется, что в 7 классе, когда ты узнал про существование линейной функции ( y=ax+b), например, ( y=2{x}-3).
Напомню, ты строил ее по точкам. Помнишь?
Ты выбирал произвольное число ( x), подставлял ее в формулу ( y=2{x}-3) и вычислял таким образом ( y).
Например, если ( x=0), то ( y=2cdot 0-3=-3), если же ( x=1), то ( y=2cdot 1-3=-1)и т. д.
Что же ты получал в итоге?
А получал ты точки с координатами: ( Aleft( 0,-3 right)) и ( Bleft( 1,-1 right)).
Далее ты рисовал «крестик» (систему координат ( X0Y)), выбирал на ней масштаб (сколько клеточек у тебя будет единичным отрезком) и отмечал на ней полученные тобою точки, которые затем соединял прямой линией, полученная линия и есть график функции ( y=2{x}-3).
Тут есть несколько моментов, которые стоит объяснить тебе чуть подробнее:
- Единичный отрезок ты выбираешь из соображений удобства, так, чтобы все красиво и компактно умещалось на рисунке;
- Принято, что ось ( displaystyle X) идет слева направо, а ось ( displaystyle Y) – cнизу вверх;
- Они пересекаются под прямым углом, а точка их пересечения называется началом координат. Она обозначается буквой ( displaystyle O);
- В записи координаты точки, например ( displaystyle Aleft( 0,-3 right)), слева в скобках стоит координата точки по оси ( displaystyle X), а справа, по оси ( displaystyle Y). В частности, ( displaystyle Aleft( 0,-3 right)) просто означает, что у точки ( displaystyle A) ( displaystyle x=0,~y=-3.);
- Для того, чтобы задать любую точку на координатной оси, требуется указать ее координаты (2 числа);
- Для любой точки, лежащей на оси ( displaystyle Ox,), ( displaystyle y=0.);
- Для любой точки, лежащей на оси ( displaystyle Oy), ( displaystyle x=0.);
- Ось ( displaystyle Ox) называется осью абсцисс;
- Ось ( displaystyle Oy) называется осью ординат.
Векторы
Теперь давай с тобой сделаем следующий шаг: отметим две точки ( displaystyle Aleft( {{x}_{1}},{{y}_{1}} right)) ( displaystyle Bleft( {{x}_{2}},{{y}_{2}} right)).
Соединим эти две точки отрезком. И поставим стрелочку так, как будто мы проводим отрезок из точки ( displaystyle A) к точке ( displaystyle B):
То есть мы сделаем наш отрезок направленным!
Вспомни, как еще называется направленный отрезок? Верно, он называется вектором!
Вектором называется направленный отрезок, имеющий начало и конец.
Таким образом, если мы соединим точку ( displaystyle A) c точкой ( displaystyle B), причем началом у нас будет точка A, а концом – точка B, то мы получим вектор ( displaystyle overrightarrow{AB}).
Это построение ты тоже делал в 8 классе, помнишь?
Координаты вектора
Оказывается, векторы, как и точки, можно обозначать двумя цифрами: эти цифры называются координатами вектора.
Вопрос: как ты думаешь, достаточно ли нам знать координаты начала и конца вектора, чтобы найти его координаты?
Оказывается, что да! И делается это очень просто:
Координаты вектора = координаты точки конца – координаты точки начала.
Таким образом, так как в векторе ( displaystyle overrightarrow{AB}) точка ( displaystyle Aleft( {{x}_{1}},{{y}_{1}} right)) – начало, а ( displaystyle Bleft( {{x}_{2}},{{y}_{2}} right)) – конец, то вектор ( displaystyle overrightarrow{AB}) имеет следующие координаты:
( displaystyle overrightarrow{AB}left( {{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}} right))
Например, если ( displaystyle Aleft( 2,0 right))( displaystyle Bleft( 1,2 right)), то координаты вектора ( displaystyle overrightarrow{AB})
( displaystyle overrightarrow{AB}left( 1-2,2-0 right)=overrightarrow{AB}left( -1,2 right))
Теперь давай сделаем наоборот, найдем координаты вектора ( displaystyle overrightarrow{BA}).
Что нам для этого нужно поменять? Да, нужно поменять местами начало и конец: теперь начало вектора будет в точке ( displaystyle B), а конец – в точке ( displaystyle A).
Тогда:
( displaystyle overrightarrow{BA}left( 2-1,text{ }!!~!!text{ }0-2 right)=overrightarrow{BA(}1,-2).)
Посмотри внимательно, чем отличаются векторы ( displaystyle overrightarrow{AB}) и ( displaystyle overrightarrow{BA})?
Единственное их отличие – это знаки в координатах. Они противоположны. Этот факт принято записывать вот так:
( displaystyle overrightarrow{AB}=-overrightarrow{BA})
Иногда, если не оговаривается специально, какая точка является началом вектора, а какая – концом, то векторы обозначают не двумя заглавными буквами, а одной строчной, например: ( displaystyle {vec{a}}), ( displaystyle {vec{p}}) и т. д.
Еще больше о векторах и проекциях (эту тему мы непременно затронем) ты можешь прочитать в статье по физике «Большая теория по векторам» 🙂
Действия с векторами
Что еще можно делать с векторами?
Да почти все то же самое, что и с обычными числами:
- Векторы можно складывать друг с другом;
- Векторы можно вычитать друг из друга;
- Векторы можно умножать (или делить) на произвольное ненулевое число;
- Векторы можно умножать друг на друга.
Что же происходит при выполнении этих действий с координатами векторов?
1. При сложении (вычитании) двух векторов, мы складываем (вычитаем) поэлементно их координаты.
То есть:
( vec{a}left( {{x}_{1}},{{y}_{1}} right)+vec{b}left( {{x}_{2}},{{y}_{2}} right)=vec{c}left( {{x}_{1}}+{{x}_{2}},{{y}_{1}}+{{y}_{2}} right))
( vec{a}left( {{x}_{1}},{{y}_{1}} right)-vec{b}left( {{x}_{2}},{{y}_{2}} right)=vec{c}left( {{x}_{1}}-{{x}_{2}},{{y}_{1}}-{{y}_{2}} right))
2. При умножении (делении) вектора на число, все его координаты умножаются (делятся) на это число:
( kcdot vec{a}left( {{x}_{1}},{{y}_{1}} right)=vec{b}left( k{{x}_{1}},k{{y}_{1}} right))
Например:
Найдите сумму координат вектора ( vec{a}+vec{b}).
Вектор растягивается или сжимается или меняет направление при умножении или делении на число:
Давай вначале найдем координаты каждого из векторов.
Оба они имеют одинаковое начало – точку начала координат. Концы у них разные.
Тогда ( vec{a}left( 2-0,6-0 right)=vec{a}left( 2,6 right)), ( vec{b}left( 8-0,4-0 right)=vec{b}left( 8,4 right)).
Теперь вычислим координаты вектора ( vec{c}=vec{a}+vec{b}=vec{c}left( 2+8,4+6 right)=vec{c}left( 10,10 right))
Тогда сумма координат полученного вектора равна ( 20).
Ответ: ( 20)
Теперь реши сам следующую задачу:
Найти сумму координат вектора ( 3vec{a}-2vec{b})
Проверяем:
- ( vec{a}=vec{a}left( 4-2,10-4 right)=vec{a}left( 2,6 right));
- ( vec{b}=vec{b}left( 10-2,6-2 right)=vec{b}left( 8,4 right));
- ( vec{c}=3vec{a}-2vec{b}=3vec{a}left( 2,6 right)-2vec{b}left( 8,4 right)=left( 6,18 right)-left( 16,8 right)=vec{c}left( -10,10 right));
- ( -10+10=0).
Ответ: ( 0)
Расстояние между двумя точками на координатной плоскости
Давай рассмотрим теперь следующую задачу: у нас есть две точки на координатной плоскости. Как найти расстояние между ними?
Пусть первая точка будет ( {{P}_{1}}({{x}_{1}},{{y}_{1}})), а вторая ( {{P}_{2}}left( {{x}_{2}},{{y}_{2}} right)).
Обозначим расстояние между ними через ( d). Давай сделаем для наглядности следующий чертеж:
Что я сделал?
Я, во-первых, соединил точки ( {{P}_{1}}left( {{x}_{1}},{{y}_{1}} right)) и ( {{P}_{2}}left( {{x}_{2}},{{y}_{2}} right)).
А также из точки ( {{P}_{1}}) провел линию, параллельную оси ( Ox), а из точки ( {{P}_{2}}) провел линию, параллельную оси ( Oy).
Они пересеклись в точке ( R), образовав при этом замечательную фигуру. Чем она замечательна?
Да мы с тобой почти что все знаем про прямоугольный треугольник. Ну уж теорему Пифагора – точно!
Искомый отрезок – это гипотенуза этого треугольника, а отрезки ( {{P}_{1}}R,~{{P}_{2}}R) – катеты.
Чему равны координаты точки ( R)?
Да, их несложно найти по картинке: ( Rleft( {{x}_{2}},{{y}_{1}} right).~)
Так как отрезки ( {{P}_{1}}R,~{{P}_{2}}R) параллельны осям ( Ox) и ( Oy) соответственно, то их длины легко найти: если обозначить длины отрезков ( {{P}_{1}}R,~{{P}_{2}}R) соответственно через ( left| {{P}_{1}}Rleft| ,~ right|{{P}_{2}}R right|), то
( left| {{P}_{1}}R right|={{x}_{2}}-{{x}_{1}})
( left| {{P}_{2}}R right|={{y}_{2}}-{{y}_{1}})
Теперь воспользуемся теоремой Пифагора. Длины катетов нам известны, гипотенузу мы найдем:
( {{d}^{2}}=text{ }!!~!!text{ }left| {{P}_{1}}{{P}_{2}} right|=text{ }!!~!!text{ }{{left| {{P}_{1}}R right|}^{2}}+{{left| {{P}_{2}}R right|}^{2}}=({{x}_{2}}-{{x}_{1}}){{~}^{2}}+({{y}_{2}}-{{y}_{1}}){{~}^{2}}~)
( d=~sqrt{({{x}_{2}}-{{x}_{1}}){{~}^{2}}+({{y}_{2}}-{{y}_{1}}){{~}^{2}}})
Таким образом, расстояние между двумя точками – это корень из суммы квадратов разностей из координат.
Или же – расстояние между двумя точками – это длина отрезка, их соединяющего.
Легко заметить, что расстояние между точками не зависит от направления.
Тогда:
( d=left| overrightarrow{{{P}_{1}}{{P}_{2}}} right|=left| overrightarrow{{{P}_{2}}{{P}_{1}}} right|=sqrt{({{x}_{2}}-{{x}_{1}}){{~}^{2}}+({{y}_{2}}-{{y}_{1}}){{~}^{2}}})
Отсюда делаем три вывода:
- Длина вектора = корень из суммы квадратов его координат;
- Найти расстояние между двумя точками = найти длину вектора, их соединяющего (в любом направлении);
- Длины векторов, соединяющих две точки в разном направлении, равны.
Давай немного поупражняемся в вычислении расстояния между двумя точками:
Например, если ( Aleft( 1,2 right),~Bleft( 3,4 right)), то расстояние между ( A) и ( B) равно
( d=sqrt{{{left( 3-1 right)}^{2}}+{{left( 4-2 right)}^{2}}}=sqrt{4+4}=sqrt{8}=2sqrt{2})
Или пойдем по-другому: найдем координаты вектора ( overrightarrow{AB})
( overrightarrow{AB}left( 3-1,4-2 right)=overrightarrow{AB}left( 2,2 right))
И найдем длину вектора:
( left| overrightarrow{AB} right|=sqrt{{{2}^{2}}+{{2}^{2}}}=sqrt{8}=2sqrt{2})
Как видишь, одно и то же!
Теперь немного потренируйся сам:
Задание. Найти расстояние между указанными точками:
- ( Aleft( 2,sqrt{3} right),~Bleft( 5,2sqrt{3} right));
- ( Cleft( 2,4 right),~Dleft( 1,-5 right));
- ( Fleft( sqrt{12},1 right),~Gleft( sqrt{3},-1 right)).
Проверяем:
- ( d=sqrt{{{left( 5-2 right)}^{2}}+{{left( 2sqrt{3}-sqrt{3} right)}^{2}}}=sqrt{9+3}=sqrt{12}=2sqrt{3});
- ( displaystyle d=sqrt{{{left( 1-2 right)}^{2}}+{{left( -5-4 right)}^{2}}}=sqrt{1+81}=sqrt{82});
- ( displaystyle d=sqrt{{{left( sqrt{3}-sqrt{12} right)}^{2}}+{{left( -1-1 right)}^{2}}}=sqrt{left( 3-2sqrt{3}sqrt{12}+12 right)+4}=); ( displaystyle=sqrt{3-2sqrt{36}+12+4}=sqrt{3-12+12+4}=sqrt{7}).
Вот еще пара задачек на ту же формулу, правда звучат они немного по-другому:
1. Найдите квадрат длины вектора ( vec{a}-vec{b}).
2. Найдите квадрат длины вектора ( overrightarrow{AB})
Я так думаю, ты с ними без труда справился? Проверяем:
1. А это на внимательность) Мы уже нашли координаты векторов ( displaystyle {vec{a}}) и ( displaystyle {vec{b}}) ранее: ( displaystyle vec{a}left( 2,6 right),~vec{b}left( 8,4 right)). Тогда вектор ( displaystyle vec{a}-vec{b}) имеет координаты ( displaystyle left( 2-8,6-4 right)=left( -6,2 right)). Квадрат его длины будет равен:
( displaystyle {{d}^{2}}={{left( -6 right)}^{2}}+{{2}^{2}}=36+4=40.)
2. Найдем координаты вектора ( displaystyle overrightarrow{AB}=overrightarrow{AB}left( 8-2,6-4 right)=overrightarrow{AB}left( 6,2 right))
Тогда квадрат его длины равен
( displaystyle {{d}^{2}}={{6}^{2}}+{{2}^{2}}=36+4=40.)
Ничего сложного, правда? Обычная арифметика, не более того.
Следующие задачки нельзя однозначно классифицировать, они скорее на общую эрудицию и на умение рисовать простенькие картинки.
Задача 1. Найдите синус угла наклона отрезка, соединяющего точки ( displaystyle Oleft( 0;~0 right)),( displaystyle Aleft( 6;~8 right)) с осью абсцисс.
Как мы будем поступать здесь?
Нужно найти синус угла между ( displaystyle OA) и осью ( displaystyle Ox).
А где мы умеем искать синус? Верно, в прямоугольном треугольнике.
Так что нам нужно сделать? Построить этот треугольник!
Поскольку координаты точки ( displaystyle A-6) и ( displaystyle 8), то отрезок ( displaystyle OB) равен ( displaystyle 6), а отрезок ( displaystyle AB-8).
Нам нужно найти синус угла ( displaystyle angle AOB).
Напомню тебе, что синус – это отношение противолежащего катета к гипотенузе, тогда
( displaystyle sinangle AOB=frac{AB}{OA})
Что нам осталось сделать?
Найти гипотенузу.
Ты можешь сделать это двумя способами: по теореме Пифагора (катеты-то известны!) или по формуле расстояния между двумя точками (на самом деле одно и то же, что и первый способ!).
Я пойду вторым путем:
( displaystyle OA=sqrt{{{left( 6-0 right)}^{2}}+{{left( 8-0 right)}^{2}}}=10)
Тогда
( displaystyle sinangle AOB=frac{AB}{OA}=frac{8}{10}=0.8)
Ответ: ( displaystyle 0.8)
Следующая задача покажется тебе еще проще. Она – на координаты точки.
Задача 3. В условиях предыдущей задачи найти сумму расстояний от точки ( displaystyle A) до осей координат.
Задача – вообще элементарная, если знать, что такое расстояние от точки до осей.
Ты знаешь?
Я надеюсь, но все же напомню тебе:
Расстояние от точки до осей координат – это длины перпендикуляров, опущенных из точки к осям.
Итак, на моем рисунке, расположенном чуть выше, я уже изобразил один такой перпендикуляр. К какой он оси?
К оси ( displaystyle Ox).
И чему же равна тогда его длина?
Она равна ( displaystyle 8).
Теперь сам проведи перпендикуляр к оси ( displaystyle Oy) и найди его длину. Она будет равна ( displaystyle 6), ведь так?
Тогда их сумма равна ( displaystyle 14).
Ответ: ( displaystyle 14).
Задача 4. В условиях задачи 2, найдите ординату точки, симметричной точке ( displaystyle A) относительно оси абсцисс.
Решение:
Я думаю, тебе интуитивно ясно, что такое симметрия?
Очень многие объекты ею обладают: многие здания, столы, самолеты, многие геометрические фигуры: шар, цилиндр, квадрат, ромб и т. д.
Грубо говоря, симметрию можно понимать вот как: фигура состоит из двух (или более) одинаковых половинок. Такая симметрия называется осевой.
А что тогда такое ось?
Это как раз та линия, по которой фигуру можно, условно говоря, «разрезать» на одинаковые половинки (на данной картинке ось симметрии – прямая ( displaystyle l)):
Теперь давай вернемся к нашей задаче.
Нам известно, что мы ищем точку, симметричную относительно оси ( displaystyle Ox).
Тогда эта ось – ось симметрии.
Значит, нам нужно отметить такую точку ( displaystyle {{A}_{1}}), чтобы ось ( displaystyle Ox) разрезала отрезок ( displaystyle A{{A}_{1}}) на две равные части.
Попробуй сам отметить такую точку. А теперь сравни с моим решением:
У тебя получилось так же?
Хорошо! У найденной точки нас интересует ордината.
Она равна ( displaystyle -8)
Ответ: ( displaystyle -8)
Теперь задачка на параллелограмм:
Задача 5. Точки ( displaystyle Oleft( 0;~0 right),~Aleft( 6;~8 right),~Cleft( 0;~6 right)~) являются вершинами параллелограмма. Найдите ординату точки ( displaystyle B).
Можно решать эту задачу двумя способами: логикой и методом координат.
Я вначале применю метод координат, а потом расскажу тебе, как можно решить иначе.
Совершенно ясно, что абсцисса точки ( displaystyle B) равна ( displaystyle 6). (она лежит на перпендикуляре, проведенной из точки ( displaystyle A) к оси абсцисс).
Нам нужно найти ординату.
Воспользуемся тем, что наша фигура – параллелограмм, это значит, что ( displaystyle CA=OB).
Найдем длину отрезка ( displaystyle CA), используя формулу расстояния между двумя точками:
( d=sqrt{{{left( 6-0 right)}^{2}}+{{left( 8-6 right)}^{2}}}=sqrt{40})
Тогда ( OB=sqrt{40}.~~)
Опускаем перпендикуляр, соединяющий точку ( B) с осью ( Ox).
Точку пересечения обозначу буквой ( D).
Длина отрезка ( OD) равна ( 6). (найди сам задачу, где мы обсуждали этот момент), тогда найдем длину отрезка ( BD) по теореме Пифагора:
( BD=sqrt{40-36}=2)
Длина отрезка – в точности совпадает с его ординатой.
Ответ: ( 2).
Другое решение (я просто приведу рисунок, который его иллюстрирует)
Ход решения:
- Провести ( CE);
- Найти координаты точки ( E) и длину ( AE);
- Доказать, что ( BD=AE).
Еще одна задачка на длину отрезка:
Точки ( Oleft( 0;~0 right),~Aleft( 6;~8 right),~Bleft( 8;~2 right)) являются вершинами треугольника. Найдите длину его средней линии ( CD), параллельной ( OA).
Ты помнишь, что такое средняя линия треугольника?
Тогда для тебя эта задача элементарна. Если не помнишь, то я напомню: средняя линия треугольника – это линия, которая соединяет середины противоположных сторон.
Она параллельна основанию и равна его половине.
Основание – это отрезок ( OA).
Его длину нам приходилось искать ранее, оно равно ( 10).
Тогда длина средней линии вдвое меньше и равна ( 5).
Ответ: ( 5).
Комментарий: эту задачу можно решить и другим способом, к которому мы обратимся чуть позже.
А пока – вот тебе несколько задачек, потренируйся на них, они совсем простые, но помогают «набивать руку», на использовании метода координат!
1. Точки ( Oleft( 0;~0 right),~Aleft( 10;~0 right),~Bleft( 8;~6 right),~Cleft( 2;~6 right)) являются вершинами трапеции. Найдите длину ее средней линии ( DE).
2. Точки ( Oleft( 0;~0 right),~Bleft( 8;~2 right),~Cleft( 2;~6 right)) и ( A) являются вершинами параллелограмма. Найдите ординату точки ( A).
3. Найдите длину отрезка, соединяющего точки ( Aleft( 6 ;~8 right)) и ( Bleft( -2;~2 right).)
4. Найдите площадь закрашенной фигуры на координатной плоскости.
5. Окружность с центром в начале координат проходит через точку ( displaystyle Pleft( 8;text{ }6 right)). Найдите ее радиус.
6. Найдите радиус окружности, описанной около прямоугольника ( displaystyle ABCD), вершины которого имеют координаты соответственно ( displaystyle left( -2;~-2 right),~left( 6;~-2 right),~left( 6;~4 right),~left( -2;~4 right).)
Решения:
1. Известно, что средняя линия трапеции равна полусумме ее оснований.
Основание ( displaystyle CB) равно ( displaystyle 6), а основание ( displaystyle OA-10).
Тогда ( displaystyle ED=frac{CB+OA}{2}=frac{16}{2}=8)
Ответ: ( displaystyle 
2. Проще всего решить эту задачу так: заметить, что ( displaystyle overrightarrow{OA}=overrightarrow{OC}+overrightarrow{OB}) (правило параллелограмма).
Вычислить координаты векторов ( displaystyle overrightarrow{OC}) и ( displaystyle overrightarrow{OB}) не представляет труда: ( displaystyle overrightarrow{OC}left( 2,6 right),~overrightarrow{OB}left( 8,2 right)).
При сложении векторов координаты складываются.
Тогда ( displaystyle overrightarrow{OA}) имеет координаты ( displaystyle left( 10,8 right)).
Эти же координаты имеет и точка ( displaystyle A), поскольку начало вектора ( displaystyle overrightarrow{OA}) – это точка с координатами ( displaystyle left( 0,0 right)).
Нас интересует ордината. Она равна ( displaystyle 8).
Ответ: ( displaystyle 
3. Действуем сразу по формуле расстояния между двумя точками:
( displaystyle d=sqrt{{{left( 6-left( -2 right) right)}^{2}}+{{left( 8-2 right)}^{2}}}=sqrt{64+36}=10)
Ответ: ( displaystyle 10)
4. Посмотри на картинку и скажи, между какими двумя фигурами «зажата» заштрихованная область?
Она зажата между двумя квадратами. Тогда площадь искомой фигуры равна площади большого квадрата минус площадь маленького.
Сторона маленького квадрата – это отрезок, соединяющий точки ( displaystyle left( 0,2 right)) и ( displaystyle left( 2,0 right).) Его длина равна
( displaystyle {{d}_{1}}=sqrt{{{left( 0-2 right)}^{2}}+{{left( 2-0 right)}^{2}}}=sqrt{8})
Тогда площадь маленького квадрата равна
( displaystyle {{S}_{1}}=d_{1}^{2}={{sqrt{8}}^{2}}=8)
Точно так же поступаем и с большим квадратом: его сторона – это отрезок, соединяющий точки ( displaystyle left( 0,4 right)) и ( displaystyle left( 4,0 right).)
Его длина равна
( displaystyle {{d}_{2}}=sqrt{{{left( 0-4 right)}^{2}}+{{left( 4-0 right)}^{2}}}=sqrt{32}).
Тогда площадь большого квадрата равна
( displaystyle {{S}_{2}}=d_{2}^{2}={{sqrt{32}}^{2}}=32)
Площадь искомой фигуры найдем по формуле:
( displaystyle S={{S}_{2}}-{{S}_{1}}=32-8=24)
Ответ: ( displaystyle 24)
5. Если окружность имеет в качестве центра начало координат и проходит через точку ( displaystyle P), то ее радиус ( displaystyle R) будет в точности равен длине отрезка ( displaystyle OP) (сделай рисунок и ты поймешь, почему это очевидно).
Найдем длину этого отрезка:
( displaystyle R=sqrt{{{6}^{2}}+{{8}^{2}}}=10)
Ответ: ( displaystyle 10)
6. Известно, что радиус описанной около прямоугольника окружности равен половине его диагонали.
Найдем длину любой из двух диагоналей (ведь в прямоугольнике они равны!)
( displaystyle left| AC right|=sqrt{{{left( 6-left( -2 right) right)}^{2}}+{{left( 4-left( -2 right) right)}^{2}}}=10)
Тогда
( displaystyle R=frac{1}{2}left| AC right|=5)
Ответ: ( displaystyle 5)
Ну что, ты со всем справился?
Было не очень сложно разобраться, ведь так? Правило здесь одно – уметь сделать наглядную картинку и просто «считать» с нее все данные.
Нам осталось совсем немного. Есть еще буквально два момента, которые бы мне хотелось обсудить:
- как найти координаты середины отрезка и
Координаты середины отрезка
Давай попробуем решить вот такую нехитрую задачку.
Пусть даны две точки ( displaystyle Aleft( {{x}_{1}},{{x}_{2}} right)~) и ( displaystyle Bleft( {{x}_{2}},{{y}_{2}} right)).
Найти координаты середины отрезка ( displaystyle AB). Решение этой задачки следующее: пусть точка ( displaystyle D) – искомая середина, тогда ( displaystyle D) имеет координаты:
( displaystyle Dleft( frac{{{x}_{1}}+{{x}_{2}}}{2},frac{{{y}_{1}}+{{y}_{2}}}{2} right))
То есть: координаты середины отрезка = среднее арифметическое соответствующих координат концов отрезка.
Это правило очень простое и как правило не вызывает затруднений у учащихся. Давай посмотрим, в каких задачках и как оно употребляется:
1. Найдите ординату середины отрезка, соединяющего точки ( displaystyle Aleft( 6,~8 right)~) и ( displaystyle Bleft( -2,~2 right).)
2. Точки ( displaystyle Oleft( 0;~0 right),~Aleft( 6;~8 right),~Bleft( 6;~2 right),~Cleft( 0;~6 right)) являются вершинами четырехугольника. Найдите ординату точки ( displaystyle P) пересечения его диагоналей.
3. Найдите абсциссу центра окружности, описанной около прямоугольника ( displaystyle ABCD), вершины которого имеют координаты соответственно ( displaystyle left( -2;~-2 right),~left( 6;~-2 right),~left( 6;~4 right),~left( -2;~4 right)).
Решения:
1. Первая задачка – просто классика. Действуем сразу по определению середины отрезка. Она имеет координаты ( displaystyle left( frac{6-2}{2},~frac{8+2}{2} right)=left( 2,5 right)).
Ордината равна ( displaystyle 5).
Ответ: ( displaystyle 5)
2. Легко видеть, что данный четырехугольник является параллелограммом (даже ромбом!). Ты и сам можешь это доказать, вычислив длины сторон и сравнив их между собой.
Что я знаю про параллелограмм?
Его диагонали точкой пересечения делятся пополам! Ага! Значит точка пересечения диагоналей – это что?
Это середина любой из диагоналей!
Выберу, в частности диагональ ( displaystyle OA). Тогда точка ( displaystyle P) имеет координаты ( displaystyle left( frac{6+0}{2},frac{8+0}{2} right)=left( 3,4 right).)
Ордината точки ( displaystyle P) равна ( displaystyle 4).
Ответ: ( displaystyle 4)
3. С чем совпадает центр описанной около прямоугольника окружности?
Он совпадает с точкой пересечения его диагоналей. А что ты знаешь про диагонали прямоугольника?
Они равны и точкой пересечения делятся пополам. Задача свелась к предыдущей.
Возьму, например, диагональ ( displaystyle AC). Тогда если ( displaystyle P) – центр описанной окружности, то ( displaystyle P) – середина ( displaystyle AC).
Ищу координаты: ( displaystyle Pleft( frac{-2+6}{2},frac{-2+4}{2} right)=Pleft( 2,1 right).) Абсцисса равна ( displaystyle 2).
Ответ: ( displaystyle 2)
Теперь потренируйся немного самостоятельно, я лишь приведу ответы к каждой задачи, чтобы ты мог себя проверить.
1. Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты ( displaystyle left( 8;~0 right),~left( 0;~6 right),~left( 8;~6 right).)
2. Найдите ординату центра окружности, описанной около треугольника, вершины которого имеют координаты ( displaystyle left( 8;~0 right),~left( 0;~6 right),~left( 8;~6 right).)
3. Какого радиуса должна быть окружность с центром в точке ( displaystyle Pleft( 8;~6 right),) чтобы она касалась оси абсцисс?
4. Найдите ординату точки пересечения оси ( displaystyle Oy) и отрезка, соединяющего точки ( displaystyle Aleft( 6;text{ }8 right)) и ( displaystyle Bleft( -6;text{ }0 right).)
Ответы:
- ( displaystyle 5);
- ( displaystyle 3);
- ( displaystyle 6);
- ( displaystyle 4).
Умножение векторов
Все удалось? Очень на это надеюсь! Теперь – последний рывок.
Сейчас будь особенно внимателен. Тот материал, который я сейчас буду объяснять, имеет непосредственное отношение не только к простым задачам на метод координат, но также встречается повсеместно и в задачах повышенной сложности.
Какое из своих обещаний я еще не сдержал?
Вспомни, какие операции над векторами я обещал ввести и какие в конечном счете ввел? Я точно ничего не забыл?
Забыл! Забыл объяснить, что значит умножение векторов.
Есть два способа умножить вектор на вектор. В зависимости от выбранного способа у нас будут получаться объекты разной природы:
- Скалярное произведение (результат – число);
- Векторное произведение (результат – вектор).
Векторное произведение выполняется довольно хитро. Как его делать и для чего оно нужно, мы с тобой обсудим чуть позже. А пока мы остановимся на скалярном произведении.
Есть аж два способа, позволяющих нам его вычислить:
- Через координаты векторов;
- Через длины векторов и угол между ними.
Как ты догадался, результат должен быть один и тот же! Итак, давай вначале рассмотрим первый способ:
Найдите скалярное произведение векторов ( displaystyle {vec{a}}) и ( displaystyle {vec{b}})
Справился? Может, и подвох небольшой заметил? Давай проверим:
( displaystyle vec{a}left( 2,6 right)), ( displaystyle vec{b}left( 8,4 right)) – координаты векторов, как в прошлой задаче! Ответ: ( displaystyle 40).
Скалярное произведение через длины векторов и косинус угла между ними
Помимо координатного, есть и другой способ вычислить скалярное произведение, а именно, через длины векторов и косинус угла между ними:
( displaystyle left( vec{a},~vec{b} right)=left| {vec{a}} right|left| {vec{b}} right|coswidehat{vec{a},~vec{b}})
( displaystyle widehat{vec{a},~vec{b}}) – обозначает угол между векторами ( displaystyle {vec{a}}) и ( displaystyle {vec{b}}).
То есть скалярное произведение равно произведению длин векторов на косинус угла между ними.
Зачем же нам эта вторая формула, если у нас есть первая, которая намного проще, в ней по крайней мере нет никаких косинусов?
А нужна она для того, что из первой и второй формулы мы с тобой сможем вывести, как находить угол между векторами!
Пусть ( displaystyle vec{a}left( {{x}_{1}},{{y}_{1}} right),~vec{b}left( {{x}_{2}},{{y}_{2}} right).) Тогда вспоминай формулу для длины вектора!
( displaystyle left| {vec{a}} right|=sqrt{x_{1}^{2}+y_{1}^{2}})
( displaystyle left| {vec{b}} right|=sqrt{x_{2}^{2}+y_{2}^{2}})
Тогда если я подставлю эти данные в формулу скалярного произведения, то я получу:
( displaystyle left( vec{a},~vec{b} right)=sqrt{x_{1}^{2}+y_{1}^{2}}cdot sqrt{x_{2}^{2}+y_{2}^{2}}coswidehat{vec{a},~vec{b}})
Но с другой стороны:
( displaystyle left( vec{a},~vec{b} right)={{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}})
Тогда
( displaystyle {{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}=sqrt{x_{1}^{2}+y_{1}^{2}}cdot sqrt{x_{2}^{2}+y_{2}^{2}}coswidehat{vec{a},~vec{b}})
Или
( displaystyle coswidehat{vec{a},~vec{b}}=frac{{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}}{sqrt{x_{1}^{2}+y_{1}^{2}}cdot sqrt{x_{2}^{2}+y_{2}^{2}}})
Таким образом, что же мы с тобой получили?
У нас теперь есть формула, позволяющая вычислять угол между двумя векторами! Иногда ее для краткости записывают еще и так:
( displaystyle coswidehat{vec{a},~vec{b}}=frac{left( vec{a},~vec{b} right)}{left| {vec{a}} right|left| {vec{b}} right|})
Решение:
1. Эти вектора – наши старые знакомые. Их скалярное произведение мы уже считали и оно было равно ( displaystyle 40).
Координаты у них такие: ( displaystyle vec{a}left( 2,6 right)), ( displaystyle vec{b}left( 8,4 right)). Тогда найдем их длины:
( left| {vec{a}} right|=sqrt{{{2}^{2}}+{{6}^{2}}}=sqrt{40})
( left| {vec{b}} right|=sqrt{{{8}^{2}}+{{4}^{2}}}=sqrt{80})
Тогда ищем косинус между векторами:
( coswidehat{vec{a},~vec{b}}=frac{left( vec{a},~vec{b} right)}{left| {vec{a}} right|left| {vec{b}} right|}=frac{40}{sqrt{40}sqrt{80}}=frac{sqrt{40}sqrt{40}}{sqrt{40}sqrt{80}}=frac{1}{sqrt{2}})
Косинус какого угла равен ( frac{1}{sqrt{2}})? Это угол ( 45{}^circ ).
Ответ: ( 45)
Ну а теперь сам реши вторую задачу, а потом сравним! Я приведу лишь очень краткое решение:
2. ( vec{a}+vec{b}) имеет координаты ( left( 10,10 right)), ( vec{a}-vec{b}) имеет координаты ( left( -6,2 right)).
( left( vec{a}+vec{b},vec{a}-vec{b} right)=-60+20=-40)
( left| vec{a}+vec{b} right|=sqrt{{{10}^{2}}+{{10}^{2}}}=10sqrt{2})
( left| vec{a}-vec{b} right|=sqrt{{{left( -6 right)}^{2}}+{{2}^{2}}}=sqrt{40}).
Пусть ( a) – угол между векторами ( vec{a}+vec{b}) и ( vec{a}-vec{b}), тогда
( cosa=frac{-40}{10sqrt{2}sqrt{40}}=-frac{sqrt{40}}{10sqrt{2}}=-frac{sqrt{20}}{10}=-frac{sqrt{5}}{5})
Ответ: ( -frac{sqrt{5}}{5})
Метод координат (продвинутый уровень)
Мы с тобой продолжаем изучать метод координат. В прошлой части мы вывели ряд важных формул, которые позволяют:
- Находить координаты вектора;
- Находить длину вектора (альтернативно: расстояние между двумя точками);
- Складывать, вычитать векторы. Умножать их на вещественное число;
- Находить середину отрезка;
- Вычислять скалярное произведение векторов;
- Находить угол между векторами.
Конечно, в эти 6 пунктов не укладывается весь координатный метод.
Он лежит в основе такой науки, как аналитическая геометрия, с которой тебе предстоит познакомиться в ВУЗе. Я лишь хочу построить фундамент, который позволит тебе решать задачи ЕГЭ любого уровня сложности!
Этот раздел будет посвящен методу решения тех задач, в которых будет разумно перейти к методу координат. Эта разумность определяется тем, что в задаче требуется найти, и какая фигура дана.
Когда стоит применять метод координат
Итак, я бы стал применять метод координат, если ставятся вопросы:
- Найти угол между двумя плоскостями;
- Найти угол между прямой и плоскостью;
- Найти угол между двумя прямыми;
- Найти расстояние от точки до плоскости;
- Найти расстояние от точки до прямой;
- Найти расстояние от прямой до плоскости;
- Найти расстояние между двумя прямыми.
Подходящими фигурами для метода координат являются:
- Куб;
- Прямоугольный параллелепипед;
- Прямая призма (треугольная, шестиугольная…);
- Пирамида (треугольная, четырехугольная, шестиугольная);
- Тетраэдр (одно и то же, что и треугольная пирамида).
Неподходящими фигурами для метода координат являются тела вращения:
- шар;
- цилиндр;
- конус
По моему опыту, нецелесообразно использовать метод координат для:
- Нахождения площадей сечений;
- Вычисления объемов тел.
Однако следует сразу отметить, что три «невыгодные» для метода координат ситуации на практике достаточно редки.
В большинстве же задач он может стать твоим спасителем, особенно если ты не очень силен в трехмерных построениях (которые порою бывают довольно замысловатыми).
Как применять метод координат
Какими являются все перечисленные мною выше фигуры?
Они уже не плоские, как, например, квадрат, треугольник, окружность, а объемные! Соответственно, нам нужно рассматривать уже не двухмерную, а трехмерную систему координат.
Строится она достаточно легко: просто помимо оси абсцисс и ординат, мы введем еще одну ось, ось аппликат. На рисунке схематично изображено их взаимное расположение:
Все они являются взаимно перпендикулярными, пересекаются в одной точке ( displaystyle O), которую мы будем называть началом координат.
Ось абсцисс, как и прежде, будем обозначать ( Ox), ось ординат – ( Oy), а введенную ось аппликат – ( Oz).
Если раньше каждая точка на плоскости характеризовалась двумя числами – абсциссой и ординатой, то каждая точка в пространстве уже описывается тремя числами – абсциссой, ординатой, аппликатой.
Например:
Соответственно абсцисса точки ( displaystyle P) равна ( displaystyle 1), ордината – ( displaystyle 2), а аппликата – ( displaystyle 3).
Иногда абсциссу точки еще называют проекцией точки на ось абсцисс, ординату – проекцией точки на ось ординат, а аппликату – проекцией точки на ось аппликат. Соответственно, если задана точка ( Aleft( x,y,z right)) то, точку с координатами:
( Aleft( x,y,0 right)) называют проекцией точки ( Aleft( x,y,z right)) на плоскость ( Oxy)
( Aleft( x,0,z right)) называют проекцией точки ( Aleft( x,y,z right)) на плоскость ( Oxz)
( Aleft( 0,y,z right)) называют проекцией точки ( Aleft( x,y,z right)) на плоскость ( Oyz)
Встает естественный вопрос: справедливы ли все формулы, выведенные для двухмерного случая, в пространстве?
Ответ утвердительный, они справедливы и имеют тот же самый вид. За маленькой деталью. Я думаю, ты уже сам догадался, за какой именно.
Во все формулы мы должны будем добавить еще один член, отвечающий за ось аппликат.
Формулы метода координат для трехмерных фигур
1. Если заданы две точки: ( Aleft( {{x}_{1}},{{y}_{1}},{{z}_{1}} right)), ( Aleft( {{x}_{2}},{{y}_{2}},{{z}_{2}} right)), то:
- Координаты вектора ( overrightarrow{AB}): ( overrightarrow{AB}left( {{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}},{{z}_{2}}-{{z}_{1}} right));
- Расстояние между двумя точками (или длина вектора ( overrightarrow{AB})) ( d=left| overrightarrow{AB} right|=sqrt{{{left( {{x}_{2}}-{{x}_{1}} right)}^{2}}+{{left( {{y}_{2}}-{{y}_{1}} right)}^{2}}+{{left( {{z}_{2}}-{{z}_{1}} right)}^{2}}});
- Середина ( D) отрезка ( AB) имеет координаты
- ( Dleft( frac{{{x}_{1}}+{{x}_{2}}}{2},frac{{{y}_{1}}+{{y}_{2}}}{2},frac{{{z}_{1}}+{{z}_{2}}}{2} right)).
2. Если дано два вектора: ( vec{a}left( {{x}_{1}},{{y}_{1}},{{z}_{1}} right)) и ( vec{b}left( {{x}_{2}},{{y}_{2}},{{z}_{2}} right)), то:
- Их скалярное произведение равно: ( left( vec{a},~vec{b} right)=left| {vec{a}} right|left| {vec{b}} right|cosoverset{}{widehat{vec{a},~vec{b}}},) или ( left( vec{a},~vec{b} right)={{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}+{{z}_{1}}{{z}_{2}});
- Косинус угла между векторами равен:
- ( cosoverset{}{widehat{vec{a},~vec{b}}},=frac{left( vec{a},~vec{b} right)}{left| {vec{a}} right|left| {vec{b}} right|}=frac{{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}+{{z}_{1}}{{z}_{2}}}{sqrt{x_{1}^{2}+y_{1}^{2}+z_{1}^{2}}cdot sqrt{x_{2}^{2}+y_{2}^{2}+z_{2}^{2}}}).
Плоскость — как «обобщение» прямой
Однако с пространством не все так просто.
Как ты понимаешь, добавление еще одной координаты вносит существенное разнообразие в спектр фигур, «живущих» в этом пространстве. И для дальнейшего повествования мне потребуется ввести некоторое, грубо говоря, «обобщение» прямой.
Этим «обобщением» будет плоскость. Что ты знаешь про плоскость? Попробуй ответить на вопрос, а что такое плоскость? Очень сложно сказать.
Однако мы все интуитивно представляем, как она выглядит:
Грубо говоря, это некий бесконечный «лист», засунутый в пространство. «Бесконечность» следует понимать, что плоскость распространяется во все стороны, то есть ее площадь равна бесконечности.
Однако, это объяснение «на пальцах» не дает ни малейшего представления о структуре плоскости. А нас будет интересовать именно она.
Давай вспомним одну из основных аксиом геометрии: через две различные точки на плоскости проходит прямая, притом только одна.
Или ее аналог в пространстве: через три точки, не лежащие на одной прямой, проходит плоскость, притом только одна.
Уравнение прямой в плоскости и пространстве
Конечно, ты помнишь, как по двум заданным точкам вывести уравнение прямой, это совсем нетрудно: если первая точка имеет координаты: ( Aleft( {{x}_{0}},{{y}_{0}} right)) а вторая ( Bleft( {{x}_{1}},{{y}_{1}} right)), то уравнение прямой будет следующим:
( frac{x-{{x}_{0}}}{{{x}_{1}}-{{x}_{0}}}=frac{y-{{y}_{0}}}{{{y}_{1}}-{{y}_{0}}})
( left( x-{{x}_{0}} right)left( {{y}_{1}}-{{y}_{0}} right)=left( y-{{y}_{0}} right)left( {{x}_{1}}-{{x}_{0}} right))
Это ты проходил еще в 7 классе.
В пространстве уравнение прямой выглядит вот так: пусть у нас даны две точки с координатами: ( Aleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right)), ( Bleft( {{x}_{1}},{{y}_{1}},{{z}_{1}} right)), то уравнение прямой, через них проходящей, имеет вид:
( frac{x-{{x}_{0}}}{{{x}_{1}}-{{x}_{0}}}=frac{y-{{y}_{0}}}{{{y}_{1}}-{{y}_{0}}}=frac{z-{{z}_{0}}}{{{z}_{1}}-{{z}_{0}}})
Например, через точки ( Aleft( 1,2,3 right)), ( Bleft( 4,5,6 right)) проходит прямая:
( frac{x-1}{4-1}=frac{y-2}{5-2}=frac{z-3}{6-3})
( frac{x-1}{3}=frac{y-2}{3}=frac{z-3}{3})
( x-1=y-2=z-3)
Как это следует понимать?
Это следует понимать вот как: точка ( Dleft( x,y,z right)) лежит на прямой, если ее координаты удовлетворяют следующей системе:
( displaystyle left{ begin{array}{l}x-1=y-2\x-1=z-3end{array} right.)
Нас не очень будет интересовать уравнение прямой, но нам нужно обратить внимание на очень важное понятие направляющего вектора прямой.
Направляющий вектор прямой
Направляющий вектор прямой – любой ненулевой вектор, лежащий на данной прямой или параллельный ей.
Например, оба вектора ( overrightarrow{{{M}_{0}}{{M}_{1}}}), ( vec{s}) являются направляющими векторами прямой ( l). Пусть ( Mleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right)) – точка, лежащая на прямой, а ( vec{p}left( m,n,q right)) – ее направляющий вектор.
Тогда уравнение прямой можно записать в следующем виде:
( frac{x-{{x}_{0}}}{m}=frac{y-{{y}_{0}}}{n}=frac{z-{{z}_{0}}}{p})
Еще раз повторюсь, мне не очень будет интересно уравнение прямой, но мне очень нужно, чтобы ты запомнил, что такое направляющий вектор!
Еще раз: это ЛЮБОЙ ненулевой вектор, лежащий на прямой, или параллельный ей.
Уравнение плоскости
Вывести уравнение плоскости по трем заданным точкам уже не так тривиально, и обычно этот вопрос не рассматривается в курсе средней школы.
А зря!
Этот прием жизненно необходим, когда мы прибегаем к методу координат для решения сложных задач. Однако, я предполагаю, что ты полон желания научиться чему-то новому?
Более того, ты сможешь поразить своего преподавателя в ВУЗе, когда выяснится, что ты уже умеешь с методикой, которую обычно изучают в курсе аналитической геометрии. Итак, приступим.
Уравнение плоскости не слишком отличается от уравнения прямой на плоскости, а именно оно имеет вид:
( Ax+By+Cz+D=0)
( A,B,C,D-) некоторые числа (не все равные нулю), а ( x,y,z-~) переменные, например: ( 3x+2y-z+1=0,~0.5x-2z-2=0,~x+y=0) и т.д.
Как видишь, уравнение плоскости не очень отличается от уравнения прямой (линейной функции). Однако, вспомни, что мы с тобой утверждали? Мы говорили, что если у нас есть три точки ( Aleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right),~Bleft( {{x}_{1}},{{y}_{1}},{{z}_{1}} right),~Cleft( {{x}_{2}},{{y}_{2}},{{z}_{2}} right)), не лежащие на одной прямой, то уравнение плоскости однозначно по ним восстанавливается.
Но как? Попробую тебе объяснить.
Поскольку уравнение плоскости имеет вид:
( Ax+By+Cz+D=0)
А точки ( Aleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right),~Bleft( {{x}_{1}},{{y}_{1}},{{z}_{1}} right),~Cleft( {{x}_{2}},{{y}_{2}},{{z}_{2}} right)) принадлежат этой плоскости, то при подстановке координат каждой точки в уравнение плоскости мы должны получать верное тождество:
( A{{x}_{0}}+B{{y}_{0}}+C{{z}_{0}}+D=0)
( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D=0)
( A{{x}_{2}}+B{{y}_{2}}+C{{z}_{2}}+D=0)
Таким образом, встает необходимость решать три уравнения аж с ( displaystyle 4) неизвестными!
Дилемма! Однако всегда можно предполагать, что ( D=1) (для этого нужно разделить ( ~Ax+By+Cz+D=0) на ( D)).
Таким образом, мы получим три уравнения с тремя неизвестными ( displaystyle A,B,C):
( A{{x}_{0}}+B{{y}_{0}}+C{{z}_{0}}+1=0)
( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+1=0)
( A{{x}_{2}}+B{{y}_{2}}+C{{z}_{2}}+1=0)
Однако мы не будем решать такую систему, а выпишем загадочное выражение, которое из него следует:
Уравнение плоскости, проходящей через три заданные точки
(left| {begin{array}{*{20}{c}}{x — {x_0}}&{{x_1} — {x_0}}&{{x_2} — {x_0}}\{y — {y_0}}&{{y_1} — {y_0}}&{{y_2} — {y_0}}\{z — {z_0}}&{{z_1} — {z_0}}&{{z_2} — {z_0}}end{array}} right| = 0)
Стоп! Это еще что такое? Какой-то очень необычный модуль!
Однако объект, который ты видишь перед собой не имеет ничего общего с модулем. Этот объект называется определителем третьего порядка.
Определитель третьего порядка
Отныне и впредь, когда ты будешь иметь дело с методом координат на плоскости, тебе очень часто будут встречаться эти самые определители.
Что же такое определитель третьего порядка? Как ни странно, это всего-навсего число. Осталось понять, какое конкретно число мы будем сопоставлять с определителем.
Давай вначале запишем определитель третьего порядка в более общем виде:
( left| {begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}end{array}} right|),
Где ( {{a}_{ij}}) – некоторые числа.
Причем под первым индеком ( displaystyle i) мы понимаем номер строки, а под индеком ( displaystyle j) – номер столбца.
Например, ( {{a}_{23}}) означает, что данное число стоит на пересечении второй строки и третьего столбца.
Давай поставим следующий вопрос: каким именно образом мы будем вычислять такой определитель?
То есть, какое конкретно число мы будем ему сопоставлять?
Для определителя именно третьего порядка есть эвристическое (наглядное) правило треугольника оно выглядит следующим образом:
Как его читать? А понимать его надо следующим образом: мы составляем два выражения:
- Произведение элементов главной диагонали (с верхнего левого угла до нижнего правого) ( displaystyle +) произведение элементов, образующих первый треугольник «перпендикулярный» главной диагонали ( displaystyle +) произведение элементов, образующих второй треугольник «перпендикулярный» главной диагонали;
- Произведение элементов побочной диагонали (с верхнего правого угла до нижнего левого) ( displaystyle +) произведение элементов, образующих первый треугольник «перпендикулярный» побочной диагонали ( displaystyle +) произведение элементов, образующих второй треугольник «перпендикулярный» побочной диагонали;
- Тогда определитель равен разности значений, полученных на шаге ( displaystyle 1) и ( displaystyle 2).
Если записать все это цифрами, то мы получим следующее выражение:
( left| {begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}end{array}} right| = )
( = {a_{11}}{a_{22}}{a_{33}} + {a_{12}}{a_{23}}{a_{31}} + {a_{21}}{a_{32}}{a_{13}} — left( {{a_{13}}{a_{22}}{a_{31}} + {a_{23}}{a_{32}}{a_{11}} + {a_{21}}{a_{12}}{a_{33}}} right))
Тем не менее, запоминать способ вычисления в таком виде не нужно, достаточно в голове просто держать треугольники и саму идею, что с чем складывается и что из чего затем вычитается).
Давай проиллюстрируем метод треугольников на примере:
Метод треугольников на примере
1. Вычислить определитель: ( left| {begin{array}{*{20}{c}}2&3&{ — 1}\{11}&{21}&{ — 5}\4&6&9end{array}} right|)
Давай разбираться, что мы складываем, а что – вычитаем.
Слагаемые, которые идут с «плюсом»:
Это главная диагональ: произведение элементов равно
( 2cdot 21cdot 9=378)
Первый треугольник, «перпендикулярный главной диагонали: произведение элементов равно
( 3cdot left( -5 right)cdot 4=-60)
Второй треугольник, «перпендикулярный главной диагонали: произведение элементов равно
( 11cdot 6cdot left( -1 right)=-66)
Складываем три числа: ( 378-60-66=252)
Слагаемые, которые идут с «минусом»:
Это побочная диагональ: произведение элементов равно
( left( -1 right)cdot 21cdot 4=-84)
Первый треугольник, «перпендикулярный побочной диагонали: произведение элементов равно
( 3cdot 11cdot 9=297)
Второй треугольник, «перпендикулярный побочной диагонали: произведение элементов равно
( 6cdot left( -5 right)cdot 2=-60)
Складываем три числа:
( -84+297-60=153)
Все, что осталось сделать – это вычесть из суммы слагаемых «с плюсом» сумму слагаемых «с минусом»:
( 252-153=99)
Таким образом,
( left| {begin{array}{*{20}{c}}2&3&{ — 1}\{11}&{21}&{ — 5}\4&6&9end{array}} right| = 99)
Как видишь, ничего сложного и сверхъестественного в вычислении определителей третьего порядка нет. Просто важно помнить про треугольники и не допускать арифметических ошибок.
Теперь попробуй самостоятельно вычислить:
( left| {begin{array}{*{20}{c}}2&{ — 2}&4\3&2&5\1&2&2end{array}} right|)
Проверяем:
- Главная диагональ: ( 2cdot 2cdot 2=8);
- Первый треугольник, перпендикулярный главной диагонали: ( left( -2 right)cdot 5cdot 1=-10);
- Второй треугольник, перпендикулярный главной диагонали: ( 3cdot 2cdot 4=24);
- Сумма слагаемых с плюсом: ( 8-10+24=22);
- Побочная диагональ: ( 1cdot 2cdot 4=8);
- Первый треугольник, перпендикулярный побочной диагонали: ( 2cdot 5cdot 2=20);
- Второй треугольник, перпендикулярный побочной диагонали: ( left( -2 right)cdot 3cdot 2=-12);
- Сумма слагаемых с минусом: ( 8+20-12=16);
- Сумма слагаемых с плюсом минус сумма слагаемых с минусом: ( 22-16=6).
Вывод:
( left| {begin{array}{*{20}{c}}2&{ — 2}&4\3&2&5\1&2&2end{array}} right| = 6)
Вот тебе еще пара определителей, вычисли их значения самостоятельно и сравни с ответами:
- ( left| {begin{array}{*{20}{c}}1&3&{ — 1}\0&4&2\{ — 3}&2&0end{array}} right|);
- ( left| {begin{array}{*{20}{c}}3&1&7\6&2&{14}\{ — 1}&0&8end{array}} right|).
Ответы:
- ( displaystyle -34);
- ( displaystyle 0).
Ну что, все совпало?
Отлично, тогда можно двигаться дальше! Если же есть затрудения, то совет мой таков: в интернете есть куча программ вычисления определителя онлайн.
Все, что тебе нужно – придумать свой определитель, вычислить его самостоятельно, а потом сравнить с тем, что посчитает программа.
И так до тех пор, пока результаты не начнут совпадать. Уверен, этот момент не заставит себя долго ждать!
Теперь давай вернемся к тому определителю, который я выписал, когда говорил про уравнение плоскости, проходящей через три заданные точки:
( left| {begin{array}{*{20}{c}}{x — {x_0}}&{{x_1} — {x_0}}&{{x_2} — {x_0}}\{y — {y_0}}&{{y_1} — {y_0}}&{{y_2} — {y_0}}\{z — {z_0}}&{{z_1} — {z_0}}&{{z_2} — {z_0}}end{array}} right| = 0)
Все, что тебе нужно – это вычислить его значение непосредственно (методом треугольников) и приравнять результат к нулю.
Естественно, поскольку ( displaystyle x,y,z) – переменные, то ты получишь некоторое выражение, от них зависящее.
Именно это выражение и будет уравнением плоскости, проходящей через три заданные точки, не лежащие на одной прямой!
( Ax+By+Cz+D=0)
Давай проиллюстрируем сказанное на простом примере:
1. Построить уравнение плоскости, проходящей через точки
( displaystyle {{M}_{1}}left( -3,2,-1 right), {{M}_{2}}left( -1,2,4 right), {{M}_{3}}left( 3,3,-1 right))
Cоставляем для этих трех точек определитель:
( left| {begin{array}{*{20}{c}}{x — left( { — 3} right)}&{ — 1 — left( { — 3} right)}&{3 — left( { — 3} right)}\{y — 2}&{2 — 2}&{3 — 2}\{z — left( { — 1} right)}&{4 — left( { — 1} right)}&{ — 1 — left( { — 1} right)}end{array}} right|).
Упрощаем:
( left| {begin{array}{*{20}{c}}{x + 3}&2&6\{y — 2}&0&1\{z + 1}&5&0end{array}} right|)
Теперь вычисляем его непосредственно по правилу треугольников:
[{left| {begin{array}{*{20}{c}}{x + 3}&2&6\{y — 2}&0&1\{z + 1}&5&0end{array}} right| = left( {x + 3} right) cdot 0 cdot 0 + 2 cdot 1 cdot left( {z + 1} right) + left( {y — 2} right) cdot 5 cdot 6 — }]
( displaystyle -left( left( z+1 right)cdot 6cdot 0+left( x+3 right)cdot 5cdot 1+left( y-2 right)cdot 2cdot 0 right)=)
( displaystyle=2left( z-1 right)+30left( y-2 right)-5left( x+3 right)=-5x+30y+2z-73)
Таким образом, уравнение плоскости, проходящей через точки ( displaystyle {{M}_{1}}left( -3,2,-1 right), {{M}_{2}}left( -1,2,4 right), {{M}_{3}}left( 3,3,-1 right)), имеет вид:
( -5x+30y+2z-73=0)
То есть ( A=-5,~B=30,~C=2,~D=-73)
Теперь попробуй решить одну задачку самостоятельно, а потом мы ее обсудим:
2. Найти уравнение плоскости, проходящей через точки
( {{M}_{1}}left( 1,2,-1 right),~{{M}_{2}}left( -1,0,4 right),~{{M}_{3}}left( -2,-1,1 right))
Ну что, давай теперь обсудим решение:
Составляем определитель:
( left| {begin{array}{*{20}{c}}{x — 1}&{ — 2}&{ — 3}\{y — 2}&{ — 2}&{ — 3}\{z + 1}&5&2end{array}} right|)
И вычисляем его значение:
( begin{array}{l}left| {begin{array}{*{20}{c}}{x — 1}&{ — 2}&{ — 3}\{y — 2}&{ — 2}&{ — 3}\{z + 1}&5&2end{array}} right| = \ = — 4left( {x — 1} right) — 15left( {y — 2} right) + 6left( {z + 1} right) + 15left( {x — 1} right) + 4left( {y — 2} right) — 6left( {z + 1} right) = \ = 11x — 11y + 11end{array})
Тогда уравнение плоскости имеет вид:
( 11x-11y+11=0)
Или же, сократив на ( 11), получим:
( x-y+1=0)
То есть, ( A=1,B=-1,C=0,D=1.)
Теперь две задачи для самоконтроля:
- Построить уравнение плоскости, проходящей через три точки: ( Kleft( 2,3,4 right),~Lleft( 6,-3,4 right),~Mleft( -4,6,-4 right).);
- Построить уравнение плоскости, проходящей через три точки:
- ( Aleft( 5,-1,3 right),~Bleft( 2,2,0 right),~Cleft( -1,1,1 right).).
Проверим:
- ( 6x+4y-3z-12=0);
- ( y+z-2=0).
Все совпало?
Опять-таки, если есть определенные затруднения, то мой совет таков: берешь из головы три точки (с большой степенью вероятности они не будут лежать на одной прямой), строишь по ним плоскость.
А потом проверяешь себя онлайн. Например, на сайте:
http://www.webmath.ru/web/prog9_1.php
Однако при помощи определителей мы будем строить не только уравнение плоскости.
Вспомни, я говорил тебе, что для векторов определено не только скалярное произведение. Есть еще векторное, а также смешанное произведение.
Векторное произведение векторов
И если скалярным произведением двух векторов и будет число, то векторным произведением двух векторов ( vec{a}) и ( vec{b}) будет вектор ( ~vec{c}=vec{a}cdot vec{b}), причем данный вектор будет перпендикулярен к заданным:
Причем его модуль будет равен площади параллелограмма, построенного на векторах ( vec{a}) и ( vec{b}).
Данный вектор понадобится нам для вычисления расстояния от точки до прямой. Как же нам считать векторное произведение векторов ( vec{a}) и ( vec{b}), если их координаты заданы?
На помощь к нам опять приходит определитель третьего порядка.
Однако, прежде чем я перейду к алгоритму вычисления векторного произведения, я вынужден сделать небольшое лирическое отступление.
Данное отступление касается базисных векторов.
Базисными векторами в трехмерном пространстве называются три вектора:
( vec{i}left( 1,0,0 right),~vec{j}left( 0,1,0 right),~vec{k}left( 0,0,1 right))
Схематично они изображены на рисунке:
Как ты думаешь, а почему они называется базисными? Дело в том, что любой вектор в трехмерном пространстве можно представить через сумму трех базисных векторов:
( vec aleft( {x,y,z} right) = x cdot vec i + y cdot vec j + z cdot vec k.)
Или на картинке:
Справедливость этой формулы очевидна, ведь:
( begin{array}{l}xcdot vec{i}=left( x,0,0 right)\ycdot vec{j}=left( 0,y,0 right)\zcdot vec{k}=left( 0,0,z right)end{array})
Тогда
( vec{a}left( x,y,z right)=xcdot vec{i}+ycdot vec{j}+zcdot vec{k}=left( x,0,0 right)+left( 0,y,0 right)+left( 0,0,z right)=left( x,y,z right)=vec{a}.)
Смешанное произведение трех векторов
Последняя конструкция, которая мне понадобится – это смешанное произведение трех векторов.
Оно, как и скалярное, является числом. Есть два способа его вычисления. ( displaystyle 1) – через определитель, ( displaystyle 2) – через смешанное произведение.
А именно, пусть у нас даны три вектора:
( vec{a}left( {{x}_{1}},{{y}_{1}},{{z}_{1}} right),~vec{b}left( {{x}_{2}},{{y}_{2}},{{z}_{2}} right),~vec{c}left( {{x}_{3}},{{y}_{3}},{{z}_{3}} right)), тогда смешанное произведение трех векторов, обозначаемое через ( (vec{a},vec{b},vec{c})) можно вычислить как:
1. ( left( vec{a},vec{b},vec{c} right)=left( vec{a},vec{b}cdot vec{c} right)) – то есть смешанное произведение – это скалярное произведения вектора на векторное произведение двух других векторов
2. ( left( {vec a,vec b,vec c} right) = left| {begin{array}{*{20}{c}}{{x_1}}&{{y_1}}&{{z_1}}\{{x_2}}&{{y_2}}&{{z_2}}\{{x_3}}&{{y_3}}&{{z_3}}end{array}} right|)
Например, смешанное произведение трех векторов ( vec{a}left( 2,3,5 right),~vec{b}left( 1,4,4 right),~vec{c}left( 3,5,7 right)) равно:
( left( {vec a,vec b,vec c} right) = left| {begin{array}{*{20}{c}}2&3&5\1&4&4\3&5&7end{array}} right| = — 4)
Самостоятельно попробуй вычислить его через векторное произведение и убедись, что результаты совпадут!
И опять – два примера для самостоятельного решения:
- ( vec{a}left( 1,2,3 right),~vec{b}left( 1,1,1 right),~vec{c}left( 1,2,1 right));
- ( vec{a}left( 1,2,3 right),~vec{b}left( 1,-1,1 right),~vec{c}left( 2,0,-1 right)).
Ответы:
- ( displaystyle 2);
- ( displaystyle 1).
Выбор системы координат
Ну вот, теперь у нас есть весь необходимый фундамент знаний, чтобы решать сложные стереометрические задачи по геометрии.
Однако прежде чем приступать непосредственно к примерам и алгоритмам их решения, я считаю, что будет полезно остановиться еще вот на каком вопросе: как именно выбирать систему координат для той или иной фигуры.
Ведь именно выбор взаимного расположения системы координат и фигуры в пространстве в конечном счете определит, насколько громоздкими будут вычисления.
Я напомню, что в этом разделе мы рассматриваем следующие фигуры:
- куб;
- Прямоугольный параллелепипед;
- Прямая призма (треугольная, шестиугольная…);
- Пирамида (треугольная, четырехугольная);
- Тетраэдр (одно и то же, что и треугольная пирамида).
Для каждой из фигур я дам практические рекомендации, как выбирать систему координат.
Я неслучайно расположил задачи в таком порядке. Пока ты еще не успел начать ориентироваться в методе координат, я сам разберу наиболее «проблемные» фигуры, а тебе предоставлю разобраться с простейшим кубом!
Постепенно тебе предстоит научиться работать со всеми фигурами, сложность задач я буду увеличивать от теме к теме.
Приступаем к решению задач:
1. Рисуем тетраэдр, помещаем его в систему координат так, как я предлагал ранее. Поскольку тетраэд правильный – то все его грани (включая основание) – правильные треугольники.
Поскольку нам не дана длина стороны, то я могу принять ее равной ( 1). Я думаю, ты понимаешь, что угол на самом деле не будет зависеть от того, насколько наш тетраэдр будет «растянут»?
Также проведу в тетраэдре высоту и медиану ( displaystyle BM).
Попутно я нарисую его основание (оно нам тоже пригодится).
Мне нужно найти угол между ( displaystyle DH) и ( displaystyle BM). Что нам известно?
Нам известна только координата точки ( displaystyle B). Значит, надо найти еще координаты точек ( displaystyle D,H,M).
Теперь думаем: точка ( displaystyle H) – это точка пересечения высот (или биссектрисс или медиан) треугольника ( displaystyle ABC).
А точка ( displaystyle D) – это приподнятая точка ( displaystyle H).
Точка же ( displaystyle M) – это середина отрезка ( displaystyle AD).
Тогда окончательно нам надо найти: координаты точек: ( displaystyle A,D,H,M).
Начнем с самого простого: координаты точки ( displaystyle A).
Смотри на рисунок: Ясно, что аппликата точки ( displaystyle A) равна нулю (точка лежит на плоскости ( displaystyle Oxy)).
Её ордината равна ( displaystyle 0,5) (так как ( displaystyle AK) – медиана).
Сложнее найти ее абсциссу. Однако это легко делается на основании теоремы Пифагора: Рассмотрим треугольник ( displaystyle BAS). Его гипотенуза ( displaystyle BA) равна ( displaystyle 1), а один из катетов ( displaystyle AS) равен ( displaystyle 0,5)
Тогда:
( BS=sqrt{B{{A}^{2}}-A{{S}^{2}}}=sqrt{1-frac{1}{4}}=frac{sqrt{3}}{2})
Окончательно имеем: ( Aleft( frac{sqrt{3}}{2},frac{1}{2},0 right)).
Теперь найдем координаты точки ( displaystyle H).
Ясно, что ее аппликата опять равна нулю, а ее ордината такая же, как у точки ( displaystyle A), то есть ( 0,5).
Найдем ее абсциссу. Это делается достаточно тривиально, если помнить, что высоты равностороннего треугольника точкой пересечения делятся в пропорции ( displaystyle mathbf{2}:mathbf{1}), считая от вершины. Так как: ( AK=BS=frac{sqrt{3}}{2}), то искомая абсцисса точки, равная длине отрезка ( displaystyle KH), равна: ( KH=frac{AK}{3}=frac{sqrt{3}}{6}). Т
аким образом, координаты точки ( displaystyle H) равны:
( Hleft( frac{sqrt{3}}{6},frac{1}{2},0 right).)
Найдем координаты точки ( displaystyle D).
Ясно, что ее абсцисса и ордината совпадают с абсциссой и ординатой точки ( displaystyle H). А аппликата равна длине отрезка ( displaystyle DH). ( displaystyle DH) – это один из катетов треугольника ( displaystyle DAH). Гипотенуза треугольника ( displaystyle DAH) – это отрезок ( AD=AB=1.) ( displaystyle AH) – катет.
Он ищется из соображений, которые я выделил жирным шрифтом:
( AH=frac{2}{3}cdot frac{sqrt{3}}{2}=frac{sqrt{3}}{3})
Тогда:
( DH=sqrt{1-{{left( frac{sqrt{3}}{3} right)}^{2}}}=sqrt{frac{2}{3}})
Отсюда:
( Dleft( frac{sqrt{3}}{6},frac{1}{2},sqrt{frac{2}{3}} right).)
Точка ( M) – это середина отрезка ( AD). Тогда нам нужно вспомнить формулу координат середины отрезка:
( Mleft( frac{frac{sqrt{3}}{2}+frac{sqrt{3}}{6}}{2},~frac{frac{1}{2}+frac{1}{2}}{2},frac{0+sqrt{frac{2}{3}}}{2} right)=Mleft( frac{sqrt{3}}{3},frac{1}{2},frac{1}{sqrt{6}} right).~)
Ну все, теперь мы можем искать координаты направляющих векторов:
( overrightarrow{BM}left( frac{sqrt{3}}{3},frac{1}{2},frac{1}{sqrt{6}} right))
( overrightarrow{DH}left( 0,0,-sqrt{frac{2}{3}} right))
Ну что, все готово: подставляем все данные в формулу:
( displaystyle cosvarphi =frac{left| frac{1}{sqrt{6}}cdot left( -sqrt{frac{2}{3}} right) right|}{sqrt{{{left( frac{sqrt{3}}{3} right)}^{2}}+{{left( frac{1}{2} right)}^{2}}+{{left( frac{1}{sqrt{6}} right)}^{2}}}cdot sqrt{{{left( -sqrt{frac{2}{3}} right)}^{2}}}}=frac{frac{1}{3}}{sqrt{frac{19}{36}}cdot sqrt{frac{2}{3}}}=frac{frac{1}{3}}{sqrt{frac{19}{54}}}=frac{sqrt{54}}{3sqrt{19}}=sqrt{frac{6}{19}})
Таким образом, ( varphi =arccossqrt{frac{6}{19}}.)
Ответ: ( varphi =arccossqrt{frac{6}{19}}.)
Тебя не должны пугать такие «страшные» ответы: для задач С2 это обычная практика. Я бы скорее удивился «красивому» ответу в этой части. Также, как ты заметил, я практически не прибегал ни к чему, кроме как к теореме Пифагора и свойству высот равностороннего треугольника. То есть для решения стереометрической задачи я использовал самый минимум стереометрии. Выигрыш в этом частично «гасится» достаточно громоздкими вычислениями. Зато они достаточно алгоритмичны!
2. Изобразим правильную шестиугольную пирамиду вместе с системой координат, а также ее основание:
Нам нужно найти угол между прямыми ( displaystyle SB) и ( displaystyle CD).
Таким образом, наша задача сводится к поиску координат точек: ( displaystyle S,B,C,D).
Координаты последних трех мы найдем по маленькому рисунку, а коодинату вершины ( displaystyle S) найдем через координату точки ( displaystyle O).
Работы навалом, но надо к ней приступать!
a) Координата ( displaystyle D): ясно, что ее аппликата и ордината равны нулю.
Найдем абсциссу. Для этого рассмотрим прямоугольный треугольник ( displaystyle EDP). Увы, в нем нам известна только гипотенуза, которая равна ( displaystyle 1). Катет ( displaystyle DP) мы будем стараться отыскать (ибо ясно, что удвоенная длина катета ( displaystyle DP) даст нам абсциссу точки ( displaystyle D)).
Как же нам ее искать?
Давай вспомним, что за фигура у нас лежит в основании пирамиды? Это правильный шестиугольник.
А что это значит? Это значит, что у него все стороны и все углы равны. Надо бы найти один такой угол. Есть идеи?
Идей масса, но есть формула:
Сумма углов правильного n-угольника равна ( left( n-2 right)cdot 180{}^circ ).
Таким образом, сумма углов правильного шестиугольника равна ( displaystyle 720) градусов. Тогда каждый из углов равен:
( frac{720{}^circ }{6}=120{}^circ )
Вновь смотрим на картинку.
Ясно, что отрезок ( displaystyle EB) – биссектрисса угла ( displaystyle DEF). Тогда угол ( displaystyle DEP) равен ( displaystyle 60) градусам.
Тогда:
( sin60{}^circ =frac{sqrt{3}}{2}=frac{DP}{ED}=frac{DP}{1}=DP)
Тогда ( DP=frac{sqrt{3}}{2}), откуда ( DF=2DP=sqrt{3}).
Таким образом, ( displaystyle D) имеет координаты ( Dleft( sqrt{3},0,0 right))
b) Теперь легко найдем координату точки ( C): ( Cleft( sqrt{3},1,0 right)).
c) Найдем координаты точки ( displaystyle B).
Так как ее абсцисса совпадает с длиной отрезка ( FP) то она равна ( frac{sqrt{3}}{2}).
Найти ординату тоже не очень сложно: если мы соединим точки ( displaystyle C) и ( displaystyle A) а точку пересечения прямой ( displaystyle AC) обозначим, скажем за ( displaystyle M). (сделай сам несложное построение). Тогда ( BM=EP.)
Таким образом, ордината точки B равна сумме длин отрезков ( PM+MB). Вновь обратимся к треугольнику ( displaystyle DEP).
Тогда
( frac{1}{2}=cos60{}^circ =frac{EP}{ED}=EP)
Тогда так как ( PM=DC=1,~mo~PB=1+frac{1}{2}=frac{3}{2}.) Тогда точка ( B) имеет координаты ( Bleft( frac{sqrt{3}}{2},frac{3}{2},0 right).)
d) Теперь найдем координаты точки ( displaystyle O).
Рассмотри прямоугольник ( displaystyle ACDF) и докажи, что ( PO=frac{1}{2}.)
Таким образом, координаты точки ( displaystyle O): ( Oleft( frac{sqrt{3}}{2},frac{1}{2},0 right).)
e) Осталось найти координаты вершины ( S). Ясно, что ее абсцисса и ордината совпадает с абсциссой и ординатой точки ( O).
Найдем аппликату. Так как ( FC=EB=2), то ( OF=1). Рассмотрим прямоугольный треугольник ( displaystyle OFS). По условию задачи боковое ребро ( FS=2). Это гипотенуза моего треугольника.
Тогда высота пирамиды ( displaystyle OS) – катет.
( OS=sqrt{F{{S}^{2}}-O{{F}^{2}}}=sqrt{4-1}=sqrt{3})
Тогда точка ( S) имеет координаты: ( Sleft( frac{sqrt{3}}{2},frac{1}{2},sqrt{3} right).)
Ну все, у меня есть координаты всех интересующих меня точек. Ищу координаты направляющих векторов прямых:
( overrightarrow{SB}left( frac{sqrt{3}}{2}-frac{sqrt{3}}{2},frac{1}{2}-frac{3}{2},sqrt{3}-0 right)=overrightarrow{SB}left( 0,-1,sqrt{3} right).)
( overrightarrow{CD}left( sqrt{3}-sqrt{3},0-1,0 right)=overrightarrow{CD}left( 0,-1,0 right).)
Ищем угол между этими векторами:
( cosvarphi =frac{left| 0+left( -1 right)cdot left( -1 right)+sqrt{3}cdot 0 right|}{sqrt{{{left( -1 right)}^{2}}+{{left( sqrt{3} right)}^{2}}}cdot sqrt{{{left( -1 right)}^{2}}}}=frac{1}{2})
Тогда ( varphi =arccos left( frac{1}{2} right)=60{}^circ )
Ответ: ( 60{}^circ )
Опять-таки, при решении этой задачи я не использовал никаких изошренных приемов, кроме формулы суммы углов правильного n-угольника, а также определения косинуса и синуса прямоугольного треугольника.
3. Поскольку нам опять не даны длины ребер в пирамиде, то я буду считать их равными единице.
Таким образом, поскольку ВСЕ ребра, а не только боковые, равны между собой, то в основании пирамиды и меня лежит квадрат, а боковые грани – правильные треугольники.
Изобразим такую пирамиду, а также ее основание на плоскости, отметив все данные, приведенные в тексте задачи:
Ищем угол между ( displaystyle BM) и ( displaystyle PH).
Я буду делать очень краткие выкладки, когда буду заниматься поиском координат точек. Тебе необходимо будет «расшифровать» их:
a) ( Bleft( 0,1,0 right))
b) ( displaystyle H) – середина отрезка ( displaystyle AC). Её координаты:
( Hleft( frac{1}{2},frac{1}{2},0 right))
c) Длину отрезка ( displaystyle AH) я найду по теореме Пифагора в треугольнике ( displaystyle AHD). ( AH=frac{sqrt{2}}{2}.) Найду ( displaystyle PH) по теореме Пифагора в треугольнике ( displaystyle AHP).
( PH=sqrt{1-frac{1}{2}}=frac{1}{sqrt{2}})
Координаты ( P): ( Pleft( frac{1}{2},frac{1}{2},frac{1}{sqrt{2}} right).)
d) ( M) – середина отрезка ( AP). Ее координаты равны ( Mleft( frac{1}{4},frac{1}{4},frac{1}{2sqrt{2}} right).)
e) Координаты вектора ( overrightarrow{PH}:~overrightarrow{PH}left( 0,0,-frac{1}{sqrt{2}} right).~)
f) Координаты вектора ( overrightarrow{BM}:~overrightarrow{BM}left( frac{1}{4},-frac{3}{4},frac{1}{2sqrt{2}} right).)
g) Ищем угол: ( cosvarphi =frac{frac{1}{4}}{frac{1}{sqrt{2}}cdot frac{sqrt{3}}{2}}=frac{1}{sqrt{6}})
h) Ответ: ( arccosfrac{1}{sqrt{6}})
Куб – простейшая фигура. Я уверен, что с ней ты разберешься самостоятельно. Ответы к задачам 4 и 5 следующие:
4. ( arccosfrac{4}{sqrt{30}})
5. ( arccosfrac{1}{sqrt{15}})
Нахождение угла между прямой и плоскостью
Ну что, время простых задачек окончено!
Теперь примеры будут еще сложнее. Для отыскания угла между прямой и плоскостью мы будем поступать следующим образом:
- По трем точкам строим уравнение плоскости: ( Ax+By+Cz+D=0), используя определитель третьего порядка;
- По двум точкам ищем координаты направляющего вектора прямой: ( vec{s}left( l,m,n right));
- Применяем формулу для вычисления угла между прямой и плоскостью: ( sinvarphi =frac{left| Al+Bm+Cn right|}{sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}~}cdot sqrt{{{l}^{2}}+{{m}^{2}}+{{n}^{2}}}})
Как видишь, эта формула очень похожа на ту, что мы применяли для поиска углов между двумя прямыми.
Структура правой части просто одинакова, а слева мы теперь ищем синус, а не косинус, как раньше. Ну и добавилось одно противное действие – поиск уравнения плоскости.
Опять я решу первые две задачи подробно, третью – кратко, а последние две оставляю тебе для самостоятельного решения.
К тому же тебе уже приходилось иметь дело с треугольной и четырехугольной пирамидами, а вот с призмами – пока что нет.
Решения:
1. Изобразим призму, а также ее основание. Совместим ее с системой координат и отметим все данные, которые даны в условии задачи:
Извиняюсь за некоторое несоблюдение пропорций, но для решения задачи это, по сути, не так важно. Плоскость ( BC{{C}_{1}}) – это просто «задняя стенка» моей призмы. Достаточно просто догадаться, что уравнение такой плоскости имеет вид:
( x=0)
Однако, это можно показать и непосредственно:
Выберем произвольные три точки на этой плоскости: например, ( Bleft( 0,0,0 right),~Cleft( 0,8,0 right),~{{B}_{1}}left( 0,0,3 right)).
Составим уравнение плоскости:
( left| {begin{array}{*{20}{c}}x&0&0\y&8&0\z&0&3end{array}} right| = 0)
Упражнение тебе: самостоятельно вычислить этот определитель. У тебя получилось ( 24x)? Тогда уравение плоскости имеет вид:
( 24x=0)
Или просто
( x=0)
Таким образом, ( A=1,B=0,C=0,D=0.)
Для решения примера мне нужно найти координаты направляющего вектора прямой ( B{{A}_{1}}).
Так как точка ( B) cовпала с началом координат, то координаты вектора (overrightarrow{B{{A}_{1}}}) просто совпадут с координатами точки ( {{A}_{1}}.)
Для этого найдем вначале координаты точки ( displaystyle A).
Для этого рассмотрим треугольник ( displaystyle ABC).
Проведем высоту (она же – медиана и биссектрисса) из вершины ( displaystyle A).
Так как ( BC=8), то ордината точки ( displaystyle A) равна ( displaystyle 4).
Для того, чтобы найти абсциссу этой точки, нам нужно вычислить длину отрезка ( displaystyle AT).
По теореме Пифагора имеем:
( AT=sqrt{A{{B}^{2}}-B{{T}^{2}}}=sqrt{25-16}=3.)
Тогда точка ( displaystyle A) имеет координаты:
( Aleft( 3,4,0 right))
Точка ( {{A}_{1}})– это «приподнятая» на ( displaystyle 3) точка ( displaystyle A):
( {{A}_{1}}left( 3,4,3 right))
Тогда координаты вектора ( overrightarrow{B{{A}_{1}}}):
( overrightarrow{B{{A}_{1}}}left( 3,4,3 right).)
( sinvarphi =frac{left| 3cdot 1+4cdot 0+3cdot 0 right|}{sqrt{{{1}^{2}}+{{0}^{2}}+{{0}^{2}}}cdot sqrt{{{3}^{2}}+{{4}^{2}}+{{3}^{2}}}}=frac{3}{sqrt{34}}.)
( varphi =arcsinfrac{3}{sqrt{34}}.)
Ответ: ( arcsinfrac{3}{sqrt{34}}.)
Как видишь, ничего принципиально сложного при решении таких задач нет. На самом деле процесс еще немного упрощает «прямота» такой фигуры, как призма.
Теперь давай перейдем к следующему примеру:
2. Рисуем параллелепипед, проводим в нем плоскость и прямую, а также отдельно вычерчиваем его нижнее основание:
Вначале найдем уравнение плоскости: Координаты трех точек, лежащих в ней:
( Aleft( 0,0,0 right),~Bleft( 0,2,0 right),{{C}_{1}}left( 1,2,1 right)) (первые две координаты получены очевидным способом, а последнюю координату ты легко найдешь по картинке из точки ( C)). Тогда составляем уравнение плоскости:
( left| {begin{array}{*{20}{c}}x&0&1\y&2&2\z&0&1end{array}} right| = 0)
Вычисляем:
( 2x-2z=0,~x-z=0)
Тогда ( A=1,B=0,C=-1,D=0.)
Ищем координаты направляющего вектора ( overrightarrow{A{{B}_{1}}}): Ясно, что его координаты совпадают с координатами точки ( {{B}_{1}}), не правда ли?
Как найти координаты ( {{B}_{1}})?
Это же координаты точки ( B), приподнятые по оси аппликат на единицу! ( {{B}_{1}}left( 0,2,1 right)). Тогда ( overrightarrow{A{{B}_{1}}}left( 0,2,1 right).)
Ищем искомый угол:
( sinvarphi =frac{left| 1cdot 0+0cdot 2+left( -1 right)cdot 1 right|}{sqrt{{{1}^{2}}+{{left( -1 right)}^{2}}+{{0}^{2}}~}cdot sqrt{0+{{2}^{2}}+{{1}^{2}}}}=frac{1}{sqrt{10}}.)
( ~varphi =arcsinfrac{1}{sqrt{10}}.)
Ответ: ( arcsinfrac{1}{sqrt{10}}.)
3. Рисуем правильную шестиугольную призму, а затем проводим в ней плоскость и прямую.
Тут даже плоскость нарисовать проблемно, не говоря уже о решении этой задачи, однако методу координат все равно! Именно в его универсальности и заключается его основное преимущество!
Плоскость проходит через три точки: ( A,C,{{D}_{1}}). Ищем их координаты:
1) ( Aleft( 0,0,0 right),~left( frac{sqrt{3}}{2},frac{3}{2},0 right), {{D}_{1}}left( sqrt{3},1,1 right)). Сам выведи координаты для последних двух точек. Тебе пригодится для этого решение задачи с шестиугольной пирамидой!
2) Строим уравнение плоскости:
( left| {begin{array}{*{20}{c}}x&{frac{{sqrt 3 }}{2}}&{sqrt 3 }\y&{frac{3}{2}}&1\z&0&1end{array}} right| = 0)
( -sqrt{3}x+y+2z=0)
( A=-sqrt{3},B=1,C=2,D=0.)
Ищем координаты вектора ( overrightarrow{A{{C}_{1}}}): ( text{ }!!~!!text{ }overrightarrow{A{{C}_{1}}}left( frac{sqrt{3}}{2},frac{3}{2},1 right)). (снова смотри задачу с треугольной пирамидой!)
3) Ищем угол:
( sinvarphi =frac{left| -sqrt{3}cdot frac{sqrt{3}}{2}+frac{3}{2}+2 right|}{sqrt{{{left( frac{sqrt{3}}{2} right)}^{2}}+{{left( frac{3}{2} right)}^{2}}+{{1}^{2}}~}cdot sqrt{{{left( -sqrt{3} right)}^{2}}+{{1}^{2}}+{{2}^{2}}}}=frac{2}{2sqrt{8}}=frac{1}{2sqrt{2}}.)
Ответ: ( arcsinfrac{1}{2sqrt{2}}.)
Как видишь, ничего сверхъестественно сложного в этих задачах нет. Нужно лишь быть очень внимательным с корнями. К последним двум задачам я дам лишь ответы:
4. ( text{arcsin}frac{12}{sqrt{193}}~)
5. ( text{arcsin}frac{1}{sqrt{6}}~)
Как ты мог убедиться, техника решения задач везде одинаковая: основная задача найти координаты вершин и подставить их в некие формулы. Нам осталось рассмотреть еще один класс задач на вычисление углов, а именно: вычисление углов между двумя плоскостями.
Решения задач:
1. Сторона основания правильной треугольной призмы ( ABC{{A}_{1}}{{B}_{1}}{{C}_{1}}) равна ( 2), а диагональ боковой грани равна ( sqrt{5}). Найдите угол между плоскостью ( {{A}_{1}}BC) и плоскостью основания призмы.
Рисую правильную (в основании – равносторонний треугольник) треугольную призму и отмечаю на ней плоскости, которые фигурируют в условии задачи:
Нам нужно найти уравнения двух плоскостей: ( ABC~и~BC{{A}_{1}}.) Уравнение основания получается тривиально: ты можешь составить соответствующий определитель по трем точкам, я же составлю уравнение сразу:
( z=0.)
То есть:
( {{A}_{1}}=0, {{B}_{1}}=0, {{C}_{1}}=1, {{D}_{1}}=0.)
Теперь найдем уравнение ( BC{{A}_{1}}.) Точка ( B) имеет координаты ( Bleft( 0,0,0 right).) Точка ( C) – ( Cleft( 0,1,0 right).)
Так как ( AO) – медиана и высота треугольника ( ABC), то ( BO=OC=1.) ( AO) легко находится по теореме Пифагора в треугольнике ( BAO:) ( AO=sqrt{4-1}=sqrt{3}).
Тогда точка ( A) имеет координаты: ( Aleft( sqrt{3},1,0 right).)
Найдем аппликату точки ( {{A}_{1}}.) Для этого рассмотрим прямоугольный треугольник ( {{A}_{1}}AC.~)
( A{{A}_{1}}=sqrt{{{A}_{1}}{{C}^{2}}-A{{C}^{2}}}=1.)
Тогда получаем вот такие координаты: ( {{A}_{1}}left( sqrt{3},1,1 right).) Cоставляем уравнение плоскости ( BC{{A}_{1}}).
( left| {begin{array}{*{20}{c}}x&0&{sqrt 3 }\y&1&1\z&0&1end{array}} right| = 0.)
( x+sqrt{3}z-sqrt{3}z-sqrt{3}y=0)
( x-sqrt{3}z=0)
Тогда
( {{A}_{2}}=1, {{B}_{2}}=0, {{C}_{2}}=-sqrt{3}, {{D}_{2}}=0.)
Вычисляем угол между плоскостями:
( cosvarphi =frac{left| -sqrt{3} right|}{sqrt{1+{{left( -sqrt{3} right)}^{2}}}}=frac{sqrt{3}}{2}.)
Отсюда
( varphi =30{}^circ .)
Ответ: ( 30{}^circ .)
2. В правильной четырехугольной пирамиде ( displaystyle SABCD), все ребра которой равны ( displaystyle 1), найдите синус угла между плоскостью ( displaystyle SAD) и плоскостью, проходящей через точку ( displaystyle A) перпендикулярно прямой ( displaystyle BD).
Делаем рисунок:
Самое сложное – это понять, что это такая за таинственная плоскость, проходящая через точку ( A) перпендикулярно ( DB).
Ну что же, главное, это что? Главное – это внимательность! В самом деле, прямая ( AC) перпендикулярна ( BD). Прямая ( OS) также перпендикулярна ( BD).
Тогда плоскость, проходящая через эти две прямые, будет перпендикулярна прямой ( BD), и, кстати, проходить через точку ( A). Эта плоскость также проходит через вершину пирамиды.
Тогда искомая плоскость – ( SAC.) А плоскость ( SAD) нам уже дана. Ищем координаты точек ( displaystyle S,A,C,D).
- ( displaystyle Aleft( 0,1,0 right))
- ( displaystyle Cleft( 1,0,0 right))
- ( displaystyle Dleft( 0,0,0 right))
Координату точки ( S) найдем через точку ( O). Из маленького рисунка легко вывести, что координаты у точки ( O) будут такие: ( Oleft( frac{1}{2},frac{1}{2},0 right).~)
Что теперь осталось найти, чтобы найти координаты вершины пирамиды?
Еще нужно вычислить ее высоту.
Это делается при помощи все той же теоремы Пифагора: вначале докажи, что ( OB=frac{sqrt{2}}{2}) (тривиально из маленьких треугольничков, образующих квадрат в основании).
Так как по условию ( SB=1), то имеем:
( OS=sqrt{1-{{left( frac{sqrt{2}}{2} right)}^{2}}}=frac{1}{sqrt{2}}.)
Теперь все готово: координаты вершины:
( Sleft( frac{1}{2},frac{1}{2},frac{1}{sqrt{2}} right).~)
Составляем уравнение плоскости ( displaystyle DAS):
( left| {begin{array}{*{20}{c}}x&0&{frac{1}{2}}\y&1&{frac{1}{2}}\z&0&{frac{1}{{sqrt 2 }}}end{array}} right| = 0)
Ты уже спец в вычислении определителей. Без труда ты получишь:
( frac{1}{sqrt{2}}x-frac{1}{2}z=0)
Или иначе (если домножим обе части на корень из двух)
( x-frac{1}{sqrt{2}}z=0.)
Теперь найдем уравнение плоскости ( displaystyle SAC):
( left| {begin{array}{*{20}{c}}{x — 1}&{ — 1}&{ — frac{1}{2}}\y&1&{frac{1}{2}}\z&0&{frac{1}{{sqrt 2 }}}end{array}} right| = 0)
(ты ведь не забыл, как мы получаем уравнение плоскости, правда?
Если ты не понял, откуда взялась эта минус единица, то вернись к определению уравнения плоскости! Просто всегда до этого оказывалось так, что моей плоскости принадлежало начало координат!)
Вычисляем определитель:
( begin{array}{l}frac{x-1}{sqrt{2}}-frac{1}{2}z+frac{1}{2}z+frac{y}{sqrt{2}}=0\frac{x-1}{sqrt{2}}+frac{y}{sqrt{2}}=0\x+y-1=0end{array}).
(Ты можешь заметить, что уравнение плоскости совпало с уравнением прямой, проходящей через точки ( displaystyle A) и ( displaystyle C)! Подумай, почему!)
Теперь вычисляем угол:
( cosvarphi =frac{left| 1+1cdot 0-frac{1}{sqrt{2}}cdot 0 right|}{sqrt{1+{{left( -frac{1}{sqrt{2}} right)}^{2}}}cdot sqrt{{{1}^{2}}+{{1}^{2}}}~~}=frac{1}{sqrt{3}}.)
Нам же нужно найти синус:
( sinvarphi =sqrt{1-{{cos }^{2}}varphi }=sqrt{1-frac{1}{3}}=sqrt{frac{2}{3}}).
Ответ: ( sqrt{frac{2}{3}}.)
3. В правильной четырехугольной призме ( ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) стороны основания равны ( displaystyle 1), а боковые ребра равны ( displaystyle 5). На ребре ( A{{A}_{1}}) отмечена точка ( displaystyle E) так, что ( AE:E{{A}_{1}}=2:3). Найдите угол между плоскостями ( ABC) и ( BE{{D}_{1}}.)
Каверзный вопрос: а что такое прямоугольная призма, как ты думаешь? Это же всего-то навсего хорошо известный тебе параллелепипед! Сразу же делаем чертеж! Можно даже отдельно не изображать основание, пользы от него здесь немного:
Плоскость ( ABC), как мы уже раньше заметили, записывается в виде уравнения:
( z=0.)
Теперь составляем плоскость ( BE{{D}_{1}}.)
( Bleft( 0,0,0 right),~Eleft( 1,0,2 right),~{{D}_{1}}left( 1,1,5 right).)
Cразу же составляем уравнение плоскости:
( left| {begin{array}{*{20}{c}}x&1&1\y&0&1\z&2&5end{array}} right| = 0)
( begin{array}{l}2y+z-2x-5y=0\-2x-3y+z=0\2x+3y-z=0end{array})
Ищем угол:
( cosvarphi =frac{1}{sqrt{4+9+1}}=frac{1}{sqrt{14}})
Ответ: ( arccos frac{1}{sqrt{14}}~~)
Теперь ответы к последним двум задачам:
4. ( arccosfrac{2}{3})
5. ( sqrt{frac{2}{3}})
Ну что же, теперь самое время немного передохнуть, ведь мы с тобой молодцы и проделали огромную работу!
Вычисление расстояния от точки до плоскости
Что нам потребуется для решения этой задачи?
- Координаты точки ( Mleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right).)
- Уравнение плоскости ( Ax+By+Cz+D=0.)
Итак, как только мы получим все необходимые данные, то применяем формулу:
( d=frac{left| A{{x}_{0}}+B{{y}_{0}}+C{{z}_{0}}+D right|}{sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}}})
Как мы строим уравнение плоскости тебе уже должно быть известно из предыдущих задач, которые я разбирал в прошлой части. Давай сразу приступим к задачам.
Схема следующая: 1, 2 –я помогаю тебе решать, причем довольно подробно, 3, 4 – только ответ, решение ты проводишь сам и сравниваешь. Начали!
Решения:
1. Рисуем кубик с единичными ребрами, строим отрезок и плоскость, середину отрезка ( B{{C}_{1}}) обозначим буквой ( M)
Вначале давай начнем с легкого: найдем координаты точки ( displaystyle M). Так как ( displaystyle Bleft( 0,1,0 right),~{{C}_{1}}left( 1,1,1 right),~) то ( displaystyle Mleft( frac{1}{2},1,frac{1}{2} right).) (вспомни координаты середины отрезка!)
Теперь составляем уравнение плоскости по трем точкам ( displaystyle Aleft( 0,0,0 right),~{{B}_{1}}left( 0,1,1 right),~{{D}_{1}}left( 1,0,1 right).)
(left| {begin{array}{*{20}{c}}x&0&1\y&1&0\z&1&1end{array}} right| = 0)
( displaystyle x+y-z=0.)
( displaystyle A=1,B=1,C=-1,~D=0.)
Теперь я могу приступать к поиску расстояния:
( displaystyle d=frac{left| frac{1}{2}+1-frac{1}{2} right|}{sqrt{1+1+1}}=frac{1}{sqrt{3}})
Ответ: ( displaystyle frac{1}{sqrt{3}})
2. Вновь начинаем с чертежа, на котором отмечаем все данные!
Для пирамиды было бы полезно отдельно рисовать ее основание.
Даже тот факт, что я рисую как курица лапой, не помешает нам с легкостью решить эту задачу!
1. ( AO=OC=frac{1}{2}AC=frac{sqrt{{{2}^{2}}+{{2}^{2}}}}{2}=sqrt{2}).
Тогда ( OS=sqrt{S{{C}^{2}}-O{{C}^{2}}}=sqrt{3}.)
Теперь легко найти координаты точки ( S.)
Так как координаты точки ( O:Oleft( 1,1,0 right),~), то ( Sleft( 1,1,sqrt{3} right).)
2. Так как координаты точки ( C:) ( Cleft( 2,2,0 right),) а ( M) – середина отрезка ( SC), то
( Mleft( frac{3}{2},frac{3}{2},frac{sqrt{3}}{2} right).)
Без проблем найдем и координаты еще двух точек на плоскости ( ADM.) ( Dleft( 1,0,0 right),~Aleft( 0,0,0 right).) Составляем уравнение плоскости и упростим его:
(left| {left| {begin{array}{*{20}{c}}x&1&{frac{3}{2}}\y&0&{frac{3}{2}}\z&0&{frac{{sqrt 3 }}{2}}end{array}} right|} right| = 0)
( frac{3}{2}z-frac{sqrt{3}}{2}y=0)
( sqrt{3}y-3z=0)
( y-sqrt{3}z=0.)
Так как точка ( B) имеет координаты: ( Bleft( 0,2,0 right)), то вычисляем расстояние:
( d=frac{2}{sqrt{1+3}}=1.)
Ответ (очень редкий!): ( 1)
Ну что, разобрался?
Мне кажется, что здесь все так же технично, как и в тех примерах, что мы рассматривали с тобой в предыдущей части. Так что я уверен, что если ты овладел тем материалом, то тебе не составит труда решить оставшиеся две задачи.
Я лишь приведу ответы:
- ( frac{3sqrt{39}}{4})
- ( frac{sqrt{3}}{2})
Вычисление расстояния от прямой до плоскости
На самом деле, здесь нет ничего нового. Как могут располагаться прямая и плоскость друг относительно друга?
У них есть всего ( 2) возможности: пересечься, или прямая параллельна плоскости. Как ты думаешь, чем равно расстояние от прямой до плоскости, с которой данная прямая пересекается?
Мне кажется, что тут ясно, что такое расстояние равно нулю. Неинтересный случай.
Второй случай хитрее: тут уже расстояние ненулевое. Однако, так как прямая параллельна плоскости, то каждая точка прямой равноудалена от этой плоскости:
Таким образом:
Расстояние от плоскости до параллельной ей прямой равно расстоянию от любой точки прямой до плоскости.
А это значит, что моя задача свелась к предыдущей: ищем координаты любой точки на прямой, ищем уравнение плоскости, вычисляем расстояние от точки до плоскости.
На самом деле, такие задачи в ЕГЭ встречаются крайне редко. Мне удалось найти лишь одну задачу, и то данные в ней были такими, что метод координат к ней был не очень-то и применим!
Теперь перейдем к другому, гораздо более важному классу задач:
Вычисление расстояния точки до прямой
Что нам потребуется?
- Координаты точки, от которой мы ищем расстояние: ( {{M}_{0}}left( {{x}_{0}},{{y}_{0}},{{z}_{0}} right).)
- Координаты любой точки, лежащей на прямой ( {{M}_{1}}left( {{x}_{1}},{{y}_{1}},{{z}_{1}} right))
- Координаты направляющего вектора прямой ( vec{s}left( m,n,p right))
Какую применяем формулу?
Ответ: ( d=frac{left| overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s} right|}{sqrt{{{m}^{2}}+{{n}^{2}}+{{p}^{2}}}})
Что означает знаменатель данной дроби тебе и так должно быть ясно: это длина направляющего вектора прямой. Здесь очень хитрый числитель!
Выражение ( left| overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s} right|) означает модуль (длина) векторного произведения векторов ( overrightarrow{{{M}_{0}}{{M}_{1}}}) и ( vec{s}.)
Как вычислять векторное произведение, мы с тобой изучали в предыдущей части работы. Освежи свои знания, нам они сейчас очень пригодятся!
Таким образом, алгоритм решения задач будет следующий:
- Ищем координаты точки, от которой мы ищем расстояние: ( {{M}_{0}}left( {{x}_{0}},{{y}_{0}},{{z}_{0}} right).)
- Ищем координаты любой точки на прямой, до которой мы ищем расстояние: ( {{M}_{1}}left( {{x}_{1}},{{y}_{1}},{{z}_{1}} right))
- Строим вектор ( overrightarrow{{{M}_{0}}{{M}_{1}}}:) ( overrightarrow{{{M}_{0}}{{M}_{1}}}left( {{x}_{1}}-{{x}_{0}},{{y}_{1}}-{{y}_{0}},{{z}_{1}}-{{z}_{0}} right).)
- Строим направляющий вектор прямой ( vec{s}left( m,n,p right))
- Вычисляем векторное произведение ( overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s})
- Ищем длину полученного вектора: ( left| overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s} right|)
- Вычисляем расстояние: ( d=frac{left| overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s} right|}{sqrt{{{m}^{2}}+{{n}^{2}}+{{p}^{2}}}})
Работы у нас много, а примеры будут достаточно сложными! Так что теперь сосредоточь все внимание!
1. Дана правильная треугольная пирамида ( DABC) с вершиной ( D). Сторона основания пирамиды равна ( sqrt{6}), высота равна ( sqrt{30}).
Найдите расстояние от середины бокового ребра ( BD) до прямой ( MT), где точки ( M) и ( T) — середины ребер ( AC) и ( AB) соответственно.
2. Длины ребер ( AB,A{{A}_{1}}) и ( AD) прямоугольного параллелепипеда ( ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) равны соответственно ( 12,text{ }16~) и ( 15.)
Найдите расстояние от вершины ( {{A}_{1}}) до прямой ( B{{D}_{1}}.)
3. В правильной шестиугольной призме ( ABCDEF{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}{{E}_{1}}{{F}_{1}}) все ребра которой равны ( 1) найдите расстояние от точки ( B) до прямой ( {{E}_{1}}{{F}_{1}}.)
Решения:
1. Делаем аккуратный чертеж, на котором отмечаем все данные:
Ну что же, работы нам предстоит немало! Принимаемся за нее, засучив рукава!
1. Чтобы найти координаты высоты пирамиды, нам нужно знать координаты точки ( displaystyle O.) Её аппликата равна нулю, а ордината равна ( displaystyle frac{sqrt{6}}{2}.)
Абсцисса ее равна длине отрезка ( displaystyle OS.) ( displaystyle AS=sqrt{A{{B}^{2}}-S{{B}^{2}}}=sqrt{6-frac{6}{4}}=frac{3}{sqrt{2}}.~)
Так как ( displaystyle AS) – высота равностороннего треугольника ( displaystyle ABC), то она делится в отношении ( displaystyle 2:1), считая от вершины, отсюда ( displaystyle OS=frac{3}{3sqrt{2}}=frac{1}{sqrt{2}}).
Окончательно, получили координаты:
( displaystyle Oleft( frac{1}{sqrt{2}},frac{sqrt{6}}{2},0 right).)
Тогда ( displaystyle D(left( frac{1}{sqrt{2}},frac{sqrt{6}}{2},sqrt{30} right)).
Координаты точки ( displaystyle A:Aleft( frac{3}{sqrt{2}},frac{sqrt{6}}{2},0 right).)
2. ( displaystyle K) – середина отрезка ( displaystyle BD:)
( displaystyle Kleft( frac{1}{2sqrt{2}},frac{sqrt{6}}{4},frac{sqrt{30}}{2} right).~)
3. ( displaystyle M) – середина отрезка ( displaystyle AC:)
( displaystyle Mleft( frac{3}{2sqrt{2}},~frac{frac{sqrt{6}}{2}+sqrt{6}}{2},0 right)=Mleft( frac{3}{2sqrt{2}},~frac{3sqrt{6}}{4},0 right).)
( displaystyle T) – середина отрезка ( displaystyle AB)
( displaystyle Tleft( frac{3}{2sqrt{2}},~frac{sqrt{6}}{4},0 right).~)
4. Координаты( displaystyle overrightarrow{KT}:overrightarrow{KT}left( frac{3}{2sqrt{2}}-frac{1}{2sqrt{2}},frac{sqrt{6}}{4}-frac{sqrt{6}}{4},~0-frac{sqrt{30}}{2} right)=overrightarrow{KT}left( frac{1}{sqrt{2}},~0,~-frac{sqrt{30}}{2} right).)
Координаты вектора ( displaystyle overrightarrow{TM}:)
( displaystyle overrightarrow{TM}left( 0,frac{3sqrt{6}}{4}-frac{sqrt{6}}{4},0 right)=overrightarrow{TM}left( 0,~frac{sqrt{6}}{2},0 right).)
5. Вычисляем векторное произведение:
( displaystyle overrightarrow{KT}times overrightarrow{TM}=frac{1}{sqrt{2}}cdot frac{sqrt{6}}{2}cdot overrightarrow{k}-frac{sqrt{30}}{2}cdot frac{sqrt{6}}{2}cdot vec{i}=frac{3sqrt{5}}{2}vec{i}+frac{sqrt{3}}{2}overrightarrow{k}=left( frac{3sqrt{5}}{2},0,~frac{sqrt{3}}{2} right).)
6. Длина вектора ( displaystyle TM): проще всего заменить, что отрезок ( displaystyle TM) – средняя линия треугольника ( displaystyle ABC), а значит, он равен половине основания ( displaystyle BC). Так что ( displaystyle left| text{ }!!~!!text{ }overrightarrow{TM} right|=frac{sqrt{6}}{2}).
7. Считаем длину векторного произведения:
( displaystyle left| overrightarrow{KT}times overrightarrow{TM} right|=sqrt{{{left( frac{3sqrt{5}}{2} right)}^{2}}+{{left( frac{sqrt{3}}{2} right)}^{2}}}=2sqrt{3}.)
8. Наконец, находим расстояние:
( displaystyle d=frac{left| overrightarrow{KT}times overrightarrow{TM} right|}{text{ }!!~!!text{ }left| text{ }!!~!!text{ }overrightarrow{TM} right|}=frac{2sqrt{3}}{frac{sqrt{6}}{2}}=2sqrt{2})
Уф, ну все!
Честно тебе скажу: решение этой задачи традиционными методами (через построения), было бы намного быстрее.
Зато здесь я все свел к готовому алгоритму!
Я так думаю, что алгоритм решения тебе ясен? Поэтому попрошу тебя решить оставшиеся две задачи самостоятельно. Сравним ответы?
2. ( displaystyle 12)
3. ( displaystyle 2)
Опять-таки повторюсь: эти задачи проще (быстрее) решать через построения, а не прибегая к координатному методу.
Я продемонстрировал такой способ решения лишь затем, чтобы показать тебе универсальный метод, который позволяет «ничего не достраивать».
Наконец, рассмотрим последний класс задач: Вычисление расстояния между скрещивающимися прямыми.
Вычисление расстояния между скрещивающимися прямыми
Здесь алгоритм решения задач будет схож с предыдущим. Что у нас есть:
- Направляющий вектор первой прямой: ( overrightarrow{{{a}_{1}}(}{{x}_{1}},{{y}_{1}},{{z}_{1}}).)
- Направляющий вектор второй прямой: ( overrightarrow{{{a}_{2}}(}{{x}_{2}},{{y}_{2}},{{z}_{2}}).)
- Любой вектор, соединяющий точки первой и второй прямой: ( overrightarrow{{{a}_{3}}}left( {{x}_{0}},{{y}_{0}},{{z}_{0}} right))
Как мы ищем расстояние между прямыми?
Формула следующая:
( d=frac{left| left( overrightarrow{{{a}_{3}}},~overrightarrow{{{a}_{1}}},overrightarrow{{{a}_{2}}} right) right|}{left| overrightarrow{{{a}_{1}}}times overrightarrow{{{a}_{2}}} right|})
Числитель – это модуль смешанного произведения (мы его вводили в предыдущей части), а знаменатель – как и в предыдущей формуле (модуль векторного произведения направляющих векторов прямых, расстояние между которыми мы с тобой ищем).
Я напомню тебе, что
тогда формулу для расстояния можно переписать в виде:
[d = frac{{left| begin{array}{l}begin{array}{*{20}{c}}{{x_0}}&{{y_0}}&{{z_0}}end{array}\begin{array}{*{20}{c}}{{x_1}}&{{y_1}}&{{z_1}}end{array}\begin{array}{*{20}{c}}{{x_2}}&{{y_2}}&{{z_2}}end{array}end{array} right|}}{{left| begin{array}{l}begin{array}{*{20}{c}}{overrightarrow i }&{overrightarrow j }&{overrightarrow k }end{array}\begin{array}{*{20}{c}}{{x_1}}&{{y_1}}&{{z_1}}end{array}\begin{array}{*{20}{c}}{{x_2}}&{{y_2}}&{{z_2}}end{array}end{array} right|}}]
Этакий определитель делить на определитель! Хотя, если честно, мне здесь совсем не до шуток!
Данная формула, на самом деле, очень громоздка и приводит к достаточно сложным вычислениям. На твоем месте я бы прибегал к ней только в самом крайнем случае!
Давай попробуем решить несколько задач, используя изложенный выше метод:
- В правильной треугольной призме ( ABC{{A}_{1}}{{B}_{1}}{{C}_{1}}), все рёбра которой равны ( 1), найдите расстояние между прямыми ( A{{A}_{1}}) и ( B{{C}_{1}}).
- Дана правильная треугольная призма ( ABC{{A}_{1}}{{B}_{1}}{{C}_{1}}) все рёбра основания которой равны ( 2sqrt{7}) Сечение, проходящее через боковое ребро ( A{{A}_{1}}) и середину ( M) ребра ( {{B}_{1}}{{C}_{1}}) является квадратом. Найдите расстояние между прямыми ( {{A}_{1}}B) и ( AM.)
Первую решаю я, а опираясь на нее, вторую решаешь ты!
1. Рисую призму и отмечаю прямые ( A{{A}_{1}}) и ( B{{C}_{1}}.)
Координаты точки С: ( C:Cleft( frac{sqrt{3}}{2},frac{1}{2},0 right),) тогда ( {{C}_{1}}left( frac{sqrt{3}}{2},frac{1}{2},1 right).~)
Координаты точки ( B:Bleft( 0,1,0 right).~)
Координаты вектора ( overrightarrow{B{{C}_{1}}}:~overrightarrow{B{{C}_{1}}}left( frac{sqrt{3}}{2},-frac{1}{2},1 right).)
Координаты точки ( {{A}_{1}}:{{A}_{1}}left( 0,0,1 right).)
Координаты вектора ( overrightarrow{A{{A}_{1}}}:~overrightarrow{A{{A}_{1}}}left( 0,0,1 right).)
Координаты вектора ( overrightarrow{AB}left( 0,1,0 right).)
[left( {B,overrightarrow {A{A_1}} overrightarrow {B{C_1}} } right) = left| {begin{array}{*{20}{l}}{begin{array}{*{20}{c}}0&1&0end{array}}\{begin{array}{*{20}{c}}0&0&1end{array}}\{begin{array}{*{20}{c}}{frac{{sqrt 3 }}{2}}&{ — frac{1}{2}}&1end{array}}end{array}} right| = frac{{sqrt 3 }}{2}]
Считаем векторное произведение между векторами ( AA) и ( overrightarrow{B{{C}_{1}}}:)
[overrightarrow {A{A_1}} cdot overrightarrow {B{C_1}} = left| begin{array}{l}begin{array}{*{20}{c}}{overrightarrow i }&{overrightarrow j }&{overrightarrow k }end{array}\begin{array}{*{20}{c}}0&0&1end{array}\begin{array}{*{20}{c}}{frac{{sqrt 3 }}{2}}&{ — frac{1}{2}}&1end{array}end{array} right| — frac{{sqrt 3 }}{2}overrightarrow k + frac{1}{2}overrightarrow i ]
Теперь считаем его длину:
( left| overrightarrow{A{{A}_{1}}}times overrightarrow{B{{C}_{1}}} right|=sqrt{{{left( -frac{sqrt{3}}{2} right)}^{2}}+{{left( frac{1}{2} right)}^{2}}}=1)
Тогда
( d=frac{frac{sqrt{3}}{2}}{1}=frac{sqrt{3}}{2}.)
Ответ: ( frac{sqrt{3}}{2}.)
Теперь постарайся аккуратно выполнить вторую задачу. Ответом на нее будет: ( frac{sqrt{6}}{2}).
Для
начала вспомним, какие действия над векторами вам известны.
Итак,
это сложение двух векторов по правилу треугольника или параллелограмма и
нескольких векторов по правилу многоугольника. Вектор разности векторов мы
получали как вектор суммы векторов .
Также
вам знакомо правило умножение вектора на число.
Сегодня
вы познакомитесь с ещё одним действием над векторами — скалярным умножением
векторов.
Определение.
Скалярным произведением двух векторов называется произведение их длин
на косинус угла между ними.
Скалярное
произведение векторов обозначают
так .
Или
возможна запись без знака умножения.
Оно
равно произведению длин данных векторов на косинус угла между ними.
Стоит
вспомнить, что угол между векторами получают, откладывая данные векторы от
одной точки. При этом выбирают угол меньший 180°
Обратите
внимание, ранее, при выполнении сложения, вычитания векторов и умножения
вектора на число, результатом каждого из этих действий мы получали некоторый
вектор.
Результатом
же скалярного произведения векторов является число.
Сейчас
подробнее рассмотрим случай, когда скалярное произведение векторов равно 0.
Понятно,
что для этого хотя бы один из множителей должен быть равен нулю.
Такими
будут случаи, когда хотя бы один из векторов в произведении является нулевым.
Если
же векторы ненулевые,
то косинус угла между ними должен быть равен 0.
Среди
возможных значений градусной меры угла между двумя векторами только лишь косинус
угла в 90° равен 0.
Отсюда
получаем, что векторы перпендикулярны.
Подытожим.
Скалярное произведение равно нулю, если хотя бы один из векторов сомножителей является
нулевым.
Ну,
а скалярное произведение ненулевых векторов равно нулю тогда и только
тогда, когда эти векторы перпендикулярны.
Из
формулы скалярного произведения также можно заметить, что, если векторы не
нулевые, то их длины всегда больше нуля, поэтому их произведение тоже
положительно. А вот значение косинуса угла между ними может принимать как
положительные, так и отрицательные значения.
Можно
сказать, что скалярное произведение двух ненулевых векторов больше нуля, если
угол между векторами острый. Равно нулю, если угол между ним прямой. И меньше
нуля, если угол между данными векторами тупой. Ещё раз обратим внимание на то,
что эти заключения верны для ненулевых векторов .
Задача.
Найти скалярное произведение векторов и
,
пользуясь данными рисунков.
Решение.
а)
б)
в)
г)
Мы
рассмотрели примеры применения формулы скалярного произведения двух векторов и
убедились, что скалярное произведение ненулевых векторов больше нуля, если угол
между ними является острым, равно нулю — если векторы перпендикулярны, и меньше
нуля — если угол между векторами тупой.
А
сейчас рассмотрим сонаправленные векторы и
.
Запишем формулу их скалярного произведения.
Вы
должны помнить с прошлых уроков, что угол между сонаправленными векторами равен
нулю. А косинус угла в 0° равен 1. Тогда получаем, что скалярное произведение
сонаправленных векторов равно произведению их длин.
Говоря
о противоположно направленных векторах, можно вспомнить, что угол между ними
равен 180°. Значит, косинус равен -1.
Тогда
скалярное произведение противоположно направленных векторов равно .
Что
касается, скалярного произведения вектора на самого себя, то его называют скалярным
квадратом вектора. Этот случай можно рассматривать в контексте
сонаправленных векторов. Действительно, ведь векторы равны, а значит, и
сонаправлены. Такое произведение равно произведению длин данного вектора.
Тогда
получаем, что скалярный квадрат вектора равен квадрату его длины.
Задача.
Найдём скалярные квадраты векторов ,
,
и
.
Решение.
Скалярное
произведение векторов применяется не только в математике. Например, из курса
механики известно, что работа постоянной силы F
при перемещении из точки М в точку Н равна .
Тем
самым получаем, что работа силы F
равна скалярному произведению вектора силы и
вектора перемещения .
Вернёмся
к скалярному произведению в математике и решим несколько задач.
Задача.
К одной и той же точке приложены и
,
действующие под углом в друг
к другу. ,
.
Найти величину равнодействующей силы .
Решение.
1
способ
,
2
способ
,
Ответ:
.
Задача.
В ,
где
,
проведена высота .
Вычислить ,
,
,
.
Решение
,
так как
Подведём
итоги нашего урока.
Сегодня
вы познакомились с новым действием над векторами — скалярным умножением
векторов.
Скалярным
произведением двух векторов называют произведение длин данных векторов на
косинус угла между ними.
Проанализировав
эту формулу, мы заметили, что скалярное произведение равно нулю, если хотя бы
один из векторов сомножителей является нулевым. Ну, а скалярное произведение
ненулевых векторов рано нулю, тогда и только тогда, когда данные векторы
перпендикулярны.
Также,
пользуясь знаниями об углах между сонаправленными и противоположно
направленными векторами, мы выяснили, что скалярное произведение сонаправленных
векторов равно произведению их длин, а скалярное произведение противоположно
направленных векторов противоположно произведению их длин.
Введя
понятия скалярного квадрата вектора, мы получили, что он равен квадрату длины
данного вектора.
Знания
о скалярном произведении векторов можно применять не только на уроках
математики. Так же они широко используются в физике.
Скалярное произведение двух векторов 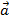
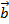
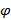
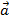
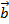
Свойства скалярного произведения
1.
2.
3.
4.
5.
Теорема 1: Если 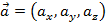
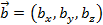
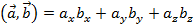
Следствие 1: 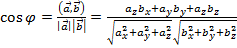
Векторное произведение векторов
Векторным произведением двух векторов 
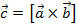
1. 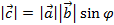
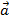
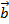
2. 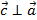
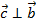
3. Направление 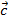
Свойства векторного произведения
1.
2.
3.
4.
Теорема 1: Если 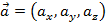
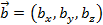
Геометрический смысл векторного произведения – определение площади параллелограмма S, из которого можно найти площадь треугольника
Следствие 1: 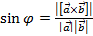
Направляющие косинусы
Пусть 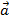
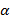
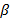
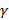

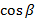
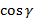
Вектор с координатами из направляющих косинусов – отнормированный вектор
Смешанное произведение векторов
Смешанным произведением трех векторов 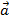
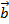
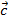
Теорема 1: Если 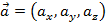
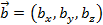
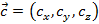
Геометрический смысл смешанного произведения – определение объема параллелепипеда V и пирамиды
Свойства смешанного произведения
1.
2.
3.
Признаки расположения векторов
Пусть 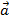
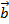
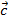
1.
2.
3. 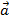
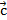
Правила проверки на линейную зависимость векторов
Два вектора линейно зависимы, если присутствует пропорциональность их координат: 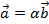
Три вектора линейно зависимы, если они компланарны: 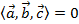
Четыре и более векторов в трехмерном пространстве 
Аналитическая геометрия
Прямая на плоскости
Уравнение с угловым коэффициентом 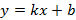
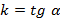
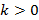
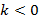
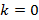
Рисунок 5. Прямая, заданная уравнением с угловым коэффициентом.
Вертикальная прямая имеет уравнение 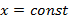
Прямая, проходящая через точку 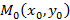
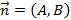
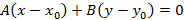
Рисунок 6. Прямая, проходящая через заданную точку и вектор нормали.
Для построения такого вида прямых задается дополнительная точка
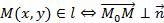
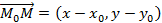
Преобразовав уравнение прямой, проходящей через точку и вектор нормали, можно получить общее уравнение прямой вида 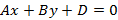
Преобразовав уже общее уравнение прямой, будет получено уравнение в прямой в отрезках вида
Построение прямой такого вида представлено на рисунке 7.
Рисунок 7. Построение прямой, заданном в уравнении в отрезках.
Дальнейший анализ возможности задать прямую на плоскости приведет еще к двум видам уравнений. Первым из них является параметрическое уравнение прямой, проходящей через точку 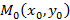
Из полученного уравнения вытекает каноническое уравнение прямой
Построение прямой по последним двум последним уравнениям представлены на рисунке 8.
Рисунок 8. Построение прямой, заданной точкой и направляющим вектором.
Помимо всех вышеуказанных способов существует еще способ задания прямой с помощью двух точек 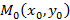
Пример прямой такого вида представлен на рисунке 9.
Рисунок 9. Прямая, заданная с помощью двух точек.
Помимо способов задания прямой на плоскости, следует определить признаки взаимного расположения прямых на плоскости. Если прямые заданы уравнением с угловым коэффициентом, тогда тангенс угла между заданными прямыми 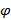
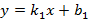
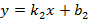
Исходя из этого уравнения, выделены признаки взаимного расположения прямых: при
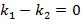
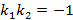
Рассматривая общие уравнения прямых, которые имеют вид 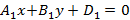
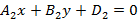
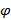
Аналогично предыдущему случаю, из этого уравнения вытекают признаки параллельности прямых, если 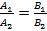
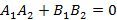
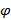
Используя общее уравнение прямой 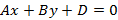
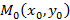
Расстоянием считается минимальный отрезок (перпендикуляр) от заданной точки до указанной прямой.
Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.
Таким образом, длина
вектора рассчитывается, как корень
квадратный из суммы квадратов его
координат

Аналогично рассчитывается длинаn-мерного вектора
Если вспомнить, что каждая координата
вектора – это разность между координатами
конца и начала, то мы получим формулу
длины отрезка, т.е. евклидова расстояния
между точками.
Скалярное произведение
двух векторов на плоскости – это
произведение длин этих векторов на
косинус угла между ними:
Можно доказать, что скалярное произведение
двух векторов

(y 1 , y 2) равно сумме произведений
соответствующих координат этих векторов:
х 1 * y 1 + х 2 * y 2 .
В n-мерном
пространстве скалярное произведение
векторовX= (х 1 ,
х 2 ,…,х n) иY=
(y 1 , y 2 ,…,y n)
определяется, как сумма произведений
их соответствующих координат:X*Y= х 1 * y 1 + х 2 * y 2 +
… + х n * y n .
Операция умножения
векторов друг на другу аналогична
умножению матрицы-строки на матрицу-столбец.
Подчеркнем, что в результате будет
получено число, а не вектор.
Скалярное произведение
векторов обладает следующими свойствами
(аксиомы):
1) Коммутативное
свойство: X*Y=Y*X.
2) Дистрибутивное
относительно сложения свойство:
X(Y+Z) =X*Y+X*Z.
3) Для любого
действительного числа 
4)

еслиX– не нулевой вектор;
Линейное векторное
пространство, в котором задано скалярное
произведение векторов, удовлетворяющее
четырем соответствующим аксиомам,
называется евклидовым линейным
векторным
пространством
.
Легко заметить, что
при умножении любого вектора самого на
себя мы получим квадрат его длины
.
Поэтому по-другомудлину
вектора
можно определить, как корень квадратный
из его скалярного квадрата:.
Длина вектора обладает
следующими свойствами:
1) |X| = 0Х = 0;
2) |X|
= ||*|X|,
где– действительное число;
3) |X*Y||X|*|Y|
(неравенство Коши-Буняковского
);
4) |X+Y||X|+|Y|
(неравенство треугольника
).
Угол между векторами вn-мерном
пространстве определяется, исходя из
понятия скалярного произведения. В
самом деле, если
то
Эта дробь не больше единицы (согласно
неравенству Коши-Буняковского), поэтому
отсюда можно найти.
Два вектора называют
ортогональными
илиперпендикулярными
,
если их скалярное произведение равно
нулю. Из определения скалярного
произведения следует, что нулевой вектор
ортогонален любому вектору. Если оба
ортогональных вектора ненулевые, то
обязательноcos= 0, т.е=/2
= 90 о.
Рассмотрим еще раз
рисунок 7.4. Из рисунка видно, что косинус
угла наклона вектора
к горизонтальной оси можно рассчитать
как
а косинус угланаклона вектора к вертикальной оси как
Эти числа принято называтьнаправляющими
косинусами
. Легко убедиться, что сумма
квадратов направляющих косинусов всегда
равна единице:cos 2 +cos 2 = 1. Аналогично можно ввести понятия
направляющих косинусов и для пространств
большей размерности.
Базис векторного пространства
Для векторов можно
определить понятия линейной комбинации
,линейной зависимости
инезависимости
аналогично тому, как эти понятия были
введены для строк матрицы. Также
справедливо, что если векторы линейно
зависимы, то по крайней мере один из них
можно линейно выразить через остальные
(т.е. он является их линейной комбинацией).
Верно и обратное утверждение: если один
из векторов является линейной комбинацией
остальных, то все эти векторы в совокупности
линейно зависимы.
Отметим, что если среди
векторов a l , a 2 ,…a m есть нулевой вектор, то эта совокупность
векторов обязательно линейно зависима.
В самом деле, мы получим l a l + 2 a 2 +…+ m a m = 0, если, например, приравняем коэффициент j при нулевом векторе к единице, а все
остальные коэффициенты – к нулю. При
этом не все коэффициенты будут равны
нулю ( j ≠ 0).
Кроме того, если
какая-то часть векторов из совокупности
векторов линейно зависимы, то и все эти
вектора — линейно зависимы. В самом деле,
если какие-то вектора дают нулевой
вектор в своей линейной комбинации с
коэффициентами, которые не являются
одновременно нулевыми, то к этой сумме
произведений можно добавить остальные
вектора, умноженные на нулевые
коэффициенты, и она по-прежнему будет
нулевым вектором.
Как определить, являются
ли вектора линейно зависимыми?
Например, возьмем три
вектора: а 1 = (1, 0, 1, 5), а 2 = (2,
1, 3, -2) и
а 3 = (3, 1, 4, 3). Составим из
них матрицу, в которой они будут являться
столбцами:
Тогда вопрос о линейной
зависимости сведется к определению
ранга этой матрицы. Если он окажется
равным трем, то все три столбца – линейно
независимы, а если окажется меньше, то
это будет говорить о линейной зависимости
векторов.
Так как ранг равен 2,
вектора линейно зависимы.
Отметим, что решение
задачи можно было бы начать и с рассуждений,
которые основаны на определении линейной
независимости. А именно, составить
векторное уравнение l a l + 2 a 2 + 3 a 3 = 0,
которое примет вид l *(1,
0, 1, 5) + 2 *(2, 1,
3, -2) + 3 *(3, 1, 4,
3) = (0, 0, 0, 0). Тогда мы получим систему
уравнений:
Решение этой системы
методом Гаусса сведется к получению
той же самой ступенчатой матрицы, только
в ней будет еще один столбец – свободных
членов. Они все будут равны нулю, так
как линейные преобразования нулей не
могут привести к другому результату.
Преобразованная система уравнений
примет вид:
Решением этой системы
будет (-с;-с; с), где с – произвольное
число; например, (-1;-1;1). Это означает, что
если взять l = -1; 2 =-1 и 3 = 1, то l a l + 2 a 2 + 3 a 3 = 0,
т.е. вектора на самом деле линейно
зависимы.
Из решенного примера
становится ясно, что если взять число
векторов больше, чем размерность
пространства, то они обязательно будут
линейно зависимы. В самом деле, если бы
в этом примере мы взяли пять векторов,
то получили бы матрицу 4 х 5, ранг которой
не мог бы оказаться больше четырех. Т.е.
максимальное число линейно независимых
столбцов все равно не было бы больше
четырех. Два, три или четыре четырехмерных
вектора могут оказаться линейно
независимыми, а пять и больше – не могут.
Следовательно, на плоскости могут
оказаться линейно независимыми не более
двух векторов. Любые три вектора в
двумерном пространстве – линейно
зависимы. В трехмерном пространстве
любые четыре (или более) вектора – всегда
линейно зависимы. И т.п.
Поэтому размерность
пространства можно определить, как
максимальное число линейно независимых
векторов, которые могут в нем быть.
Совокупность n линейно
независимых векторов n-мерного пространства
R называют базисом
этого пространства.
Теорема. Каждый вектор
линейного пространства можно представить
в виде линейной комбинации векторов
базиса, и притом единственным способом.
Доказательство. Пусть
векторы e l , e 2 ,…e n образуют базисn-мерного
пространства R. Докажем, что любой вектор
Х является линейной комбинацией этих
векторов. Поскольку вместе с вектором
Х число векторов станет (n +1), эти (n +1)
векторов будут линейно зависимы, т.е.
существуют числа l , 2 ,…, n ,, не равные одновременно
нулю, такие
что
l e l + 2 e 2 +…+ n e n
+Х = 0
При этом 0, т.к. в противном
случае мы получили бы l e l + 2 e 2 +…+ n e n
= 0, где не все коэффициенты l , 2 ,…, n равны нулю. Это означает, что векторы
базиса оказались бы линейно зависимы.
Следовательно, можно разделить обе
части первого уравнения на:
( l /)e l + ( 2 /)e 2 +…+ ( n /)e n
+ Х = 0
Х = -( l /)e l — ( 2 /)e 2 -…- ( n /)e n
Х = x l e l +x 2 e 2 +…+x n e n ,
где х j = -( j /),
Теперь докажем, что
такое представление в виде линейной
комбинации является единственным.
Предположим противное, т.е. что существует
другое представление:
Х = y l e l +y 2 e 2 +…+y n e n
Вычтем из него почленно
полученное ранее выражение:
0 = (y l – х 1)e l + (y 2 – х 2)e 2 +…+ (y n –
х n)e n
Так как векторы базиса
линейно независимы, получим, что
(y j — х j) = 0,
т.е.y j = х j . Итак, выражение
оказалось тем же самым. Теорема доказана.
Выражение Х = x l e l +x 2 e 2 +…+x n e n называютразложением
вектора Х по
базису e l , e 2 ,…e n ,
а числа х l , х 2 ,…х n —координатами
вектора х относительно
этого базиса, или в этом базисе.
Можно доказать, что
если nненулевых векторовn-мерного евклидова
пространства попарно ортогональны, то
они образуют базис. В самом деле, умножим
обе части равенства l e l + 2 e 2 +…+ n e n
= 0 на любой вектор е i .
Получим l
(e l *е i)
+ 2 (e 2 *е i)
+…+ n (e n *е i)
= 0
i (e i *е i)
= 0
i
= 0
для
i.
Векторы e l ,
e 2 ,…e n n-мерного
евклидова пространства образуютортонормированный базис
, если эти
векторы попарно ортогональны и норма
каждого из них равна единице, т.е. если
е i *e j = 0 приi≠jи |е i | = 1
дляi.
Теорема (без
доказательства). Во всяком n-мерном
евклидовом пространстве существует
ортонормированный базис.
Примером ортонормированного
базиса являют система n единичных
векторов е i , у которыхi-я компонента равна
единице, а остальные компоненты равны
нулю. Каждый такой вектор называетсяорт
. Например, вектора-орты (1, 0, 0),
(0, 1, 0) и (0, 0, 1) образуют базис трехмерного
пространства.
В случае плоской задачи скалярное произведение векторов a = {a x ; a y } и b = {b x ; b y } можно найти воспользовавшись следующей формулой:
a · b = a x · b x + a y · b y
Формула скалярного произведения векторов для пространственных задач
В случае пространственной задачи скалярное произведение векторов a = {a x ; a y ; a z } и b = {b x ; b y ; b z } можно найти воспользовавшись следующей формулой:
a · b = a x · b x + a y · b y + a z · b z
Формула скалярного произведения n -мерных векторов
В случае n-мерного пространства скалярное произведение векторов a = {a 1 ; a 2 ; … ; a n } и b = {b 1 ; b 2 ; … ; b n } можно найти воспользовавшись следующей формулой:
a · b = a 1 · b 1 + a 2 · b 2 + … + a n · b n
Свойства скалярного произведения векторов
1. Скалярное произведение вектора самого на себя всегда больше или равно нуля:
2. Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору:
a · a = 0 a = 0
3. Скалярное произведение вектора самого на себя равно квадрату его модуля:
4. Операция скалярного умножения коммуникативна:
5. Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны:
a ≠ 0, b ≠ 0, a · b = 0 a ┴ b
6. (αa) · b = α(a · b)
7. Операция скалярного умножения дистрибутивна:
(a + b) · c = a · c + b · c
Примеры задач на вычисление скалярного произведения векторов
Примеры вычисления скалярного произведения векторов для плоских задач
Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.
Решение:
a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20.
Найти скалярное произведение векторов a и b, если их длины |a| = 3, |b| = 6, а угол между векторами равен 60˚.
Решение:
a · b = |a| · |b| cos α = 3 · 6 · cos 60˚ = 9.
Найти скалярное произведение векторов p = a + 3b и q = 5a — 3 b, если их длины |a| = 3, |b| = 2, а угол между векторами a и b равен 60˚.
Решение:
p · q = (a + 3b) · (5a — 3b) = 5 a · a — 3 a · b + 15 b · a — 9 b · b =
5 |a| 2 + 12 a · b — 9 |b| 2 = 5 · 3 2 + 12 · 3 · 2 · cos 60˚ — 9 · 2 2 = 45 +36 -36 = 45.
Пример вычисления скалярного произведения векторов для пространственных задач
Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.
Решение:
a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 — 5 = 15.
Пример вычисления скалярного произведения для n -мерных векторов
Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.
Решение:
a · b = 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 — 5 -4 = 11.
13.
Векторным произведением векторов и вектора называется третий вектор
, определяемый следующим образом:
2) перпендикулярно, перпендикулярно. (1″»)
3) векторы ориентированы также, как и базис всего пространства (положительно или отрицательно).
Обозначают: .
Физический смысл векторного произведения
― момент силы относительно точки О; ― радиус ― вектор точки приложения силы, тогда
причем, если перенести в точку О, то тройка, должна быть ориентирована как вектора базиса.
Определение 1
Скалярное произведение векторов называют число, равное произведению дин этих векторов на косинус угла между ними.
Обозначение произведения векторов a → и b → имеет вид a → , b → . Преобразуем в формулу:
a → , b → = a → · b → · cos a → , b → ^ . a → и b → обозначают длины векторов, a → , b → ^ — обозначение угла между заданными векторами. Если хоть один вектор нулевой, то есть имеет значение 0, то и результат будет равен нулю, a → , b → = 0
При умножении вектора самого на себя, получим квадрат его дины:
a → , b → = a → · b → · cos a → , a → ^ = a → 2 · cos 0 = a → 2
Определение 2
Скалярное умножение вектора самого на себя называют скалярным квадратом.
Вычисляется по формуле:
a → , b → = a → · b → · cos a → , b → ^ .
Запись a → , b → = a → · b → · cos a → , b → ^ = a → · n p a → b → = b → · n p b → a → показывает, что n p b → a → — это числовая проекция a → на b → , n p a → a → — проекция b → на a → соостветсвенно.
Сформулируем определение произведения для двух векторов:
Скалярное произведение двух векторов a → на b → называют произведение длины вектора a → на проекцию b → на направление a → или произведение длины b → на проекцию a → соответственно.
Скалярное произведение в координатах
Вычисление скалярного произведения можно производить через координаты векторов в заданной плоскости или в пространстве.
Скаларное произведение двух векторов на плоскости, в трехмерном простарнстве называют сумму координат заданных векторов a → и b → .
При вычислении на плоскости скаларного произведения заданных векторов a → = (a x , a y) , b → = (b x , b y) в декартовой системе используют:
a → , b → = a x · b x + a y · b y ,
для трехмерного пространства применимо выражение:
a → , b → = a x · b x + a y · b y + a z · b z .
Фактически это является третьим определением скалярного произведения.
Докажем это.
Доказательство 1
Для доказательства используем a → , b → = a → · b → · cos a → , b → ^ = a x · b x + a y · b y для векторов a → = (a x , a y) , b → = (b x , b y) на декартовой системе.
Следует отложить векторы
O A → = a → = a x , a y и O B → = b → = b x , b y .
Тогда длина вектора A B → будет равна A B → = O B → — O A → = b → — a → = (b x — a x , b y — a y) .
Рассмотрим треугольник O A B .
A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos (∠ A O B) верно, исходя из теоремы косинусов.
По условию видно, что O A = a → , O B = b → , A B = b → — a → , ∠ A O B = a → , b → ^ , значит, формулу нахождения угла между векторами запишем иначе
b → — a → 2 = a → 2 + b → 2 — 2 · a → · b → · cos (a → , b → ^) .
Тогда из первого определения следует, что b → — a → 2 = a → 2 + b → 2 — 2 · (a → , b →) , значит (a → , b →) = 1 2 · (a → 2 + b → 2 — b → — a → 2) .
Применив формулу вычисления длины векторов, получим:
a → , b → = 1 2 · ((a 2 x + a y 2) 2 + (b 2 x + b y 2) 2 — ((b x — a x) 2 + (b y — a y) 2) 2) = = 1 2 · (a 2 x + a 2 y + b 2 x + b 2 y — (b x — a x) 2 — (b y — a y) 2) = = a x · b x + a y · b y
Докажем равенства:
(a → , b →) = a → · b → · cos (a → , b → ^) = = a x · b x + a y · b y + a z · b z
– соответственно для векторов трехмерного пространства.
Скалярное произведение векторов с координатами говорит о том, что скалярный квадрат вектора равен сумме квадратов его координат в пространстве и на плоскости соответственно. a → = (a x , a y , a z) , b → = (b x , b y , b z) и (a → , a →) = a x 2 + a y 2 .
Скалярное произведение и его свойства
Существуют свойства скалярного произведения, которые применимы для a → , b → и c → :
- коммутативность (a → , b →) = (b → , a →) ;
- дистрибутивность (a → + b → , c →) = (a → , c →) + (b → , c →) , (a → + b → , c →) = (a → , b →) + (a → , c →) ;
- сочетательное свойство (λ · a → , b →) = λ · (a → , b →) , (a → , λ · b →) = λ · (a → , b →) , λ — любое число;
- скалярный квадрат всегда больше нуля (a → , a →) ≥ 0 , где (a → , a →) = 0 в том случае, когда a → нулевой.
Пример 1
Свойства объяснимы благодаря определению скалярного произведения на плоскости и свойствам при сложении и умножении действительных чисел.
Доказать свойство коммутативности (a → , b →) = (b → , a →) . Из определения имеем, что (a → , b →) = a y · b y + a y · b y и (b → , a →) = b x · a x + b y · a y .
По свойству коммутативности равенства a x · b x = b x · a x и a y · b y = b y · a y верны, значит a x · b x + a y · b y = b x · a x + b y · a y .
Отсюда следует, что (a → , b →) = (b → , a →) . Что и требовалось доказать.
Дистрибутивность справедлива для любых чисел:
(a (1) → + a (2) → + . . . + a (n) → , b →) = (a (1) → , b →) + (a (2) → , b →) + . . . + (a (n) → , b →)
и (a → , b (1) → + b (2) → + . . . + b (n) →) = (a → , b (1) →) + (a → , b (2) →) + . . . + (a → , b → (n)) ,
отсюда имеем
(a (1) → + a (2) → + . . . + a (n) → , b (1) → + b (2) → + . . . + b (m) →) = = (a (1) → , b (1) →) + (a (1) → , b (2) →) + . . . + (a (1) → , b (m) →) + + (a (2) → , b (1) →) + (a (2) → , b (2) →) + . . . + (a (2) → , b (m) →) + . . . + + (a (n) → , b (1) →) + (a (n) → , b (2) →) + . . . + (a (n) → , b (m) →)
Скалярное произведение с примерами и решениями
Любая задача такого плана решается с применением свойств и формул, касающихся скалярного произведения:
- (a → , b →) = a → · b → · cos (a → , b → ^) ;
- (a → , b →) = a → · n p a → b → = b → · n p b → a → ;
- (a → , b →) = a x · b x + a y · b y или (a → , b →) = a x · b x + a y · b y + a z · b z ;
- (a → , a →) = a → 2 .
Рассмотрим некоторые примеры решения.
Пример 2
Длина a → равна 3, длина b → равна 7. Найти скалярное произведение, если угол имеет 60 градусов.
Решение
По условию имеем все данные, поэтому вычисляем по формуле:
(a → , b →) = a → · b → · cos (a → , b → ^) = 3 · 7 · cos 60 ° = 3 · 7 · 1 2 = 21 2
Ответ: (a → , b →) = 21 2 .
Пример 3
Заданны векторы a → = (1 , — 1 , 2 — 3) , b → = (0 , 2 , 2 + 3) . Чему равно скалярной произведение.
Решение
В данном примере рассматривается формула вычисления по координатам, так как они заданы в условии задачи:
(a → , b →) = a x · b x + a y · b y + a z · b z = = 1 · 0 + (- 1) · 2 + (2 + 3) · (2 + 3) = = 0 — 2 + (2 — 9) = — 9
Ответ: (a → , b →) = — 9
Пример 4
Найти скалярное произведение A B → и A C → . На координатной плоскости заданы точки A (1 , — 3) , B (5 , 4) , C (1 , 1) .
Решение
Для начала вычисляются координаты векторов, так как по условию даны координаты точек:
A B → = (5 — 1 , 4 — (- 3)) = (4 , 7) A C → = (1 — 1 , 1 — (- 3)) = (0 , 4)
Подставив в формулу с использованием координат, получим:
(A B → , A C →) = 4 · 0 + 7 · 4 = 0 + 28 = 28 .
Ответ: (A B → , A C →) = 28 .
Пример 5
Заданы векторы a → = 7 · m → + 3 · n → и b → = 5 · m → + 8 · n → , найти их произведение. m → равен 3 и n → равен 2 единицам, они перпендикулярные.
Решение
(a → , b →) = (7 · m → + 3 · n → , 5 · m → + 8 · n →) . Применив свойство дистрибутивности, получим:
(7 · m → + 3 · n → , 5 · m → + 8 · n →) = = (7 · m → , 5 · m →) + (7 · m → , 8 · n →) + (3 · n → , 5 · m →) + (3 · n → , 8 · n →)
Выносим коэффициент за знак произведения и получим:
(7 · m → , 5 · m →) + (7 · m → , 8 · n →) + (3 · n → , 5 · m →) + (3 · n → , 8 · n →) = = 7 · 5 · (m → , m →) + 7 · 8 · (m → , n →) + 3 · 5 · (n → , m →) + 3 · 8 · (n → , n →) = = 35 · (m → , m →) + 56 · (m → , n →) + 15 · (n → , m →) + 24 · (n → , n →)
По свойству коммутативности преобразуем:
35 · (m → , m →) + 56 · (m → , n →) + 15 · (n → , m →) + 24 · (n → , n →) = = 35 · (m → , m →) + 56 · (m → , n →) + 15 · (m → , n →) + 24 · (n → , n →) = = 35 · (m → , m →) + 71 · (m → , n →) + 24 · (n → , n →)
В итоге получим:
(a → , b →) = 35 · (m → , m →) + 71 · (m → , n →) + 24 · (n → , n →) .
Теперь применим формулу для скалярного произведения с заданным по условию углом:
(a → , b →) = 35 · (m → , m →) + 71 · (m → , n →) + 24 · (n → , n →) = = 35 · m → 2 + 71 · m → · n → · cos (m → , n → ^) + 24 · n → 2 = = 35 · 3 2 + 71 · 3 · 2 · cos π 2 + 24 · 2 2 = 411 .
Ответ: (a → , b →) = 411
Если имеется числовая проекция.
Пример 6
Найти скалярное произведение a → и b → . Вектор a → имеет координаты a → = (9 , 3 , — 3) , проекция b → с координатами (- 3 , — 1 , 1) .
Решение
По условию векторы a → и проекция b → противоположно направленные, потому что a → = — 1 3 · n p a → b → → , значит проекция b → соответствует длине n p a → b → → , при чем со знаком «-»:
n p a → b → → = — n p a → b → → = — (- 3) 2 + (- 1) 2 + 1 2 = — 11 ,
Подставив в формулу, получим выражение:
(a → , b →) = a → · n p a → b → → = 9 2 + 3 2 + (- 3) 2 · (- 11) = — 33 .
Ответ: (a → , b →) = — 33 .
Задачи при известном скалярном произведении, где необходимо отыскать длину вектора или числовую проекцию.
Пример 7
Какое значение должна принять λ при заданном скалярном произведении a → = (1 , 0 , λ + 1) и b → = (λ , 1 , λ) будет равным -1.
Решение
Из формулы видно, что необходимо найти сумму произведений координат:
(a → , b →) = 1 · λ + 0 · 1 + (λ + 1) · λ = λ 2 + 2 · λ .
В дано имеем (a → , b →) = — 1 .
Чтобы найти λ , вычисляем уравнение:
λ 2 + 2 · λ = — 1 , отсюда λ = — 1 .
Ответ: λ = — 1 .
Физический смысл скалярного произведения
Механика рассматривает приложение скалярного произведения.
При работе А с постоянной силой F → перемещаемое тело из точки M в N можно найти произведение длин векторов F → и M N → с косинусом угла между ними, значит работа равна произведению векторов силы и перемещения:
A = (F → , M N →) .
Пример 8
Перемещение материальной точки на 3 метра под действием силы равной 5 ньтонов направлено под углом 45 градусов относительно оси. Найти A .
Решение
Так как работа – это произведение вектора силы на перемещение, значит, исходя из условия F → = 5 , S → = 3 , (F → , S → ^) = 45 ° , получим A = (F → , S →) = F → · S → · cos (F → , S → ^) = 5 · 3 · cos (45 °) = 15 2 2 .
Ответ: A = 15 2 2 .
Пример 9
Материальная точка, перемещаясь из M (2 , — 1 , — 3) в N (5 , 3 λ — 2 , 4) под силой F → = (3 , 1 , 2) , совершила работа равную 13 Дж. Вычислить длину перемещения.
Решение
При заданных координатах вектора M N → имеем M N → = (5 — 2 , 3 λ — 2 — (- 1) , 4 — (- 3)) = (3 , 3 λ — 1 , 7) .
По формуле нахождения работы с векторами F → = (3 , 1 , 2) и M N → = (3 , 3 λ — 1 , 7) получим A = (F ⇒ , M N →) = 3 · 3 + 1 · (3 λ — 1) + 2 · 7 = 22 + 3 λ .
По условию дано, что A = 13 Д ж, значит 22 + 3 λ = 13 . Отсюда следует λ = — 3 , значит и M N → = (3 , 3 λ — 1 , 7) = (3 , — 10 , 7) .
Чтобы найти длину перемещения M N → , применим формулу и подставим значения:
M N → = 3 2 + (- 10) 2 + 7 2 = 158 .
Ответ: 158 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Если в задаче и длины векторов, и угол между ними преподнесены «на блюдечке с голубой каёмочкой», то условие задачи и её решение выглядят так:
Пример 1.
Даны векторы .
Найти скалярное произведение векторов
, если их длины и угол между ними представлены
следующими значениями:
Справедливо и другое определение, полностью равносильное определению 1.
Определение 2
. Скалярным произведением векторов называется число (скаляр), равное
произведению длины одного их этих векторов на проекцию другого вектора на ось, определяемую первым из указанных векторов. Формула согласно определению 2:
Задачу с применением этой формулы решим после следующего важного теоретического пункта.
Определение скалярного произведения векторов через координаты
То же самое число можно получить, если перемножаемые векторы заданы своими координатами.
Определение 3.
Скалярное произведение векторов — это число,
равное сумме попарных произведений их соответствующих координат
.
На плоскости
Если два вектора и
на плоскости определены своими двумя декартовыми прямоугольными координатами
то скалярное произведение этих векторов равно сумме попарных произведений их соответствующих координат:
.
Пример 2.
Найти численную величину проекции вектора
на ось, параллельную вектору
.
Решение. Находим скалярное произведение векторов, складывая попарные произведения их координат:
Теперь нам требуется приравнять полученное скалярное произведение произведению
длины вектора на проекцию
вектора на ось, параллельную
вектору (в соответствии
с формулой ).
Находим длину вектора
как квадратный корень из суммы квадратов его координат:
.
Составляем уравнение и решаем его:
Ответ. Искомая численная величина равна минус 8.
В пространстве
Если два вектора и
в пространстве определены своими тремя декартовыми прямоугольными координатами
,
то скалярное произведение этих векторов также равно сумме попарных произведений их соответствующих координат, только координат уже три:
.
Задача на нахождение скалярного произведения рассмотренным способом — после разбора свойств
скалярного произведения. Потому что в задаче потребуется определить, какой угол образуют перемножаемые
векторы.
Свойства скалярного произведения векторов
Алгебраические свойства
1. (переместительное свойство
: от перемены местами перемножаемых векторов величина их скалярного произведения не меняется).
2. (сочетательное относительно числового множителя свойство
: скалярное произведение вектора, умноженного на некоторый множитель, и другого вектора, равно скалярному произведению этих векторов, умноженному на тот же множитель).
3. (распределительное относительно суммы векторов свойство
: скалярное произведение суммы двух векторов на третий вектор равно сумме скалярных произведений первого вектора на третий вектор и второго вектора на третий вектор).
4. (скалярный квадрат вектора больше нуля
),
если — ненулевой вектор, и ,
если — нулевой вектор.
Геометрические свойства
В определениях изучаемой операции мы уже касались понятия угла между двумя векторами.
Пора уточнить это понятие.
На рисунке выше видны два вектора, которые приведены к общему началу. И первое, на что нужно
обратить внимание: между этими векторами существуют два угла — φ
1
и φ
2
. Какой из этих углов фигурирует в определениях и свойствах
скалярного произведения векторов? Сумма рассмотренных углов равна 2π
и поэтому
косинусы этих углов равны. В определение скалярного произведения входит только косинус угла, а не значение его выражения.
Но в свойствах рассматривается только один угол. И это тот из двух углов, который не превосходит π
,
то есть 180 градусов. На рисунке этот угол обозначен как φ
1
.
1. Два вектора называют ортогональными
и угол между этими векторами — прямой
(90 градусов или π
/2
), если скалярное произведение этих векторов равно нулю
:
.
Ортогональностью в векторной алгебре называется перпендикулярность двух векторов.
2. Два ненулевых вектора составляют острый угол
(от 0 до 90 градусов, или, что тоже самое — меньше π
скалярное произведение
положительно
.
3. Два ненулевых вектора составляют тупой угол
(от 90 до 180 градусов, или, что то же самое — больше π
/2
) тогда и только тогда, когда их скалярное произведение отрицательно
.
Пример 3.
В координатах даны векторы:

Вычислить скалярные произведения всех пар данных векторов. Какой угол (острый, прямой, тупой) образуют эти пары векторов?
Решение. Вычислять будем путём сложения произведений соответствующих координат.
Получили отрицательное число, поэтому векторы образуют тупой угол.
Получили положительное число, поэтому векторы образуют острый угол.
Получили нуль, поэтому векторы образуют прямой угол.
Получили положительное число, поэтому векторы образуют острый угол.
.
Получили положительное число, поэтому векторы образуют острый угол.
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними
.
Пример 4.
Даны длины двух векторов и угол между ними:
.
Определить, при каком значении числа
векторы и
ортогональны (перпендикулярны).
Решение. Перемножим векторы по правилу умножения многочленов:
Теперь вычислим каждое слагаемое:
.
Составим уравнение (равенство произведения нулю), приведём подобные члены и решим уравнение:
Ответ: мы получили значение λ
= 1,8
,
при котором векторы ортогональны.
Пример 5.
Доказать, что вектор
ортогонален (перпендикулярен) вектору
Решение. Чтобы проверить ортогональность, перемножим векторы
и
как многочлены, подставляя
вместо его выражение, данное
в условии задачи:

Для этого нужно каждый член (слагаемое) первого многочлена умножить на каждый член
второго и полученные произведения сложить:

В полученном результате дробь за счёт
сокращается. Получается следующий результат:
Вывод: в результате умножения получили нуль, следовательно, ортогональность (перпендикулярность) векторов доказана.
Решить задачу самостоятельно, а затем посмотреть решение
Пример 6.
Даны длины векторов
и
, a
угол между этими векторами равен π
/4
. Определить, при каком значении
μ
векторы и
взаимно перпендикулярны.
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними
.
Матричное представление скалярного произведения векторов и произведение n-мерных векторов
Иногда выигрышным для наглядности является представление двух перемножаемых векторов
в виде матриц. Тогда первый вектор представлен в виде матрицы-строки, а второй — в виде матрицы-столбца:
Тогда скалярное произведение векторов будет произведением этих матриц
:
Результат тот же, что и полученный способом, который мы уже рассмотрели. Получили одно
единственное число, и произведение матрицы-строки на матрицу-столбец также является одним единственным
числом.
В матричной форме удобно представлять произведение абстрактных n-мерных векторов.
Так, произведение двух четырёхмерных векторов будет произведением матрицы-строки с четырьмя элементами на
матрицу-столбец также с четырьмя элементами, произведение двух пятимерных векторов — произведением
матрицы-строки с пятью элементами на матрицу-столбец также с пятью элементами и так далее.
Пример 7.
Найти скалярные произведения пар векторов
,
используя матричное представление.
Решение. Первая пара векторов. Представляем первый вектор в виде матрицы-строки, а второй —
в виде матрицы-столбца. Находим скалярное произведение этих векторов как произведение матрицы-строки на
матрицу-столбец:
Аналогично представляем вторую пару и находим:
Как видим, результаты получились те же, что и у тех же пар из
примера 2.
Угол между двумя векторами
Вывод формулы косинуса угла между двумя векторами очень красив и краток.
Чтобы выразить скалярное произведение векторов
(1)
в координатной форме, предварительно найдём скалярные произведение ортов. Скалярное произведение вектора на само себя по определению:
То, что записано в формуле выше, означает: скалярное произведение вектора на самого себя равно квадрату его длины
.
Косинус нуля равен единице, поэтому квадрат каждого орта будет равен единице:
Так как векторы
попарно перпендикулярны, то попарные произведения ортов будут равны нулю:
Теперь выполним умножение векторных многочленов:
Подставляем в правую часть равенства значения соответствующих скалярных произведений ортов:
Получаем формулу косинуса угла между двумя векторами:
Пример 8.
Даны три точки A
(1;1;1), B
(2;2;1), C
(2;1;2).
Найти угол .
Решение. Находим координаты векторов:
,
.
По формуле косинуса угла получаем:
Следовательно, .
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними
.
Пример 9.
Даны два вектора
Найти сумму, разность, длину, скалярное произведение и угол между ними.
2.Разность
I. Скалярное произведение обращается в нуль в том и только в том случае, когда по крайней мере один из векторов является нулевым или если векторы перпендикулярны. В самом деле, если или , или то .
Обратно, если и перемножаемые векторы не являются нулевыми, то потому что из условия
при вытекает:
Так как направление нулевого вектора неопределенно, то нулевой вектор можно считать перпендикулярным к любому вектору. Поэтому указанное свойство скалярного произведения может быть сформулировано короче: скалярное произведение обращается в нуль в том и только том случае, когда векторы перпендикулярны.
II. Скалярное произведение обладает свойством переместительности:
Это свойство непосредственно вытекает из определения:
потому что различные обозначения одного и того же угла.
III. Исключительно важное значение имеет распределительный закон. Его применение столь же велико, как и в обычной арифметике или алгебре, где он формулируется так: чтобы умножить сумму, нужно умножить каждое слагаемое и сложить полученные произведения, т. е.
Очевидно, что умножение многозначных чисел в арифметике или многочленов в алгебре основано на этом свойстве умножения.
Такое же основное значение имеет этот закон и в векторной алгебре, так как на основании его мы можем применять к векторам обычное правило умножения многочленов.
Докажем, что для любых трех векторов А, В, С справедлива равенство
По второму определению скалярного произведения, выражаемому формулой получим:
Применив теперь свойство 2 проекций из § 5, найдем:
что и требовалось доказать.
IV. Скалярное произведение обладает свойством сочетательности относительно числового множителя; это свойство выражается следующей формулой:
т. е. чтобы умножить скалярное произведение векторов на число, достаточно умножить на это число один из сомножителей.
Будут и задачи для самостоятельного решения, к которым можно
посмотреть ответы.
Если в задаче и длины векторов, и угол между ними преподнесены «на блюдечке с голубой каёмочкой», то условие задачи и её решение выглядят так:
Пример 1.
Даны векторы .
Найти скалярное произведение векторов
, если их длины и угол между ними представлены
следующими значениями:
Справедливо и другое определение, полностью равносильное определению 1.
Определение 2
. Скалярным произведением векторов называется число (скаляр), равное
произведению длины одного их этих векторов на проекцию другого вектора на ось, определяемую первым из указанных векторов. Формула согласно определению 2:
Задачу с применением этой формулы решим после следующего важного теоретического пункта.
Определение скалярного произведения векторов через координаты
То же самое число можно получить, если перемножаемые векторы заданы своими координатами.
Определение 3.
Скалярное произведение векторов — это число,
равное сумме попарных произведений их соответствующих координат
.
На плоскости
Если два вектора и
на плоскости определены своими двумя декартовыми прямоугольными координатами
то скалярное произведение этих векторов равно сумме попарных произведений их соответствующих координат:
.
Пример 2.
Найти численную величину проекции вектора
на ось, параллельную вектору
.
Решение. Находим скалярное произведение векторов, складывая попарные произведения их координат:
Теперь нам требуется приравнять полученное скалярное произведение произведению
длины вектора на проекцию
вектора на ось, параллельную
вектору (в соответствии
с формулой ).
Находим длину вектора
как квадратный корень из суммы квадратов его координат:
.
Составляем уравнение и решаем его:
Ответ. Искомая численная величина равна минус 8.
В пространстве
Если два вектора и
в пространстве определены своими тремя декартовыми прямоугольными координатами
,
то скалярное произведение этих векторов также равно сумме попарных произведений их соответствующих координат, только координат уже три:
.
Задача на нахождение скалярного произведения рассмотренным способом — после разбора свойств
скалярного произведения. Потому что в задаче потребуется определить, какой угол образуют перемножаемые
векторы.
Свойства скалярного произведения векторов
Алгебраические свойства
1. (переместительное свойство
: от перемены местами перемножаемых векторов величина их скалярного произведения не меняется).
2. (сочетательное относительно числового множителя свойство
: скалярное произведение вектора, умноженного на некоторый множитель, и другого вектора, равно скалярному произведению этих векторов, умноженному на тот же множитель).
3. (распределительное относительно суммы векторов свойство
: скалярное произведение суммы двух векторов на третий вектор равно сумме скалярных произведений первого вектора на третий вектор и второго вектора на третий вектор).
4. (скалярный квадрат вектора больше нуля
),
если — ненулевой вектор, и ,
если — нулевой вектор.
Геометрические свойства
В определениях изучаемой операции мы уже касались понятия угла между двумя векторами.
Пора уточнить это понятие.
На рисунке выше видны два вектора, которые приведены к общему началу. И первое, на что нужно
обратить внимание: между этими векторами существуют два угла — φ
1
и φ
2
. Какой из этих углов фигурирует в определениях и свойствах
скалярного произведения векторов? Сумма рассмотренных углов равна 2π
и поэтому
косинусы этих углов равны. В определение скалярного произведения входит только косинус угла, а не значение его выражения.
Но в свойствах рассматривается только один угол. И это тот из двух углов, который не превосходит π
,
то есть 180 градусов. На рисунке этот угол обозначен как φ
1
.
1. Два вектора называют ортогональными
и угол между этими векторами — прямой
(90 градусов или π
/2
), если скалярное произведение этих векторов равно нулю
:
.
Ортогональностью в векторной алгебре называется перпендикулярность двух векторов.
2. Два ненулевых вектора составляют острый угол
(от 0 до 90 градусов, или, что тоже самое — меньше π
скалярное произведение
положительно
.
3. Два ненулевых вектора составляют тупой угол
(от 90 до 180 градусов, или, что то же самое — больше π
/2
) тогда и только тогда, когда их скалярное произведение отрицательно
.
Пример 3.
В координатах даны векторы:

Вычислить скалярные произведения всех пар данных векторов. Какой угол (острый, прямой, тупой) образуют эти пары векторов?
Решение. Вычислять будем путём сложения произведений соответствующих координат.
Получили отрицательное число, поэтому векторы образуют тупой угол.
Получили положительное число, поэтому векторы образуют острый угол.
Получили нуль, поэтому векторы образуют прямой угол.
Получили положительное число, поэтому векторы образуют острый угол.
.
Получили положительное число, поэтому векторы образуют острый угол.
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними
.
Пример 4.
Даны длины двух векторов и угол между ними:
.
Определить, при каком значении числа
векторы и
ортогональны (перпендикулярны).
Решение. Перемножим векторы по правилу умножения многочленов:
Теперь вычислим каждое слагаемое:
.
Составим уравнение (равенство произведения нулю), приведём подобные члены и решим уравнение:
Ответ: мы получили значение λ
= 1,8
,
при котором векторы ортогональны.
Пример 5.
Доказать, что вектор
ортогонален (перпендикулярен) вектору
Решение. Чтобы проверить ортогональность, перемножим векторы
и
как многочлены, подставляя
вместо его выражение, данное
в условии задачи:

Для этого нужно каждый член (слагаемое) первого многочлена умножить на каждый член
второго и полученные произведения сложить:

В полученном результате дробь за счёт
сокращается. Получается следующий результат:
Вывод: в результате умножения получили нуль, следовательно, ортогональность (перпендикулярность) векторов доказана.
Решить задачу самостоятельно, а затем посмотреть решение
Пример 6.
Даны длины векторов
и
, a
угол между этими векторами равен π
/4
. Определить, при каком значении
μ
векторы и
взаимно перпендикулярны.
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними
.
Матричное представление скалярного произведения векторов и произведение n-мерных векторов
Иногда выигрышным для наглядности является представление двух перемножаемых векторов
в виде матриц. Тогда первый вектор представлен в виде матрицы-строки, а второй — в виде матрицы-столбца:
Тогда скалярное произведение векторов будет произведением этих матриц
:
Результат тот же, что и полученный способом, который мы уже рассмотрели. Получили одно
единственное число, и произведение матрицы-строки на матрицу-столбец также является одним единственным
числом.
В матричной форме удобно представлять произведение абстрактных n-мерных векторов.
Так, произведение двух четырёхмерных векторов будет произведением матрицы-строки с четырьмя элементами на
матрицу-столбец также с четырьмя элементами, произведение двух пятимерных векторов — произведением
матрицы-строки с пятью элементами на матрицу-столбец также с пятью элементами и так далее.
Пример 7.
Найти скалярные произведения пар векторов
,
используя матричное представление.
Решение. Первая пара векторов. Представляем первый вектор в виде матрицы-строки, а второй —
в виде матрицы-столбца. Находим скалярное произведение этих векторов как произведение матрицы-строки на
матрицу-столбец:
Аналогично представляем вторую пару и находим:
Как видим, результаты получились те же, что и у тех же пар из
примера 2.
Угол между двумя векторами
Вывод формулы косинуса угла между двумя векторами очень красив и краток.
Чтобы выразить скалярное произведение векторов
(1)
в координатной форме, предварительно найдём скалярные произведение ортов. Скалярное произведение вектора на само себя по определению:
То, что записано в формуле выше, означает: скалярное произведение вектора на самого себя равно квадрату его длины
.
Косинус нуля равен единице, поэтому квадрат каждого орта будет равен единице:
Так как векторы
попарно перпендикулярны, то попарные произведения ортов будут равны нулю:
Теперь выполним умножение векторных многочленов:
Подставляем в правую часть равенства значения соответствующих скалярных произведений ортов:
Получаем формулу косинуса угла между двумя векторами:
Пример 8.
Даны три точки A
(1;1;1), B
(2;2;1), C
(2;1;2).
Найти угол .
Решение. Находим координаты векторов:
,
.
По формуле косинуса угла получаем:
Следовательно, .
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними
.
Пример 9.
Даны два вектора
Найти сумму, разность, длину, скалярное произведение и угол между ними.
2.Разность
Продолжаем разбираться с векторами. На первом уроке Векторы для чайников
мы рассмотрели понятие вектора, действия с векторами, координаты вектора и простейшие задачи с векторами. Если вы зашли на эту страничку впервые с поисковика, настоятельно рекомендую прочитать вышеуказанную вводную статью, поскольку для усвоения материала необходимо ориентироваться в используемых мной терминах, обозначениях, обладать базовыми знаниями о векторах и уметь решать элементарные задачи. Данный урок является логическим продолжением темы, и на нём я подробно разберу типовые задания, в которых используется скалярное произведение векторов. Это ОЧЕНЬ ВАЖНОЕ занятие
. Постарайтесь не пропускать примеры, к ним прилагается полезный бонус – практика поможет вам закрепить пройденный материал и «набить руку» на решении распространенных задач аналитической геометрии.
Сложение векторов, умножение вектора на число…. Было бы наивным думать, что математики не придумали что-нибудь ещё. Помимо уже рассмотренных действий, существует ряд других операций с векторами, а именно: скалярное произведение векторов
, векторное произведение векторов
и смешанное произведение векторов
. Скалярное произведение векторов знакомо нам со школы, два других произведения традиционно относятся к курсу высшей математики. Темы несложные, алгоритм решения многих задач трафаретен и понятен. Единственное. Информации прилично, поэтому нежелательно пытаться освоить-прорешать ВСЁ И СРАЗУ. Особенно это касается чайников, поверьте, автор совершенно не хочет чувствовать себя Чикатило от математики. Ну и не от математики, конечно, тоже =) Более подготовленные студенты могут использовать материалы выборочно, в известном смысле, «добирать» недостающие знания, для вас я буду безобидным графом Дракулой =)
Приоткроем же, наконец, дверь и увлечённо посмотрим, что происходит, когда два вектора встречают друг друга….
Определение скалярного произведения векторов.
Свойства скалярного произведения. Типовые задачи
Понятие скалярного произведения
Сначала про угол между векторами
. Думаю, всем интуитивно понятно, что такое угол между векторами, но на всякий случай чуть подробнее. Рассмотрим свободные ненулевые векторы и . Если отложить данные векторы от произвольной точки , то получится картинка, которую многие уже представили мысленно:
Признаюсь, здесь я обрисовал ситуацию только на уровне понимания. Если необходимо строгое определение угла между векторами, пожалуйста, обратитесь к учебнику, для практических же задач оно нам, в принципе, ни к чему. Также ЗДЕСЬ И ДАЛЕЕ я буду местами игнорировать нулевые векторы ввиду их малой практической значимости. Оговорку сделал специально для продвинутых посетителей сайта, которые могут меня упрекнуть в теоретической неполноте некоторых последующих утверждений.
может принимать значения от 0 до 180 градусов (от 0 до радиан) включительно. Аналитически данный факт записывается в виде двойного неравенства: либо
(в радианах).
В литературе значок угла часто пропускают и пишут просто .
Определение:
Скалярным произведением двух векторов и называется ЧИСЛО, равное произведению длин этих векторов на косинус угла между ними:
Вот это вот уже вполне строгое определение.
Акцентируем внимание на существенной информации:
Обозначение:
скалярное произведение обозначается через или просто .
Результат операции является ЧИСЛОМ
: Умножается вектор на вектор, а получается число. Действительно, если длины векторов – это числа, косинус угла – число, то их произведение тоже будет числом.
Сразу пара разминочных примеров:
Пример 1
Решение:
Используем формулу . В данном случае:
Ответ:
Значения косинуса можно найти в тригонометрической таблице
. Рекомендую её распечатать – потребуется практически во всех разделах вышки и потребуется много раз.
Чисто с математической точки зрения скалярное произведение безразмерно, то есть результат, в данном случае , просто число и всё. С точки же зрения задач физики скалярное произведение всегда имеет определенный физический смысл, то есть после результата нужно указать ту или иную физическую единицу. Канонический пример по вычислению работы силы можно найти в любом учебнике (формула в точности представляет собой скалярное произведение). Работа силы измеряется в Джоулях, поэтому, и ответ запишется вполне конкретно, например, .
Пример 2
Найти , если , а угол между векторами равен .
Это пример для самостоятельного решения, ответ в конце урока.
Угол между векторами и значение скалярного произведения
В Примере 1 скалярное произведение получилось положительным, а в Примере 2 – отрицательным. Выясним, от чего зависит знак скалярного произведения. Смотрим на нашу формулу: . Длины ненулевых векторов всегда положительны: , поэтому знак может зависеть только от значения косинуса.
Примечание:
Для более качественного понимания нижеприведенной информации лучше изучить график косинуса в методичке Графики и свойства функции
. Посмотрите, как ведёт себя косинус на отрезке .
Как уже отмечалось, угол между векторами может изменяться в пределах , и при этом возможны следующие случаи:
1) Если угол
между векторами острый
: (от 0 до 90 градусов), то
, и скалярное произведение будет положительным
сонаправлены
, то угол между ними считается нулевым , и скалярное произведение также будет положительным. Поскольку , то формула упрощается: .
2) Если угол
между векторами тупой
: (от 90 до 180 градусов), то
, и, соответственно, скалярное произведение отрицательно
: . Особый случай: если векторы направлены противоположно
, то угол между ними считается развёрнутым
: (180 градусов). Скалярное произведение тоже отрицательно, так как
Справедливы и обратные утверждения:
1) Если , то угол между данными векторами острый. Как вариант, векторы сонаправлены.
2) Если , то угол между данными векторами тупой. Как вариант, векторы направлены противоположно.
Но особый интерес представляет третий случай:
3) Если угол
между векторами прямой
: (90 градусов), то и скалярное произведение равно нулю
: . Обратное тоже верно: если , то . Компактно утверждение формулируется так: Скалярное произведение двух векторов равно нулю тогда и только тогда, когда данные векторы ортогональны
. Короткая математическая запись:
! Примечание
: повторим основы математической логики
: двусторонний значок логического следствия обычно читают «тогда и только тогда», «в том и только в том случае». Как видите, стрелки направлены в обе стороны – «из этого следует это, и обратно – из того, следует это». В чём, кстати, отличие от одностороннего значка следования ? Значок утверждает, только то
, что «из этого следует это», и не факт, что обратное справедливо. Например: , но не каждый зверь является пантерой, поэтому в данном случае нельзя использовать значок . В то же время, вместо значка можно
использовать односторонний значок. Например, решая задачу, мы выяснили, что и сделали вывод, что векторы ортогональны: – такая запись будет корректной, и даже более уместной, чем
.
Третий случай имеет большую практическую значимость
, поскольку позволяет проверить, ортогональны векторы или нет. Данную задачу мы решим во втором разделе урока.
Свойства скалярного произведения
Вернёмся к ситуации, когда два вектора сонаправлены
. В этом случае угол между ними равен нулю, , и формула скалярного произведения принимает вид: .
А что будет, если вектор умножить на самого себя? Понятно, что вектор сонаправлен сам с собой, поэтому пользуемся вышеуказанной упрощенной формулой:
Число называется скалярным квадратом
вектора , и обозначатся как .
Таким образом, скалярный квадрат вектора равен квадрату длины данного вектора:
Из данного равенства можно получить формулу для вычисления длины вектора:
Пока она кажется малопонятной, но задачи урока всё расставят на свои места. Для решения задач нам также потребуются свойства скалярного произведения
.
Для произвольных векторов и любого числа справедливы следующие свойства:
1) – переместительный или коммутативный
закон скалярного произведения.
2) – распределительный или дистрибутивный
закон скалярного произведения. Попросту, можно раскрывать скобки.
3) – сочетательный или ассоциативный
закон скалярного произведения. Константу можно вынести из скалярного произведения.
Зачастую, всевозможные свойства (которые ещё и доказывать надо!) воспринимаются студентами как ненужный хлам, который лишь необходимо вызубрить и сразу после экзамена благополучно забыть. Казалось бы, чего тут важного, все и так с первого класса знают, что от перестановки множителей произведение не меняется: . Должен предостеречь, в высшей математике с подобным подходом легко наломать дров. Так, например, переместительное свойство не является справедливым для алгебраических матриц
. Неверно оно и для векторного произведения векторов
. Поэтому, в любые свойства, которые вам встретятся в курсе высшей математики, как минимум, лучше вникать, чтобы понять, что можно делать, а чего нельзя.
Пример 3
.
Решение:
Сначала проясним ситуацию с вектором . Что это вообще такое? Сумма векторов и представляет собой вполне определенный вектор, который и обозначен через . Геометрическую интерпретацию действий с векторами можно найти в статье Векторы для чайников
. Та же петрушка с вектором – это сумма векторов и .
Итак, по условию требуется найти скалярное произведение . По идее, нужно применить рабочую формулу , но беда в том, что нам неизвестны длины векторов и угол между ними. Зато в условии даны аналогичные параметры для векторов , поэтому мы пойдём другим путём:
(1) Подставляем выражения векторов .
(2) Раскрываем скобки по правилу умножения многочленов, пошлую скороговорку можно найти в статье Комплексные числа
или Интегрирование дробно-рациональной функции
. Повторяться уж не буду =) Кстати, раскрыть скобки нам позволяет дистрибутивное свойство скалярного произведения. Имеем право.
(3) В первом и последнем слагаемом компактно записываем скалярные квадраты векторов: . Во втором слагаемом используем перестановочность скалярного произведения: .
(4) Приводим подобные слагаемые: .
(5) В первом слагаемом используем формулу скалярного квадрата , о которой не так давно упоминалось. В последнем слагаемом, соответственно, работает та же штука: . Второе слагаемое раскладываем по стандартной формуле .
(6) Подставляем данные условия , и ВНИМАТЕЛЬНО проводим окончательные вычисления.
Ответ:
Отрицательное значение скалярного произведения констатирует тот факт, что угол между векторами является тупым.
Задача типовая, вот пример для самостоятельного решения:
Пример 4
Найти скалярное произведение векторов и , если известно, что .
Теперь ещё одно распространённое задание, как раз на новую формулу длины вектора . Обозначения тут будут немного совпадать, поэтому для ясности я перепишу её с другой буквой:
Пример 5
Найти длину вектора , если .
Решение
будет следующим:
(1) Поставляем выражение вектора .
(2) Используем формулу длины: , при этом в качестве вектора «вэ» у нас выступает целое выражение .
(3) Используем школьную формулу квадрата суммы . Обратите внимание, как она здесь любопытно работает: – фактически это квадрат разности, и, по сути, так оно и есть. Желающие могут переставить векторы местами: – получилось то же самое с точностью до перестановки слагаемых.
(4) Дальнейшее уже знакомо из двух предыдущих задач.
Ответ:
Коль скоро речь идёт о длине, не забываем указать размерность – «единицы».
Пример 6
Найти длину вектора , если .
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Продолжаем выжимать полезные вещи из скалярного произведения. Снова посмотрим на нашу формулу . По правилу пропорции сбросим длины векторов в знаменатель левой части:
А части поменяем местами:
В чём смысл данной формулы? Если известны длины двух векторов и их скалярное произведение, то можно вычислить косинус угла между данными векторами, а, следовательно, и сам угол.
Скалярное произведение – это число? Число. Длины векторов – числа? Числа. Значит, дробь тоже является некоторым числом . А если известен косинус угла: , то с помощью обратной функции легко найти и сам угол:
.
Пример 7
Найти угол между векторами и , если известно, что .
Решение:
Используем формулу:
На заключительном этапе вычислений использован технический приём – устранение иррациональности в знаменателе. В целях устранения иррациональности я домножил числитель и знаменатель на .
Итак, если , то:
Значения обратных тригонометрических функций можно находить по тригонометрической таблице
. Хотя случается это редко. В задачах аналитической геометрии значительно чаще появляется какой-нибудь неповоротливый медведь вроде , и значение угла приходится находить приближенно, используя калькулятор. Собственно, такую картину мы ещё неоднократно увидим.
Ответ:
Опять, не забываем указывать размерность – радианы и градусы. Лично я, чтобы заведомо «снять все вопросы», предпочитаю указывать и то, и то (если по условию, конечно, не требуется представить ответ только в радианах или только в градусах).
Теперь вы сможете самостоятельно справиться с более сложным заданием:
Пример 7*
Даны – длины векторов , и угол между ними . Найти угол между векторами , .
Задание даже не столько сложное, сколько многоходовое.
Разберём алгоритм решения:
1) По условию требуется найти угол между векторами и , поэтому нужно использовать формулу 
2) Находим скалярное произведение (см. Примеры № 3, 4).
3) Находим длину вектора и длину вектора (см. Примеры № 5, 6).
4) Концовка решения совпадает с Примером № 7 – нам известно число , а значит, легко найти и сам угол:
Краткое решение и ответ в конце урока.
Второй раздел урока посвящен тому же скалярному произведению. Координаты. Будет даже проще, чем в первой части.
Скалярное произведение векторов,
заданных координатами в ортонормированном базисе
Ответ:
Что и говорить, иметь дело с координатами значительно приятнее.
Пример 14
Найти скалярное произведение векторов и , если
Это пример для самостоятельного решения. Здесь можно использовать ассоциативность операции, то есть не считать , а сразу вынести тройку за пределы скалярного произведения и домножить на неё в последнюю очередь. Решение и ответ в конце урока.
В заключение параграфа провокационный пример на вычисление длины вектора:
Пример 15
Найти длины векторов , если
Решение:
снова напрашивается способ предыдущего раздела: , но существует и другая дорога:
Найдём вектор :
И его длину по тривиальной формуле :
Скалярное произведение здесь вообще не при делах!
Как не при делах оно и при вычислении длины вектора :
Стоп. А не воспользоваться ли очевидным свойством длины вектора? Что можно сказать о длине вектора ? Данный вектор длиннее вектора в 5 раз. Направление противоположно, но это не играет роли, ведь разговор о длине. Очевидно, что длина вектора равна произведению модуля
числа на длину вектора :
– знак модуля «съедает» возможный минус числа .
Таким образом:
Ответ:
Формула косинуса угла между векторами, которые заданы координатами
Теперь у нас есть полная информация, чтобы ранее выведенную формулу косинуса угла между векторами выразить через координаты векторов :
Косинус угла между векторами плоскости
и , заданными в ортонормированном базисе , выражается формулой
:.
Косинус угла между векторами пространства
, заданными в ортонормированном базисе , выражается формулой
:
Пример 16
Даны три вершины треугольника . Найти (угол при вершине ).
Решение:
По условию чертёж выполнять не требуется, но всё-таки:
Требуемый угол помечен зелёной дугой. Сразу вспоминаем школьное обозначение угла: – особое внимание на среднюю
букву – это и есть нужная нам вершина угла. Для краткости можно было также записать просто .
Из чертежа совершенно очевидно, что угол треугольника совпадает с углом между векторами и , иными словами: .
Проведённый анализ желательно научиться выполнять мысленно.
Найдём векторы:
Вычислим скалярное произведение:
И длины векторов:
Косинус угла:
Именно такой порядок выполнения задания рекомендую чайникам. Более подготовленные читатели могут записывать вычисления «одной строкой»:
Вот и пример «плохого» значения косинуса. Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.
Найдём сам угол:
Если посмотреть на чертёж, то результат вполне правдоподобен. Для проверки угол также можно измерить и транспортиром. Не повредите покрытие монитора =)
Ответ:
В ответе не забываем, что спрашивалось про угол треугольника
(а не про угол между векторами), не забываем указать точный ответ: и приближенное значение угла: , найденное с помощью калькулятора.
Те, кто получил удовольствие от процесса, могут вычислить углы , и убедиться в справедливости канонического равенства
Пример 17
В пространстве задан треугольник координатами своих вершин . Найти угол между сторонами и
Это пример для самостоятельного решения. Полное решение и ответ в конце урока
Небольшой заключительный раздел будет посвящен проекциям, в которых тоже «замешано» скалярное произведение:
Проекция вектора на вектор. Проекция вектора на координатные оси.
Направляющие косинусы вектора
Рассмотрим векторы и :
Спроецируем вектор на вектор , для этого из начала и конца вектора опустим перпендикуляры
на вектор (зелёные пунктирные линии). Представьте, что на вектор перпендикулярно падают лучи света. Тогда отрезок (красная линия) будет «тенью» вектора . В данном случае проекцией вектора на вектор является ДЛИНА отрезка . То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.
Данное ЧИСЛО обозначается следующим образом: , «большим вектором» обозначают вектор КОТОРЫЙ
проецируют, «маленьким подстрочным вектором» обозначают вектор НА
который проецируют.
Сама запись читается так: «проекция вектора «а» на вектор «бэ»».
Что произойдёт, если вектор «бэ» будет «слишком коротким»? Проводим прямую линию, содержащую вектор «бэ». И вектор «а» будет проецироваться уже на направление вектора «бэ»
, попросту – на прямую, содержащую вектор «бэ». То же самое произойдёт, если вектор «а» отложить в тридесятом царстве – он всё равно легко спроецируется на прямую, содержащую вектор «бэ».
Если угол
между векторами острый
(как на рисунке), то
Если векторы
ортогональны
, то (проекцией является точка, размеры которой считаются нулевыми).
Если угол
между векторами тупой
(на рисунке мысленно переставьте стрелочку вектора ), то (та же длина, но взятая со знаком минус).
Отложим данные векторы от одной точки:
Очевидно, что при перемещении вектора его проекция не меняется
Содержание:
- Векторы
- Действия над векторами
- Умножение вектора на число
- Скалярное произведение векторов
- Векторное произведение
- Смешенное произведение векторов
- Разложение вектора по базису
- Действия над векторами, заданными своими координатами
- Проекция вектора на ось
- Проекции вектора на оси координат
- Направляющие косинусы вектора
- Разложение вектора по ортам
- Действия над векторами, заданными в координатной форме
- Вектор — основные определения
- Операции над векторами и их свойства
- Сформулируем и докажем ещё одну важную для решения некоторых задач теорему.
- Координаты вектора
- Скалярное произведение векторов и его свойства
- Векторы и их решение
- Собственные числа и собственные векторы
- Векторная алгебра
- Векторы: основные определения, линейные операции
- Линейные операции над векторами
- Умножения вектора на скаляр
- Основные свойства проекции вектора на ось
- Прямоугольная система координат в пространстве. Координатная и алгебраическая формы задания векторов
- Скалярное, векторное, смешанное произведения векторов
- Векторное произведение двух векторов
- Смешанное произведение векторов, заданных в координатной форме
- Простейшие задачи аналитической геометрии
- Задача об определении площади треугольника
- Задача о деление отрезка в заданном отношении
Векторы
В математике вектором называют величину, которая характеризуется только числом и направлением. Так определённые векторы ещё называют свободными векторами. Примером физических величин, которые имеют векторный характер являются скорость, сила, ускорение. Геометрически вектор — это направленный отрезок, хотя правильней говорить про целый класс направленных отрезков, которые все параллельны между собой, имеют одинаковые длину и направление.
Векторы обозначают малыми латинскими буквами с чертой сверху 


Действия над векторами
Рассмотрим основные действия, определённые над векторами.
1. Сложение векторов. Суммой векторов 





Учитывая, что 

Вычитание векторов сводится к сложению противоположного вектора
Запишем основные свойства действий сложения векторов:
Заметим, что сумма нескольких векторов находится последовательным сложением двух из них, например:
Геометрически сумма нескольких векторов находится их последовательным отложением один за одним так, чтоб начало следующего совпадало с концом предыдущего. Суммой является вектор, который будет соединять начало первого с концом последнего (рис. 4). Если такая последовательность векторов даёт замкнутую ломаную то суммой векторов является 
Умножение вектора на число
Произведением вектора 


а) 
б) 




Запишем основные свойства действий умножения вектора на число:
Скалярное произведение векторов
Скалярным произведением 






Очевидно, что скалярное произведение двух ненулевых векторов будет равно нулю тогда и только тогда когда эти вектора перпендикулярны (ортогональны). Действительно, если 

Наоборот, если 

Например, скалярное произведение 
Запишем основные свойства действий скалярного умножения векторов:
Векторное произведение
Векторным произведением 



1) модуль вектора 


2) вектор 


3) вектор 





Модуль векторного произведения равен площади параллелограмма, построенного на векторах 







Приведём основные свойства векторного произведения:
1) векторное произведение 


2) от перестановки местами векторов-сомножителей векторное произведение меняет знак на противоположный: 
3) 
4) 
Физическое содержание векторного произведения такое. Если 







Смешенное произведение векторов
Смешенным произведением векторов 



Как результат скалярного произведения векторов 


Действительно, 




Объём V параллелепипеда, построенного на векторах 
Однако, знак смешенного произведения совпадает со знаком 




Из геометрического содержания смешенного произведения выходит, что
1) смешанное произведение равно нулю тогда и только тогда, когда перемноженные вектора копланарные (условие компланарных векторов);
2)
Учитывая коммутативность скалярного произведения и антикоммутативность векторного, для произвольных векторов 
Пример 1.
Доказать, что когда М — точка АВС и О — произвольные точки пространства, то выполняется равенство:
Решение.
Пусть 



тогда
Пример 2.
У прямоугольного параллелепипеда рёбра 




Решение.
Пусть 

рис. 9.
Далее,
Этим закончен «перевод» условия задачи на «язык» векторов.
Теперь произведём вычисления с векторами:
Наконец «переводим» полученные вектора равенства снова на «геометрический язык». Поскольку 

Далее поскольку 




Разложение вектора по базису
Базисом на площади называют упорядоченную пару неколлинеарных векторов и точку отсчёта.
Теорема. Любой вектор 



Доказательство.
Пусть векторы 





Тогда по правилу параллелограмма 
Но 

Числа, которые стоят при базисных векторах в разложении вектора за двумя неколлинеарными векторами называют координатами вектора в данном базисе и обозначают 
Соответственно в пространстве базисом называется упорядоченная тройка некомпланарных векторов и точки отсчёта. Для четырёх некомпланарных векторов справедлива следующая теорема.
Теорема. Любой вектор 




Доказательство.
От точки О отложим векторы 


в котором вектор 
Числа х,у,z которые стоят при базисных векторах в разложении вектора по трём некомпланарным векторам называют координатами вектора в пространстве и обозначают 






Отсюда легко установить длину вектора как расстояние между двумя точками:
Действия над векторами, заданными своими координатами
1. При сложении двух, или более векторов их соответствующие координаты складываются:
Действительно:
2. При вычитании векторов соответствующие координаты вычитаются:
Доказательство аналогично предыдущему.
3. При умножении вектора на число все координаты умножаются на это число.
Правда, для вектора 

4. Скалярное произведение двух векторов 
Правда:
Поскольку 

5. Векторное произведение векторов 
6. Смешенное произведение трёх векторов 
Пример 1.
Зная координаты векторов 

Решение:
Ответ: 
Пример 2.
Зная координаты векторов 

Решение.
Ответ: 
Пример 3.
Зная координаты векторов 
а) скалярное произведение векторов
б) векторное произведение векторов
в) смешенное произведение векторов 
Решение.
Ответ:
На основании приведённых выше формул действий над векторами можно установить следующие условия и соотношения для нулевых векторов
1. Угол между векторами.
2. Условие перпендикулярности двух векторов:
(векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю).
3. Условие коллинеарности двух векторов: 
4. Условие компланарности трёх векторов.
(три вектора компланарны тогда и только тогда, когда их смешенное произведение равно нулю).
5. Деление отрезка АВ в заданном отношении.
Если точка 

Если точка М делит отрезок АВ на пополам то 
Действия над векторами (теория)
а) Произведение вектора на число.
Определение 1. Произведением вектора 

который имеет длину 

Рис. 12.
Условие 
является условием коллинеарности двух векторов.
б) Сложение векторов.
Определение 2. Суммой двух векторов 






Рис. 13.
Понятно, что вектор 


Для векторной суммы справедливый переместительный закон
Легко убедиться, что для векторной суммы имеет место соединительный
закон 
Исходя из определения 2, легко находим сумму, например, четырех векторов 
Рис. 14.
Вектор 


в) Вычитание векторов.
Действие вычитание векторов можно рассматривать как обратное действие относительно сложения векторов.
Определение. Разностью 



Рис. 15.
Как видно из рис. 15, одна диагональ 




Дадим еще одно определение разности векторов.
Определение. Разностью двух векторов 


Проекция вектора на ось
Пусть имеем произвольную ось l на плоскости и некоторый вектор 
Рис. 16.
Опустим из начала A вектора и из конца B перпендикуляры на ось l. Основаниями перпендикуляров будут точки A1 и B1, которые называются проекциями точек A и B.
Величина A1B1 называется проекцией вектора 


Определение 1. Проекцией вектора 
Из точки A проведем прямую, параллельную оси l, которая пересечет отрезок BB1 в точке C. Вектор 


Определение 2. Проекция вектора на любую ось равна произведению длины этого вектора на косинус угла между осью и вектором.
Если угол φ острый, то проекция 

Свойства проекций.
1. Если векторы 


2. Проекция суммы векторов на любую ось равна сумме проекций слагаемых на ту же ось, то есть:
3. Проекция разности двух векторов на ось l равна разности величин проекций на ту же ось, то есть:
4. Если вектор 

Проекции вектора на оси координат
Рассматривается прямоугольная система координат Oxyz в пространстве и произвольный вектор 
Пусть 
Проекции x, y, z вектора 

Если заданы две точки A (x1; y1; z1) и B (x2; y2; z2), то координаты вектора 
x = x2 – x1, y = y2 – y1, z = z2 – z1 .
Рис. 17
Действительно, проведем через точки A и B плоскости, перпендикулярные оси Ox и обозначим точки их пересечения соответственно A1 и B1 (рис.17). Точки A1 и B1 имеют на оси Ox координаты x1 и x2 , но 
x = x2 – x1 . Аналогично доказывается, что y = y2 – y1, z = z2 – z1 .
Направляющие косинусы вектора
Пусть имеем вектор 
Рис. 18
Через точку M проведем плоскости, перпендикулярные к осям координат, и вместе с координатными плоскостями они образуют параллелепипед, диагональ которого — отрезок OM (рис.18). Через α, β, γ обозначим углы, которые образует вектор 


Квадрат диагонали прямоугольного параллелепипеда равна сумме квадратов длин трех его измерений.
Поэтому


Формула (2.8) выражает длину вектора через его координаты. Тогда на основе формул (2.7) и (2.8) получим
Отсюда для направляющих косинусов получаем

Для направляющих косинусов справедливо равенство 
Разложение вектора по ортам
Рассмотрим прямоугольную систему координат в пространстве и вектор, начало которого в точке O (рис.19) .
Рис. 19.
Обозначим орты осей координат Ox, Oy, Oz соответственно через 
Спроецируем вектор 
Из прямоугольника ODMC видно, что вектор 

Тогда

Вектор 
Векторы 




Подставляя эти значения в равенство (2.10), учитывая, что 

Слагаемые 

Тройка векторов 

Пример 1. Построить вектор 
Рис. 20.
Решение. Компоненты вектора 


соответствует прямоугольный параллелепипед, диагональ которого является искомый вектор (рис. 20).
Действия над векторами, заданными в координатной форме
Если векторы заданы в координатной форме, то действия сложения, вычитания, умножения вектора на число можно заменить простыми арифметическими операциями над координатами этих векторов по таким правилам.
Правило 1. При сложении векторов их одноименные координаты складываются
Пусть имеем векторы 





Сложив эти равенства, получим

Итак, координаты вектора 
Правило 2. Чтобы отнять от вектора 



Правило 3. Чтобы умножить вектор 


Пример 1. Найти вектор 
Решение. Выполним действия последовательно и найдем

Значит,
Вектор — основные определения
Определение вектора в пространстве ничем не отличается от определения вектора на плоскости.
Определение 1. Вектором называется направленный отрезок, т.е. отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.
Так же как и на плоскости, векторы обозначаются 
Определение 2. Длиной (или модулем) вектора 


Длина вектора 


Любая точка пространства также считается вектором, который называется нулевым. Начало такого вектора совпадает с его концом, а длина равна нулю. Обозначения нулевого вектора:
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Определение 3. Векторы 

Если ненулевые векторы 







Ясно, что сонаправленные векторы, в силу их определения, коллинеарны. Если два коллинеарных вектора не сонаправлены, то они называются противоположно направленными. Обозначения остаются обычными: 





Определение 4. Векторы 



Теорема 1. От любой тонки пространства можно отложить вектор, равный данному, и притом только один.
Доказательство этой теоремы аналогично доказательству соответствующей планиметрической теоремы.
Возможно вам будут полезны данные страницы:
Операции над векторами и их свойства
Операции над векторами в пространстве аналогичны соответствующим операциям на плоскости.
Пусть даны два вектора 








Теорема 2. Сумма 




Правило треугольника можно сформулировать и так: для любых трёх точек 
Кроме того, сумму двух неколлинеарных векторов с общим началом можно построить и по правилу параллелограмма: 




Все свойства операции сложения векторов, справедливые на плоскости, остаются справедливыми и в пространстве:
1)
2) 
3) 
Здесь 
Определение 5. Два ненулевых вектора называются противоположными, если их длины равны и эти векторы противоположно направлены.
Вектор, противоположный данному ненулевому вектору 
Определение 6. Разностью двух векторов 



Разность векторов 



Разность векторов 



Из законов сложения векторов следует, что сумма нескольких векторов не зависит от порядка слагаемых.
Умножение (произведение) вектора на число и его свойства, так же как и свойства операции сложения, не претерпевают изменений и в пространстве.
Определение 7. Произведением ненулевого вектора 








Таким образом, по определению, 






Свойства умножения вектора на число не отличаются от аналогичных свойств на плоскости:
-
— ассоциативность (сочетательный закон);
-
—дистрибутивность относительно сложения векторов (1-й распределительный закон);
-
— дистрибутивность относительно сложения чисел (2-й распределительный закон).
Здесь 


Справедлива также и лемма о коллинеарных векторах: если векторы 


что 

Сформулируем и докажем ещё одну важную для решения некоторых задач теорему.
Теорема 3. Пусть 



Доказательство
1. Из равенства 





2. Пусть 




З. Компланарные и некомпланарные векторы
Следующее понятие уже не имеет аналога в планиметрии.
Определение 8. Векторы называются компланарными, если лучи, задающие их направления, параллельны некоторой плоскости.
Замечание. Из определения 8 следует, что при откладывании от одной точки векторов, равных нескольким данным компланарным векторам, получим векторы, лежащие в одной плоскости. Таким образом, компланарные векторы лежат либо в одной плоскости, либо в параллельных плоскостях.
Очевидно, что любые два вектора компланарны и любые три вектора, два из которых коллинеарны, также являются компланарными (поясните). Рассмотрим теперь условия, при которых три вектора, из которых никакие два не коллинеарны, являются компланарными.
Теорема 4. Векторы 




Доказательство
1. Пусть векторы 
точки 
















Докажем, что векторы 






Отложим от произвольной точки 







Если векторы 






Следующая теорема, называемая теоремой о разложении вектора по трём некомпланарным векторам, является основной во всей элементарной (школьной) векторной алгебре.
Теорема 5. Любой вектор 




2. Пусть векторы 





















3. Докажем теперь, что разложение вектора 



Тогда
отсюда
— т. е. векторы
компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора
по данным векторам
единственно. Теорема доказана.
Итак, любой вектор 





Координаты вектора
Так же как и на плоскости, в пространстве помимо координат точки вводятся координаты вектора. Рассмотрим три попарно перпендикулярных вектора 












Свойства векторов пространства, заданных своими координатами, аналогичны соответствующим свойствам векторов на плоскости:
- Два вектора равны в том и только том случае, если равны их координаты.
- Координаты суммы (разности) двух векторов равны суммам (разностям) соответствующих координат этих векторов, т.е. для векторов
получаем
- При умножении вектора на число каждая его координата умножается на это число, т.е. для вектора
и действительного числа
получаем
Докажем, например, свойство 2. Так как 



Скалярное произведение векторов и его свойства
Определение скалярного произведения векторов 

Определение 11. Скалярным произведением векторов 

Теорема 8. Два ненулевых вектора 

Доказательство этой теоремы вытекает из формулы (9).
Определение 12. Скалярным квадратом вектора 


Так как 
Таким образом, длина вектора равна квадратному корню из его скалярного квадрата.
Замечание. Скалярное произведение есть число, поэтому грубой ошибкой явилась бы запись:
Если векторы 


Теорема 9. Скалярное произведение векторов равно сумме произведений их соответственных координат, т. е.
Доказательство. Отложим от произвольной точки 







итак как 


поэтому
Решение любой геометрической задачи на вычисление сводится, в сущности, к нахождению величин двух типов: расстояний и углов. Если в пространстве задан некоторый базис (в частности, прямоугольный), т. е. тройка некомпланарных векторов, то на основании теоремы 5 любой вектор пространства можно разложить по векторам этого базиса, причём единственным образом.
Если известны длины векторов, образующих базис, углы между ними и разложение некоторого вектора по векторам этого базиса, то, используя свойства скалярного произведения, можно определить длину такого вектора и угол, образуемый им с любым другим вектором, разложение которого по векторам этого базиса известно.
Таким образом, векторы позволяют находить решения довольно широкого класса геометрических задач, а умение определять разложение вектора по базисным векторам является важнейшим фактором их решения.
Для решения задач о разложении вектора по трём данным некомпланарным векторам, разумеется, необходимо, помимо теоремы 5, знание предшествующего ей материала.
Примеры с решением
Задача 1.
Основанием четырёхугольной пирамиды 






Решение (см. рис. 14).
1. 

2. Так как 


Ответ:
Заметим, что в разложении вектора 








Задача 2.
Пусть 


Решение (см. рис. 15). Пусть 






Ответ:
Векторы и их решение
Вектором называется направленный отрезок. Направление отрезка показывается стрелкой. Различают начало и конец отрезка.
Два вектора называются равными между собой, если каждый из них можно получить параллельными перенесениями другого.
Равные векторы являются параллельными (колинеарными), имеют одно и то же направление и одинаковую длину. Длина вектора 
Вектор называется нулевым (ноль- вектором), если он имеет нулевую длину, то есть его конец сходится с началом.
Чтобы найти сумму двух векторов 



Суммой 






Для складывания векторов имеют место такие законы:
1) переставной (коммутативный)
2) связующий
3) для каждого вектора 

4)
5) для некоторых двух векторов 

Если вектор 



Пусть вектор имеет начало в точке 





Если вектор 
Произведением вектора 






Любой вектор 
где 



Пример 1.73
Даны два вектора: 

Найти вектор
Решение
Признаком колинеарности двух векторов 

Скалярным произведением двух векторов 


Скалярное произведение можно записать в таком виде:
Если векторы 

Учитывая формулы (1.18) и (1.19), можно найти косинус угла между векторами 

Отсюда получается условие перпендикулярности двух векторов: если 

Среди свойств скалярного произведения отметим так:
Векторным произведением вектора 


1) длина вектора 
2) вектор 

3) из конца вектора 


Заметим, что 


В координатной форме векторное произведение векторов 

Смешанным или скалярно — векторным произведением трех векторов 



Если векторы 
Если известные координаты сомножителей 
Если три ненулевых 
Следует, в координатной форме условие компланарности трех ненулевых векторов имеет вид:
Решение примеров:
Пример 1.74
Заданы координатами точек 


1) вектор 
2) угол между векторами 
3) координаты вектора
4) объем пирамиды с вершинами в точках
Решение
1) По формуле (1.14) находим
тогда
2) Косинус угла между векторами 

Поскольку косинус угла отрицательный, то угол 
3) Координаты векторного произведения находим по формуле (1.22):
4) Чтобы найти объем пирамиды, найдем сначала смешанное произведение векторов, что выходят из одной вершины пирамиды:
Тогда объем пирамиды
Собственные числа и собственные векторы
Вектор — столбец 




Тут 



Координаты собственного вектора 

Собственный вектор обозначаются с точностью к постоянному множителю.
Решение примеров:
Пример 1.90.
Обозначить собственные определения и собственные векторы матрицы
Решение. Характеристические уравнения данной матрицы имеет вид (1.24):

отсюда получается, что матрица 





которое приводится к одному уравнению
Возьмем 
Следует, первый собственный вектор является
Второй вектор 

Эта система уравнений так же приводится к одному уравнению 


Таким образом, матрица 




Пример 1.91
Найти собственные векторы и собственные значения матрицы
Решение. Характеристическое уравнение
Раскрыв определитель получим:
Корень 


Система уравнений для определения собственных векторов имеет вид:
Последовательно подставим 

Фундаментальная система уравнений получается, если свободным переменным 
Получили два линейно независимые собственные векторы. Вся совокупность векторов, что соответствуют собственному значению 
Фундаментальная система решений получается, если взять
Векторная алгебра
Понятие «вектор» (от лат. vector — носитель), как отрезка, имеет определенную длину и определенное направление, впервые появилось в работах по построению числовых систем в ирландского математика Уильяма Гамильтона (1805-1865). Это понятие связано с объектами, которые характеризуются величиной и направлением, например, скорость, сила, ускорение. При этом скорость можно понимать в широком смысле: скорость изменения издержек производства, доходов, спроса, потребления и предложения и др. Вектор может указывать направление наибольшего возрастания или убывания функции, описывающей различные экономические процессы. Векторы, рассмотренные в данном разделе, является частным случаем 
Для графического изображения решения экономических задач на плоскости и в пространстве применяются средства аналитической геометрии. Аналитическая геометрия — математическая наука, объектом изучения которой являются геометрические фигуры, а предметом — установление их свойств средствами алгебры с помощью координатного метода. Теоретической базой этой науки является частично известна из школы векторная алгебра.
Основателем метода координат и, вместе с тем, аналитической геометрии является Рене Декарт (1596-1650) — французский философ, математик, физик и физиолог. Его именем и названа известная «декартова прямоугольная система координат», которая позволяет определить положение фигуры на плоскости и тела в пространстве.
После изучения данной темы вы сможете:
● использовать инструмент векторной алгебры для геометрического изображения и анализа объектов экономических процессов;
● применять уравнение прямой линии на плоскости для геометрической интерпретации зависимости между функциональному признаку и аргументом, что на нее влияет;
● применять уравнение кривых второго порядка при построении нелинейных математических моделей экономических задач;
● осуществлять геометрическую интерпретацию решений экономических задач с помощью поверхностей и плоскостей.
Векторы: основные определения, линейные операции
Выберем на произвольной прямой (в 






алфавита с чертой: 
Рис. 6.1
В применимых задачах естественных наук существенным является обстоятельство — где, в какой точке находится начало вектора. Например, результат действия силы зависит не только от ее величины и направления действия, но и от того, в какой точке она прикладывается.
Вектор, для которого фиксированная (не фиксирована) начальная точка называется связанным (свободным). Векторы, которые применяются в экономических задачах, как правило, не являются связанными, поэтому в дальнейшем будем рассматривать преимущественно свободные векторы
Длиной, или модулем, вектора называется длина соответствующего отрезка и обозначается одним из символов:
Нулевым вектором 0, или ноль-вектором, называется вектор, длина которого равна нулю, а направление его считается произвольным (неопределенным).
Единичным вектором 
Равными векторами называются векторы, которые принадлежат одной прямой или параллельным прямым, одинаково направлены и имеют равные длины.
Взаимно противоположными называются векторы, которые принадлежат одной прямой или параллельным прямым, имеют равные длины, но противоположно направлены. Вектор, противоположный вектору 

Коллинеарными называют векторы, которые принадлежат одной прямой или параллельным прямым.
Компланарными называются векторы, которые принадлежат одной плоскости или параллельным плоскостям.
Линейные операции над векторами
Будем считать, что векторы 



1. Суммой векторов 


Параллельный перенос можно осуществить и так, что объединятся начала векторов 

Рис. 6.2
Правило треугольника обобщается на произвольное конечное число векторов. Если параллельным переносом расположить векторы так, что конец предыдущего вектора (начиная с первого) является началом следующего, то результирующим будет вектор, соединяющий начало первого вектора слагаемого с концом последнего (рис. 6.3):
Рис. 6.3
Соответствующее правило называют правилом многоугольника.
Свойства суммы векторов:
1) переставная, или коммутативна:
2) соединительная, или ассоциативная:
3)
4)
Разницу 

Умножения вектора на скаляр
Пусть 










Рис. 6.4
При


Свойства умножения вектора на скаляр:
1) переставной или коммутативных закон:

2) соединительный, или ассоциативный закон:

3) распределительный или дистрибутивный закон:

4)
5)
Из определения умножения вектора на скаляр следует необходимое и достаточное условие коллинеарности двух векторов: вектора 

Известно, что три ненулевые векторы 


Рассмотрим понятие, имеет очень важное значение в теории векторов — проекции вектора на ось (прямую, имеет направление; заданное направление считать положительным, противоположное направление — отрицательным).
Компонентой вектора 





Рис. 6.5
Проекцией вектора 






Основные свойства проекции вектора на ось
1. Проекция вектора на ось 

2. Проекция суммы двух векторов на эту ось равна сумме их проекций на эту ось:
Это свойство обобщается на любое конечное число векторов.
3. Проекция на ось произведения вектора со скаляром равна произведению со скаляром проекции самого вектора на ось:
Прямоугольная система координат в пространстве. Координатная и алгебраическая формы задания векторов
Пусть в трехмерном векторном пространстве 


Рис. 6.6
Выберем в пространстве произвольную точку 





Под декартовыми прямоугольными координатами точки 

Точка 





Измерениями параллелепипеда есть модули координат точки 
Углы 


откуда:
Косинусы направляющих углов называются направляющими косинусами радиус-вектора 
1) направляющие косинусы являются координатами единичного радиус-вектора:
2) сумма квадратов направляющих косинусов вектора 
Понятие «координата», «направляющие углы», «направляющие косинусы» без изменений переносятся на любые свободные векторы, потому начало каждого из них параллельным переносом можно поместить в начало 
Координатами любого вектора 



Задача вектора тройкой его координат 
Для единичных векторов 

Длина произвольного вектора 
Найти длину и направляющие косинусы вектора
По формулам (6.5) имеем:
Установим связь между координатами вектора — числами — и его компонентами — векторами — с помощью единичных векторов 
Рис. 6.7
Компонентами вектора 


Следовательно, любой вектор 
Изображение вектора с 
Согласно свойствами операций над векторами, алгебраическая форма задания дает возможность установить результаты действий над векторами, заданными в координатной форме.
1. При добавлении (вычитании) двух векторов с 


Действительно, по свойствам ассоциативности и дистрибутивности имеем:
2. При умножении вектора 

Действительно, согласно распределительным свойствам умножения скаляра на сумму векторов имеем:
Скалярное, векторное, смешанное произведения векторов
Скалярным произведением двух векторов 



Вместо 


Для определения угла 







Основные свойства скалярного произведения векторов вытекают из его определения (6.7).
1. Скалярное произведение 
2. Скалярный квадрат вектора равен квадрату его модуля, то есть
3. Скалярное произведение подчиняется всем законам арифметики чисел относительно линейных операций:
4. Скалярное произведение двух векторов равно произведению модуля одного из них с проекцией второго на ось, направление которого определяется первым вектором:
Доказательство этого свойства основывается на определении (6.3).
Скалярное произведение векторов 

1. Вычислим скалярные произведения единичных векторов 

2. Находим произведение 
Раскрываем скобки и получаем:
Скалярное произведение двух векторов равно сумме произведений одноименных координат. Это полностью совпадает с определением скалярного произведения 
Как следствие из (6.12) при 
Определим угол между двумя ненулевыми векторами 

Следовательно, косинус угла между двумя векторами определяется формулой:
Отсюда
В результате с соотношением (6.13) получим критерий ортогональности двух векторов, заданных в координатной форме:
Критерием коллинеарности векторов 

Векторное произведение двух векторов
Пусть 








1) модуль его численно равен площади параллелограмма, построенного на векторах 

2) он перпендикулярный плоскости параллелограмма 



Рис. 6.9
Векторное произведение обозначается символами: 
Следовательно,
где 




Основные свойства векторного произведения вытекают из его определения.
1. Векторное произведение ненулевых векторов равно ноль-вектору тогда и только тогда, когда векторы 

Еще одним критерием коллинеарности векторов является равенство нулевому вектору их векторного произведения.
2. Векторные произведения с разным порядком сомножителей являются взаимно противоположными векторами:
Это означает, что векторное произведение не подчиняется переставному (коммутативному) закону.
3. Векторное произведение подчиняется ассоциативному закону относительно скалярного множителя и дистрибутивному закону относительно сложения:
где
Векторное произведение векторов 

1. Определяем векторные произведения ортов 
Векторное произведение одноименных векторов по свойству 1 дает ноль вектор:
Однако все векторные произведения разноименных единичных векторов будут давать единичные векторы:
Рис. 6.10
Рассмотрим, например, произведение 




2. Находим произведение 
Множители при 
Коэффициенты при единичных векторах в соотношении (6.20) являются координатами вектора 


Если символы 

Найдем векторное произведение векторов 
Модуль векторного произведения 

Смешанным произведением трех векторов 


Смешанное произведение можно обозначать тройкой векторов 





Геометрическая интерпретация смешанного произведения. Пусть 

Рис. 6.11
Вектор 





Согласно (6.11) скалярное произведение 



где 




Модуль смешанного произведения трех векторов численно равен объему параллелепипеда 
Основные свойства смешанного произведения вытекают из его определения и геометрической интерпретации.
1. Смешанное произведение ненулевых векторов равно нулю, если по крайней мере два из трех векторов коллинеарны или все три — компланарны, и наоборот.
Необходимым и достаточным условием компланарности трех ненулевых векторов является равенство нулю их смешанного произведения:

Свяжем с изображенными на плоскости векторами 
2. Циклическая перестановка трех сомножителей смешанного произведения не меняет его величины, а отрицательное перестановки меняет его знак на противоположный:
Смешанное произведение векторов, заданных в координатной форме
Пусть имеем три ненулевые векторы 
Полученная сумма произведений является расписанием определителя 3-го порядка, составленный из координат векторов, по элементам его третьей строки, то есть:
Векторы 

С помощью смешанного произведения векторов легко определить, относятся ли четыре точки 
Простейшие задачи аналитической геометрии
Задача об определении длины отрезка. Найти длину отрезка 

1. Введем в рассмотрение вектор 



2. Определим координаты вектора 


3. Находим модуль вектора 

Задача об определении площади треугольника
Найдем площадь треугольника, заданного координатами вершин:
По аксиомой стереометрии известно, что три точки в пространстве определяют плоскость и притом только одну. Для упрощения изложения, не нарушает общего подхода к решению задачи, договоримся рассматривать треугольник 



1. Введем в рассмотрение векторы:
и найдем их векторное произведение
По соотношению (6.20) имеем:
2. Вычислим модуль вектора 


Тогда для площади треугольника 
Знак 

Если треугольник принадлежит не плоскости 
Найдем площадь треугольника с вершинами 

Введем в рассмотрение векторы: 


Тогда

Задача о деление отрезка в заданном отношении
Пусть в пространстве заданы две точки 







Рис. 6.15
Число 
называется отношением, в котором точка 



Задача о деление отрезка в заданном отношении формулируется так: найти координаты точки 




Пусть точкам 




С этого векторного равенства найдем вектор
или в координатах:
Отсюда, если отрезок разделить на две равные части точкой 

Можно доказать, что координаты точки пересечения медиан треугольника, заданного координатами его вершин 
Лекции:
- Объем конуса
- Разложение на множители
- Деление многочлена на многочлен
- Правила дифференцирования
- Теорема Пифагора
- Асимптотическое поведение функций. Сравнение бесконечно малых функций
- Прямая линия на плоскости
- Выпуклость и вогнутость графика функции
- Матанализ для чайников
- Производные некоторых элементарных функций



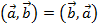
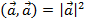
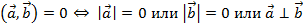
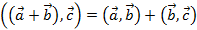
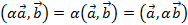
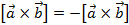
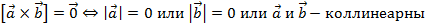
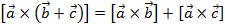
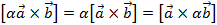
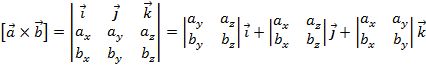
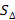
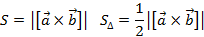
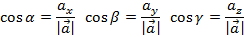
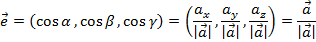
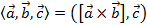
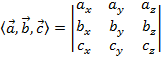
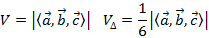
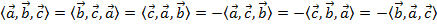
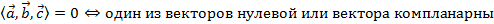
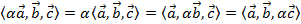
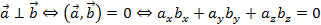
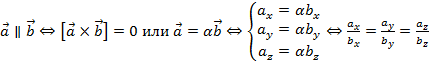
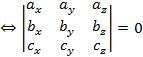
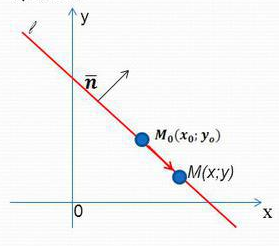
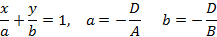
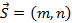
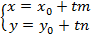
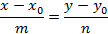
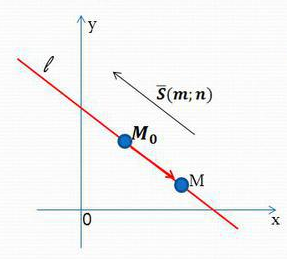
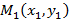
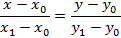
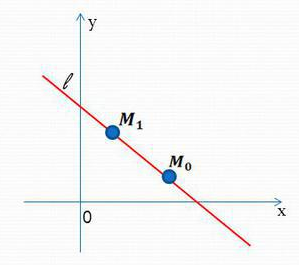
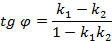

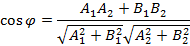
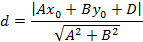
















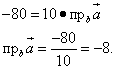











































































































 — ассоциативность (сочетательный закон);
— ассоциативность (сочетательный закон); —дистрибутивность относительно сложения векторов (1-й распределительный закон);
—дистрибутивность относительно сложения векторов (1-й распределительный закон); — дистрибутивность относительно сложения чисел (2-й распределительный закон).
— дистрибутивность относительно сложения чисел (2-й распределительный закон).











 отсюда
отсюда 
 — т. е. векторы
— т. е. векторы  компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора
компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора  по данным векторам
по данным векторам  единственно. Теорема доказана.
единственно. Теорема доказана.

 получаем
получаем 
 и действительного числа
и действительного числа  получаем
получаем 











































































































































































































