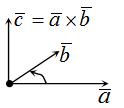Как найти квадрат векторного произведения

Векторное произведение векторов и его свойства

Вектор называется векторным произведением неколлинеарных векторов и , если:

1) его длина равна произведению длин векторов и на синус угла между ними: (рис.1.42);

2) вектор ортогонален векторам и ;

3) векторы , , (в указанном порядке) образуют правую тройку.

Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.

Векторное произведение обозначается (или ).

---

Алгебраические свойства векторного произведения

Для любых векторов , , и любого действительного числа :

1. ;

2. ;

3. .

Первое свойство определяет антисимметричность векторного произведения, второе и третье — аддитивность и однородность по первому множителю. Эти свойства аналогичны свойствам произведения чисел: первое свойство «противоположно» закону коммутативности умножения чисел (закон антикоммутативности), второе свойство соответствует закону дистрибутивности умножения чисел по отношению к сложению, третье — закону ассоциативности умножения. Поэтому рассматриваемая операция и называется произведением векторов. Поскольку ее результатом является вектор, то такое произведение векторов называется векторным.

Докажем первое свойство, предполагая, что векторы и не коллинеарны (в противном случае обе части доказываемого равенства равны нулевому вектору). По определению векторы и имеют равные длины и коллинеарны (так как оба вектора перпендикулярны одной плоскости). По определению тройки векторов и — правые, т.е. вектор направлен так, что кратчайший поворот от к происходит в положительном направлении (против часовой стрелки), если смотреть из конца вектора , а вектор направлен так, что кратчайший поворот от к происходит в положительном направлении, если смотреть из конца вектора (рис. 1.43). Это означает, что векторы и противоположно направлены. Следовательно, , что и требовалось доказать. Доказательство остальных свойств приведено ниже (см. пункт 1 замечаний 1.13).

Замечания 1.12

1. Свойства аддитивности и однородности векторного произведения означают линейность векторного произведения по первому множителю:

для любых векторов и любых действительных чисел и .

2. В силу антисимметричности векторное произведение линейно и по второму множителю, т.е. линейно по любому множителю.

---

Геометрические свойства векторного произведения

1. Модуль векторного произведения численно равен площади параллелограмма, построенного на множителях (рис. 1.42,6).

2. Векторное произведение равняется нулевому вектору тогда и только тогда, когда множители коллинеарны, т.е.

, в частности, .

Первое свойство следует из определения. Докажем второе свойство. Равенство возможно в трех случаях: , или , или . В каждом из этих случаев векторы и коллинеарны (см. разд. 1.1).

---

Пример 1.19. Вычислить площади параллелограмма и треугольника, построенных на векторах , где , угол между векторами и равен (рис. 1.44).

Решение. Используя алгебраические свойства, найдем сначала векторное произведение

а затем его модуль .

По первому геометрическому свойству векторного произведения искомая площадь параллелограмма равна , а площадь треугольника в 2 раза меньше: .

---

Выражение векторного произведения через координаты векторов

Пусть в пространстве задан ортонормированный (стандартный) базис . Векторные произведения базисных векторов находятся по определению:

Формулы (1.14) можно получить, используя диаграмму (рис. 1.45): если на этой схеме кратчайший поворот от первого множителя ко второму совершается в положительном направлении (указанном стрелкой), то произведение равно третьему вектору, а если — в отрицательном направлении, то произведение равно третьему вектору, взятому со знаком минус (противоположному вектору).

Найдем выражение векторного произведения через координаты множителей. Пусть в стандартном базисе векторы и имеют координаты и соответственно. Тогда, используя линейность векторного произведения по любому множителю (см. пункт 2 замечаний 1.12) и формулы (1.14), получаем

Запишем это равенство при помощи определителей второго порядка:

Правую часть (1.15) можно представить как результат разложения символического определителя третьего порядка по первой строке

---

Формула вычисления векторного произведения

Теорема 1.8 (формула вычисления векторного произведения). Если векторы и в правом ортонормированием базисе имеют координаты и соответственно, то векторное произведение этих векторов находится по формуле (1.15), которую принято записывать в виде

Если и — координатные столбцы векторов и в стандартном базисе, то координатный столбец векторного произведения находится по формуле

В самом деле, выполняя умножение матрицы на столбец, получаем

Тогда , что совпадает с (1.15).

---

Пример 1.20. Параллелограмм построен на векторах (рис. 1.46). Найти:

а) векторные произведения и ;
б) площадь параллелограмма ;
в) направляющие косинусы такого вектора , перпендикулярного плоскости параллелограмма ,

для которого тройка , , — левая.

Решение. а) Векторное произведение находим по формуле (1.16):

Для нахождения векторного произведения можно использовать матричную запись формулы (1.15) (см. теорему 1.8). Векторам и соответствуют координатные столбцы .

По указанной формуле получаем координатный столбец вектора :

то есть . Результаты совпадают.

Векторное произведение находим, используя алгебраические свойства:

Следовательно, .

б) Площадь параллелограмма находим как модуль векторного произведения :

в) Вектор, противоположный вектору , удовлетворяет перечисленным в условии требованиям, поэтому

Разделив этот вектор на его длину , получим единичныи вектор:

Согласно его координатами служат направляющие косинусы

.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Векторное произведение векторов

Определение

Определение

Векторным произведением векторов $ overline{a} $ и $ overline{b} $ является вектор $ overline{c} $, который расположен перпендикулярно к плоскости, образуемой векторами $ overline{a} $ и $ overline{b} $. Само произведение обозначается как $ [overline{a},overline{b}] $, либо $ overline{a} times overline{b} $.

Векторное произведение векторов, формула которого зависит от исходных данных задачи, можно найти двумя способами.

Формула

Формула 1

Если известен синус угла между векторами $ overline{a} $ и $ overline{b} $, то найти векторное произведение векторов можно по формуле: $$ [overline{a},overline{b}] = |overline{a}| cdot |overline{b}| cdot sin (overline{a},overline{b}) $$

Формула 2

В случае когда векторы $ overline{a} $ и $ overline{b} $ заданы в координатной форме, то их произведение определяется по формуле: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} $$ где векторы $ overline{i},overline{j},overline{k} $ называются единичными векторами соответствующих осей $ Ox, Oy, Oz $.

Определитель во второй формуле можно раскрыть по первой строке:

$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} = overline{i} (a_2 b_3 — a_3 b_2) — overline{j} (a_1 b_3 — a_3 b_1) + overline{k} (a_1 b_2 — a_2 b_1) $$

Итого вторая формула приобретает окончательный короткий вид:

$$ overline{a} times overline{b} = (a_2 b_3 — a_3 b_2; a_3 b_1 — a_1 b_3; a_1 b_2 — a_2 b_1) $$

Свойства

1. При изменении порядка множителей меняется знак на противоположный: $$ [overline{a},overline{b}] = -[overline{b},overline{a}] $$
2. Вынос константы за знак произведения: $$ lambda [overline{a},overline{b}] = [lambda overline{a}, overline{b}] = [overline{a}, lambda overline{b}] $$
3. $$ [overline{a}+overline{b}, overline{c}] = [overline{a},overline{c}] + [overline{b}, overline{c}] $$

Примеры решений

Пример 1

Найти векторное произведение векторов, заданных координатами $$ overline{a} = (2,1,-3) $$ $$ overline{b} = (1,2,-1) $$

Решение

Составляем определитель, первая строка которого состоит из единичных векторов, а вторая и третья из координат векторов $ overline{a} $ и $ overline{b} $: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ 2&1&-3\1&2&-1 end{vmatrix} = overline{i} (-1+6) — overline{j}(-2+3) + overline{k}(4-1) = 5overline{i} — overline{j} + 3overline{k} $$ Полученный ответ можно записать в удобном виде: $$ overline{a} times overline{b} = (5, -1, 3) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ overline{a} times overline{b} = (5, -1, 3) $$

Геометрический смысл

• Модуль векторного произведения векторов $ overline{a} $ и $ overline{b} $ в геометрическом смысле равен площади параллелограмма, построенного на этих векторах: $$ S_{parall} = |overline{a} times overline{b}| $$
• Половина этого модуля это площадь треугольника: $$ S_Delta = frac{1}{2} |overline{a} times overline{b} | $$
• Если векторное произведение равно нулю $ overline{a} times overline{b} = 0 $, то векторы коллинеарны.

 

Пример 2

Найти площадь треугольника по заданным векторам $$ overline{a} = (2,1,3) $$ $$ overline{b} = (-1,2,1) $$

Решение

Используя геометрический смысл, в частности вторую формулу находим половину модуля векторного произведения векторов. Находим определитель: $$ begin{vmatrix} overline{i}&overline{j}&overline{k}\2&1&3\-1&2&1 end{vmatrix} = overline{i}(1-6) — overline{j}(2+3) + overline{k}(4+1) = -5overline{i} — 5overline{j} + 5overline{k} $$ Вычисляем модуль полученного вектора как корень квадратный из суммы квадратов координат этого вектора: $$ |overline{a} times overline{b}| = sqrt{(-5)^2 + (-5)^2 + 5^2} = sqrt{25 + 25 + 25} = sqrt{75} $$ По формуле нахождения площади треугольника имеем: $$ S_Delta = frac{1}{2} |overline{a} times overline{b}| = frac{1}{2} sqrt{75} = 4.33 $$

Ответ

$$ S_Delta = 4.33 $$

Векторное произведение векторов

Так же, как и скалярное произведение, векторное произведение своим появлением обязано необходимости решения физических задач. Рассмотрим одну из таких – задачу о вычислении момента силы.

Принято считать моментом силы , приложенной в точке А относительно точки О, вектор , имеющий модуль, равный произведению модуля силы на кратчайшее расстояние (плечо силы) от этой точки до линий действия силы (рис 3.33). Если вектор связывает точку О с началом вектора , а  – угол между векторами И , то .

Поэтому .

Вектор перпендикулярен плоскости, в которой лежат сила и точка О, и ориентирован в ту сторону, откуда вращение тела вокруг точки О видно как вращение, происходящее против часовой стрелки. Таким образом, двум векторным величинам И Ставится в соответствие тоже векторная величина. Это новый тип соответствия отличен от уже введенного скалярного произведения. Существуют разнообразные физические процессы, в которых соответствие между векторами осуществляется подобным образом. Вот почему в математике вводится еще одно действие умножения векторов – векторное произведение.

Рис. 3.33. Момент силы относительно точки О.

ВЕКТОРНЫМ ПРОИЗВЕДЕНИЕМ вектора на вектор называется вектор , обозначаемый , обладающий следующими свойствами (рис. 3.34):

1. Его модуль равен произведению модулей данных векторов на синус угла между ними.

2. Он перпендикулярен плоскости, в которой располагаются данные векторы.

3. Его ориентация такова, что векторы , и образуют правую координатную тройку (то есть из конца вектора поворот от вектора до совмещения с вектором на кратчайший угол виден как поворот, осуществляемый против часовой стрелки).

По определению имеем:

Геометрически это означает, что равняется площади параллелограмма, построенного на векторах и как на сторонах.

Возвращаясь к задаче о вычислении момента силы, можно заключить, что

и .

Очевидно, что векторное произведение обращается в нуль , если векторы коллинеарны или же какой-нибудь из них нулевой.

Рассмотрим алгебраические свойства векторного произведения. Не все они сохраняются в том же виде, что и для скалярного произведения.

1.  – антипереместительный закон.

Действительно, векторы и перпендикулярны одной и той же плоскости, в которой располагаются векторы и , но ориентированы в противоположные стороны, так как, если векторы , , образуют правую тройку, то векторы , , будут образовывать уже левую тройку векторов, что и доказывает данный закон.

2.  – распределительный закон. Приведем его без доказательства.

3.  – сочетательный закон относительно скалярного множителя.

Действительно, векторы и (рис. 3.35) имеют одинаковые модули. Их ориентация совпадает с ориентацией вектора , если , и противоположны ему при .

Рис. 3.35. Сочетательный закон для векторного
произведения векторов относительно скалярного
Множителя.

Очевидно, что векторный квадрат вектора равен нулю:

Получим формулы векторного произведения в координатном виде. Пусть даны векторы:

Поэтому

Векторные квадраты координатных ортов равны нулю:

А произведения определяются следующим образом:

Тогда

Эта запись может быть представлена в компактной форме с помощью определителя третьего порядка.

Определителем третьего порядка, составленного из таблицы девяти элементов

Называется выражение

.

Произведения элементов определителя, которые берутся со знаком плюс, символично для запоминания могут быть представлены следующей схемой:

Последние три слагаемых определителя, имеющие знак минус, получаются по другой схеме:

В курсе алгебры при решении систем линейных уравнений рассматриваются определители различных порядков, элементами которого чаще всего являются числа, а потому и определитель есть число.

Легко проверить справедливость формулы:

В заключение получим интересную формулу, связывающую скалярное и векторное произведения.

Так как

То очевидно соотношение:

Отсюда можно получить два полезных неравенства:

< Предыдущая		Следующая >

В данной публикации мы рассмотрим, каким образом можно найти векторное произведение двух векторов, приведем геометрическую интерпретацию, алгебраическую формулу и свойства этого действия, а также разберем пример решения задачи.

Геометрическая интерпретация

Векторное произведение двух ненулевых векторов a и b – это вектор c, который обозначается как [a, b] или a x b.

Длина вектора c равна площади параллелограмма, построенного с помощью векторов a и b.

При этом c перпендикулярен плоскости, в которой расположены a и b, и расположен так, чтобы наименьшее вращение от a к b выполнялось против часовой стрелки (с точки зрения конца вектора).

Формула векторного произведения

Произведение векторов a = {a_x; a_y, a_z} и b = {b_x; b_y, b_z} вычисляется с помощью одной из формул ниже:

Свойства векторного произведения

1. Векторное произведение двух ненулевых векторов равняется нулю тогда и только тогда, когда эти векторы являются коллинеарными.

[a, b] = 0, если

a || b

.

2. Модуль векторного произведения двух векторов равняется площади параллелограмма, образованного этими векторами.

S_парал. = |a x b|

3. Площадь треугольника, образованного двумя векторами, равняется половине их векторного произведения.

S_Δ = ¹/₂ · |a x b|

4. Вектор, являющийся векторным произведением двух других векторов, перпендикулярен им.

c ⟂ a, c ⟂ b.

5. a x b = –b x a

6. (m a) x a = a x (m b) = m (a x b)

7. (a + b) x c = a x c + b x c

Пример задачи

Вычислим векторное произведение a = {2; 4; 5} и b = {9; -3; 1}.

Решение:

Ответ: a x b = {19; 43; -42}.