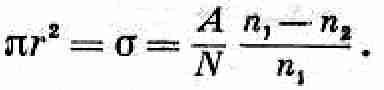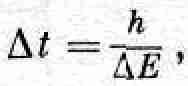Как найти время, зная расстояние
Навыки определения времени, которое понадобится телу на преодоление расстояния, могут пригодиться не только на школьных уроках физики и алгебры. Подобные знания с пользой можно использовать и на практике.

Инструкция
Предположим, нужно узнать точное время, требующееся на преодоление расстояния на автомобиле в 1000 километров. Получить ответ на этот вопрос можно несколькими способами, так как наиболее удобный метод нахождения времени может изменяться в зависимости от исходных условий задачи.
Первый способ. Воспользуйтесь формулой S=Vt, где S – расстояние (измеряется в километрах),V – скорость (измеряется в километрах в час), t – время (измеряется в часах). В случае если S дано в километрах, а V в метрах в секунду, то расстояние S переведите в метры, чтобы уравнять величины.
Теперь, чтобы вычислить время из исходной формулы S=Vt, примените правило нахождения неизвестного множителя: «Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель». Таким образом, t=S/V. Если скорость движения автомобиля известна (пусть V=50 км/ч), то в полученную формулу подставьте исходные значения. Получится: t=1000 км / 50 км/ч, t=20 ч.
Второй способ (используется в задачах, где отсутствует скорость, но известно ускорение). Воспользуйтесь формулой S=(at^2)/2, где S – расстояние (измеряется в километрах), a – ускорение (измеряется в метрах в секунду), t^2 – время в квадрате. Чтобы вычислить время в квадрате, умноженное на ускорение, примените правило нахождения неизвестного делимого: «Чтобы найти неизвестное делимое, нужно частное умножить на делитель». Таким образом, at^2=2S, t^2=2S/a (правило нахождения неизвестного множителя), t=корень квадратный из (2S/a).
Далее необходимо уравнять величины. Так как a (ускорение) дано нам в м/c, то S (расстояние) переведите в метры: 1000 км=1000000 м. Если ускорение известно (пусть 2 м/с), то в полученную формулу подставьте исходные значения. Получится: t=корень квадратный из 2000000 м / 2 м/c, t=1000 c. Переведите полученное время в часы: t=16,7 ч.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Видео
Пространство-время
Эмиль Ахмедов
Сохранить в закладки
16334
589
Сохранить в закладки
Физик Эмиль Ахмедов о втором законе Ньютона, метрике Минковского и природе пространства-времени
20.09.2017
Над материалом работали

Эмиль Ахмедов
доктор физико-математических наук, ведущий научный сотрудник и профессор МФТИ и ИТЭФ

Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
WTF Кимберлитовая трубка «Мир»

Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
ПРОМО Вы нужны нам: как поддержать ПостНауку
Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
FAQ Тезаурус: Производственные технологии

Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
Журнал Мир в пределах наноразмерной шкалы

Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
Видео
17967
535
Носимая электроника в медицине

Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
FAQ Перспективы интеллектуальных агентов

Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
FAQ FAQ: Химия высоких энергий

Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
Видео
3089
221
Магнетизм Земли

Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
tv Как будут передаваться данные в 5G?
2017-04-02
Одним из основоволожников современной физики по праву считается итальянский ученый Галилео Галилей. В начале XVII века он экспериментально исследовал движение различных тел под действием притяжения к Земле. Ему удалось доказать, что такое движение является равноускоренным и не зависящим от массы тела (если пренебречь силами сопротивления). В частности, Г.Галилей подробно исследовал качение шаров (в качестве которых использовал пушечные ядра) по наклонной плоскости.
Воспроизведем результаты опытов Г. Галилея. В качестве наклонной плоскости используется желоб длиной $L = 5,0 м$ (конечно, во времена Галилея в Италии употреблялись другие единицы длины), один из концов которого приподнят на высоту $h$.
Для того, чтобы отмерять равные промежутки времени, Г.Галилей использовал маятник — груз подвешенный на нити.
В Таблице 1 приведены значения пути £, пройденного шаром, за время, равное целому числу $n$ колебаний маятника, при разных значениях высоты $h$ (проскальзывание отсутствует).
Таблица 1.
На основании приведенных данных
1. Покажите, что движение ядра по желобу действительно является равноускоренным.
2. Найдите, как зависит ускорение ядра от высоты $h$. Объясните эту зависимость.
3. Вычислите путь, который пройдет ядро за пять колебаний маятника при высоте $h = 50 см$?
Решение:
При равноускоренном движении тела с нулевой начальной скоростью пройденный путь зависит от времени по закону
$S = frac{at^{2}}{2}$, (1)
где $a$ — ускорение тела. Иными словами, пройденный путь пропорционален квадрату времени. Постоянный период колебаний маятника в данном случае может служить единицей измерения времени, поэтому можно переписать формулу (1) в виде
$S = frac{An^{2}}{2}$, (2)
где $A$ — ускорение тела, измеренное в «метрах на период в квадрате», а $n$ — число периодов.
Построим графики зависимости пройденного пути от квадрата времени (то есть, $n^{2}$). Как видно, эти зависимости представляют прямые линии, следовательно эксперимент подтверждает формулу (2), то есть движение действительно является равноускоренным. 2. По наклону графиков определим ускорения шаров при каждом значении высоты $h$:
$A = 2 frac{ Delta S}{ Delta n^{2}}$. (3)
Получим следующие значения
$h = 20 см, A approx 0,09 м$
$h = 30 см, A approx 0,14 м$
$h = 40 см, A approx 0,18 м$
Можно заметить, что ускорение прямо пропорционально высоте $h$. Еще лучше построить график зависимости $A(h)$ и убедится в ее прямой пропорциональности.
С помощью графика, либо непосредственно по численным значениям легко определить коэффициент пропорциональности. Окончательно получаем $A approx 0,46h$, где высота $h$ измеряется в метрах.
Легко показать, что ускорение при движении по наклонной плоскости пропорционально синусу угла наклона, который при постоянной длине желоба пропорционален высоте $h$. Действительно, кинетическая энергия катящегося шара пропорциональна квадрату скорости $E_{кин} = C v^{2}$, где $C$ — постоянный коэффициент, зависящий не только от распределения масс внутри шара, но и от глубины желоба. Пренебрегая работой против сил трения качения, можем приравнять кинетическую энергию в конце желоба к начальной потенциальной энергии
$Cv^{2} = mgh$. (4)
С другой стороны при равноускоренном движении справедлива формула
$L = frac{v^{2}}{2a}$, (5)
где $a$ — ускорение шара. Из формул (4)-(5) следует $a = frac{mgh}{2CL} infty h$.
3. При высоте $h = 50 см$ ускорение примерно равно $A approx 0,23$. Поэтому путь пройденным шаром за пять колебаний маятника
$S = frac{An^{2}}{2} approx 2,88 м$.
Глава 5
ВРЕМЯ И РАССТОЯНИЕ
§ 1. Движение
§ 2. Время
§ 3. Короткие времена
§ 4. Большие времена
§ 5. Единицы и стандарты времени
§ 6. Большие расстояния
§ 7. Малые расстояния
§ 1. Движение
В этой главе мы рассмотрим понятия время и расстояние. Мы уже говорили, что физика, как, впрочем, любая другая наука, основывается на наблюдениях. Можно даже сказать, что развитие физических наук до их современного уровня в огромной степени зависело от фактов, основанных на количественных наблюдениях. Только с помощью количественных наблюдений можно получить количественные соотношения — сердце современной физики.
Многие считают, что физика берет свое начало с опыта, проведенного Галилеем 350 лет назад, а сам Галилей является первым физиком. До этого времени изучение движения было чисто философским и основывалось на доводах, которые были плодом фантазии. Большинство этих доводов были придуманы Аристотелем и другими греческими философами и рассматривались как «доказанные». Но Галилей был скептиком и поставил следующий опыт: по наклонной плоскости он пускал шар и наблюдал за его движением (фиг. 5.1).
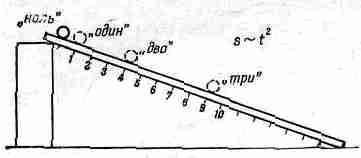
Фиг.5.1. Шарик катится по наклонной плоскости.
Галилей не просто смотрел, как катится шар, а измерял то расстояние, которое прошел шар, и определял время, в течение которого шар проходил это расстояние. Способ измерения расстояний был хорошо известен еще задолго до Галилея, однако точного способа измерения времени, особенно коротких интервалов, не было. Хотя впоследствии Галилей изобрел более совершенные часы (отнюдь не похожие на современные), но в своих первых опытах для отсчета равных промежутков времени он использовал собственный пульс. Давайте сделаем то же самое.
Будем отсчитывать удары пульса в то время, пока шарик катится вниз: «Один… два… три… четыре… пять… шесть… семь… восемь…». Пусть кто-нибудь отмечает положение шарика на каждый счет. Теперь можно измерить расстояние, которое шарик прошел за один, два, три и т. д. равных интервала времени. Галилей сформулировал результат своих наблюдений следующим образом: если отмечать положения шарика через 1, 2, 3,4,… единицы времени от начала движения, то окажется, что эти отметки удалены от начального положения пропорционально числам 1, 4, 9,16, … . Сейчас мы сказали бы, что расстояние пропорционально квадрату времени:
S~ t2.
Таким образом, изучение процесса движения (основы современной физики) начинается с вопросов: где и когда?
§ 2. Время
Разберем сначала, что мы понимаем под словом время. Что же это такое? Неплохо было бы найти подходящее определение понятия «время». В толковом словаре Вебстера, например, «время» определяется как «период», а сам «период» — как «время». Однако пользы от этого определения мало. Но и в определении «время — это то, что меняется, когда больше ничего не изменяется» не больше смысла. Быть может, следует признать тот факт, что время — это одно из понятий, которое определить невозможно, и просто сказать, что это нечто известное нам: это то, что отделяет два последовательных события! Дело, однако, не в том, как дать определение понятия «время», а в том, как его измерить. Один из способов измерить время — это использовать нечто регулярно повторяющееся, нечто периодическое. Например, день. Казалось бы, дни регулярно следуют один за другим. Но, поразмыслив немного, сталкиваешься с вопросом: периодичны ли они? Все ли дни имеют одинаковую длительность? Создается впечатление, что летние дни длиннее зимних. Впрочем, некоторые зимние дни кажутся ужасно длинными, особенно если они скучны. О них обычно говорят: «Ужасно длинный день!»
Однако, по-видимому, все дни в среднем одинаковы. Можно [и проверить, действительно ли они одинаковы и от одного дня до другого, хотя бы в среднем, проходит ли одно и то же время? Для этого необходимо произвести сравнение с каким-то другим периодическим процессом. Давайте посмотрим, как такое сравнение можно, например, провести с помощью песочных часов. С помощью таких часов мы можем создать периодический процесс, если будем стоять возле них день и ночь и переворачивать каждый раз, когда высыплются последние крупинки песка.
Если затем подсчитать число переворачиваний песочных часов от каждого утра до следующего, то можно обнаружить, что число «часов» (т. е. число переворачиваний) в разные дни различно. Кто же виноват в этом? Может быть, Солнце? Может быть, часы? А может, и то и другое? После некоторых размышлений можно прийти к мысли, что следует считать «часы» не от утра до утра, а от полудня до полудня (полдень — это, конечно, не 12 часов, а момент, когда Солнце находится в наивысшем положении). На этот раз оказывается, что в каждых сутках число «часов» одинаково.
Теперь можно утверждать, что «час» и «сутки» имеют регулярную периодичность, т. е. отмечают последовательные равные интервалы времени, хотя нами и не доказано, что каждый из процессов действительно периодичен. Нас могут спросить: а вдруг есть некое всемогущее существо, которое замедляет течение песка ночью и убыстряет днем? Наш эксперимент, конечно, не может дать ответа на такого рода вопросы. Очевидно лишь то, что периодичность одного процесса согласуется с периодичностью другого. Поэтому при определении понятия «время» мы просто будем исходить из повторения некоторых очевидно периодических событий.
§ 3. Короткие времена
Заметим, что в процессе проверки «воспроизводимости» дней мы нашли метод измерения части дня, т. е. метод измерения меньших промежутков времени. Нельзя ли этот процесс продолжить и научиться измерять еще меньшие промежутки времени?
Галилей предположил, что каждый маятник отклоняется и возвращается назад за равные интервалы времени (если отклонения невелики). Сравнение числа отклонений маятника с «часом» показывает, что это действительно так. Таким способом можно измерять доли «часа». Если для подсчета числа колебаний маятника применить механический счетчик, то мы получим маятниковые часы наших дедов.
Договоримся теперь, что если маятник отклонится 3600 раз в час (и если в сутках 24 часа), то период колебаний такого маятника мы назовем «секундой». Итак, нашу первоначальную единицу «сутки» мы разделили приблизительно на 105 частей. Используя тот же принцип сравнения, можно и секунду разделить на все меньшие и меньшие части. Для этого оказывается более удобным использовать не простой механический, а электрический маятник, называемый осциллятором, период колебаний которого может быть очень малым. В таких электронных осцилляторах роль маятника выполняет электрический ток, который течет то в одном, то в другом направлении.
Давайте представим себе целый ряд таких осцилляторов, что период колебаний каждого последующего в десять раз меньше предыдущего. Это можно проверить путем простого подсчета числа колебаний последующего осциллятора за одно колебание предыдущего; только теперь этот подсчет трудно провести без устройства, расширяющего возможности наблюдения, своеобразного «микроскопа времени». Таким устройством может служить электронно-лучевой осциллограф, на светящемся экране которого строится график зависимости электрического тока, (или напряжения) от времени. I
Соединяя осциллограф сначала с одним осциллятором, а| затем с другим, мы получим на экране графики зависимости тока от времени в одном и в другом осцилляторе (фиг. 5.2).
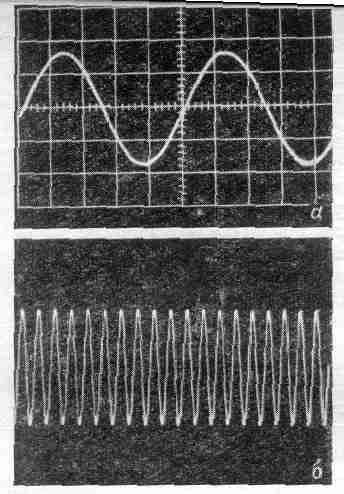
Фиг. 5.2. Две осциллограммы, снятые с экрана осциллографа.
а — при осциллографе, подключенном к одному осциллятору; б — при осциллографе, подключенном к осциллятору, период колебаний которого в десять раз меньше первого.
А теперь нетрудно подсчитать, какое число периодов «быстрого» осциллятора укладывается в одном периоде «медленного».
Современная электроника позволяет создавать осцилляторы с периодами 10-12сек, которые выверяются (калибруются) методом сравнения, подобным вышеописанному, на стандартную единицу времени — секунду. В последние несколько лет в связи с изобретением и усовершенствованием «лазера», или усилителя света, появилась возможность сделать осцилляторы с еще более коротким периодом. Пока еще невозможно калибровать их тем же методом, однако, несомненно, что и это скоро будет достигнуто.
Можно измерять промежутки времени, гораздо более короткие, чем 10-12 сек, но для этого используются совершенно другие методы. В сущности используется другое определение понятия «время». Один из таких методов — это измерение расстояния между двумя событиями, происходящими на движущемся объекте. Например, пусть в движущемся автомобиле сначала включают, а затем выключают фары. Если известно, где были включены и выключены фары и какова была скорость автомобиля, то можно вычислить, сколько времени они горели. Для этого нужно расстояние, на протяжении которого горели фары, разделить на скорость автомобиля.
Именно таким методом в последние годы измерялось время жизни p°-мезона. При наблюдении в микроскоп мельчайших следов, оставленных на фотоэмульсии, в которой родился p°-мезон, было обнаружено следующее: p°-мезон, двигаясь со скоростью, близкой к скорости света, прежде чем распасться, проходит в среднем расстояние около 10-7 м. Таким образом, время жизни p°-мезона составляет всего лишь 10-16 сек! Необходимо подчеркнуть, что здесь было использовано несколько другое определение понятия «время», но, поскольку оно не приводит к каким-либо противоречиям, можно быть уверенным в том, что эти определения в достаточной мере эквивалентны друг другу.
Развивая технику эксперимента, а если необходимо, меняя определение понятия «время», можно обнаружить еще более быстрые физические процессы. Мы, например, можем говорить о периоде вибраций ядра или о времени жизни недавно обнаруженных «странных» резонансов (частиц), которые уже упоминались в гл. 2. Время жизни этих частиц лишь ненамного больше 10-24 сек! Приблизительно столько времени требуется свету (который имеет наибольшую скорость распространения), чтобы пройти расстояние, равное диаметру ядра водорода (наименьший из известных объектов).
Что можно сказать о еще более коротких интервалах времени? Имеет ли смысл вообще говорить о них, если невозможно не только измерить, но даже разумно судить о процессах, происходящих в течение столь коротких интервалов? Возможно, нет. Это один из тех вопросов, на которые нет ответа. Может быть, кому-нибудь из вас посчастливится ответить на него в ближайшие 20—30 лет.
§ 4. Большие времена
Рассмотрим теперь промежутки времени, большие «суток». Измерять большие времена легко: нужно просто считать дни, пока не придумаем что-нибудь лучшего. Первое, с чем мы сталкиваемся, это год — вторая естественная периодичность, состоящая приблизительно из 365 дней. Интересно, что в природе существуют естественные счетчики лет в виде годовых колец у деревьев или отложений речного ила. В некоторых случаях можно использовать эти естественные счетчики для определения времени, отделяющего нас от какого-либо отдаленного события в прошлом.
Но, когда невозможно считать годы для очень больших отрезков времени, нужно искать какие-то другие способы измерения. Одним из наиболее эффективных методов является использование в качестве «часов» радиоактивного вещества. Здесь мы сталкиваемся с «регулярностью» иного рода, чем в случае, скажем, маятника. Радиоактивность любого вещества для последовательных равных интервалов времени изменяется в одно и то же число раз.

Если начертить график зависимости радиоактивности от времени, то мы получим кривую типа изображенной на фиг. 5.3.
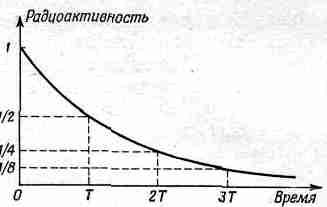
Фиг. 5.3. Уменьшение радиоактивности со временем.
Радиоактивность падает в два раза за каждый период полураспада Т.
Мы видим, что если радиоактивность за Т дней (период полураспада) уменьшается вдвое, то за 2Т дней она уменьшится в четыре раза и т. д. Произвольный интервал времени t содержит tIT «периодов полураспада», и, следовательно, количество начального вещества уменьшится в 2t/T раза.
Если мы знаем, что какой-то материал, например дерево, при своем образовании содержал некоторое количество А радиоактивного вещества, а прямые измерения показывают, что теперь он содержит количество В, то возраст этого материала можно просто вычислить, решив уравнение
(1/2)t/T=B/A.
А такие случаи, когда мы знаем первоначальное количество радиоактивного вещества, к счастью, существуют. Известно, например, что углекислый газ в воздухе содержит малую долю радиоактивного изотопа С14, период полураспада которого составляет 5000 лет. Количество его благодаря действию космических лучей постоянно пополняется взамен распавшегося. Если мы измеряем полное содержание углерода в каком-то предмете и знаем, что определенная доля этого углерода была первоначально радиоактивным С14, то нам известно и первоначальное количество А и мы можем пользоваться приведенной выше формулой. Если же путем точных измерений установлено, что оставшееся количество С14 соответствует 20 периодам полураспада, то можно сказать, что этот органический предмет жил приблизительно 100 000 лет назад.
Хотелось бы, однако, узнать возраст еще более древних вещей. Это можно сделать, измерив содержание других радиоактивных элементов с большими периодами полураспада. Уран, например, имеет изотоп с периодом полураспада около 109 лет, так что если какой-то материал при своем образовании 109 лет назад содержал уран, то сегодня от него осталась только половина первоначального количества. При своем распаде уран превращается в свинец. Как определить возраст горной породы, которая образовалась много-много лет назад в результате какого-то химического процесса? Свинец по своим химическим свойствам отличается от урана, поэтому они первоначально входили в разные виды горных пород. Если взять такой вид породы, который вначале должен был содержать только уран, то мы обнаружим в нем некоторое количество свинца. Сравнивая доли свинца и урана, можно определить ту часть урана, которая в результате распада превратилась в свинец. Этим методом было установлено, что возраст некоторых горных пород составляет несколько миллиардов лет. Применяя шире этот метод путем сравнения содержания урана и свинца не только в некоторых горных породах, но и в воде океанов, а затем усредняя различные данные по всему земному шару, установили, что нашей планете исполнилось примерно 5,5 миллиарда лет.
Интересно, что возраст метеоритов, падающих на Землю, вычисленный по урановому методу, совпадает с возрастом самой Земли. Более того, оказалось, что и метеориты, и горные породы Земли составлены из одного и того же материала, поэтому существует мнение, что Земля образовалась из пород, «плававших» некогда в «околосолнечном» пространстве.
Некогда, во времена, еще более древние, чем возраст Земли (т. е. 5 миллиардов лет назад), начала свою историю Вселенная. Сейчас считают, что возраст по крайней мере нашей части Вселенной достигает примерно 10—12 миллиардов лет. Нам неизвестно, что было до этого. В сущности опять можно спросить: «А есть ли смысл говорить о том, что было до этого? И имеет ли смысл само понятие «время» до «рождения» Вселенной?»
§ 5. Единицы и стандарты времени
Мы уже говорили, что счет времени удобно вести в каких-то стандартных единицах, скажем в днях или секундах, и измерять длительности в количествах этой единицы или ее долях. Но что же выбрать за основную стандартную единицу? Можно ли, например, принять за отправную единицу человеческий пульс? Очевидно, нет. Уж очень непостоянна эта единица. Лучше обстоит дело с часами. Двое часов согласуются гораздо лучше, чем пульс. Вы скажете: ладно, давайте возьмем часы. Но чьи? Существует предание об одном швейцарском мальчике, которому хотелось, чтобы все часы в его городе отзванивали полдень и в одно и то же время. Он ходил по городу и доказывал всем, насколько это важно. Каждый считал, что это действительно было бы чудесно, если бы все другие часы в городе звонили полдень по его часам! В самом деле, очень трудно решить, чьи же часы мы должны выбрать в качестве стандарта. К счастью, существуют часы, которые признают все,— это наша Земля. Долгое время в качестве стандарта выбирался период вращения Земли. Однако по мере того, как измерения становились все более точными, обнаруживалось, что вращение Земли не строго периодично, если сравнивать его с лучшими часами. А этим «лучшим часам» можно доверять, ибо они согласуются друг с другом. Сейчас известно, что по разным причинам одни дни оказываются длиннее других и, кроме того, средний период вращения Земли на протяжении столетий несколько удлиняется.
Вплоть до самого последнего времени не было найдено ничего более точного, чем вращение Земли, и поэтому все часы сверялись с длиной астрономических суток, а секунда определялась как 1/86 400 часть средних суток. Однако сейчас мы научились работать с некоторыми естественными осцилляторами, которые являются более точными стандартами времени, чем вращение Земли. Это так называемые «атомные часы». В основе их лежат колебания атомов, период которых нечувствителен к температуре и другим внешним воздействиям. Эти часы позволяют измерять время с точностью, лучшей 10-7%. В последние два года профессор Гарвардского университета Норман Рамзей спроектировал и построил улучшенные атомные часы, работающие на колебаниях атомов водорода. Он считает, что эти часы могут быть еще в сто раз более точными. Сейчас ведутся измерения, которые покажут, насколько он прав.
А поскольку оказалось возможным создать часы гораздо более точные, чем астрономические, то ученые договариваются определять единицу времени с помощью новых стандартов — атомных часов .
§ 6. Большие расстояния
Вернемся теперь к вопросу о расстоянии. Как далеко отстоят от нас окружающие предметы и как велики они? Всем известно, что для измерения расстояния нужно взять какую-то единицу длины и считать, сколько этих единиц укладывается на данном отрезке. Но как измерить те предметы, которые меньше единицы длины? Как подразделить выбранную единицу длины? А точно так же, как и время: мы берем меньшую единицу длины и считаем, сколько таких единиц укладывается в большей. Таким методом мы сможем измерять все меньшие и меньшие длины.
Однако под расстоянием мы понимаем не только то, что можно измерить метром. Как, например, измерить метром расстояние между вершинами двух гор? Здесь на помощь приходит уже другой метод измерения расстояний — триангуляция. Хотя это означает использование другого определения понятия «расстояние», но в тех случаях, когда есть возможность применить оба метода, они дают одинаковый результат. Пространство все же более или менее соответствует представлениям Евклида, поэтому оба определения эквивалентны. Ну, а раз они согласуются на Земле, то мы более уверены в законности применения триангуляции и для больших расстояний. Этим методом была измерена, например, высота первого спутника (фиг. 5.4).
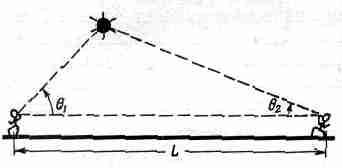
Фиг. 5.4. Определение высоты искусственного спутника методом триангуляции.
Она оказалась равной приблизительно 5·105 м. При большей тщательности измерений тем же самым методом определялось расстояние до Луны. Направления двух телескопов в различных точках Земли дают два необходимых угла. Оказалось, что Луна удалена от нас на расстояние 4·108 м. Однако для Солнца таких измерений провести нельзя, по крайней мере до сих пор никому не удавалось. Дело в том, что точность, с которой можно сфокусировать телескоп на данную точку Солнца и с которой можно измерить углы, не достаточна для вычисления расстояния до Солнца. Как же все-таки определить его? Необходимо как-то расширить принцип триангуляции. Астрономические наблюдения позволяют измерить относительное расстояние между планетами и Солнцем и определить их относительное расположение. Таким образом, мы получаем план солнечной системы в неизвестном масштабе. Чтобы определить масштаб, требуется только абсолютное расстояние, которое было найдено многими различными способами. Один из способов, считавшийся до самого последнего времени наиболее точным, заключается в определении расстояния от Земли до Эроса — малой планеты, которая по временам проходит недалеко от Земли. С помощью триангуляции можно определить расстояние до этого небольшого объекта и получить необходимый масштаб. Зная относительные расстояния, можно определить, например, все абсолютные расстояния от Земли до Солнца или до планеты Плутон.
В последний год достигнуты большие успехи в определении масштаба солнечной системы. В Лаборатории ракетных двигателей с помощью прямой радиолокационной связи были проведены очень точные измерения расстояния от Земли до Венеры. Здесь мы имеем дело еще с одним определением понятия «расстояние». Нам известна скорость распространения света (а стало быть, и скорость распространения радиоволн), и мы предполагаем, что эта скорость постоянна на всем протяжении между Землей и Венерой. Послав радиоволну по направлению к Венере, мы считаем время до прихода обратно отраженной волны. А зная время и скорость, мы получаем расстояние.
А как измерить расстояние до еще более отдаленных объектов, например до звезд? К счастью, здесь снова можно возвратиться к нашему методу триангуляции, ибо движение Земли вокруг Солнца позволяет измерить расстояние до объектов, находящихся вне солнечной системы. Если мы направим телескоп на некую звезду один раз зимой, а другой раз летом (фиг. 5.5), то можно надеяться достаточно точно измерить углы и определить расстояние до этой звезды.
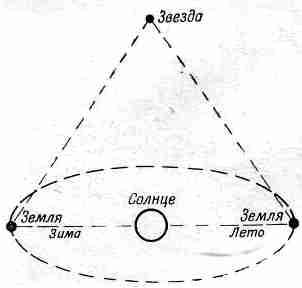
Фиг. 5.5. Определение расстояния до ближайшей звезды методом триангуляции.
В качестве базы используется диаметр орбиты Земли.
Но что делать, если звезда находится настолько далеко от нас, что уже невозможно пользоваться методом триангуляции? Астрономы всегда изобретают все новые и новые способы определения расстояний. Так, они научились определять размер и яркость звезд по их цвету. Оказалось, что цвет и истинная яркость многих близлежащих звезд, расстояние до которых определялось методом триангуляции, в большинстве случаев связаны между собой гладкой зависимостью. Если теперь измерить цвет отдаленной звезды, то по этой зависимости можно определить ее истинную яркость, а измеряя видимую яркость звезды (вернее, по тому, насколько звезда нам кажется тусклой), можно вычислить расстояние до нее. (Для данной истинной яркости видимая яркость уменьшается как квадрат расстояния.) Правильность этого метода нашла неожиданное подтверждение в результатах измерений, проведенных для группы звезд, известных под названием «шарового скопления». Фотография этой группы звезд приведена на фиг. 5.6.

Фиг. 5.6. Скопление звезд вблизи центра нашей Галактики, удаленное от нас на расстояние 30 000 световых лет, или около 3·1020 м.
Достаточно взглянуть на фотографию, чтобы убедиться, что все эти звезды расположены в одном месте. Тот же результат получается и с помощью метода сравнения цвета и яркости.
Изучение многих шаровых скоплений дает еще одну важную информацию. Оказалось, что существует участок неба с большой концентрацией таких шаровых скоплений, причем большинство из них находится на одном и том же расстоянии от нас. Сравнивая эти данные с некоторыми другими, мы приходим к заключению, что эти скопления являются центром нашей Галактики. Таким образом мы определяем, что расстояние до центра Галактики составляет приблизительно 1020 м.
Данные о размере нашей Галактики дают ключ к определению еще больших межгалактических расстоянии. На фиг. 5.7 приведена фотография галактики, которая по форме очень похожа на нашу Галактику.

Фиг. 5.7. Спиральная галактика, подобная нашей. Если предположить, что диаметр этой галактики равен диаметру нашей Галактики, та, исходя из ее кажущегося размера, можно подсчитать расстояние; оно оказывается равным 30 миллионам световых лет (3·1023 м).
Возможно, что и размер ее тот же. (Есть еще ряд соображений, согласно которым размеры всех галактик приблизительно одинаковы.) А если это так, то можно узнать расстояние до нее. Мы измеряем угловой размер галактики (т. е. угол, который она занимает на небесном своде), знаем ее диаметр, а стало быть, можем вычислить расстояние. Опять триангуляция!
Недавно с помощью гигантского Паломарского телескопа были получены фотографии неимоверно далеких галактик. Одна из этих фотографий приведена на фиг. 5.8.

Фиг.5.8. Наиболее удаленный от нас объект ЗС295 в созвездии Волопаса (указан стрелкой), который измерялся в 1960 г. с помощью 200-дюймового телескопа.
Сейчас полагают, что расстояние до некоторых из них приблизительно равно половине размера Вселенной (1026 м) — наибольшего расстояния, которое можно себе представить!
§ 7. Малые расстояния
Обратимся теперь к малым расстояниям. Подразделить метр просто. Без особых трудностей можно разделить его на тысячу равных частей. Таким же путем, хотя и несколько сложнее (используя хороший микроскоп), можно разделить миллиметр на тысячу частей и получить микрон (миллионную долю метра). Однако продолжать это деление становится трудно, поскольку невозможно «увидеть» объекты, меньшие, чем длина волны видимого света (около 5·10-7 м).
Все же мы не останавливаемся на том, что недоступно глазу. С помощью электронного микроскопа можно получить фотографии, помогающие увидеть и измерить еще меньшие объекты — вплоть до 10-8м (фиг. 5.9).
Фиг. 5.9. Фотография вирусов, полученная с помощью электронного микроскопа. Видна «большая» сфера, показанная для сравнения: диаметр ее равен 2·10-7 м, или 2000 Е.
А с помощью косвенных измерений (своего рода триангуляции в микроскопическом масштабе) можно измерять все меньшие и меньшие объекты. Сначала из наблюдений отражения света короткой длины волны (рентгеновских лучей) от образца с нанесенными на известном расстоянии метками измеряется длина волны световых колебаний.
Затем по картине рассеяния того же света на кристалле можно определить относительное расположение в нем атомов, причем результат хорошо согласуется с данными о расположении атомов, полученными химическим путем. Таким способом определяется диаметр атомов (около 10-10 м).
Дальше в шкале расстояний имеется довольно большая незаполненная «щель» между атомными размерами 10-10 м и в 105 раз меньшими ядерными размерами (около 10-15 м). Для определения ядерных размеров применяются уже совершенно другие методы: измеряется видимая площадь s, или так называемое эффективное поперечное сечение, Если же мы хотим определить радиус, то пользуемся формулой s = pr2, поскольку ядра можно приближенно рассматривать как сферические.
Эффективные сечения ядер можно определить, пропуская пучок частиц высокой энергии через тонкую пластинку вещества и измеряя число частиц, не прошедших сквозь нее. Эти высокоэнергетические частицы прорываются сквозь легкое облачко электронов, но при попадании в тяжелое ядро останавливаются или отклоняются. Предположим, что у нас имеется пластинка толщиной 1 см. На такой толщине укладывается приблизительно 108 атомных слоев. Однако ядра настолько малы, что вероятность того, что одно ядро закроет другое, очень незначительна. Можно себе представить, что высокоэнергетическая частица, налетающая на пластинку углерода толщиной 1 см, «видит» приблизительно то, что в сильно увеличенном масштабе показано на фиг. 5.10.

Фиг. 5.10. Воображаемая пластинка углерода толщиной 1 см при сильном увеличении (если бы были видны только ядра атомов).
Вероятность того, что очень малая частица столкнется с ядром, равна отношению площади, занимаемой ядрами (черные точки), к общей площади рисунка. Пусть над областью с площадью А по всей толщине пластинки находится N атомов (разумеется, каждый с одним ядром). Тогда доля площади, закрытая ядрами, будет равна Ns/А. Пусть теперь число частиц в нашем пучке до пластинки будет равно n1, а после нее равно n2; тогда доля частиц, не прошедших через пластинку, будет (n1-n2)/n1, что должно быть равно доле площади, занимаемой ядрами. Радиус же ядер вычисляется из равенства
Из таких экспериментов мы находим, что радиусы ядер лежат в пределах от 1·10-15 до 6·10-15 м. Кстати, единица длины 10-15 м называется ферми в честь Энрико Ферми (1901—1958).
Что можно ожидать в области еще меньших расстояний? Можно ли их измерять? На этот вопрос пока еще нет ответа. Может быть, именно здесь, в каком-то изменении понятия пространства или измерения на малых расстояниях, кроется разгадка тайны ядерных сил.
Несколько слов о стандарте длины. Разумно в качестве стандарта использовать какую-то естественную единицу длины, например радиус Земли или некоторую его долю. Именно таким образом возник метр. Первоначально он определялся как (p/2)·10-7 доля радиуса Земли. Однако такое определение нельзя считать ни особенно точным, ни удобным. Поэтому в течение долгого времени по международному соглашению в качестве эталона метра принималась длина между двумя метками, сделанными на особом брусе, который хранится в специальной лаборатории во Франции. Только много позднее поняли, что и такое определение метра не столь уж точно, как это необходимо, и не так уж универсально и постоянно, как этого хотелось бы. Поэтому сейчас принят новый стандарт длины как некоторое заранее установленное число длин волн определенной спектральной линии.
· · ·
Результаты измерения расстояний и времени зависят от наблюдателя. Два наблюдателя, движущиеся друг относительно друга, измеряя один и тот же предмет или длительность одного и того же процесса, получат разные значения, хотя, казалось бы, мерили одно и то же. Расстояния и интервалы времени в зависимости от системы координат (т. е. системы отсчета), в которой производят измерения, имеют различную величину. В последующих главах мы будем более подробно разбирать этот вопрос.
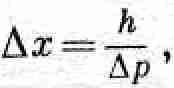
Законы природы не позволяют выполнять абсолютно точные измерения расстояний или интервалов времени. Мы уже упоминали ранее, что ошибка в определении положения предмета не может быть меньше, чем
где h — малая величина, называемая «постоянной Планка», а Dр — ошибка в измерении импульса (массы, умноженной на скорость) этого предмета. Как уже говорилось, эта неопределенность в измерении положения связана с волновой природой частиц.
Относительность пространства и времени приводит к тому, что измерения интервалов времени также не могут быть точнее, чем
где DЕ — ошибка в измерении энергии того процесса, продолжительностью которого мы интересуемся. Чтобы знать более точно, когда что-то произошло, мы вынуждены довольствоваться тем, что меньше знаем, что же именно произошло, поскольку наши знания об энергии, участвующей в процессе, будут менее точными. Эта неопределенность времени, так же как и неопределенность положения, связана с волновой природой вещества.
* Об этом ученые договорились в конце 1964 г., когда готовилось русское издание этой книги.— Прим. ред.
* Это равенство справедливо только тогда, когда площадь, занимаемая ядрами, составляет малую долю общей площади, т. е. (n1-n2)/n1 много меньше единицы. В противном же случае необходимо учитывать поправку на частичное «загораживание» одного ядра другим.

(возвращение к теме)
Я вполне осознаю, что понятие смыслового принципа «квадрата времени» несколько затруднено для восприятия читателями. Поверьте, что не менее сложно это понятие изложить. И для попыток интеллектуального проникновения в сущность этого принципа необходима изрядная доля интереса, интуиции и внимательной сосредоточенности.
Для меня также совершенно понятно, что неким препятствием для привлечения сосредоточенного внимания и интеллектуального проникновения в это понятие в известной мере служит так называемый «феномен социального кумира». То есть, если бы об этом принципе «квадрата времени» говорил какой-либо научный деятель, обладающий неоспоримым авторитетом в обществе, то его объяснения непременно привлекли бы и интерес, и внимание, и сосредоточение. Ибо, в этом случае всё сказанное было бы принято на веру без интеллектуального проникновения в сущность сказанного.
Несмотря на то, что я не научный деятель, обладающий таким общественным авторитетом, я всё-таки решил ещё раз затронуть тему, поднятую мной в статье «Смысловой принцип квадрата или «квадрат времени». Ибо, в конце концов, никому не возбраняются интеллектуальные попытки проникновения в тайны мировосприятия, миропонимания и мировоззрения.
При этом я особо хочу подчеркнуть, что эта тема относится именно к сфере мировоззрения, а совсем не к сфере математики.
Я напомню вам изображение этого «квадрата времени».

Обращаю ваше внимание на то, что сумма трёх чисел по любому направлению равняется числу 15. Цифровой синтез смыслов которого равен числу 6.
При этом замечу, что это только принцип.
Несмотря на то, что этот феномен не математический, он может быть выражен математически. Что и сделал в форме теоремы Пьер Ферма в 1637 году. То есть, сформулировал математическое выражение смыслового принципа квадрата – для любого натурального числа n > 2 уравнение an+ bn= cnне имеет натуральных решений a,b и c. О чём я упоминал в статье «Всесильна ли «царица» всех наук?».
Причём, в этой формуле при n = 2, число 2 означает два смысловых линейных единообразия. А все значения числа n > 2, это так сказать «от лукавого». Вот это «от лукавого» и пытался доказать российский математик Перельман.
Иными словами, двухтактное время разворачивает точку в два смысловых линейных единообразия, представляющих в пространстве двух степеней мерности смысловой квадрат времени.
Далее я представлю вам некое объёмное изображение, которое я также уже упоминал в статье «Смысловой принцип квадрата или «квадрат времени». И которое демонстрирует процесс разворачивания двух смысловых линейных единообразий в пространстве трёх степеней мерности.

Вот так два смысловых линейных единообразия разворачиваются в трёхмерном пространстве. Образуя своеобразный куб материального бытия – инкубатор. (N.b. ин – куб – АТ – ОР).
Обратите внимание на то, что линейная сумма любых трёх чисел в каждой из трёх степеней мерности составляет число 15, цифровой синтез смыслов которого равен числу 6.
То есть, материальное бытие существует внутри трёхмерного пространства (куба), определяемого числом зверя – 666. Числом, которое также называется числом человеческим.
Кстати сказать, в нынешнее время человеческая цивилизация считается очень развитой, а каждый её представить считает себя если не высоким интеллектуалом, то, по крайней мере, человеком весьма неглупым. И в то же время, как всё человечество, так отдельные его представители до сих пор не могут проникнуть в сущность того, что было сформулировано в далёкие незапамятные времена. Вот и попытайте теперь возразить, что эта интеллектуальная немощь не очевидное проявление некоего феномена, который называется человеческой гордыней разума. А ведь эта гордыня разума и есть не что иное, как свидетельство всеобщего понижения человеческого интеллекта в результате всеобщей деградации человечества и дегенерации самого человека.
Теперь об обобщённой категории меры времени.
Ни для кого не является секретом, что обобщёнными категориями меры пространства являются длина, ширина и высота.
А вы никогда не задумывались, как называется обобщённая категория меры времени? Ведь она называется угол (N.b. у – ГО – Л). О чём я также уже упоминал в статье «Алмазная психология порока».
И это должно быть для вас очевидно, поскольку мы исчисляем время по мере угла поворота часовых стрелок, идущих по кругу.
Несмотря на то, что часовая стрелка проходит по кругу дважды – 2х12, общий полный круг времени оборота Земли вокруг своей оси, всё-таки, составляет 24 часа.
В то же время мы знаем, что полный круг пространства составляет 360 угловых градусов. А названия дробных единиц измерения углов в круге и названия дробных единиц измерения времени на часовом циферблате полностью совпадают – секунды и минуты.
Название же главной единицы измерения времени человеческого бытия – час – не совпадает с названием главной единицы углового измерения в круге – градус. Тогда вычислим, а сколько же угловых градусов пространства содержится в одном часе времени.
360 : 24 = 15 (!)
Таким образом, каждый час составляет 15 градусов пространства (в цифровом смысловом синтезе 6). А это совпадает с линейными показателями сумм и их цифровых синтезов, которые мы видели в изображении смыслового квадрата.
Следовательно, мы исчисляем время по принципу смыслового квадрата.
Поскольку же пространство мы измеряем посредством времени, то в сфере его пространства (т.е. пространства времени) естественно действует тот же принцип смыслового квадрата.
На основании изложенного вполне правомерно сделать вывод, что любой предмет, двигаясь в трёхмерном пространстве времени, в каждый данный момент времени может совершать своё перемещение только (и всего лишь) в двух степенях. То есть, вектор его перемещения всегда определяется лишь двумя степенями. И при любых изменениях направления движения в процессе такого изменения меняется лишь подбор двух степеней ориентации из трёх. Таким образом, изменение вектора движения материального тела в пространстве времени непрерывно изменяет сами двуединые линейные пространственные координаты материального тела. То есть, для движущегося в пространстве времени материального тела постоянно меняется координационная структура пространства. И это непреложный закон смыслового квадрата времени физического существования материального мира в трёхмерном пространства времени.
Для тех, кому трудно это представить и кому до сих пор в это не верится, я продемонстрирую явление этого феномена на примере часового циферблата. На котором очень наглядно показан принцип двух линейных единообразий. То есть, смысловой принцип квадрата времени.
Когда-то, очень давно я вдруг совершенно интуитивно осознал, что часовой циферблат, это штука несоизмеримо более сложная, чем сам часовой механизм. И что этот циферблат содержит в себе какие-то основополагающие тайны нашего бытия.
Я полагаю, что конструктор циферблата начинал не с чисел, а со смыслов. Смысл полного углового размера пространства времени он обозначил следующими символами цифр:
– 3 = триединство Бога, как основополагающий принцип бытия;
– 6 = область материального бытия;
– 0 = пространство времени;
Таким образом, полный угловой размер пространства времени был обозначен этими цифровыми символами – 360. И основная единица измерения угла (у – ГО – Л) была названа градус.
Далее число полного углового размера пространства времени было разделено на числовой линейный размер смыслового квадрата времени.
360 : 15 = 24
Этими расчётами был определён числовой угловой размер одного оборота Земли вокруг своей оси. Основная единица этого измерения оборота Земли, предназначенная для человека, была названа час, состоящий из 15 угловых градусов.
Далее был необходим некий материальный числовой инструмент для этих измерений. Был сконструирован круговой часовой циферблат.
Казалось бы, что остальное всё просто. Взять 24 часа и равномерно распределить их по круговому циферблату. Однако конструктор пошёл по иному пути. Он разделил 24 часа на две половины по 12 часов каждая. И на одном круге часового циферблата разместил обе половины, наложив одну на другую.
То есть, стрелка, указывающая числовое значение часового угла, при первом обороте указывала числовые значения первой половины из 24-х часов. А при втором обороте – числовые значения второй половины.
Интересно, для чего было сделано такое усложнение. И какую цель оно преследовало. Давайте посмотрим.
Сложим числовые значения первого круга.
1+2+3+4+5+6+7+8+9+10+11+12 = 78
Цифровой синтез смыслов – 15 = 6.
Теперь сложим числовые значения второго круга.
13+14+15+16+17+18+19+20+21+22+23+24 = 222
Цифровой синтез смыслов – 6.
Таким образом, конструктор часового циферблата зафиксировал в своей конструкции смысловой принцип квадрата времени. И отразил смысловой принцип двух линейных единообразий материального бытия в пространстве времени на круговом часовом циферблате.
В.П. Белоусов
Чтобы оставить комментарий Вы можете или зарегистрироваться, или войти, или прокомментировать статью с Вашим ip-адресом.