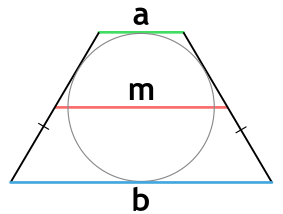
Определения
Трапеция — это такой четырехугольник, у которого две стороны параллельны (они являются основаниями трапеции, указанные на рисунках a и b), а две другие — нет.
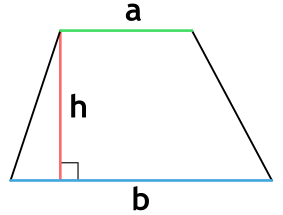
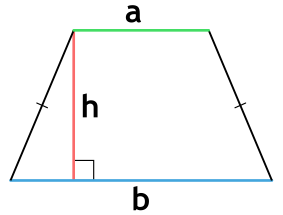
Высота трапеции — это такой отрезок h, который проведен перпендикулярно основаниям.
Нахождение высоты по площади и основаниям
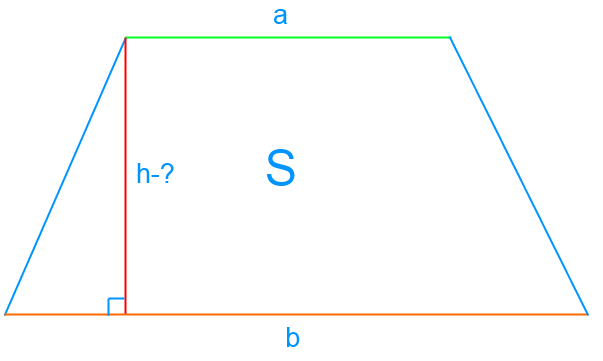
Чтобы вычислить площадь S трапеции мы используем формулу:
[S=frac{((a+b) times h)}{2}]
Здесь h — высота трапеции, а сегменты a и b являются ее основаниями.
Можем найти h:
[h=frac{2 times S}{(a+b)}]
Пример 1
Площадь трапеции S составляет 50 см2, длина ее основания a = 4 см, длина второго основания b равна 6 см, то для нахождения высоты h мы используем формулу:
[h=frac{2 times 50}{(4+6)}=10 mathrm{~cm}]
Ответ: 10 см.
Нахождение высоты, зная площадь и среднюю линию
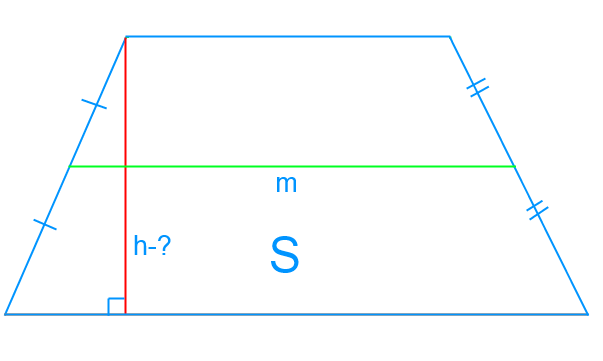
Мы используем формулу, с помощью которой можно рассчитать площадь трапеции:
S = m × h,
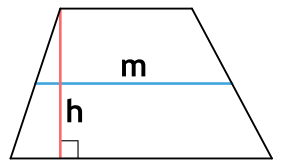
Здесь h — это высота трапеции, m — ее средняя линия.
Можем найти h:
[h=frac{S}{m}], будет ответом.
Пример 2
Средняя линия трапеции, обозначенная буквой m, равна 20 см, а площадь S, которая составляет 200 см2. Давайте найдем значение высоты трапеции h.
[h=frac{200}{20}=10 mathrm{~cm}]
Ответ: 10 см
Высота прямоугольной трапеции
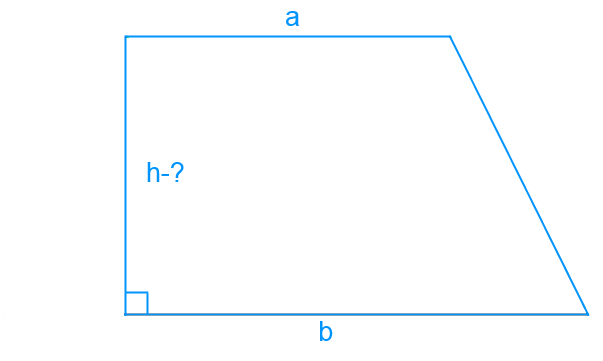
Определение
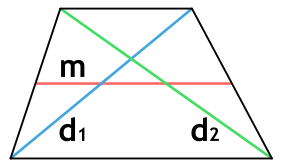
Диагональ — это сегмент, соединяющий пару противоположных вершин трапеции. Когда трапеция прямоугольная, используя диагональ, мы находим высоту данной фигуры.
Трапецию, одна из боковых сторон которой перпендикулярна основаниям, называют прямоугольной трапецией.
Таким образом, рассмотрим подобную трапецию ABCD, где AD — высота, AC — диагональ, DC-основание. Мы используем теорему Пифагора, которая говорит, что в прямоугольном треугольнике ADC квадрат гипотенузы AC равен сумме квадратов его сторон — катетов AB и BC.
Тогда мы сможем написать:
AC² = AD² + DC².
AD — это катет треугольника, сторона трапеции и, одновременно, ее высота. Так как отрезок перпендикулярен основаниям. Длина катета будет находиться как:
[A D=sqrt{left(A C^{2}-D C^{2}right)}]
Таким образом, у нас есть формула, которая поможет при вычислении найти высоту трапеции AD.
Пример 3
Основания трапеции с прямым углом(DC) равно 14 см, а ее диагональ (AC) равна 15 см, мы будем использовать теорему Пифагора для получения высоты (сторона AD).
Пусть x — неизвестная часть прямоугольного треугольника (AD), тогда
[A C^{2}=A D^{2}+D C^{2}] может быть записан
[15^{2}=14^{2}+x^{2}]
[x=sqrt{left(15^{2}-14^{2}right)}=sqrt{(225-196)}=sqrt{29} mathrm{см}]
Ответ: [sqrt{29} mathrm{см}], что составляет приблизительно 5,385 см
Нет времени решать самому?
Наши эксперты помогут!
Нахождение высоты через стороны
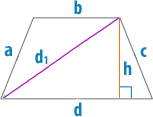
Существует еще один способ найти высоту — через стороны. Помимо высоты в трапеции стоит провести также ее диагональ, которая образует треугольник с прямым углом и даст возможность найти высоты несколькими различными способами через различные треугольники.
Если выразить все длины сторон таких треугольников через стороны трапеции и привести подобные слагаемые, то получится следующая формула:
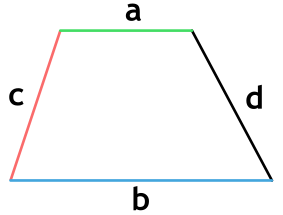
[mathrm{h}=sqrt{C^{2}-left(frac{(a-b)^{2}+e^{2} d^{2}}{2(a-b)}right)^{2}}]
Пример 4
Дана трапеция, в ней известны основания a и b. Эти основания соответственно равны 4,5 см и 2,5 см. Известны и ее боковые стороны d и c, которые равны 2 см и используем формулу:
[h=sqrt{2^{2}-left(frac{(4,5-2,5)^{2}+2^{2}-2 sqrt{2}^{2}}{2(4,5-2,5)}right)^{2}}=sqrt{4}=2 см]
Ответ: h=2 см.
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту трапеции, а также разберем примеры решения задач для закрепления материала.
Напомним, высотой трапеции называется отрезок, соединяющий оба ее основания и перпендикулярный им.
-
Нахождение высоты трапеции
- Через длины сторон
- Через боковую сторону и прилежащий угол
- Через диагонали и угол между ними
- Через площадь
- Примеры задач
Нахождение высоты трапеции
Через длины сторон
Если известны длины всех четырех сторон трапеции, ее высота рассчитывается по формуле ниже:
Через боковую сторону и прилежащий угол
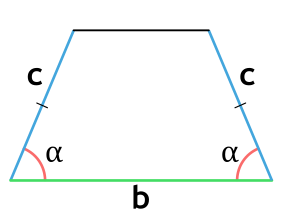
Высоту трапеции можно вычислить, если знать длину любой из ее боковых сторон и значение прилежащего к ней и основанию угла.
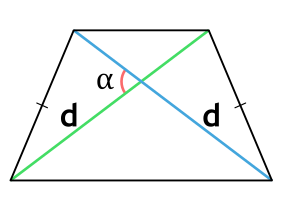
Через диагонали и угол между ними
Зная длину оснований трапеции, а также диагоналей и угол между ними, вычислить высоту удастся по формуле:
Если сумму оснований заменить длиной средней линии (m), то формула будет выглядеть следующим образом:
Средняя линия трапеции (m) равняется полусумме ее оснований, т.е m = (a+b)/2.
Через площадь
Высоту трапеции можно вычислить, если известны ее площадь и длины оснований (или средней линии).
Примечание: формулы для нахождения высоты равнобедренной и прямоугольной трапеций представлены на нашем сайте в отдельных публикациях.
Примеры задач
Задание 1
Найдите высоту трапеции, если ее основания равны 9 и 6 см, а боковые стороны – 4 и 5 см.
Решение
Т.к. у нас есть длины всех сторон, мы можем воспользоваться первой формулой для вычисления требуемого значения:
Кстати, т.к. высота равна одной из боковой сторон трапеции, значит она является прямоугольной.
Задание 2
Площадь трапеции равна 26 см2. Найдите ее высоту, если основания равны 10 и 3 см.
Решение
В данном случае можно применить последнюю из рассмотренных формул:
математика — Найти квадрат высоты трапеции
|
0 |
Трапеция ABCD с основаниями BC=4 и AD=5 вписана в окружность. Продолжение средней линии MN трапеции за точку M пересекает окружность в точке K. Найдите квадрат высоты трапеции, если MK=1. математика задача геометрия
задан Clarkkent 71% принятых изменен Deleted Аналогичная задача была разобрана здесь. (27 Ноя ’13 15:46)
|
Знаете, кто может ответить? Поделитесь вопросом в Twitter или ВКонтакте.
Ваш ответ
Если вы не нашли ответ, задайте вопрос.
Здравствуйте
Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Присоединяйтесь!
регистрация »
отмечен:
математика
×4,435
геометрия
×3,291
задача
×575
задан
27 Ноя ’13 15:39
показан
1466 раз
обновлен
27 Ноя ’13 15:46
Связанные исследования
Модель многомерного пространства и его необычные свойства
Конвертирование из MathType в (La)Tex
Непознанный угольник
Связанные вопросы
0
Задача по геометрий
0
Правильно ли нарисовано задачи по условию , решать не надо
0
Задача по геометрии (желательно с картинкой!!!!)
0
Как расположены проекций отрезков
0
Задача про вписанный параллелограмм
2
Чему равен радиус сферы?
0
Наведите на решение, не совсем понимаю как решать
0
Дайте идею к решению задачи
2
Найти углы смежные (при стороне) к стороне
0
Помогите, не совсем пойму
Отслеживать вопрос
по почте:
Зарегистрировавшись, вы сможете подписаться на любые обновления
по RSS:
Ответы
Ответы и Комментарии
Трапецией принято называть выпуклую четырёхугольную четырехугольник с парой параллельных и двумя не
параллельными сторонами. Отрезки, которые создают параллельные прямы называются «основанием
трапеции», две других стороны играют роль «боковой стороны трапеции». Средняя линия трапеции будет
соединять два центра боковых сторон.
- Высота трапеции через боковую сторону и прилегающий угол
при основании - Высота трапеции через площадь и длины оснований
- Высота трапеции через площадь и среднию линию
- Высота трапеции через основании, диагонали и угол между
диагоналями - Высота трапеции через среднию линию, диагонали и угол между
диагоналями
Как найти высоту при помощи боковой стороны и прилегающего угла при основании
Для вычисления высоты трапеции через боковую сторону и прилегающий угол при основании нужно
воспользоваться нижеприведенной формулой:
h = a · sin α
где h — это искомая высота трапеции, a — известная боковая сторона, sin α — угол
при основании.
Цифр после
запятой:
Результат в:
Пример. Чтобы разобраться с применением формулы, давайте рассмотрим пример. Дана
некая трапеция. Нам известно, что боковая сторона равна 10 сантиметрам, а прилегающих угол
составляет 30 гр. Нам нужно найти высоту данной трапеции. Для решения у нас есть вся нужная
информация и формула выше. Подставляем значения в формулу: h = a · sin, h = 10 · sin 30, h = 10 · 1/2, h = 5 см
Как найти высоту трапецию при помощи длины основания и площади трапеции
Чтобы найти высоту трапеции через известные длины основания и площадь, нужно воспользоваться
формулой:
h = (2S) / (a + b)
где h — это искомая высота трапеции, S — известная площадь фигуры, a и b — длины
обеих оснований.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: Нам известно, что в трапеции АВСD основания a и b равны
5 и 10 сантиметров. Площадь фигуры равна 30 квадратных сантиметров. Для решения нужно
воспользоваться формулой. h = (2S) / (a + b), h = (2 х 30) / (5 + 10), h = 60 /15, h = 4 см.
Высота трапеции равна 4 см.
Как найти высоту при помощи диагоналей, углу между диагоналями и средней линией трапеции
Чтобы найти высоту трапеции через среднюю линию, известные диагонали и угол между ними, нужно
прибегнуть к применению выведенной формулы:
h = ((D x d) / (2m)) x sin (α)
где h — это искомая высота трапеции, D и d — известные диагонали, m — средняя
линия, sin(α) — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: Дана трапеция с диагоналями 5 и 12 сантиметров.
Известно, что средняя линия фигуры равна 6 см, а угол между диагоналями – 30 градусов. Применив
формулу выше, мы сможем с легкостью найти высоту трапеции. h = ((D x d) / (2m)) x sin (α), h = ((5 x 12) / (2 х 6)) x sin (30), h = (60 /12) x 0.5, h = 2.5 см.
Высота трапеции равна 2.5 см.
Как найти высоту при помощи средней линии и площади трапеции
Чтобы найти высоту трапеции через площадь и среднюю линию воспользуемся выведенной формулой:
h = (2S) / m
где h — это искомая высота трапеции, S — известная площадь фигуры, а m — средняя
линия.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: Площадь произвольной трапеции составляет 30 квадратных
сантиметров. Средняя линия фигуры равна 5 см. Нужно найти высоту по формуле. h = (2S) / m, h = (2 х 30) / 5, h = 60 / 5, h = 12 см. 12
см – высота трапеции.
Как найти высоту при помощи известного основания, диагоналей трапеции и угла между диагоналями
Для нахождения высоты трапеции при помощи известного основания, диагонали и углу между диагоналями
используют нижеприведенную формулу:
h = ((Dd) / (a + b)) x sin (α)
где h — это искомая высота трапеции, D и d — известные диагонали, a и b — длины
обеих оснований, sin(α) — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: В трапеции ABCD диагонали равны 10 см каждая. Известно,
что сумма основ фигура равна 20 см. Угол, созданный между диагоналями – 30 градусов. Нужно найти
высоту. Для этого нужно воспользоваться выше предоставленной формулой. h = ((Dd) / (a+b)) x sin (α), h = ((10 х 10) / (20)) x sin (30), h = 5 x sin (30), h = 2.5 см.
Высота трапеции равна 2.5 см
Можно выделить 2 разновидности трапеции:
- Трапеция, в которой одна из боковых сторон лежит под перпендикулярным углом с обеими основами
называется прямоугольной. - Трапеции с равными боковыми сторонами называется равнобедренной.
Высотой трапеции принято называть отрезок, которой показывает самое короткое расстояние между верхним
и нижним основанием фигуры. Существует большое количество математических задач разного уровня
сложности, для решения которых активно применяют высоту. Стоит разобраться со всеми возможными
формулами, которые используются для нахождения высоты трапеции.

{S = dfrac{1}{2} (a + b) cdot h}
Площадь трапеции можно найти множеством способов. Для вас мы собрали все возможные варианты нахождения площади. Для вашего удобства для каждой формулы создан калькулятор, который поможет рассчитать площадь трапеции по известным данным. От вас требуется только подставить значения и в режиме онлайн мгновенно получить ответ. Формулы и калькуляторы сгруппированы по типам трапеций — обычная, равнобедренная (равнобокая).
- Калькулятор площади трапеции
- Площадь трапеции
- через основания и высоту
- через среднюю линию и высоту
- через диагонали и среднюю линию
- через 4 стороны
- через диагонали и угол между ними
- через основания и углы при основании
- через площади треугольников
- через диагонали и высоту
- через радиус вписанной окружности и основания
- через перпендикулярные диагонали
- Площадь равнобедренной (равнобокой) трапеции
- через основания и высоту
- через 3 стороны (формула Брахмагупты)
- через верхнее основание, боковую сторону и угол при нижнем основании
- через нижнее основание, боковую сторону и угол при нижнем основании
- через основания и угол
- через диагонали и угол между ними
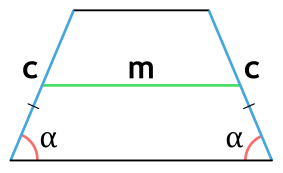
- через боковую сторону, угол при основании и среднюю линию
- через радиус вписанной окружности и угол при основании
- Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
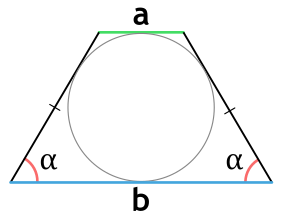
- через высоту (диаметр вписанной окружности) и угол при основании
- через основания и угол при основании
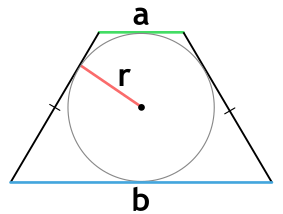
- через основания и радиус вписанной окружности
- через основания
- через основания и боковую сторону
- через основания и среднюю линию
- Примеры задач
Площадь трапеции
Трапеция — выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Площадь трапеции через основания и высоту
{S = dfrac{1}{2} (a + b) cdot h}
a и b — основания трапеции
h — высота, проведенная к основанию
Площадь трапеции через среднюю линию и высоту
{S = m cdot h}
m — средняя линия трапеции
h — высота трапеции
Площадь трапеции через диагонали и среднюю линию
{S = sqrt{p(p-d_1)(p-d_2)(p-2m)}}
{p = dfrac{d_1+d_2+2m}{2}}
d1 и d2 — диагонали трапеции
m — средняя линия трапеции
Площадь трапеции через 4 стороны
{S = dfrac{a+b}{2} sqrt{c^2 — {Big( dfrac{(a-b)^2 + c^2 — d^2}{2(a-b)} Big)}^2}}
a, b, c и d — стороны трапеции
Площадь трапеции через диагонали и угол между ними
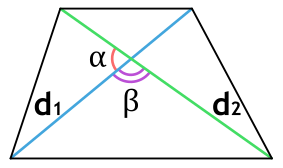
{S = dfrac{d_1 cdot d_2}{2}cdot sin(alpha); S = dfrac{d_1 cdot d_2}{2}cdot sin(beta)}
d1 и d2 — диагонали трапеции
α или β — угол между диагоналями трапеции
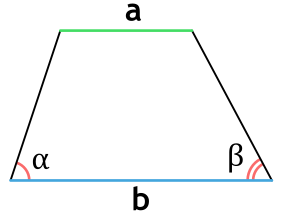
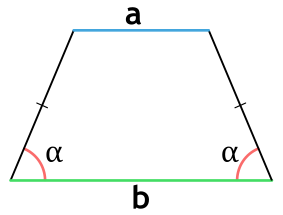
Площадь трапеции через основания и углы при основании
{S = dfrac{b^2 — a^2}{2} cdot dfrac{sin(alpha) cdot sin(beta)}{sin(alpha + beta)}}
a и b — основания трапеции
α или β — прилежащие к основанию трапеции углы
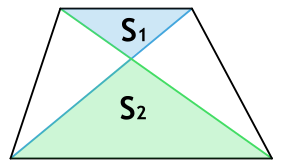
Площадь трапеции через площади треугольников
{S = (sqrt{S_1} + sqrt{S_2})^2}
S1 и S2 — площади образованных пересечением диагоналей трапеции треугольников
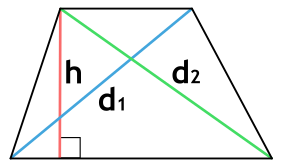
Площадь трапеции через диагонали и высоту
{S = dfrac{sqrt{{d_2}^2-h^2}+sqrt{{d_1}^2-h^2}}{2} cdot h}
d1 и d2 — диагонали трапеции
h — высота трапеции
Площадь трапеции через радиус вписанной окружности и основания
{S = (a+b)cdot r}
a и b — основания трапеции
r — радиус вписанной в трапецию окружности
Площадь трапеции через перпендикулярные диагонали
{S = dfrac{1}{2} cdot d_1 cdot d_2}
d1 и d2 — перпендикулярные диагонали трапеции
Площадь равнобедренной (равнобокой) трапеции
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
Площадь равнобедренной трапеции через основания и высоту
{S = dfrac{a+b}{2} cdot h}
a и b — основания равнобедренной трапеции
h — высота, проведенная к основанию равнобедренной трапеции
Площадь равнобедренной трапеции через 3 стороны (формула Брахмагупты)
{S = sqrt{(p-a)(p-b)(p-c)^2}}
{p = dfrac{a+b+2c}{2}}
a и b — основания равнобедренной трапеции
c — боковая сторона равнобедренной трапеции
Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании
{S = c cdot sin(alpha) cdot (a+c cdot cos(alpha))}
a — верхнее основание равнобедренной трапеции
c — боковая сторона равнобедренной трапеции
α — прилежащие к нижнему основанию трапеции углы
Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании
{S = c cdot sin(alpha) cdot (b-c cdot cos(alpha))}
b — нижнее основание равнобедренной трапеции
c — боковая сторона равнобедренной трапеции
α — прилежащий к нижнему основанию трапеции угол
Площадь равнобедренной трапеции через основания и угол
{S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha)}
a и b — основания равнобедренной трапеции
α — прилежащий к основанию трапеции угол
Площадь равнобедренной трапеции через диагонали и угол между ними
{S = dfrac{1}{2}d^2 cdot sin(alpha)}
a — диагональ равнобедренной трапеции
α — угол между диагоналями равнобедренной трапеции
Площадь равнобедренной трапеции через боковую сторону, угол при основании и среднюю линию
{S = m cdot c cdot sin(alpha)}
m — средняя линия равнобедренной трапеции
c — боковая сторона равнобедренной трапеции
α — угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции через радиус вписанной окружности и угол при основании
{S = dfrac{4r^2}{sin(alpha)}}
r — радиус вписанной окружности
α — угол при основании равнобедренной трапеции
Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
В трапецию можно вписать окружность тогда и только тогда, когда суммы ее противоположных сторон равны.
Площадь равнобедренной трапеции, в которую можно вписать окружность, через высоту (диаметр вписанной окружности) и угол при основании
{S = dfrac{h^2}{sin(alpha)}}
h — высота равнобедренной трапеции
α — угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и угол при основании
{S = dfrac{a cdot b}{sin(alpha)}}
a и b — основания равнобедренной трапеции
α — угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и радиус вписанной окружности
{S = r(a+b); r=dfrac{sqrt{a cdot b}}{2}}
a и b — основания равнобедренной трапеции
r — радиус вписанной окружности
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания
{S = sqrt{a cdot b} cdot dfrac{a+b}{2}}
a и b — основания равнобедренной трапеции
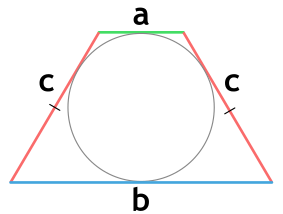
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и боковую сторону
{S = c cdot sqrt{a cdot b}}
a и b — основания равнобедренной трапеции
c — боковая сторона равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и среднюю линию
{S = m cdot sqrt{a cdot b}}
a и b — основания равнобедренной трапеции
m — средняя линия равнобедренной трапеции
Примеры задач на нахождение площади трапеции
Задача 1
Найдите площадь трапеции, если основания равны 6см и 9 см, а высота трапеции равна 5 см.
Решение
Для решения задачи воспользуемся первой формулой.
S = dfrac{1}{2} (a + b) cdot h = dfrac{1}{2} (6 + 9) cdot 5 = dfrac{1}{2} cdot 15 cdot 5 = dfrac{1}{2} cdot 75 = 37dfrac{1}{2} : см^2
Ответ: 37.5 см²
Полученный ответ легко проверить с помощью калькулятора .
Задача 2
Найдите площадь трапеции средняя линия которой равна 18 см, а высота 9 см.
Решение
С решением этой задачи нам поможет вторая формула.
S = m cdot h = 18 cdot 9 = 162 : см^2
Ответ: 162 см²
Воспользуемся калькулятором для проверки результата.
Задача 3
Найдите площадь трапеции диагонали которой равны 10 и 8, а средняя линия равна 3.
Решение
Для решения этой задачи нам поможет третья формула.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{10+8+2 cdot 3}{2} = dfrac{10+8+6}{2} = dfrac{24}{2} = 12
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-10)(12-8)(12-2 cdot 3)} = sqrt{12 cdot 2 cdot 4 cdot 6} = sqrt{576} = 24 : см^2
Ответ: 24 см²
Осталось проверить полученный ответ.
Задача 4
Найдите площадь трапеции диагонали которой равны 17 и 15, а средняя линия равна 4.
Решение
Задача похожа на ту, что мы только что решили. Поэтому повторим шаги.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{17+15+ 2 cdot 4}{2} = dfrac{17+15+8}{2} = dfrac{40}{2} = 20
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{20(20-17)(20-15)(20-2 cdot 4)} = sqrt{20 cdot 3 cdot 5 cdot 12} = sqrt{3600} = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 5
Найдите площадь трапеции диагонали которой равны 8 и 6 а средняя линия равна 5.
Решение
Еще одна типовая задача. Повторим действия как в задачах выше.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{8+6+ 2 cdot 5}{2} = dfrac{8+6+10}{2} = dfrac{24}{2} = 12
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-8)(12-6)(12-2 cdot 5)} = sqrt{12 cdot 4 cdot 6 cdot 2} = sqrt{576} = 24 : см^2
Ответ: 24 см²
Проверка .
Задача 6
Найдите площадь равнобедренной трапеции если её основания равны 5 см и 17 см, а боковая сторона равна 10 см.
Решение
Для решения этой задачи используем формулу Брахмагупты.
Сначала вычислим p:
p = dfrac{a+b+2c}{2} = dfrac{5+17+2 cdot 10}{2} = dfrac{22+20}{2} = dfrac{42}{2} = 21
А теперь можно вычислить площадь трапеции:
S = sqrt{(p-a)(p-b)(p-c)^2} = sqrt{(21-5)(21-17)(21-10)^2} = sqrt{16 cdot 4 cdot 11^2} = sqrt{16 cdot 4 cdot 121} = sqrt{7744}= 88 : см^2
Ответ: 88 см²
Проверка .
Задача 7
Острый угол равнобедренной трапеции равен 45°, а основания равны 8 и 6 см. Найдите площадь трапеции.
Решение
Для решения этой задачи воспользуемся формулой.
S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha) = dfrac{1}{2}(8^2-6^2) cdot tg(45°)
Тангенс 45° = 1, продолжим вычисления:
S = dfrac{1}{2}(8^2-6^2) cdot tg(45°) = dfrac{1}{2}(64-36) cdot 1 = dfrac{1}{2} cdot 28 = 14 : см^2
Ответ: 14 см²
Убедиться в правильности решения нам поможет калькулятор .