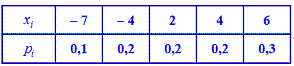
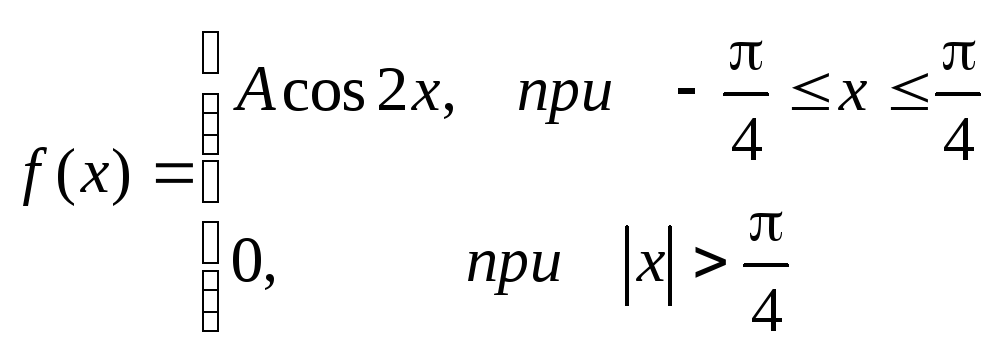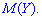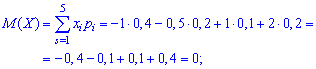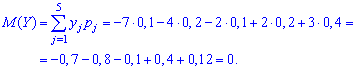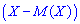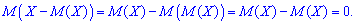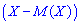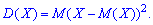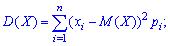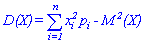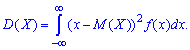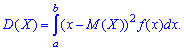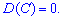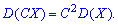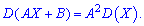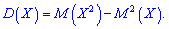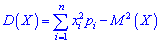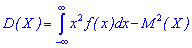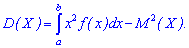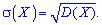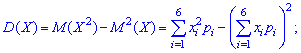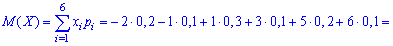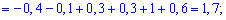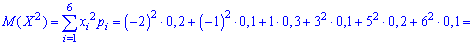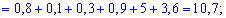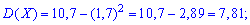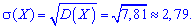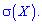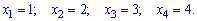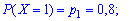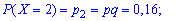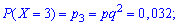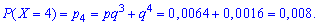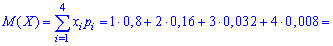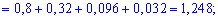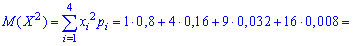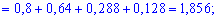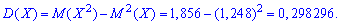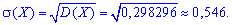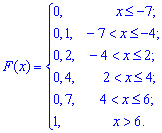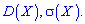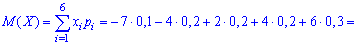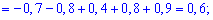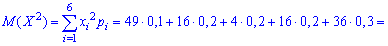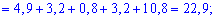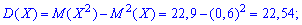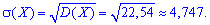Математическое ожидание, дисперсия, среднее квадратичное отклонение
Эти величины определяют некоторое
среднее значение, вокруг которого
группируются значения случайной
величины, и степень их разбросанности
вокруг этого среднего значения.
Математическое ожидание Mдискретной случайной величины — это
среднее значение случайной величины,
равное сумме произведений всех возможных
значений случайной величины на их
вероятности.
Свойства математического ожидания:
-
Математическое ожидание постоянной
величины равно самой постоянной . -
Постоянный множитель можно выносить
за знак математического ожидания . -
Математическое ожидание произведения
двух независимых случайных величин
равно произведению их математических
ожиданий . -
Математическое ожидание суммы двух
случайных величин равно сумме
математических ожиданий слагаемых
Для описания многих практически важных
свойств случайной величины необходимо
знание не только ее математического
ожидания, но и отклонения возможных ее
значений от среднего значения.
Дисперсия случайной величины— мера разброса случайной величины,
равная математическому ожиданию квадрата
отклонения случайной величины от ее
математического ожидания.
.
Принимая во внимание свойства
математического ожидания, легко показать
что
Казалось бы естественным рассматривать
не квадрат отклонения случайной величины
от ее математического ожидания, а просто
отклонение. Однако математическое
ожидание этого отклонения равно нулю.
Это объясняется тем, что одни возможные
отклонения положительны, другие
отрицательны, и в результате их взаимного
погашения получается ноль. Можно было
бы принять за меру рассеяния математическое
ожидание модуля отклонения случайной
величины от ее математического ожидания,
но как правило, действия связанные с
абсолютными величинами, приводят к
громоздким вычислениям.
Свойства дисперсии:
-
Дисперсия постоянной равна нулю.
-
Постоянный множитель можно выносить
за знак дисперсии, возводя его в квадрат. -
Если x и y независимые случайные величины
, то дисперсия суммы этих величин равна
сумме их дисперсий.
Средним квадратическим отклонением
случайной величины(иногда применяется
термин «стандартное отклонение случайной
величины») называется число равное
.
Среднее квадратическое отклонение,
является, как и дисперсия, мерой рассеяния
распределения, но измеряется, в отличие
от дисперсии, в тех же единицах, которые
используют для измерения значений
случайной величины.
Решение задач:
1)Дана случайная величина Х:
-
xi
-3
-2
0
1
2
pi
0,1
0,2
0,05
0,3
0,35
Найти М(х), D(X).
Решение:
.
=9
=2,31.
.
2) Известно, что М(Х)=5, М(Y)=2.
Найти математическое ожидание случайной
величиныZ=6X-2Y+9-XY.
Решение:М(Z)=6М(Х)-2М(Y)+9-M(X)M(Y)=30-4+9-10=25.
Пример:Известно, чтоD(Х)=5,D(Y)=2. Найти
математическое ожидание случайной
величиныZ=6X-2Y+9.
Решение:D(Z)=62D(Х)-22D(Y)+0=180-8=172.
Тема 7. Непрерывные случайные величины
Задача 14
Случайная
величина, значения которой заполняют
некоторый промежуток, называется
непрерывной.
Плотностью распределениявероятностей непрерывной случайной
величины Х называется функцияf(x)– первая производная от функции
распределенияF(x).
Плотность
распределения также называют
дифференциальной
функцией.
Для описания дискретной случайной
величины плотность распределения
неприемлема.
Зная плотность распределения, можно
вычислить вероятность того, что некоторая
случайная величина Х примет значение,
принадлежащее заданному интервалу.
Вероятность того, что непрерывная
случайная величина Х примет значение,
принадлежащее интервалу (a,
b), равна определенному
интегралу от плотности распределения,
взятому в пределах от a
до b.
Функция распределения может быть легко
найдена, если известна плотность
распределения, по формуле:
Свойства плотности распределения.
1) Плотность распределения – неотрицательная
функция.
2) Несобственный интеграл
от плотности распределения в пределах
от -доравен единице.
Решение задач.
1.Случайная величина подчинена
закону распределения с плотностью:
Требуется найти коэффициент а,
определить вероятность того, что
случайная величина попадет в интервал
от 0 до
.
Решение:
Для нахождения коэффициента авоспользуемся свойством
.
2 .Задана непрерывная случайная
величинахсвоей функцией распределенияf(x).
Требуется определить
коэффициент А, найти функцию распределения,
определить вероятность того, что
случайная величинахпопадет в
интервал
.
Решение:
Найдем коэффициент А.
Найдем функцию распределения:
1) На участке
:
2) На участке
3) На участке
Итого:
Найдем вероятность попадания случайной
величины в интервал
.
Ту же самую вероятность можно искать
и другим способом:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Математическое ожидание не дает достаточно полной информации о случайной величине, поскольку одному и тому же значению математического ожидания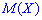 
может соответствовать множество случайных величин, будут различаться не только возможными значениями, но и характером распределения и самой природой возможных значений.
Например. Законы распределения двух случайных величин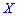 
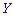
и 
заданные таблицами:
Вычислить математическое ожидание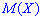 
и 
Решение. Находим математическое ожидание по класической формуле
Получили, что для двух различных законов распределения математическое ожидание принимает одинаковое значения (0), при этом возможные значения случайных величин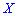
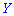
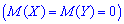
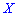
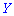
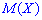
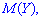
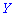
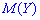
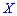
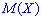
и 
различаются. Из приведенного примера видно, что в случае равенства математических ожиданий 
случайные величин 
и 
имеют тенденцию к колебаниям относительно 
и 
причем 
имеет больший размах рассеяния относительно 
сравнительно случайной величине 
относительно 
. Поэтому математическое ожидание еще называют центром рассеяния. Для определения рассеяния вводится числовая характеристика, называемая дисперсией.
Для определения дисперсии рассматривается отклонение случайной величины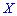 
от своего математического ожидания 
Математическое ожидание такого отклонения случайной величины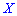 
всегда равна нулю. В этом легко убедиться из следующего соотношения
Таки образом, отклонение не может быть мерой рассеивания случайной величины.
Дисперсией случайной величины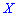 
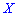
называют математическое ожидание квадрата отклонения случайной величины 
от своего математического ожидания 
Для дискретной случайной величины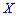 
дисперсия вычисляется по формуле
для непрерывной находят интегрированием
Если непрерывная величина заданная на интервале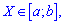 
то дисперсия равна интегралу с постоянными пределами интегрирования
Дисперсия обладает следующими свойствами
1. Если случайная величина состоит из одной тотчки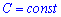 
— постоянная величина, то дисперсия равна нулю
2. Дисперсия от произведения постоянной на случайную величину равна квадрату постоянной умноженной на дисперсию случайной величины
3. Если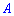 
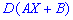
и 
— постоянные величины, то для дисперсии 
справедлива зависимость
Это следует из двух предыдущих свойств.
Дисперсию можно вычислить по упрощенной формуле:
которая в случае дискретной случайной величины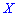 
имеет вид
для непрерывной определяется зависимостью
и для непрерывной на промежутке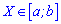 
соотношением
Приведенные формулы очень удобны в вычислениях, и их, в отличие от предыдущих, используют в обучении
Также следует помнить, что дисперсия всегда принимает неотрицательные значения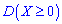 
. Она характеризует рассеяние случайной величины относительно своего математического ожидания. Если случайная величина измерена в некоторых единицах, то дисперсия будет измеряться в этих же единицах, но в квадрате.
Для сравнения удобно пользоваться числовыми характеристиками одинаковой размерности случайной величиной. Для этого вводят в рассмотрение среднее квадратичное отклонение – корень квадратный из дисперсии. Ее обозначают греческой буквой «сигма»
—————————————-
Рассмотрим примеры для ознакомления с практической стороной определения этих величин.
Пример 1. Закон распределения дискретной случайной величины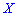 
заданы таблицей:
Вычислить дисперсию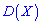 
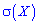
и среднее квадратическое отклонение 
.
Решение. Согласно свойствами дисперсии получим:
—————————————-
Пример2. Есть четыре электрические лампочки, каждая из которых имеет дефект с вероятностью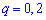 
(
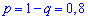
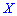
— вероятность того, что лампочка без дефекта). Последовательно берут по одной лампочке, вкручивают в патрон и включают электрический ток. При включении тока лампочка может перегореть, и ее заменяют на другую. Построить закон распределения дискретной случайной величины 
— число лампочек, которые будут опробованы. Вычислить среднее квадратическое отклонение 
Решение. Дискретная случайная величина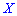 
— число лампочек, которые будут опробованы — приобретает такие возможных значений:
Вычислим соответствующие вероятности:
Последнюю вероятность можно трактовать следующим образом: четвертая лампочка будет испытана, когда третья перегорит, а четвертая — нет, или если и четвертая перегорит.
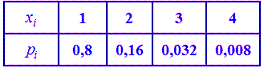
В табличной форме закон распределения 
иметь следующий вид:
Для нахождения среднего квадратического отклонения найдем сначала значение дисперсии. Для дискретной случайной величины она примет значение:
Среднее квадратичное отклонение находим добычей корня квадратного из дисперсии.
—————————————-
Пример 3. Закон распределения вероятностей дискретной случайной величины 
заданы в виде функции
Вычислить среднее квадратическое отклонение и дисперсию 
Решение. С помощью функции распределения вероятностей формируем закон распределения в виде таблицы
На основе таблицы распределения вычисляем дисперсию
————————
Подобных примеров можно привести множество, основная их суть в правильном применении приведенных в начале статьи формул для вычисления дисперсии и математического ожидания. Применяйте их там где это необходимо и не допускайте ошибок при определении дисперсии.
Загрузить PDF
Загрузить PDF
Вычислив среднеквадратическое отклонение, вы найдете разброс значений в выборке данных.[1]
Но сначала вам придется вычислить некоторые величины: среднее значение и дисперсию выборки. Дисперсия – мера разброса данных вокруг среднего значения.[2]
Среднеквадратическое отклонение равно квадратному корню из дисперсии выборки. Эта статья расскажет вам, как найти среднее значение, дисперсию и среднеквадратическое отклонение.
-
1
Возьмите наборе данных. Среднее значение – это важная величина в статистических расчетах.[3]
- Определите количество чисел в наборе данных.
- Числа в наборе сильно отличаются друг от друга или они очень близки (отличаются на дробные доли)?
- Что представляют числа в наборе данных? Тестовые оценки, показания пульса, роста, веса и так далее.
- Например, набор тестовых оценок: 10, 8, 10, 8, 8, 4.
-
2
Для вычисления среднего значения понадобятся все числа данного набора данных.[4]
- Среднее значение – это усредненное значение всех чисел в наборе данных.
- Для вычисления среднего значения сложите все числа вашего набора данных и разделите полученное значение на общее количество чисел в наборе (n).
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
-
3
Сложите все числа вашего набора данных.[5]
- В нашем примере даны числа: 10, 8, 10, 8, 8 и 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. Это сумма всех чисел в наборе данных.
- Сложите числа еще раз, чтобы проверить ответ.
-
4
Разделите сумму чисел на количество чисел (n) в выборке. Вы найдете среднее значение.[6]
- В нашем примере (10, 8, 10, 8, 8 и 4) n = 6.
- В нашем примере сумма чисел равна 48. Таким образом, разделите 48 на n.
- 48/6 = 8
- Среднее значение данной выборки равно 8.
Реклама
-
1
Вычислите дисперсию. Это мера разброса данных вокруг среднего значения.[7]
- Эта величина даст вам представление о том, как разбросаны данные выборки.
- Выборка с малой дисперсией включает данные, которые ненамного отличаются от среднего значения.
- Выборка с высокой дисперсией включает данные, которые сильно отличаются от среднего значения.
- Дисперсию часто используют для того, чтобы сравнить распределение двух наборов данных.
-
2
Вычтите среднее значение из каждого числа в наборе данных. Вы узнаете, насколько каждая величина в наборе данных отличается от среднего значения.[8]
- В нашем примере (10, 8, 10, 8, 8, 4) среднее значение равно 8.
- 10 — 8 = 2; 8 — 8 = 0, 10 — 2 = 8, 8 — 8 = 0, 8 — 8 = 0, и 4 — 8 = -4.
- Проделайте вычитания еще раз, чтобы проверить каждый ответ. Это очень важно, так как полученные значения понадобятся при вычислениях других величин.
-
3
Возведите в квадрат каждое значение, полученное вами в предыдущем шаге.[9]
- При вычитании среднего значения (8) из каждого числа данной выборки (10, 8, 10, 8, 8 и 4) вы получили следующие значения: 2, 0, 2, 0, 0 и -4.
- Возведите эти значения в квадрат: 22, 02, 22, 02, 02, и (-4)2 = 4, 0, 4, 0, 0, и 16.
- Проверьте ответы, прежде чем приступить к следующему шагу.
-
4
Сложите квадраты значений, то есть найдите сумму квадратов.[10]
- В нашем примере квадраты значений: 4, 0, 4, 0, 0 и 16.
- Напомним, что значения получены путем вычитания среднего значения из каждого числа выборки: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- Сумма квадратов равна 24.
-
5
Разделите сумму квадратов на (n-1). Помните, что n – это количество данных (чисел) в вашей выборке. Таким образом, вы получите дисперсию.[11]
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
- n-1 = 5.
- В нашем примере сумма квадратов равна 24.
- 24/5 = 4,8
- Дисперсия данной выборки равна 4,8.
Реклама
-
1
Найдите дисперсию, чтобы вычислить среднеквадратическое отклонение.[12]
- Помните, что дисперсия – это мера разброса данных вокруг среднего значения.
- Среднеквадратическое отклонение – это аналогичная величина, описывающая характер распределения данных в выборке.
- В нашем примере дисперсия равна 4,8.
-
2
Извлеките квадратный корень из дисперсии, чтобы найти среднеквадратическое отклонение.[13]
- Как правило, 68% всех данных расположены в пределах одного среднеквадратического отклонения от среднего значения.
- В нашем примере дисперсия равна 4,8.
- √4,8 = 2,19. Среднеквадратическое отклонение данной выборки равно 2,19.
- 5 из 6 чисел (83%) данной выборки (10, 8, 10, 8, 8, 4) находится в пределах одного среднеквадратического отклонения (2,19) от среднего значения (8).
-
3
Проверьте правильность вычисления среднего значения, дисперсии и среднеквадратического отклонения. Это позволит вам проверить ваш ответ.[14]
- Обязательно записывайте вычисления.
- Если в процессе проверки вычислений вы получили другое значение, проверьте все вычисления с самого начала.
- Если вы не можете найти, где сделали ошибку, проделайте вычисления с самого начала.
Реклама
Об этой статье
Эту страницу просматривали 64 925 раз.
Была ли эта статья полезной?
Дисперсия и ее свойства.
Среднее квадратическое отклонение
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Дисперсия и формула для ее вычисления
На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. Например, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели, которая должна быть поражена.
На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения случайной величины и затем найти их среднее значение. Однако такой путь ничего не даст, так как среднее значение отклонения, т. е. M[X-M(X)], для любой случайной величины равно нулю. Это свойство объясняется тем, что одни возможные отклонения положительны, а другие — отрицательны; в результате их взаимного погашения среднее значение отклонения равно нулю. Эти соображения говорят о целесообразности заменить возможные отклонения их абсолютными значениями или их квадратами. Так и поступают на деле. Правда, в случае, когда возможные отклонения заменяют их абсолютными значениями, приходится оперировать с абсолютными величинами, что приводит иногда к серьезным затруднениям. Поэтому чаще всего идут по другому пути, то есть вычисляют среднее значение квадрата отклонения, которое и называют дисперсией.
Дисперсией называется
математическое ожидание квадрата отклонения случайной величины
от
:
Для того чтобы найти дисперсию, достаточно вычислить сумму произведений возможных значений квадрата отклонения на их вероятности.
Для вычисления дисперсии
на практике удобно пользоваться следующей формулой:
Свойства дисперсии
Свойство 1.
Дисперсия равна разности между
математическим ожиданием квадрата случайной величины
и
квадратом ее математического ожидания.
Свойство 2.
Дисперсия константы
равна нулю:
Свойство 3.
Постоянный множитель
выносится из-под знака дисперсии в квадрате:
Свойство 4.
Дисперсия суммы
случайных величин:
где
–
ковариация случайных величин
и
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Следствия из свойств дисперсии.
В частности, если
и
независимы, то
Прибавление константы
в
случайной величине не меняет ее дисперсии:
Дисперсия разности равна сумме дисперсий:
Среднеквадратическое отклонение
Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.
Стандартное (среднее
квадратичное) отклонение случайной величины
определяется
как корень из дисперсии и обозначается
Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то ее размерность совпадает с размерностью X. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию. Например, если X выражается в линейных метрах, то среднее квадратичное отклонение X будет выражаться также в линейных метрах, a дисперсия X — в квадратных метрах.
Смежные темы решебника:
- Математическое ожидание и его свойства
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
В коробке 20 конфет, из которых 4 с
вареньем. Х – число конфет с вареньем среди двух случайно выбранных. Найти
дисперсию случайной величины Х.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Случайная
величина
– число конфет с вареньем, может принимать
значения 0,1,2
Найдем
соответствующие вероятности:
Проверка:
Получаем
следующий закон распределения СВ
:
Математическое
ожидание:
Дисперсию
можно вычислить по формуле:
Искомая
дисперсия:
Пример 2
Даны
законы распределения независимых случайных величин X и Y:
и
Найти
закон распределения суммы (X+Y). Проверить равенство D(X+Y)=D(X)+D(Y).
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Распределение суммы
:
Окончательно получаем:
|
|
2 | 3 | 4 | Итого |
|
|
0.2 | 0.5 | 0.3 | 1 |
Вычислим математические ожидания:
Вычислим
дисперсии:
Проверим
равенство
:
Равенство
выполняется.
Пример 3
Вероятность
изготовления бракованной детали на первом станке составляет 3%, на втором
станке 5%. На первом станке было изготовлено 20 деталей, на втором 40 деталей.
Найти математическое ожидание и дисперсию числа бракованных деталей.
Решение
Математическое
ожидание биномиального распределения:
Дисперсия:
Математическое
ожидание величины
– числа бракованных деталей на 1-м станке:
Дисперсия:
Математическое
ожидание величины
– числа бракованных деталей на 2-м станке:
Дисперсия:
Математическое
ожидание числа бракованных деталей:
Дисперсия
числа бракованных деталей:
Ответ:
;
.
Пример 4
Случайные
величины X,Y распределены по закону
Пуассона. Найдите M{(X+Y)2}, если M(X)=40 и
M(Y)=70, а коэффициент корреляции X и Yравен 0,8.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Поскольку
случайные величины
и
распределены по закону Пуассона и известны их
математические ожидания, соответствующие дисперсии равны:
Пользуясь
свойствами математического ожидания и дисперсии:
Подставляя
числовые значения, получаем:
Ответ:
.
Задачи контрольных и самостоятельных работ
Задача 1
Независимые случайные величины X и Y
заданы следующими законами:
| x | 2.3 | 2.5 | 2.7 | 2.9 |
| p | 0.4 | 0.3 | 0.2 | 0.1 |
Укажите
законы распределения случайной величины X+Y, X-Y и найдите их
математическое ожидание и дисперсию.
Задача 2
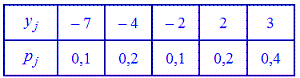
Найти
дисперсию, математическое ожидания, среднекваратическое отклонение ДСВ X,
заданной законом распределения.
| x | -5 | 2 | 3 | 4 |
| p | 0,4 | 0,3 | 0,1 | 0,2 |
Написать F(x) и построить ее график.
Задача 3
Случайная
величина X имеет плотность вероятности
Требуется
найти дисперсию Dx.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Вероятность
того, что прибор исправен, равна 0,8. X – число исправных приборов
из двух выбранных. Найти дисперсию случайной величины X.
Задача 5
Случайные
величины X и Y независимы. Найти
дисперсию случайной величины Z=2X+3Y, если известно, что D(X)=4, D(Y)=5.
Задача 6
Найти
дисперсию дискретной случайной величины X – числа отказов элемента
некоторого устройства в десяти независимых опытах, если вероятность отказа
элемента в каждом опыте равна 0,9.
Задача 7
Дискретная
случайная величина X имеет только два возможных значения: x1 и x2, причем x2>x1. Вероятность того, что X
примет значение x1, равна 0,6. Найти закон распределения величины X, если
математическое ожидание и дисперсия известны: M(X)=1,4; D(X)=0,24.
Задача 8
Закон
распределения случайной величины ξ имеет вид:
| ξ | -1 | 2 | 3 | 5 |
| P | 1/4 | 1/2 | 1/8 | 1/8 |
Найти функцию распределения случайной величины ξ,
вычислить ее математическое ожидание, дисперсию и среднее квадратическое
отклонение. Вычислить вероятность P{5⁄2<ξ<5}.
Задача 9
Дискретная
случайная величины X принимает лишь два значения. Большее из значений 3
она принимает с вероятностью 0,4. Кроме того, известна дисперсия случайной
величины D(X)=6. Найти математическое
ожидание случайной величины.
Задача 10
Найти
дисперсию по заданному непрерывному закону распределения случайной величины X,
заданному плотностью вероятности
при
и
в остальных точках.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Числовые характеристики распределения вероятностей. Математическое ожидание, дисперсия и стандартное отклонение
- Закон распределения дискретной случайной величины
- Математическое ожидание
- Дисперсия
- Среднее квадратичное отклонение
- Правило трёх сигм
- Примеры
п.1. Закон распределения дискретной случайной величины
Законом распределения дискретной случайной величины называют соответствие между полученными на опыте значениями этой величины X= {xi} и их вероятностями pi = P(xi).
При этом сумма всех вероятностей равна 1: (mathrm{sum_{i=1}^n p_i=1})
Закон распределения можно задать таблицей, графиком или аналитически (в виде формулы).
Например:
Закон распределения случайной величины X = {0;1;2;3}, равной числу выпадения орлов при 3 бросках монеты, аналитически задаётся формулой: $$ mathrm{ p_i=P(x_i)=P_3(i)=frac{C_3^{i}}{2^3}, i={0;1;2;3} } $$
В табличном виде:
|
xi |
pi |
|
0 |
1/8 |
|
1 |
3/8 |
|
2 |
3/8 |
|
3 |
1/8 |
В виде графика:
п.2. Математическое ожидание
Математическое ожидание дискретной случайной величины X = {xi} равно сумме произведений всех возможных значений xi на соответствующие вероятности pi: $$ mathrm{ M(X)=x_1p_1+x_2p_2+…+x_{n}p_{n}=sum_{i=1}^n x_{i}p_{i} } $$ Математическое ожидание является средним значением величины X.
Свойства математического ожидания
1) Размерность математического ожидания равна размерности случайной величины.
2) Математическое ожидание может быть любым действительным числом: положительным, равным 0, отрицательным.
3) Математическое ожидание постоянной величины равно этой постоянной:
M(C) = C
4) Математическое ожидание суммы независимых случайных величин равно сумме математических ожиданий:
M(X + Y) = M(X) + M(Y)
5) Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий:
M(XY) = M(X) · M(Y)
6) Постоянный множитель можно вынести за знак математического ожидания:
M(CX) = C · M(X)
Например:
Пусть в результате экспериментов получено следующее распределение случайной величины X – числа появления белых шаров (см. пример 1, §40 данного справочника):
| Число белых шаров, xi | 0 | 1 | 2 | 3 | 4 | 5 |
| pi | (mathrm{C_5^0q^5}) | (mathrm{C_5^1pq^4}) | (mathrm{C_5^2p^2q^3}) | (mathrm{C_5^3p^3q^2}) | (mathrm{C_5^4p^4q}) | (mathrm{C_5^5p^5}) |
| 0,0074 | 0,0618 | 0,2060 | 0,3433 | 0,2861 | 0,0954 |
Найдём математическое ожидание для данного распределения:
M(X) = 0 · 0,0074 + 1 · 0,0618 + … + 5 · 0,0954 = 3,125
п.3. Дисперсия
Дисперсия дискретной случайной величины X = {xi} – это математическое ожидание квадрата отклонения случайной величины от её математического ожидания: $$ mathrm{ D(X)=M(X-M(X))^2 } $$ На практике дисперсия рассчитывается по формуле: $$ mathrm{ D(X)=M(X)^2-M^2(X)=sum_{i=1}^n x_i^2p_i-M^2(X) } $$
Свойства дисперсии
1) Размерность дисперсии равна квадрату размерности случайной величины.
2) Дисперсия может быть любым неотрицательным действительным числом.
3) Дисперсия постоянной величины равна нулю:
D(C) = 0
4) Дисперсия суммы независимых случайных величин равна сумме дисперсий:
D(X + Y) = D(X) + D(Y)
5) Постоянный множитель можно вынести за знак дисперсии:
D(CX) = C2 · D(X)
Например:
Продолжим исследование и найдём дисперсию для распределения случайной величины X – числа появления белых шаров. Составим расчётную таблицу:
pi
0,0074
0,0618
0,2060
0,3433
0,2861
0,0954
1
xip1
0
0,0618
0,4120
1,0300
1,1444
0,4768
3,125
(mathrm{x_i^2})
0
1
4
9
16
25
–
(mathrm{x_i^2p_i})
0
0,0618
0,8240
3,0899
4,5776
2,3842
10,9375
Получаем: D(X) = 10,9375 – 3,1252 ≈ 1,1719.
п.4. Среднее квадратичное отклонение
Среднее квадратичное отклонение (СКО) дискретной случайной величины X = {xi} – это корень квадратный от дисперсии: $$ mathrm{ sigma(X)=sqrt{D(X)} } $$ СКО характеризует степень отклонения случайной величины от среднего значения.
Свойства СКО
1) Размерность СКО равна размерности случайной величины.
2) СКО может быть любым неотрицательным действительным числом.
3) СКО постоянной величины равно нулю:
σ(C) = 0
4) Постоянный множитель можно вынести за знак СКО:
σ(CX) = C · σ(X)
п.5. Правило трёх сигм
Большое количество случайных величин, измеряемых в экспериментах (например, в школьных лабораторных работах), имеет так называемое нормальное распределение.
В частности, при больших n, биномиальное распределение можно с хорошей точностью описывать как нормальное с M(X) = np и (mathrm{sigma(X)=sqrt{npq}}).
График плотности нормального распределения p(x) похож на колокол, с максимумом, соответствующим M(X) = Xcp – среднему значению измеряемой величины.
Величина СКО σ(X) характеризует степень отклонения X от среднего значения M(X).
Если величина X имеет нормальное распределение, то в пределах
±σ лежит 68,26% значений, принимаемых этой величиной
±2σ лежит 95,44% значений, принимаемых этой величиной
±3σ лежит 99,72% значений, принимаемых этой величиной
Вероятность того, что нормально распределённая величина примет значение, отклоняющееся от среднего больше, чем на «три сигмы», равна 0,28%, т.е. пренебрежимо мала.
п.6. Примеры
Пример 1. Найдите математическое ожидание, дисперсию и СКО при бросании кубика.
Закон распределения величины X – очки на верхней грани при бросании кубика и расчётная таблица:
pi
1/6
1/6
1/6
1/6
1/6
1/6
1
xip1
1/6
1/3
1/2
2/3
5/6
1
3,5
(mathrm{x_i^2})
1
4
9
16
25
36
–
(mathrm{x_i^2p_i})
(mathrm{frac16})
(mathrm{frac23})
(mathrm{1frac12})
(mathrm{2frac23})
(mathrm{4frac16})
6
(mathrm{15frac16})
Получаем: begin{gather*} mathrm{ M(X)=sum_{i=1}^6 x_ip_i=3,5 }\ mathrm{ D(X)=sum_{i=1}^6 x_i^2p_i-M^2(X)=15frac16-3,5^3=2frac{11}{12} }\ mathrm{ sigma(X)=sqrt{D(X)}=sqrt{2frac{11}{12}}approx 1,7 } end{gather*} Ответ: (mathrm{M(X)=3,5; D(X)=2frac{11}{12}; sigma(X)approx 1,7}).
Пример 2*. Найти математическое ожидание, дисперсию и СКО суммы очков при бросании двух кубиков.
Используем свойства мат.ожиданий и дисперсий.
Пусть X – очки на первом кубике, Y – на втором.
Параметры распределения для каждого из кубиков рассчитаны в примере 1.
(mathrm{M(X)=M(Y)=3,5, D(X)=D(Y)=2frac{11}{12}}).
Для суммы очков получаем:
(mathrm{M(X+Y)=M(X)+M(Y)=3,5+3,5=7})
(mathrm{D(X+Y)=D(X)+D(Y)=2frac{11}{12}+2frac{11}{12}=5frac56})
(mathrm{sigma(X+Y)=sqrt{D(X+Y)}=sqrt{5frac56}approx 2,4})
Ответ: (mathrm{M(X+Y)=7; D(X+Y)=5frac56; sigma(X+Y)approx 2,4}).
Пример 3*. Докажите, что в опытах по схеме Бернулли математическое ожидание M(X)=np, а дисперсия D(X)=npq.
Проведем один опыт. В нём может быть только два исхода: «успех» и «неудача».
Составим расчётную таблицу:
(mathrm{x_i^2p_i})
0
p
p
Мат.ожидание первого опыта (mathrm{M(X)=sum x_ip_i=p}).
Общее число успехов при n опытах складывается из числа успехов при каждом опыте, т.е. (mathrm{X=X_1+X_2+…+X_n}). Все опыты между собой независимы.
По свойству мат.ожидания суммы независимых событий: begin{gather*} mathrm{ M(X)=M(X_1+X_2+…+X_n)=M(X_1)+M(X_2)+…+M(X_n)= }\ mathrm{=underbrace{p+p+…+p}_{n text{раз}}=np } end{gather*} Дисперсия первого опыта (mathrm{D(X)=sum x_i^2p_i-M(X)=p-p^2=p(1-p)=pq})
По свойству дисперсии суммы независимых событий: begin{gather*} mathrm{ D(X)=D(X_1+X_2+…+X_n)=D(X_1)+D(X_2)+…+D(X_n)= }\ mathrm{=underbrace{pq+pq+…+pq}_{n text{раз}}=npq } end{gather*} Что и требовалось доказать.
Пример 4. 100 канцелярских кнопок высыпали на стул. Вероятность, что кнопка упала острием вверх, равна 0,4. Найдите среднее количество, дисперсию и СКО для числа кнопок, упавших острием вверх. Найдите интервал оценки для количества этих кнопок по правилу «трёх сигм».
По условию n = 100, p = 0,4.
Для каждой кнопки может быть два исхода: упасть острием вверх или вниз.
Таким образом, это испытание Бернулли с биномиальным распределением случайной величины. begin{gather*} mathrm{ M(X)=np=100cdot 0,4=40 }\ mathrm{D(X)=npq=100cdot 0,4cdot 0,6=24 }\ mathrm{sigma(X)=sqrt{D(X)}=sqrt{24}approx 4,9} end{gather*} Интервал оценки «три сигмы»: begin{gather*} mathrm{ M(X)-3sigma(X)lt Xlt M(X)+3sigma(X) }\ mathrm{40-3cdot 4,9lt Xlt 40+3cdot 4,9 }\ mathrm{25,3lt Xlt 54,7}\ mathrm{26leq Xleq 54} end{gather*} Скорее всего (99,7%), от 26 до 54 кнопок будут острием вверх.
Ответ: (mathrm{M(X)=40; D(X)=24; sigma(X)approx 4,9; 26leq Xleq 54})
Пример 5*. В тесте 10 задач с 4 вариантами ответов. Ответы выбираются наугад. Постройте распределение величины X = «количество угаданных ответов», найдите числовые характеристики этого распределения.
Найдите интервал оценки для количества угаданных ответов по правилу «трёх сигм».
Какова вероятность угадать хотя бы 1 ответ? Хотя бы 5 ответов? Угадать все 10 ответов?
По условию: (mathrm{n=10, p=frac14, q=frac34}).
Для каждого ответа может быть два исхода: «угадал»/ «не угадал».
Таким образом, это испытание Бернулли с биномиальным распределением случайной величины. $$ mathrm{ P_{10}(k)=C_{10}^kp^kq^{10-k}=C_{10}^kfrac{3^{10-k}}{4^{10}}=left(frac34right)^{10}frac{C_{10}^k}{3^k} } $$ Строим расчётную таблицу. Для (mathrm{C_{10}^k}) используем рекуррентную формулу (см. §36 данного справочника): $$ mathrm{ C_{n}^k=frac{n-k+1}{k}C_n^{k-1} } $$
| (mathrm{x_i=k}) | (mathrm{C_k}) | (mathrm{3^k}) | (mathrm{p_i(x_i)}) | (mathrm{x_icdot p_i}) | (mathrm{x_i^2}) | (mathrm{x_i^2cdot p_i}) |
| 0 | 1 | 1 | 0,0563135 | 0,0000000 | 0 | 0,0000000 |
| 1 | 10 | 3 | 0,1877117 | 0,1877117 | 1 | 0,1877117 |
| 2 | 45 | 9 | 0,2815676 | 0,5631351 | 4 | 1,1262703 |
| 3 | 120 | 27 | 0,2502823 | 0,7508469 | 9 | 2,2525406 |
| 4 | 210 | 81 | 0,1459980 | 0,5839920 | 16 | 2,3359680 |
| 5 | 252 | 243 | 0,0583992 | 0,2919960 | 25 | 1,4599800 |
| 6 | 210 | 729 | 0,0162220 | 0,0973320 | 36 | 0,5839920 |
| 7 | 120 | 2187 | 0,0030899 | 0,0216293 | 49 | 0,1514053 |
| 8 | 45 | 6561 | 0,0003862 | 0,0030899 | 64 | 0,0247192 |
| 9 | 10 | 19683 | 0,0000286 | 0,0002575 | 81 | 0,0023174 |
| 10 | 1 | 59049 | 0,0000010 | 0,0000095 | 100 | 0,0000954 |
| Σ | 1 | 2,5 | 8,125 |
Получаем: begin{gather*} mathrm{ M(X)=sum_{i=0}^{10} x_ip_i=2,5 }\ mathrm{ D(X)=sum_{i=0}^{10} x_i^2p_i-M^2(X)=8,125=2,5^2=1,875 }\ mathrm{ sigma(X)=sqrt{D(X)}=sqrt{1,875}approx 1,37 } end{gather*} 
Интервал оценки «три сигмы»: begin{gather*} mathrm{ M(X)-3sigma(X) lt Xlt M(X)+3sigma(X) }\ mathrm{ 2,5-3cdot 1,37lt X lt 2,5+3cdot 1,37 }\ mathrm{ -1,61lt Xlt 6,61 }\ mathrm{ 0leq Xleq 6 } end{gather*} Скорее всего (по расчетам – 99,65%), вы угадаете от 0 до 6 ответов.
Вероятность угадать хотя бы один ответ: begin{gather*} mathrm{ P(Xgeq 1)=1-p_0approx 1-0,0563=0,9437 }end{gather*} Очень хорошие шансы – 94,37%.
Вероятность угадать хотя бы 5 ответов: begin{gather*} mathrm{ P(Xgeq 5)=1-left(sum_{i=0}^{4}{p_i} right)approx 1-(0,0563+0,1877+…+0,1460)=0,0781 }end{gather*} Шансов мало – 7,81%. Т.е. «средний балл» при сдаче тестов мало достижим методом научного тыка.
Вероятность угадать все 10 ответов: p10≈ 0,000001. Шанс – один из миллиона.