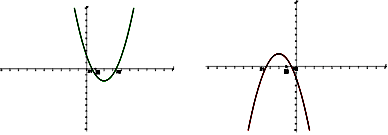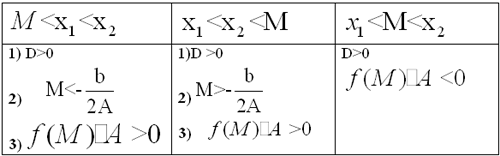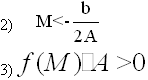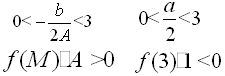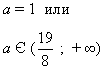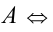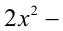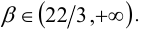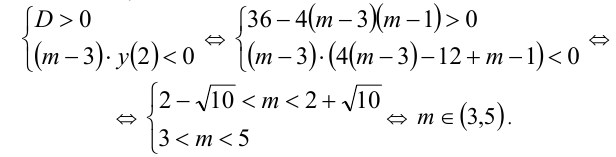Как найти квадратное уравнение по точкам

Как определить a, b и c по графику параболы

Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.

Коэффициент (a) можно найти с помощью следующих фактов:

— Если (a>0), то ветви параболы направленных вверх, если (a 1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:

Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.

Решаем систему.
Пример:

Вычтем из второго уравнения первое:

Подставим (9a) вместо (b):

Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

Подставим в первое уравнение (a):

Получается квадратичная функция: (y=-x^2-9x-15).

Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:

Сложим 2 уравнения:

Подставим во второе уравнение:

Теперь найдем точки пересечения двух функций:

Теперь можно найти ординату второй точки пересечения:

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Главный недостаток этого способа — вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).

– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.

– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.

График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.

У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:

Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).

Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).

Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).

Как построить параболу? Что такое парабола? Как решаются квадратные уравнения?

Урок: как построить параболу или квадратичную функцию?

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Парабола — это график функции описанный формулой ax 2 +bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:

1 ) Формула параболы y=ax 2 +bx+c,
если а>0 то ветви параболы направленны вверх,
а 2 +bx+c=0;

a) Полное квадратное уравнение имеет вид ax 2 +bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax 2 +bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);

4) Найти несколько дополнительных точек для построения функции.

ПРАКТИЧЕСКАЯ ЧАСТЬ

И так теперь на примере разберем все по действиям:
Пример №1:
y=x 2 +4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x 2 +4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x₁=(-4+2)/2=-1
x₂=(-4-2)/2=-3

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2

х -4 -3 -1 0
у 3 0 0 3

Подставляем вместо х в уравнение y=x 2 +4x+3 значения
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2

Пример №2:
y=-x 2 +4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1 2 +4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x 2 +4x=0
Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4.

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x 2 +4x значения
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2

Пример №3
y=x 2 -4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x 2 -4=0
Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x 2 =4
x₁=2
x₂=-2

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x 2 -4 значения
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0

Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.

Квадратичная функция. Построение параболы

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ: наглядно.

• Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.

Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.

Построение квадратичной функции

Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:

График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :

Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:

x

y

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.

График функции y = –x 2 выглядит, как перевернутая парабола:

Зафиксируем координаты базовых точек в таблице:

x

y

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

• Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
• Если старший коэффициент меньше нуля a 2 + bx + c, для построения которой нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

1. Если D 0,то график выглядит так:

1. Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
2. Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:

Если a > 0, то график выглядит как-то так:

0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>

На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.

Разберем общий алгоритм на примере y = 2x 2 + 3x — 5.

Как строим:

1. Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена 2x 2 + 3x — 5.

D = b 2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

2x 2 + 3x — 5 = 0 2 + 3x — 5 = 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAPoAAAAyCAYAAAB1V8bkAAAJyElEQVR4Ae2c16sUwRLGfdRX/wXFB30QFFQUQUyIKCIGBEEQzCCoKIgB01ExZwVz4JpzztljwJxzzjlnrcuvL33unD2zOzO7OzvuThU0u5N6uuvrr7u6unrKiYpqQDVQ8BooV/A11AqqBlQDokTXRqAaiIEGlOgxAFmrqBpQomsbUA3EQANK9BiArFVUDSjRtQ2oBmKgASV6DEDWKqoGlOjaBlQDMdBAQRH9z58/8vv3b5P+/v2bMXy/fv0S8kxMGWesGRgNpIMXz7jhkg28CxmWgiH69+/f5dSpU7JixQpZtmyZXLx4UX7+/JkUOxoGjSaVTJw4UVatWiUbNmwoSYcPH071iF7zqYGgeNlsT58+LZMnTy7BA2y2bNkib9++tbfor4sGCobogD19+nR5/fq1nDx5Upo0aSLHjh2TZD39x48f5ebNmy4q+d8pRo327dtLo0aNTF6NGzeWevXqCeRXyVwDQfHijXTMmzZtMjiAL6lu3brSuXNnuXfvXuaFKuAcCobojOQDBgwwgD948EAg5ubNm42Z54bfjRs3ZMqUKW6XzDk6jP379wsjD/LmzRtZt26dvHr1KukzesG/BoLiRc5gceXKFZM4/vbtmxw6dEguXbokP3788P/yGN5ZMET/8uWLvHv3Tt6/f2/Muh49esj169eTQupF9MQHIfm1a9cST+txmhoIipfba86fPy9Hjx4VrDOV1BooGKJTTYh++fJlGTt2rCxevNgcJ6t+EKIz3587d26yrPR8mhoIglfiK549e2Y6dHBU8dZA3hH9+PHjYhNmnFO+fv1qTOwDBw5Ily5dhF+nQ47ndu/ebdLChQule/fuJcecp9E477d5d+zYUW7fvm0P9TeABixW/AbBCz+LffbChQtl3rh69WpZsmSJjuZlNON+Iu+IDkGZW+N427Ztm6nVp0+f5MiRI6Zh2Dl1hw4dZOjQoaVGdebc1oM+a9Ys48Sxx/y6zfUePnwoVapUcdeenvXUQLp4LV261OA8bdo0g5nzRR8+fJBhw4YJeav400DeEf3Ro0dmZGD+/fLlS1NLzLjhw4fLmDFjhEaA4DHv16+fGeHdVOHXdKczqVy5slsWes6HBtLF6/HjxwZn/CLPnz8v9aZbt25Jt27dlOiltJL6IO+I7lYdTPY1a9bIjBkz5M6dO7Jjxw5hRN++fXtSb6xfos+ZM0cqVark9trQzrEmXFxc7LnOH1oBQs44HbycRTpz5oy0a9funyA6DkGW/NavX19mauIsc+J/OkCmJliRL168ME7FVM7jxOeDHhcE0ak05KD3P3v2rFkWO3HihHz+/DmpPlh3XbRoUdLr9gL5LF++3B6G+nv//n3ZuHGjDBw4UDp16pS0kwq1EDnKPChezmI9efJEtm7dmnJVxXl/WP8PHjxopoxXr141RG3Tpo0JsPLzPqaaLVq0kDp16kjDhg2lb9++JgbEz7Pp3FMwRKfyBLkwX2fpxivqjbm8Nf1TKY77WK/NhVBuGvGoUaNMHID1N+Ti3VG8IwhezvIR5gwm/EYlrBgMGTJE9u3bZxy4YDV69Gjf/py9e/fKypUrjSVKLEDYqwcFRfSoQM/2e2fOnGmivgqd6NnWWy7zI3CqefPmUlRUVOIXgrzly5cXfEZewr2Y/XTuyaI3vfIIcj1tolM4lpyIBZ83b56MGzdO9uzZY0YjwkSfPn0apBx6r0MDYRBd8XIoOAt/sRiZU0N4az2OHz9eKlSo4MvSgOgs6RKIBYdIYUraRMfsYpkL84m5cc+ePY1DYv78+dKnTx/B2eAlmKldu3b1TISy5luII8s/XnWbNGmSMC9PlDCIrniJcXB6YcJ15s9+JHEkrlq1qixYsMDPowLRcRqzSgSHiOkI0xeUNtHpxXBUIQQ3tGrVKnLniC8N58FNYRBd8QoOPES2Php8Agw2dvR25gZRcaaNHDnSeTrlf/JxdhTsuMQacJ5LmUHAi2kT3b6HyrNBoXXr1uYUBXVThr3f+YuCcGp4JZRsFYAV8K8lt1hremqveuE4RAeJEgbR7Tvigpfb1JG6e2HCde5DCJbCM16rVi2T2D9BiLVT6Agwv3GsgSXPumHqfAZ+sLqCNWfbNQ455ve8MwxJm+gsXeF0YFcXPRlRaAiebD/OCO5l/XDQoEGeCTPHhqZWq1ZN/rVElF2iTJ061bNemHkEhiRKGESPG141atRIVKtZevXT3tjz7kcYgIioZDRmtyM6Zk09sf0zbYIndkBgabFt27ZmeZeYAgQzvmLFimWe9VMOP/ekTXTWMXv37m16uF69esmECRNMZdgDzgcgVIJrwLm8Vr9+fSECjM4wG6J4ZUOL/8+DgQdSwwGccIRkk4jITBRGaZZM8V/ZlRRGdIJlwJzBsX///gKPwpK0iY7HkArSgKgwu8XYMnju3LmkgSr0ZNZUCatCfvLFtKIHtj2sn2dycY8NmCGcF6cQIwXx+dmQfMMLfEj/qjA1Yx29ZcuWpRLmfaLcvXtXBg8eLCNGjChxUoM1mBAdt3btWmP9ZatTT3w/x2kTHcKytAB5EeYmyYiDecpWz9mzZyf9EIRb4cI6Rw/KikGcLI98w4vlWkKYC0Uw5xkEMeGt4A/Akc28P+wBMG2i28L6+WV7IruRmjVrVmK6+HkujHuYL+3atcuUhbm/SlkNRI0Xn/iqWbOmaTNlS5d/ZzDzITOhslFJTohO5Rg98WDaOUoUFabXpBExV2JThBI9OQpR4YX1x3SQb/UxOBSCYO2yA48RPCqJFdGZmxN8w/q/Ej11k4uK6ERXMqflw4+FQvTUms7N1VgRnYgndq2RlOipG1gURCf2myhLpldNmzZVoqeGKNDV2BAdj+bOnTuNcpTo3m0k10THrCVohCAiRInujVGQO2JDdJYA8bQTpIJHt3bt2mZtk1FEpawGck10PrRB4BEf4QQjgqIIK2UbqErmGsgJ0fE2AmL16tWFj/oRwpprYcRgVCcR+URsPkELBCyolNZAFHgRVcZyrcWoQYMGwtd97KfBSpdQj4JqICdEZ3kBkwwQIZZXLHDQSvi9H687G/wJgyREkl+7McdvHnG4L0q8WG9mUOCDnASf4DxVyVwDOSF65sXMXg6QnYbMMh+/fjfgZK8EmlMqDYAPzji7WyyqQSFVGfPxWuyIno8gaZlVA5lqQImeqQb1edVAHmhAiZ4HIGkRVQOZakCJnqkGI3m+WIrKlZOi45G8XF+ahxpQouchaKbIx4uU6PmKXQTlVqJHoPTMX/lM/tOuSIozz0hziIkGlOgxAVqrGW8NKNHjjb/WPiYaUKLHBGitZrw1oESPN/5a+5hoQIkeE6C1mvHWwH8BSUfSiO3XWNEAAAAASUVORK5CYII=»>

1. Координаты вершины параболы:

1. Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
2. Нанести эти точки на координатную плоскость и построить график параболы:
   2 + 3x — 5 = 0″ height=»671″ src=»https://lh6.googleusercontent.com/TYyA5dFfh0ZKINaPSps3Y_X1mCv8Mhv_8bNG3_dPbZud1AEsvo7UBFmVQNm1GcR1CQFo6HE1lNjYaAgepQUTQiK_ay_Fnuv7LEsB53woHkFO66W0R1PP8QfGsFcYzaR_h4AJdLxC» width=»602″>

Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀

Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.

Рассмотрим пример: y = 2 * (x — 1) 2 + 4.

Как строим:

1. Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:

• построить y = x 2 ,
• умножить ординаты всех точек графика на 2,
• сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• сдвинуть его вдоль оси OY на 4 единицы вверх.

1. Построить график параболы для каждого случая. 2 + y₀» height=»431″ src=»https://lh5.googleusercontent.com/_zgF-CXWf4Yy0p2OnBYSJkUm0zO-mNetq5feU6LIPEbIgSrO9kdr2ti_tr7Gg3yTMOlJVnuZgG0HleAFfAzG7yr7ELHT6KSMqMrRHkHqt-VcgIiSZx80cVj0zlPMBzEM0wAWQ-L6″ width=»602″>

Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)

Рассмотрим следующий пример: y = (x − 2) × (x + 1).

Как строим:

Данный вид уравнения позволяет быстро найти нули функции:

(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.

Определим координаты вершины параболы:

Найти точку пересечения с осью OY:

с = ab = (−2) × (1) = −2 и ей симметричная.

Отметим эти точки на координатной плоскости и соединим плавной прямой.

источники:

http://tutomath.ru/uroki/kak-postroit-parabolu.html

http://skysmart.ru/articles/mathematic/kvadratichnaya-funkciya-parabola

Как найти квадратное уравнение по 2 точкам? Квадратное уравнение — это полиномиальное уравнение, в котором наибольшая степень неизвестной переменной является квадратичным членом. Квадратное уравнение можно найти по двум точкам.

Содержание

• 1 Как найти квадратное уравнение по 2 точкам?
• 2 Как найти квадратное уравнение по двум точкам?
• 3 Как найти квадратное уравнение по двум точкам и вершине?
• 4 Как найти квадратное уравнение, зная точку пересечения Y и две точки?
• 5 Как найти квадратное уравнение с двумя корнями?
• 6 Как найти квадратное уравнение?
• 7 Как найти форму вершины по двум точкам?
• 8 Как найти уравнение квадратичной функции?
• 9 Как найти координату y двух точек?
• 10 Как написать квадратное уравнение с точкой пересечения Y?
• 11 Как найти точку пересечения y квадратного уравнения?
• 12 Как найти r1 и r2 квадратного уравнения?
• 13 Как найти квадратное уравнение с одним корнем?
• 14 Откуда взялась квадратичная формула?
• 15 Какие 4 способа решения квадратного уравнения?
• 16 Какие 5 примеров квадратного уравнения?
• 17 Как найти вершину квадратичной функции?
• 18 Как записать квадратичную функцию в стандартной форме с двумя точками?
• 19 Как найти квадратичную функцию в вершинной форме?
• 20 Какова формула параболы?
• 21 Как найти вторую точку?
• 22 Как найти наклон двух заданных точек?
• 23 Что такое P и Q в квадратном уравнении?
• 24 Как найти точку пересечения нуля и оси Y квадратного уравнения?
• 25 Что такое вершинная форма?
• 26 Что такое дискриминантная формула?
• 27 Как найти сумму корней?
• 28 Если корни квадратного уравнения равны 2 и 3, то уравнение равно?
• 29 Что такое квадратное уравнение, если его корни равны 0 и 4*?
• 30 Как составить квадратное уравнение с нулями?
• 31 Какие 3 способа решения квадратного уравнения?
• 32 Как проще всего решать квадратные уравнения?
• 33 Как решать квадратные уравнения для чайников?
• 34 Как найти вершину и точку пересечения Y квадратичной функции?
• 35 Нахождение квадратного уравнения по 2 точкам на параболе
• 36 Определение квадратного уравнения по вершине и точке
• 37 Как написать уравнение параболы по трём точкам
• 38 Нахождение квадратного уравнения по трем точкам

Смотрите также, во сколько начинается Путь огня

Предполагая вертикальную ось симметрии, уравнение будет иметь вид у = ах ^ 2 + Ьх + с что также можно записать как y = a (x — h) ^ 2 + k. Случай 1: если две точки имеют одинаковое значение y, то ось симметрии пройдет через середину отрезка между ними.

Как найти квадратное уравнение по 2 точкам?

Как найти квадратное уравнение по двум точкам?

Как найти квадратное уравнение по двум точкам и вершине?

Как найти квадратное уравнение, зная точку пересечения Y и две точки?

Как найти квадратное уравнение с двумя корнями?

Как найти квадратное уравнение?

Как найти форму вершины из двух точек?

1. Вершинная форма квадратного уравнения: y=a(x-h)2+k, где (h,k) — вершина параболы.
2. Вершина параболы – это точка в верхней или нижней части параболы.
3. «h» равно -6, первая координата в вершине.
4. ‘k’ равно -4, вторая координата в вершине.
5. «x» равно -2, первая координата в другой точке.

Как найти уравнение квадратичной функции?

Как найти координату Y двух точек?

Шаги

1. Вычислить уклон по 2 точкам. Например, две точки (3, 5) и (6, 11)
2. Подставьте наклон (м) в форму уравнения с пересечением наклона.
3. Подставьте любую точку в уравнение. Вы можете использовать либо (3,5), либо (6,11).
4. Найдите b, который является точкой пересечения линии по оси y.
5. Подставьте b в уравнение.

Как написать квадратное уравнение с точкой пересечения Y?

Как найти точку пересечения y квадратного уравнения?

Стандартная форма квадратного уравнения записывается как y=ax2+bx+c, где x и y — переменные, а a, b и c — известные константы. Чтобы найти точку пересечения по оси y из квадратного уравнения, подставьте 0 вместо значения x и решите. Точка пересечения с осью y всегда равна значению c в уравнении.

Как найти r1 и r2 квадратного уравнения?

Как найти квадратное уравнение с одним корнем?

Откуда взялась квадратная формула?

То персидский математик 9 века Мухаммад ибн Муса аль-Хорезми решал квадратные уравнения алгебраически. Квадратичная формула, охватывающая все случаи, была впервые получена Симоном Стевином в 1594 году. В 1637 году Рене Декарт опубликовал «Геометрию», содержащую частные случаи квадратичной формулы в той форме, которую мы знаем сегодня.

Какими 4 способами можно решить квадратное уравнение?

Четыре метода решения квадратного уравнения: разложение на множители, использование квадратных корней, завершение квадрата и квадратичная формула.

Каковы 5 примеров квадратного уравнения?

Примеры стандартной формы квадратного уравнения (ax² + bx + c = 0) включают:

• 6x² + 11x — 35 = 0.
• 2x² – 4x – 2 = 0.
• -4x² – 7x +12 = 0.
• 20x² -15x – 10 = 0.
• х² -х – 3 = 0.
• 5x² – 2x – 9 = 0.
• 3x² + 4x + 2 = 0.
• -x² +6x + 18 = 0.

См. также, почему растения важны для животных.

Как найти вершину квадратичной функции?

Мы находим вершину квадратного уравнения со следующими шагами:

1. Получите уравнение в виде y = ax2 + bx + c.
2. Вычислить -б/2а. Это x-координата вершины.
3. Чтобы найти координату y вершины, просто подставьте значение -b / 2a в уравнение для x и найдите y.

Как записать квадратичную функцию в стандартной форме с двумя точками?

Эти сценарии относятся непосредственно к конкретной форме квадратного уравнения:

1. y = a(x – h)2 + k (или форма вершины, где (h, k) – расположение вершины).
2. y = a (x — p) (x — q) (или форма пересечения x, где p и q — пересечения x).
3. y = ax2 + bx + c (или стандартная форма).

Как найти квадратичную функцию в вершинной форме?

Вершинная форма квадратичной функции f(x) = a(x – h)2 + k, где a, h и k — константы. параболы находится в точке (h, k). Когда квадратичная родительская функция f(x) = x2 записана в вершинной форме, y = a(x – h)2 + k, a = 1, h = 0 и k = 0.

Как найти квадратное уравнение по 2 точкам?

Какова формула параболы?

Общее уравнение параболы у = х² в котором х-квадрат является параболой. Обработав его сторону, он становится y² = x или математически выражается как y = √x. Формула уравнения параболы. При известном фокусе (h, k) и направляющей y = mx+b уравнение параболы имеет вид y−mx–b² / m²+1 = (x – h)² + (y – k)² .

Как найти вторую точку?

Как найти наклон двух заданных точек?

Используйте формулу наклона, чтобы найти наклон линии, зная координаты двух точек на линии. Формула наклона м=(у2-у1)/(х2-х1), или изменение значений y по сравнению с изменением значений x. Координаты первой точки представляют x1 и y1. Координаты второй точки x2, y2.

Что такое P и Q в квадратном уравнении?

«p» и «q» представляют x-перехваты. Х-пересечения — это точки пересечения графика с осью абсцисс. Х-пересечения находятся в точках х = -3 и х = 1. Неважно, какой х-перехват равен «р», а какой — «q».

Как найти точку пересечения нуля и оси Y квадратного уравнения?

Что такое вершинная форма?

Вершинная форма уравнения альтернативный способ записи уравнения параболы. … Из этой формы достаточно легко найти корни уравнения (там, где парабола попадает на ось x), приравняв уравнение к нулю (или используя квадратичную формулу).

Что такое дискриминантная формула?

Дискриминант является частью квадратной формулы под символом квадратного корня: b²-4ac. Дискриминант говорит нам, есть ли два решения, одно решение или нет решений.

Как найти сумму корней?

Для любого квадратного уравнения ax2 + bx + c = 0,

1. сумма корней = -b/a.
2. произведение корней = с/а.

Смотрите также, что такое максимальное значение

Если корни квадратного уравнения равны 2 и 3, то уравнение равно?

квадратное уравнение х^2-5х+6.

Что представляет собой квадратное уравнение, если его корни равны 0 и 4*?

х2+4х=0.

Как составить квадратное уравнение с нулями?

Какими тремя способами можно решить квадратное уравнение?

Существует три основных метода решения квадратных уравнений: разложение на множители по формуле квадрата и завершение квадрата.

Как проще всего решать квадратные уравнения?

Как решать квадратные уравнения для чайников?

Как найти вершину и точку пересечения Y квадратичной функции?

Нахождение квадратного уравнения по 2 точкам на параболе

Определение квадратного уравнения по вершине и точке

Как написать уравнение параболы по трем точкам

Нахождение квадратного уравнения по трем точкам

“Будущий математик, как и всякий человек учится при помощи практики и
подражания… .Ему следует решать задачи, выбирая те, которые соответствуют
его интересам, размышлять над их решением и изобретать новые задачи.”
Дьердь Пойа

Цели и задачи:

• Повторить свойства графика квадратичной функции у = aх² + bх + с, а ≠ 0;
• Повторить теорему Виета для корней квадратного уравнения ах² + bх + с =
  0;
• Рассмотреть алгоритм решения квадратного уравнения с параметром в
  котором поставлено условие для корней х₁ и х₂;
• Применять алгоритм для решения уравнений с параметром с поставленными
  условиями;
• Воспитывать чувство ответственности перед товарищами и умение работать в
  группах
• Развивать логическое мышление.

План занятия

1. Организационный момент.
2. Актуализация знаний учащихся:

• Повторение свойств графика квадратичной функции
• Повторение Теоремы Виета.

3. Изучение нового материала. Работа в группах:
Исследовательская работа. Отчет о проделанной работе.
4. Закрепление изученного материала.
5. Домашнее задание.
6. Итог занятия.

Оборудование: Мультимедийное оборудование, презентация,
(Приложение 1)

1. Организационный момент

Рассмотреть рисунки. Что общего на всех эти картинах? Что просматривается на
этих картинах? (Слайд 3, 4 ,5)

2. Актуализация знаний учащихся.

Повторение. (Слайд 6)

Парабола…
Что такое парабола?
Как может располагаться парабола в системе координат? Отчего это зависит?
(Слайд 6, 7)

3. Изучение нового материала.

Нас сегодня будет интересовать случай, когда парабола пересекает ось абсцисс
в двух точках, т.е. квадратное уравнение ах²+bх+с=0 имеет два корня.
Возьмем на оси абсцисс произвольную точку М. Давайте рассмотрим все случаи
расположения точки М и корней квадратного уравнения х₁ и х2.

Исследовательская работа в группах: (Слайд 8, 9, 10, 11)

1-я группа.

 2-я группа.

 3-я группа.

А вы, ребята, должны провести исследовательскую работу.

(Работа в группах.)

Задания даны на ваших инструкционных картах вместе с графиком.
Работаем 6–8 минут. А затем готовим выступление по своей работе.
Выводы записываем в заранее заготовленную таблицу на доске (или через
компьютерную презентацию).

Вместе вырабатываем (план) Алгоритм решения квадратного уравнения с
параметром относительно заданных точек.

Алгоритм решения. (Cлайд 12)

• Постановка проблемы.
• Путь решения.
• Составить математическую модель. (Ввести функцию.)
• Найти решение.
• Записать ответ.

5. Закрепление изученного материала. (Слайд 13)

При каких значениях а оба корня уравнения х² – ах + 2 = 0 лежат
в промежутке (0; 3)

Решение

1. Проблема поставлена условием задачи.
2. Воспользуемся первым способом решения:

1) D>0

3. Составим модель решения квадратного уравнения с параметром.

D = b² – 4ac
a² – 4•1•2 > 0

4. Решение

a² – 8 > 0
0 < a < 6
9 – 3a + 2 < 0
a² > 8
0 < a < 6
3a < 11

Решая, данную систему неравенств получаем:

Ответ:

Решаем вместе у доски:

При каких значениях а оба корня (а – 1)х2 – 2(а + 1)х + а – 3 = 0 лежат в промежутке (-1; 5)

Ответ:

Самостоятельно в тетрадях:

При каких значениях а оба корня 4х2 – (3а +1) х – а – 2 = 0 лежат в промежутке (-1; 2)

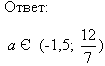6. Домашнее задание.

1) х² – ах + 2 = 0 лежат в промежутке (1; 3) Ответ:
[2√2; 3)

2) 4х² – 2х + а = 0 лежат в промежутке (-1; 1)
Ответ: (-2; 0,25]

7. Итог занятия. (Слайд 14)

“Считать несчастным тот день или тот час, в который ты не усвоил ничего
нового и ничего не прибавил к своему образованию”
Ян Амос Каминский

– Что нового узнали?
– Чему научились?

Квадратичная функция. Построение параболы

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ: наглядно.

• Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.

Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.

Построение квадратичной функции

Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:

График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :

Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:

x

y

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.

График функции y = –x 2 выглядит, как перевернутая парабола:

Зафиксируем координаты базовых точек в таблице:

x

y

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

• Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
• Если старший коэффициент меньше нуля a 2 + bx + c, для построения которой нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

1. Если D 0,то график выглядит так:

1. Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
2. Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:

Если a > 0, то график выглядит как-то так:

0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>

На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.

Разберем общий алгоритм на примере y = 2x 2 + 3x — 5.

Как строим:

1. Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена 2x 2 + 3x — 5.

D = b 2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

2x 2 + 3x — 5 = 0 2 + 3x — 5 = 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAPoAAAAyCAYAAAB1V8bkAAAJyElEQVR4Ae2c16sUwRLGfdRX/wXFB30QFFQUQUyIKCIGBEEQzCCoKIgB01ExZwVz4JpzztljwJxzzjlnrcuvL33unD2zOzO7OzvuThU0u5N6uuvrr7u6unrKiYpqQDVQ8BooV/A11AqqBlQDokTXRqAaiIEGlOgxAFmrqBpQomsbUA3EQANK9BiArFVUDSjRtQ2oBmKgASV6DEDWKqoGlOjaBlQDMdBAQRH9z58/8vv3b5P+/v2bMXy/fv0S8kxMGWesGRgNpIMXz7jhkg28CxmWgiH69+/f5dSpU7JixQpZtmyZXLx4UX7+/JkUOxoGjSaVTJw4UVatWiUbNmwoSYcPH071iF7zqYGgeNlsT58+LZMnTy7BA2y2bNkib9++tbfor4sGCobogD19+nR5/fq1nDx5Upo0aSLHjh2TZD39x48f5ebNmy4q+d8pRo327dtLo0aNTF6NGzeWevXqCeRXyVwDQfHijXTMmzZtMjiAL6lu3brSuXNnuXfvXuaFKuAcCobojOQDBgwwgD948EAg5ubNm42Z54bfjRs3ZMqUKW6XzDk6jP379wsjD/LmzRtZt26dvHr1KukzesG/BoLiRc5gceXKFZM4/vbtmxw6dEguXbokP3788P/yGN5ZMET/8uWLvHv3Tt6/f2/Muh49esj169eTQupF9MQHIfm1a9cST+txmhoIipfba86fPy9Hjx4VrDOV1BooGKJTTYh++fJlGTt2rCxevNgcJ6t+EKIz3587d26yrPR8mhoIglfiK549e2Y6dHBU8dZA3hH9+PHjYhNmnFO+fv1qTOwDBw5Ily5dhF+nQ47ndu/ebdLChQule/fuJcecp9E477d5d+zYUW7fvm0P9TeABixW/AbBCz+LffbChQtl3rh69WpZsmSJjuZlNON+Iu+IDkGZW+N427Ztm6nVp0+f5MiRI6Zh2Dl1hw4dZOjQoaVGdebc1oM+a9Ys48Sxx/y6zfUePnwoVapUcdeenvXUQLp4LV261OA8bdo0g5nzRR8+fJBhw4YJeav400DeEf3Ro0dmZGD+/fLlS1NLzLjhw4fLmDFjhEaA4DHv16+fGeHdVOHXdKczqVy5slsWes6HBtLF6/HjxwZn/CLPnz8v9aZbt25Jt27dlOiltJL6IO+I7lYdTPY1a9bIjBkz5M6dO7Jjxw5hRN++fXtSb6xfos+ZM0cqVark9trQzrEmXFxc7LnOH1oBQs44HbycRTpz5oy0a9funyA6DkGW/NavX19mauIsc+J/OkCmJliRL168ME7FVM7jxOeDHhcE0ak05KD3P3v2rFkWO3HihHz+/DmpPlh3XbRoUdLr9gL5LF++3B6G+nv//n3ZuHGjDBw4UDp16pS0kwq1EDnKPChezmI9efJEtm7dmnJVxXl/WP8PHjxopoxXr141RG3Tpo0JsPLzPqaaLVq0kDp16kjDhg2lb9++JgbEz7Pp3FMwRKfyBLkwX2fpxivqjbm8Nf1TKY77WK/NhVBuGvGoUaNMHID1N+Ti3VG8IwhezvIR5gwm/EYlrBgMGTJE9u3bZxy4YDV69Gjf/py9e/fKypUrjSVKLEDYqwcFRfSoQM/2e2fOnGmivgqd6NnWWy7zI3CqefPmUlRUVOIXgrzly5cXfEZewr2Y/XTuyaI3vfIIcj1tolM4lpyIBZ83b56MGzdO9uzZY0YjwkSfPn0apBx6r0MDYRBd8XIoOAt/sRiZU0N4az2OHz9eKlSo4MvSgOgs6RKIBYdIYUraRMfsYpkL84m5cc+ePY1DYv78+dKnTx/B2eAlmKldu3b1TISy5luII8s/XnWbNGmSMC9PlDCIrniJcXB6YcJ15s9+JHEkrlq1qixYsMDPowLRcRqzSgSHiOkI0xeUNtHpxXBUIQQ3tGrVKnLniC8N58FNYRBd8QoOPES2Php8Agw2dvR25gZRcaaNHDnSeTrlf/JxdhTsuMQacJ5LmUHAi2kT3b6HyrNBoXXr1uYUBXVThr3f+YuCcGp4JZRsFYAV8K8lt1hremqveuE4RAeJEgbR7Tvigpfb1JG6e2HCde5DCJbCM16rVi2T2D9BiLVT6Agwv3GsgSXPumHqfAZ+sLqCNWfbNQ455ve8MwxJm+gsXeF0YFcXPRlRaAiebD/OCO5l/XDQoEGeCTPHhqZWq1ZN/rVElF2iTJ061bNemHkEhiRKGESPG141atRIVKtZevXT3tjz7kcYgIioZDRmtyM6Zk09sf0zbYIndkBgabFt27ZmeZeYAgQzvmLFimWe9VMOP/ekTXTWMXv37m16uF69esmECRNMZdgDzgcgVIJrwLm8Vr9+fSECjM4wG6J4ZUOL/8+DgQdSwwGccIRkk4jITBRGaZZM8V/ZlRRGdIJlwJzBsX///gKPwpK0iY7HkArSgKgwu8XYMnju3LmkgSr0ZNZUCatCfvLFtKIHtj2sn2dycY8NmCGcF6cQIwXx+dmQfMMLfEj/qjA1Yx29ZcuWpRLmfaLcvXtXBg8eLCNGjChxUoM1mBAdt3btWmP9ZatTT3w/x2kTHcKytAB5EeYmyYiDecpWz9mzZyf9EIRb4cI6Rw/KikGcLI98w4vlWkKYC0Uw5xkEMeGt4A/Akc28P+wBMG2i28L6+WV7IruRmjVrVmK6+HkujHuYL+3atcuUhbm/SlkNRI0Xn/iqWbOmaTNlS5d/ZzDzITOhslFJTohO5Rg98WDaOUoUFabXpBExV2JThBI9OQpR4YX1x3SQb/UxOBSCYO2yA48RPCqJFdGZmxN8w/q/Ej11k4uK6ERXMqflw4+FQvTUms7N1VgRnYgndq2RlOipG1gURCf2myhLpldNmzZVoqeGKNDV2BAdj+bOnTuNcpTo3m0k10THrCVohCAiRInujVGQO2JDdJYA8bQTpIJHt3bt2mZtk1FEpawGck10PrRB4BEf4QQjgqIIK2UbqErmGsgJ0fE2AmL16tWFj/oRwpprYcRgVCcR+URsPkELBCyolNZAFHgRVcZyrcWoQYMGwtd97KfBSpdQj4JqICdEZ3kBkwwQIZZXLHDQSvi9H687G/wJgyREkl+7McdvHnG4L0q8WG9mUOCDnASf4DxVyVwDOSF65sXMXg6QnYbMMh+/fjfgZK8EmlMqDYAPzji7WyyqQSFVGfPxWuyIno8gaZlVA5lqQImeqQb1edVAHmhAiZ4HIGkRVQOZakCJnqkGI3m+WIrKlZOi45G8XF+ahxpQouchaKbIx4uU6PmKXQTlVqJHoPTMX/lM/tOuSIozz0hziIkGlOgxAVqrGW8NKNHjjb/WPiYaUKLHBGitZrw1oESPN/5a+5hoQIkeE6C1mvHWwH8BSUfSiO3XWNEAAAAASUVORK5CYII=»>

1. Координаты вершины параболы:

1. Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
2. Нанести эти точки на координатную плоскость и построить график параболы:
   2 + 3x — 5 = 0″ height=»671″ src=»https://lh6.googleusercontent.com/TYyA5dFfh0ZKINaPSps3Y_X1mCv8Mhv_8bNG3_dPbZud1AEsvo7UBFmVQNm1GcR1CQFo6HE1lNjYaAgepQUTQiK_ay_Fnuv7LEsB53woHkFO66W0R1PP8QfGsFcYzaR_h4AJdLxC» width=»602″>

Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀

Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.

Рассмотрим пример: y = 2 * (x — 1) 2 + 4.

Как строим:

1. Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:

• построить y = x 2 ,
• умножить ординаты всех точек графика на 2,
• сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• сдвинуть его вдоль оси OY на 4 единицы вверх.

1. Построить график параболы для каждого случая. 2 + y₀» height=»431″ src=»https://lh5.googleusercontent.com/_zgF-CXWf4Yy0p2OnBYSJkUm0zO-mNetq5feU6LIPEbIgSrO9kdr2ti_tr7Gg3yTMOlJVnuZgG0HleAFfAzG7yr7ELHT6KSMqMrRHkHqt-VcgIiSZx80cVj0zlPMBzEM0wAWQ-L6″ width=»602″>

Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)

Рассмотрим следующий пример: y = (x − 2) × (x + 1).

Как строим:

Данный вид уравнения позволяет быстро найти нули функции:

(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.

Определим координаты вершины параболы:

Найти точку пересечения с осью OY:

с = ab = (−2) × (1) = −2 и ей симметричная.

Отметим эти точки на координатной плоскости и соединим плавной прямой.

Как определить a, b и c по графику параболы

Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.

Коэффициент (a) можно найти с помощью следующих фактов:

— Если (a>0), то ветви параболы направленных вверх, если (a 1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:

Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.

Решаем систему.
Пример:

Вычтем из второго уравнения первое:

Подставим (9a) вместо (b):

Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

Подставим в первое уравнение (a):

Получается квадратичная функция: (y=-x^2-9x-15).

Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:

Сложим 2 уравнения:

Подставим во второе уравнение:

Теперь найдем точки пересечения двух функций:

Теперь можно найти ординату второй точки пересечения:

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Главный недостаток этого способа — вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).

– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.

– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.

График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.

У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:

Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).

Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).

Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).

Как построить параболу? Что такое парабола? Как решаются квадратные уравнения?

Урок: как построить параболу или квадратичную функцию?

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Парабола — это график функции описанный формулой ax 2 +bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:

1 ) Формула параболы y=ax 2 +bx+c,
если а>0 то ветви параболы направленны вверх,
а 2 +bx+c=0;

a) Полное квадратное уравнение имеет вид ax 2 +bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax 2 +bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);

4) Найти несколько дополнительных точек для построения функции.

ПРАКТИЧЕСКАЯ ЧАСТЬ

И так теперь на примере разберем все по действиям:
Пример №1:
y=x 2 +4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x 2 +4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x₁=(-4+2)/2=-1
x₂=(-4-2)/2=-3

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2

х -4 -3 -1 0
у 3 0 0 3

Подставляем вместо х в уравнение y=x 2 +4x+3 значения
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2

Пример №2:
y=-x 2 +4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1 2 +4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x 2 +4x=0
Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4.

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x 2 +4x значения
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2

Пример №3
y=x 2 -4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x 2 -4=0
Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x 2 =4
x₁=2
x₂=-2

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x 2 -4 значения
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0

Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.

Расположение корней квадратного трёхчлена относительно одной-двух заданных точек («метод парабол»)

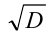
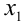
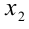
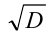
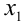
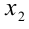
Многие задачи с параметрами сводятся к исследованию расположения корней квадратного трёхчлена относительно заданной точки или заданного промежутка (отрезка, интервала, луча). При этом если дискриминант D квадратного трёхчлена есть полный квадрат некоторого выражения (т.е. извлекается ), то в подавляющем большинстве случаев проще найти корни ,квадратного трёхчлена и подчинить их условиям задачи. Если же — не извлекается (остаётся радикал), то в принципе также можно найти корни , квадратного трёхчлена и подчинить их условиям задачи, но при этом придётся решать непростые иррациональные неравенства, которые приводят к большим и утомительным вычислениям. В этом случае более удобным оказывается следующий подход (иногда называемый методом парабол), использующий графическую интерпретацию расположения корней квадратного трёхчлена, вершины его графика по отношению к заданной точке (точкам).

Итак, пусть задана квадратичная функция

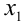
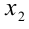
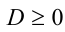
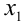
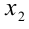
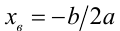
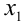
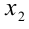
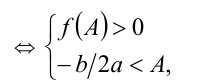
график которой имеет точки, пересечения с осью абсцисс (т.е. ). Пусть, для определённости, ветви параболы направлены вверх. Выпишем, например, условия, необходимые и достаточные для того, чтобы оба корня , были меньше заданного действительного числа А . Очевидно, что в этом случае вершина параболы должна располагаться левее точки x = А , и значение данной квадратичной функции в точке А должно быть положительно. Таким образом, оба корня , меньше заданного числа

т.е. данная система условий однозначно задаёт рассматриваемую ситуацию в расположении корней по отношению к А .

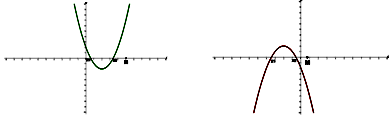
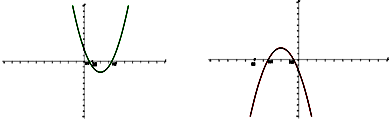
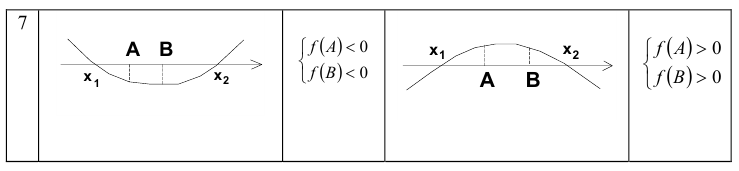
Понятно, что по отношению к одному заданному числу А возможны всего три ситуации: оба корня меньше А , оба корня больше А , корни расположены по разные стороны от А . Если же заданы два действительных числа А и В , то по отношению к ним возможны уже четыре ситуации расположения корней квадратного трёхчлена. Оформим полученный специальный метод в виде следующей таблицы.

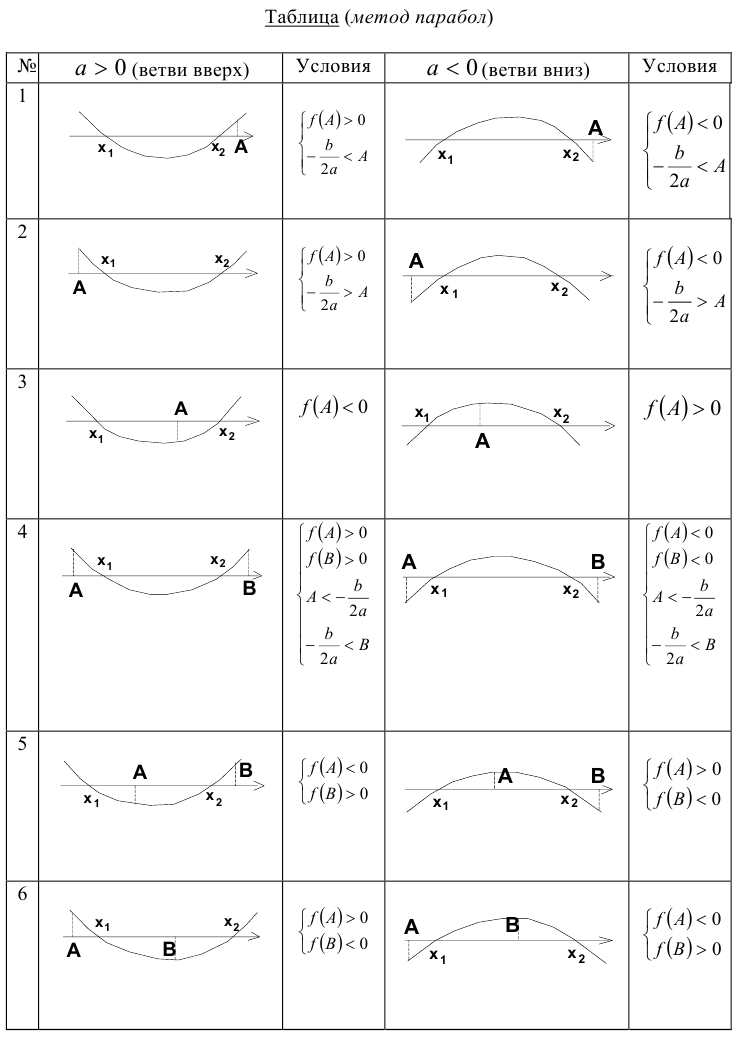
Замечание. При использовании данного метода внимательно читайте условие задачи. В зависимости от постановки задачи знак в неравенствах, приведённых в таблице, может быть как строгим, так и нестрогим. Неверно поставленный знак может привести к потере или, наоборот, к приобретению посторонних корней.

Пример №164.

Найти все значения параметра а , при которых корни уравнения 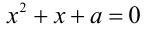действительные, различные и оба больше а .

Решение:

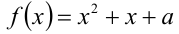
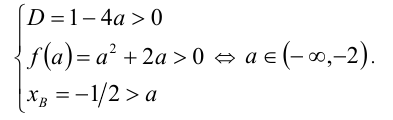
В этой задаче реализуется случай 2 из таблицы выше. Обозначим . В соответствии с методом, решение задачи сводится к системе

Пример №165.

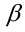
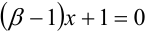
При каких значениях оба корня уравнения положительны и расположены по разные стороны от числа 3?

Решение:

Выпишем два способа решения задачи — стандартный и специальный, изложенный выше, и сравним их по эффективности.

Стандартный способ решения сводится к решению системы

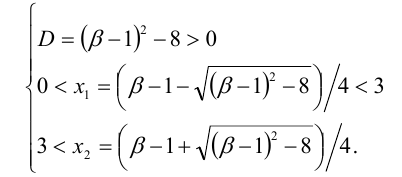
Специальный метод состоит в решении следующей системы (см. случай 6 в таблице; через f(x) обозначен многочлен в левой части уравнения):

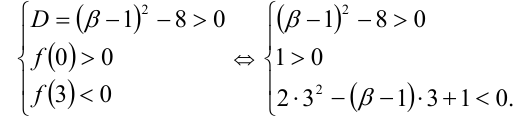
Условие положительности дискриминанта учтено в обоих способах решения. Но если при стандартном способе надо решать два иррациональных неравенства (одно из которых двойное), то при выборе второго способа вместо этого имеем два линейных неравенства (одно из которых тривиально). Безусловно, при решении данной задачи следует предпочесть второй вариант решения.

Ответ:

Пример №166.

Найти все значения параметра m , при которых один из корней квадратного трёхчлена

меньше, а другой больше двух.

Решение:

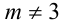
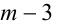
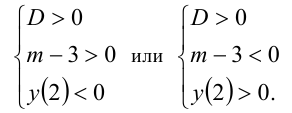
По условию . В зависимости от знака старшего коэффициента возможны два случая (см. пункт 3 в таблице):

Заметим, что эти случаи легко объединить в один:

Пример №167.

Найти наибольшее значение параметра p , при котором функция

принимает отрицательные значения в интервале (0,1).

Решение:

По условию задачи составляем систему (см. пункт 7 в таблице):

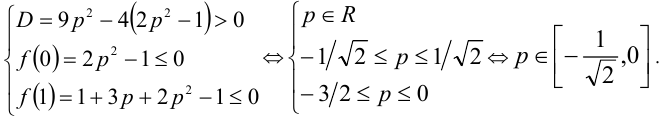
Ответ: наибольшее значение p равно 0.

Заметим, что необходимость использования приведённого метода при решении задач, связанных с корнями квадратного уравнения, возникает не всегда. Например, в следующей задаче вполне можно обойтись стандартным методом.

Пример №168.

При каких значениях параметра а больший корень уравнения

принадлежит промежутку [0,1) ?

Решение:

В данной задаче дискриминант является полным квадратом и, следовательно, корни имеют рациональные выражения: 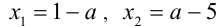. Согласно условию задачи, возможны два случая.

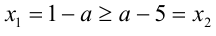
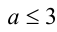
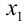
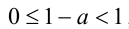
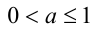
1) Если , т.е. , то большим является корень , и условие задачи приводит к неравенству , откуда .

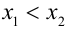
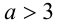
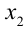
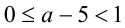
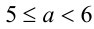
2) Если же , т.е. , то большим является корень , и условие задачи приводит к неравенству , откуда находим .

Ответ: .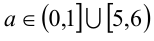

Общая рекомендация такова: если дискриминант квадратного уравнения является полным квадратом и, следовательно, корни имеют рациональный вид, во многих задачах приемлем (часто оказывается проще других методов) стандартный подход. Но если это не так и корни иррациональны, то более удобными могут оказаться специальный метод, эффективность которого была продемонстрирована выше на примерах, и теорема Виета, которые не требуют нахождения корней уравнения в явном виде.

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Предмет математика

Эти страницы возможно вам будут полезны: