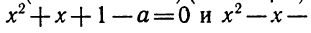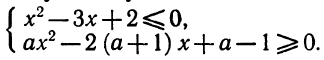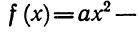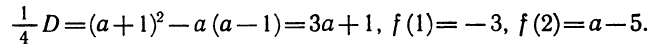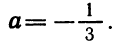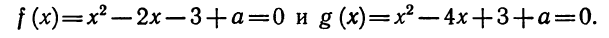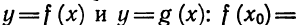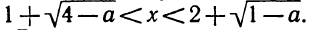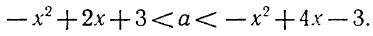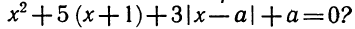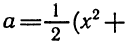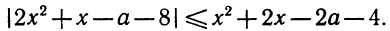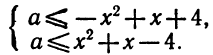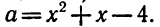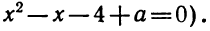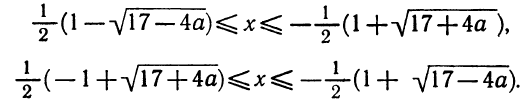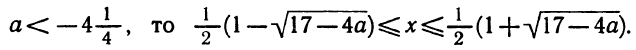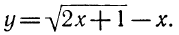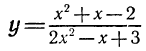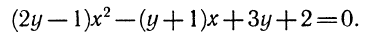Разложение квадратного трёхчлена на множители
Как разложить на множители квадратный трёхчлен
Квадратный трёхчлен — это многочлен вида ax 2 + bx + c .
В прошлых уроках мы решали квадратные уравнения. Общий вид таких уравнений выглядел так:
Левая часть этого уравнения является квадратным трёхчленом.
Одним из полезных преобразований при решении задач является разложение квадратного трёхчлена на множители. Для этого исходный квадратный трёхчлен приравнивают к нулю и решают квадратное уравнение. В этом случае говорят, что выполняется поиск корней квадратного трёхчлена.
Полученные корни x1 и x2 следует подстáвить в следующее выражение, которое и станет разложением:
Таким образом, чтобы разложить квадратный трёхчлен на множители при помощи решения квадратного уравнения, нужно воспользоваться следующей готовой формулой:
Где левая часть — исходный квадратный трёхчлен.
Пример 1. Разложить на множители следующий квадратный трёхчлен:
Найдём корни квадратного трёхчлена. Для этого приравняем данный квадратный трёхчлен к нулю и решим квадратное уравнение:
В данном случае коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента. Чтобы сэкономить время, некоторые подробные вычисления можно пропустить:
Итак, x1 = 6 , x2 = 2 . Теперь воспользуемся формулой ax 2 + bx + c = a(x − x1)(x − x2). В левой части вместо выражения ax 2 + bx + c напишем свой квадратный трёхчлен x 2 − 8x + 12. А в правой части подставим имеющиеся у нас значения. В данном случае a = 1, x1 = 6, x2 = 2
Если a равно единице (как в данном примере), то решение можно записать покороче:
Чтобы проверить правильно ли разложен квадратный трёхчлен на множители, нужно раскрыть скобки у правой части получившегося равенства.
Раскроем скобки у правой части равенства, то есть в выражении (x − 6)(x − 2) . Если мы всё сделали правильно, то должен получиться квадратный трёхчлен x 2 − 8x + 12
Пример 2. Разложить на множители следующий квадратный трёхчлен:
Приравняем данный квадратный трёхчлен к нулю и решим уравнение:
Как и в прошлом примере коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента:
Итак, x1 = 4 , x2 = 3 . Приравняем квадратный трехчлен 2x 2 − 14x + 24 к выражению a(x − x1)(x − x2) , где вместо переменных a , x1 и x2 подстáвим соответствующие значения. В данном случае a = 2
Выполним проверку. Для этого раскроем скобки у правой части получившегося равенства. Если мы всё сделали правильно, то должен получиться квадратный трёхчлен 2x 2 − 14x + 24
Как это работает
Разложение квадратного трёхчлена на множители происходит, если вместо коэффициентов квадратного трёхчлена подстáвить теорему Виета и выполнить тождественные преобразования.
Для начала рассмотрим случай, когда коэффициент a квадратного трёхчлена равен единице:
Вспоминаем, что если квадратное уравнение является приведённым, то теорема Виета имеет вид:
Тогда приведённый квадратный трехчлен x 2 + bx + c можно разложить на множители следующим образом. Сначала выразим b из уравнения x1 + x2 = −b . Для этого можно умножить обе его части на −1
Переменную c из теоремы Виета выражать не нужно — она уже выражена. Достаточно поменять местами левую и правую часть:
Теперь подставим выраженные переменные b и c в квадратный трёхчлен x 2 + bx + c
Раскроем скобки там где это можно:
В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:
Из первых скобок вынесем общий множитель x , из вторых скобок — общий множитель −x2
Далее замечаем, что выражение ( x − x1 ) является общим множителем. Вынесем его за скобки:
Но это был случай, когда исходный квадратный трёхчлен является приведённым. В нём коэффициент a равен единице. И соответственно, в формуле разложения такого квадратного трехчлена коэффициент a можно опустить.
Теперь рассмотрим случай, когда коэффициент a квадратного трёхчлена не равен единице. Это как раз тот случай, когда в формуле разложения присутствует перед скобками коэффициент a
Вспоминаем, что если квадратное уравнение не является приведённым, то есть имеет вид ax 2 + bx + c = 0 , то теорема Виета принимает следующий вид:
Это потому что теорема Виета работает только для приведённых квадратных уравнений. А чтобы уравнение ax 2 + bx + c = 0 стало приведённым, нужно разделить обе его части на a
Далее чтобы квадратный трёхчлен вида ax 2 + bx + c разложить на множители, нужно вместо b и c подставить соответствующие выражения из теоремы Виета. Но в этот раз нам следует использовать равенства и
Для начала выразим b и c . В первом равенстве умножим обе части на a . Затем обе части получившегося равенства умножим на −1
Теперь из второго равенства выразим c . Для этого умножим обе его части на a
Теперь подставим выраженные переменные b и с в квадратный трёхчлен ax 2 + bx + c . Для наглядности каждое преобразование будем выполнять на новой строчке:
Здесь вместо переменных b и c были подставлены выражения −ax1 − ax2 и ax1x2 , которые мы ранее выразили из теоремы Виета. Теперь раскроем скобки там где это можно:
В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:
Теперь из первых скобок вынесем общий множитель ax , а из вторых — общий множитель −ax2
Далее замечаем, что выражение x − x1 тоже является общим множителем. Вынесем его за скобки:
Вторые скобки содержат общий множитель a . Вынесем его за скобки. Его можно расположить в самом начале выражения:
Отметим, что если квадратный трехчлен не имеет корней, то его нельзя разложить на множители. Действительно, если не найдены корни квадратного трёхчлена, то нéчего будет подставлять в выражение a(x − x1)(x − x2) вместо переменных x1 и x2 .
Если квадратный трёхчлен имеет только один корень, то этот корень одновременно подставляется в x1 и x2 . Например, квадратный трёхчлен x 2 + 4x + 4 имеет только один корень −2
Тогда значение −2 в процессе разложения на множители будет подставлено вместо x1 и x2 . А значение a в данном случае равно единице. Её можно не записывать, поскольку это ничего не даст:
Скобки внутри скобок можно раскрыть. Тогда получим следующее:
При этом если нужно получить короткий ответ, последнее выражение можно записать в виде (x + 2) 2 поскольку выражение (x + 2)(x + 2) это перемножение двух сомножителей, каждый из которых равен (x + 2)
Примеры разложений
Пример 1. Разложить на множители следующий квадратный трёхчлен:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения. В левой части напишем квадратный трёхчлен 3x 2 − 2x − 1 , а в правой части — его разложение в виде a(x − x1)(x − x2) , где вместо a , x1 и x2 подстáвим соответствующие значения:
Во вторых скобках можно заменить вычитание сложением:
Пример 2. Разложить на множители следующий квадратный трёхчлен:
Упорядочим члены так, чтобы старший коэффициент располагался первым, средний — вторым, свободный член — третьим:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Упростим получившееся разложение. Вынесем за первые скобки общий множитель 3
Теперь воспользуемся сочетательным законом умножения. Напомним, что он позволяет перемножать сомножители в любом порядке. Умножим 3 на вторые скобки. Это позвóлит избавиться от дроби в этих скобках:
Пример 3. Разложить на множители следующий квадратный трёхчлен:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Пример 4. Найдите значение k , при котором разложение на множители трёхчлена 3x 2 − 8x + k содержит множитель (x − 2)
Если разложение содержит множитель (x − 2) , то один из корней квадратного трёхчлена равен 2 . Пусть корень 2 это значение переменной x1
Чтобы найти значение k , нужно знать чему равен второй корень. Для его определения воспользуемся теоремой Виета.
В данном случае квадратный трёхчлен не является приведённым, поэтому сумма его корней будет равна дроби , а произведение корней — дроби
Выразим из первого равенства переменную x2 и сразу подстáвим найденное значение во второе равенство вместо x2
Теперь из второго равенства выразим k . Так мы найдём его значение.
Пример 5. Разложить на множители следующий квадратный трёхчлен:
Перепишем данный трёхчлен в удобный для нас вид. Если в первом члене заменить деление умножением, то получим . Если поменять местами сомножители, то получится . То есть коэффициент a станет равным
Коэффициент b можно перевести в обыкновенную дробь. Так проще будет искать дискриминант:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Квадратные уравнения
| Решение неполных квадратных уравнений |
| Выделение полного квадрата |
| Дискриминант |
| Разложение квадратного трехчлена на множители |
| Формула для корней квадратного уравнения |
| Прямая и обратная теоремы Виета |
Квадратным трёхчленом относительно переменной x называют многочлен
где a, b и c – произвольные вещественные числа, причем
Квадратным уравнением относительно переменной x называют уравнение
где a, b и c – произвольные вещественные числа, причем
Полным квадратным уравнением относительно переменной x называют уравнение
где a, b и c – произвольные вещественные числа, отличные от нуля.
Неполными квадратными уравнениями называют квадратные уравнения следующих типов:
Решение неполных квадратных уравнений
Покажем, как решаются неполные квадратные уравнения на примерах.
Пример 1 . Решить уравнение
Пример 2 . Решить уравнение
Решение . Вынося в левой части уравнения (3) переменную x за скобки, перепишем уравнение в виде
Поскольку произведение двух сомножителей равно нулю тогда и только тогда, когда, или первый сомножитель равен нулю, или второй сомножитель равен нулю, то из уравнения (4) получаем:
Ответ : .
Пример 3 . Решить уравнение
Ответ : .
Пример 4 . Решить уравнение
Решение . Поскольку левая часть уравнения (5) положительна при всех значениях переменной x , а правая часть равна 0, то уравнение решений не имеет.
Ответ : .
Выделение полного квадрата
Выделением полного квадрата называют представление квадратного трёхчлена (1) в виде:
Для того, чтобы получить формулу (6), совершим следующие преобразования:
Формула (6) получена.
Дискриминант
Дискриминантом квадратного трёхчлена (1) называют число, которое обозначается буквой D и вычисляется по формуле:
Дискриминант квадратного трёхчлена играет важную роль, и от того, какой знак он имеет, зависят различные свойства квадратного трёхчлена.
Используя дискриминант, формулу (6) можно переписать в виде
Разложение квадратного трёхчлена на множители
Утверждение . В случае, когда , квадратный трёхчлен (1) разлагается на линейные множители. В случае, когда D , квадратный трехчлен нельзя разложить на линейные множители.
Доказательство . В случае, когда D = 0 , формула (8) и является разложением квадратного трехчлена на линейные множители:
В случае, когда D > 0 , выражение, стоящее в квадратных скобках в формуле (8), можно разложить на множители, воспользовавшись формулой сокращенного умножения «Разность квадратов»:
Таким образом, в случае, когда D > 0 , разложение квадратного трехчлена (1) на линейные множители имеет вид
В случае, когда D , выражение, стоящее в квадратных скобках в формуле (8), является суммой квадратов и квадратный трёхчлен на множители не раскладывается.
Замечание . В случае, когда D , квадратный трехчлен всё-таки можно разложить на линейные множители, но только в области комплексных чисел, однако этот материал выходит за рамки школьного курса.
Формула для корней квадратного уравнения
Из формул (9) и (10) вытекает формула для корней квадратного уравнения .
Действительно, в случае, когда D = 0 , из формулы (9) получаем:
Следовательно, в случае, когда D = 0 , уравнение (1) обладает единственным корнем, который вычисляется по формуле
В случае, когда D > 0 , из формулы (10) получаем:
Таким образом, в случае, когда D > 0 , уравнение (1) имеет два различных корня , которые вычисляются по формулам
Замечание 1 . Формулы (12) и (13) часто объединяют в одну формулу и записывают так:
Замечание 2 . В случае, когда D = 0 , обе формулы (12) и (13) превращаются в формулу (11). Поэтому часто говорят, что в случае, когда D = 0 , квадратное уравнение (1) имеет два совпавших корня , вычисляемых по формуле (11), а саму формулу (11) переписывают в виде:
Замечание 3 . В соответствии с материалом, изложенным в разделе «Кратные корни многочленов», корень (11) является корнем уравнения (1) кратности 2.
В случае, когда D = 0 , разложение квадратного трехчлена на линейные множители (9) можно переписать по-другому, воспользовавшись формулой (15):
| ax 2 + bx + c = = a (x – x1) 2 . |
(16) |
В случае, когда D > 0 , разложение квадратного трехчлена на линейные множители (10) с помощью формул (12) и (13) переписывается так:
| ax 2 + bx + c = = a (x – x1) (x – x2) . |
(17) |
Замечание 4 . В случае, когда D = 0 , корни x1 и x2 совпадают, и формула (17) принимает вид (16).
Прямая и обратная теоремы Виета
Раскрывая скобки и приводя подобные члены в правой части формулы (17), получаем равенство
Отсюда, поскольку формула (17) является тождеством, вытекает, что коэффициенты многочлена
равны соответствующим коэффициентам многочлена
Таким образом, справедливы равенства
следствием которых являются формулы
Формулы (18) и составляют содержание теоремы Виета (прямой теоремы Виета) .
Словами прямая теорема Виета формулируется так: — «Если числа x1 и x2 являются корнями квадратного уравнения (1), то они удовлетворяют равенствам (18)».
Обратная теорема Виета формулируется так: — «Если числа x1 и x2 являются решениями системы уравнений (18), то они являются корнями квадратного уравнения (1)».
Для желающих ознакомиться с примерами решений различных задач по теме «Квадратные уравнения» мы рекомендуем наше учебное пособие «Квадратный трехчлен».
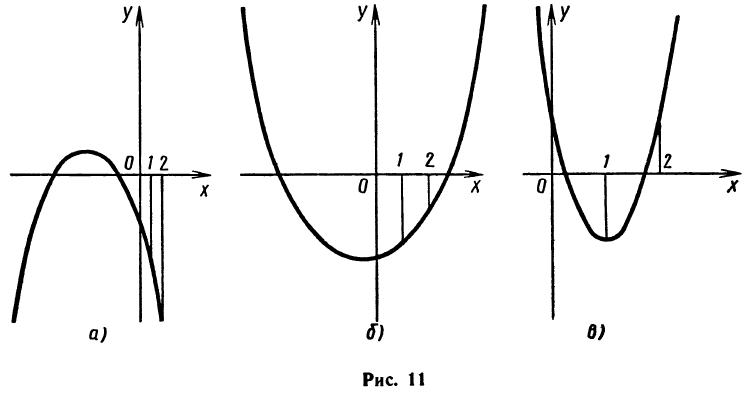
Графики парабол и решение с их помощью квадратных неравенств представлены в разделе «Парабола на координатной плоскости. Решение квадратных неравенств» нашего справочника.
Как решать квадратные уравнения
О чем эта статья:
Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, которое содержит переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.
А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Квадратные уравнения могут иметь два корня, один корень или не иметь корней.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b 2 − 4ac. А вот свойства дискриминанта:
- если D 0, есть два различных корня.
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.
Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.
Давайте-ка на примерах — вот у нас есть два уравнения:
- x 2 — 2x + 6 = 0
- x 2 — x — 1/4 = 0
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x 2 ), а значит уравнение называется приведенным.
- 2x 2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Пример 1. Превратим неприведенное уравнение: 8x 2 + 20x — 9 = 0 — в приведенное.
Для этого разделим обе части исходного уравнения на старший коэффициент 8:
Ответ: равносильное данному приведенное уравнение x 2 + 2,5x — 1,125 = 0.
Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax 2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax 2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
| Для самых любопытных объясняем откуда появились такие названия: | |
|---|---|
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. Решение неполных квадратных уравненийКак мы уже знаем, есть три вида неполных квадратных уравнений:
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам. Как решить уравнение ax 2 = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0. Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней. Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0. Пример 1. Решить −6x 2 = 0.
Как решить уравнение ax 2 + с = 0Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный. Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами. Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи. Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней. Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:
Пример 1. Найти решение уравнения 8x 2 + 5 = 0.
Разделим обе части на 8: Ответ: уравнение 8x 2 + 5 = 0 не имеет корней. Как решить уравнение ax 2 + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0. Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение: Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a. Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня: Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0 0,5x = 0,125, Ответ: х = 0 и х = 0,25. Как разложить квадратное уравнениеС помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так: Формула разложения квадратного трехчлена Если x1 и x2 — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x1) (x − x2). Дискриминант: формула корней квадратного уравненияЧтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так: где D = b 2 − 4ac — дискриминант квадратного уравнения. Эта запись означает: Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться. Алгоритм решения квадратных уравнений по формулам корнейТеперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни. В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней. Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться! Примеры решения квадратных уравненийКак решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике. Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.
Ответ: единственный корень 3,5. Пример 2. Решить уравнение 54 — 6x 2 = 0.
Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую Ответ: два корня 3 и — 3. Пример 3. Решить уравнение x 2 — х = 0.
Ответ: два корня 0 и 1. Пример 4. Решить уравнение x 2 — 10 = 39.
Ответ: два корня 7 и −7. Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.
D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112 Ответ: корней нет. В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся. Формула корней для четных вторых коэффициентовРассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b 2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула. Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней: 2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″> Для удобства вычислений обозначим выражение n 2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид: где D1 = n 2 — ac. Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения. Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
Формула ВиетаЕсли в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену. Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства: Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам. Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0. Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре: Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит: Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента: Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное. Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется: Результат проделанных вычислений в том, что мы убедились в справедливости выражения: Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она: Обратная теорема Виета Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0. Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение. Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″> Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы. Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже. Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам: Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p> Упрощаем вид квадратных уравненийЕсли мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту. Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0. Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100. Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов. Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто. А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0. Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0. Связь между корнями и коэффициентамиМы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты: Из этой формулы, можно получить другие зависимости между корнями и коэффициентами. Например, можно применить формулы из теоремы Виета: Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3. Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты: источники: http://www.resolventa.ru/spr/algebra/kv.htm http://skysmart.ru/articles/mathematic/kak-reshat-kvadratnye-uravneniya |
Разложение квадратного трехчлена на множители
Квадратный трехчлен можно разложить на множители следующим образом:
a x 2 + b x + c = a ⋅ ( x − x 1 ) ⋅ ( x − x 2 )
где a – число, коэффициент перед старшим коэффициентом,
x – переменная (то есть буква),
x 1 и x 2 – числа, корни квадратного уравнения a x 2 + b x + c = 0 , которые найдены через дискриминант.
Если квадратное уравнение имеет только один корень , то разложение выглядит так:
a x 2 + b x + c = a ⋅ ( x − x 0 ) 2
Примеры разложения квадратного трехчлена на множители:
- − x 2 + 6 x + 7 = 0 ⇒ x 1 = − 1, x 2 = 7
− x 2 + 6 x + 7 = ( − 1 ) ⋅ ( x − ( − 1 ) ) ( x − 7 ) = − ( x + 1 ) ( x − 7 ) = ( x + 1 ) ( 7 − x )
- − x 2 + 4 x − 4 = 0 ; ⇒ x 0 = 2
− x 2 + 4 x − 4 = ( − 1 ) ⋅ ( x − 2 ) 2 = − ( x − 2 ) 2
Если квадратный трехчлен является неполным ( b = 0 или c = 0 ) , то его можно разложить на множители следующими способами:
- c = 0 ⇒ a x 2 + b x = x ( a x + b )
- b = 0 ⇒ применить формулу сокращенного умножения для разности квадратов.
Задания для самостоятельного решения
№1. Квадратный трёхчлен разложен на множители: x 2 + 6 x − 27 = ( x + 9 ) ( x − a ) . Найдите a .
№2. Уравнение x 2 + p x + q = 0 имеет корни − 5 ; 7. Найдите q .
Класс: 8
«Б» Предмет: Алгебра Дата:
_______
Урок
№ 64 Тема: «Составление
квадратного трехчлена по его корням»
Цели
урока: научить составлять
квадратный трехчлена по его корням.
Задачи
урока:
Обучающая: повторить
понятие квадратного трехчлена и его корней; формировать умение составлять квадратный трехчлена по его корням.
Развивающая:
развитие логического мышления, познавательных интересов.
Воспитательная: воспитание организованности,
дисциплинированности, аккуратности, усидчивости.
Тип
урока: урок изучения нового
материала и первичного закрепления
Методы и приемы: словесный, наглядный, практический.
Материально-техническое обеспечение: дидактический материал.
План
урока:
I.
Организационный
момент
II.
Актуализация знаний
III.
Первичное усвоение новой учебной информации
IV.
Осознание и осмысление
V.
Закрепление
VI.
Информация о домашнем задании
VII.
Подведение итогов урока
Ход урока
І.
Организационный момент
|
— Цели |
Приветствие, проверка готовности |
ІІ. Актуализация знаний
|
— Давайте — Разложите — а) Х2— — Найдите — а) Х2— |
Ребята отвечают |
ІІІ. Первичное усвоение
новой учебной информации
§ 54 . Разложение квадратного трехчлена на линейные множители
В этом
параграфе мы рассмотрим следующий вопрос: в каком случае квадратный трехчлен ax2 + bx + c можно
представить в виде произведения
(a1x + b1)
(a2x + b2)
двух
линейных относительно х множителей с действительными
коэффициентами a1, b1, a2, b2 (a1 =/=0, a2 =/=0) ?
1.
Предположим, что данный квадратный трехчлен ax2 + bx + c представим
в виде
ax2 + bx
+ c = (a1x
+ b1) (a2x + b2).
(1)
Правая
часть формулы (1) обращается в нуль при х = — b1/ a1 и х = — b2/ a2 (a1иa2 по условию не равны нулю). Но
в таком случае числа — b1/ a1 и — b2/ a2 являются
корнями уравнения
ax2 + bx + c = 0.
Следовательно,
дискриминант квадратного трехчлена ax2 + bx + c должен быть неотрицательным.
2.
Обратно, предположим, что
дискриминант D = b2 — 4ас квадратного трехчлена ax2 + bx + c неотрицателен.
Тогда этот трехчлен имеет
действительные корни x1
и x2.
Используя теорему Виета, получаем:
ax2 + bx + c = а (x2 + b/a х + c/a)
= а [x2 — (x1 + x2) х + x1x2]
=
= а [(x2— x1x ) — (x2x — x1x2)]
= а [х (х — x1)
— x2(х — x1)
=
= a(х — x1)(х — x2).
Итак,
ax2 + bx + c = a(х — x1)(х — x2),
(2)
где x1 и x2 — корни трехчлена ax2 + bx + c. Коэффициент а можно отнести к любому из двух
линейных множителей, например,
a(х — x1)(х — x2)
= (aх — ax1)(х — x2).
Но это
означает, что в рассматриваемом случае квадратный трехчлен ax2 + bx + c представим в
виде произведения двух линейных множителей с действительными коэффициентами.
Объединяя
результаты, полученные в пунктах 1 и 2, мы приходим к следующей теореме.
Теорема. Квадратный трехчлен ax2 + bx + c тогда и тoлько
тогда можно представить в виде произведения двух линейных множителей с
действительными коэффициентами,
ax2 + bx + c = (aх — ax1)(х — x2),
когда
дискриминант этого квадратного трехчлена неотрицателен
(то есть когда этот трехчлен имеет
действительные корни).
Пример
1.
Разложить на линейные множители 6x2 — х —1.
Корни
этого квадратного трехчлена равны x1 = 1/2 и x2 = — 1/3.
Поэтому
по формуле (2)
6x2 — х —1 = 6 (х — 1/2)(х + 1/3)
= (2х — 1) (3x + 1).
Пример
2.
Разложить на линейные множители x2 + х + 1. Дискриминант
этого квадратного трехчлена отрицателен:
D = 12 — 4•1•1 = — 3 <
0.
Поэтому
данный квадратный трехчлен на линейные множители с
действительными коэффициентами не раскладывается.
Упражнения
Разложить
на линейные множители следующие
выражения (№ 403 — 406):
403. 6x2 —
7х + 2.
405. x2 — х + 1.
404.
2x2 —
7ах + 6а2.
406. x2 — 3ах + 2а2 — аb— b2.
Предположим,
что нам нужно составить квадратное уравнение, корнями которого
были бы числа x1 и x2. Очевидно,
что в качестве искомого уравнения можно выбрать уравнение
a(х — x1)(х — x2)
= 0,
(1)
где а — любое отличное от нуля
действительное число. С другой стороны, как было показано в § 54, каждое
квадратное уравнение с корнями x1
и x2 можно
записать в виде (1).
Таким
образом, формула (1) полностью решает поставленную выше задачу. Из всех квадратных
уравнений корни x1 и x2 имеют
уравнения вида (1) и только, они.
ІV.Осознание и осмысление
Пример. Составить квадратное уравнение,
корни которого равны 1 и — 2.
Ответ.
Корни 1 и —2 имеют все квадратные уравнения вида
а(х — 1)(х + 2) = 0,
или
ах2 + ах — 2а = 0,
где а — любое отличное от нуля
действительное число. Например, при а = 1 получается
уравнение
х2 + х — 2 = 0.
V. Закрепление
Упражнения
1.
Составить квадратное уравнение, корнями которого были бы числа:
а) 2 и
— 3; б) — 1 и — 5; в) 1/4 и 1/6;
г) — 1/2 и
— 1/3 .
2.
Составить квадратное уравнение с целыми коэффициентами так, чтобы его
корни были равны:
а) — 1/5 и
2/3; б) 4/7 и
5; в) — 3/2
и 2/9;
г) — 3/10 и — 2/5.
3.
Составить квадратное
уравнение с целыми коэффициентами, корни которого равны 5/7 и — 1/2, а сумма
всех коэффициентов равна 36.
Решение:
(х-5/7)(х-1/2)=0 х2-17/14х+5/14=0 14х2-17х+5=0
14+17+5=36
4.
Могут ли корнями квадратного уравнения с натуральными коэффициентами
быть числа 6/5 и
— 1/7?
Решение:
(х-6/5)(х+1/7)=0 35х2-37х-6=0 (да)
5.
Составить
квадратное уравнение с целыми коэффициентами, если известно, что один из
его корней равен:
а) 2 +
√3 ; б) 3
—√2
в)
√3-5
Решение
Второй корень будет сопряжён первому, т. е. x1 =
√3−5; x2 = −√3−5.
Ищем квадратное уравнение в виде x² + ax + b =
0,
тогда по теореме Виета a = −(x1+x2)
= −2•(−5) = 10, b = x1•x2 = (−5)²−(√3)² = 22.
ОТВЕТ: x²+10x+22 = 0.
Решить №3,№5 на стр.97-98 проверь себя, дополнительно №242
(1,2).
VI.Информация о домашнем задании
№228, №234+ Повторить пройденную
тему§12.
VII.Подведение итогов
урока
Давайте
теперь подведем итоги урока :
Учитель благодарит за урок и объявляет оценки.
Квадратный трехчлен – это многочлен вида (ax^2+bx+c) ((a≠0)).
Пример:
(x^2-2x+1)
(3x^2-5x+6)
Почему его называют именно так? Потому что, наибольшая степень у него – квадрат, а состоит он из трех слагаемых (одночленов). Вот и получается – квадратный трехчлен.

Примеры не квадратных трехчленов:
(x^3-3x^2-5x+6) — кубический четырёхчлен
(2x+1) — линейный двучлен
Корень квадратного трехчлена:
Значение переменной (x), при котором квадратный трехчлен обращается в ноль, называют его корнем.
Пример:
У трехчлена (x^2-2x+1) корень (1), потому что (1^2-2·1+1=0)
У трехчлена (x^2+2x-3) корни (1) и (-3), потому что (1^2+2-3=0) и ((-3)^2-6-3=9-9=0)
Например: если нужно найти корни для квадратного трехчлена (x^2-2x+1), приравняем его к нулю и решим уравнение (x^2-2x+1=0).
(D=4-4cdot1=0)
(x=frac{2-0}{2}=frac{2}{2}=1)
Готово. Корень равен (1).
Разложение квадратного трёхчлена на множители:
Квадратный трехчлен (ax^2+bx+c) можно разложить как (a(x-x_1 )(x-x_2)), если дискриминант уравнения (ax^2+bx+c=0) больше нуля (x_1) и (x_2) — корни того же уравнения).
Например, рассмотрим трехчлен (3x^2+13x-10).
У квадратного уравнения (3x^2+13x-10=0) дискриминант равен 289 (больше нуля), а корни равны (-5) и (frac{2}{3}). Поэтому (3x^2+13x-10=3(x+5)(x-frac{2}{3})). В верности этого утверждения легко убедится – если мы раскроем скобки, то получим исходный трехчлен.
Квадратный трехчлен (ax^2+bx+c) можно представить как (a(x-x_1)^2), если дискриминант уравнения (ax^2+bx+c=0) равен нулю.
Например, рассмотрим трехчлен (x^2+6x+9).
У квадратного уравнения (x^2+6x+9=0) дискриминант равен (0), а единственный корень равен (-3). Значит, (x^2+6x+9=(x+3)^2) (здесь коэффициент (a=1), поэтому перед скобкой не пишется – незачем). Обратите внимание, что тоже самое преобразование можно сделать и по формулам сокращенного умножения.
Квадратный трехчлен (ax^2+bx+c) не раскладывается на множители, если дискриминант уравнения (ax^2+bx+c=0) меньше нуля.
Например, у трехчленов (x^2+x+4) и (-5x^2+2x-1) – дискриминант меньше нуля. Поэтому разложить их на множители невозможно.
Пример. Разложите на множители (2x^2-11x+12).
Решение:
Найдем корни квадратного уравнения (2x^2-11x+12=0)
(D=11^2-4 cdot 2 cdot 12=121-96=25>0)
(x_1=frac{11-5}{4}=1,5;) (x_2=frac{11+5}{4}=4.)
Значит, (2x^2-11x+12=2(x-1,5)(x-4))
Ответ: (2(x-1,5)(x-4))
Полученный ответ, может быть, записать по-другому: ((2x-3)(x-4)).
Пример. (Задание из ОГЭ) Квадратный трехчлен разложен на множители (5x^2+33x+40=5(x++ 5)(x-a)). Найдите (a).
Решение:
(5x^2+33x+40=0)
(D=33^2-4 cdot 5 cdot 40=1089-800=289=17^2)
(x_1=frac{-33-17}{10}=-5)
(x_2=frac{-33+17}{10}=-1,6)
(5x^2+33x+40=5(x+5)(x+1,6))
Ответ: (-1,6)
Смотрите также:
Квадратный трехчлен (шпаргалка)
Квадратный трехчлен – это многочлен вида a x 2 + b x + c ( a ≠ 0 ).
Исследование квадратного трёхчлена
Задача:
C аэростата, находящегося на высоте 1000 м, сбросили груз со скоростью 20 м в секунду. На каком расстоянии от земли этот груз будет через 15 сек.? (Сопротивление воздуха в расчёт не принимается.)
Путь, проходимый падающим телом, вычисляется по формуле: 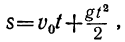
где 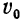
В данном случае 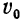
s=20t+4,9t². (2)
Такой путь пройдёт падающий груз за t секунд. Значит, через t секунд он будет находиться на высоте
x=1000-20t— 4,9t² (3)
метров от земли. Чтобы определить х — высоту груза над землёй через 15 сек., очевидно, достаточно в (3) подставить t = 15 и произвести вычисления. Получим:
x = 1000-20∙15-4,9∙15²= —402,5.
Отрицательное значение х здесь не имеет смысла, и, следовательно, наша задача не имеет решения. Почему так получилось? Чтобы ответить на этот вопрос, определим сначала, через сколько секунд сброшенный груз упадёт на землю? Очевидно, это произойдёт в тот момент, когда груз пройдёт путь, равный высоте, с которой он был сброшен, т. е. 1000 м. Значит, мы должны иметь:
20t- 4,9t² =1000,
или
4,9t² +20t-1000= 0. (4)
Решив это уравнение, найдём t =12,4 сек. (с точностью до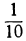
При каких же значениях t задача допускает вполне определённое решение? Очевидно, только для тех значений, при которых путь, пройденный грузом, меньше 1000 м, т. е. при условии, что
4,9t²+20t< 1000,
или, что то же,
4,9t2⅛20∕ — 1000 <0. (5)
Значит, задача имеет решение только при таких (положительных) значениях /, при которых трёхчлен 4,9t²+20t— 1000 является отрицательным числом. Это будет при t<12,4.
Во многих задачах, как в приведённой выше, требуется определить для данного трёхчлена, при каких значениях входящей в него буквы он является положительным и при каких отрицательным. В этом и заключается исследование квадратного трёхчлена.
Квадратный трёхчлен, имеющий действительные различные корни
Пример:
Пусть дан трёхчлен:
y=2x² — 7x+3. (1)
Требуется определить, при каких значениях х этот трёхчлен будет иметь положительные и при каких отрицательные значения.
Мы знаем, что всякий квадратный трёхчлен можно представить в виде произведения коэффициента при х² и разностей между переменным и корнями трёхчлена.
Найдём корни данного трёхчлена, для чего решим уравнение
2x² — 7x+3=0. (2)
Получим: 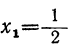
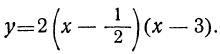
Исследуем теперь, при каких значениях х это произведение будет числом положительным и при каких отрицательным. Разберём три случая.
1. Пусть 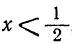
Следовательно, произведение 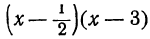
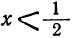
2. Пусть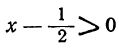
т. е. значения х заключены между корнями данного трёхчлена. Из этих неравенств, после переноса членов в левую часть, получим: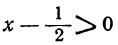
Стало быть, в произведении 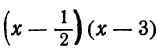
выражение (3), а следовательно, и данный трёхчлен, является отрицательным числом.
3. Пусть х>3, тогда и подавно 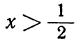
х — 3 >> 0 и х
Произведение 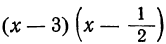
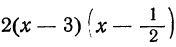
данный трёхчлен — число положительное. Итак, мы пришли к следующему выводу. Трёхчлен 2x²-7x+3 имеет положительные значения при всех значениях х, меньших 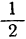
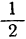
Проверка сделанных выводов на некоторых числовых значениях х дана в следующей таблице, где в верхней строке даны значения х, а в нижней — соответствующие значения трёхчлена:
| x | -5 | -3 | -1 | 0 | 1 | 2 | 4 | 7 | 10 |
| 2x²-7х+3 | 88 | 42 | 12 | 3 | -2 | -3 | 7 | 52 | 133 |
К тем же результатам мы придём, если рассмотрим график трёхчлена 2x²-7х+3. Мы знаем, что этим графиком является парабола, пересекающая ось x-ов в точках, абсциссы которых равны 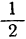
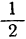
Точки же параболы, абсциссы которых заключены между 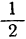
Пример:
Исследуем таким же способом трёхчлен:
y=3x²-x-10.
Решив квадратное уравнение Зх²-х-10=0, найдём корни данного трёхчлена. Они будут равны: 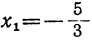
можно представить в таком виде:
или
Рассуждая так же, как и в первом примере, найдём:
1) При 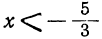
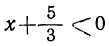
Следовательно, при этих значениях х произведение
т. е. данный трёхчлен имеет положительные значения.
2) При 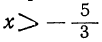
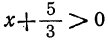
Следовательно,
т. е. трёхчлен имеет отрицательные значения.
3) При х>2 будет также и 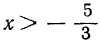
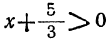
Отсюда:
и трёхчлен имеет положительные значения.
Общий вывод будет такой же, как и в первом примере: трёхчлен имеет положительные значения при всех значениях х, меньших 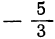
Он имеет отрицательные значения для всех значений х, заключённых между 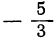
| x | -5 | -2 | -1 | 0 | 1 | 2 | 3 | 5 |
| Зх²-х-10 | 70 | 4 | -6 | -10 | -8 | 0 | 14 | 60 |
Пример:
Рассмотрим теперь такой трёхчлен, у которого первый коэффициент (т. е. коэффициент при х²) является отрицательным
числом. Пусть, например, дан трёхчлен:
y=-2x²+4x+16.
Найдя корни этого трёхчлена: x₁= — 2 и x₂=4, мы можем его переписать так:
y=-2(x+2) (x-4)
Исследуя знак этого произведения в том же порядке, как и в предыдущих примерах, мы найдём:
1. При х < 2 будет также и х<4. Отсюда:
x+2<0 и х-4<0.
Произведение этих множителей (x+2) (х-4) положительно. Но при умножении этого положительного числа на —2 получим, очевидно, отрицательное число, и, значит, данный трёхчлен при х<-2 имеет отрицательные значения.
2. При х>-2 и x<4 имеем:
x+2> 0 и х — 4<0.
Произведение (x+2) (x-4) — число отрицательное, а, значит, по умножении его на отрицательное число — 2 получится положительное число.
Следовательно, при значениях х, заключённых между корнями трёхчлена — 2 и 4, данный трёхчлен имеет положительные значения.
3. Наконец, при х>4 получим:
x+2>0 и х-4>0.
Произведение (x+2) (х-4) — число положительное. По умножении его на — 2 получим отрицательное число, и, значит, трёхчлен при х>4 имеет отрицательные значения.
Мы видим, что в этом случае мы имеем положение, обратное тому, которое наблюдали в первых двух примерах: при значениях х, меньших — 2, и при значениях, больших 4, он имеет отрицательные значения; при значениях х, заключённых между корнями трёхчлена, он имеет положительные значения. Этот вывод подтверждает и таблица для отдельных числовых значений х.
| x | -5 | -3 | -2 | -1 | 0 | 1 | 3 | 4 | 5 | 8 |
| -2x²+4x+16 | -54 | -14 | 0 | 10 | 16 | 18 | 10 | 0 | -14 | -80 |
К тому же выводу мы придём, если рассмотрим график трёхчлена -2x²+4x+16. Мы уже знаем, что при a<0 график трёхчлена αx²+bx+c будет обращён вершиной вверх и пересечёт ось х-ов в точках, абсциссы которых равны корням трёхчлена. В данном случае график имеет такой вид (черт. 38). Мы видим, что при х<-2 и при х> 4 ординаты точек кривой, т. е. значения у =- 2x²+4x+16, отрицательны, а при — 2<x< 4 — положительны.
Сопоставляя третий пример с первым и со вторым, мы замечаем, что во всех трёх случаях при значениях х, меньших меньшего корня, а также больших большего корня, трёхчлен имеет тот же знак, что и коэффициент при x²; при значениях х, заключённых между корнями, трёхчлен имеет знак, противоположный знаку коэффициента при х².
Убедимся в том, что такой вывод верен для любых значений коэффициентов а, b и с в случае действительных и различных корней. Для этого исследуем квадратный трёхчлен в общем виде.
Общий случай:
Пусть дан трёхчлен:
y=αx²+bx+c,
где а, b и с — любые действительные числа, удовлетворяющие лишь тому условию, что трёхчлен имеет действительные и различные корни (и, конечно, α≠0). Обозначим эти корни через
x₁ и x₂ (x₁<x₂)
Тогда трёхчлен может быть представлен в таком виде:
y=a(x-x₁) (x-x₂).
Исследуем, какие значения имеет этот трёхчлен при различных значениях х.
1. Пусть x<x₁, а значит, x<x₂ (так как x₁<x₂).
Отсюда имеем:
х-x₁<0 и х-x₂<0.
Следовательно, произведение (х-x₁) (х-x₂) будет числом положительным. Отсюда следует, что а (х-x₁) (х-x₂) положительно, если а положительно, и отрицательно, если а отрицательно. Другими словами, при x<x₁ значение трёхчлена ax²+bx+c имеет тот же
знак, что и коэффициент а.
2. Пусть x<x₁ и x<x₂.
Тогда:
x-x₁>0 и x-x₂<0.
Произведение (х — x₁) (х — x₂), как произведение чисел с разными знаками, будет числом отрицательным. Отсюда следует, что произведение а (х — x₁) (х — x₂) отрицательно при положительном а и положительно при отрицательном а.
Значит, в этом случае значения трёхчлена имеют знак, противоположный знаку коэффициента а.
3. Пусть х>х₂, а значит, и x>x₁ (так как x₂ >x₁).
Тогда:
х —x₂>0 и х —x₁>0
Произведение (х — x₁) (х — x₂) будет положительным, а следовательно, произведение а (х — x₁) (х — x₂) положительно при а положительном и отрицательно при а отрицательном. Значит, в этом случае числовое значение трёхчлена имеет тот же знак, что и коэффициент а.
Объединяя все три случая, мы можем теперь сделать такой общий вывод:
Если квадратный трёхчлен ax²+bx+c имеет действительные различные корни, то при значениях х, меньших меньшего из корней, и при значениях х, больших большего из корней, он имеет тот же знак, что и коэффициент при x². При значениях х, заключённых между корнями трёхчлена, он имеет знак, противоположный знаку коэффициента при х².
Примечание. Если условиться называть значения х<x₁ и х>x₂ значениями х вне промежутка между корнями, а значения x₁<x<x₂ значениями х внутри промежутка между корнями, то этот вывод можно ещё сформулировать так:
Если трёхчлен ax²+bx+c имеет действительные различные корни x₁ и x₂, то при значениях х вне промежутка между корнями трёхчлен имеет тот же знак, что и коэффициент при х²; при значениях х внутри промежутка между корнями трёхчлен имеет знак, противоположный знаку коэффициента при x².
Квадратный трёхчлен, имеющий равные корни
Пример:
Пусть требуется исследовать трёхчлен:
y=2x²-8х+8.
Найдём корни этого трёхчлена, для чего приравняем его нулю и решим уравнение:
2х² —8x+8=0.
Получим x₁= x₂=2. Значит, данный трёхчлен можно представить в таком виде:
y=2(x-2) (х-2),
или
y=2 (х — 2)².
Очевидно, что при любых действительных значениях x, кроме х=2, выражение (х — 2)² — число положительное. А значит, и по умножении его на положительное число 2 будем иметь положительное число. Следовательно, трёхчлен 2x²-8x+8 имеет положительные значения при всех значениях х, кроме значения, равного корню трёхчлена, т. е. при х=2.
(При х=2 трёхчлен равен нулю.)
Построив график трёхчлена 2x²-8x+8, мы замечаем (черт. 39), что при всех значениях х точки кривой расположены выше оси х, т. e. y>0, и только при x= 2 будет y=0. В этой точке кривая касается оси абсцисс.
Пример:
Исследуем трёхчлен:
Найдём корни этого трёхчлена, для чего решим уравнение:
Получим: x₁=x₂=3. Следовательно, данный трёхчлен можем представить в таком виде:
или
Как и в предыдущем примере, заключаем, что выражение (х-3)² при всех значениях х, кроме х=3, является числом положительным.
По умножении его на 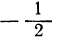
Таким образом, в этом случае при всех значениях х, кроме х=3, трёхчлен имеет отрицательные значения.
Построив график трёхчлена 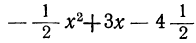
(черт. 40), что все точки параболы, кроме точки (3; 0), находятся ниже оси х-ов. Значит, ординаты всех этих точек, т. е. значения 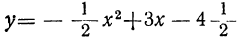
Сопоставляя оба примера, мы замечаем, что в обоих случаях знак численной величины трёхчлена совпадает со знаком коэффициента при x². Чтобы убедиться, что это имеет место при любых коэффициентах (в случае равных корней), рассмотрим трёхчлен в общем виде.
Общий случай: Пусть дан трёхчлен:
y=ax²+bx+c,
причём известно, что он имеет равные корни. Обозначив корень через x₁, представим трёхчлен в таком виде:
y = α(x- x₁) (x-x₁),
или
y = α(x- x₁)²
Отсюда заключаем: какова бы ни была разность x-x₁, если только она не равна нулю, квадрат этой разности является числом положительным. Значит, при положительном а произведение а (x-x₁ )², а следовательно, и у будут числами положительными, а при отрицательном а — отрицательными. Таким образом, мы можем сделать вывод:
Если трёхчлен имеет равные корни, то при всех значениях х, кроме значения, равного корню трёхчлена, значения трёхчлена имеют тот же знак, что и коэффициент при х².
Квадратный трёхчлен, имеющий мнимые корни
Пример:
Исследуем трёхчлен:
y=2x²-3x+3.
Решая уравнение 2x²-3x+3=0, мы получим:
Корни трёхчлена оказались мнимыми. В этом случае разности x-x₁ и x-x₂ будут мнимыми числами. Так как вопрос о знаке мнимых чисел не имеет смысла, то мы проведём исследование данного случая другим способом. Вынесем сначала за скобки первый коэффициент, получим:
Рассматривая теперь второй член 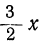
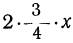
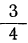
до полного квадрата, прибавив, а затем вычтя
Будем иметь:
Исследуем теперь полученное выражение. Очевидно, что при любых значениях х выражение 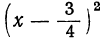
только при 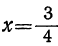
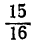
График трёхчлена y=2x²-3x+3 (черт. 41) показывает, что действительно все точки параболы расположены выше оси х-ов, т. е. их ординаты положительны.
Пример:
Исследуем трёхчлен:
y= — 3x²+2x- 1.
Решив уравнение —3x²+2x—1=0, найдём его корни.
Имеем:
Корни трёхчлена оказались мнимыми. Применим поэтому тот же способ исследования, что и в примере 1. Вынесем за скобки первый коэффициент и в скобках выделим квадрат двучлена:
Выражение 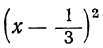
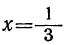
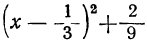
По умножении её на — 3 получим отрицательное число. Отсюда делаем вывод, что трёхчлен — 3x²+2x — 1 имеет отрицательные значения при всех значениях х. График трёхчлена (черт. 42) показывает, что все точки параболы расположены ниже оси х-ов, т. е. их ординаты отрицательны.
Сопоставляя примеры 1 и 2, замечаем, что в обоих случаях знак численной величины трёхчлена совпадал со знаком коэффициента при х² при всех без исключения значениях переменного х. Покажем, что это будет иметь место для всякого трёхчлена, имеющего мнимые корни.
Общий случай: Пусть дан трёхчлен:
y=ax²+bx+c,
причём известно, что он имеет мнимые корни. Мы знаем, что в этом случае должно быть
b² — 4αc < 0.
Преобразуем трёхчлен так же, как мы это делали в примерах 1 и 2:
или
Прибавим и вычтем по 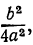
При всех значениях х выражение 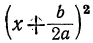
равно нулю 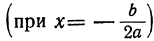
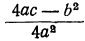
Отсюда следует, что знак численной величины трёхчлена зависит только от знака а; при а положительном и трёхчлен имеет положительные значения, при отрицательном — отрицательные.
Итак, мы можем сделать вывод:
Если трёхчлен имеет мнимые корни, то при всех значениях х его численная величина имеет тот же знак, что и коэффициент при х².
Общий вывод: Мы можем теперь подвести общий итог проведённого исследования квадратного трёхчлена. Но прежде сделаем следующие замечания.
1. Мы разбили исследование трёхчлена на три случая в зависимости от того, какие корни имеет трёхчлен. Но мы знаем что корни квадратного уравнения связаны с его дискриминантом b²—4ас следующей зависимостью:
1) Если b²— 4αc>0, то корни действительны и различны.
2) Если b² — 4αc=0, то корни действительны и равны.
3) Если b² — 4ас<0, то корни мнимы.
Следовательно, вместо того чтобы говорить, например: „если корни трёхчлена действительны и различны’, — мы можем сказать короче: „если дискриминант больше нуля’; аналогично изменяем формулировку и в остальных двух случаях.
2. Мы исследовали, какой знак имеет численная величина трёхчлена при различных численных значениях переменного. В дальнейшем для краткости вместо „знак численной величины трёхчлена’ условимся говорить короче: „знак трёхчлена’, помня, что речь идёт о знаке числа, которое получится, если вместо переменного подставить его численное значение. Точно так же вместо слов „трёхчлен имеет положительные (отрицательные) значения’ будем говорить короче: „трёхчлен положителен (отрицателен)’. Теперь мы можем сформулировать общий вывод так:
1) Если дискриминант трёхчлена ax²+bx+c положителен, то при всех значениях х, заключённых внутри промежутка между корнями, он имеет знак, противоположный знаку коэффициента а; при всех значениях х, содержащихся вне этого промежутка, трёхчлен имеет тот же знак, что и коэффициент а.
2) Если дискриминант трёхчлена равен нулю, то трёхчлен при всех значениях х, кроме значения, равного корню трёхчлена, имеет тот же знак, что и коэффициент а.
3) Если дискриминант отрицателен, то при всех значениях х трёхчлен имеет тот же знак, что и коэффициент а.
Этот вывод можно представить в виде следующей таблицы:
| Дискриминант | Значение х | Знак у = ax²+bx+c | |
| α>0 | α<0 | ||
| b² — 4αc > 0 | 1) x₁<x<x₂ 2) x<x₁; x>x₂ |
отрицательный положительный | положительный отрицательный |
| b² — 4ac = 0 | любое, кроме x=x₁=x₂ |
положительный | отрицательный |
| b² — 4αc<0 | любое | положительный | отрицательный |
Примеры:
1. у = x² -7x+10. Дискриминант: b²-4ac=49-40 = 9>0; α=1>0. Корни трёхчлена: x₁ = 2; x₂ = 5. Следовательно, при х<2 и при х>5 трёхчлен положителен, а при 2<x<5 — отрицателен.
2. у =-2x²+6x+80. Дискриминант: 36+640=676>0;
а=-2<0. Корни трёхчлена: x₁ =-5; x₂ =8. Следовательно, при -5<x<8 трёхчлен положителен; при х<-5 и при x>8 — отрицателен.
3. у = —x²+4х-15. Дискриминант: 16- 4·15=-44 <0. Следовательно, при всех значениях х трёхчлен отрицателен.
4. y=5x²-10x-5. Дискриминант: 10²-4∙5∙5=0. Корень трёхчлена: x₁= x₂=1; α=5>0. Следовательно, при всех значениях х, кроме х=1, трёхчлен положителен.
5. Определить, при каких значениях m трёхчлен 2x²-6x+m будет иметь положительные значения при любом значении х. Так как здесь α=2>0, то трёхчлен будет иметь положительные значения при любом х в том случае, если b²— 4αc<0. Подставляя сюда значения: α=2, b=-6, с=m, получим: 36-4∙2m=36- 8m. Значит, должно быть 36 — 8m<0. Отсюда находим: m >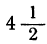
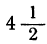
6. Определить, при каких значениях р трёхчлен x²+(p— 2) x+4-2p+l будет иметь положительные значения при любом значении х.
Дискриминант трёхчлена (р — 2)²—4(2p+1) =p²-12p=p(p—12). Следовательно, для того чтобы данный трёхчлен имел положительные значения при любом х, должно быть:
p(p-12)<0.
Решив уравнение:
р (р -12)=0,
найдём:
p₁=0; p₂=12.
Решим неравенство: р(р — 12) < 0. Оно будет верно при условии
I p< 0 и р — 12 >0 или
II р>0 и р—12≤0.
Первая система неравенств несовместна (при р < 0, очевидно, и р-12 < 0). Вторая же система даёт решение:
0<р< 12.
Итак, при всех значениях р от 0 до 12, т. е. при условии 0<p<12, данный трёхчлен имеет положительные значения при любом значении х.
Неравенства второй степени: Неравенствами второй степени с одним неизвестным называются неравенства вида:
ax²+bx+c > 0 (1)
и
ax²+bx+c < 0, (2)
где а, b и с — любые действительные числа, причём α≠0.
Так как неравенство вида (2) всегда может быть приведено к виду (1) путём умножения его на —1, то мы можем в дальнейшем ограничиться рассмотрением неравенств вида (1).
Решить неравенство — значит определить, при каких значениях х это неравенство справедливо. Для неравенства (1) это значит, что мы должны найти те значения х, при которых трёхчлен в левой части-является числом положительным.
После того как было изложено относительно знака квадратного трёхчлена, ответ на этот вопрос не представляет затруднений.
Решим несколько примеров.
Пример:
Пусть требуется решить неравенство:
2х²-13x+15> 0. (1)
Это значит, что нам нужно определить, при каких значениях х трёхчлен 2x²— 13x-f-15 является числом положительным. Решение проведём в таком порядке:
а) Устанавливаем, что первый коэффициент положителен (α=2>0).
б) Устанавливаем, что дискриминант трёхчлена 132 — 4∙2∙15>0.
Отсюда заключаем , что неравенство (1) справедливо при всех значениях х, больших большего, и при всех значениях х, меньших меньшего из корней трёхчлена.
в) Чтобы определить эти значения, решаем уравнение:
2x² — 13x+15=0.
Находим: x₁=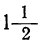
Следовательно, данное неравенство справедливо при значениях х, меньших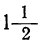
Пример:
Решить неравенство:
— 4x²+4x-1 <0. (1)
Умножив обе части на —1, получим равносильное неравенство:
4x² — 4x+1 >0. (2)
а) Коэффициент α=4>0.
б) Дискриминант 4²-4·4=0.
Следовательно, трёхчлен имеет равные корни. В этом случае, как мы знаем, трёхчлен (2) имеет положительные значения при всех значениях х, кроме значения, равного корню трёхчлена. Найдём этот корень, решив уравнение:
4x² — 4x+1=0.
Получим 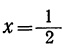
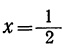
Пример:
Решить неравенство:
3x²- 5x+4 >0.
а) Коэффициент α=3 > 0.
б) Дискриминант 5²-4∙3∙4=-23 <0.
Отсюда сразу заключаем, что неравенство справедливо при любых значениях х.
Пример:
Решить неравенство:
(2х — 1) (x+3) — (x+7) (х-1) — 4х < 0.
Раскрыв скобки и произведя упрощения, получим:
x² -5x+4< 0, (1)
или по умножении на — 1:
— x²+5x-4>0. (2)
а) Коэффициент
а= —1 <0.
б) Дискриминант
5²-4-(— 1).(— 4)=9>0.
Следовательно, неравенство (2), а значит, и (1) справедливо при всех значениях х, заключённых между корнями трёхчлена. Найдём эти корни:
х² —5x+4=0,
отсюда x₁=1, x₂=4. Итак, неравенство (1) справедливо при 1<х<4.
Пример:
Решить неравенство: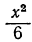
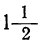
Умножив обе части на —6, получим:
— x²+6x- 9 > 0. (2)
а) Коэффициент а=-1<0.
б) Дискриминант 6²- 4·(—1)∙(—9)=0. Отсюда сразу заключаем, что неравенство (1) не имеет решений (при х=3 трёхчлен (2) равен 0, при всех остальных значениях — отрицателен).
Пример:
Решить неравенство:
— 3x²+4x- 10 >0.
Так как а=-3<0 и дискриминант 4²-120<0, то непосредственно заключаем, что неравенство решений не имеет.
Решённые примеры, а также рассмотрение таблицы приводят к следующему общему выводу для неравенства:
ax²+bx+-c>0.
I. Если b²-4αc<0, то:
а) при α > 0 неравенство справедливо при любых значениях х;
б) при α < 0 неравенство не имеет решений.
II. Если b²- 4αc=0, то:
а) при α > 0 неравенство справедливо при всех значениях х, кроме значения, равного корню трёхчлена в левой части;
б) при α < 0 не имеет решений.
III. Если b² — 4ас > 0, то:
а) при α > 0 неравенство справедливо при значениях х, больших большего, и при значениях х, меньших меньшего из корней трёхчлена в левой части (или, как мы условились говорить короче: „при значениях х вне промежутка между корнями трёхчлена»);
б) при α< 0 неравенство справедливо при значениях х, заключённых между корнями трёхчлена в левой части (или при значениях х внутри промежутка между корнями).
Примечание. Во всех приведённых примерах мы проводили решение, полностью основываясь на результатах исследования квадратного трёхчлена. Но, конечно, в каждом случае возможно и вполне самостоятельное исследование. Так, в примере 1, решив уравнение 2x²—13x+15=0 и найдя x₁=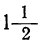
Теперь решение данного неравенства привелось к решению двух систем неравенств первой степени:
Первая система даёт х > 5, вторая: х <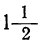
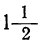
Мы пришли к тому же результату, что и в первом примере, но гораздо более длинным путём.
Решим теперь несколько неравенств более сложного вида.
Пример:
Решить неравенство:
Решение этого неравенства приводится к решению двух систем:
Решим первую систему неравенств. Так как 8²-4 ∙7=36>0, то трёхчлен x²-8x+7 имеет действительные и различные корни. Решив уравнение х²-8x+7=0, найдём: x₁=1; x₂=7. В таком случае, как мы знаем, неравенство (1) будет иметь место при x<1 и при х>7.
Но решив неравенство (2), найдём х>3. Значит, обоим неравенствам удовлетворяют лишь значения х>7.
Решим вторую систему. Неравенство (3) будет справедливо при всех значениях х, заключающихся между 1 и 7, т. е. при 1 < x < 7. Но неравенство (4) даёт x<3. Следовательно, обоим неравенствам вместе удовлетворяют лишь значения х, заключённые между 1 и 3, т. е. при 1 < x < 3. Теперь мы можем сделать общий вывод: данное неравенство справедливо:
при 1< x< 3 и при х > 7.
Проверьте правильность решения подстановкой в данное неравенство значений: x=- 1; 0; 1; 2; 4; 6; 8; 10.
Пример:
Решить неравенство:
Решение приводится к решению систем:
или
Так как 9²-56=25>0 и 5²-16=9>0, то оба трёхчлена имеют действительные и различные корни. Решив соответствующие уравнения, найдём для первого трёхчлена: x₁=2; x₂=7, второго трёхчлена: x₁=1;x₂=4. Отсюда заключаем:
1) Неравенство (1) справедливо при x<2 и х>7, а неравенство (2) — при х<1 и x>4. Следовательно, оба неравенства вместе будут верны лишь при х<4 и х >7.
2) Неравенство (3) верно при 2<x<7, а неравенство (4)—при 1<х<4. Следовательно, оба неравенства одновременно будут иметь место лишь при 2<x<4. Итак, решениями данного неравенства будут следующие значения х: 1) х<1; 2) 2<x<4; 3) x>7.
Замечание:
Найдя корни обоих трёхчленов, мы могли данное неравенство представить в таком виде:
Тогда решение этого неравенства свелось бы к решению двух систем:
или
Решение каждого из этих неравенств мы можем провести подобно тому, как это было сделано в первом примере. Очевидно, что мы пришли бы к тому же результату, как и выше, но ход решения был бы значительно более длинным.
Пример:
Решить неравенство:
Решение сводится к решению систем:
или
Дискриминанты трёхчленов: 3²+4∙ 10=49>0 и 3²-4∙10= =-31<0. Отсюда сразу заключаем, что система I не имеет решений. Действительно, раз дискриминант трёхчлена (2) меньше нуля, то трёхчлен положителен при любых значениях х и, следовательно, неравенство (2) не может иметь места.
Обращаемся к системе II. Мы уже знаем, что неравенство (4) верно при всех значениях х. Значит, остаётся решить неравенство (3). Найдя корни трёхчлена x²-Зх-10, получим: x₁=-2; x₂=5. Следовательно, решениями неравенства (3), а значит, и системы II будут лишь значения х, заключённые между -2 и 5.
Итак, данное неравенство будет верно при —2≤x≤5.
Квадратный трехчлен и квадратные неравенства
Умение решать квадратные неравенства необходимо каждому учащемуся, готовящемуся к выпускным экзаменам в школе и вступительным экзаменам в вузе. Чтобы успешно решать квадратные неравенства и сводящиеся к ним, следует твердо знать свойства квадратного трехчлена и квадратичной функции.
График квадратичной функции.
Функцию
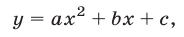
где а,b,с — действительные числа, причем 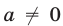
Применив метод выделения полного квадрата, запишем квадратичную функцию (1) в виде
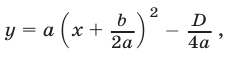
где
Введем следующие обозначения:
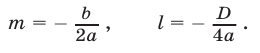
Тогда формула (1) примет вид
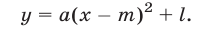
Из формулы (4) следует, что графиком квадратичной функции является такая же парабола, как 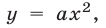
Знак числа а определяет направление ветвей параболы: при а > 0 ветви параболы направлены вверх, при а < 0 — вниз. Ось симметрии параболы — прямая, параллельная оси Оу и проходящая через вершину А параболы.
График функции 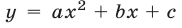
1) найти координаты вершины А(m;l) параболы, пользуясь формулами (3) или применяя метод выделения полного квадрата;
2) построить ось параболы;
3) найти точки пересечения параболы с осью Оу и осью Ох (найти корни уравнения 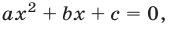
4) нарисовать эскиз графика функции, используя найденные точки и учитывая роль знака числа а.
Для более точного изображения параболы найти координаты нескольких ее точек.
На рис. 20.1 изображен график функции
Теорема:
Квадратичная функция 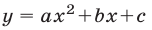
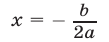
Для доказательства этой теоремы можно воспользоваться формулой
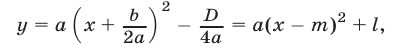
где
Замечание:
Эта теорема имеет простой геометрический смысл. Если а > 0, то самая нижняя точка параболы 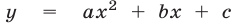
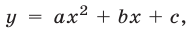
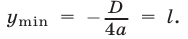
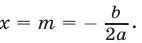
Исследование квадратного трехчлена
Теорема:
Если 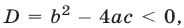
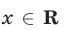
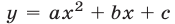
Теорема:
Если D = 0, то при всех 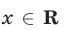
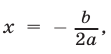
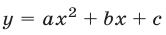
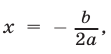
Теорема:
Если D > 0, то знак квадратичной функции
а) совпадает со знаком числа а для всех х, лежащих вне отрезка 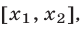
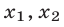
такие, что 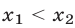
б) противоположен знаку числа а при всех х таких, что 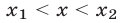
Теоремы 2 и 3 можно доказать с помощью формулы (5), записанной в виде
а теорему 4 — с помощью разложения квадратного трехчлена на множители:
Теорема:
Квадратичная функция 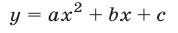
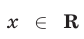
Доказательство:
Достаточность следует из теоремы 2. В самом деле, если 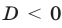
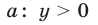
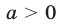
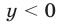
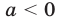
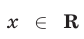
Докажем необходимость, т. е. покажем, что если 
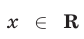
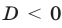
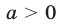
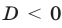

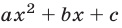
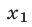
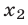
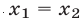
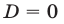
что противоречит условию ( 
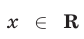
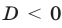
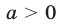
Квадратные неравенства.
Пусть 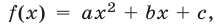
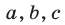
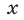
называют квадратными неравенствами или неравенствами второй степени, причем первые два из этих неравенств называют строгими, остальные — нестрогими.
Перейдем к нахождению решений квадратных неравенств. Ограничимся рассмотрением строгих неравенств и заметим, что всякое строгое квадратное неравенство можно привести к одному из следующих видов:
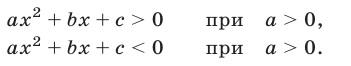
Из теорем 2-4 следует:
1) если
то решениями неравенства (1) являются все действительные числа (см. рис. 20.3), а неравенство (2) не имеет решений;
2) если 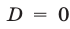
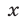
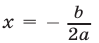
3) если 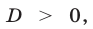
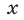


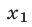
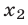
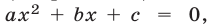
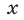
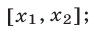
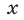
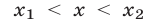
Примеры с решениями:
Пример:
Определить знаки чисел 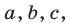
Решение:
Ветви параболы направлены вверх и поэтому 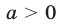
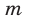
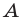
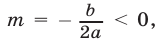
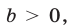
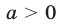
Наконец, 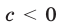
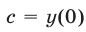
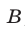
Ответ.
Пример:
Квадратичная функция 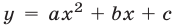
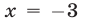
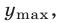
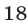
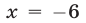
Решение:
Так как 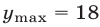
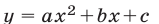
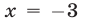
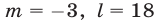
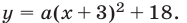
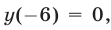
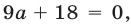

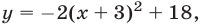
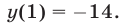
Ответ.
Пример:
Квадратный трехчлен 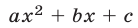
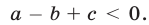
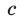
Решение:
По условию график квадратичной функции 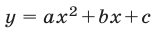
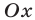
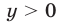
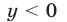
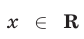
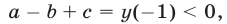
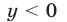
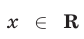
Ответ. 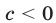
Пример:
Квадратичная функция 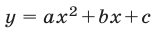

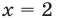
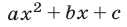
Решение:
Предположим, что квадратный трехчлен не имеет действительных корней. Тогда парабола 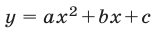
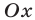
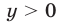
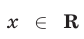
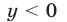
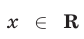
Пример:
Решить неравенство:
Решение:
а) Неравенство 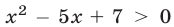
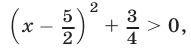
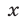
б) Неравенство 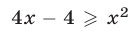
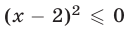
в) Уравнение 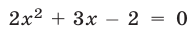
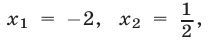
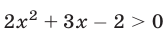
все числа 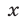
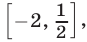
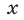
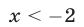
г) Уравнение 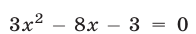
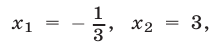
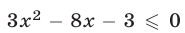
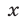
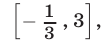
Пример:
Решить неравенство
Решение:
Полагая 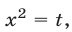
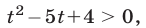
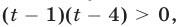
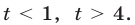
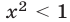
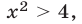
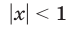
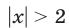
Ответ.
Пример:
Найти все значения 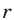
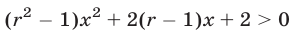
верно для всех 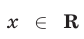
Решение:
Если 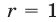
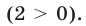
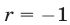
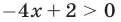
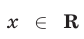
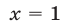
Пусть 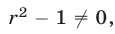
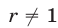
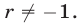
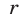
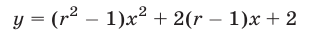
принимает положительные значения для всех 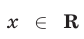
По теореме 5 это имеет место тогда и только тогда, когда дискриминант квадратного трехчлена (4) отрицателен, а коэффициент при 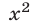
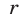
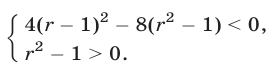
Неравенство (5) равносильно каждому из неравенств 

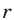
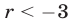
Неравенство (6) справедливо при 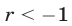
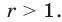
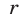
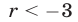
Ответ.
Пример:
Найти все значения 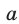
верно для всех значений 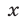
Решение:
Так как
для всех 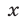
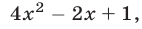
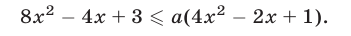
Неравенство
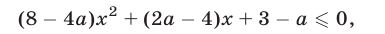
равносильное неравенству (7), не является верным при
Если 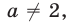
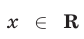
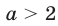
Отсюда следует, что 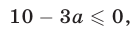
Ответ.
Пример:
Найти все значения 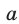
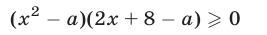
верно для всех значений
Решение:
Пусть неравенство (9) является верным для каждого 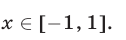
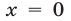
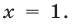
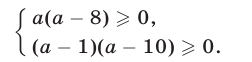
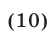
Первому неравенству системы (10) удовлетворяют значения 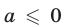
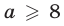
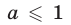


Таким образом, условия (11) являются необходимыми (искомыми значениями 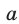
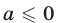

Покажем, что условия (11) являются достаточными. Пусть 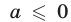
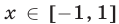
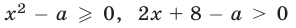
Пусть 
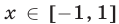
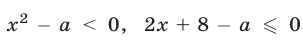
Ответ.
Пример:
Решить неравенство
Решение:
Данное неравенство равносильно системе неравенств
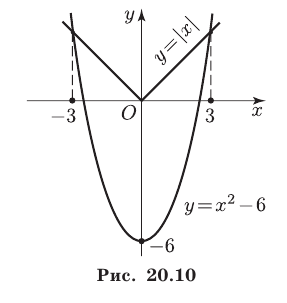
которая равносильна следующей системе:
Множество решений первого неравенства — интервал 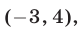
Ответ.
Пример:
Решить неравенство
Решение:
На рис. 20.10 изображены графики четных функций 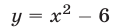
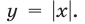
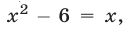
График функции 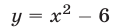
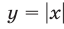
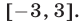
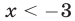
Ответ.
Пример:
Решить неравенство
Решение:
Данное неравенство равносильно совокупности неравенств
и
Множество решений первого неравенства, равносильного неравенству
представляет собой объединение промежутков 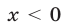
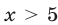
есть интервал
Ответ.
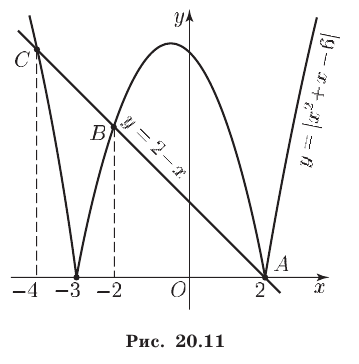
Пример:
Решить неравенство
Решение:
Первый способ. Число 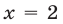
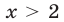
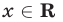
Если 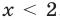
Эти неравенства равносильны неравенствам
соответственно. Решив систему
получаем
Аналогично, из системы
следует, что 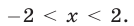
Ответ.
Второй способ. Построим графики функций 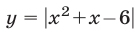
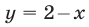
Эти графики имеют общую точку 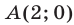
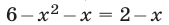
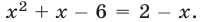
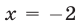
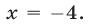
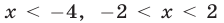
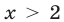
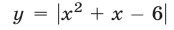
Пример:
Решить неравенство
Решение:
Воспользуемся тем, что неравенство 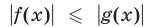
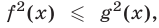
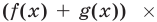
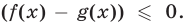
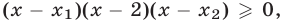
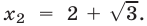
Ответ.
Пример:
Найти множество значений функции 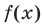
Решение:
а) Число а принадлежит множеству значений функции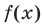
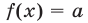
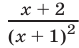
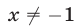
можно записать в виде 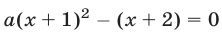
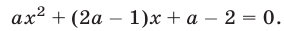
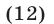
Уравнение (12) при 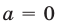
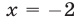
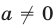
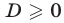
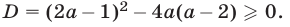
Ответ.
б) Пусть 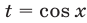
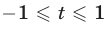
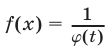
График функции 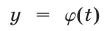
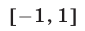
Из рис. 20.12 видно, что 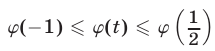
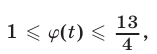
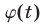
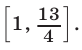
Ответ.
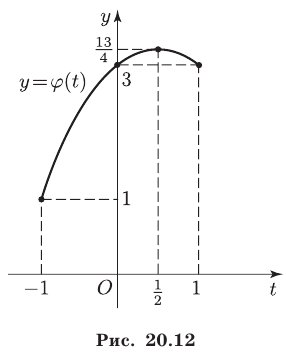
Пример:
Найти все значения 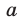
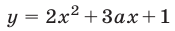
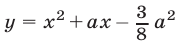
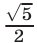
Решение:
Для нахождения координат вершин парабол воспользуемся методом выделения полного квадрата. Получим
Пусть 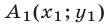
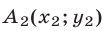
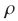
Пусть 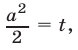
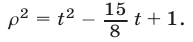
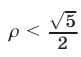
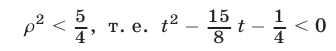
Так как 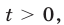
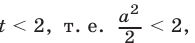
Ответ.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Решение задач по математике
Возможно вам будут полезны эти страницы:
Квадратный трехчлен и алгоритм решения с примерами
Почти вся теория квадратного трехчлена, а также решение многих задач, связанных с ним, основываются на приеме, называемом «выделение полного квадрата». Применяя этот прием к квадратному трехчлену 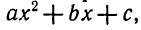
Нет необходимости эту формулу запоминать. Гораздо важнее в каждом конкретном случае уметь проделать соответствующие преобразования и выделить полный квадрат. Например,
Выражение 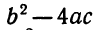
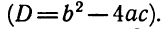
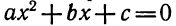
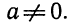
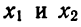
Правда, нумерация корней условна. Обычно стараются за нумеровать их в порядке возрастания, но это не обязательно.
Дадим два практических совета. Во-первых, если второй коэффициент (b) четный (причем он может быть просто четным числом, а может иметь вид b = 2k), то удобнее пользоваться для нахождения корней формулами
Во-вторых, старайтесь по возможности «работать» с квадратным трехчленом, у которого старший коэффициент (а — коэффициент при 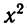
Задачи, связанные с квадратным трехчленом, встречающиеся в школьной и конкурсной практике, чрезвычайно разнообразны.
Нередки среди них такие, где основное, что требуется от учащегося,— это внимательность к формулировке. Например:
1.Определить все значения параметра а, при которых уравнение 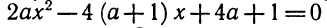
Решение:
Здесь главное — не забыть про случай а = 0, поскольку в условии не сказано, что рассматривается квадратное уравнение. При а = 0 имеем линейное уравнение 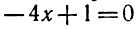
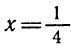
Ответ.
К азбуке квадратного трехчлена относится и теорема Виета. Для того чтобы 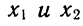
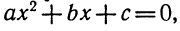
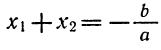
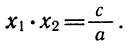
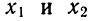
Некоторые логические и терминологические проблемы возникают в случае D = 0, но мы их не будем обсуждать. Заметим лишь, что выражения «квадратное уравнение, имеющее одно решение» и «квадратное уравнение с равными корнями» означают одно и то же.
Из теоремы Виета следует следующее разложение на множители квадратного трехчлена:
На теореме Виета основан целый ряд традиционных задач и методов решения.
2.Решить уравнение
Решение:
Решение этого уравнения непосредственно по формуле корней квадратного уравнения приводит к большим вычислительным трудностям.
Если же заметить, что 319-1988+1669 = 0, откуда следует, что 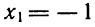
Ответ.
Сталкиваясь с квадратным уравнением, решение которого требует громоздких арифметических или алгебраических пре образований, попытайтесь выяснить, не имеет ли это уравнение «хорошего» целого корня, в частности 1 (в этом случае имеет место равенство а+b + с = 0) или —1 (а —b + с = 0).
3.Пусть 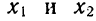
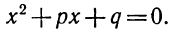
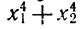
Решение:
Нам нужно выразить 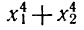
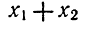
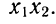
Ответ.
4. Разложить на множители выражение
Решение:
Данное выражение можно рассматривать как квадратное относительно любого входящего в него переменного. Сгруппируем его члены и расположим их по степеням х. Получим
Коэффициент при х представляет собой квадратный трехчлен относительно у (можно z) 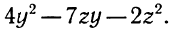
Следовательно,
Таким образом, в каждом из коэффициентов квадратного трех члена (1) есть множитель у — 2z. Вынося его за скобки, получим
Квадратный трехчлен 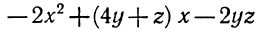
Ответ.
Решая эту задачу, мы сознательно не стали использовать некоторые соображения, которые могли бы привести к цели быстрее. Так, например, выделив множитель (у — 2z), учитывая цикличность исходного выражения (оно не меняется при замене х на у, у на z, z на х), можно было сразу получить требуемое разложение на множители. В данном случае мы следовали по говоркам: «От добра добра не ищут» и «Тише едешь…» Однако в других, более сложных случаях подобного рода особенности могут сыграть решающую роль. И еще на одно очень важное обстоятельство следует обратить внимание: надо учиться «видеть» квадратный трехчлен в тех случаях, когда он не задан в стандарт ной канонической форме; уметь выделять переменное, параметр, алгебраическое выражение, относительно которого данное выражение представляет собой квадратный трехчлен; делать замену переменного, превращающую его в квадратный трехчлен.
Существование корней квадратного уравнения. Знаки корней
Как мы знаем, для того чтобы квадратное уравнение 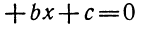
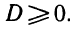
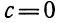
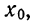
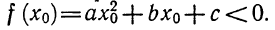
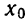
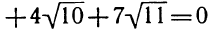
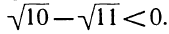
5. Доказать, что при любом а уравнение
имеет решение.
Решение:
Можно, конечно, попытаться найти дискриминант и доказать, что он положителен. Но не будем спешить.
Обозначим левую часть данного уравнения через f (х). Сразу видно, что 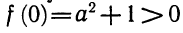
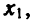
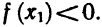
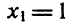
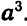
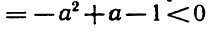
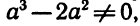
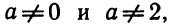
Мы не будем обсуждать здесь проблему, в какой мере допустимо и законно использование тех или иных графических соображений в условиях конкурсного экзамена. Общими словами здесь не отделаешься — истина конкретна. К сожалению, четких и согласованных критериев, которых бы придерживались комиссии разных вузов (и даже члены одной комиссии), нет. Нам все же кажется, что степень обоснованности решений, аппелирующих к графическому образу квадратного трехчлена, зачастую гораздо выше, чем это считают некоторые чрезмерно педантичные экзаменаторы.
Мы советуем ученикам почаще обращаться в процессе поиска решения к «картинкам», искать соответствующую графическую интерпретацию.
Теорема Виета очевидным образом используется в задачах, в которых требуется определить знаки корней квадратного уравнения.
6. При каких значениях параметра а уравнение
имеет решение? Определить знаки корней в зависимости от а.
Решение:
Прежде всего, если 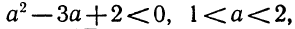
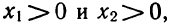
откуда а >5. Точно так же рассматриваются другие случаи.
Ответ. Если а<1 или 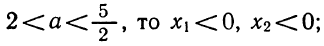
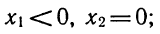
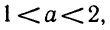
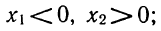
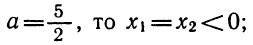
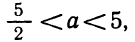
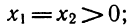
Ответ выглядит сложнее, чем решение задачи.
Расположение корней квадратного трехчлена
Выделим прежде всего два наиболее распространенных типа задач, связанных с расположением корней квадратного трех члена. Первый тип — задачи, в которых изучается расположение корней относительно заданной точки А. Возможны три случая, не считая случая отсутствия корней: оба корня меньше А; один корень меньше, а другой больше А; оба корня больше А. Задачи первого типа без труда сводятся к проблеме,— определению знаков корней квадратного трехчлена. Это делается при помощи замены t = х —A, х =t+A, в результате которой трехчлен относительно х переходит в трехчлен относительно t. Знаки корней нового квадратного трехчлена очевидным образом определяют расположение корней исходного квадратного трехчлена относительно А. Можно и не делать замену.
7. При каком значении параметра а один корень уравнения 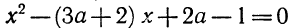
Решение:
Решение легко получается на основании следующего простого графического соображения. График функции 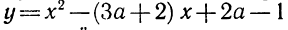
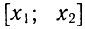
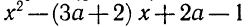
Ответ. а> —2.
В общем случае для того, чтобы уравнение 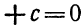
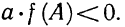
это самостоятельно.) Не следует последнее условие заучивать. Необходимо понять принцип его получения и уметь провести необходимые рассуждения в конкретных задачах.
8. При каких значениях параметра а оба корня уравнения
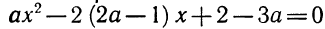
Решение:
Для того чтобы оба корня уравнения
были больше 1, необходимо и достаточно выполнения следующих условий:
Необходимость условия 1) очевидна. Неравенство 2) означает, что знак f (х) при х=1 совпадает со знаком старшего коэффициента. Квадратные трехчлены, удовлетворяющие условиям 1) и 2), обладают тем свойством, что все они имеют два корня и оба эти корня либо меньше 1, либо больше 1 (рис. 8). Неравенство 3) выделяет из них те трехчлены, у которых оба корня больше 1. Оно означает, что вершина параболы расположена правее прямой х = 1.
Система неравенств 1) —3) дает нам необходимое и достаточное условие для того, чтобы оба корня данного уравнения были больше 1. Неравенство 2) дает 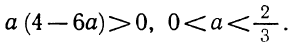
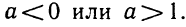
Ответ. Ни при каких.
В задачах второго типа исследуется расположение корней квадратного трехчлена относительно заданного отрезка [А; В].
Здесь можно выделить 6 возможных случаев расположения корней (оба меньше А, один меньше А, а другой на отрезке [А; В] и т. д.). Если же отдельно рассматривать ситуацию, когда D = 0, то добавится еще 3 случая. Мы вновь не будем заниматься по строением общей теории, а рассмотрим конкретные примеры.
9. При каких значениях параметра а все решения уравнения 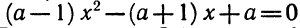
Решение:
Обозначим 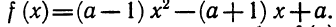
(Проверьте, что если f (х) имеет корни на данном отрезке, то все неравенства выполняются. Проверьте обратное утверждение, что если выполняются все неравенства, то корни f (х) расположены на отрезке [0; 3]. Покажите, что ни одно из не равенств нельзя отбросить, т. е. если выполняются все неравенства, кроме одного, то квадратный трехчлен не удовлетворяет условию задачи.)
Оба неравенства 2) и 3) выполняются при 
Решим неравенство 4): 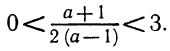
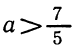
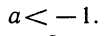
Значит, система неравенств 2), 3), 4) имеет решение 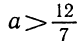
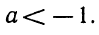
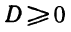
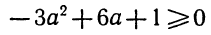
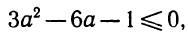
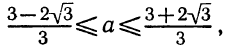
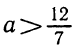
Отдельно рассматривается случай а=1.
Ответ.
Заметим, что если бы в условии требовалось, чтобы оба корня располагались на заданном отрезке, т. е. указывалось на наличие двух различных корней, то правое нестрогое неравенство ответа следовало бы заменить на строгое и исключить случай а= 1.
10. Определить, как расположены корни уравнения 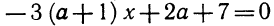
Решение:
Решим эту задачу несколько иначе, способом, который можно назвать «обобщенным методом интервалов».
Сначала определим, где обращается в ноль дискриминант уравнения. Имеем
При 1<а<9 корней у данного уравнения нет. Обозначив, как обычно, левую часть уравнения через f (х), найдем f (—1) = 6а+10, f(4) = 6a —5. Как видно, f(— 1) и f (4) меняют знаки соответственно при 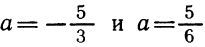
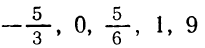
Рассмотрим эти 6 случаев.
Имеем
Можно проверить, что при
будет
Значит, уравнение имеет корни, ветви
параболы направлены вниз, значения f (х) при х= —1 и х=4 отрицательны, вершина параболы расположена между прямыми х=-1 и х = 4 (рис. 9,б). Следовательно, в этом случае оба корня расположены между — 1 и 4.
2) 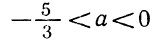
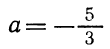
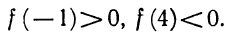
Точно так же рассматриваются остальные случаи.
Ответ. При 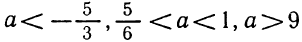
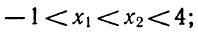
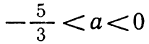
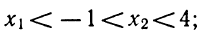
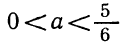
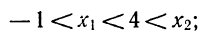
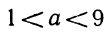
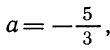
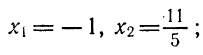
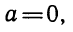
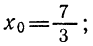
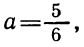
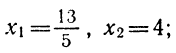
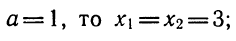
11. Определить, как расположены корни уравнения
относительно отрезка [1; 3].
Решение:
В данном случае приемы, которые мы использовали при решении предыдущего примера, не нужны; все гораздо проще, рассматриваемое уравнение всегда (при 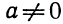
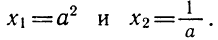
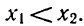
Вывод очевиден — при решении задач не стоит увлекаться общими теориями, следует попытаться сначала выявить специфику данного конкретного примера.
Взаимное расположение корней двух квадратных трехчленов
12. Найти все значения параметра а, при которых уравнения 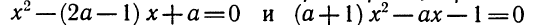
Решение:
Решение основывается на следующей простой идее: если два уравнения 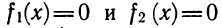
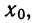
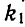
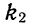
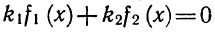
Возьмем сначала 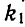
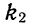
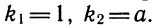
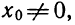
Затем выберем 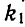
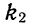
Получим уравнение
Так как х должен удовлетворять обоим полученным линейным уравнениям, для а должно выполняться соотношение
Далее получаем 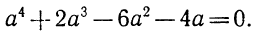
Ответ.
Два замечания. 1. Для каждого из найденных значений а необходимо убедиться, что соответствующие уравнения имеют решения, (Достаточно проверить существование корней у одного из них.) 2. Заданную пару квадратных уравнений можно рассматривать как систему из двух уравнений с неизвестными х и а.
13. Расположить корни уравнений
в порядке возрастания.
Решение:
Обозначим 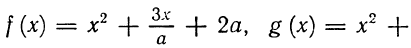
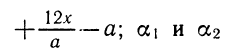
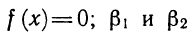
Найдем значения х, при которых 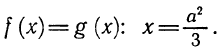
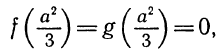
Таким образом, множество значений параметра а, при которых оба уравнения имеют корни, разбито на три интервала (рис. 10, а). Концы интервалов удобнее рассматривать отдельно. Возникают три случая.
Имеем
С точностью до обозначений, какая из двух парабол соответствует f(х), а какая g (х), возможны два случая (рис. 10, б, в). Посмотрим, как расположены вершины каждой из парабол по отношению к прямой 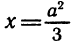
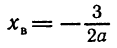
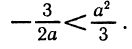
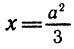
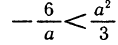
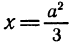
Если 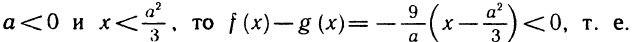
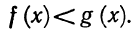
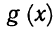
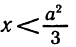
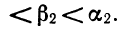
2) 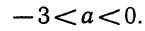
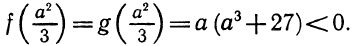
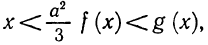

3) 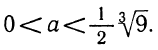
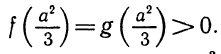
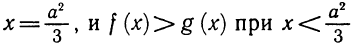
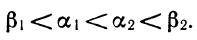
Заметим, что получить правильный ответ в данном примере можно было бы несколько проще, хотя и менее законно. Из соображений непрерывности следует, что на каждом из трех интервалов имеет место один и тот же порядок следования корней (граничными точками такого рода интервалов являются: запрещенные значения параметра, в данном случае а = 0; нули дискриминантов— точки 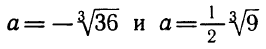
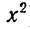
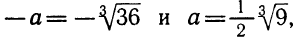
Уравнения, неравенства и системы с параметром
В большинстве задач, рассмотренных в предыдущих пунктах, требовалось узнать «при каких значениях параметра…?». Подобного рода вопрос для уравнений, неравенств, систем уравнений или неравенств с параметром не всегда фигурирует в условии задачи. Однако наличие параметра заранее предполагает специальную форму записи ответа, такую, чтобы по ней можно было указать, каков будет ответ для любого допустимого значения параметра.
14. Решить уравнение
Решение:
Обозначим 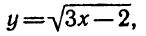

которое надо решить при условии 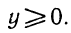
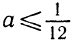
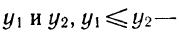
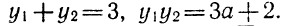
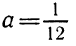
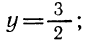
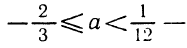
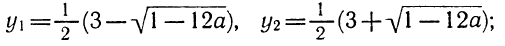
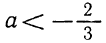
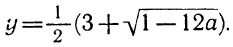
Ответ. Если 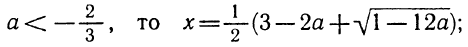
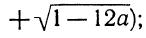
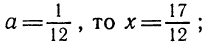
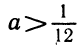
Если решать уравнение 14 более обычным путем, возводя в квадрат обе его части, то приходим к уравнению 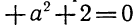
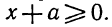
15. Решить уравнение
Решение:
Возводим обе части уравнения в квадрат (условие 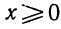
Еще раз возводим в квадрат (условие 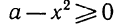
среди решений которого надо найти те, для которых 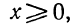
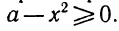
Найдем дискриминант, надеясь, что он окажется полным квадратом:
Итак, наши надежды оправдались. Теперь правая часть уравнения раскладывается на множители 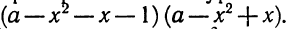
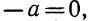
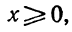
Начнем с уравнения 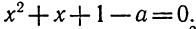
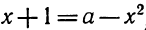
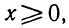
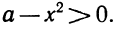
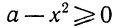
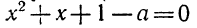
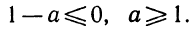
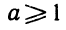
Перейдем ко второму уравнению 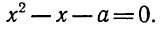
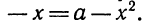
Ответ. Если 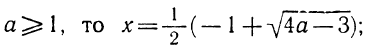
16. Для каждого неотрицательного значения параметра а
решить неравенство
Решение:
Левая часть неравенства представляет собой многочлен как относительно х, так и относительно параметра а. Степени соответственно равны 4 и 3. Однако если умножить многочлен на а, а затем сделать замену у = ах, то в новом многочлене максимальная степень параметра а будет равна 2. Случай а = 0 дает нам ответ 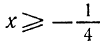
Левая часть представляет собой квадратный трехчлен относительно а:
Раскладывая левую часть неравенства на множители, получим
или
Второй множитель положителен при всех у, если а>0. Приходим к неравенству 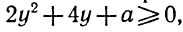
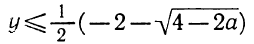
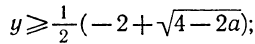
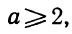
Ответ. Если а=0, то 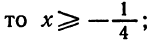
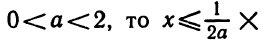
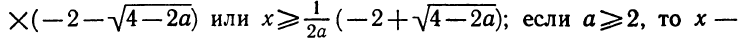
Очень часто уравнения, неравенства, системы с параметром сводятся к задачам о расположении корней одного или двух квадратных трехчленов. Основные методы решения подобных задач мы рассматривали в двух предыдущих пунктах.
17. Решить систему неравенств
Решение:
Поскольку решением первого неравенства является 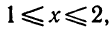
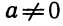
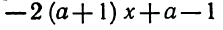
Область изменения параметра а оказалась разделенной на 4 части (не считая граничных точек).
1) Если а 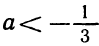
2) Если 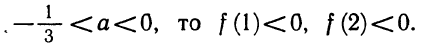
параболы выполняется неравенство 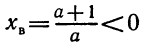
Следовательно, множество решений второго неравенства не содержит
точек отрезка [1; 2] Система не имеет решения. То же имеет место и при а = 0.
3) Если 0<а<5, то f (1)<0, f(2)<0 (рис. 11, б). Значит, на всем отрезке [1; 2] f (х)<0. Система вновь не имеет решения.
4) Если 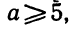
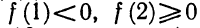
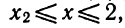
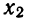
Ответ. Если а <5, система не имеет решения; если 
18. Решить систему неравенств
Решение:
Задача, по существу, сводится к выяснению, в каком порядке следуют корни уравнений
Вычисляя их дискриминанты, получим, что первое уравнение имеет корни, если 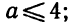
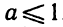
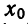
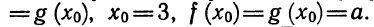
1) a<0 (рис. 12). Если 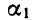
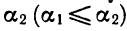
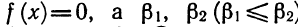
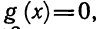
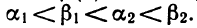
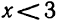
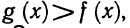
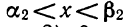
2) 0<а<1. В этом случае порядок следования корней будет 
Если 
3) 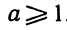
Ответ. Если а<0, то 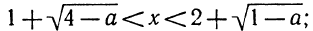
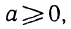
Уравнения, неравенства и системы с параметром. Графические интерпретации
Начнем с того, что еще раз решим систему неравенств 18.
Эту систему можно переписать в виде двойного неравенства
Рассмотрим координатную плоскость (х; а). Множество точек, координаты которых удовлетворяют нашей системе неравенств, ограничено графиками двух квадратных трехчленов 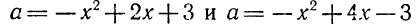
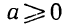
Чтобы найти решение системы неравенств при некотором 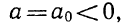
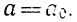
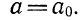
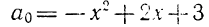
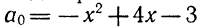
Рассмотрим еще несколько примеров.
19. При каких значениях а уравнение х |х —2а| —За + 2=0 имеет один корень?
Решение:
Рассмотрим функцию у = х|х — 2а| — За + 2. Ее график состоит из частей двух парабол: если 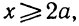
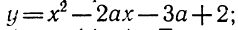
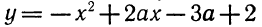
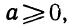
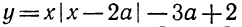
Нетрудно сделать вывод, что, для того чтобы уравнение 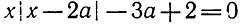
Получаем неравенство для а:
Найдем, где обращается в ноль первый множитель: а|а| — За + 2 =0. Если 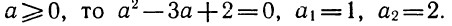
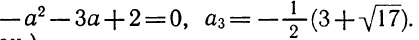
Второй множитель обращается в ноль при 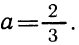
отрицателен, т. е. (а|а| — За + 2)( — За + 2)<0. При переходе через отмеченные точки знак меняется.
Ответ.
20. Сколько корней в зависимости от а имеет уравнение
Решение:
Изобразим на плоскости (х; а) все точки, удовлетворяющие данному уравнению. Если 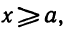

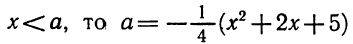
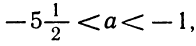
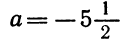
21. Решить неравенство
Решение:
Напомним, что неравенство 

Изобразим на плоскости (х; а) множество точек, координаты которых удовлетворяют полученной системе (рис. 16). При конкретном значении параметра а =а, решением нашего неравенства будут абсциссы тех точек горизонтальной прямой а = а, которые находятся в заштрихованной области. Найдем точки пересечения А (2; 2), В ( — 2; —2) наших парабол и вершину С ( — 0,5; —4,25) параболы
Далее получаем: если а>2, решений нет; горизонтальная прямая не пересекается с заштрихованной областью.
Если 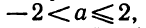
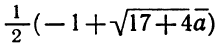
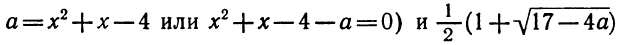
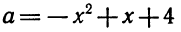
Если 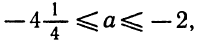
Если
Подведем итог этому пункту. Мы рассмотрели здесь задачи, при решении которых использовались наглядно-графические соображения. Подчеркнем два характерных приема.
Первый прием (использовался при решении задачи 19). На плоскости (х; у) рассматривается семейство кривых, зависящих от параметра a: y = f(x; а). Затем в этом семействе выделяется множество кривых, обладающих требуемым свойством. При этом очень часто поступают следующим образом: изучают, как перемещается кривая семейства при изменении параметра, и находят граничные значения параметра, отделяющие множество значений параметра, которым соответствуют кривые, имеющие нужное свойство. (Правда, в задаче 19 путь решения был несколько иной. Нам удалось сразу получить удобное необходимое и достаточное условие, выделяющее искомое множество кривых.)
Второй прием состоит в том, что рассматривается плоскость (х; а), на которой изображается множество точек, координаты которых удовлетворяют данному уравнению или неравенству (см. решения задач 20 и 21). После этого, проводя прямые, параллельные оси х, находят решение этого уравнения или не равенства при соответствующем значении параметра. Значения параметра, при переходе через которые меняется формула, дающая решение, естественным образом определяются построенным множеством.
Задачи на максимум-минимум. Доказательство неравенств
Простейший прием нахождения наибольших и наименьших значений, основанный на свойствах квадратичной функции, состоит в том, что исследуемая функция при помощи преобразований или замены переменной приводится к квадратичной, после чего выделяется полный квадрат.
22. Найти наибольшее значение функции
Решение:
Обозначим 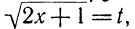
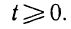
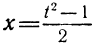
наибольшее значение функции 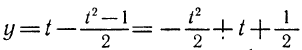
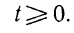
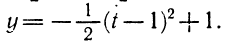
Другой прием иллюстрирует следующая задача.
23. Найти наибольшее и наименьшее значения функции
Решение:
Рассмотрим данное равенство как уравнение с неизвестным х и параметром у. (Можно для создания большего психологического комфорта заменить у на а.) После преобразований получим
Для того чтобы это уравнение имело решение, необходимо и достаточно, чтобы выполнялось неравенство
откуда
Слева в неравенстве стоит наименьшее значение у, справа — наибольшее.
Интересно сравнить данное решение задачи с решением, использующим производные.
Идея, на которой основано решение задачи 23, чрезвычайно проста. Чтобы найти наибольшее и наименьшее значения функции y=f(x) мы, рассматривая данное равенство как уравнение с неизвестным х, решаем задачу, при каких у это уравнение имеет решение.
Рассмотрим еще два примера, в которых работает эта же идея с небольшими вариациями.
24. Найти наибольшее и наименьшее значения выражения
2х— Зу, если
Решение:
Обозначим 2х — 3y = s, тогда 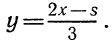
Для того чтобы это уравнение (относительно х) имело решение, необходимо и достаточно выполнения неравенства
откуда
Как и в предыдущем случае, слева в двойном неравенстве стоит наименьшее значение s = 2x —Зу, справа — наибольшее.
25. Найти наибольшее и наименьшее значения выражения 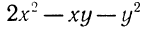
Решение:
Задача сводится к определению наибольшего и наименьшего значений а, при которых система
имеет решение.
Левые части каждого из уравнений представляют собой однородные многочлены второй степени относительно х и у. Умножим первое уравнение на 4, второе на — а и сложим получившиеся уравнения. Получим
Разделив это уравнение на 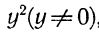
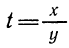
Нам необходимо, чтобы дискриминант этого уравнения был неотрицателен:
откуда 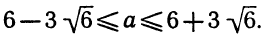
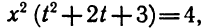
Ответ. Наименьшее значение 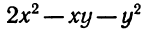
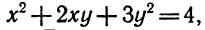
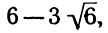
Рассмотрим еще две задачи, решение которых основывается на графических соображениях.
26. Пусть М — точка на прямой у = 2х+1, а N — точка на параболе 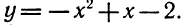
Решение:
Найдем уравнение прямой, параллельной данной прямой у = 2х+1 и касающейся параболы 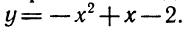
имеет дискриминант, равный нулю: 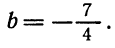
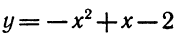
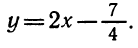
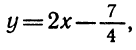
Теперь очевидно, что наименьшее значение длины отрезка МN равно расстоянию между параллельными прямыми у = 2х+1 и 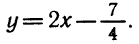
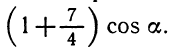
Ответ.
Замечание:
Возможно, более простым будет следующее решение. Найдем наименьшее значение разности 
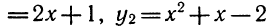
искомое наименьшее значение равно 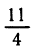
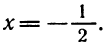
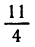
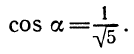
27. Найти все значения параметра а, для которых наименьшее значение функции 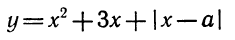
Решение:
График данной функции состоит из частей двух парабол, «склеенных» в точке с абсциссой 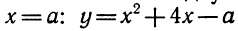
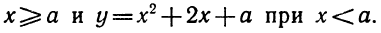
Мы перечислили все возможные значения аргумента, которые «подозреваются на минимум». (Не беда, если среди них окажутся лишние. Единственное следствие — некоторое увеличение объема вычислительной работы.) Следовательно» условию задачи удовлетворяют все те значения (и только те) параметра а, для которых выполняется хотя бы одно из трех неравенств
Все три неравенства объединены квадратной скобкой, что означает, что нам надо, решив каждое из них, полученные ответы объединить (а не находить множество значений параметра а, удовлетворяющее всем трем одновременно, как это делается в системах уравнений или неравенств).
Решая неравенства, получим для каждого из них соответственно
Ответ.
Мы не будем здесь подробно рассматривать задачи на доказательство неравенств, решения которых основываются на использовании тех или иных свойств квадратного трехчлена. (Выделение полного квадрата, оценка дискриминанта и т. д.) Ограничимся одним известным и полезным неравенством, при доказательстве которого свойства квадратного трехчлена используются весьма нестандартно.
28. Доказать, что для любых 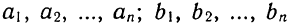
(неравенство Коши-Буняковского).
Решение:
Рассмотрим следующую квадратичную функцию от х:
При всех х функция 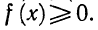
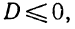
Значит,
откуда получаем требуемое неравенство. Легко видеть, что равенство в неравенстве Коши-Буняковского имеет место, если существует х, обращающий в ноль все слагаемые в выражении для 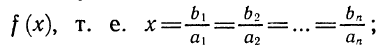
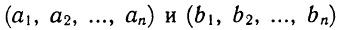
Доказанное неравенство имеет очевидную геометрическую интерпретацию. Для n = 2; 3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведения их длин. Так же можно
интерпретировать неравенство Коши-Буняковского и для произвольных n.
Из полученного неравенства можно получить следствия. На пример, возьмем 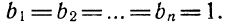
Небольшой обзор различных типов и видов задач, относящихся к теме «Квадратный трехчлен», показывает, сколь разно образны по тематике, методам решения, уровню сложности за дачи, составляющие эту тему. Многие идеи, рассмотренные в нашем обзоре, носят достаточно общий характер и с успехом могут быть использованы при решении задач, относящихся к самым различным разделам алгебры и анализа.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат


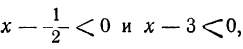
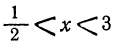
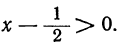
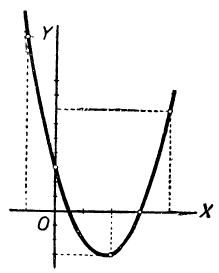
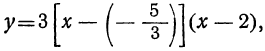
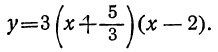
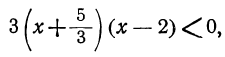
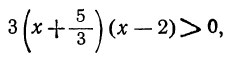
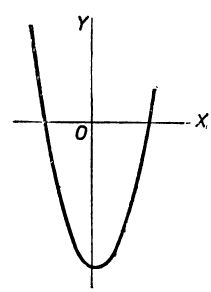
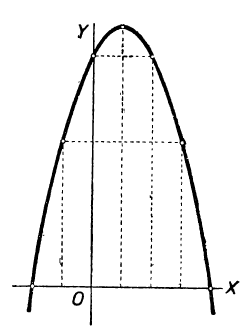
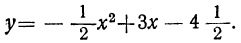
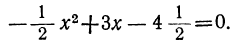
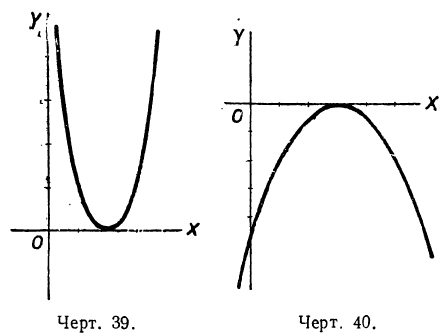
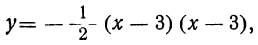
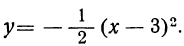
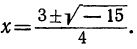
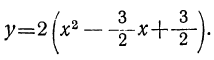
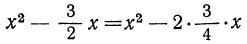
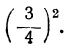
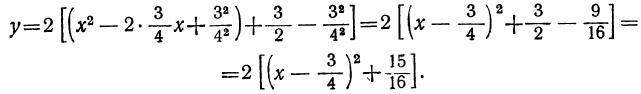
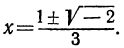
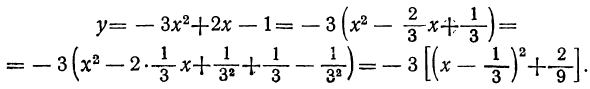
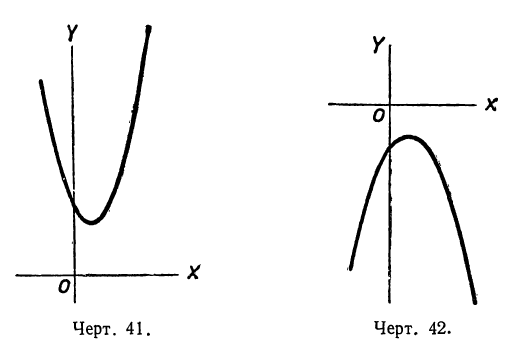
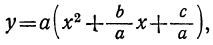
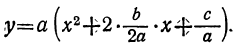
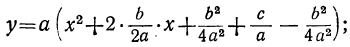
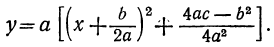
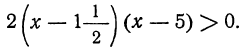
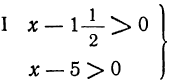
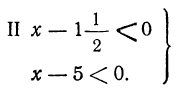
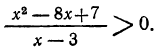
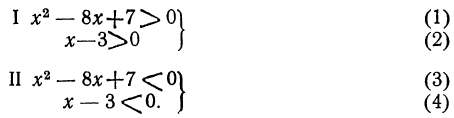
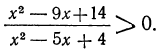
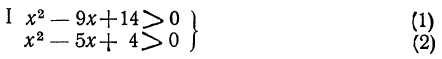
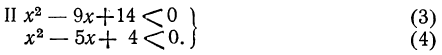
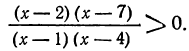
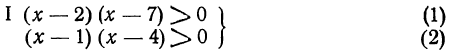
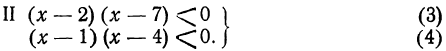
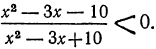

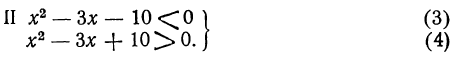
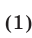
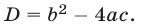
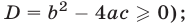
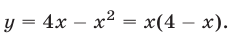
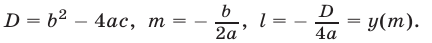
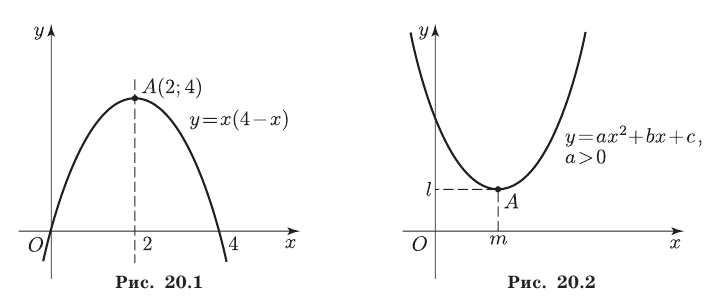
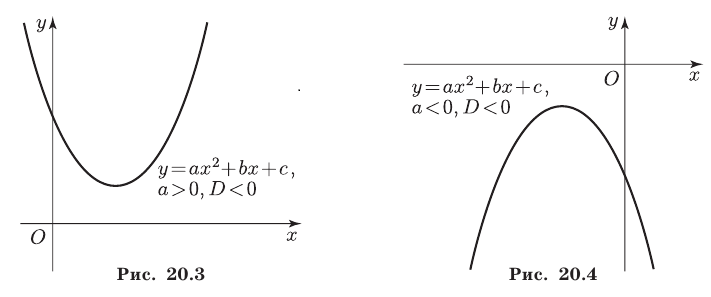
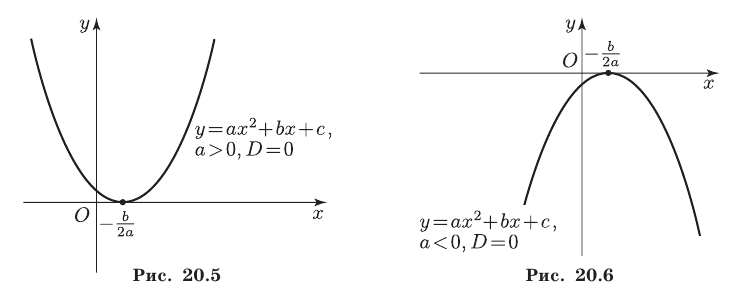
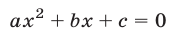
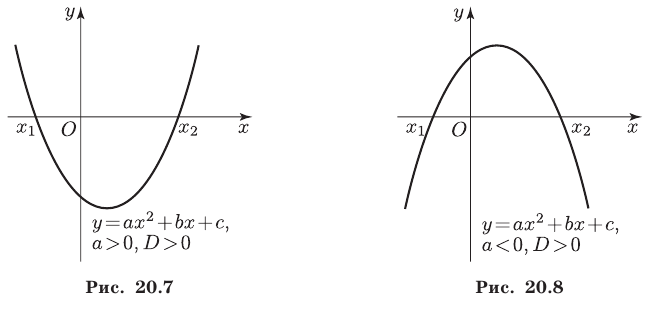
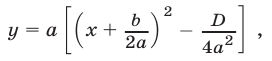
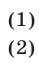
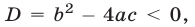
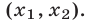
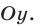
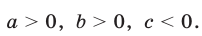
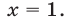
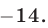
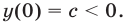
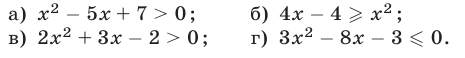
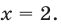
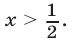
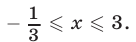
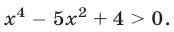
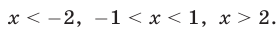
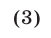
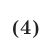
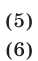
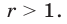
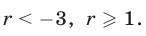
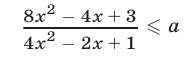
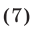
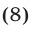
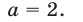
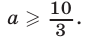
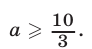
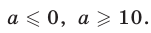
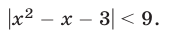
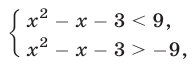
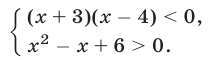
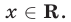
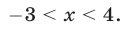
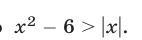
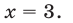
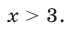
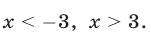
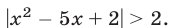
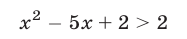
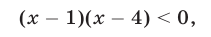
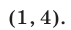
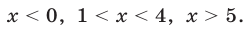
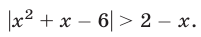
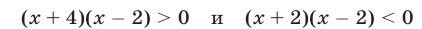
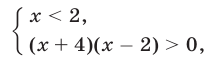
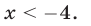
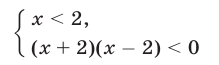
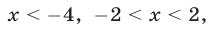
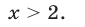
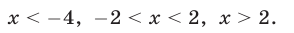
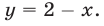
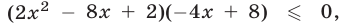
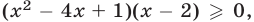
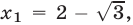
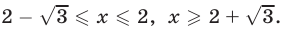
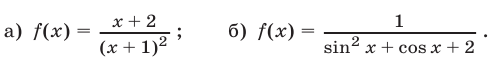
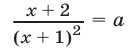
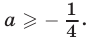
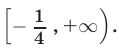
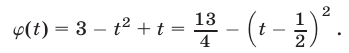
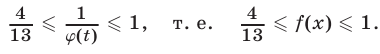
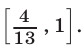
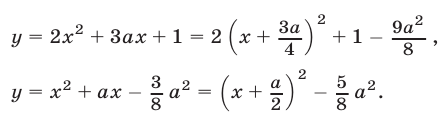
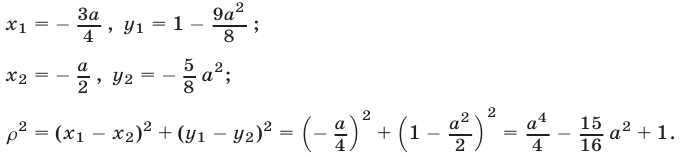
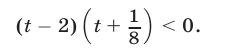
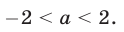
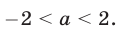
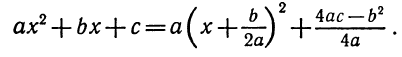
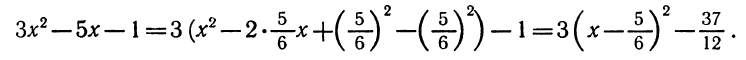
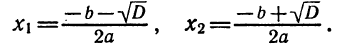
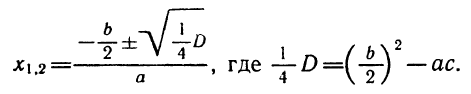
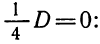
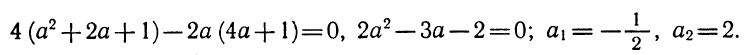
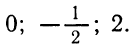
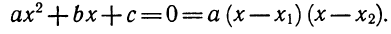
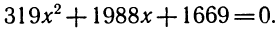
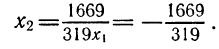
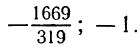
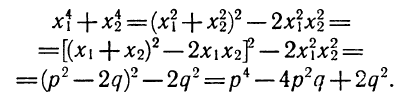
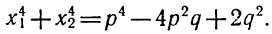
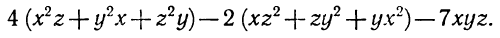
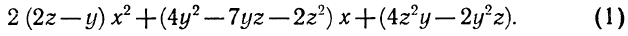
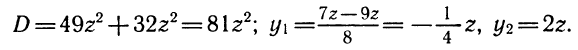
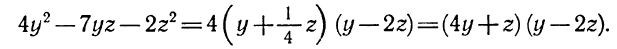
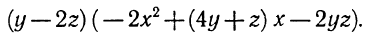
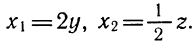
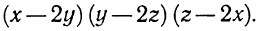
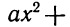
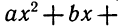
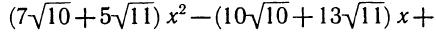
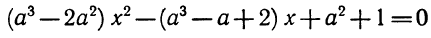
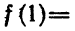
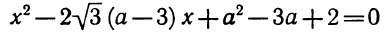
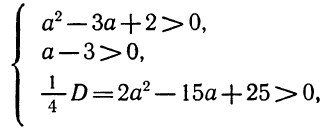
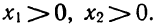
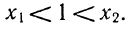
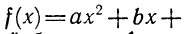
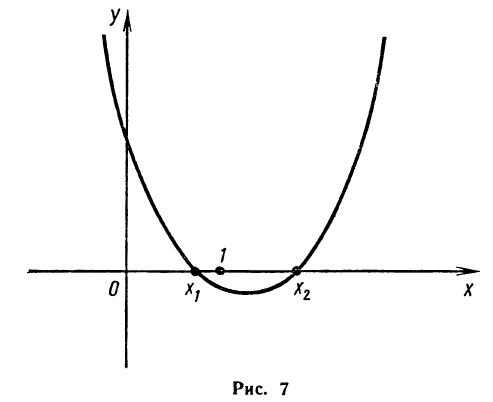
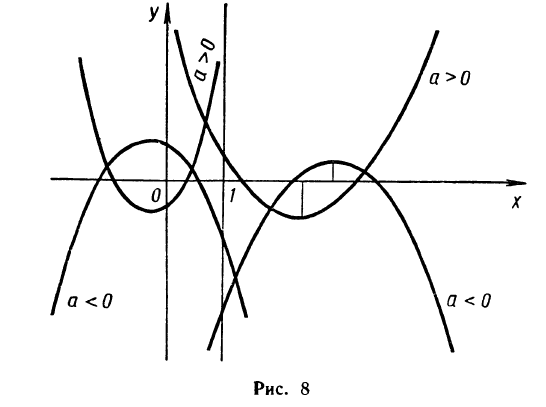
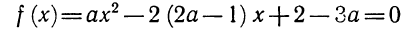
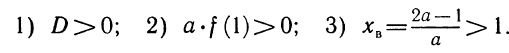
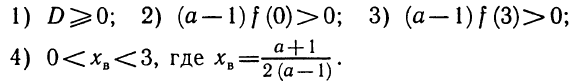
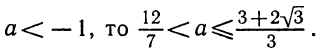
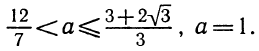
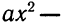
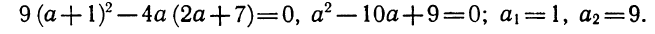
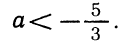 Имеем
Имеем 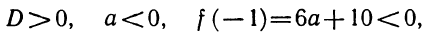
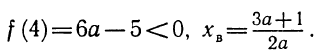 Можно проверить, что при
Можно проверить, что при 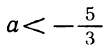 будет
будет 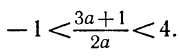 Значит, уравнение имеет корни, ветви
Значит, уравнение имеет корни, ветви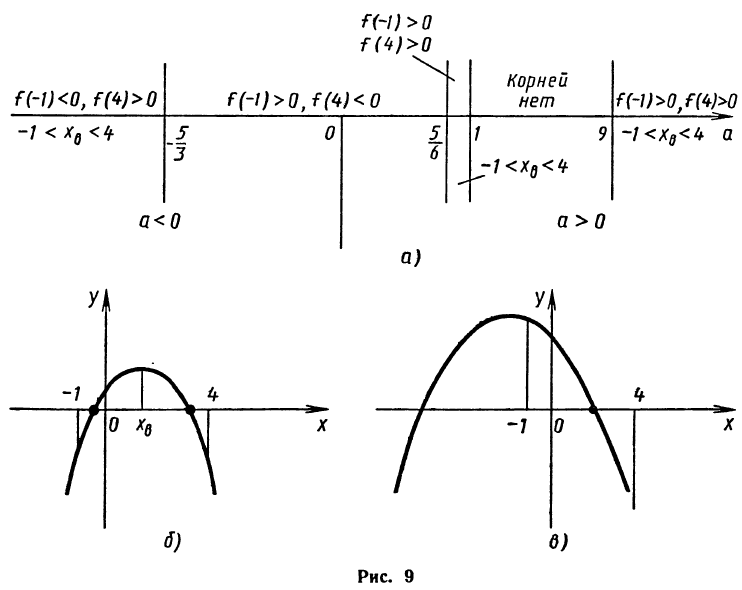
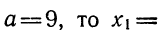
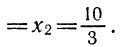
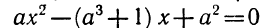
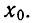
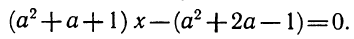
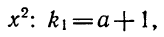

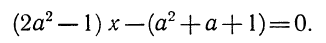
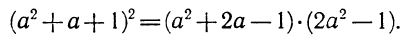
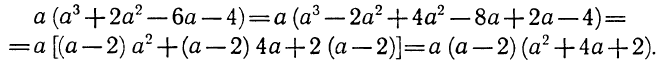
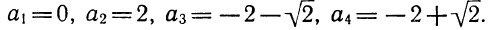
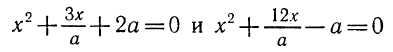
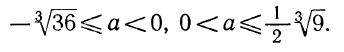
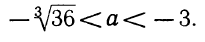 Имеем
Имеем