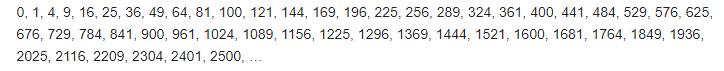Как найти квадраты целых положительных чисел - Исправление недочетов и поиск решений вместе с Examum.ru

Что такое точные квадратные числа?

Определение полного квадратного числа можно понимать как положительное натуральное целое число, квадратный корень которого также является натуральным положительным целым числом.

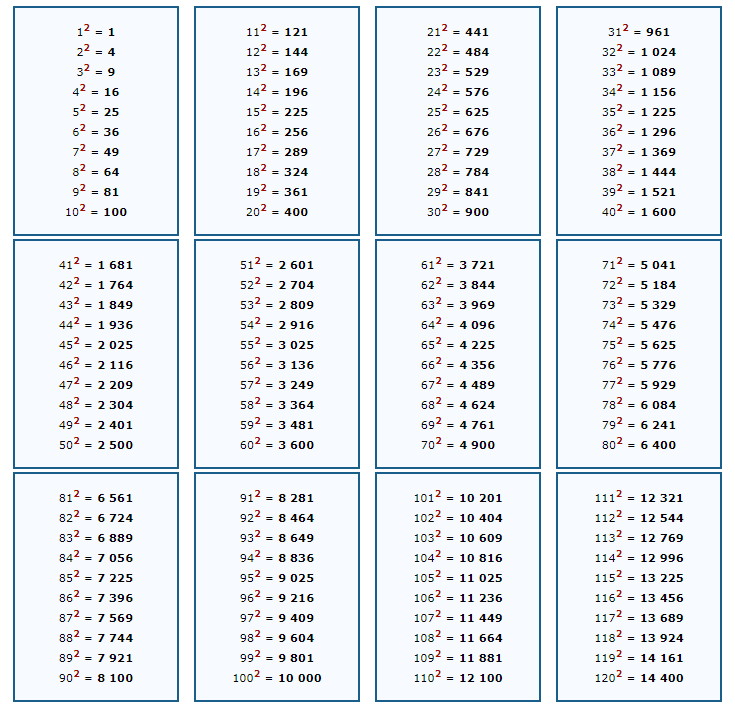
Итак, мы имеем: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100…

√1 = 1, √4 = 2, √9 = 3, √16 = 4, √25 = 5, √36 = 6, √49 = 7, √64 = 8, √81 = 9, √100 = 10…

Таблица умножения и вывески полных квадратных чисел до 15

Если мы возьмем за основу геометрию, мы можем думать, что квадрат — это фигура, стороны которой имеют одинаковую меру.

Таким образом, площадь квадрата равна l × l или l ².

Любой квадрат, стороны которого являются целыми числами, будет идеальным квадратом.

Примеры квадратов: 1 ² = 1 и 4 ² = 16

Как вычислить, является ли число полным квадратом?

Исходя из факторизации числа, если оно имеет точный квадратный корень и является результатом квадрата других чисел, мы можем сказать, что это полный квадрат.

Пример:

2704 — идеальный квадрат?

Чтобы ответить на вопрос, необходимо разложить 2704 на множитель, то есть вычислить

Следовательно, имеем: 2704 = 2 × 2 × 2 × 2 × 13 × 13 = 2 ⁴ × 13 ^2.

√2704 = √ (2 ² × 2 ² × 13 ²⁾ = 2 × 2 × 13 = 52

2704 — идеальное квадратное число 52.

Правила идеального квадрата

Совершенное квадратное число — это число, имеющее точный корень.
Нечетное совершенное квадратное число имеет нечетный корень, а четное — четное.
Полные квадратные числа никогда не заканчиваются числами 2, 3, 7 и 8.
У чисел, оканчивающихся на 0, есть квадраты, заканчивающиеся на 00.
У чисел, оканчивающихся на 1 или 9, квадраты заканчиваются на 1.
У чисел, оканчивающихся на 2 или 8, квадраты заканчиваются на 4.
У чисел, заканчивающихся на 3 или 7, есть квадраты, заканчивающиеся на 9.
У чисел, заканчивающихся на 4 или 6, есть квадраты, заканчивающиеся на 6.
У чисел, заканчивающихся на 5, есть квадраты, заканчивающиеся на 25.

Другие отношения

Квадрат числа равен произведению его соседей плюс один. Например: квадрат семи (7 ²) равен произведению смежных чисел (6 и плюс один. 7 ² = 6 × 8 + 1 = 48 + 1 = 49. х ² = (х-1). (х + 1) + 1.

Совершенные квадраты являются результатом математической последовательности между предыдущим точным квадратом и арифметической прогрессией.

1 ² = 1

2 ² = 1 + 3 = 4

3 ² = 4 + 5 = 9

4 ² = 9 + 7 = 16

5 ² = 16 + 9 = 25

6 ² = 25 + 11 = 36

7 ² = 36 + 13 = 49

8 ² = 49 + 15 = 64

9 ² = 64 + 17 = 81

10 ² = 81 + 19 = 100…

Смотрите также:

Источник

Учитывая положительное целое число n, найдите минимальное количество квадратов, которое в сумме дает n.

Например,

Input: 100
Output: 1
100 is a perfect square. It can be represented as 10².

Input: 10
Output: 2
10 can be represented as 3² + 1².

Input: 63
Output: 4
63 can be represented as 7² + 3² + 2² + 1².

Потренируйтесь в этой проблеме

Идея состоит в том, чтобы использовать рекурсия. Для каждого положительного целого числа i <= √n, повторяться для n-i² и найдите минимальное количество квадратов, сумма которых равна n. Это показано ниже на C++ и Java:

C++

#include <iostream>

#include <cmath>

using namespace std;

// Вспомогательная функция для проверки, является ли заданное число `n` идеальным квадратом или нет

bool isPerfectSquare(int n)

{

// найти значение с плавающей запятой квадратного корня из `n`

long double sqr = sqrt(n);

// вернуть true, если квадратный корень является целым числом

return sqr == floor(sqr);

}

// Рекурсивная функция для нахождения минимального количества квадратов, сумма которых равна `n`

int findMinSquares(int n)

{

// базовый случай: `n` — идеальный квадрат

if (isPerfectSquare(n)) {

return 1;

}

// инициализируем результат максимально возможным количеством квадратов

int result = n;

// перебираем все положительные целые числа, меньшие квадратного корня из `n`

for (int i = 1; i*i < n; i++)

{

// повторить для `n-i×i` и обновить результат, если найдено меньшее значение

result = min(result, 1 + findMinSquares(n — i*i));

}

return result;

}

int main()

{

int n = 63;

cout << «The minimum number of squares is « << findMinSquares(n) << endl;

return 0;

}

Скачать Выполнить код

результат:

The minimum number of squares is 4

Java

class Main

{

// Вспомогательная функция для проверки, является ли заданное число `n` идеальным квадратом или нет

public static boolean isPerfectSquare(int n)

{

// найти значение с плавающей запятой квадратного корня из `n`

double sqr = Math.sqrt(n);

// вернуть true, если квадратный корень является целым числом

return sqr == Math.floor(sqr);

}

// Рекурсивная функция для нахождения минимального количества квадратов, сумма которых равна `n`

public static int findMinSquares(int n)

{

// базовый случай: `n` — идеальный квадрат

if (isPerfectSquare(n)) {

return 1;

}

// инициализируем результат максимально возможным количеством квадратов

int result = n;

// перебираем все положительные целые числа, меньшие квадратного корня из `n`

for (int i = 1; i*i < n; i++)

{

// повторить для `n-i×i` и обновить результат, если найдено меньшее значение

result = Integer.min(result, 1 + findMinSquares(n — i*i));

}

return result;

}

public static void main(String[] args)

{

int n = 63;

System.out.println(«The minimum number of squares is « + findMinSquares(n));

}

Скачать Выполнить код

результат:

The minimum number of squares is 4

Временная сложность приведенного выше решения экспоненциальна и требует дополнительного места для рекурсии (стека вызовов). Проблема может быть рекурсивно разбита на более мелкие подзадачи, и каждая подзадача повторяется несколько раз. Повторяющиеся подзадачи легко увидеть, нарисовав дерево рекурсии.

Поскольку задача удовлетворяет оптимальное основание а также перекрывающиеся подзадачи свойства динамическое программирование, решение подзадачи может быть получено восходящим способом. Ниже приведено решение для динамического программирования на C, Java и Python, где вспомогательный массив используется для хранения решений более мелких подзадач:

C

#include <stdio.h>

// Вспомогательная функция для поиска минимума среди двух целых чисел `x` и `y`

int min(int x, int y) {

return x < y ? x : y;

}

// Итерационная функция для нахождения минимального количества квадратов, сумма которых равна `n`

int findMinSquares(int n)

{

// создаем вспомогательный массив T[], где T[i] хранит минимальное число

// квадратов, сумма которых равна `i`

int T[n + 1];

// заполняем вспомогательный массив T[] снизу вверх

for (int i = 0; i <= n; i++)

{

// инициализируем T[i] максимально возможным количеством квадратов

T[i] = i;

// перебрать все положительные целые числа, меньшие или равные

// квадратный корень из `i`

for (int j = 1; j*j <= i; j++)

{

// вычисляем значение T[i], используя результат меньшего

// подзадача T[i-j×j]

T[i] = min(T[i], 1 + T[i — j*j]);

}

return T[n];

}

int main(void)

{

int n = 63;

printf(«The minimum number of squares is %d», findMinSquares(n));

return 0;

}

Скачать Выполнить код

результат:

The minimum number of squares is 4

Java

class Main

{

// Итерационная функция для нахождения минимального количества квадратов, сумма которых равна `n`

public static int findMinSquares(int n)

{

// создаем вспомогательный массив T[], где T[i] хранит минимальное число

// квадратов, сумма которых равна `i`

int[] T = new int[n + 1];

// заполняем вспомогательный массив T[] снизу вверх

for (int i = 0; i <= n; i++)

{

// инициализируем T[i] максимально возможным количеством квадратов

T[i] = i;

// перебрать все положительные целые числа, меньшие или равные

// квадратный корень из `i`

for (int j = 1; j*j <= i; j++)

{

// вычисляем значение T[i], используя результат меньшего

// подзадача T[i-j×j]

T[i] = Integer.min(T[i], 1 + T[i — j*j]);

}

return T[n];

}

public static void main(String[] args)

{

int n = 63;

System.out.println(«The minimum number of squares is « + findMinSquares(n));

}

Скачать Выполнить код

результат:

The minimum number of squares is 4

Python

# Итеративная функция для нахождения минимального количества квадратов, сумма которых равна `n`

def findMinSquares(n):

# создает вспомогательный массив T[], где T[i] хранит минимальное число

# квадратов, сумма которых равна `i`

T = [0] * (n + 1)

# заполняет вспомогательный массив T[] снизу вверх

for i in range(n + 1):

# инициализирует T[i] максимально возможным количеством квадратов

T[i] = i

# перебирает все положительные целые числа, меньшие или равные

# квадратный корень из `i`

j = 1

while j*j <= i:

# рассчитывает значение T[i], используя результат меньшего

# Подзадача # T[i-j×j]

T[i] = min(T[i], 1 + T[i — j*j])

j += 1

return T[n]

if __name__ == ‘__main__’:

n = 63

print(‘The minimum number of squares is’, findMinSquares(n))

Скачать Выполнить код

результат:

The minimum number of squares is 4

Временная сложность приведенного выше решения равна O(n.√n), а дополнительное пространство, используемое программой, равно O(n).

Источник

В этой статье мы поговорим, что такое квадрат числа, как его найти, а также каким образом производятся подобные вычисления в программировании.

Квадратом Х называют произведение 2-х множителей, каждый из которых равен Х.

Обозначение квадрата осуществляется с помощью степени, то есть Х² читается «Х в квадрате».

Если говорить еще более простым языком, то квадратом можно назвать число, которое умножено само на себя. Таким образом, мы можем написать простейшую формулу вычисления Х²:

Х² = Х ⋅ Х

Почему вообще такое выражение называют квадратом X? Дело в том, что именно данной формулой выражают площадь квадрата, сторона которого равна X, то есть геометрически это значение можно представить в виде площади квадрата, имеющего целочисленную сторону.

Вывод тут прост: для решение поставленной задачи следует требуемое значение взять в качестве множителя дважды, а потом вычислить произведение. Соответственно:

3² = 3 ⋅ 3 = 9

5² = 5 ⋅ 5 = 25

10² = 10 ⋅ 10 = 100

Это все элементарно и проходится в начальных классах средней школы. Решить такой пример в математике не проблема, а когда числовые значения выходят за рамки классической таблицы умножения, используют таблицу, ускоряющую расчеты.

Также описанную математическую операцию можно рассматривать в контексте частного случая возведения в степень — ведь именно этим, по сути, она и является — возведением в степень 2.

Интерес представляет и числовая последовательность для квадратов целых чисел, являющихся неотрицательными (речь идет о последовательности A000290 в OEIS):

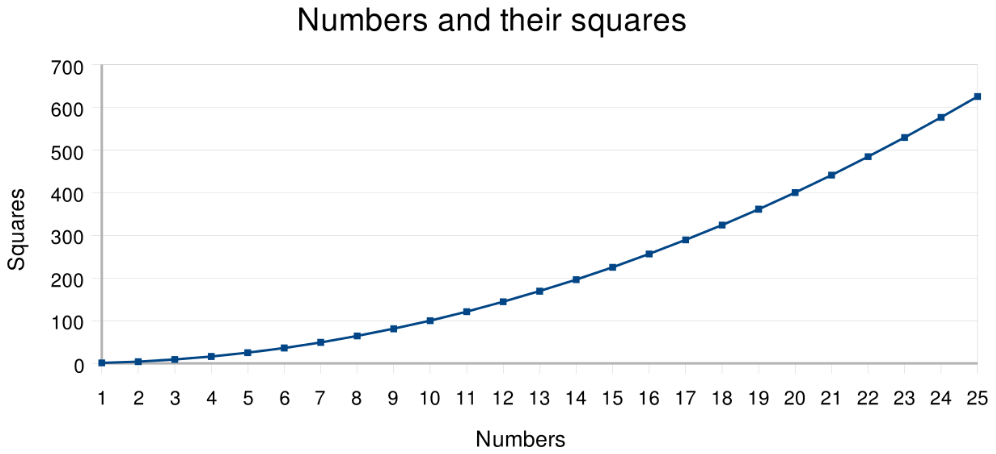
Нельзя не сказать и про график y=x², где представлены целые значения x на отрезке 1-25.

Квадратные числа

Если же говорить о натуральных числах из последовательности, упомянутой выше, в историческом контексте, то их всегда называли «квадратными». Квадратное числовое значение также называют полным либо точным квадратом, то есть целым значением, квадратный корень из которого можно извлечь нацело. К примеру, найти корень из 9 несложно (√9 = 3, т. к. 3 ⋅ 3 = 9). Не составляет проблем и вычислить корень из ста: (√100 = 10, ведь десять на десять равно сто).

Легко понять, что сто — это квадратное число, так как его можно записать в виде 10 ⋅ 10, плюс оно может быть представлено, как было сказано выше, в качестве площади квадрата со стороной, равной десяти. Таким образом, можно сделать вывод, что квадратное число включено в категорию классических фигурных чисел, то есть чисел, которые мы можем представить в виде геометрических фигур. Но в эту тему углубляться пока не будем.

А что в программировании?

Теперь давайте посмотрим, как все это работает в программировании. Для примера возьмем такой язык программирования, как Java (кстати, статья о том, как выполнять возведение в степень в Java, уже была).

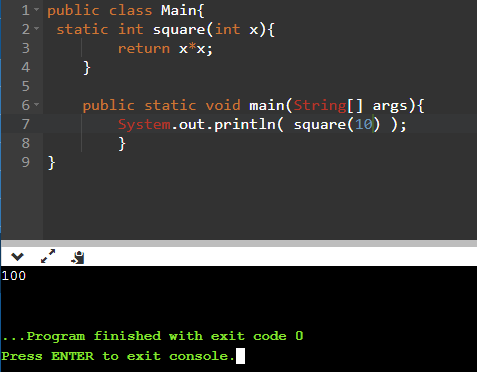
Напишем простой метод по возведению любых числовых значений в квадрат:

public class Main{

static int square(int x){

return x*x;

}

public static void main(String[] args){

System.out.println( square(10) );

}

Вы можете воспользоваться любым онлайн-компилятором для проверки этого кода. Также никто не мешает вписать любое число вместо десяти.

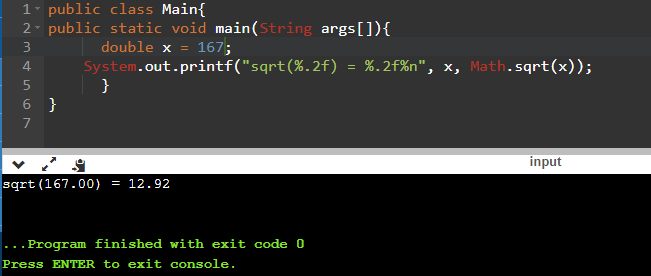
Теперь воспользуемся простейшей программой для того, чтобы найти квадратный корень из 100:

public class Main{

public static void main(String args[]){

double x = 100;

System.out.printf("sqrt(%.2f) = %.2f%n", x, Math.sqrt(x));

}

Программа позволяет извлекать корень и из неквадратных значений. Ниже мы находим корень из 167:

Да, в современную эпоху калькуляторов мало кто считает в уме. Вдобавок ко всему, сегодня даже не надо покупать настоящий калькулятор, так как калькулятор есть в любом мобильном телефоне, не говоря уже об онлайн-калькуляторах, коих существует огромное количество. Однако это не значит, что можно забыть азы алгебры. Не зря же великий русский ученый Михаил Ломоносов когда-то сказал:

По материалам:

https://calculator888.ru/tablitsa-kvadratov;
http://www.for6cl.uznateshe.ru/kvadrat-chisla/;
https:/ru.wikipedia.org/.

Источник

ИДЕАЛЬНЫЙ КВАДРАТ: ЧТО ЭТО ТАКОЕ, КАК РАССЧИТАТЬ, ПРИМЕРЫ И ПРАВИЛА — МАТЕМАТИКА — 2022

То есть они являются результатом умножения числа на само себя.

1 × 1 = 1
2 × 2 = 4
3 × 3 = 9
4 × 4 = 16

Формула полного квадрата представлена следующим образом: n × n = a или n 2 = a. Таким образом, n — натуральное число, а a — точное квадратное число.

Что такое точные квадратные числа?

Итак, мы имеем: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100.

√1 = 1, √4 = 2, √9 = 3, √16 = 4, √25 = 5, √36 = 6, √49 = 7, √64 = 8, √81 = 9, √100 = 10.

Таблица умножения и вывески полных квадратных чисел до 15

Таким образом, площадь квадрата равна l × l или l 2 .

Любой квадрат, стороны которого являются целыми числами, будет идеальным квадратом.

Примеры квадратов: 1 2 = 1 и 4 2 = 16

Как вычислить, является ли число полным квадратом?

Пример:

2704 — идеальный квадрат?

Чтобы ответить на вопрос, необходимо разложить 2704 на множитель, то есть вычислить

Следовательно, имеем: 2704 = 2 × 2 × 2 × 2 × 13 × 13 = 2 4 × 13 2.

√2704 = √ (2 2 × 2 2 × 13 2) = 2 × 2 × 13 = 52

2704 — идеальное квадратное число 52.

Правила идеального квадрата

Совершенное квадратное число — это число, имеющее точный корень.
Нечетное совершенное квадратное число имеет нечетный корень, а четное — четное.
Полные квадратные числа никогда не заканчиваются числами 2, 3, 7 и 8.
У чисел, оканчивающихся на 0, есть квадраты, заканчивающиеся на 00.
У чисел, оканчивающихся на 1 или 9, квадраты заканчиваются на 1.
У чисел, оканчивающихся на 2 или 8, квадраты заканчиваются на 4.
У чисел, заканчивающихся на 3 или 7, есть квадраты, заканчивающиеся на 9.
У чисел, заканчивающихся на 4 или 6, есть квадраты, заканчивающиеся на 6.
У чисел, заканчивающихся на 5, есть квадраты, заканчивающиеся на 25.

Другие отношения

Квадрат числа равен произведению его соседей плюс один. Например: квадрат семи (7 2 ) равен произведению смежных чисел (6 и плюс один. 7 2 = 6 × 8 + 1 = 48 + 1 = 49. х 2 = (х-1). (х + 1) + 1.

математика — Точный квадрат

Это выражение означает квадрат целого числа. Точные квадраты — это в точности числа 0, 1, 4, 9, 16, 25, . и так далее. Иногда, если изначально речь идёт о натуральных числах, 0 сюда не включается. Это понятие очень часто встречается в теоретико-числовых задачах — в том числе олимпиадных. Иногда употребляется выражение «полный квадрат», означающее по отношению к числам то же самое.

отвечен 27 Апр ’13 19:38

Точный квадрат это целое неотрицательное число, которое является квадратом целого числа.

PS: а выражение вида $%(a+b)^2$% обычно называется полным квадратом.

отвечен 27 Апр ’13 19:39

Здравствуйте

Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.

Свойства квадрата целого числа

Цель:формирование знаний, умений и навыков при решении в целых числах уравнений, содержащих квадрат целого числа; создание условий для преодоления у выпускников трудностей при решении заданий ( ) ЕГЭ по математике.

Задачи:

помочь обучающимся сформулировать основные свойства квадрата целого числа;
познакомить с различными подходами к решению задач, содержащих точный квадрат числа;
показать на примерах олимпиадных задач и задач из ЕГЭ по математике ( ) применение свойств квадрата целого числа в решении задач на делимость.

Тип занятия: урок изучения нового материала.

Ход урока

I. Постановка цели

В 2009-2010 учебном году на ЕГЭ по математике задания в основном состояли из задач на делимость. Большинство выпускников 11-х классов даже не приступали к этим задачам, увидев в них нагромождение различных символов, функций и значков. Для решения таких задач необходимо знать некоторые свойства делимости целых чисел и овладеть приёмами применения этих свойств. Сегодня на занятии мы решим ряд задач на делимость, в которых используются простейшие свойства точного квадрата числа.

II. Актуализация опорных знаний

При решении задач нам пригодятся признаки делимости чисел, с которыми вы познакомились ещё в 6-ом и последующих классах, а также определение числа

Напомните, пожалуйста, признаки делимости:

на «2» – (если число оканчивается чётной цифрой);
на «3» – (если сумма цифр числа делится на 3);
на «4» – (если две последние цифры в записи числа образуют двузначное число, кратное 4);
на «5» – (если число оканчивается 0 или 5);
на «8» – (если три последние цифры в записи числа образуют трёхзначное число, кратное 8);
на «9» – (если сумма цифр числа делится на 9);
на «10» – (если число оканчивается 0).

И ещё вопрос: что такое и как найти значения 1!, 2!, 3!, 4!, 5!, 6!, … Посмотрите, как изменяется последняя цифра числа

n! = 1 2 3 4 5 6 … n– произведение первых n натуральных чисел.
1! = 1
2! = 1 2 = 2
3! = 1 2 3 = 6
4! = 1 2 3 4 = 24
5! = 1 2 3 4 5 = 120
6! =1 2 3 4 5 6 = 720 и т.д.

При n≥5 число n! всегда оканчивается нулём.

III. Ознакомление с новым материалом

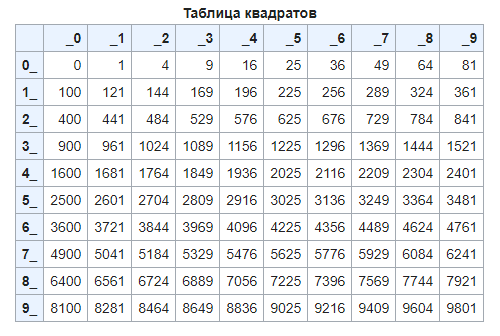
Рассмотрим таблицу квадратов натуральных чисел. Все свойства точного квадрата числа спрятаны в этой таблице. Нам только надо проявить наблюдательность при анализе данных в таблице.

Обратите внимание на последние цифры квадратов чисел. Что вы заметили?

На какие натуральные числа может делиться точный квадрат числа?

Свойства квадрата целого числа

1. Точный квадрат целого числа не может оканчиваться цифрами 2, 3, 7, 8, а также нечётным количеством нулей.
Первое свойство очевидное и доказательства не требует.

2. Квадрат натурального числа либо делится на 4, либо при делении на 8 даёт остаток 1.
Доказательство:
Если а – число чётное, то есть а = 2к, то = 4 – делится на 4.
Если а – число нечётное, то есть а = 2к + 1, то = ( = 4 + 4к + 1 = 4к (к+1) + 1 – при делении на 8 даёт остаток 1.

3. Квадрат натурального числа либо делится на 9, либо при делении на 3 даёт остаток 1.
Доказательство:
Если число а кратно 3, значит а = 3к, тогда = ( = 9 — делится на 9.
Если же число а не кратно 3, то оно имеет вид а = 3к ± 1, тогда = ( = 9 ± 6к + 1 = 3к (3к±2) + 1 – при делении на 3 даёт остаток 1.

Вот мы и сформулировали свойства точного квадрата числа. Теперь вашему вниманию я предлагаю ряд задач, в решении которых используются вышеперечисленные свойства.

1. Найти все натуральныеn, при которых число является точным квадратом.

Решение:

Если n=1, то – не является точным квадратом.
Если n=2, то – не является точным квадратом.
Если n=3, то – не является точным квадратом.
Если n=4, то , значит, при n=4 число является точным квадратом числа.
Если , то оканчивается 0, тогда оканчивается 7, но по свойству (1) квадрат целого числа не может оканчиваться цифрой 7. Значит, других натуральных чисел n, удовлетворяющих данному условию, не существует.

Ответ: при n=4.

Эта задача могла быть сформулирована иначе:

Решить в целых числах уравнение .

Способ решения тот же. Только надо помнить, что по определению

Ответ: .

2. Решить в целых числах уравнение: .

Решение:

Так как – произведение первых натуральных чисел, значит, , а целым может быть только k.
Если n=1, то
Если n=2, то
Если n=3, то
Если n=4, то

Но по свойству (1) квадрат целого числа не может оканчиваться ни 3, ни 8, значит, других целых решений уравнение не имеет.

Ответ: .

3. Решить в целых числах уравнение: .

Решение:

В решении этого уравнения надо использовать тот же приём, что и в предыдущих. Его легко решить устно.

Но тогда оканчивается 8 или 3, а это противоречит свойству (1). Значит, при уравнение не имеет решений в целых числах. Поэтому решения уравнения следует искать для
Если n=1, то
Если n=2, то .
Если n=3, то .
Если n=4, то .
Как видим, ни при каком число не является точным квадратом.

Ответ:уравнение не имеет целых решений.

4. Решить уравнение в целых числах: .

Решение:

, и опираемся на свойство(1) квадрата целого числа.

Значит, оканчивается 7, но тогда и оканчивается 7.
Но квадрат целого числа не может оканчиваться 7, значит, целых решений нет.
Значит, решения уравнения следует искать при = 1, 2, 3, 4.
Если n=1, то
Если n=2, то
Если n=3, то
Если n=4, то

Ответ: .

5. Решить в натуральных числах уравнение .

Решение:

В этом уравнении должны быть натуральными числами, а в остальном – решение аналогично предыдущим.

Но квадрат целого числа не может оканчиваться 3, значит, при натуральных решений уравнение не имеет. Остаётся проверить наличие решений при =1, 2, 3, 4.
Если n=1, то
Если n=2, то
Если n=3, то
Если n=4, то

Ответ:

6. Решить уравнение в целых числах: 1!+2!+3!+…+

Решение:

Если =1, то 1! = , тогда
Если =2, то 1!+2! = – число не целое.
Если =3, то 1!+2!+3! =
Если =4, то 1!+2!+3!+4! = – число не целое.
Если , то 1!+2!+3!+4!+…+х! оканчивается цифрой 3, но квадрат целого числа не может оканчиваться 3.
Значит, при

Ответ: =1, 2) =3,

7. Доказать, что уравнение не имеет решений в целых числах.

Доказательство:

если делится на 5, а это возможно, если оканчивается 0 или 5, тогда

Но квадрат целого числа не может оканчиваться ни цифрой 3, ни цифрой 8.

Значит, уравнение не имеет целых решений. Что и требовалось доказать.

8. Решить в целых числах уравнение .

Решение:

Если n=1, то
Если n=2, то
Если n=3, то
Если n=4, то
Если уравнение целых решений не имеет, так как при чётном
1 2 3 4 … ( 1 2 3 4 … ( =
=1 2 3 4 … (
При нечётном
1 2 3 4 … ( 1 2 3 4 … ( =1 2 3 4 … ( – не делится на 4, а при делении на 8 даёт остаток 3, а не 1.

Ответ: 1)

9. Решить уравнение в целых числах: .

Решение:

Если =4, то
При (1 2 4 5 … +1) = – левая часть уравнения делится на 3, значит, число должно делиться на 9.
Но 1 2 4 5 … +1 на 3 не делится, поэтому левая часть уравнения не кратна 9 Значит, при уравнение не имеет целых решений.

10. Решить в целых числах уравнение:

Решение:

1) Если m – число чётное, то – числа нечётные и их произведение
– тоже число нечётное, но правая часть уравнения – чётное число. Значит, при чётном m уравнение не имеет решений.
2) Если m – число нечётное, то – числа чётные, причем, – два последовательных чётных числа, одно из которых кратно 2, а другое – 4. Тогда , значит, , но квадрат целого числа делится на 4 или при делении на 8 даёт остаток 1. А лишь в единственном случае, если n=0. При n=0 уравнение примет вид:

Ответ: .

11. Решить в целых числах уравнение:

Решение:

1) Если n – число четное, то – числа нечётные, значит, – тоже нечетное число, а это возможно лишь тогда, когда , т.е. . При всех других чётных уравнение целых решений не имеет.
2) Если n – число нечётное, то – два последовательных чётных числа, одно из которых кратно 2, а другое – 4. Тогда их произведение . Значит, и левая часть уравнения
, но – число нечётное, значит, только
. Это возможно, если . При .
При ,
.
Если же , то , а правая часть уравнения , значит, других решений уравнение не имеет.

Ответ: 1) 2)

12. Решить в целых числах уравнение:

Решение:

– имеет решение, если:
1) = 0, тогда
— число нечётное, . Тогда, ,

.
( ) – нечётное число при . Значит, тоже должно быть нечётным, а это возможно, если . Тогда при исходное уравнение примет вид .

Ответ: 1) ; 2)

13. Доказать, что число, оканчивающееся двумя одинаковыми цифрами, отличными от 0 и 4, не может быть точным квадратом.

Доказательство:

Так как квадрат любого числа может оканчиваться цифрами: 0; 1; 4; 5; 6; 9, то кроме 0 и 4 последними цифрами могут быть: 11; 55; 66; 99.

Источник

Оглавление:

Что такое точные квадратные числа?

Как вычислить, является ли число полным квадратом?

Правила идеального квадрата

Другие отношения

C++

Java

C

Java

Python

Квадратные числа

А что в программировании?

ИДЕАЛЬНЫЙ КВАДРАТ: ЧТО ЭТО ТАКОЕ, КАК РАССЧИТАТЬ, ПРИМЕРЫ И ПРАВИЛА — МАТЕМАТИКА — 2022

Что такое точные квадратные числа?

Как вычислить, является ли число полным квадратом?

Правила идеального квадрата

Другие отношения

математика — Точный квадрат

Здравствуйте

Свойства квадрата целого числа