Python для анализа данных¶
Полное описание для scipy.stats доступно по ссылке. По ссылке можно прочитать полную документацию по работе с непрерывными (Continuous), дискретными (Discrete) и многомерными (Multivariate) распределениями. Пакет также предоставляет некоторое количество статистических методов, которые рассматриваются в курсах статистики. А описание для numpy.random находится по следующей ссылке.
In [1]:
import scipy.stats as sps import numpy as np import ipywidgets as widgets import matplotlib.pyplot as plt from numpy import random import seaborn as sns sns.set(palette='Set2', style='whitegrid', font_scale=1.3)
1. Работа с библиотекой numpy.random.¶
Базовые функции
-
randint(low[, high, size, dtype])— случайное число в диапазоне; -
choice(a[, size, replace, p])— Генерирует случайную выборку из заданного одномерного массива; -
shuffle(x)— Премешивает выходные значения массива; -
permutation(x)— Перемешивает значения самого массива и возвращает его перемешанным.
Создание простого случайного массива¶
Сгенерируем 5 случайных чисел из равномерного распределения [0, 1):
Out[2]:
array([0.53404185, 0.33336281, 0.74879742, 0.18810245, 0.33417001])
Создание случайных целых чисел:¶
Создадим случайный целочисленный массив размером 5×5 в диапазоне от 10 (включительно) до 20 (включительно)
In [3]:
np.random.randint(10, 20, (5, 5))
Out[3]:
array([[18, 11, 10, 19, 19],
[14, 15, 10, 15, 19],
[11, 12, 15, 17, 17],
[13, 11, 17, 17, 19],
[16, 14, 19, 17, 18]])
Также возможна генерация случайных чисел из конкретных распределений:¶
beta(a, b[, size])— бета-распределение;binomial(n, p[, size])— биномиальное распределение;exponential([scale, size])— экспоненциальное распределение;gamma(shape[, scale, size])— гамма-распределение;geometric(p[, size])— геометрическое распределение;normal([loc, scale, size])— нормальное распределение;poisson([lam, size])— пуассоновское распределение;uniform([low, high, size])— равномерное распределение.
Сгенерируем 5 случайных чисел из стандартного нормального распределения
Out[4]:
array([ 0.5770148 , -1.68602927, 0.21022454, 0.57520789, -0.32360461])
Укажем параметры распределения
In [5]:
np.random.normal(70, 10, 5)
Out[5]:
array([73.68257501, 56.80081027, 63.90140038, 81.41057287, 62.30318935])
Генерация из пуассоновского распределения
In [6]:
np.random.poisson(lam=2.5, size=5)
Многомерное нормальное распределение:¶
Генерация случайных выборок из многомерного нормального распределения выполняется с помощью функции multivariate_normal(mean, cov[, size, ...]).
Сгенерируем 800 векторов из двумерного нормального распределения со средним [0, 0] и ковариационной матрицей [[6, -3], [-3, 3.5]].
In [7]:
mean = (1, 2) cov = [[1, 0], [0, 1]] x = np.random.multivariate_normal(mean, cov, (3, 3)) cov = np.array([[6, -3], [-3, 3.5]]) pts = np.random.multivariate_normal([0, 0], cov, size=800)
Мы можем визуализировать эти данные с помощью точечной диаграммы. Ориентация облака точек иллюстрирует отрицательную корреляцию компонентов этой выборки.
In [8]:
plt.figure(figsize=(6, 6)) plt.plot(pts[:, 0], pts[:, 1], '.', alpha = 0.5) plt.axis('equal') plt.show()
2. Работа с библиотекой scipy.stats.¶
Общий принцип:
Пусть $X$ — класс, реализующий некоторое распределение. Конкретное распределение с параметрами params можно получить как X(params). У него доступны следующие методы:
X(params).rvs(size=N)— генерация выборки размера $N$ (Random VariateS). Возвращаетnumpy.array;X(params).cdf(x)— значение функции распределения в точке $x$ (Cumulative Distribution Function);X(params).logcdf(x)— значение логарифма функции распределения в точке $x$;X(params).ppf(q)— $q$-квантиль (Percent Point Function);X(params).mean()— математическое ожидание;X(params).median()— медиана ($1/2$-квантиль);X(params).var()— дисперсия (Variance);X(params).std()— стандартное отклонение = корень из дисперсии (Standard Deviation).
Кроме того для непрерывных распределений определены функции
X(params).pdf(x)— значение плотности в точке $x$ (Probability Density Function);X(params).logpdf(x)— значение логарифма плотности в точке $x$.
А для дискретных
X(params).pmf(k)— значение дискретной плотности в точке $k$ (Probability Mass Function);X(params).logpdf(k)— значение логарифма дискретной плотности в точке $k$.
Все перечисленные выше методы применимы как к конкретному распределению X(params), так и к самому классу X. Во втором случае параметры передаются в сам метод. Например, вызов X.rvs(size=N, params) эквивалентен X(params).rvs(size=N).
Параметры могут быть следующими:
loc— параметр сдвига;scale— параметр масштаба;- и другие параметры (например, $n$ и $p$ для биномиального).
Для примера сгенерируем выборку размера $N = 200$ из распределения $mathcal{N}(1, 9)$ и посчитаем некоторые статистики.
В терминах выше описанных функций у нас $X$ = sps.norm, а params = (loc=1, scale=3).
Примечание. Выборка — набор независимых одинаково распределенных случайных величин. Часто в разговорной речи выборку отождествляют с ее реализацией — значения случайных величин из выборки при «выпавшем» элементарном исходе.
In [9]:
sample = sps.norm(loc=1, scale=3).rvs(size=200) print('Первые 10 значений выборки:n', sample[:10]) print('Выборочное среденее: %.3f' % sample.mean()) print('Выборочная дисперсия: %.3f' % sample.var())
Первые 10 значений выборки: [-4.77722498 0.38477431 -0.39011306 3.35800245 -1.63958325 -0.65691616 0.7098962 -0.9834454 1.89568372 2.81589159] Выборочное среденее: 0.938 Выборочная дисперсия: 9.002
Вероятностные характеристики
In [10]:
print('Плотность:tt', sps.norm(loc=1, scale=3).pdf([-1, 0, 1, 2, 3])) print('Функция распределения:t', sps.norm(loc=1, scale=3).cdf([-1, 0, 1, 2, 3]))
Плотность: [0.10648267 0.12579441 0.13298076 0.12579441 0.10648267] Функция распределения: [0.25249254 0.36944134 0.5 0.63055866 0.74750746]
$p$-квантиль распределения с функцией распределения $F$ — это число $min{x: F(x) geqslant p}$.
In [11]:
print('Квантили:', sps.norm(loc=1, scale=3).ppf([0.05, 0.1, 0.5, 0.9, 0.95]))
Квантили: [-3.93456088 -2.8446547 1. 4.8446547 5.93456088]
Cгенерируем выборку размера $N = 200$ из распределения $Bin(10, 0.6)$ и посчитаем некоторые статистики.
В терминах выше описанных функций у нас $X$ = sps.binom, а params = (n=10, p=0.6).
In [12]:
sample = sps.binom(n=10, p=0.6).rvs(size=200) print('Первые 10 значений выборки:n', sample[:10]) print('Выборочное среденее: %.3f' % sample.mean()) print('Выборочная дисперсия: %.3f' % sample.var())
Первые 10 значений выборки: [9 4 5 8 7 5 7 8 6 7] Выборочное среденее: 5.815 Выборочная дисперсия: 2.511
In [13]:
print('Дискретная плотность:t', sps.binom(n=10, p=0.6).pmf([-1, 0, 5, 5.5, 10])) print('Функция распределения:t', sps.binom(n=10, p=0.6).cdf([-1, 0, 5, 5.5, 10]))
Дискретная плотность: [0.00000000e+00 1.04857600e-04 2.00658125e-01 0.00000000e+00 6.04661760e-03] Функция распределения: [0.00000000e+00 1.04857600e-04 3.66896742e-01 3.66896742e-01 1.00000000e+00]
In [14]:
print('Квантили:', sps.binom(n=10, p=0.6).ppf([0.05, 0.1, 0.5, 0.9, 0.95]))
Квантили: [3. 4. 6. 8. 8.]
Отдельно есть класс для многомерного нормального распределения.
Для примера сгенерируем выборку размера $N=200$ из распределения $mathcal{N} left( begin{pmatrix} 1 \ 1 end{pmatrix}, begin{pmatrix} 2 & 1 \ 1 & 2 end{pmatrix} right)$.
In [15]:
sample = sps.multivariate_normal( mean=[1, 1], cov=[[2, 1], [1, 2]] ).rvs(size=200) print('Первые 10 значений выборки:n', sample[:10]) print('Выборочное среденее:', sample.mean(axis=0)) print('Выборочная матрица ковариаций:n', np.cov(sample.T))
Первые 10 значений выборки: [[ 0.85484709 2.77930705] [ 2.08602217 2.47692174] [-1.36896172 -2.80735273] [ 0.15274979 -0.10392857] [ 2.12666431 2.54083453] [ 0.65826516 2.39020483] [-0.13879247 -0.10071583] [-0.82272378 1.12570173] [ 2.17156211 2.44109516] [ 0.8552283 2.99134069]] Выборочное среденее: [1.1563024 1.21146554] Выборочная матрица ковариаций: [[2.14874013 1.10612854] [1.10612854 2.03850564]]
In [16]:
sample = sps.norm(loc=np.arange(10), scale=0.1).rvs(size=10) print(sample)
[-3.71478133e-03 9.25683322e-01 2.01936398e+00 3.04612388e+00 3.91695761e+00 5.01249749e+00 5.83371327e+00 7.10138435e+00 8.00572921e+00 9.08765149e+00]
Бывает так, что надо сгенерировать выборку из распределения, которого нет в `scipy.stats`.
Для этого надо создать класс, который будет наследоваться от класса rv_continuous для непрерывных случайных величин и от класса rv_discrete для дискретных случайных величин.
Пример из документации.
Для примера сгенерируем выборку из распределения с плотностью $f(x) = frac{4}{15} x^3 I{x in [1, 2] = [a, b]}$.
In [17]:
class cubic_gen(sps.rv_continuous): def _pdf(self, x): return 4 * x ** 3 / 15 cubic = cubic_gen(a=1, b=2, name='cubic') sample = cubic.rvs(size=200) print('Первые 10 значений выборки:n', sample[:10]) print('Выборочное среденее: %.3f' % sample.mean()) print('Выборочная дисперсия: %.3f' % sample.var())
Первые 10 значений выборки: [1.91569466 1.6333686 1.71335385 1.98595286 1.39090471 1.13319513 1.18916208 1.93276106 1.62536501 1.99435283] Выборочное среденее: 1.641 Выборочная дисперсия: 0.079
Если дискретная случайная величина может принимать небольшое число значений, то можно не создавать новый класс, как показано выше, а явно указать эти значения и из вероятности.
In [18]:
some_distribution = sps.rv_discrete( name='some_distribution', values=([1, 2, 3], [0.6, 0.1, 0.3]) # значения и вероятности ) sample = some_distribution.rvs(size=200) print('Первые 10 значений выборки:n', sample[:10]) print('Выборочное среденее: %.3f' % sample.mean()) print('Частота значений по выборке:', (sample == 1).mean(), (sample == 2).mean(), (sample == 3).mean())
Первые 10 значений выборки: [1 3 1 3 2 1 1 1 3 1] Выборочное среденее: 1.695 Частота значений по выборке: 0.59 0.125 0.285
3. Как генерируются случайные числа¶
Генерация случайных чисел разделена на два компонента: генератор битов и генератор случайных чисел.
-
BitGeneratorуправляет состоянием и предоставляет функции для создания случайных бинарных последовательностей. -
Генератор случайных чисел
Generatorпринимает набор из генератора битов, и преобразует их целевые распределения, например, нормальное распределение.
Генератор — пользовательский объект, который почти идентичен устаревшему RandomState . Он принимает экземпляр генератора битов в качестве аргумента. В настоящее время по умолчанию используется PCG64.
Можно воспользоваться функцие default_rng
In [19]:
rng = np.random.default_rng(12345) print(rng)
Можно также создать экземпляр генератора напрямую с помощью экземпляра BitGenerator.
Чтобы использовать генератор бит PCG64 по умолчанию, можно создать его экземпляр напрямую и передать его генератору:
In [21]:
rng = np.random.Generator(np.random.PCG64(12345)) print(rng)
Аналогично использованию более старого генератора бит MT19937 (не рекомендуется), можно создать его экземпляр напрямую и передать его генератору:
In [22]:
rng = np.random.Generator(np.random.MT19937(12345)) print(rng)
Random.seed:¶
Данная функция используется для генерации одних и тех же случайных чисел при многократном выполнении кода на одной или разных машинах. По умолчанию генератор случайных чисел использует текущее системное время.
random.seed(svalue, version)
Параметр svalue является необязательным, и это начальное значение, необходимое для генерации случайного числа. Значение по умолчанию — None, и в таком случае генератор использует текущее системное время.
Если вы дважды используете одно и то же начальное значение, вы получите один и тот же результат
In [23]:
np.random.seed(10) print(random.random()) np.random.seed(10) print(random.random())
0.771320643266746 0.771320643266746
Другой пример, в котором мы генерируем одно и то же случайное число много раз
In [24]:
for i in range(5): # устанавливаем опцию генератора np.random.seed(11) # генерируем число от 1 до 1000. print(np.random.randint(1, 1000))
4. Производительность¶
Если вам нужно только сгенерировать случайный набор чисел без дополнительной работы с распределениями, рекомендуется использовать функции из numpy. Покажем это на примерах
Сравним время генерации 1000 случайных чисел двумя библиотеками
In [26]:
%timeit x = np.random.uniform(size=size, high=2)
10.8 µs ± 249 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
In [27]:
%timeit x = sps.uniform.rvs(size=size, scale=2)
54.1 µs ± 1.63 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
Как видим, numpy генерирует в 5 раз быстрее.
Если же мы будем иначе передавать параметры распределения в scipy, то будет еще дольше
In [28]:
%timeit x = sps.uniform(scale=2).rvs(size=size)
618 µs ± 34.2 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
Это объясняется тем, что код sps.uniform(scale=2) создает объект распределения, на что тратится достаточно много времени
In [29]:
%timeit x = sps.uniform(scale=2)
495 µs ± 17.3 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
Посмотрим также примеры с нормальным распределением
In [30]:
%timeit x = np.random.normal(size=size, loc=2, scale=5)
28.2 µs ± 1.19 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
In [31]:
%timeit x = sps.norm.rvs(size=size, loc=2, scale=5)
68.4 µs ± 1.68 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
In [32]:
%timeit x = sps.norm(loc=2, scale=5).rvs(size=size)
672 µs ± 29.8 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
5. Свойства абсолютно непрерывных распределений¶
Прежде чем исследовать свойства распределений, напишем вспомогательную функцию для отрисовки плотности распределения.
In [33]:
def show_pdf(pdf, xmin, xmax, ymax, grid_size, distr_name, **kwargs): """ Рисует график плотности непрерывного распределения pdf - плотность xmin, xmax - границы графика по оси x ymax - граница графика по оси y grid_size - размер сетки, по которой рисуется график distr_name - название распределения kwargs - параметры плотности """ grid = np.linspace(xmin, xmax, grid_size) plt.figure(figsize=(10, 5)) plt.plot(grid, pdf(grid, **kwargs), lw=5) plt.grid(ls=':') plt.xlabel('Значение', fontsize=18) plt.ylabel('Плотность', fontsize=18) plt.xlim((xmin, xmax)) plt.ylim((None, ymax)) title = 'Плотность {}'.format(distr_name) plt.title(title.format(**kwargs), fontsize=20) plt.show()
2.1 Нормальное распределение¶
$mathcal{N}(a, sigma^2)$ — нормальное распределение.
Параметры в scipy.stats:
loc= $a$,scale= $sigma$.
Свойства распределения:
- математическое ожидание: $a$,
- дисперсия: $sigma^2$.
Посмотрим, как выглядит плотность нормального стандартного распределения $mathcal{N}(0, 1)$:
In [34]:
show_pdf( pdf=sps.norm.pdf, xmin=-3, xmax=3, ymax=0.5, grid_size=100, distr_name=r'$N({loc}, {scale})$', loc=0, scale=1 )
Сгенерируем значения из нормального стандартного распределения и сравним гистограмму с плотностью:
In [35]:
sample = sps.norm.rvs(size=1000) # выборка размера 1000 grid = np.linspace(-3, 3, 1000) # сетка для построения графика plt.figure(figsize=(12, 5)) plt.hist(sample, bins=30, density=True, alpha=0.6, label='Гистограмма выборки') plt.plot(grid, sps.norm.pdf(grid), color='red', lw=5, label='Плотность случайной величины') plt.title(r'Случайная величина $xi sim mathcal{N}$(0, 1)', fontsize=20) plt.legend(fontsize=14, loc=1) plt.show()
Исследуем, как меняется плотность распределения в зависимости от параметров.
In [36]:
# создать виджет, но не отображать его ip = widgets.interactive(show_pdf, pdf=widgets.fixed(sps.norm.pdf), grid_size=widgets.IntSlider(min=25, max=300, step=25, value=100), xmin=widgets.FloatSlider(min=-10, max=0, step=0.1, value=-5), xmax=widgets.FloatSlider(min=0, max=10, step=0.1, value=5), ymax=widgets.FloatSlider(min=0, max=2, step=0.1, value=1), loc = widgets.FloatSlider(min=-10, max=10, step=0.1, value=0), scale = widgets.FloatSlider(min=0.01, max=2, step=0.01, value=1), distr_name = r'$N$({loc}, {scale})' ); # отображаем слайдеры группами display(widgets.HBox(ip.children[:2])) display(widgets.HBox(ip.children[2:4])) display(widgets.HBox(ip.children[5:7])) # отображаем вывод функции display(ip.children[-1]) ip.update() # чтобы функция запустилась до первого изменения слайдеров
Показательный пример с разными значениями параметров распределения:
In [37]:
grid = np.linspace(-7, 7, 1000) # сетка для построения графика loc_values = [0, 3, 0] # набор значений параметра a sigma_values = [1, 1, 2] # набор значений параметра sigma plt.figure(figsize=(12, 6)) for i, (a, sigma) in enumerate(zip(loc_values, sigma_values)): plt.plot(grid, sps.norm(a, sigma).pdf(grid), lw=5, label='$mathcal{N}' + '({}, {})$'.format(a, sigma)) plt.legend(fontsize=16) plt.title('Плотности нормального распределения', fontsize=20) plt.xlabel('Значение', fontsize=18) plt.ylabel('Плотность', fontsize=18) plt.show()
Значения параметров определяют положение и форму кривой на графике распределения, каждой комбинации параметров соответствует уникальное распределение.
Для нормального распределения:
- Параметр $loc = a$ отвечает за смещение кривой вдоль $mathcal{Ox}$, тем самым определяя положение вертикальной оси симметрии плотности распределения. Вероятность того, что значение случайной величины $x$ попадет в отрезок $mathcal{[m; n]}$, равна площади участка, зажатого кривой плотности, $mathcal{Ox}$ и вертикальными прямыми ${x = m}$, ${x = n}$. В точке $a$ значение плотности распределения наибольшее, соответственно вероятность того, что значение случайной величины, имеющей нормальное распределение, попадет в окрестность точки $а$ — наибольшая.
- параметр ${scale = sigma}$ отвечает за смещение экстремума вдоль $mathcal{Oy}$ и «прижимание» кривой к вертикальной прямой ${x = a}$, тем самым увеличивая площадь под кривой плотности в окрестности точки $а$. Другими словами, этот параметр отвечает за дисперсию — меру разброса значений случайной величины. При уменьшении параметра $sigma$ увеличивается вероятность того, что нормально распределенная случайная величина будет равна $a$. Это соответствует мере разброса значений случайной величины относительно её математического ожидания, то есть дисперсии $sigma^2$.
Проверим несколько полезных свойств нормального распределения.
Пусть $xi_1 sim mathcal{N}(a_1, sigma_1^2)$ и $xi_2 sim mathcal{N}(a_2, sigma_2^2)$ — независимые случайные величины. Тогда $xi_3 = xi_1 + xi_1 sim mathcal{N}(a_1 + a_2, sigma_1^2 + sigma_2^2)$
In [38]:
sample1 = sps.norm(loc=-1, scale=3).rvs(size=1000) sample2 = sps.norm(loc=1, scale=4).rvs(size=1000) sample3 = sample1 + sample2 grid = np.linspace(-15, 15, 1000) plt.figure(figsize=(12, 5)) plt.hist(sample3, density=True, bins=30, alpha=0.6, label=r'Гистограмма суммы $xi_3 = xi_1 + xi_1$') plt.plot(grid, sps.norm(-1 + 1, np.sqrt(3*3 + 4*4)).pdf(grid), color='red', lw=5, label=r'Плотность $mathcal{N}(0, 25)$') plt.title( r'Распределение $xi_3=xi_1+xi_1simmathcal{N}(-1 + 1, 3^2 + 4^2)$ ', fontsize=20 ) plt.xlabel('Значение', fontsize=17) plt.ylabel('Плотность', fontsize=17) plt.legend(fontsize=16) plt.show()
Пусть $xi$ из $mathcal{N}(a, sigma^2)$. Тогда $xi_{new} = cxisimmathcal{N}(c a, c^2 sigma^2)$
In [39]:
sample = sps.norm(loc=5, scale=3).rvs(size=1000) grid = np.linspace(-5, 30, 1000) c = 2 new_sample = c*sample plt.figure(figsize=(12,5)) plt.hist(new_sample, density=True, bins=30, alpha=0.6, label=r'Гистограмма $xi_{new} = c xi$') plt.plot(grid, sps.norm(c*5, c*3).pdf(grid), color='red', lw=5, label=r'Плотность $mathcal{N}(10, 36)$') plt.title( r'Распределение $xi_{new}=c xisimmathcal{N}(2cdot5, 4cdot9)$', fontsize=20 ) plt.xlabel('Значение', fontsize=17) plt.ylabel('Плотность', fontsize=17) plt.legend(fontsize=16) plt.show()
2.2 Равномерное распределение¶
${U}(a, b)$ — равномерное распределение.
Параметры в scipy.stats:
loc= $a$,scale= $b-a$.
Свойства распределения:
- математическое ожидание: $frac{a+b}{2}$,
- дисперсия: $frac{(b-a)^2}{12}$.
In [40]:
show_pdf( pdf=sps.uniform.pdf, xmin=-0.5, xmax=1.5, ymax=2, grid_size=10000, distr_name=r'$U(0, 1)$', loc=0, scale=1 )
In [41]:
grid = np.linspace(-3, 3, 10001) # сетка для построения графика sample = sps.uniform.rvs(size=1000) # выборка размера 1000 plt.figure(figsize=(12, 5)) plt.hist(sample, bins=30, density=True, alpha=0.6, label='Гистограмма случайной величины') plt.plot(grid, sps.uniform.pdf(grid), color='red', lw=5, label='Плотность случайной величины') plt.title(r'Случайная величина $xisim U(0, 1)$', fontsize=20) plt.xlim(-0.5, 1.5) plt.legend(fontsize=14, loc=1) plt.show()
In [42]:
# создать виджет, но не отображать его ip = widgets.interactive( show_pdf, pdf=widgets.fixed(sps.uniform.pdf), grid_size=widgets.IntSlider(min=25, max=300, step=25, value=500), xmin=widgets.FloatSlider(min=-10, max=0, step=0.1, value=-5), xmax=widgets.FloatSlider(min=0, max=10, step=0.1, value=5), ymax=widgets.FloatSlider(min=0, max=2, step=0.1, value=1.4), loc=widgets.FloatSlider(min=-4, max=0, step=0.1, value=0), scale=widgets.FloatSlider(min=0.01, max=4, step=0.01, value=1), distr_name=r'$U$({loc}, {loc} + {scale})' ); # отображаем слайдеры группами display(widgets.HBox(ip.children[:2])) display(widgets.HBox(ip.children[2:4])) display(widgets.HBox(ip.children[5:7])) # отображаем вывод функции display(ip.children[-1]) ip.update() # чтобы функция запустилась до первого изменения слайдеров
In [43]:
grid = np.linspace(-3, 7, 1000) # сетка для построения графика loc_values = [0, 0, 4] # набор значений параметра a scale_values = [1, 2, 1] # набор значений параметра scale plt.figure(figsize=(12, 5)) for i, (loc, scale) in enumerate(zip(loc_values, scale_values)): plt.plot(grid, sps.uniform(loc, scale).pdf(grid), lw=5, alpha=0.7, label='$U' + '({}, {})$'.format(loc, scale)) plt.legend(fontsize=16) plt.title('Плотности равномерного распределения', fontsize=20) plt.xlabel('Значение', fontsize=18) plt.ylabel('Плотность', fontsize=18) plt.show()
Для равномерного распределения:
- Параметр ${loc = a}$ определяет начало отрезка, на котором случайная величина равномерно распределена.
- Параметр ${scale = b-a}$ определяет длину отрезка, на котором задана случайная величина. Значение плотности распределения на данном отрезке убывает с ростом данного параметра, то есть с ростом длины этого отрезка. Чем меньше длина отрезка, тем больше значение плотности вероятности на отрезке.
Время на прочтение
9 мин
Количество просмотров 15K
Пост №3 для начинающих посвящен генерированию распределений, их свойствам, а также графикам для их сопоставительного анализа. Предыдущий пост см. здесь.
Булочник и Пуанкаре
Существует легенда, почти наверняка апокрифическая, которая дает возможность детальнее рассмотреть вопрос о том, каким образом центральная предельная теорема позволяет рассуждать о принципе формирования статистических распределений. Она касается прославленного французского эрудита XIX-ого века Анри Пуанкаре, который, как гласит легенда, в течение одного года каждый день занимался тем, что взвешивал свежую буханку хлеба.
В те времена хлебопекарное ремесло регламентировалось государством, и Пуанкаре обнаружил, что, хотя результаты взвешивания буханок хлеба подчинялись нормальному распределению, пик находился не на публично афишируемом 1 кг, а на 950 г. Он сообщил властям о булочнике, у которого он регулярно покупал хлеб, и тот был оштрафован. Такова легенда ;-).
В следующем году Пуанкаре продолжил взвешивать буханки хлеба того же булочника. Он обнаружил, что среднее значение теперь было равно 1 кг, но это распределение больше не было симметричным вокруг среднего значения. Теперь оно было смещено вправо. А это соответствовало тому, что булочник теперь давал Пуанкаре только самые тяжелые из своих буханок хлеба. Пуанкаре снова сообщил о булочнике властям, и булочник был оштрафован во второй раз.
Было ли это на самом деле или нет здесь не суть важно; этот пример всего лишь служит для того, чтобы проиллюстрировать ключевой момент — статистическое распределение последовательности чисел может сообщить нам нечто важное о процессе, который ее создал.
Генерирование распределений
В целях развития нашего интуитивного понимания относительно нормального распределения и дисперсии, давайте смоделируем честного и нечестного булочников, и для этого воспользуемся функцией генерирования нормально распределенных случайных величин stats.norm.rvs. (rvs от англ. normal variates, т.е. нормально-распределенные случайные величины). Честного булочника можно смоделировать в виде нормального распределения со средним значением 1000, что соответствует справедливой буханке хлеба весом 1 кг. При этом мы допустим наличие дисперсии в процессе выпекания, которая приводит к стандартному отклонению в 30г.
def honest_baker(mu, sigma):
'''Модель честного булочника'''
return pd.Series( stats.norm.rvs(loc, scale, size=10000) )
def ex_1_18():
'''Смоделировать честного булочника на гистограмме'''
honest_baker(1000, 30).hist(bins=25)
plt.xlabel('Честный булочник')
plt.ylabel('Частота')
plt.show()Приведенный выше пример построит гистограмму, аналогичную следующей:
Теперь смоделируем булочника, который продает только самые тяжелые буханки хлеба. Мы разобьем последовательность на группы по тринадцать элементов (на «чертовы дюжины») и отберем максимальное значение в каждой:
def dishonest_baker(mu, sigma):
'''Модель нечестного булочника'''
xs = stats.norm.rvs(loc, scale, size=10000)
return pd.Series( map(max, bootstrap(xs, 13)) )
def ex_1_19():
'''Смоделировать нечестного булочника на гистограмме'''
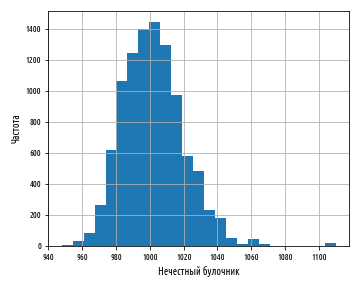
dishonest_baker(950, 30).hist(bins=25)
plt.xlabel('Нечестный булочник')
plt.ylabel('Частота')
plt.show()Приведенный выше пример создаст гистограмму, аналогичную следующей:
Совершенно очевидно, что эта гистограмма выглядит не совсем так, как другие, которые мы видели. Среднее значение по-прежнему равно 1 кг, но разброс значений вокруг среднего больше не является симметричным. Мы говорим, что эта гистограмма показывает смещенное нормальное распределение.
Асимметрия
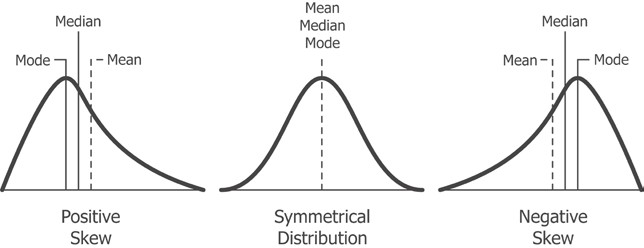
Асимметрией называется смещение распределения относительно ее моды. Отрицательная асимметрия, или левое смещение кривой, указывает на то, что площадь под графиком больше на левой стороне моды. Положительная асимметрия, или правое смещение кривой, указывает на то, что площадь под графиком больше на правой стороне моды.
Библиотека pandas располагает функцией skew для измерения асимметрии:
def ex_1_20():
'''Получить коэффициент асимметрии нормального распределения'''
s = dishonest_baker(950, 30)
return { 'среднее' : s.mean(),
'медиана' : s.median(),
'асимметрия': s.skew() }{'асимметрия': 0.4202176889083849,
'медиана': 998.7670301469957,
'среднее': 1000.059263920949}Приведенный выше пример показывает, что коэффициент асимметрии в выпечке от нечестного булочника составляет порядка 0.4. Этот коэффициент количественно определяет степень скошенности, которая видна на гистограмме.
Графики нормального распределения
Ранее в этой серии постов мы познакомились с квантилями как средством описания статистического распределения данных. Напомним, что функция quantile принимает число между 0 и 1 и возвращает значение последовательности в этой точке. 0.5-квантиль соответствует значению медианы.
Изображение квантилей данных относительно квантилей нормального распределения позволяет увидеть, каким образом наши измеренные данные соотносятся с теоретическим распределением. Подобные графики называются квантильными графиками, или диаграммами квантиль-квантиль, графиками Q-Q, от англ. Q-Q plot. Они предоставляют быстрый и интуитивно понятный способ определить степень нормальности статистического распределения. Для данных, которые близки к нормальному распределению, квантильный график покажет прямую линию. Отклонения от прямой линии показывают, каким образом данные отклоняются от идеализированного нормального распределения.
Теперь построим квантильные графики для честного и нечестного булочников. Функция qqplot принимает список точек данных и формирует график выборочных квантилей, отображаемых относительно квантилей из теоретического нормального распределения:
def qqplot( xs ):
'''Квантильный график (график квантиль-квантиль, Q-Q plot)'''
d = {0:sorted(stats.norm.rvs(loc=0, scale=1, size=len(xs))),
1:sorted(xs)}
pd.DataFrame(d).plot.scatter(0, 1, s=5, grid=True)
df.plot.scatter(0, 1, s=5, grid=True)
plt.xlabel('Квантили теоретического нормального распределения')
plt.ylabel('Квантили данных')
plt.title ('Квантильный график', fontweight='semibold')
def ex_1_21():
'''Показать квантильные графики
для честного и нечестного булочников'''
qqplot( honest_baker(1000, 30) )
plt.show()
qqplot( dishonest_baker(950, 30) )
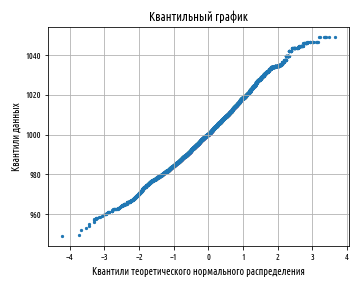
plt.show()Приведенный выше пример создаст следующие ниже графики:
Выше показан квантильный график для честного булочника. Далее идет квантильный график для нечестного булочника:
Тот факт, что линия имеет изогнутую форму, показывает, что данные положительно асимметричны; наклон в другую сторону будет означать отрицательную асимметрию. Квантильный график в сущности позволяет легко различить целый ряд отклонений от стандартного нормального распределения, как показано на следующем ниже рисунке:
Надписи: нормально распределенные, тяжелые хвосты, легкие хвосты, скошенность влево, скошенность вправо, раздельные кластеры
Квантильные графики сопоставляют статистическое распределение честного и нечестного булочника с теоретическим нормальным распределением. В следующем разделе мы сравним несколько альтернативных способов визуального сопоставления двух (или более) измеренных последовательностей значений.
Технические приемы сопоставительной визуализации
Квантильные графики дают замечательную возможность сопоставить измеренное эмпирическое (выборочное) распределение с теоретическим нормальным распределением. Однако если мы хотим сопоставить друг другу два или более эмпирических распределения, то графики нормального распределения для этого не подойдут. Впрочем, у нас есть несколько других вариантов, как показано в следующих двух разделах.
Коробчатые диаграммы
Коробчатые диаграммы, или диаграммы типа «ящик с усами», — это способ визуализации таких описательных статистик, как медиана и дисперсия. Мы можем сгенерировать их с помощью следующего исходного кода:
def ex_1_22():
'''Показать коробчатую диаграмму
с данными честного и нечестного булочников'''
d = {'Честный булочник' :honest_baker(1000, 30),
'Нечестный булочник':dishonest_baker(950, 30)}
pd.DataFrame(d).boxplot(sym='o', whis=1.95, showmeans=True)
plt.ylabel('Вес буханки (гр.)')
plt.show()Этот пример создаст следующую диаграмму:
Ящики в центре диаграммы представляют интерквартильный размах. Линия поперек ящика — это медиана. Большая точка — это среднее. Для честного булочника линия медианы проходит через центр окружности, показывая, что среднее и медиана примерно одинаковые. Для нечестного булочника среднее отодвинуто от медианы, что указывает на смещение.
Усы показывают на диапазон данных. Выбросы представлены полыми кругами. Всего одна диаграмма позволяет яснее увидеть расхождение между двумя статистическими распределениями, чем рассматривать их отдельно на гистограмме или квантильном графике.
Интегральные функции распределения
Интегральные функции распределения (ИФР), также именуемые кумулятивными функциями распределения, от англ. Cumulative Distribution Function (CDF), описывают вероятность, что значение, взятое из распределения, будет меньше x. Как и все распределения вероятностей, их значения лежат в диапазоне между 0 и 1, где 0 — это невозможность, а 1 — полная определенность. Например, представьте, что я собираюсь бросить шестигранный кубик. Какова вероятность, что выпадет значение меньше 6?
Для уравновешенного кубика вероятность выпадения пятерки или меньшего значения равна 5/6. И наоборот, вероятность, что выпадет единица, равна всего 1/6. Тройка или меньше соответствуют равным шансам — то есть вероятности 50%.
ИФР выпадения чисел на кубике следует той же схеме, что и все ИФР — для чисел на нижнем краю диапазона ИФР близка к нулю, что соответствует низкой вероятности выбора чисел в этом диапазоне или ниже. На верхнем краю диапазона ИФР близка к единице, поскольку большинство значений, взятых из последовательности, будет ниже.
ИФР и квантили тесно друг с другом связаны — ИФР является инверсией квантильной функции. Если 0.5-квантиль соответствует значению 1000, тогда ИФР для 1000 составляет 0.5.
Подобно тому, как функция pandas quantile позволяет нам отбирать значения из распределения в конкретных точках, эмпирическая ИФР empirical_cdf позволяет нам внести значение из последовательности и вернуть значение в диапазоне между 0 и 1. Это функция более высокого порядка, т.е. она принимает значение (в данном случае последовательность значений) и возвращает функцию, которую потом можно вызывать, сколько угодно, с различными значениями на входе, и возвращая ИФР для каждого из них.
Функции более высокого порядка — это функции, которые принимают или возвращают функции.
Построим график ИФР одновременно для честного и нечестного булочников. Для этих целей можно воспользоваться функцией библиотеки pandas построения двумерного графика plot для визуализации ИФР, изобразив на графике исходные данные — то есть выборки из распределений честного и нечестного булочников — в сопоставлении с вероятностями, вычисленными относительно эмпирической ИФР. Функция plot ожидает, что значения x и значения y будут переданы в виде двух раздельных последовательностей значений. Для этих целей мы воспользуемся конструктором кадра данных pandas DataFrame.
Чтобы изобразить оба распределения на одном графике, мы должны передать функции plot несколько серий. Для многих своих графиков pandas предоставляет функции, которые позволяют добавлять дополнительные серии. В случае с функцией plot мы можем присвоить указатель на создаваемый график, присвоив временной переменной (ax) результат первого вызова функции plot, и затем при повторных вызовах указывать эту переменную в именованном аргументе функции (ax=ax). Можно также передать необязательную метку серии. Мы выполним это в следующем ниже примере, чтобы на готовом графике отличить две серии друг от друга. Сначала определим универсальную функцию построения эмпирической ИФР против теоретической, которая получает на вход кортеж из двух серий (tp[1] и tp[3]) и их названий и метки осей, и затем вызовем ее:
def empirical_cdf(x):
'''Вернуть эмпирическую ИФР для x'''
sx = sorted(x)
return pd.DataFrame( {0: sx, 1:sp.arange(len(sx))/len(sx)} )
def ex_1_23():
'''Показать графики эмпирической ИФР
честного булочника в сопоставлении с нечестным'''
df = empirical_cdf(honest_baker(1000, 30))
df2 = empirical_cdf(dishonest_baker(950, 30))
ax = df.plot(0, 1, label='Честный булочник')
df2.plot(0, 1, label='Нечестный булочник', grid=True, ax=ax)
plt.xlabel('Вес буханки')
plt.ylabel('Вероятность')
plt.legend(loc='best')
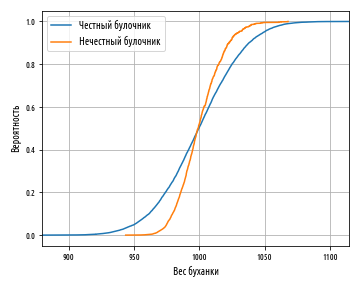
plt.show()Приведенный выше пример сгенерирует следующий график:
Несмотря на то, что этот график выглядит совсем по-другому, он в сущности показывает ту же самую информацию, что и коробчатая диаграмма. Мы видим, что две линии пересекаются примерно в медиане 0.5, соответствующей 1000 гр. Линия нечестного булочника обрезается в нижнем хвосте и удлиняется на верхнем хвосте, что соответствует асимметричному распределению.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
Следующая часть, часть 4, серии постов «Python, исследование данных и выборы» посвящена техническим приемам визуализации данных.
Все курсы > Программирование на Питоне > Занятие 10 (часть 3)
Рассмотрим равномерное и нормальное распределения непрерывной случайной величины.
Продолжим работать в том же ноутбуке⧉
Непрерывное вероятностное распределение
Как уже было сказано, в отличие от дискретной величины, непрерывная величина может принимать любое значение в заданном интервале.
Непрерывное равноемерное распределение
Непрерывное равномерное распределение (continuous uniform distribution) описывает случайную величину, вероятность значений которой одинакова на заданном интервале от a до b.
$$ X sim U(a, b) $$
Например, если мы знаем, что автобус приходит на остановку каждые 12 минут, то время ожидания автобуса на остановке равномерно распределено между 0 и 12 минутами.
$$ X sim U(0, 12) $$
Плотность вероятности
Непрерывное распределение (в отличие от дискретного) задается плотностью вероятности (probability density function, pdf). Для равномерного непрерывного распределения плотность вероятности задается вот такой несложной функцией.
$$ pdf(x) = begin{cases} frac{1}{b-a}, x in [a, b] 0, x notin [a, b] end{cases} $$
В примере с ожиданием автобуса вероятность его приезда в любой момент в пределах заданного интервала равна
$$ pdf(x) = begin{cases} frac{1}{12-0} = frac{1}{12}, x in [0, 12] 0, x notin [0, 12] end{cases} $$
На графике равномерное распределение представляет собой прямоугольник, площадь которого всегда равна единице.
Если мы хотим посчитать вероятность приезда автобуса в пределах заданного интервала ожидания, нам, по сути, нужно рассчитать отдельный участок площади прямоугольника.
Например, вероятность приезда автобуса при ожидании до 12 минут включительно составляет 1.00 или 100%, потому что такой промежуток включает всю площадь прямоугольника.
Теперь давайте рассчитаем вероятность ожидания автобуса до 7 минут включительно. Нас будет интересовать интервал от 0 до 7 минут и соответствующий участок площади прямоугольника.
Применив несложную формулу, мы без труда вычислим площадь этого участка.
$$ P(7) = frac{1}{12} times 7 approx 0,583 $$
Матожидание и дисперсия
Остается рассчитать матожидание (среднее время ожидания автобуса) и дисперсию.
$$ {mathbb E}[X] = frac{a + b}{2} = frac{0 + 12}{2} = 6 $$
$$ {mathbb D}[X] = frac{(b-a)^2}{12} = frac{(12-0)^2}{12} = 12 $$
Реализация на Питоне
Воспользуемся функцией np.random.uniform() для того, чтобы создать равномерное распределение с параметрами U(0, 12).
|
# создадим распределение с параметрами a = 0 и b = 12 # повторим экспермиент 1 000 000 раз res = np.random.uniform(0, 12, 1000000) # посмотрим на первые десять значений res[:10] |
|
array([ 7.14186749, 4.37660571, 0.06450744, 6.73305271, 10.75884493, 6.38060282, 9.36585218, 1.94345171, 1.64757201, 10.72732251]) |
Посмотрим на результат с помощью гистограммы.
Посмотрим на среднее значение и дисперсию.
Теперь экспериметнальным путем найдем вероятность ожидания автобуса до семи минут включительно.
|
# разделим количество значений <= 7 на общее количество значений len(res[res <= 7])/len(res) |
Разница между np.random.random(), np.random.rand() и np.random.uniform()
Как вы заметили, мы использовали три функции для генерирования равномерного распределения.
Функция np.random.random(size = None) создает равномерное распределение в полуоткрытом интервале [0, 1). Параметр size задает размер этого распределения (количество экспериментов).
|
# создадим массив 2 x 3 в интервале от [0, 1) np.random.seed(42) # для этого передадим параметры в виде кортежа np.random.random((2, 3)) |
|
array([[0.37454012, 0.95071431, 0.73199394], [0.59865848, 0.15601864, 0.15599452]]) |
Функция np.random.rand() практически идентична.
|
# единственное отличие — размеры массива передаются отдельными параметрами, а не кортежем np.random.seed(42) np.random.rand(2, 3) |
|
array([[0.37454012, 0.95071431, 0.73199394], [0.59865848, 0.15601864, 0.15599452]]) |
Для функции np.random.uniform(low = 0.0, high = 1.0, size = None) интервал [0, 1) является интервалом по умолчанию, при этом можно задать любой другой промежуток (как мы и сделали выше).
Приведем несколько примеров.
|
# сгенерируем одно значение из равномерного распределения в интервале [0, 9) np.random.uniform(9) |
|
# создадим двумерный массив 2 х 5 со значениями в промежутке [0, 1) np.random.seed(42) np.random.uniform(size = (2, 5)) |
|
array([[0.37454012, 0.95071431, 0.73199394, 0.59865848, 0.15601864], [0.15599452, 0.05808361, 0.86617615, 0.60111501, 0.70807258]]) |
Напоследок замечу, что равномерное непрерывное распределение является частным случаем бета-распределения с параметрами Beta(1, 1). О том что это такое мы поговорим с вами на курсе статистики вывода.
Нормальное распределение
На занятии по описательной статистике мы начали изучать количественные данные с примера роста мужчин в России. При этом интересно, что рост людей, как и многие другие величины (например, вес человека, артериальное давление, некоторые природные явления и многое другое) имеют так называемое нормальное распределение (normal distribution).
Функция плотности нормального распределения
Функция плотности (pdf) нормального распределения случайной величины X определяется функцией Гаусса и поэтому нормальное распределение также называется распределением Гаусса (Gauss distribution).
$$ pdf(x, mu, sigma) = frac{1}{sigma sqrt{2pi}} e^{-frac{1}{2} (frac{x-mu}{sigma})^2} $$
Как видно из формулы, единственными неизвестными параметрами являются μ («мю», матожидание) и σ («сигма», среднее квадратическое отклонение, СКО). Именно они и определяют нормальное распределение.
$$ X sim {mathcal N}(mu, sigma) $$
Здесь важно напомнить, что среднее квадратическое отклонение (standard deviation) равно квадратному корню из дисперсии (variance).
$$ sigma = sqrt{sigma^2} $$
Функция np.random.normal()
На Питоне нормальное распределение создается с помощью функции np.random.normal(). Мы уже использовали ее, в частности, для создания данных о росте мужчин и женщин в ноутбуке⧉ к десятому занятию вводного курса. Повторим этот код, увеличив размер массива до 100 000.
|
# зададим точку отсчета np.random.seed(42) # создадим 100 000 значений нормально распределенной величины с матожиданием 180 см и СКО 10 см height_men = np.round(np.random.normal(180, 10, 100000)) # создадим еще одно распределение, но матожидание будет равно 160 см height_women = np.round(np.random.normal(160, 10, 100000)) |
Посмотрим на результат.
|
print(height_men[:10]) print(height_women[:10]) |
|
[185. 179. 186. 195. 178. 178. 196. 188. 175. 185.] [153. 157. 154. 161. 172. 152. 170. 152. 152. 168.] |
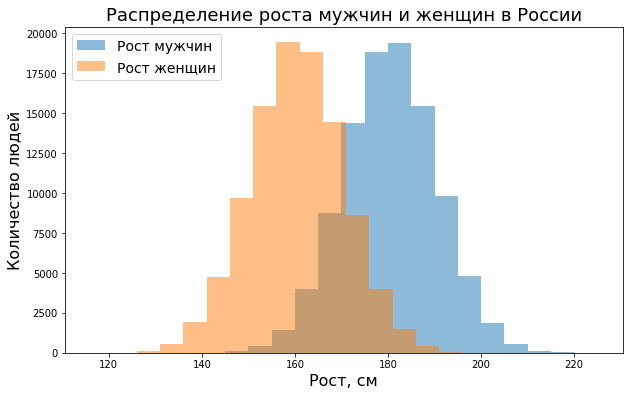
Для визуализации нормального распределения можно использовать несколько типов графиков. Например, можно использовать уже знакомую нам гистограмму.
|
# выведем результат с помощью гистограммы plt.figure(figsize = (10,6)) # зададим 18 интервалов (bin) и уровень прозрачности графиков plt.hist(height_men, 18, alpha = 0.5, label = ‘Рост мужчин’) plt.hist(height_women, 18, alpha = 0.5, label = ‘Рост женщин’) # пропишем расположение и размер шрифта легенды plt.legend(loc = ‘upper left’, prop = {‘size’: 14}) # добавим подписи plt.xlabel(‘Рост, см’, fontsize = 16) plt.ylabel(‘Количество людей’, fontsize = 16) plt.title(‘Распределение роста мужчин и женщин в России’, fontsize = 18) plt.show() |
Также можно использовать график плотности (density plot) распределения случайной величины.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# импортируем библиотеку seaborn import seaborn as sns # зададим размер графиков plt.figure(figsize = (10,6)) # и построим график функции плотности sns.kdeplot(height_men, fill = True, label = ‘Рост мужчин’) sns.kdeplot(height_women, fill = True, label = ‘Рост женщин’) # пропишем расположение и размер шрифта легенды plt.legend(loc = ‘upper left’, prop = {‘size’: 14}) # добавим подписи plt.xlabel(‘Рост, см’, fontsize = 16) plt.ylabel(‘Количество людей’, fontsize = 16) plt.title(‘Распределение роста мужчин и женщин в России’, fontsize = 18) plt.show() |
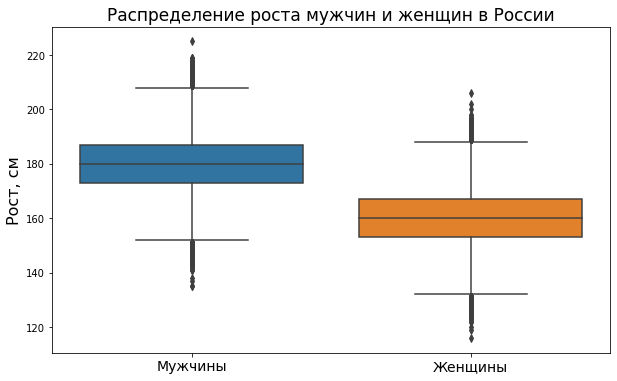
Еще одной полезной визуализацией является так называемый boxplot (ящик с усами или диаграмма размаха).
|
# boxplot, как и многие другие графики, удобно строить из библиотеки Pandas import pandas as pd # создадим датафрейм из словаря, включающего два массива с данными о росте data = pd.DataFrame({‘Мужчины’ : height_men, ‘Женщины’ : height_women}) data.head() |
|
# зададим размер графика plt.figure(figsize = (10,6)) # и построим два вертикальных boxplots, передав датафрейм с данными в параметр data sns.boxplot(data = data) # дополнительно укажем размер подписей каждого из графиков по оси x plt.xticks(fontsize = 14) # подпись к оси y plt.ylabel(‘Рост, см’, fontsize = 16) # и заголовок графика plt.title(‘Распределение роста мужчин и женщин в России’, fontsize = 17) plt.show() |
Boxplot позволяет увидеть медиану (median), первый и третий квартили (Quartile 1, Q1 и Quartile 3, Q3), межквартильный размах (Interquartile Range, IQR), а также, что очень важно, так называемые выбросы (outliers), то есть значения, сильно отличающиеся от среднего (на графике выше они обозначены точками). Ни гистограмма, ни график плотности вероятности этой информации не выводят.
На рисунке ниже можно увидеть связь между boxplot и графиком плотности вероятности.
С σ («сигма»), обозначающей среднее квадратическое отклонение мы уже знакомы, а вот что такое квартиль, межквартильный размах и о том, что измеряют Q1 − 1.5 x IQR и Q3 + 1.5 x IQR мы поговорим на следующем курсе по анализу и обработке данных.
Дополнительно приведу пример того, как можно совместить boxplot с гистограммой на Питоне.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# создадим два подграфика f, (ax_box, ax_hist) = plt.subplots(nrows = 2, # из двух строк ncols = 1, # и одного столбца sharex = True, # оставим только нижние подписи к оси Х gridspec_kw = {‘height_ratios’: (.15, .85)}, # зададим разную высоту строк figsize = (12,8)) # зададим размер графика # в первом подграфике построим boxplot sns.boxplot(x = height_men, ax = ax_box) # во втором гистограмму sns.histplot(data = height_men, bins = 15, ax = ax_hist) # зададим заголовок и подписи к осям ax_box.set_title(‘Распределение роста мужчин в России’, fontsize = 17) ax_hist.set_xlabel(‘Рост, см’, fontsize = 15) ax_hist.set_ylabel(‘Количество людей’, fontsize = 15) plt.show() |
Расчет вероятности
Теперь давайте рассчитаем вероятность того, что рост случайно встретившегося нам человека на улице составляет менее 190 см.
Разумеется, для того, чтобы это утверждать мы должны допустить, что наши данные действительно отражают генеральную совокупность, то есть рост всех людей.
Вначале рассчитаем теоретическую вероятность. Для создания «идеального» теоретического распределения воспользуемся библиотекой scipy.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# импортируем объект norm из модуля stats библиотеки scipy from scipy.stats import norm # зададим размер графика plt.figure(figsize = (10,6)) # пропишем среднее значение и СКО mean, std = 180, 10 # создадим пространство из 1000 точек в диапазоне +/- трех СКО от среднего значения x = np.linspace(mean — 3 * std, mean + 3 * std, 1000) # рассчитаем значения по оси y с помощью метода .pdf() # т.е. функции плотности вероятности f = norm.pdf(x, mean, std) # и построим график plt.plot(x, f) plt.show() |
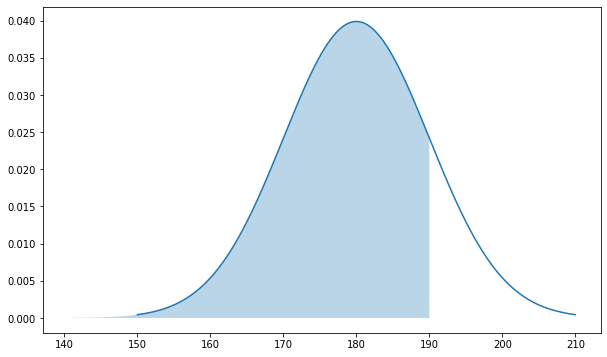
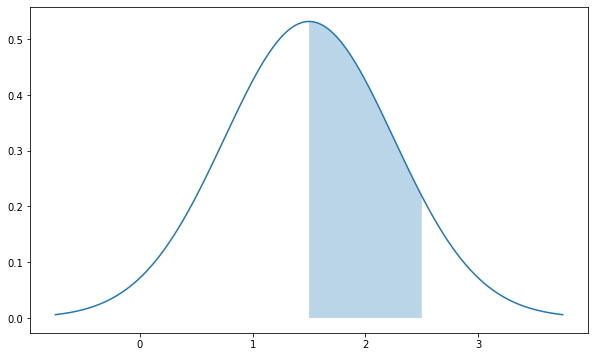
Как и в случае с равномерным распределением задача сводится к нахождению площади под кривой от минус бесконечности до 190 включительно.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# зададим размер графика plt.figure(figsize = (10,6)) # пропишем среднее значение и СКО mean, std = 180, 10 # создадим пространство из 1000 точек в диапазоне +/- трех СКО от среднего значения x = np.linspace(mean — 3 * std, mean + 3 * std, 1000) # рассчитаем значения по оси y с помощью метода .pdf() # т.е. функции плотности вероятности f = norm.pdf(x, mean, std) # и построим график plt.plot(x, f) # дополнительно создадим точки на оси х для закрашенной области px = np.linspace(mean — 3 * std, 190, 1000) # и заполним в пределах этих точек по оси x пространство # от кривой нормального распределения до оси y = 0 plt.fill_between(px, norm.pdf(px, mean, std), alpha = 0.3) # выведем оба графика на экран plt.show() |
Для нахождения площади можно воспользоваться одним из многочисленных онлайн-калькуляторов⧉.
На Питоне это вычисление можно выполнить с помощью функции распределения (cumulative density function, cdf).
|
# передадим методу .cdf() границу (рост), среднее значение (loc) и СКО (scale) area = norm.cdf(190, loc = 180, scale = 10) # на выходе мы получим площадь под кривой area |
Обратное вычисление, то есть нахождение значения (роста) по площади выполняется с помощью квантиль-функции (percent point function, ppf).
|
# с помощью метода .ppf() можно узнать значение (рост) по площади height = norm.ppf(area, loc = 180, scale = 10) height |
Рассчитать вероятность того, что нам встретится человек выше 190 см очень просто. Так как мы знаем, что площадь под кривой нормального распределения равна единице, нам достаточно вычесть найденную площадь слева от 190 см из одного.
|
# рассчитаем вероятность встретить человека выше 190 см 1 — norm.cdf(190, loc = 180, scale = 10) |
Так мы получим площадь справа от заданной границы. Посмотрим, как это выглядит на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# зададим размер графика plt.figure(figsize = (10,6)) # пропишем среднее значение и СКО mean, std = 180, 10 # создадим пространство из 1000 точек в диапазоне +/- трех СКО от среднего значения x = np.linspace(mean — 3 * std, mean + 3 * std, 1000) # рассчитаем значения по оси y с помощью метода .pdf() # т.е. функции плотности вероятности f = norm.pdf(x, mean, std) # и построим график plt.plot(x, f) # дополнительно создадим точки на оси х для закрашенной области px = np.linspace(190, mean + 3 * std, 1000) # и заполним в пределах этих точек по оси x пространство # от кривой нормального распределения до оси y = 0 plt.fill_between(px, norm.pdf(px, mean, std), alpha = 0.3) # выведем оба графика на экран plt.show() |
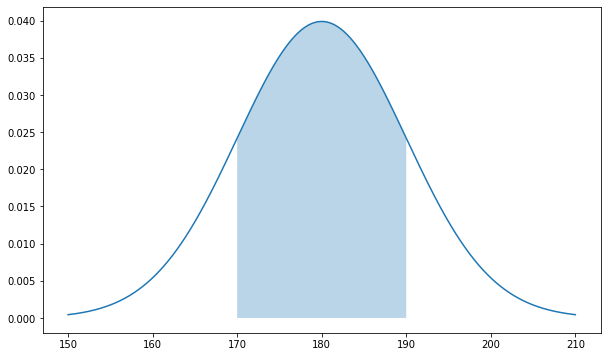
Если нужно вычислить площадь между двумя значениями a и b, например, между 170 и 190 см, из большего, находящегося правее значения функции распределения, можно вычесть меньшее, находящееся левее.
|
# рассчитаем меньшую площадь до нижней границы lowerbound = norm.cdf(170, loc = 180, scale = 10) # рассчитаем большую площадь до верхней границы upperbound = norm.cdf(190, loc = 180, scale = 10) # вычтем меньшую площадь из большей upperbound — lowerbound |
Посмотрим на этот участок на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# зададим размер графика plt.figure(figsize = (10,6)) # пропишем среднее значение и СКО mean, std = 180, 10 # создадим пространство из 1000 точек в диапазоне +/- трех СКО от среднего значения x = np.linspace(mean — 3 * std, mean + 3 * std, 1000) # рассчитаем значения по оси y с помощью метода .pdf() # т.е. функции плотности вероятности f = norm.pdf(x, mean, std) # и построим график plt.plot(x, f) # дополнительно создадим точки на оси х для закрашенной области px = np.linspace(170, 190, 1000) # и заполним в пределах этих точек по оси x пространство # от кривой нормального распределения до оси y = 0 plt.fill_between(px, norm.pdf(px, mean, std), alpha = 0.3) # выведем оба графика на экран plt.show() |
Теперь вернемся к нашим данным и рассчитаем эмпирическую вероятность встретить человека с ростом не более 190 см.
|
# разделим количество людей с ростом <= 190 на общее количество наблюдений len(height_men[height_men <= 190])/len(height_men) |
В целом результат близок к найденному аналитическому решению.
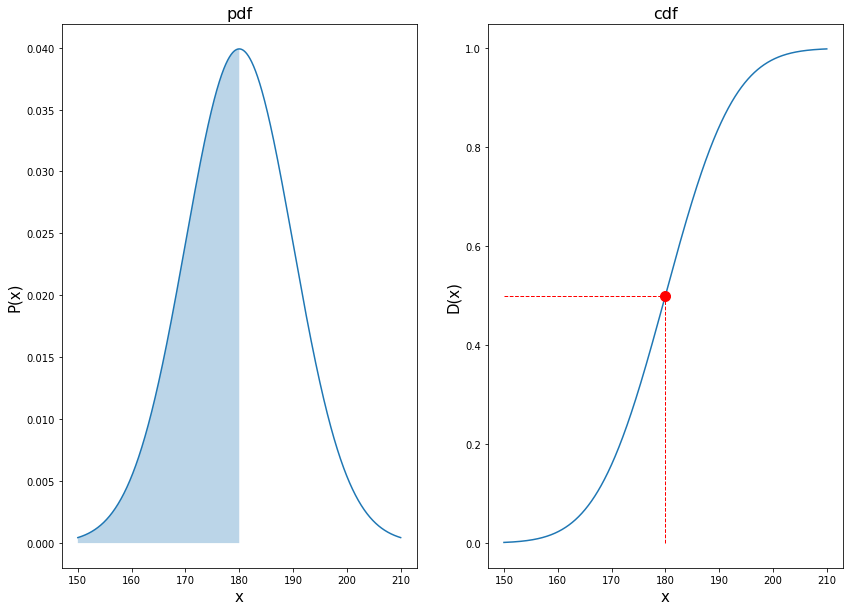
Функция плотности и функция распределения
Рассмотрим связь функции плотности (pdf) и функции распределения (cdf). Напомню, что функция плотности нормального распределения определяется по формуле
$$ P(x) = frac{1}{sigma sqrt{2pi}} e^{-frac{1}{2} (frac{x-mu}{sigma})^2} $$
При этом вот что мы успели про нее узнать:
- Вероятность того, что случайная величина примет значение не более заданного в интервале (−∞; x] равна площади под кривой функции плотности на этом промежутке
- Эта площадь вычисляется с помощью функции распределения
Одновременно, известно, что площадь под кривой определяется как интеграл функции этой кривой на заданном промежутке.
Значит функция распределения (cdf) есть интеграл функции плотности (pdf).
Математически это выражается так.
$$ D(x) = int_{-infty}^{x} P(x) dx $$
Тема интегрирования выходит за рамки сегодняшнего занятия, однако давайте попробуем на уровне интуиции понять, как связаны функция плотности и функция распределения через нахождение интеграла.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
# зададим размер графика plt.figure(figsize = (14,10)) # определим среднее значение и СКО mean, std = 180, 10 # зададим последовательность точек на оси x x = np.linspace(mean — 3 * std, mean + 3 * std, 1000) # найдем значения функции плотности y1 = norm.pdf(x, mean, std) # и функции распределения y2 = norm.cdf(x, mean, std) # на левом графике (row 1, col 2, index 1) plt.subplot(1, 2, 1) # построим функцию плотности plt.plot(x, y1) # и заполним пространство под кривой вплоть до точки x = 180 px = np.linspace(mean — 3 * std, 180, 1000) plt.fill_between(px, norm.pdf(px, mean, std), alpha = 0.3) # добавим заголовок и подписи к осям plt.title(‘pdf’, fontsize = 16) plt.xlabel(‘x’, fontsize = 15) plt.ylabel(‘P(x)’, fontsize = 15) # на правом графике (row 1, col 2, index 2) plt.subplot(1, 2, 2) # построим функцию распределения plt.plot(x, y2) # а также горизонтальную и вертикальную пунктирные линии, plt.hlines(y = 0.5, xmin = 150, xmax = 180, linewidth = 1, color = ‘r’, linestyles = ‘—‘) plt.vlines(x = 180, ymin = 0, ymax = 0.5, linewidth = 1, color = ‘r’, linestyles = ‘—‘) # которые сойдутся в точке (180, 0.5) plt.plot(180, 0.5, marker = ‘o’, markersize = 10, markeredgecolor = ‘r’, markerfacecolor = ‘r’) # добавим заголовок и подписи к осям plt.title(‘cdf’, fontsize = 16) plt.xlabel(‘x’, fontsize = 15) plt.ylabel(‘D(x)’, fontsize = 15) plt.show() |
Вначале обратимся к графику слева. Как мы видим, вероятность встретить человека не более 180 см составляет 0,5 (закрашенный синим участок). Одновременно, проинтегрировав функцию плотности на интервале (−∞; 180], на графике справа мы видим, что «накопленная» вероятность составляет 0,5, и именно эту вероятность нам показывает график функции распределения на отметке x = 180.
Продолжим исследовать связь функции плотности и функции распределения.
Если функция распределения есть интеграл функции плотности, то плотность вероятности (pdf) является производной функции распределения (cdf).
Приведем формулу.
$$ P(x) = D'(x) $$
Хотя опять же тему дифференцирования (то есть нахождения производной) мы будем разбирать на курсе по оптимизации, ничто не мешает нам начать знакомиться с ней прямо сейчас.
Совместим обе функции на одном графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# зададим функции pdf и cdf на оси x x = np.linspace(mean — 3 * std, mean + 3 * std, 1000) # при этом возникает проблема: по оси y них разный масштаб y1 = norm.pdf(x, mean, std) y2 = norm.cdf(x, mean, std) # эту проблему можно решить через функции subplots() и twinx() # создадим сетку из одной ячейки fig, ax_left = plt.subplots(nrows = 1, ncols = 1, figsize = (12,8)) # создадим новую ось с правой стороны ax_right = ax_left.twinx() # на оси x и левой оси y построим график функции плотности (pdf) ax_left.plot(x, y1, label = ‘pdf’) # на оси x и правой оси y построим график функции распределения (cdf) ax_right.plot(x, y2, color = ‘orange’, label = ‘cdf’) # также построим вертикальную прямую и точку ax_left.vlines(x = 180, ymin = 0, ymax = 0.040, linewidth = 1, color = ‘r’, linestyles = ‘—‘) ax_left.plot(180, 0.020, marker = ‘o’, markersize = 5, markeredgecolor = ‘r’, markerfacecolor = ‘r’) # из-за двух осей с легендой придется повозиться fig.legend(loc = ‘upper right’, bbox_to_anchor = (1,1), bbox_transform = ax_right.transAxes, prop = {‘size’: 15}) plt.show() |
Здесь вначале посмотрим на функцию распределения (cdf, оранжевый график). В промежутке от 150 до 210 см эта функция непрерывно возрастает, при этом она возрастает с разной скоростью. До точки x = 180 (она называется точкой перегиба, inflection point) скорость возрастания функции увеличивается, после нее убывает.
Именно это изменение описывает производная от нее функция плотности (pdf, синий график). На участке от 150 до 180 она возрастает, а потом в интервале от 180 до 210 постоянно убывает.
Таким образом, плотность вероятности описывает скорость изменения функции распределения.
Дополнительно продемонстрирую взаимосвязь двух рассматриваемых функций с помощью Питона.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# воспользуемся модулем integrate библиотеки scipy import scipy.integrate as integrate # зададим среднее значение и СКО mu, sigma = 180, 10 # и границы интервала от 190 до + бесконечности lowerbound = 190 upperbound = np.inf # функция quad() в качестве первого аргумента ожидает функцию для интегрирования # напишем функцию gauss() с одним параметром def gauss(x): return norm.pdf(x, mu, sigma) # передадим в функцию quad() функцию Гаусса, а также нижний и верхний пределы # поместим первое выводимое значение в переменную integral integral = integrate.quad(gauss, lowerbound, upperbound)[0] # так как мы получили вероятность от 190 см и выше (то есть площадь справа) # для нахождения вероятности не более 190 см результат нужно вычесть из единицы 1 — integral |
Как вы видите, результат, найденный через интегрирование, ничем не отличается от результата, полученного через функцию распределения.
Вероятность конкретного значения
Важный и немного контринтуитивный момент. Вероятность того, что случайная величина непрерывного распределения примет конкретное значение (то есть нам встретится человек определенного роста) равна нулю. Это легко продемонстрировать. Ранее мы находили вероятность встретить человека ростом от 170 до 190 сантиметров, вычитая меньшую площадь под кривой из большей.
$$ P(170 leq x leq 190) = P(x leq 190)-P(x leq 170) approx 0,68 $$
При этом если мы таким же способом постараемся найти вероятность встретить человека ростом ровно 190 сантиметров, то она очевидно будет равна нулю.
$$ P(x = 190) = P(x leq 190)-P(x leq 190) = 0 $$
Формирование выборки
Сделаем небольшое отступление и рассмотрим процесс формирования выборки (sampling). Все очень несложно, мы берем некоторый набор элементов и из него случайным образом достаем какое-то их количество.
Пусть таким набором элементов будет мешок с разноцветными шарами.
|
# возьмем вот такой мешок с разноцветными шарами bag = [‘red’, ‘yellow’, ‘green’, ‘gray’, ‘black’, ‘orange’, ‘white’, ‘blue’, ‘brown’, ‘pink’] |
При этом формировать выборку можно двумя способами. В первом случае мы случайным образом достаем элемент, но, прежде чем взять следующий, кладем этот элемент обратно. Такой процесс называют выборкой с возвращением (sampling with replacement), и имитировать его можно с помощью функции np.random.choice().
|
np.random.seed(42) # выберем с возвращением восемь шаров np.random.choice(bag, 8) |
|
array([‘white’, ‘gray’, ‘blue’, ‘black’, ‘white’, ‘pink’, ‘green’, ‘white’], dtype='<U6′) |
Обратите внимание, белый шар повторяется дважды.
Кроме того, можно сформировать выборку без возвращения (sampling without replacement). В этом случае мы не кладем элемент обратно, а откладываем в сторону и только потом достаем следующий элемент. Для этого функции np.random.choice() нужно задать параметр replace = False.
|
np.random.seed(42) # сделаем то же самое, только возвращать шары не будем np.random.choice(bag, 8, replace = False) |
|
array([‘brown’, ‘yellow’, ‘orange’, ‘red’, ‘blue’, ‘green’, ‘pink’, ‘black’], dtype='<U6′) |
Теперь при том же seed ни один элемент не повторяется. Дополнительно замечу, что эта функция работает также и с числами.
|
np.random.seed(42) # выберем 5 чисел из массива от 0 до 9 # «под капотом» массив из 10 чисел формируется с помощью np.arange(10) np.random.choice(10, 5) |
Центральная предельная теорема
Помимо процессов в организме и природных явлений, нормальное распределение имеет большое значение для Центральной предельной теоремы (Central Limit Theorem).
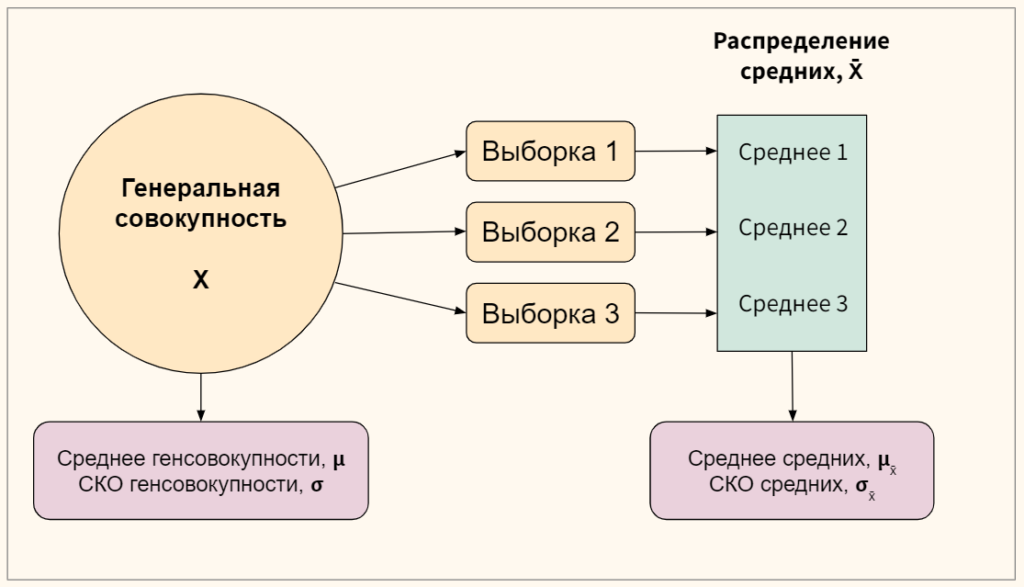
Определения и нотация
Вначале вспомним несколько терминов и введем полезные обозначения.
Во-первых, напомню, что данные могут представлять собой генеральную совокупность (population) или выборку из нее (sample). Если мы берем несколько выборок из одной генеральной совокупности и измеряем для каждой из них определенный параметр (например, среднее арифметическое, sample mean), то совокупность этих средних формирует выборочное распределение (sampling distribution).
При изучении Центральной предельной теоремы нас будет интересовать поведение именно этого распределения, его среднее арифметическое и среднее квадратическое отклонение.
Теперь перейдем к сути.
ЦПТ и нормальное распределение
Мы уже знаем, что среднее средних нескольких выборок (mean of sampling distribution of sample means) из одной генеральной совокупности будет стремиться к истинному среднему этой генеральной совокупности.
$$ mu_bar{x} = mu $$
Однако это не все. При соблюдении двух условий, а именно, (1) выборки сформированы случайным образом, (2) размер каждой выборки составляет не менее 30 элементов, выборочные средние будут следовать нормальному распределению.
Более того, распределение самой генеральной совокупности при этом не обязательно должно быть нормальным.
Одновременно, среднее квадратическое отклонение распределения средних будет стремиться к СКО генсовокупности, разделенному на корень размера одной выборки.
$$ sigma_bar{x} = frac{sigma}{sqrt{n}} $$
Математически эти выводы можно записать так
$$ X sim dist(mu, sigma) rightarrow bar{X} sim {mathcal N}(mu, frac{sigma}{sqrt{n}}) $$
Проверим на Питоне
А теперь давайте проверим истинность ЦПТ с помощью Питона. Для начала создадим скошенное вправо распределение (right skewed distribution). Такое распределение может характеризовать, например, зарплаты людей.
|
# скошенное распределение мы будем строить # с помощью объекта skewnorm модуля stats библиотеки scipy from scipy.stats import skewnorm # сгенерируем массив с данными о зарплате, задав искуссвенные параметры salaries = skewnorm.rvs(a = 20, # скошенность (skewness) loc = 20, # среднее значение без учета скошенности scale = 80, # отклонение от среднего size = 100000, # размер генерируемого массива random_state = 42) # воспроизводимость результата |
Посмотрим на график этого распределения.
|
# зададим размер графика plt.figure(figsize = (10,6)) # и построим график функции плотности sns.kdeplot(salaries, fill = True) # добавим подписи plt.xlabel(‘Зарплата, тыс. рублей’, fontsize = 15) plt.ylabel(‘Плотность распределения’, fontsize = 15) plt.title(‘Распределение заработной платы’, fontsize = 17) plt.show() |
Большая часть зарплат находится в нижней границе диапазона, при этом справа есть большой хвост тех немногих, чья заработная плата существенно выше среднего. Рассчитаем среднее значение и медиану.
Как и должно быть, медианное значение меньше среднего арифметического, на которое влияют небольшое количество очень высоких зарплат. По этой причине, как мы уже говорили, для измерения средней зарплаты предпочтительнее использовать медиану.
Рассчитаем СКО.
Выборки с возвращением. Теперь давайте брать выборки из нашей скошенной генеральной совокупности salaries и смотреть, что произойдет с распределением выборочных средних. Вначале создадим необходимое количество выборок.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# зададим точку отсчета np.random.seed(42) # создадим список, в который будем записывать выборочные средние sample_means = [] # зададим количество и размер выборок n_samples = 1000 sample_size = 30 # в цикле будем формировать выборки for i in range(n_samples): # путем отбора нужного количества элементов из генеральной совокупности sample = np.random.choice(salaries, sample_size, replace = False) # для каждой выборки рассчитаем среднее значение и поместим в список выборочных средних sample_means.append(np.mean(sample)) # убедимся, что сформировали нужно количество выборок len(sample_means) |
Посмотрим на результат.
|
# зададим размер графика plt.figure(figsize = (10,6)) # и построим график функции плотности sns.kdeplot(sample_means, fill = True) # добавим подписи plt.xlabel(‘Средние значения выборок’, fontsize = 15) plt.ylabel(‘Плотность распределения’, fontsize = 15) plt.title(‘Распределение выборочных средних’, fontsize = 17) plt.show() |
Обратите внимание, распределение выборочных средних гораздо ближе к нормальному распределению, нежели исходное распределение salaries. Остается рассчитать значения, к которым, согласно ЦПТ, должны стремиться среднее значение и СКО выборочных средних.
|
np.mean(salaries), np.std(salaries)/np.sqrt(sample_size) |
|
(83.84511076271755, 8.830476539330403) |
Посмотрим так ли это.
|
np.mean(sample_means), np.std(sample_means) |
|
(83.93586714203595, 8.94762726282006) |
Как мы видим, ЦПТ выполняется.
Выборки без возвращения. Теперь в качестве упражнения, давайте понаблюдаем, как будет меняться распределение выборочных средних при различных значениях количества выборок и их размера.
Кроме того, на этот раз будем делать выборку без возвращения, потому что если вы обратите внимание, несмотря на указанный параметр replace = False, на каждой итерации приведенного выше алгоритма мы формировали выборку из одной и той же генеральной совокупности, а значит элементы могли повторяться.
Важно, что при формировании выборки без возвращения ЦПТ будет выполняться, если размер одной выборки состаляет не более 5% от размера генеральной совокупности.
Для формирования распределения выборок без возвращения напишем собственную функцию sample_means(). На входе она будет принимать следующие параметры:
- data — набор данных (генеральную совокупность)
- n_samples — количество выборок
- sample_size — размер одной выборки
- replace = True — с возвращением делать выборки или без
- random_state = None — воспроизводимость результата
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# объявим собственную функцию для формирования распределения выборочных средних def sample_means(data, n_samples, sample_size, replace = True, random_state = None): # создадим список, в который будем записывать выборочные средние sample_means = [] # пропишем воспроизводимость np.random.seed(random_state) # в цикле будем формировать выборки for i in range(n_samples): # путем отбора нужного количества элементов из генеральной совокупности sample = np.random.choice(data, sample_size, replace = False) # для каждой выборки рассчитаем среднее значение и поместим в список выборочных средних sample_means.append(np.mean(sample)) # если указано, что выборки делаются без возвращения if replace == False: # удалим эту выборку из данных о зарплате data = np.array(list(set(data) — set(sample))) # вернем список с выборочными средними return sample_means |
Протестируем эту функцию.
|
# сформируем 100 выборок без возвращения по 30 элементов в каждой res = sample_means(salaries, 100, 30, replace = False, random_state = 42) |
|
# зададим размер графика plt.figure(figsize = (10,6)) # и построим график функции плотности sns.kdeplot(res, fill = True) # добавим подписи plt.xlabel(‘Средние значения выборок’, fontsize = 15) plt.ylabel(‘Плотность распределения’, fontsize = 15) plt.title(‘Распределение выборочных средних’, fontsize = 17) plt.show() |
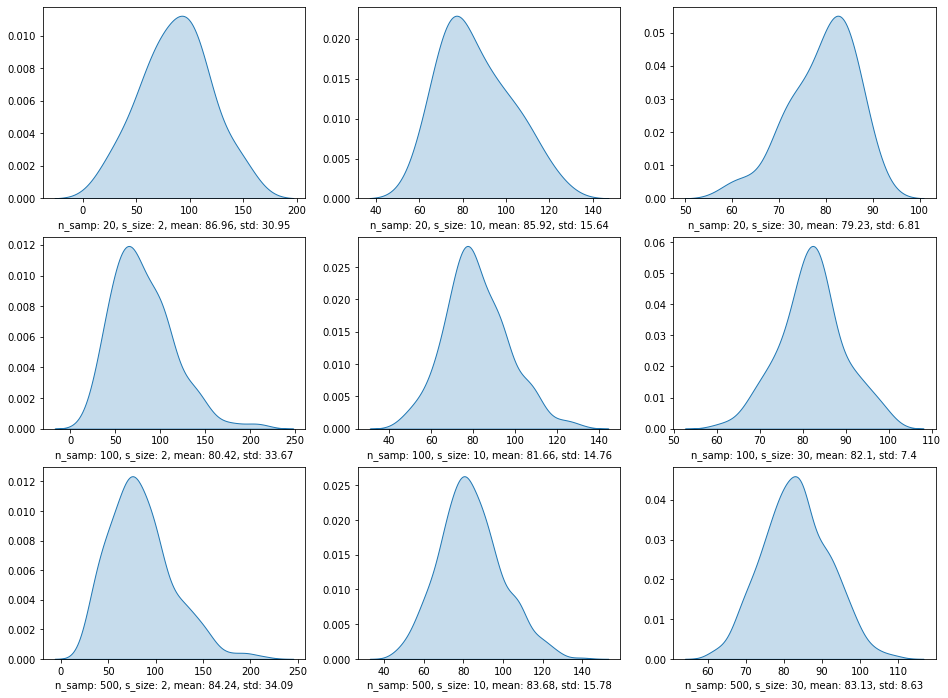
Теперь сгенерируем несколько распределений выборочных средних с 20, 100 и 500 выборками в распределении и размером выборки в 2, 10 и 30 значений.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
# создадим сетку подграфиков 3 x 3 fig, ax = plt.subplots(nrows = 3, ncols = 3, figsize = (16,12)) # списки с разным количеством number_of_samples_list = [20, 100, 500] # и размером выборок sample_size_list = [2, 10, 30] # кроме этого, создадим списки для учета получившихся # средних значений mean_list = [] # и СКО std_list = [] # по строкам сетки 3 x 3 разместим разное количество выборок for i, n_samples in enumerate(number_of_samples_list): # по столбцам разный размер выборки for j, sample_size in enumerate(sample_size_list): # на каждой итерации будем генерировать «свежую» генеральную совокупность salaries = skewnorm.rvs(a = 20, loc = 20, scale = 80, size = 100000, random_state = 42) # и создавать распределение с заданными параметрами res = sample_means(salaries, n_samples, sample_size, replace = False, random_state = 42) # кроме того, мы вычисляем среднее значение и СКО mean = np.mean(res).round(2) std = np.std(res).round(2) # и записываем их в соответствующие списки mean_list.append(mean) std_list.append(std) # помещаем график плотности распределения в «ячейку» с координатами [i, j] sns.kdeplot(res, fill = True, ax = ax[i, j]) # а под графиком выводим количество выборок, размер выборки, среднее значение и СКО ax[i, j].set_xlabel(‘n_samp: {}, s_size: {}, mean: {}, std: {}’.format(n_samples, sample_size, mean, std)) # подпись к оси y оставляем пустой ax[i, j].set_ylabel(») # выведем результат plt.show() |
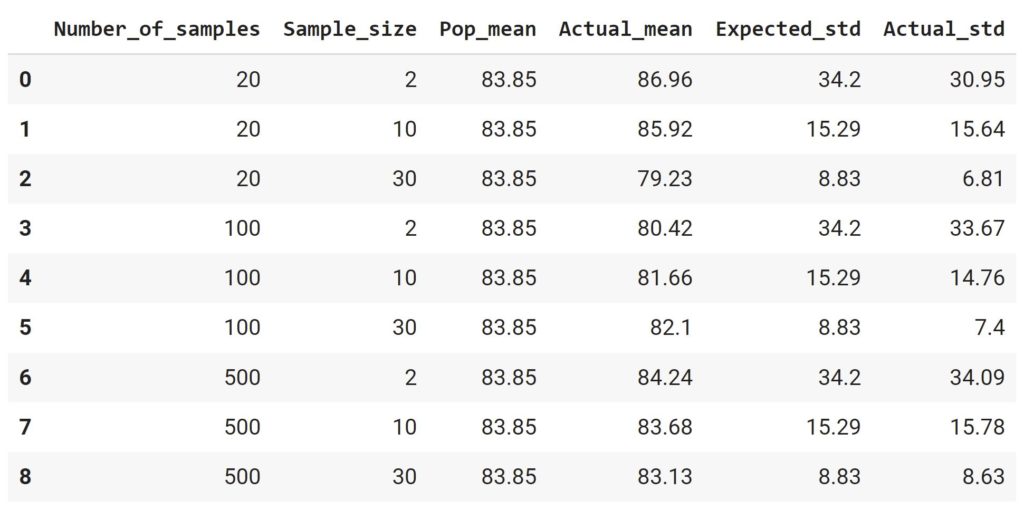
Кроме того, давайте посмотрим на параметры этих распределений в табличной форме и сравним с «целевыми» показателями, основанными на ЦПТ.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# вновь создадим генеральную совокупность salaries = skewnorm.rvs(a = 20, loc = 20, scale = 80, size = 100000, random_state = 42) # в словарь sampling_distributions поместим sampling_distributions = { # количество выборок в каждом из девяти распределений ‘Number_of_samples’ : np.repeat(number_of_samples_list, 3), # размер каждой выборки ‘Sample_size’ : sample_size_list * 3, # среднее значение генеральной совокупности ‘Pop_mean’ : [np.mean(salaries)] * 9, # фактическое среднее значение каждого распределения ‘Actual_mean’ : mean_list, # расчетное СКО (в соответствии с ЦПТ) ‘Expected_std’ : [np.std(salaries) / np.sqrt(n) for n in sample_size_list * 3], # фактическое СКО каждого распределения ‘Actual_std’ : std_list } # превратим словарь в датафрейм и округлим значения pd.DataFrame(sampling_distributions).round(2).astype(str) |
Как мы видим, на выполняемость ЦПТ влияет не только размер выборки, но и количество этих выборок. Очевидно, что наибольшую близость к расчетным показателям демонстрируют распределения из 500 выборок.
Стандартное нормальное распределение
Любое нормальное распределение со средним значением μ и СКО σ можно привести к стандартному нормальному распределению (standard normal distribution) со средним значением ноль и СКО равным единице.
$$ Z sim {mathcal N}(0, 1) $$
Для этого воспользуемся следующей формулой.
$$ z = frac{x-mu}{sigma} $$
Таким образом мы приводим каждое значение x к соответствующей z-оценке (z-score), вычитая среднее μ и деля результат на СКО σ. Например, приведем данные о росте мужчин к стандартному виду (для этого воспользуемся векторизацией и трансляцией кода).
|
height_men_standard = (height_men — np.mean(height_men))/np.std(height_men) height_men_standard[:10] |
|
array([ 0.49836188, -0.10076518, 0.59821639, 1.49690697, -0.20061969, -0.20061969, 1.59676148, 0.7979254 , -0.50018322, 0.49836188]) |
Посмотрим на результат на графике.
|
# зададим размер графика plt.figure(figsize = (10,6)) # построим график плотности sns.kdeplot(height_men_standard, fill = True) # добавим подписи plt.xlabel(‘z-score’, fontsize = 15) plt.ylabel(‘Плотность распределения’, fontsize = 15) plt.title(‘Стандартное распределение роста мужчин’, fontsize = 17) plt.show() |
Стоит сказать, что ровно такого же результата можно добиться, применив метод .fit_transform() класса ScandardScaler модуля preprocessing библиотеки sklearn.
|
# импортируем класс StandardScaler from sklearn.preprocessing import StandardScaler # создаем объект этого класса scaler = StandardScaler() # применяем метод .fit_transform() к данным о росте, предварительно превратив их в двумерный массив scaled_height_men = scaler.fit_transform(height_men.reshape(—1, 1)) # убираем второе измерение scaled_height_men = scaled_height_men.flatten() # и сравниваем получившийся результат с ранее стандартизированными данными np.array_equiv(height_men_standard, scaled_height_men) |
Мы уже использовали этот инструмент для нормализации данных в рамках вводного курса (в задачах классификации и кластеризации), а также при работе с файлами в Google Colab.
Добавлю, что стандартное нормальное распределение можно также создать с помощью функции np.random.standard_normal().
|
# создадим массив из 10 000 значений st_norm = np.random.standard_normal(10000) # посмотрим на первые 10 st_norm[:10] |
|
array([-0.76366945, -1.11864174, -0.77088274, 0.96929238, -0.69869956, -1.34853749, -0.94994848, 0.99902749, 0.30575659, -0.45619504]) |
Посмотрим на результат.
|
# зададим размер графика plt.figure(figsize = (10,6)) # построим график плотности sns.kdeplot(st_norm, fill = True) # добавим подписи plt.xlabel(‘z-score’, fontsize = 15) plt.ylabel(‘Плотность распределения’, fontsize = 15) plt.title(‘Стандартное нормальное распределение’, fontsize = 17) plt.show() |
Создаваемый массив также может быть многомерным.
|
# для этого измерения нужно передать в виде кортежа np.random.standard_normal((2, 3)) |
|
array([[-0.40187015, -0.0797878 , -0.21066058], [-0.70034594, 0.10488661, 0.85464581]]) |
Как и в случае обычного нормального распределения, мы можем найти значение (в данном случае z-score) по площади с помощью квантиль-функции.
|
# вычислим z-score, соответствующий 95 процентам площади под кривой # loc = 0, scale = 1 можно не указывать, это параметры по умолчанию zscore = norm.ppf(0.95) zscore |
Убедиться в верности результата можно с помощью функции распределения.
Критерии нормальности распределения
Давайте еще раз посмотрим на распределение выборочных средних. Мы сказали, что при определенных условиях оно стремится к нормальному.
Одновременно пока что мы определяли нормальность распределения «на глаз» (с помощью гистограммы, графика плотности или boxplot), хотя в некоторых случаях полезно иметь более надежный критерий нормальности. Это важно, например, при оценке:
- Распределения остатков модели линейной регрессии
- Распределения наблюдений в классах модели линейного дискриминантного анализа (Linear Discriminant Analysis, LDA)
Рассмотрим два способа оценки нормальности распределения.
Способ 1. График нормальной вероятности
График нормальной вероятности (normal probability plot) показывает соотношение упорядоченных по возрастанию данных и соответствующих им квантилей нормального распределения.
Если данные распределены нормально, все точки будут лежать на одной прямой, если нет — мы будем наблюдать отклонения.
Алгоритм создания графика нормальной вероятности следующий:
- Сортируем исходные данные по возрастанию
- Находим накопленную вероятность (cumulative probability) каждого значения
- С помощью квантиль-функции выясняем, какому квантилю соответствовала бы эта вероятность, если бы распределение было нормальным
- По оси x отмечаем квантили, по оси y — отсортированные данные
Накопленную вероятность будем вычислять по формуле
$$ P = frac{i-0.375}{n+0.25} $$
где i — это индекс (начиная с единицы) значения в перечне отсортированных данных, а n — количество наблюдений.
С помощью Питона построим график нормальной вероятности для данных о росте.
|
# вначале отсортируем данные о росте height_men_srt = sorted(height_men) # рассчитаем длину массива n = len(height_men_srt) # вычислим накопленную вероятность cum_probability = [(i — 0.375)/(n + 0.25) for i in range(1, n + 1)] # рассчитаем квантили, как если бы данные были нормально распределены quantiles = norm.ppf(cum_probability) |
|
# как и должно быть, накопленная вероятность — это значения от 0 до 1 cum_probability[0], cum_probability[—1] |
|
(6.249984375039063e-06, 0.999993750015625) |
|
# также посмотрим на соответствующие им квантили quantiles[0], quantiles[—1] |
|
(-4.368680139037586, 4.368680139037566) |
|
# зададим размер графика plt.figure(figsize = (10,8)) # на точечной диаграмме по оси x разместим теоретические квантили # по оси y — отсортированные по возрастанию данные plt.scatter(quantiles, height_men_srt) # добавим подписи plt.xlabel(‘Теоретические квантили’, fontsize = 15) plt.ylabel(‘Отсортированные данные’, fontsize = 15) plt.title(‘График нормальной вероятности’, fontsize = 17) plt.show() |
Как мы видим, в целом данные распределены нормально (что разумеется ожидаемо, потому что мы генерировали их с помощью функции np.random.normal()).
Можно также воспользоваться функцией probplot() модуля stats библиотеки scipy.
|
from scipy.stats import probplot |
Построим график для тех же данных о росте.
|
plt.figure(figsize = (10,8)) # параметр dist = ‘norm’ указывает на сравнение данных с нормальным распределением # plot = plt строит график с помощью matplotlib.pyplot probplot(height_men, dist = ‘norm’, plot = plt) plt.show() |
Эта функция использует другую формулу для вычисления накопленной вероятности (а именно Filliben’s estimate), поэтому квантили незначительно, но будут отличаться от написанного нами алгоритма.
|
# функция probplot() при параметрах plot = None, fit = False возвращает два массива: # квантили и отсортированные данные, возьмем первый массив [0] quantiles = probplot(height_men, dist = ‘norm’, plot = None, fit = False)[0] # по посмотрим на первое и последнее значения quantiles[0], quantiles[—1] |
|
(-4.346021549886044, 4.346021549886044) |
Давайте построим график нормальной вероятности для скошенного вправо распределения (мы договорились, что это распределение зарплат).
|
plt.figure(figsize = (10,8)) probplot(salaries, dist = ‘norm’, plot = plt) plt.show() |
Здесь мы видим, что график нормальной вероятности довольно сильно отклоняется от «идеальных» значений, лежащих на диагонали.
Остается построить график для распределения выборочных средних.
|
# снова воспользуемся функцией sample_means() с параметрами n_samples = 500, sample_size = 30 sampling_dist = sample_means(salaries, 500, 30, replace = False, random_state = 42) # построим график нормальной вероятности plt.figure(figsize = (10,8)) probplot(sampling_dist, dist = ‘norm’, plot = plt) plt.show() |
Как и должно быть, это распределение гораздо ближе к нормальному.
Способ 2. Тест Шапиро-Уилка
Тест Шапиро-Уилка (Shapiro-Wilk test) позволяет сделать статистически значимый вывод о нормальности распределения.
- Нулевая гипотеза предполагает, что распределение нормально
- Альтернативная гипотеза утверждает обратное
Тест Шапиро-Уилка чувствителен к количеству элементов (N) в наборе данных и теряет точность при N > 5000.
Проведем тест для распределений роста и распределения зарплат при пороговом значении 0,05, однако вначале создадим распределения с меньшим количеством элементов.
|
np.random.seed(42) height_men = np.round(np.random.normal(180, 10, 1000)) salaries = skewnorm.rvs(a = 20, loc = 20, scale = 80, size = 1000, random_state = 42) |
Начнем с роста.
|
from scipy.stats import shapiro _, p_value = shapiro(height_men) p_value |
Теперь посмотрим на зарплаты.
|
_, p_value = shapiro(salaries) p_value |
Как и ожидалось, в первом случае мы не смогли отвергнуть нулевую гипотезу о нормальном распределении (p-value > 0,05), во втором случае мы можем это сделать (p-value < 0,05).
Нормальное приближение биномиального распределения
Теорема Муавра-Лапласа
Теорема Муавра-Лапласа (de Moivre–Laplace theorem), частный случай Центральной предельной теоремы, утверждает, что при определенных условиях нормальное распределение может быть использовано в качестве приближения биномиального распределения (Normal Approximation to Binomial Distribution).
Напомню формулу биномиального распределения
$$ P(X = k) = binom{n}{k} p^k (1-p)^{n-k} $$
где n — количество испытаний, k — количество успехов, а p — вероятность успеха. Так вот если np ≥ 5 и n(1−p) ≥ 5, то выполняется следующее
$$ B(n, p) sim {mathcal N}(np, sqrt{np(1-p)}) $$
Другими словами, если взять вероятность успеха p близкое к 0,5, либо достаточно большое количество испытаний n, то биномиальное распределение по мере увеличения n будет приближаться нормальному распределению.
Проиллюстрируем теорему с помощью Питона. Будем подбрасывать несимметричную монету (p = 0,8) по 3, 5, 10, 15, 25 и 50 раз и сравнивать получившиеся распределения с нормальным.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
# создадим список с количеством испытаний (подбрасываний монеты) n_list = [3, 5, 10, 15, 25, 50] # подграфики будут расположены в одном столбце с количеством строк, # равном длине списка n_list fig, ax = plt.subplots(nrows = len(n_list), ncols = 1, # размер графика также будет определяться длиной списка n_list figsize = (8, 4 * len(n_list)), # constrained_layout регулирует пространство между подграфиками constrained_layout = True) # пройдемся по списку n_list for i, n in enumerate(n_list): # зададим вероятность успеха p = 0.8 # и проверим выполняются ли условия при заданном p и n cond1, cond2 = n * p, n * (1 — p) # сгенерируем биномиальное распределение с заданными p и n np.random.seed(42) res = np.random.binomial(n = n, p = p, size = 1000) # запишем успешные серии подбрасываний и их количество successes, counts = np.unique(res, return_counts = True) # с помощью столбчатой диаграммы выведем относительную частоту каждого значения случайной величины ax[i].bar(successes, counts / len(res), alpha = 0.5) # в подписи к графике выведем n, p, а также результат проверки условий ax[i].set_xlabel(‘n: {}, p: {}, np: {}, n * (1 — p): {}’.format(n, p, round(cond1), round(cond2))) # рассчитаем среднее значение и СКО согласно теореме Муавра-Лапласа mean, std = n * p, np.sqrt(n * p * (1 — p)) # создадим 1000 точек в +/- 3 СКО от среднего значения x = np.linspace(mean — 3 * std, mean + 3 * std, 1000) # найдем точки на оси y по формуле Гаусса f_norm = norm.pdf(x, mean, std) # построим график плотности нормального распределения ax[i].plot(x, f_norm) # дополнительно можно вывести «идеальное» биномиальное распределение с помощью функции binom() # from scipy.stats import binom # x2 = np.arange(n) # binom_p = binom.pmf(x2, n, p) # ax[i].stem(x2, binom_p, use_line_collection = True) plt.show() |
Как мы видим, вначале (например, при n = 3), распределение было ожидаемо скошенным, при этом по мере увеличения количества бросков оно стало все больше «вписываться» в график плотности нормального распределения.
Поправка на непрерывность распределения
Нормальное приближение биномиального распределения удобно использовать, когда нужно посчитать вероятность большого числа исходов. Однако прежде внесем одно уточнение.
На графике ниже видно, что для расчета биномиальной вероятности нам нужно сложить площади столбцов гистограммы. Например, чтобы найти вероятность выпадения не более одного орла при трех последовательных подбрасываниях монеты, нужно сложить первый и второй столбцы.
Получаем
$$ P_B(X ≤ 1) = P_B(X = 0) + P_B(X = 1) = frac{1}{8} + frac{3}{8} = frac{4}{8} = frac{1}{2} $$
При этом, если мы хотим рассчитать эту же площадь с помощью кривой нормального распределения, нам нужно сместить границу таким образом, чтобы захватить все интересующие нас столбцы. В данном случае прибавить 0,5. То есть PN (X < 1,5).
Воспользуемся теоремой Муавра-Лапласа для расчета среднего и СКО (напомню n = 3, p = 0,5).
$$ mu = np = 3 times 0,5 = 1,5 $$
$$ sigma = sqrt{np(1-p)} = sqrt{3 times 0,5 times 0,5} = 0,75 $$
Остается воспользоваться Питоном для нахождения площади под кривой нормального распределения.
|
# передадим методу .cdf() границу, среднее значение (loc) и СКО (scale) area = norm.cdf(1.5, loc = 1.5, scale = 0.75) # на выходе мы получим площадь под кривой area |
Посмотрим на результат на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# зададим размер графика plt.figure(figsize = (10,6)) # пропишем среднее значение и СКО mean, std = 1.5, 0.75 # создадим пространство из 1000 точек в диапазоне +/- трех СКО от среднего значения x = np.linspace(mean — 3 * std, mean + 3 * std, 1000) # рассчитаем зачения по оси y с помощью метода .pdf() # т.е. функции плотности вероятности f = norm.pdf(x, mean, std) # и построим график plt.plot(x, f) # дополнительно создадим создадим точки на оси x для закрашенной области px = x = np.linspace(mean — 3 * std, mean, 1000) # и заполним пространство в пределах этих точек по оси x пространство # от кривой нормального распределения до оси y = 0 plt.fill_between(px, norm.pdf(px, mean, std), alpha = 0.3) # выведем оба графика на экран plt.show() |
Если же нас попросят найти вероятность конкретного значения, например, выпадения двух орлов PB(X = 2) (то есть площадь одного столбца гистограммы), то при расчете площади под кривой нормального распределения нужен интервал PN(1,5 < X < 2,5). Другими словами мы прибавили по 0,5 с обеих сторон.
Рассчитаем площадь с помощью Питона.
|
# передадим методу .cdf() границу, среднее значение (loc) и СКО (scale) area = norm.cdf(2.5, loc = 1.5, scale = 0.75) — norm.cdf(1.5, loc = 1.5, scale = 0.75) # на выходе мы получим площадь под кривой area |
Напомню, площадь столбца составляет PB(X = 2) = 3/8 или 0,375, что довольно существенно отличается от площади под кривой. Это связано с тем, что мы взяли слишком маленькое n и условия $np geq 5$ и $ n(1-p) geq 5 $ в данном случае не выполняются.
По мере увеличения n поправка на непрерывность распределения становится все менее значимой.
Выведем результат на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# зададим размер графика plt.figure(figsize = (10,6)) # пропишем среднее значение и СКО mean, std = 1.5, 0.75 # создадим пространство из 1000 точек в диапазоне +/- трех СКО от среднего значения x = np.linspace(mean — 3 * std, mean + 3 * std, 1000) # рассчитаем зачения по оси y с помощью метода .pdf() # т.е. функции плотности вероятности f = norm.pdf(x, mean, std) # и построим график plt.plot(x, f) # дополнительно создадим создадим точки на оси x для закрашенной области px = x = np.linspace(1.5, 2.5, 1000) # и заполним пространство в пределах этих точек по оси x пространство # от кривой нормального распределения до оси y = 0 plt.fill_between(px, norm.pdf(px, mean, std), alpha = 0.3) # выведем оба графика на экран plt.show() |
Пример приближения
Для закрепления пройденного материала рассмотрим более жизненный пример. Предположим, вам поставили партию из 500 единиц оборудования. При этом вам известно, что в среднем 2% (то есть 0,02) оборудования имеют различные дефекты. Какова вероятность того, что в партии не менее 15 бракованных единиц оборудования?
Речь идет о биномиальном распределении, так как мы последовательно достаем из партии одну единицу оборудования, и в ней либо будет дефект, либо нет.
$$ B(n, p) = B(500; 0,02) rightarrow P_B(X geq 15) $$
|
# импортируем объект binom из модуля stats библиотеки scipy from scipy.stats import binom # зададим параметры биномиального распределения n, p = 500, 0.02 # метод .cdf() рассчитывает вероятность до значения включительно (!), # таким образом, чтобы найти X >= 15, # мы берем значения вплоть до 14 и вычитаем результат из единицы 1 — binom.cdf(14, n, p) |
Теперь решим эту задачу с помощью нормального приближения. По теореме Муавра-Лапласа выводим следующее.
$$ B(500; 0,02) sim {mathcal N}(10; sqrt{9.8}) rightarrow P_N(X > 14,5) $$
Таким образом, задача сводится к нахождению площади под кривой с учетом внесенной поправки на непрерывность распределения (15 − 0,5 = 14,5).
|
# рассчитаем среднее значение и СКО mean, std = n * p, np.sqrt(n * p * (1 — p)) # рассчитаем площадь под кривой слева от границы и вычтем результат из единицы 1 — norm.cdf(14.5, loc = mean, scale = std) |
Посмотрим, как это выглядит на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# зададим размер графика plt.figure(figsize = (10,6)) # создадим 1000 точек в +/- 3 СКО от среднего значения x = np.linspace(mean — 3 * std, mean + 3 * std, 1000) # найдем точки на оси y по формуле Гаусса f_norm = norm.pdf(x, mean, std) # построим график плотности нормального распределения plt.plot(x, f_norm) # дополнительно создадим точки на оси х для закрашенной области px = np.linspace(14.5, mean + 3 * std, 1000) # и заполним в пределах этих точек по оси x пространство # от кривой нормального распределения до оси y = 0 plt.fill_between(px, norm.pdf(px, mean, std), alpha = 0.3) plt.show() |
Перейдем к комбинаторике.
To add to the confusion around Q-Q plots and probability plots in the Python and R worlds, this is what the SciPy manual says:
«
probplotgenerates a probability plot, which should not be confused
with a Q-Q or a P-P plot. Statsmodels has more extensive functionality
of this type, see statsmodels.api.ProbPlot.»
If you try out scipy.stats.probplot, you’ll see that indeed it compares a dataset to a theoretical distribution. Q-Q plots, OTOH, compare two datasets (samples).
R has functions qqnorm, qqplot and qqline. From the R help (Version 3.6.3):
qqnormis a generic function the default method of which produces a
normal QQ plot of the values in y.qqlineadds a line to a
“theoretical”, by default normal, quantile-quantile plot which passes
through the probs quantiles, by default the first and third quartiles.
qqplotproduces a QQ plot of two datasets.
In short, R’s qqnorm offers the same functionality that scipy.stats.probplot provides with the default setting dist=norm. But the fact that they called it qqnorm and that it’s supposed to «produce a normal QQ plot» may easily confuse users.
Finally, a word of warning. These plots don’t replace proper statistical testing and should be used for illustrative purposes only.
You are calling the normal pdf, with parameters $mu=2$ and $sigma=9$, evaluated at the points 0,1,2,3,4. It cannot be interpreted as a probability as is. Are you interested in probabilities or quantiles?
If you want quantiles, try
scipy.stats.norm.ppf( [.05,.5, .95], 2, 9)
will give you the quantiles at the points 0.05, .5 and .95. For example, the solution to $P( N_{2,9} < q ) = 0.05$ is scipy.stats.norm.ppf(.05, 2,9).