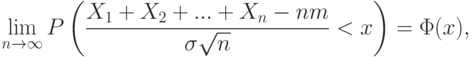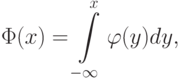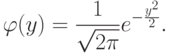В примерах в данной статье данные генерятся при каждой загрузке страницы. Если Вы хотите посмотреть пример с другими значениями —
обновите страницу .
Параметры дискретного закона распределения
В статье описано как найти среднее значение и стандартное отклонение. Вы узнаете, что такое квантиль и каких он бывает видов, а также,
как построить доверительный интервал.
Математическое описание
Смотря на закон распределения, мы можем понять, какова вероятность того или иного события,
можем сказать, какова вероятность, что произойдёт группа событий, а в этой статье мы рассмотрим, как наши выводы «на глаз» перевести
в математически обоснованное утверждение.
Крайне важное определение: математическое ожидание — это площадь под графиком распределения. Если мы говорим о дискретном распределении —
это сумма событий умноженных на соответсвующие вероятности, также известно как момент:
(2) E(X) = Σ(pi•Xi) E — от английского слова Expected (ожидание)
Для математического ожидания справедливы равенства:(3) E(X + Y) = E(X) + E(Y)
(4) E(X•Y) = E(X) • E(Y)
Момент степени k:
(5) νk = E(Xk)
Центральный момент степени k:
(6) μk = E[X — E(X)]k
Среднее значение
Среднее значение (μ) закона распределения — это математическое ожидание случайной величины
(случайная величина — это событие), например, сколько в среднем посетителей заходит в магазин в час:
| Кол-во посетителей | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Количество наблюдений | 87 | 130 | 79 | 48 | 20 | 10 | 26 |
| Таблица 1. Количество посетителей в час |
График 1. Количество посетителей в час
Чтобы найти среднее значение всех результатов необходимо сложить всё вместе и разделить на количество результатов:
μ = (87 • 0 + 130 • 1 + 79 • 2 + 48 • 3 + 20 • 4 + 10 • 5 + 26 • 6) / 400 = 718/400 = 1.8
То же самое мы можем проделать используя формулу 2:
μ = M(X) = Σ(Xi•pi) = 0 • 0.22 + 1 • 0.33 + 2 • 0.2 + 3 • 0.12 + 4 • 0.05 + 5 • 0.03 + 6 • 0.07 = 1.8 Момент первой степени, формула (5)
Собственно, формула 2 представляет собой среднее арифметическое всех значений
Итог: в среднем, 1.8 посетителя в час
| Количество посетителей | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Вероятность (%) | 21.8 | 32.5 | 19.8 | 12 | 5 | 2.5 | 6.5 |
| Таблица 2. Закон распределения количества посетителей |
Отклонение от среднего
Посмотрите на это распределение, можно предположить, что в среднем случайная величина равна 100±5, поскольку
кажется, что таких значений несравнимо больше чем тех, что меньше 95 или больше 105:
График 2. График функции вероятности. Распределение ≈ 100±5
Среднее значение по формуле (2): μ = 99.95, но как посчитать, насколько далеко все значения находятся от среднего? Вам должна быть
знакома запись 100±5. Что бы получить это значение ±, нам необходимо определить диапазон значений вокруг среднего. И мы могли бы
использовать в качестве меры удалённости «разность» между средним и случайными величинами:
(7) xi — μ
но сумма таких расстояний, а следовательно и любое производное от этого числа, будет равно нулю, поэтому в качестве меры выбрали квадрат разниц
между величинами и средним значением:
(8) (xi — μ)2
Соответственно, среднее значение удалённости — это математическое ожидание квадратов удалённости:
(9) σ2 = E[(X — E(X))2]
Поскольку вероятности любой удалённости равносильны — вероятность каждого из них — 1/n, откуда:
(10) σ2 = E[(X — E(X))2] = ∑[(Xi — μ)2]/n
Она же формула центрального момента (6) второй степени
σ возведена в квадрат, поскольку вместо расстояний мы взяли квадрат расстояний. σ2 называется дисперсией. Корень из дисперсии
называется средним квадратическим отклонением, или среднеквадратическим отклоненим, и его используют в качестве меры разброса:
(11) μ±σ
(12) σ = √(σ2) = √[∑[(Xi — μ)2]/n]
Возвращаясь к примеру, посчитаем среднеквадратическое отклонение для графика 2:
σ = √(∑(x-μ)2/n) = √{[(90 — 99.95)2 + (91 — 99.95)2 + (92 — 99.95)2 + (93 — 99.95)2 + (94 — 99.95)2 + (95 — 99.95)2 + (96 — 99.95)2 + (97 — 99.95)2 + (98 — 99.95)2 + (99 — 99.95)2 + (100 — 99.95)2 + (101 — 99.95)2 + (102 — 99.95)2 + (103 — 99.95)2 + (104 — 99.95)2 + (105 — 99.95)2 + (106 — 99.95)2 + (107 — 99.95)2 + (108 — 99.95)2 + (109 — 99.95)2 + (110 — 99.95)2]/21} = 6.06
Итак, для графика 2 мы получили:
X = 99.95±6.06 ≈ 100±6 , что немного отличается от полученного «на глаз»
Квантиль
График 3. Функция распределения. Медиана
График 4. Функция распределения. 4-квантиль или квартиль
График 5. Функция распределения. 0.34-квантиль
Для анализа функции распределения ввели понятие квантиль. Квантиль — это случайная величина при заданном уровне вероятности, т.е.:
квантиль для уровня вероятности 50% — это случайная величина на графике плотности вероятности, которая имеет вероятность 50%.
На примере с графиком 3, квантиль уровня 0.5 = 99 (ближайшее значение, поскольку распределение дискретно и события со значением 99.3 просто не существует)
- 2-квантиль — медиана
- 4-квантиль — квартиль
- 10-квантиль — дециль
- 100-квантиль — перцентиль
То есть, если мы говорим о дециле (10-квантиле), то это означает, что мы разбили график на 10 частей, что соответствует девяти линяям,
и для каждого дециля нашли значение случайной величины.
Также, используется обозначение x-квантиль, где х — дробное число, например, 0.34-квантиль, такая запись означает значение случайной величины при
p = 0.34.
Для дискретного распределения квантиль необходимо выбирать следующим образом: квантиль гарантирует вероятность, поэтому, если рассчитанный
квантиль не совпадает с одним и значений, необходимо выбирать меньшее значение.
Построение интервалов
Квантили используют для построения доверительных интервалов, которые необходимы для исследования статистики не одного конкретного события (например,
интерес — случайное число = 98), а для группы событий (например, интерес — случайное число между 96 и 99). Доверительный интервал бывает двух видов:
односторонний и двусторонний. Параметр доверительного интервала — уровень доверия. Уровень доверия означает процент событий, которые можно считать успешными.
Двусторонний доверительный интервал
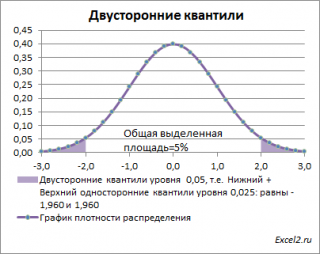
Двусторонний доверительный интервал строится следующим образом: мы задаёмся уровнем значимости, например, 10%, и выделяем область на графике так, что 90% всех
событий попадут в эту область. Поскольку интервал двусторонний, то мы отсекаем по 5% с каждой стороны, т.е. мы ищем 5й перцентиль, 95й перцентиль и значения
случайной величины между ними будут являться доверительной областью, значения за пределами доверительной области называются «критическая область»
График 6. Плотность вероятности
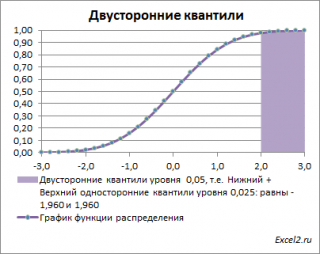
График 7. Функция распределения с 5 и 95 перцентилями. Цветом выделен доверительный интервал с уровнем доверия 0.9
График 8. Функция вероятности и двусторонний доверительный интервал с уровнем доверия 90%
Доверительный интервал
Левосторонний и правосторонний доверительные интервалы строятся аналогично двустороннему: для левостороннего интервала мы находим перцентиль уровня
[‘один’ минус ‘уровень значимости’]. Таким образом, для построения доверительного левостороннего интервала уровня значимости 4% нам необходимо найти четвёртый перцентиль
и всё, что справа — доверительный интервал, всё что слева — критическая область.
График 9. Левосторонний доверительный интервал с уровнем значимости 4%. Заливкой выделен доверительный интервал
График 10. Правосторонний доверительный интервал с уровнем значимости 4%. Заливкой выделен доверительный интервал
Итого
Среднее значение — математическое ожидание случайной величины, находится по формуле:
μ = E(X) = Σ(pi•Xi)
Среднеквадратичное отклонение — математическое ожидание удалённости значений от среднего, находится по формуле:
σ = √(σ2) = √[∑[(Xi — μ)2]/n]
n-квантиль — разделение функции распределения на n равных отрезков, основные типы квантилей:
- 2-квантиль — медиана
- 4-квантиль — квартили
- 10-квантиль — децили
- 100-квантиль — перцентили
Доверительный интервал уровня α — участок функции вероятности, содержащий α всех возможных значений. Двусторонний доверительный
интервал строится отсечением (1-α)/2 справа и слева. Левосторонний и правосторонний доверительные интервалы строятся отсечением
области (1-α) слева и справа соответственно.
Построить ряд распределения
Предположим, мы имеем 100 значений и все разные, например: масса тела Сомалийских пиратов.
Такой набор данных обрабатывать неудобно, мы даже не можем представить их на обычном графике.
Поэтому нам необходимо категоризировать имеющиеся данные и для этого мы делаем следующее:
Запишем наши данные в таблицу:
| 111 | 58 | 73 | 112 | 103 | 112 | 95 | 75 | 81 | 86 |
| 56 | 87 | 61 | 53 | 74 | 84 | 72 | 114 | 97 | 74 |
| 68 | 87 | 77 | 63 | 52 | 85 | 110 | 69 | 87 | 77 |
| 106 | 95 | 114 | 58 | 95 | 85 | 92 | 96 | 93 | 105 |
| 66 | 61 | 106 | 106 | 109 | 56 | 107 | 56 | 104 | 72 |
| 104 | 72 | 65 | 64 | 109 | 95 | 63 | 75 | 78 | 102 |
| 62 | 83 | 110 | 85 | 69 | 91 | 63 | 67 | 64 | 112 |
| 112 | 111 | 100 | 63 | 65 | 66 | 61 | 72 | 112 | 83 |
| 99 | 75 | 78 | 93 | 73 | 84 | 88 | 104 | 54 | 62 |
| 112 | 82 | 80 | 58 | 104 | 99 | 80 | 102 | 112 | 97 |
| Таблица 3. Вес сомалийских пиратов |
Данные разобьём на группы, для начала предлагаю разбить на десять интервалов:
Узнаём максимальное и минимальное значения, вычитаем их друг из друга и делим на количество
интервалов — получили отрезки:
Максимальное значение: 114
Минимальное значение: 52
Разница: 114 — 52 = 62
Длина интервала: 62 / 10 = 6.2
Теперь посчитаем количество пиратов (весов, я имею ввиду) в каждом интервале:
| # | Интервал | Количество элементов |
|---|---|---|
| 1. | 52 — 58.2 | 9 |
| 2. | 58.2 — 64.4 | 11 |
| 3. | 64.4 — 70.6 | 8 |
| 4. | 70.6 — 76.8 | 11 |
| 5. | 76.8 — 83 | 8 |
| 6. | 83 — 89.2 | 12 |
| 7. | 89.2 — 95.4 | 8 |
| 8. | 95.4 — 101.6 | 6 |
| 9. | 101.6 — 107.8 | 12 |
| 10. | 107.8 — 114 | 13 |
| Таблица 4. Количество элементов в интервалах |
Вуа-ля, наше распределение на графике:
График 11. Ряд распределения массы тела сомалийских пиратов
Бонус
Интервалы лучше брать целыми числами, поэтому, если с выбранным количеством интервалов
размер выходит нецелым, то можно раздвинуть диапазон значений, пример:
Значение интервала равно 6.2, число не является целым, поэтому
отодвигаем верхнюю границу:
Остаток от деления: [(114 — 52) / 10] = 2
Подвинуть на: 8
Новый диапазон: [52;122]
Диапазон можно двигать как вверх, так и вниз, но лучше в обе стороны.
Совет
Принято делить распределение на 7-8 интервалов, но в каждой конкретной ситуации
Вы можете выбрать отличное количество интервалов, впрочем, как и сделать их
различной длины.
Список параметров
Итак, вот список основных параметров дискретного закона распределения:
| Название | Символ | Формула |
|---|---|---|
| Математическое ожидание (среднее) | E(X) | Σ(pi•Xi) |
| Центральный момент (среднеквадратичное отклонение) |
σx | σ = √(σ2) = √[∑[(Xi — μ)2]/n] |
| Длина интервала | R | max(x) — min(x) |
| Мода | mo | max P(x = mo) |
| 1й квантиль | — | F(x) = 0.25 |
| Медиана | me | F(x) = 0.5 |
| Дециль | — | F(x) = 0.1 |
| Таблица 5. Основные параметры дискретного закона распределения |
Шаблон гистограммы в OpenOffice Calc
Файл histogram_mock.ods содержит шаблон
построения гистограммы.
Вам понравилась статья?
/
Просмотров: 16 114
Мода и медиана случайной величины.
Квантиль уровня случайной величины
- Краткая теория
- Примеры решения задач
Краткая теория
Кроме
математического ожидания и дисперсии, в теории вероятностей применяется еще ряд
числовых характеристик, отражающих те или иные особенности распределения.
Мода непрерывной и дискретной случайной величины
Модой
случайной величины называется ее наиболее вероятное значение, для которого
вероятность
или плотность вероятности
достигает максимума.
В
частности, наивероятнейшее значение числа успехов в схеме Бернулли – это мода
биномиального распределения.
Если
вероятность или плотность вероятности достигает максимума не в одной, а в
нескольких точках, распределение называется полимодальным.
Полимодальное распределение
Медиана непрерывной и дискретной случайной величины
Медианой случайной величины
называют число
, такое, что
.
То есть вероятность того, что
случайная величина
примет
значение, меньшее медианы
или больше ее,
одна и та же и равна
.
Для дискретной случайной величины
это число может
не совпадать ни с одним из значений
. Поэтому медиану дискретной случайной величины
определяют как любое число
, лежащее между двумя соседними возможными значениями
и
такими, что
.
Для непрерывной случайной величины,
геометрически, вертикальная прямая
, проходящая через точку с абсциссой, равной
, делит площадь фигуры под кривой распределения на две
равные части.
Медиана на графике плотности вероятности непрерывной
случайной величины
Очевидно, что в точке
функция распределения непрерывной случайной
величины равна
, то есть
.
Медиана на графике функции распределения непрерывной
случайной величины
Квантили и процентные точки случайной величины
Наряду с отмеченными выше числовыми
характеристиками для описания случайной величины используется понятие квантилей
и процентных точек.
Квантилем уровня
(или
– квантилем)
называется такое значение
случайной
величины, при котором функция ее распределения принимает значение, равное
, то есть:
Некоторые квантили получили особое
называние. Очевидно, что введенная выше медиана случайной величины есть
квантиль уровня 0,5, то есть
. Квантили
и
получили
название соответственно верхнего и нижнего квантилей. Также в литературе
встречаются термины: децили (под которыми понимают квантили
) и процентили (квантили
).
С понятием квантиля тесно связано
понятие процентной точки. Под
точкой
подразумевается квантиль
, то есть такое значение случайной величины
, при котором
.
Смежные темы решебника:
- Структурные средние в статистике — мода, медиана, квантиль, дециль
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Найти
моду, медиану, квантиль
и 40%-ну точку случайной величины
c плотностью распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Производная
не обращается в нуль.
Значения
на концах отрезка:
Следовательно,
мода:
Медиану
найдем из условия:
В нашем
случае получаем:
Значение
принадлежит отрезку
,
следовательно, искомая медиана:
Квантиль
найдем из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомый квантиль:
Найдем
40%-ную точку случайной величины
, или квантиль
из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомая точка:
Ответ:
.
Пример 2
Найти
моду, медиану, квантиль
случайной величины
, заданной функцией
распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Найдем
плотность распределения:
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Значения
функции
в стационарных точках и на концах отрезка:
Распределение
полимодальное:
Медиану
найдем из уравнения:
Итак,
медиана:
Квантиль
найдем из уравнения:
Итак:
Ответ:
.
- Краткая теория
- Примеры решения задач
2.4. Случайные величины и их распределения
Распределения случайных величин и функции распределения. Распределение числовой случайной величины – это функция, которая однозначно определяет вероятность того, что случайная величина принимает заданное значение или принадлежит к некоторому заданному интервалу.
Первое – если случайная величина принимает конечное число значений. Тогда распределение задается функцией 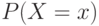


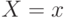
Второе – если случайная величина принимает бесконечно много значений. Это возможно лишь тогда, когда вероятностное пространство, на котором определена случайная величина, состоит из бесконечного числа элементарных событий. Тогда распределение задается набором вероятностей 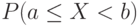


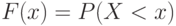


Это соотношение показывает, что как распределение может быть рассчитано по функции распределения, так и наоборот, функция распределения – по распределению.
Используемые в вероятностно-статистических методах принятия решений и других прикладных исследованиях функции распределения бывают либо дискретными, либо непрерывными, либо их комбинациями.
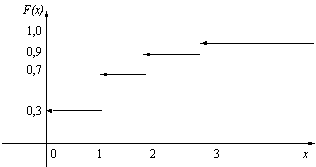
Дискретные функции распределения соответствуют дискретным случайным величинам, принимающим конечное число значений или же значения из множества, элементы которого можно перенумеровать натуральными числами (такие множества в математике называют счетными). Их график имеет вид ступенчатой лестницы (
рис.
2.1).
Пример 1. Число 

рис.
2.1.
Рис.
2.1.
График функции распределения числа дефектных изделий
Непрерывные функции распределения не имеют скачков. Они монотонно возрастают1В некоторых случаях, например, при изучении цен, объемов выпуска или суммарной наработки на отказ в задачах надежности, функции распределения постоянны на некоторых интервалах, в которые значения исследуемых случайных величин не могут попасть. при увеличении аргумента – от 0 при 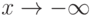
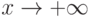
Непрерывные функции распределения, используемые в вероятностно-статистических методах принятия решений, имеют производные. Первая производная 

По плотности вероятности можно определить функцию распределения:
Для любой функции распределения
а потому
Перечисленные свойства функций распределения постоянно используются в вероятностно-статистических методах принятия решений. В частности, из последнего равенства вытекает конкретный вид констант в формулах для плотностей вероятностей, рассматриваемых ниже.
Пример 2. Часто используется следующая функция распределения:
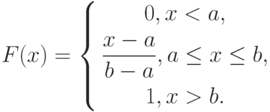 |
( 1) |
где 


(в точках 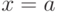


Случайная величина с функцией распределения (1) называется «равномерно распределенной на отрезке ![[a; b]](https://intuit.ru/sites/default/files/tex_cache/65c152d51ed08a1761f5a8cb653eafe5.png)
Смешанные функции распределения встречаются, в частности, тогда, когда наблюдения в какой-то момент прекращаются. Например, при анализе статистических данных, полученных при использовании планов испытаний на надежность, предусматривающих прекращение испытаний по истечении некоторого срока. Или при анализе данных о технических изделиях, потребовавших гарантийного ремонта.
Пример 3. Пусть, например, срок службы электрической лампочки – случайная величина с функцией распределения 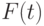
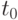
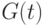
Функция 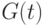
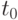
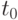
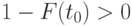
Характеристики случайных величин. В вероятностно-статистических методах принятия решений используется ряд характеристик случайных величин, выражающихся через функции распределения и плотности вероятностей.
При описании дифференциации доходов, при нахождении доверительных границ для параметров распределений случайных величин и во многих иных случаях используется такое понятие, как «квантиль порядка 
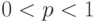
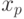




рис.
2.2). Может случиться, что это условие выполняется для всех значений 


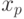

рис.
2.2), причем
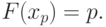 |
( 2) |
Рис.
2.2.
Пример 4. Найдем квантиль 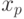


При 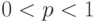
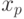
т.е. 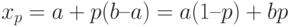



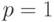
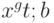
Для дискретных распределений, как правило, не существует 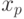
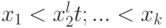
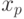


Для перечисленных 

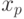
для всех 

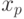
![(x_m; x_m+1]](https://intuit.ru/sites/default/files/tex_cache/fbd0f166d182a5d5000c4216d283d6d5.png)



то 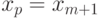
Рассмотренное свойство дискретных распределений создает значительные трудности при табулировании и использовании подобных распределений, поскольку невозможно точно выдержать типовые численные значения характеристик распределения. В частности, это так для критических значений и уровней значимости непараметрических статистических критериев (см. ниже), поскольку распределения статистик этих критериев дискретны.
Большое значение в статистике имеет квантиль порядка 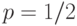



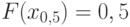
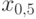
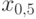
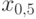
Медиана указывает «центр» распределения. С точки зрения одной из современных концепций – теории устойчивых статистических процедур – медиана является более хорошей характеристикой случайной величины, чем математическое ожидание [
[
1.15
]
,
[
2.16
]
]. При обработке результатов измерений в порядковой шкале (см. лекцию о теории измерений) медианой можно пользоваться, а математическим ожиданием – нет.
Ясный смысл имеет такая характеристика случайной величины, как мода – значение (или значения) случайной величины, соответствующее локальному максимуму плотности вероятности для непрерывной случайной величины или локальному максимуму вероятности для дискретной случайной величины.
Если 

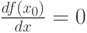
У случайной величины может быть много мод. Так, для равномерного распределения (1) каждая точка 
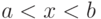
Математическое ожидание для дискретных случайных величин с конечным числом значений рассмотрено в 2.2. Для непрерывной случайной величины 
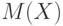
являющемуся аналогом формулы (5) из утверждения 2 
Пример 5. Математическое ожидание для равномерно распределенной случайной величины 
Для рассматриваемых в настоящем параграфе случайных величин верны все те свойства математических ожиданий и дисперсий, которые были рассмотрены ранее в 2.2 для дискретных случайных величин с конечным числом значений. Однако доказательства этих свойств не приводим, поскольку они требуют углубления в математические тонкости, не являющиеся необходимыми для понимания и квалифицированного применения вероятностно-статистических методов принятия решений.
Замечание. В настоящем учебнике сознательно обходятся математические тонкости, связанные, в частности, с понятиями измеримых множеств и измеримых функций, 
[
2.2
]
].
Каждая из трех характеристик – математическое ожидание, медиана, мода – описывает «центр» распределения вероятностей. Понятие «центр» можно определять разными способами – отсюда три разные характеристики. Однако для важного класса распределений – симметричных унимодальных – все три характеристики совпадают.
Плотность распределения 

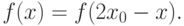 |
( 3) |
Равенство (3) означает, что график функции 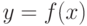
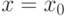
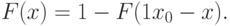 |
( 4) |
Для симметричного распределения с одной модой математическое ожидание, медиана и мода совпадают и равны 
Наиболее важен случай симметрии относительно 0, т.е. 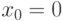
 |
( 5) |
и
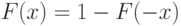 |
( 6) |
соответственно. Приведенные соотношения показывают, что симметричные распределения нет необходимости табулировать при всех 
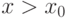
Отметим еще одно свойство симметричных распределений, постоянно используемое в вероятностно-статистических методах принятия решений и других прикладных исследованиях. Для непрерывной функции распределения
где 


Часто используют другую формулировку рассматриваемого утверждения: если
Если 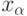
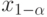

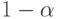
От характеристик положения – математического ожидания, медианы, моды – перейдем к характеристикам разброса случайной величины 
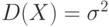


«Различные виды статистических данных»
. Для непрерывных случайных величин
Среднее квадратическое отклонение – это неотрицательное значение квадратного корня из дисперсии:
Коэффициент вариации – это отношение среднего квадратического отклонения к математическому ожиданию:
Коэффициент вариации применяется при 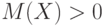
Пример 6. Для равномерно распределенной случайной величины Х найдем дисперсию, среднеквадратическое отклонение и коэффициент вариации. Дисперсия равна:
Замена переменной 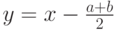
где 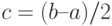
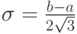

По каждой случайной величине 





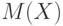


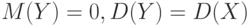
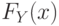



Для плотностей этих случайных величин справедливо равенство
Нормированная случайная величина 


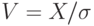


где 

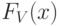
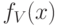

где 


Приведенная случайная величина 
Для приведенной случайной величины
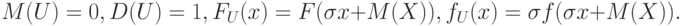 |
( 7) |
Нормированные, центрированные и приведенные случайные величины постоянно используются как в теоретических исследованиях, так и в алгоритмах, программных продуктах, нормативно-технической и инструктивно-методической документации. В частности потому, что равенства 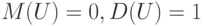
Используются преобразования случайных величин и более общего плана. Так, если 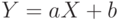


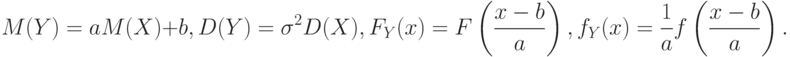 |
(
|
Пример 7. Если 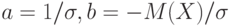

С каждой случайной величиной 

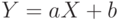
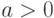


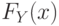

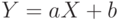
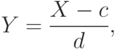 |
( 9) |
где
Число 





Для масштабно-сдвигового семейства (9) распределение 
Применяют и другие преобразования случайных величин. Например, для положительной случайной величины 
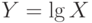
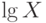

связывает функции распределения 

При обработке данных используют такие характеристики случайной величины 

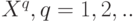

Для непрерывной случайной величины
Моменты порядка 


Так, дисперсия – это центральный момент порядка 2.
Нормальное распределение и центральная предельная теорема. В вероятностно-статистических методах принятия решений часто идет речь о нормальном распределении. Иногда его пытаются использовать для моделирования распределения исходных данных (эти попытки не всегда являются обоснованными – см. ниже). Более существенно, что многие методы обработки данных основаны на том, что расчетные величины имеют распределения, близкие к нормальному.
Пусть 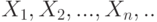
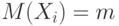
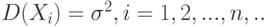
Рассмотрим приведенную случайную величину 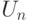

Как следует из формул (7), 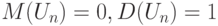
Центральная предельная теорема (для одинаково распределенных слагаемых). Пусть 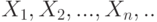
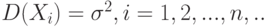

где 
Подробнее о функции 

Центральная предельная теорема (ЦПТ) носит свое название по той причине, что она является центральным, наиболее часто применяющимся математическим результатом теории вероятностей и математической статистики. История ЦПТ занимает около 200 лет – с 1730 г., когда английский математик А.Муавр (1667–1754) опубликовал первый результат, относящийся к ЦПТ (о теореме Муавра-Лапласа см. ниже), по двадцатые – тридцатые годы ХХ в., когда финн Дж. У. Линдеберг, француз Поль Леви (1886–1971), югослав В. Феллер (1906–1970), русский А.Я. Хинчин (1894–1959) и другие ученые получили необходимые и достаточные условия справедливости классической центральной предельной теоремы.
Развитие рассматриваемой тематики на этом отнюдь не прекратилось – изучали случайные величины, не имеющие дисперсии, т.е. те, для которых
(академик Б.В.Гнеденко и др.), ситуацию, когда суммируются случайные величины (точнее, случайные элементы) более сложной природы, чем числа (академики Ю.В.Прохоров, А.А.Боровков и их соратники), и т.д.
Функция распределения 
где 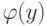
Здесь 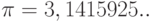

При обработке результатов наблюдений функцию нормального распределения не вычисляют по приведенным формулам, а находят с помощью специальных таблиц или компьютерных программ. Лучшие на русском языке «Таблицы математической статистики» составлены членами-корреспондентами АН СССР Л.Н. Большевым и Н.В.Смирновым [
[
2.1
]
].
Вид плотности стандартного нормального распределения 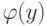
Для иллюстрации приводим небольшие таблицы функции распределения 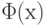
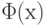
 |
 |
 |
 |
 |
 |
| -5,0 | 0,00000029 | -1,0 | 0,158655 | 2,0 | 0,9772499 |
| -4,0 | 0,00003167 | -0,5 | 0,308538 | 2,5 | 0,99379033 |
| -3,0 | 0,00134990 | 0,0 | 0,500000 | 3,0 | 0,99865010 |
| -2,5 | 0,00620967 | 0,5 | 0,691462 | 4,0 | 0,99996833 |
| -2,0 | 0,0227501 | 1,0 | 0,841345 | 5,0 | 0,99999971 |
| -1,5 | 0,0668072 | 1,5 | 0,9331928 |
 |
Квантиль порядка 
|
 |
Квантиль порядка 
|
| 0,01 | -2,326348 | 0,60 | 0,253347 |
| 0,025 | -1,959964 | 0,70 | 0,524401 |
| 0,05 | -1,644854 | 0,80 | 0,841621 |
| 0,10 | -1,281552 | 0,90 | 1,281552 |
| 0,30 | -0,524401 | 0,95 | 1,644854 |
| 0,40 | -0,253347 | 0,975 | 1,959964 |
| 0,50 | 0,000000 | 0,99 | 2,326348 |
Если случайная величина 

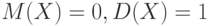
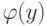


Рассмотрим вычисление квантилей для некоторых функций распределений, представленных в
MS
EXCEL
.
Понятие
Квантиля
основано на определении
Функции распределения
. Поэтому, перед изучением
Квантилей
рекомендуем освежить в памяти понятия из статьи
Функция распределения вероятности
.
Содержание статьи:
- Определение
- Квантили специальных видов
- Квантили стандартного нормального распределения
- Квантили распределения Стьюдента
- Квантили распределения ХИ-квадрат
- Квантили F-распределения
- Квантили распределения Вейбулла
- Квантили экспоненциального распределения
Сначала дадим формальное определение
квантиля,
затем приведем примеры их вычисления в MS EXCEL.
Определение
Пусть случайная величина
X
, имеет
функцию распределения
F
(
x
).
α-квантилем
(
альфа-
квантиль,
x
a
,
квантиль
порядка
α, нижний
α-
квантиль
) называют решение уравнения
x
a
=F
-1
(α), где
α
— вероятность, что случайная величина х примет значение меньшее или равное x
a
, т.е. Р(х<= x
a
)=
α.
Из определения ясно, что нахождение
квантиля
распределения является обратной операцией нахождения вероятности. Т.е. если при вычислении
функции распределения
мы находим вероятность
α,
зная x
a
, то при нахождении
квантиля
мы, наоборот, ищем
x
a
зная
α
.
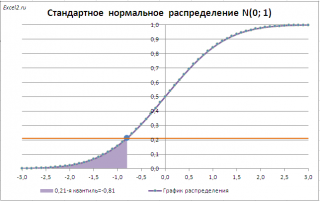
Чтобы пояснить определение, используем график функции
стандартного нормального распределения
(см.
файл примера Лист Определение
):
Примечание
: О построении графиков в MS EXCEL можно прочитать статью
Основные типы диаграмм в MS EXCEL
.
Например, с помощью графика вычислим 0,21-ю
квантиль
, т.е. такое значение случайной величины, что Р(X<=x
0,21
)=0,21.
Для этого найдем точку пересечения горизонтальной линии на уровне вероятности равной 0,21 с
функцией распределения
. Абсцисса этой точки равна -0,81. Соответственно, 0,21-я
квантиль
равна -0,81. Другими словами, вероятность того, что случайная величина, распределенная
стандартному нормальному закону,
примет значение
меньше
-0,81, равна 0,21 (21%).
Примечание
: При вычислении
квантилей
в MS EXCEL используются
обратные функции распределения
:
НОРМ.СТ.ОБР()
,
ЛОГНОРМ.ОБР()
,
ХИ2.ОБР(),
ГАММА.ОБР()
и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Точное значение
квантиля
в нашем случае можно найти с помощью формулы
=НОРМ.СТ.ОБР(0,21)
СОВЕТ
: Процедура вычисления
квантилей
имеет много общего с вычислением
процентилей
выборки
(см. статью
Процентили в MS EXCEL
).
Квантили специальных видов
Часто используются
Квантили
специальных видов:
-
процентили
x
p/100
, p=1, 2, 3, …, 99 -
квартили
x
p/4
, p=1, 2, 3 -
медиана
x
1/2
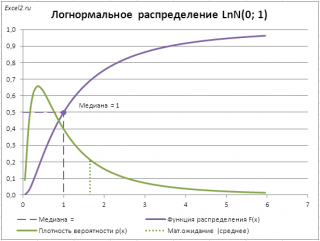
В качестве примера вычислим
медиану (0,5-квантиль)
логнормального распределения
LnN(0;1) (см.
файл примера лист Медиана
).
Это можно сделать с помощью формулы
=ЛОГНОРМ.ОБР(0,5; 0; 1)
Квантили стандартного нормального распределения
Необходимость в вычислении квантилей
стандартного нормального распределения
возникает при
проверке статистических гипотез
и при
построении доверительных интервалов.
Примечание
: Про
проверку статистических гипотез
см. статью
Проверка статистических гипотез в MS EXCEL
. Про
построение доверительных интервалов
см. статью
Доверительные интервалы в MS EXCEL
.
В данных задачах часто используется специальная терминология:
Нижний квантиль уровня
альфа
(
α
percentage point)
;
Верхний квантиль уровня альфа (upper
α
percentage point)
;
Двусторонние квантили уровня
альфа
.
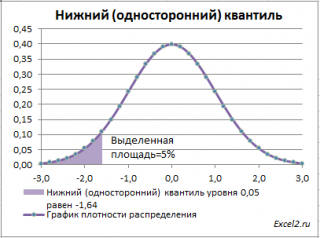
Нижний квантиль уровня альфа
— это обычный
α-квантиль.
Чтобы пояснить название «
нижний» квантиль
, построим график
плотности вероятности
и
функцию вероятности
стандартного нормального
распределения
(см.
файл примера лист Квантили
).
Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение меньше
α-квантиля
. Из определения
квантиля
эта вероятность равна
α
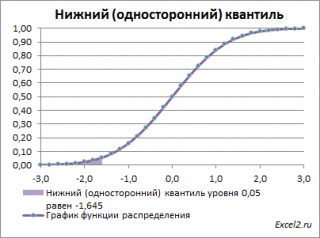
. Из графика
функции распределения
становится понятно, откуда происходит название »
нижний квантиль» —
выделенная область расположена в нижней части графика.
Для
α=0,05,
нижний 0,05-квантиль
стандартного нормального распределения
равен -1,645. Вычисления в MS EXCEL можно сделать по формуле:
=НОРМ.СТ.ОБР(0,05)
Однако, при
проверке гипотез
и построении
доверительных интервалов
чаще используется «верхний»
α-квантиль.
Покажем почему.
Верхним
α
—
квантилем
называют такое значение x
α
, для которого вероятность, того что случайная величина X примет значение
больше или равное
x
α
равна
альфа:
P(X>= x
α
)=
α
. Из определения понятно, что
верхний альфа
—
квантиль
любого распределения равен
нижнему (1-
α)
—
квантилю.
А для распределений, у которых
функция плотности распределения
является четной функцией,
верхний
α
—
квантиль
равен
нижнему
α
—
квантилю
со знаком минус
.
Это следует из свойства четной функции f(-x)=f(x), в силу симметричности ее относительно оси ординат.
Действительно, для
α=0,05,
верхний 0,05-квантиль
стандартного нормального распределения
равен 1,645. Т.к.
функция плотности вероятности
стандартного нормального
распределения
является четной функцией, то вычисления в MS EXCEL
верхнего квантиля
можно сделать по двум формулам:
=НОРМ.СТ.ОБР(1-0,05)
=-НОРМ.СТ.ОБР(0,05)
Почему применяют понятие
верхний
α
—
квантиль?
Только из соображения удобства, т.к. он при
α<0,5
всегда положительный (в случае
стандартного нормального
распределения
). А при проверке гипотез
α
равно
уровню значимости
, который обычно берут равным 0,05, 0,1 или 0,01. В противном случае, в процедуре
проверки гипотез
пришлось бы записывать условие отклонения
нулевой гипотезы
μ>μ
0
как Z
0
>Z
1-
α
, подразумевая, что Z
1-
α
–
обычный
квантиль
порядка
1-
α
(или как Z
0
>-Z
α
). C верхнем квантилем эта запись выглядит проще Z
0
>Z
α
.
Примечание
: Z
0
— значение
тестовой статистики
, вычисленное на основе
выборки
. Подробнее см. статью
Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна)
.
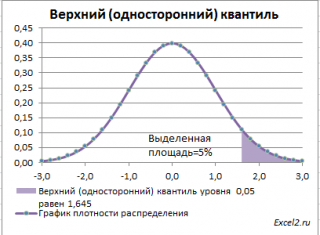
Чтобы пояснить название «
верхний»
квантиль
, построим график
плотности вероятности
и
функцию вероятности
стандартного нормального
распределения
для
α=0,05.
Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение больше
верхнего 0,05-квантиля
, т.е.
больше
значения 1,645. Эта вероятность равна 0,05.
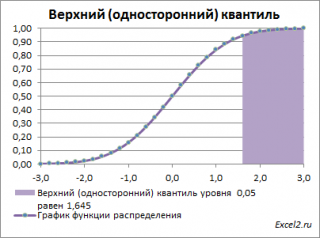
На графике
плотности вероятности
площадь выделенной области равна 0,05 (5%) от общей площади под графиком (равна 1). Из графика
функции распределения
становится понятно, откуда происходит название «верхний»
квантиль
—
выделенная область расположена в верхней части графика. Если Z
0
больше
верхнего квантиля
, т.е. попадает в выделенную область, то
нулевая гипотеза
отклоняется.
Также при
проверке двухсторонних гипотез
и построении соответствующих
доверительных интервалов
иногда используется понятие «двусторонний»
α-квантиль.
В этом случае условие отклонения
нулевой гипотезы
звучит как |Z
0
|>Z
α
/2
, где Z
α
/2
–
верхний
α/2-квантиль
. Чтобы не писать
верхний
α/2-квантиль
, для удобства используют «двусторонний»
α-квантиль.
Почему двусторонний? Как и в предыдущих случаях, построим график
плотности вероятности стандартного нормального распределения
и график
функции распределения
.
Невыделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение
между
нижним квантилем уровня α
/2 и
верхним квантилем
уровня α
/2, т.е. будет между значениями -1,960 и 1,960 при α=0,05. Эта вероятность равна в нашем случае 1-(0,05/2+0,05/2)=0,95. Если Z
0
попадает в одну из выделенных областей, то
нулевая гипотеза
отклоняется.
Вычислить
двусторонний
0,05
—
квантиль
это можно с помощью формул MS EXCEL:
=НОРМ.СТ.ОБР(1-0,05/2)
или
=-НОРМ.СТ.ОБР(0,05/2)
Другими словами,
двусторонние α-квантили
задают интервал, в который рассматриваемая случайная величина попадает с заданной вероятностью α.
Квантили распределения Стьюдента
Аналогичным образом
квантили
вычисляются и для
распределения Стьюдента
. Например, вычислять
верхний
α/2-
квантиль
распределения Стьюдента с
n
-1 степенью свободы
требуется, если проводится
проверка двухсторонней гипотезы
о
среднем значении
распределения при
неизвестной
дисперсии
(
см. эту статью
).
Для
верхних квантилей
распределения Стьюдента
часто используется запись t
α/2,n-1
. Если такая запись встретилась в статье про
проверку гипотез
или про построение
доверительного интервала
, то это именно
верхний квантиль
.
Примечание
:
Функция плотности вероятности распределения Стьюдента
, как и
стандартного нормального распределения
, является четной функцией.
Чтобы вычислить в MS EXCEL
верхний
0,05/2
—
квантиль
для t-распределения с 10 степенями свободы (или тоже самое
двусторонний
0,05-квантиль
), необходимо записать формулу
=СТЬЮДЕНТ.ОБР.2Х(0,05; 10)
или
=СТЬЮДРАСПОБР(0,05; 10)
или
=СТЬЮДЕНТ.ОБР(1-0,05/2; 10)
или
=-СТЬЮДЕНТ.ОБР(0,05/2; 10)
.2X означает 2 хвоста, т.е.
двусторонний квантиль
.
Квантили распределения ХИ-квадрат
Вычислять
квантили
распределения ХИ-квадрат
с
n
-1 степенью свободы
требуется, если проводится
проверка гипотезы
о
дисперсии нормального распределения
(см. статью
Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения
).
При
проверке таких гипотез
также используются
верхние квантили.
Например, при
двухсторонней гипотезе
требуется вычислить 2
верхних
квантиля
распределения
ХИ
2
: χ
2
α/2,n-1
и
χ
2
1-
α/2,n-1
. Почему требуется вычислить два
квантиля
, не один, как при
проверке гипотез о среднем
, где используется
стандартное нормальное распределение
или
t-распределение
?
Дело в том, что в отличие от
стандартного нормального распределения
и
распределения Стьюдента
, плотность распределения
ХИ
2
не является четной (симметричной относительно оси х). У него все
квантили
больше 0, поэтому
верхний альфа-квантиль
не равен
нижнему (1-альфа)-квантилю
или по-другому:
верхний альфа-квантиль
не равен
нижнему альфа-квантилю
со знаком минус.
Чтобы вычислить
верхний
0,05/2
—
квантиль
для
ХИ
2
-распределения
с
числом степеней свободы
10, т.е.
χ
2
0,05/2,n-1
, необходимо в MS EXCEL записать формулу
=ХИ2.ОБР.ПХ(0,05/2; 10)
или
=ХИ2.ОБР(1-0,05/2; 10)
Результат равен 20,48. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике
функции распределения
.
Чтобы вычислить
верхний
(1-0,05/2)-
квантиль
при том же
числе степеней свободы
, т.е.
χ
2
1-0,05/2,n-1
и необходимо записать формулу
=ХИ2.ОБР.ПХ(1-0,05/2; 10)
или
=ХИ2.ОБР(0,05/2; 10)
Результат равен 3,25.
Квантили F-распределения
Вычислять
квантили
распределения Фишера
с
n
1
-1 и
n
2
-1 степенями свободы
требуется, если проводится
проверка гипотезы
о равенстве
дисперсий двух нормальных распределений
(см. статью
Двухвыборочный тест для дисперсии: F-тест в MS EXCEL
).
При
проверке таких гипотез
используются, как правило,
верхние квантили.
Например, при
двухсторонней гипотезе
требуется вычислить 2
верхних
квантиля
F
-распределения:
F
α/2,n1-1,
n
2
-1
и
F
1-α/2,n1-1,
n
2
-1
. Почему требуется вычислить два
квантиля
, не один, как при
проверке гипотез о среднем
? Причина та же, что и для распределения ХИ
2
– плотность
F-распределения
не является четной
.
Эти
квантили
нельзя выразить один через другой как для
стандартного нормального распределения
.
Верхний альфа-квантиль
F
-распределения
не равен
нижнему альфа-квантилю
со знаком минус.
Чтобы вычислить
верхний
0,05/2-квантиль
для
F
-распределения
с
числом степеней свободы
10 и 12, необходимо записать формулу
=F.ОБР.ПХ(0,05/2;10;12) =FРАСПОБР(0,05/2;10;12) =F.ОБР(1-0,05/2;10;12)
Результат равен 3,37. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике
функции распределения
.
Квантили распределения Вейбулла
Иногда
обратная функция распределения
может быть представлена в явном виде с помощью элементарных функций, например как для
распределения Вейбулла
. Напомним, что функция этого распределения задается следующей формулой:
После логарифмирования обеих частей выражения, выразим x через соответствующее ему значение F(x) равное P:
Примечание
: Вместо обозначения
α-квантиль
может использоваться
p
—
квантиль.
Суть от этого не меняется.
Это и есть обратная функция, которая позволяет вычислить
P
—
квантиль
(
p
—
quantile
). Для его вычисления в формуле нужно подставить известное значение вероятности P и вычислить значение х
p
(вероятность того, что случайная величина Х примет значение меньше или равное х
p
равна P).
Квантили экспоненциального распределения
Задача
:
Случайная величина имеет
экспоненциальное распределение
:
Требуется выразить
p
-квантиль
x
p
через параметр распределения λ и заданную вероятность
p
.
Примечание
: Вместо обозначения
α-квантиль
может использоваться
p-квантиль
. Суть от этого не меняется.
Решение
: Вспоминаем, что
p
-квантиль
– это такое значение x
p
случайной величины X, для которого P(X<=x
p
)=
p
. Т.е. вероятность, что случайная величина X примет значение меньше или равное x
p
равна
p
. Запишем это утверждение с помощью формулы:
По сути, мы записали
функцию вероятности экспоненциального распределения
: F(x
p
)=
p
.
Из определения
квантиля
следует, что для его нахождения нам потребуется
обратная функция распределения
.
Проинтегрировав вышеуказанное выражение, получим:
Используя это уравнение, выразим x
p
через λ и вероятность
p
.
Конечно, явно выразить
обратную функцию распределения
можно не для всех
функций распределений
.
Плотность вероятности нормального распределения с отображением квартилей. Площадь под красной кривой одинакова в интервалах (−∞, Q 1 ) , ( Q 1 , Q 2 ) , ( Q 2 , Q 3 ) и ( Q 3 , + ∞) .
В статистике и вероятности , квантили разрежут точки , делящие диапазон от более распределения вероятностей в непрерывные интервалы с равными вероятностями, или разделяющие наблюдения в выборке таким же образом. На один квантиль меньше, чем количество созданных групп. Общие квантили имеют специальные названия, например квартили (четыре группы), децили (десять групп) и процентили (100 групп). Созданные группы называются половинками, третями, четвертями и т. Д., Хотя иногда термины для квантиля используются для созданных групп, а не для точек отсечения.
Q — квантили являются значениямикоторые разбиением на конечное множество значений в д подмножества из (почти) одинакового размера. Существует q — 1 из q -квантилей, по одному для каждого целого числа k, удовлетворяющего 0 < k < q . В некоторых случаях значение квантиля не может быть определено однозначно, как это может быть в случае медианы (2-квантиль) равномерного распределения вероятностей для набора четного размера. Квантили также можно применять к непрерывным распределениям, что дает возможность обобщить статистику рангов на непрерывные переменные (см. Процентильный ранг ). Когда функция распределения из случайной величины известна, Q -quantiles является применением функции квантиля (The обратной функции от функции распределения ) до значений {1 / д , 2 / д , …, ( д — 1) / q }.
Специализированные квантили
Некоторые q- квантили имеют специальные имена:
- Единственный 2-квантиль называется медианой.
- 3-квантили называются тертили или terciles → T
- 4-квантили называются квартилями → Q; разница между верхним и нижним квартилями также называется межквартильным размахом , средний или средний пятьдесят → IQR = Q 3 — Q 1 .
- 5-квантили называются квинтилями → QU.
- 6-квантили называются секстилями → S
- 7-квантили называются септилами.
- 8-квантили называются октилями.
- 10-квантили называются децилями → D
- 12-квантили называются дуодецилями или додецилями.
- 16-квантили называются гексадецилями → H
- 20-квантили называются вентилями , вигинтилями или полу-децилями → V
- 100-квантили называются процентилями → P
- 1000-квантили были названы пермилями или миллилями, но они редки и в значительной степени устарели.
Квантили населения
Как и при вычислении, например, стандартного отклонения , оценка квантиля зависит от того, работаете ли человек со статистической совокупностью или с выборкой, взятой из нее. Для совокупности дискретных значений или для непрерывной плотности населения k -й q -квантиль представляет собой значение данных, в котором кумулятивная функция распределения пересекает k / q . То есть x является k -м q -квантилем для переменной X, если
- Pr [ X < x ] ≤ k / q или, что то же самое, Pr [ X ≥ x ] ≥ 1 — k / q
а также
- Pr [ X ≤ x ] ≥ k / q .
Это эквивалентно тому, что x — наименьшее значение такое, что Pr [ X ≤ x ] ≥ k / q . Для конечной совокупности N равновероятных значений, проиндексированных 1,…, N от наименьшего к наибольшему, k -я q -квантиль этой совокупности может быть эквивалентно вычислена через значение I p = N k / q . Если I p не является целым числом, округлите до следующего целого числа, чтобы получить соответствующий индекс; соответствующее значение данных является k -м q -квантилем. С другой стороны, если I p является целым числом, то любое число от значения данных в этом индексе до значения данных следующего может быть принято в качестве квантиля, и принято (хотя и произвольно) брать среднее из этих двух значения (см. Оценка квантилей по выборке ).
Если вместо использования целых чисел k и q « p- квантиль» основан на действительном числе p с 0 < p <1, тогда p заменяет k / q в приведенных выше формулах. Эта более широкая терминология используется, когда квантили используются для параметризации непрерывных распределений вероятностей . Более того, некоторые программы (включая Microsoft Excel ) рассматривают минимум и максимум как 0-й и 100-й процентили соответственно. Однако эта более широкая терминология выходит за рамки традиционных статистических определений.
Примеры
В следующих двух примерах используется определение квантиля ближайшего ранга с округлением. Для объяснения этого определения см. Процентили .
Равномерное население
Рассмотрим упорядоченную совокупность из 10 значений данных {3, 6, 7, 8, 8, 10, 13, 15, 16, 20}. Что такое 4-квантили («квартили») этого набора данных?
| Квартиль | Расчет | Результат |
|---|---|---|
| Нулевой квартиль | Хотя это не является общепринятым, можно также говорить о нулевом квартиле. Это минимальное значение набора, поэтому нулевой квартиль в этом примере будет равен 3. | 3 |
| Первый квартиль | Ранг первого квартиля составляет 10 × (1/4) = 2,5, что округляется до 3, что означает, что 3 — это ранг в генеральной совокупности (от наименьшего к наибольшему значениям), при котором примерно 1/4 значений меньше чем значение первого квартиля. Третье значение в популяции — 7. | 7 |
| Второй квартиль | Ранг второго квартиля (так же, как и медианы) равен 10 × (2/4) = 5, что является целым числом, в то время как количество значений (10) является четным числом, поэтому среднее значение как для пятого, так и для шестого значения берутся — то есть (8 + 10) / 2 = 9, хотя любое значение от 8 до 10 может быть принято в качестве медианы. | 9 |
| Третий квартиль | Ранг третьего квартиля составляет 10 × (3/4) = 7,5, что округляется до 8. Восьмое значение в генеральной совокупности — 15. | 15 |
| Четвертый квартиль | Хотя это не является общепринятым, можно также говорить о четвертом квартиле. Это максимальное значение набора, поэтому четвертый квартиль в этом примере будет равен 20. Согласно определению квантиля ближайшего ранга ранг четвертого квартиля — это ранг самого большого числа, поэтому ранг четвертого квартиля будет быть 10. | 20 |
Итак, первый, второй и третий 4-квантили («квартили») набора данных {3, 6, 7, 8, 8, 10, 13, 15, 16, 20} — это {7, 9, 15}. Если также требуется, нулевой квартиль равен 3, а четвертый квартиль равен 20.
Нестандартное население
Рассмотрим упорядоченную совокупность из 11 значений данных {3, 6, 7, 8, 8, 9, 10, 13, 15, 16, 20}. Что такое 4-квантили («квартили») этого набора данных?
| Квартиль | Расчет | Результат |
|---|---|---|
| Нулевой квартиль | Хотя это не является общепринятым, можно также говорить о нулевом квартиле. Это минимальное значение набора, поэтому нулевой квартиль в этом примере будет равен 3. | 3 |
| Первый квартиль | Первый квартиль определяется как 11 × (1/4) = 2,75, что округляется до 3, что означает, что 3 — это ранг в генеральной совокупности (от наименьшего к наибольшему значениям), при котором примерно 1/4 значений меньше, чем значение первого квартиля. Третье значение в популяции — 7. | 7 |
| Второй квартиль | Значение второго квартиля (то же, что и медиана) определяется как 11 × (2/4) = 5,5, что округляется до 6. Следовательно, 6 — это ранг в генеральной совокупности (от наименьшего к наибольшему значениям), при котором примерно 2 / 4 значения меньше значения второго квартиля (или медианы). Шестое значение в генеральной совокупности — 9. | 9 |
| Третий квартиль | Значение третьего квартиля для исходного примера выше определяется как 11 × (3/4) = 8,25, что округляется до 9. Девятое значение в генеральной совокупности равно 15. | 15 |
| Четвертый квартиль | Хотя это не является общепринятым, можно также говорить о четвертом квартиле. Это максимальное значение набора, поэтому четвертый квартиль в этом примере будет равен 20. Согласно определению квантиля ближайшего ранга, ранг четвертого квартиля — это ранг самого большого числа, поэтому ранг четвертого квартиля будет быть 11. | 20 |
Таким образом, первый, второй и третий 4-квантили («квартили») набора данных {3, 6, 7, 8, 8, 9, 10, 13, 15, 16, 20} равны {7, 9, 15} . Если также требуется, нулевой квартиль равен 3, а четвертый квартиль — 20.
Отношение к среднему
Для любого распределения вероятностей популяции на конечном числе значений и, как правило, для любого распределения вероятностей со средним значением и дисперсией это тот случай, когда

где Q p — значение p -квантиля для 0 < p <1 (или, что то же самое, k -й q -квантиль для p = k / q ), где μ — среднее арифметическое распределения , а σ — стандартное отклонение . В частности, медиана ( p = k / q = 1/2) никогда не превышает одного стандартного отклонения от среднего.
Оценка квантилей по выборке
Одна из проблем , которая часто возникает оценивание квантиля (очень больших или бесконечные) населений , основанные на конечную выборке объема N .
Асимптотическое распределение p -го квантиля выборки хорошо известно: оно асимптотически нормально вокруг -го квантиля генеральной совокупности с дисперсией, равной
где f ( x p ) — значение плотности распределения в p -м квантиле населения. Однако это распределение основывается на знании распределения населения; что эквивалентно знанию квантилей населения, которые мы пытаемся оценить! Таким образом, современные статистические пакеты полагаются на другой метод — или выбор методов — для оценки квантилей.
Хайндман и Фан составили таксономию из девяти алгоритмов, используемых различными программными пакетами. Все методы вычисляют Q p , оценку p -квантиля ( k -й q -квантиль, где p = k / q ) из выборки размера N путем вычисления действительного индекса h . Когда h является целым числом, h -ое наименьшее из N значений, x h , является оценкой квантиля. В противном случае закругления или интерполяция схема используется для вычисления оценки квантиля от ч , х ⌊ ч ⌋ и х ⌈ ч ⌉ . (Обозначения см. В функциях пола и потолка ).
Первые три являются кусочно-постоянными, резко меняющимися в каждой точке данных, в то время как последние пять используют линейную интерполяцию между точками данных и отличаются только тем, как выбирается индекс h, используемый для выбора точки вдоль кривой кусочно-линейной интерполяции.
Языки программирования Mathematica , Matlab , R и GNU Octave поддерживают все девять примеров методов квантилей. SAS включает пять примеров методов квантилей, SciPy и Maple включают восемь, EViews включает шесть кусочно-линейных функций, Stata включает две, Python включает две, а Microsoft Excel включает две. Mathematica и SciPy поддерживают произвольные параметры для методов, которые допускают использование других нестандартных методов.
Используемые типы оценок и схемы интерполяции включают:
| Тип | час | Q p | Примечания |
|---|---|---|---|
| Р ‑ 1, САС ‑ 3, Клен ‑ 1 | Np + 1/2 | х ⌈ ч — 1 / 2⌉ | Обратная эмпирическая функция распределения . |
| Р ‑ 2, САС ‑ 5, Клен ‑ 2, Стата | Np + 1/2 | ( x ⌈ h — 1 / 2⌉ + x ⌊ h + 1 / 2⌋ ) / 2 | То же, что и Р-1, но с усреднением на несплошностях. |
| Р-3, САС-2 | Np | х ⌊ ч ⌉ | Наблюдение имеет ближайший к Np . Здесь ⌊ ч ⌉ указывает округление до ближайшего целого числа, выбирая даже целое число в случае равенства . |
| R ‑ 4, SAS ‑ 1, SciPy‑ (0,1), Maple ‑ 3 | Np | x ⌊ h ⌋ + ( h — ⌊ h ⌋) ( x ⌈ h ⌉ — x ⌊ h ⌋ ) | Линейная интерполяция эмпирической функции распределения. |
| Р ‑ 5, SciPy‑ (1 / 2,1 / 2), Клен ‑ 4 | Np + 1/2 | Кусочно-линейная функция, где узлы — это значения на полпути между шагами эмпирической функции распределения. | |
| R ‑ 6, Excel, Python, SAS ‑ 4, SciPy‑ (0,0), Maple ‑ 5, Stata ‑ altdef | ( N + 1) п | Линейная интерполяция математических ожиданий для статистики порядка для равномерного распределения на [0,1]. То есть это линейная интерполяция между точками ( p h , x h ) , где p h = h / ( N +1) — вероятность того, что последнее из ( N +1 ) случайно выбранных значений не превысит h — наименьшее из первых N случайно выбранных значений. | |
| R ‑ 7, Excel, Python, SciPy‑ (1,1), Maple ‑ 6, NumPy, Julia | ( N — 1) p + 1 | Линейная интерполяция режимов для порядковой статистики для равномерного распределения на [0,1]. | |
| Р ‑ 8, SciPy‑ (1 / 3,1 / 3), Клен ‑ 7 | ( N + 1/3) p + 1/3 | Линейная интерполяция приблизительных медиан для статистики заказов. | |
| Р ‑ 9, SciPy‑ (3 / 8,3 / 8), Клен ‑ 8 | ( N + 1/4) p + 3/8 | Результирующие оценки квантилей приблизительно несмещены для ожидаемой статистики порядка, если x имеет нормальное распределение. |
Примечания:
- От R ‑ 1 до R ‑ 3 кусочно-постоянные, с разрывами.
- R ‑ 4 и последующие являются кусочно линейными, без разрывов, но отличаются способом вычисления h .
- R ‑ 3 и R ‑ 4 несимметричны в том смысле, что они не дают h = ( N + 1) / 2 при p = 1/2 .
- PERCENTILE.EXC в Excel и «эксклюзивный» метод Python по умолчанию эквивалентны R ‑ 6.
- PERCENTILE и PERCENTILE.INC в Excel и необязательный «включающий» метод Python эквивалентны R ‑ 7. Это метод R по умолчанию.
- Пакеты отличаются тем , как они оценивают квантили за пределы самых низких и самых высоких значений в выборке, т.е. р <1 / N и р > ( N — 1) / N . Возможные варианты включают возврат значения ошибки, вычисление линейной экстраполяции или принятие постоянного значения.
Из методов Хайндман и Фан рекомендуют R-8, но большинство пакетов статистического программного обеспечения выбрали R-6 или R-7 по умолчанию.
Стандартная ошибка из оценки квантильной в общем случае может быть оценена с помощью начальной загрузки . Также можно использовать метод Марица – Джарретта.
Приблизительные квантили из потока
Вычисление приблизительных квантилей из данных, поступающих из потока, может быть выполнено эффективно с использованием сжатых структур данных. Наиболее популярные методы — t-digest и KLL. Эти методы непрерывно считывают поток значений и в любой момент могут быть запрошены о приблизительном значении указанного квантиля.
Оба алгоритма основаны на схожей идее: сжатие потока значений путем суммирования идентичных или похожих значений с помощью веса. Если поток состоит из 100-кратного повторения v1 и 100-кратного v2, нет причин хранить отсортированный список из 200 элементов, достаточно сохранить два элемента и два счетчика, чтобы можно было восстановить квантили. При большем количестве значений эти алгоритмы поддерживают компромисс между количеством сохраненных уникальных значений и точностью получаемых квантилей. Некоторые значения могут быть исключены из потока и вносить вклад в вес ближайшего значения без значительного изменения результатов квантилей. t-digest использует подход, основанный на кластеризации k-средних, для группировки похожих значений, тогда как KLL использует более сложный метод «уплотнения», который позволяет лучше контролировать границы ошибок.
Оба метода принадлежат к семейству набросков данных, которые являются подмножествами алгоритмов потоковой передачи с полезными свойствами: эскизы t-digest или KLL можно комбинировать. Вычисление эскиза для очень большого вектора значений можно разделить на тривиально параллельные процессы, в которых эскизы вычисляются для параллельных разделов вектора и объединяются позже.
Обсуждение
Например, результаты стандартизированных тестов обычно указываются в виде оценок учащихся «в 80-м процентиле». Здесь используется альтернативное значение слова «процентиль» как интервал между (в данном случае) 80-м и 81-м скалярным процентилем. Это отдельное значение процентиля также используется в рецензируемых научных статьях. Используемое значение может быть получено из его контекста.
Если распределение симметрично, то медиана — это среднее значение (пока последнее существует). Но в целом медиана и среднее значение могут отличаться. Например, для случайной переменной, имеющей экспоненциальное распределение , любая конкретная выборка этой случайной величины будет иметь примерно 63% шанс быть меньше среднего. Это связано с тем, что экспоненциальное распределение имеет длинный хвост для положительных значений и нулевое значение для отрицательных чисел.
Квантили — полезные меры, потому что они менее восприимчивы, чем средние, к распределениям с длинным хвостом и выбросам. Эмпирически, если анализируемые данные на самом деле не распределяются в соответствии с предполагаемым распределением, или если есть другие потенциальные источники выбросов, которые очень далеки от среднего, то квантили могут быть более полезной описательной статистикой, чем средние и другие статистические данные, связанные с моментами. .
С этим тесно связан метод наименьших абсолютных отклонений , метод регрессии, который более устойчив к выбросам, чем метод наименьших квадратов, в котором вместо квадрата ошибки используется сумма абсолютных значений наблюдаемых ошибок. Связь состоит в том, что среднее — это единственная оценка распределения, которая минимизирует ожидаемую квадратичную ошибку, в то время как медиана минимизирует ожидаемую абсолютную ошибку. Наименьшие абсолютные отклонения обладают способностью быть относительно нечувствительными к большим отклонениям в отдаленных наблюдениях, хотя доступны даже лучшие методы надежной регрессии .
Квантили случайной величины сохраняются при возрастающих преобразованиях в том смысле, что, например, если m — медиана случайной величины X , то 2 m — медиана 2 X , если только не был сделан произвольный выбор из диапазон значений для определения определенного квантиля. (См. Квантильную оценку выше для примеров такой интерполяции.) Квантили также можно использовать в случаях, когда доступны только порядковые данные.
Смотрите также
- Flashsort — сортировка по первому сегменту по квантилю
- Межквартильный размах
- Описательная статистика
- Квартиль
- Q – Q график
- Квантильная функция
- Квантильная нормализация
- Квантильная регрессия
- Квантование
- Сводные статистические данные
- Интервал допуска (« доверительные интервалы для p- го квантиля»)
использованная литература
дальнейшее чтение
- Серфлинг, Р. Дж. (1980). Аппроксимационные теоремы математической статистики . Джон Вили и сыновья. ISBN 0-471-02403-1.
внешние ссылки
-
СМИ, связанные с Quantiles, на Викискладе?


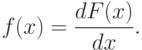
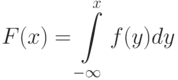
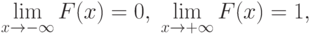
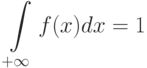
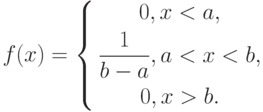


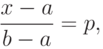
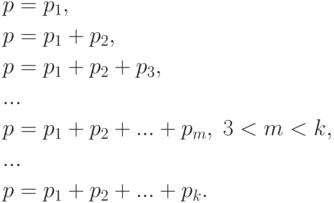
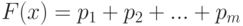
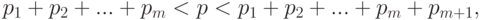
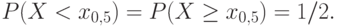
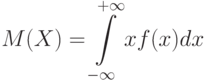
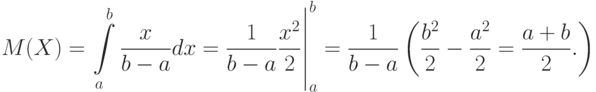
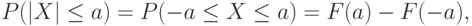



![D(X)=M[(X-M(X))^2]=intlimits_{-infty}^{+infty}(x-M(X))^2 f(x)dx.](https://intuit.ru/sites/default/files/tex_cache/a621dce410482b68ec5a69c3e1fb2517.png)
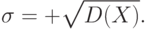
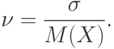
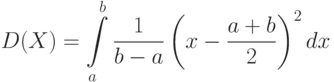
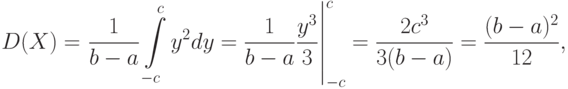
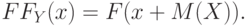
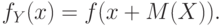
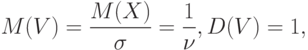

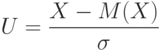
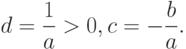

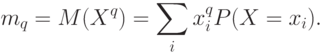
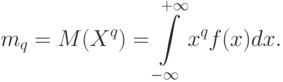
![mu_q=M[(X-M(X))^q],;q=2,3,...](https://intuit.ru/sites/default/files/tex_cache/7b7bfe61aca346f804d0c3147505d6a5.png)