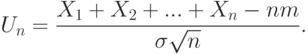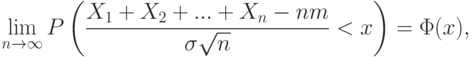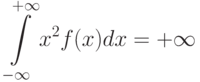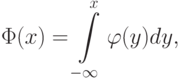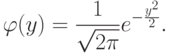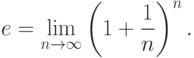Рассмотренные
выборочные параметры: среднее, дисперсия
и коэффициент корреляции выборки
являются приближенными оценками
соответствующих генеральных параметров.
Погрешность этих оценок будет тем
меньше, чем больше объем выборки. Есть
способы, с помощью которых можно оценить
саму погрешность. Для этого переходят
от точечных оценок параметров к оцениванию
доверительных интервалов параметров.
При получении интервальных оценок часто
используют так называемые квантили.
Квантилем,
отвечающий заданному уровню вероятностиР, называют такое значение, при котором функция распределения
принимает значение, равноеР, т.е.
гдеР– заданный уровень вероятности.
Другими словами
квантильесть такое значение
случайной величины,
при котором
Вероятность Р, задаваемая в процентах, дает название
соответствующему квантилю, например,
называется 40%-ым квантилем.
Квантили стандартного
нормального распределения (распределение
с параметрами
)
обозначаются буквой.
Они легко находятся в соответствующих
таблицах. Если,
то подбирая такое,
для которогои находим
.
Если,
то подбираем такое,
для которогои тогда
.
Например, 40 % квантиль будет равен85 %, квантиль
и т.д.
Квантиль общего
нормального распределения
с параметрами
и
выражается через квантиль
:
. (2.5)
Если известны два
квантиля случайной величины
и
,
то
Понятие
квантиля используется не только для
нормального , но и для большинства
встречающихся распределений.
Квантиль
называетсямедианой распределения.
Если распределение случайной величины
симметрично, то.
Например,
распределение случайных ошибок
симметрично. Поэтому для этого
распределения можно использовать как
математическое ожидание, так и медиану.
2.5. Получение интервальных оценок
Все
выборочные параметры являются случайными
величинами, а следовательно и их
отклонения от генеральных параметров,
т.е. погрешности, также будут случайными.
Поэтому оценка этих погрешностей носит
вероятностный характер. Можно лишь
указать вероятность той или иной
погрешности. Чтобы решить подобную
задачу нужно найти вероятность того,
что отклонения выборочного параметра
от исследуемого генерального
не превосходит по абсолютной величине
некоторого заданного числа,
т.е. находятся в пределах отдо
.
Обозначим отклонение через.
Поставленную задачу можно легко решить
если известна функция распределенияили плотность распределения
величины
:
(2.6)
Распределение
иногда удается точно определить по
элементам выборки. В других случаях это
распределение зависит только от объема
выборкии его можно вывести теоретически. Если
бы при этом было известно математическое
ожидание выборочного параметра,
то разность
дает точное значение
генерального параметра. К сожалению
,
как правило, не известно.
Определим генеральный
параметр. Находят по выборке одно
значение
выборочного параметра
и принимают его за приближенное значение
генерального параметра.
Затем, используя выражение (2.6) оценивают
это приближение. Действительно, задаваясь
некоторым положительным числом,
мы можем найти вероятность того, что.
Но так какесть одно из допустимых значений
выборочного параметра,
то вероятность неравенстватакже равна этой вероятности. Отсюда
получаем формулу
которая
позволяет сравнивать найденное значение
выборочного параметра с неизвестным
генеральным параметром.
Неизвестный
генеральный параметр можно представить
в виде
.
Это
неравенство отличается тем, что
неизвестная величина
,
которая является неслучайной величиной,
оценивается случайными границами, т.к.
выборочный параметр является случайным.
Таким
образом, любая статистическая оценка
есть оценка вида
где
некоторые
случайные величины.
Придавая
конкретные значения, мы сможем вычислять
вероятность соответствующей оценки.
В
качестве границ
наиболее удобно брать квантили случайной
величины.
При обработке наблюдений для оценок
генерального параметра берут симметричные
квантили. В этом случае вероятностиРсоответствует оценка
Рассмотрим
как пользоваться оценками на практике.
Для этого дадим следующие определения.
Событиеназываетсяабсолютно достоверным,
если оно появляется при любом осуществлении
комплекса основных факторов. Абсолютную
достоверность нельзя установить никакой
самой длительной проверкой. Ее можно
вывести лишь теоретически , путем
логических умозаключений. Сюда относят
обычно математические истины.
Большинство
же привычных достоверных событий при
рассмотрении не является абсолютно
достоверным. Например, нельзя считать
абсолютно достоверным тот факт, что
подброшенная монета упадет гербом или
числом, т.к. у монеты есть и другие
состояния равновесия — это ребро. Однако,
в данном случае мы можем утверждать,
что монета упадет либо гербом , либо
числом. Такая достоверность называется
практической достоверностью.
Использования
принципа практической достоверности
позволяет не доводить вероятность
оценки до единицы. Принимаемый при этом
уровень вероятности называется
доверительной вероятностью. В
зависимости от конкретных обстоятельств
в качестве доверительной вероятности
берут обычно значения: 0.950.99;
реже 0.90;0.999.
Соответствующие
доверительной вероятности квантильные
границы называются доверительными
границами, а образуемый ими интервал
—доверительным интерваломили
еще называютдоверительной оценкойилиинтервальной оценкой.
Величина
называетсяуровнем значимости.
Уровень значимости соответствует
практически невозможному событию.
Уровень значимости и уровень достоверности
в сумме дают единицу. Обычно значения
уровней значимости берутся в пределах:
0.050.01
и реже 0.1; 0.001.
Соседние файлы в папке model-00ae89b6
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Время на прочтение
8 мин
Количество просмотров 24K
Как понять, что выборка данных принадлежит определенному распределению? Есть 2 метода: аналитический тест Колмогорова-Смирнова (тест Шапиро-Уилка для нормального) и графический метод при помощи графика квантиль-квантиль плот.
Чем так замечателен второй вариант? Q-Q plot позволяет кроме принадлежности:
-
оценить степень отклонения данных от теоретического распределения
-
графически проиллюстрировать такие параметры как расположение данных, масштаб и скошенность. Читаем: медиану, дисперсию и наклон функции плотности распределения.
-
сравнить две выборки между собой
-
делать выводы, не основываясь на таких спорных показателях как p.value.
Фактически, p.value в случае Q-Q Plot будет оценивать человеческий мозг на основе визуального изучения.
Графический метод является мощнейшим инструментом анализа, но как сказано в англоязычной статье википедии про Q-Q Plots, требует серьезных навыков для интерпретации. В данной статье я представляю дорожную карту пути к пониманию квантильных графиков.
С чего начинать? Сперва стоит посмотреть видео на YouTube от StatQuest. Это тот самый автор, который на обложке видеороликов пишет «… Clearly Explained». Если у вас Яндекс-браузер, то вы можете смотреть его видео почти на русском. Есть упомянутая статья в википедии, а также отличный текст на Медиуме. Мне показалось, что это лучшее, что можно найти в поиске по теории, если просто вбивать в строку браузера «Understanding QQ-Plots». Напишите в комментариях вашу любимую статью по квантильным графикам.
Несмотря на замечательные материалы, которые я упомянул, у меня не сложилось полноценного понимания QQ-Plots. Я до сих пор не могу с ходу представить в голове распределение, если мне показать квантильный график. Но в процессе их изучения я смог осознать несколько важных тезисов, с которыми и хочу вас познакомить при помощи визуализаций на Wolfram Mathematica.
В статье я представляю идеальные квантильные графики. Выводы, сделанные на их основе легко переносятся на соответствующие распределения выборочных данных в случае большого их объема (см. Рис. 1). На графиках в статье по горизонтальной оси я буду откладывать только теоретические квантили стандартного нормального распределения.
1. Квантили
Начнем с трех важнейших определений: дискретный квантиль выборки, дискретный квантиль функции плотности распределения и квантиль-функция.
Квантиль дискретной выборки — это одна из точек, делящих упорядоченную последовательность чисел на равные части.
Обращаю ваше внимание, что понятия 0.25 квантиль, 1 квартиль и 25 персентиль обозначают одно и то же, как и 2 квартиль, 0.5 квантиль и 50 персентиль.
Квантиль непрерывного распределения — это одна из точек, делящих функцию плотности распределения на участки, вероятность попадания в которые одинакова, то есть на участки одинаковой площади.
Квантиль-функция — это функция, которая по значению вероятности возвращает такое число (квантиль)
, что вероятность того, что случайная величина примет значение меньше
равняется
.
Можно представлять себе квантиль-функцию непрерывного распределения, как зависимость арифметического уровня воды в вазе, стенками которой является функция плотности вероятности от объема налитой воды. Эта интерпретация хорошо показана в видео одного бразильского инструктора по статистике.
2. Главный квантильный график
Для начала построим базовый Q-Q Plot — теоретических квантилей стандартного нормального распределения от теоретических квантилей стандартного нормального распределения. На следующей картинке (рисунок слева) в виде непрерывной прямой показана зависимость этих теоретических квантилей. Горизонтальные прямые делят распределение оси y на 8 равных по площади промежутков, а вертикальные прямые делят распределение на оси x на 8 равных промежутков и визуализируют появление непрерывной прямой, которую вы наблюдаете.
На рисунке справа я тоже построил квантильный график, но в этом случае по оси y отложил квантили выборки из 200 чисел, случайно выбранных из стандартного нормального распределения. Обращаю ваше внимание, что в случае квантильного графика выборки, за квантиль выбирается каждая точка наших данных, как показано в нижней части на рисунке 1. Далее в статье я буду опускать построение выборочного квантильного графика. Повторюсь, что на больших объемах выборки квантильный график будет полностью повторять теоретическую зависимость.
Как мы видим, в случае одинаковых распределений Q-Q Plot представляет собой прямую линию , причем масштаб нормальных распределений не имеет значения, главное, чтобы у них совпадали средние значения и стандартное отклонение. Этот вывод переносится на случай произвольных распределений.
3. Физический смысл коэффициентов прямой
Что произойдет с прямой, если у распределения на оси y поменять среднее значение (и медиану, соответственно)? Построенная прямая сместится таким образом, чтобы медиане квантилей на оси x соответствовала медиана квантилей на оси y. На рисунке слева визуально ничего не изменилось, только по оси y отложены квантили нормального распределения со средним 5 стандартным отклонением 1.
Таким образом:
-
При построении Q-Q Plot от теоретических квантилей стандартного нормального распределения значение квантильной зависимости в нуле имеет смысл медианы распределения, которое мы строим на оси y.
А что произойдет с прямой, если у распределения на оси y поменять стандартное отклонение?
Ответ представлен на Рисунке 6. Поигравшись с параметрами можно сделать следующий вывод:
-
При построении Q-Q Plot от теоретических квантилей стандартного нормального распределения тангенс наклона прямой имеет смысл стандартного отклонения распределения, которое мы строим на оси y. Если прямая положе, чем y = x (Рис. 4а), то нормальное распределение, построенное на вертикальной оси менее дисперсно, чем распределение, построенное на горизонтальной оси. Если прямая круче, чем y = x (Рис. 4б), то распределение, построенное не вертикальной оси более дисперсно, чем распределение, построенное на горизонтальной оси.
Мы разобрались с основными понятиями и выяснили, что QQ-Plot нормального распределения или выборки из нормального распределения хорошо визуализирует медиану и стандартное отклонение, чем являются коэффициенты прямой.
4. Линия главного тренда на примере скошенных распределений
Все бы хорошо, да кроме нормальных распределений есть еще много других. Если в случае построения околонормального распределения все точки стелятся вдоль прямой линии как на Рис. 4б (коэффициенты которой очень легко интерпретируются), то в случае, например, скошенных распределений точки на прямую ложиться не будут.
При построении Q-Q Plot многие программные пакеты подбирают и изображают некоторую прямую, которая называется линией главного тренда (англ. Reference Line).
SkewNormalDistr(0, 1, 3) и (б) скошенного влево нормального распределения SkewNormalDistr(0, 1, -3)
— от теоретических квантилей стандартного нормального распределения N(0, 1).
Intercept и slope этой контрольной прямой имеют смысл среднего и стандартного отклонения нормального распределения, «наилучшим образом» подходящего к нашим данным. Как написано в замечательном гайде по q-q plots на языке SAS есть 3 способа это сделать:
-
Провести прямую по двум точкам: через 1 и 3 квартили.
-
Провести прямую методом наименьших квадратов.
-
К выборочным данным подобрать среднее и стандартное отклонение генеральной совокупности, используя метод максимального правдоподобия и провести прямую, иллюстрирующую зависимость теоретических квантилей подобранного идеального нормального распределения от теоретических квантилей стандартного нормального (или любого другого, используемого при построении).
Мнение автора по интерпретации 1 и 2 способа.
В первом случае «идеальная прямая» будет соответствовать нормальному распределению со средним, равным среднему значению 1 и 3 квартилей выборки и стандартным отклонением, равным отношению межквартильного размаха распределения на оси y и межквартильного размаха распределения на оси x.
где IQR(x) и IQR(y) — межквартильный размах распределений, построенных на осях y и x соответственно. Для стандартного нормального распределения IQR(x) примерно равен 1.35.
Во втором случае тангенс наклона прямой будет равен произведению корреляции квантилей изображенных распределений — на стандартное отклонение распределения на оси y.
где corr — корреляция, а sd — стандартное отклонение. Это следует из формул для коэффициентов регрессионной прямой, а также из того факта, что для стандартного нормального распределения sd(x) = 1.
Я не нашел подтверждения полученных умозаключений в литературе и не представляю, как использовать эту информацию в реальном анализе.
Разные программные пакеты строят эту линию, используя один из указанных подходов. Если есть большая потребность узнать методы построения, можно заглянуть в документацию. Но если это не принципиально, можно ориентироваться на главную идею: линия главного тренда представляет прямую идеального нормального распределения для наших данных.
Выводы:
-
Если оба конца квантильного графика находятся выше прямой главного тренда, то скорее всего это распределение скошено вправо.
-
Если оба конца квантильного графика находится ниже прямой главного тренда, то скорее всего это распределение скошено влево.
5. Изогнутые Q-Q Plots: Равномерное, Бимодальное и t-распределения.
Следующие 4 графика предназначены для настройки машинного обучения в голове. С помощью них можно научиться отличать равномерное распределение от двугорбого.
Квантиль-квантиль плот для равномерного и бимодальных распределений представляют собой — Образную кривую. В случае равномерного распределения кривая стелется вдоль линии главного тренда, а в случае бимодального пересекает ее. Обращаю также ваше внимание на поведение буквы
в нуле в случае бимодального распределения. Если разрыв между горбами велик, то квантильная зависимость в этом месте становится почти вертикальной.
Стоит прямо здесь научиться распознавать распределение Стьюдента, которое, как известно имеет более толстые хвосты, по сравнению со стандартным нормальном. Внимание на экран.
Здесь мы тоже видим змееобразную кривую, но она представляет собой букву зеркально-отраженную относительно линии главного тренда.
Бонус: Экспоненциальное распределение
На следующем рисунке изображён первый график из англоязычной статьи Википедии про Q-Q Plots. Обращаю еще раз ваше внимание на то, что значение квантильного графика в нуле — это медиана распределения, которое мы строим вдоль оси y. На данном квантильном графике не изображена линия главного тренда. Пунктирная прямая представляет график функции y = x.
Заключение
Если делать summary, то главным является следующее.
-
Если точки на графике Q-Q Plot стелятся вдоль какой-то прямой, то наши данные неплохо соответствуют теоретическим квантилям, отложенным по горизонтальной оси.
Если мы строим Q-Q Plot от теоретических квантилей стандартного нормального распределения, то:
-
Значение получившейся функции в нуле — это медиана нашей выборки. Вообще все квантили нашей выборки соответствуют квантилям распределения на оси x, а не только медиана
-
Тангенс линии тренда соответствует стандартному отклонению нормального распределения, наилучшим образом описывающем нашу выборку. Значение линии главного тренда в нуле соответствует его среднему значению
-
Равномерное распределение — это S-образная кривая, стелющаяся вдоль линии тренда, бимодальное распределение — это S-образная кривая, пересекающая линию тренда. t-распределение — это зеркально отраженная S-образная кривая.
Я буду рад, если моя статья поможет кому-то в понимании QQ-Plots. Поделитесь в комментариях вашим любимым учебным материалом по квантильным графикам или примером реального их использования в анализе данных.
Благодарю Анастасию Котликову за ценное обсуждение способов построения линии главного тренда и за помощь в интерпретации ее коэффициентов.
В примерах в данной статье данные генерятся при каждой загрузке страницы. Если Вы хотите посмотреть пример с другими значениями —
обновите страницу .
Параметры дискретного закона распределения
В статье описано как найти среднее значение и стандартное отклонение. Вы узнаете, что такое квантиль и каких он бывает видов, а также,
как построить доверительный интервал.
Математическое описание
Смотря на закон распределения, мы можем понять, какова вероятность того или иного события,
можем сказать, какова вероятность, что произойдёт группа событий, а в этой статье мы рассмотрим, как наши выводы «на глаз» перевести
в математически обоснованное утверждение.
Крайне важное определение: математическое ожидание — это площадь под графиком распределения. Если мы говорим о дискретном распределении —
это сумма событий умноженных на соответсвующие вероятности, также известно как момент:
(2) E(X) = Σ(pi•Xi) E — от английского слова Expected (ожидание)
Для математического ожидания справедливы равенства:(3) E(X + Y) = E(X) + E(Y)
(4) E(X•Y) = E(X) • E(Y)
Момент степени k:
(5) νk = E(Xk)
Центральный момент степени k:
(6) μk = E[X — E(X)]k
Среднее значение
Среднее значение (μ) закона распределения — это математическое ожидание случайной величины
(случайная величина — это событие), например, сколько в среднем посетителей заходит в магазин в час:
| Кол-во посетителей | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Количество наблюдений | 66 | 123 | 0 | 31 | 68 | 31 | 81 |
| Таблица 1. Количество посетителей в час |
График 1. Количество посетителей в час
Чтобы найти среднее значение всех результатов необходимо сложить всё вместе и разделить на количество результатов:
μ = (66 • 0 + 123 • 1 + 0 • 2 + 31 • 3 + 68 • 4 + 31 • 5 + 81 • 6) / 400 = 1129/400 = 2.82
То же самое мы можем проделать используя формулу 2:
μ = M(X) = Σ(Xi•pi) = 0 • 0.17 + 1 • 0.31 + 2 • 0 + 3 • 0.08 + 4 • 0.17 + 5 • 0.08 + 6 • 0.2 = 2.82 Момент первой степени, формула (5)
Собственно, формула 2 представляет собой среднее арифметическое всех значений
Итог: в среднем, 2.82 посетителя в час
| Количество посетителей | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Вероятность (%) | 16.5 | 30.8 | 0 | 7.8 | 17 | 7.8 | 20.3 |
| Таблица 2. Закон распределения количества посетителей |
Отклонение от среднего
Посмотрите на это распределение, можно предположить, что в среднем случайная величина равна 100±5, поскольку
кажется, что таких значений несравнимо больше чем тех, что меньше 95 или больше 105:
График 2. График функции вероятности. Распределение ≈ 100±5
Среднее значение по формуле (2): μ = 99.95, но как посчитать, насколько далеко все значения находятся от среднего? Вам должна быть
знакома запись 100±5. Что бы получить это значение ±, нам необходимо определить диапазон значений вокруг среднего. И мы могли бы
использовать в качестве меры удалённости «разность» между средним и случайными величинами:
(7) xi — μ
но сумма таких расстояний, а следовательно и любое производное от этого числа, будет равно нулю, поэтому в качестве меры выбрали квадрат разниц
между величинами и средним значением:
(8) (xi — μ)2
Соответственно, среднее значение удалённости — это математическое ожидание квадратов удалённости:
(9) σ2 = E[(X — E(X))2]
Поскольку вероятности любой удалённости равносильны — вероятность каждого из них — 1/n, откуда:
(10) σ2 = E[(X — E(X))2] = ∑[(Xi — μ)2]/n
Она же формула центрального момента (6) второй степени
σ возведена в квадрат, поскольку вместо расстояний мы взяли квадрат расстояний. σ2 называется дисперсией. Корень из дисперсии
называется средним квадратическим отклонением, или среднеквадратическим отклоненим, и его используют в качестве меры разброса:
(11) μ±σ
(12) σ = √(σ2) = √[∑[(Xi — μ)2]/n]
Возвращаясь к примеру, посчитаем среднеквадратическое отклонение для графика 2:
σ = √(∑(x-μ)2/n) = √{[(90 — 99.95)2 + (91 — 99.95)2 + (92 — 99.95)2 + (93 — 99.95)2 + (94 — 99.95)2 + (95 — 99.95)2 + (96 — 99.95)2 + (97 — 99.95)2 + (98 — 99.95)2 + (99 — 99.95)2 + (100 — 99.95)2 + (101 — 99.95)2 + (102 — 99.95)2 + (103 — 99.95)2 + (104 — 99.95)2 + (105 — 99.95)2 + (106 — 99.95)2 + (107 — 99.95)2 + (108 — 99.95)2 + (109 — 99.95)2 + (110 — 99.95)2]/21} = 6.06
Итак, для графика 2 мы получили:
X = 99.95±6.06 ≈ 100±6 , что немного отличается от полученного «на глаз»
Квантиль
График 3. Функция распределения. Медиана
График 4. Функция распределения. 4-квантиль или квартиль
График 5. Функция распределения. 0.34-квантиль
Для анализа функции распределения ввели понятие квантиль. Квантиль — это случайная величина при заданном уровне вероятности, т.е.:
квантиль для уровня вероятности 50% — это случайная величина на графике плотности вероятности, которая имеет вероятность 50%.
На примере с графиком 3, квантиль уровня 0.5 = 99 (ближайшее значение, поскольку распределение дискретно и события со значением 99.3 просто не существует)
- 2-квантиль — медиана
- 4-квантиль — квартиль
- 10-квантиль — дециль
- 100-квантиль — перцентиль
То есть, если мы говорим о дециле (10-квантиле), то это означает, что мы разбили график на 10 частей, что соответствует девяти линяям,
и для каждого дециля нашли значение случайной величины.
Также, используется обозначение x-квантиль, где х — дробное число, например, 0.34-квантиль, такая запись означает значение случайной величины при
p = 0.34.
Для дискретного распределения квантиль необходимо выбирать следующим образом: квантиль гарантирует вероятность, поэтому, если рассчитанный
квантиль не совпадает с одним и значений, необходимо выбирать меньшее значение.
Построение интервалов
Квантили используют для построения доверительных интервалов, которые необходимы для исследования статистики не одного конкретного события (например,
интерес — случайное число = 98), а для группы событий (например, интерес — случайное число между 96 и 99). Доверительный интервал бывает двух видов:
односторонний и двусторонний. Параметр доверительного интервала — уровень доверия. Уровень доверия означает процент событий, которые можно считать успешными.
Двусторонний доверительный интервал
Двусторонний доверительный интервал строится следующим образом: мы задаёмся уровнем значимости, например, 10%, и выделяем область на графике так, что 90% всех
событий попадут в эту область. Поскольку интервал двусторонний, то мы отсекаем по 5% с каждой стороны, т.е. мы ищем 5й перцентиль, 95й перцентиль и значения
случайной величины между ними будут являться доверительной областью, значения за пределами доверительной области называются «критическая область»
График 6. Плотность вероятности
График 7. Функция распределения с 5 и 95 перцентилями. Цветом выделен доверительный интервал с уровнем доверия 0.9
График 8. Функция вероятности и двусторонний доверительный интервал с уровнем доверия 90%
Доверительный интервал
Левосторонний и правосторонний доверительные интервалы строятся аналогично двустороннему: для левостороннего интервала мы находим перцентиль уровня
[‘один’ минус ‘уровень значимости’]. Таким образом, для построения доверительного левостороннего интервала уровня значимости 4% нам необходимо найти четвёртый перцентиль
и всё, что справа — доверительный интервал, всё что слева — критическая область.
График 9. Левосторонний доверительный интервал с уровнем значимости 4%. Заливкой выделен доверительный интервал
График 10. Правосторонний доверительный интервал с уровнем значимости 4%. Заливкой выделен доверительный интервал
Итого
Среднее значение — математическое ожидание случайной величины, находится по формуле:
μ = E(X) = Σ(pi•Xi)
Среднеквадратичное отклонение — математическое ожидание удалённости значений от среднего, находится по формуле:
σ = √(σ2) = √[∑[(Xi — μ)2]/n]
n-квантиль — разделение функции распределения на n равных отрезков, основные типы квантилей:
- 2-квантиль — медиана
- 4-квантиль — квартили
- 10-квантиль — децили
- 100-квантиль — перцентили
Доверительный интервал уровня α — участок функции вероятности, содержащий α всех возможных значений. Двусторонний доверительный
интервал строится отсечением (1-α)/2 справа и слева. Левосторонний и правосторонний доверительные интервалы строятся отсечением
области (1-α) слева и справа соответственно.
Построить ряд распределения
Предположим, мы имеем 100 значений и все разные, например: масса тела Сомалийских пиратов.
Такой набор данных обрабатывать неудобно, мы даже не можем представить их на обычном графике.
Поэтому нам необходимо категоризировать имеющиеся данные и для этого мы делаем следующее:
Запишем наши данные в таблицу:
| 120 | 112 | 106 | 117 | 100 | 134 | 112 | 66 | 67 | 120 |
| 127 | 75 | 108 | 130 | 108 | 89 | 112 | 92 | 64 | 137 |
| 113 | 81 | 129 | 65 | 98 | 83 | 102 | 65 | 92 | 72 |
| 133 | 131 | 115 | 128 | 110 | 113 | 113 | 120 | 85 | 77 |
| 130 | 131 | 100 | 142 | 97 | 128 | 105 | 76 | 67 | 108 |
| 81 | 79 | 128 | 92 | 110 | 129 | 110 | 101 | 126 | 65 |
| 131 | 103 | 64 | 116 | 77 | 95 | 76 | 99 | 115 | 117 |
| 81 | 117 | 87 | 106 | 139 | 100 | 66 | 79 | 66 | 106 |
| 90 | 66 | 96 | 66 | 98 | 97 | 72 | 98 | 135 | 98 |
| 126 | 75 | 142 | 72 | 127 | 118 | 104 | 106 | 82 | 132 |
| Таблица 3. Вес сомалийских пиратов |
Данные разобьём на группы, для начала предлагаю разбить на восемь интервалов:
Узнаём максимальное и минимальное значения, вычитаем их друг из друга и делим на количество
интервалов — получили отрезки:
Максимальное значение: 142
Минимальное значение: 64
Разница: 142 — 64 = 78
Длина интервала: 78 / 8 = 9.75
Теперь посчитаем количество пиратов (весов, я имею ввиду) в каждом интервале:
| # | Интервал | Количество элементов |
|---|---|---|
| 1. | 64 — 73.75 | 15 |
| 2. | 73.75 — 83.5 | 13 |
| 3. | 83.5 — 93.25 | 7 |
| 4. | 93.25 — 103 | 14 |
| 5. | 103 — 112.75 | 16 |
| 6. | 112.75 — 122.5 | 13 |
| 7. | 122.5 — 132.25 | 15 |
| 8. | 132.25 — 142 | 5 |
| Таблица 4. Количество элементов в интервалах |
Вуа-ля, наше распределение на графике:
График 11. Ряд распределения массы тела сомалийских пиратов
Бонус
Интервалы лучше брать целыми числами, поэтому, если с выбранным количеством интервалов
размер выходит нецелым, то можно раздвинуть диапазон значений, пример:
Значение интервала равно 9.75, число не является целым, поэтому
отодвигаем верхнюю границу:
Остаток от деления: [(142 — 64) / 8] = 6
Подвинуть на: 2
Новый диапазон: [64;144]
Диапазон можно двигать как вверх, так и вниз, но лучше в обе стороны.
Совет
Принято делить распределение на 7-8 интервалов, но в каждой конкретной ситуации
Вы можете выбрать отличное количество интервалов, впрочем, как и сделать их
различной длины.
Список параметров
Итак, вот список основных параметров дискретного закона распределения:
| Название | Символ | Формула |
|---|---|---|
| Математическое ожидание (среднее) | E(X) | Σ(pi•Xi) |
| Центральный момент (среднеквадратичное отклонение) |
σx | σ = √(σ2) = √[∑[(Xi — μ)2]/n] |
| Длина интервала | R | max(x) — min(x) |
| Мода | mo | max P(x = mo) |
| 1й квантиль | — | F(x) = 0.25 |
| Медиана | me | F(x) = 0.5 |
| Дециль | — | F(x) = 0.1 |
| Таблица 5. Основные параметры дискретного закона распределения |
Шаблон гистограммы в OpenOffice Calc
Файл histogram_mock.ods содержит шаблон
построения гистограммы.
Вам понравилась статья?
/
Просмотров: 16 107
Рассмотрим вычисление квантилей для некоторых функций распределений, представленных в
MS
EXCEL
.
Понятие
Квантиля
основано на определении
Функции распределения
. Поэтому, перед изучением
Квантилей
рекомендуем освежить в памяти понятия из статьи
Функция распределения вероятности
.
Содержание статьи:
- Определение
- Квантили специальных видов
- Квантили стандартного нормального распределения
- Квантили распределения Стьюдента
- Квантили распределения ХИ-квадрат
- Квантили F-распределения
- Квантили распределения Вейбулла
- Квантили экспоненциального распределения
Сначала дадим формальное определение
квантиля,
затем приведем примеры их вычисления в MS EXCEL.
Определение
Пусть случайная величина
X
, имеет
функцию распределения
F
(
x
).
α-квантилем
(
альфа-
квантиль,
x
a
,
квантиль
порядка
α, нижний
α-
квантиль
) называют решение уравнения
x
a
=F
-1
(α), где
α
— вероятность, что случайная величина х примет значение меньшее или равное x
a
, т.е. Р(х<= x
a
)=
α.
Из определения ясно, что нахождение
квантиля
распределения является обратной операцией нахождения вероятности. Т.е. если при вычислении
функции распределения
мы находим вероятность
α,
зная x
a
, то при нахождении
квантиля
мы, наоборот, ищем
x
a
зная
α
.
Чтобы пояснить определение, используем график функции
стандартного нормального распределения
(см.
файл примера Лист Определение
):
Примечание
: О построении графиков в MS EXCEL можно прочитать статью
Основные типы диаграмм в MS EXCEL
.
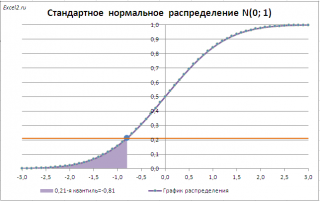
Например, с помощью графика вычислим 0,21-ю
квантиль
, т.е. такое значение случайной величины, что Р(X<=x
0,21
)=0,21.
Для этого найдем точку пересечения горизонтальной линии на уровне вероятности равной 0,21 с
функцией распределения
. Абсцисса этой точки равна -0,81. Соответственно, 0,21-я
квантиль
равна -0,81. Другими словами, вероятность того, что случайная величина, распределенная
стандартному нормальному закону,
примет значение
меньше
-0,81, равна 0,21 (21%).
Примечание
: При вычислении
квантилей
в MS EXCEL используются
обратные функции распределения
:
НОРМ.СТ.ОБР()
,
ЛОГНОРМ.ОБР()
,
ХИ2.ОБР(),
ГАММА.ОБР()
и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Точное значение
квантиля
в нашем случае можно найти с помощью формулы
=НОРМ.СТ.ОБР(0,21)
СОВЕТ
: Процедура вычисления
квантилей
имеет много общего с вычислением
процентилей
выборки
(см. статью
Процентили в MS EXCEL
).
Квантили специальных видов
Часто используются
Квантили
специальных видов:
-
процентили
x
p/100
, p=1, 2, 3, …, 99 -
квартили
x
p/4
, p=1, 2, 3 -
медиана
x
1/2
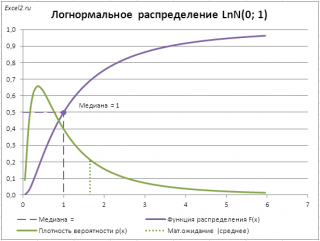
В качестве примера вычислим
медиану (0,5-квантиль)
логнормального распределения
LnN(0;1) (см.
файл примера лист Медиана
).
Это можно сделать с помощью формулы
=ЛОГНОРМ.ОБР(0,5; 0; 1)
Квантили стандартного нормального распределения
Необходимость в вычислении квантилей
стандартного нормального распределения
возникает при
проверке статистических гипотез
и при
построении доверительных интервалов.
Примечание
: Про
проверку статистических гипотез
см. статью
Проверка статистических гипотез в MS EXCEL
. Про
построение доверительных интервалов
см. статью
Доверительные интервалы в MS EXCEL
.
В данных задачах часто используется специальная терминология:
Нижний квантиль уровня
альфа
(
α
percentage point)
;
Верхний квантиль уровня альфа (upper
α
percentage point)
;
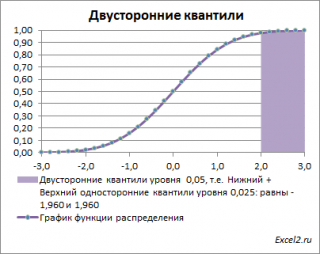
Двусторонние квантили уровня
альфа
.
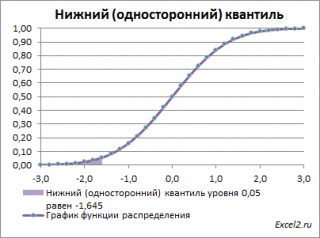
Нижний квантиль уровня альфа
— это обычный
α-квантиль.
Чтобы пояснить название «
нижний» квантиль
, построим график
плотности вероятности
и
функцию вероятности
стандартного нормального
распределения
(см.
файл примера лист Квантили
).
Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение меньше
α-квантиля
. Из определения
квантиля
эта вероятность равна
α
. Из графика
функции распределения
становится понятно, откуда происходит название »
нижний квантиль» —
выделенная область расположена в нижней части графика.
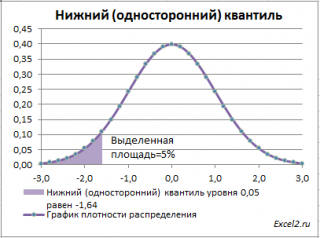
Для
α=0,05,
нижний 0,05-квантиль
стандартного нормального распределения
равен -1,645. Вычисления в MS EXCEL можно сделать по формуле:
=НОРМ.СТ.ОБР(0,05)
Однако, при
проверке гипотез
и построении
доверительных интервалов
чаще используется «верхний»
α-квантиль.
Покажем почему.
Верхним
α
—
квантилем
называют такое значение x
α
, для которого вероятность, того что случайная величина X примет значение
больше или равное
x
α
равна
альфа:
P(X>= x
α
)=
α
. Из определения понятно, что
верхний альфа
—
квантиль
любого распределения равен
нижнему (1-
α)
—
квантилю.
А для распределений, у которых
функция плотности распределения
является четной функцией,
верхний
α
—
квантиль
равен
нижнему
α
—
квантилю
со знаком минус
.
Это следует из свойства четной функции f(-x)=f(x), в силу симметричности ее относительно оси ординат.
Действительно, для
α=0,05,
верхний 0,05-квантиль
стандартного нормального распределения
равен 1,645. Т.к.
функция плотности вероятности
стандартного нормального
распределения
является четной функцией, то вычисления в MS EXCEL
верхнего квантиля
можно сделать по двум формулам:
=НОРМ.СТ.ОБР(1-0,05)
=-НОРМ.СТ.ОБР(0,05)
Почему применяют понятие
верхний
α
—
квантиль?
Только из соображения удобства, т.к. он при
α<0,5
всегда положительный (в случае
стандартного нормального
распределения
). А при проверке гипотез
α
равно
уровню значимости
, который обычно берут равным 0,05, 0,1 или 0,01. В противном случае, в процедуре
проверки гипотез
пришлось бы записывать условие отклонения
нулевой гипотезы
μ>μ
0
как Z
0
>Z
1-
α
, подразумевая, что Z
1-
α
–
обычный
квантиль
порядка
1-
α
(или как Z
0
>-Z
α
). C верхнем квантилем эта запись выглядит проще Z
0
>Z
α
.
Примечание
: Z
0
— значение
тестовой статистики
, вычисленное на основе
выборки
. Подробнее см. статью
Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна)
.
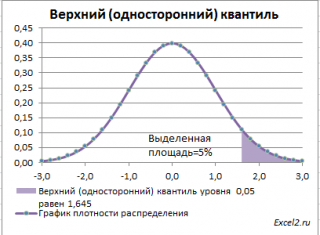
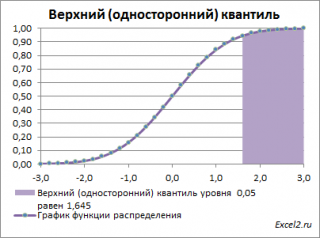
Чтобы пояснить название «
верхний»
квантиль
, построим график
плотности вероятности
и
функцию вероятности
стандартного нормального
распределения
для
α=0,05.
Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение больше
верхнего 0,05-квантиля
, т.е.
больше
значения 1,645. Эта вероятность равна 0,05.
На графике
плотности вероятности
площадь выделенной области равна 0,05 (5%) от общей площади под графиком (равна 1). Из графика
функции распределения
становится понятно, откуда происходит название «верхний»
квантиль
—
выделенная область расположена в верхней части графика. Если Z
0
больше
верхнего квантиля
, т.е. попадает в выделенную область, то
нулевая гипотеза
отклоняется.
Также при
проверке двухсторонних гипотез
и построении соответствующих
доверительных интервалов
иногда используется понятие «двусторонний»
α-квантиль.
В этом случае условие отклонения
нулевой гипотезы
звучит как |Z
0
|>Z
α
/2
, где Z
α
/2
–
верхний
α/2-квантиль
. Чтобы не писать
верхний
α/2-квантиль
, для удобства используют «двусторонний»
α-квантиль.
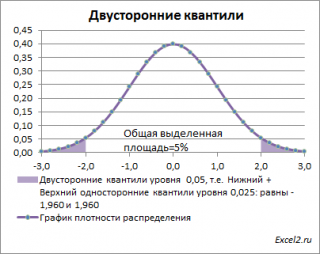
Почему двусторонний? Как и в предыдущих случаях, построим график
плотности вероятности стандартного нормального распределения
и график
функции распределения
.
Невыделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение
между
нижним квантилем уровня α
/2 и
верхним квантилем
уровня α
/2, т.е. будет между значениями -1,960 и 1,960 при α=0,05. Эта вероятность равна в нашем случае 1-(0,05/2+0,05/2)=0,95. Если Z
0
попадает в одну из выделенных областей, то
нулевая гипотеза
отклоняется.
Вычислить
двусторонний
0,05
—
квантиль
это можно с помощью формул MS EXCEL:
=НОРМ.СТ.ОБР(1-0,05/2)
или
=-НОРМ.СТ.ОБР(0,05/2)
Другими словами,
двусторонние α-квантили
задают интервал, в который рассматриваемая случайная величина попадает с заданной вероятностью α.
Квантили распределения Стьюдента
Аналогичным образом
квантили
вычисляются и для
распределения Стьюдента
. Например, вычислять
верхний
α/2-
квантиль
распределения Стьюдента с
n
-1 степенью свободы
требуется, если проводится
проверка двухсторонней гипотезы
о
среднем значении
распределения при
неизвестной
дисперсии
(
см. эту статью
).
Для
верхних квантилей
распределения Стьюдента
часто используется запись t
α/2,n-1
. Если такая запись встретилась в статье про
проверку гипотез
или про построение
доверительного интервала
, то это именно
верхний квантиль
.
Примечание
:
Функция плотности вероятности распределения Стьюдента
, как и
стандартного нормального распределения
, является четной функцией.
Чтобы вычислить в MS EXCEL
верхний
0,05/2
—
квантиль
для t-распределения с 10 степенями свободы (или тоже самое
двусторонний
0,05-квантиль
), необходимо записать формулу
=СТЬЮДЕНТ.ОБР.2Х(0,05; 10)
или
=СТЬЮДРАСПОБР(0,05; 10)
или
=СТЬЮДЕНТ.ОБР(1-0,05/2; 10)
или
=-СТЬЮДЕНТ.ОБР(0,05/2; 10)
.2X означает 2 хвоста, т.е.
двусторонний квантиль
.
Квантили распределения ХИ-квадрат
Вычислять
квантили
распределения ХИ-квадрат
с
n
-1 степенью свободы
требуется, если проводится
проверка гипотезы
о
дисперсии нормального распределения
(см. статью
Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения
).
При
проверке таких гипотез
также используются
верхние квантили.
Например, при
двухсторонней гипотезе
требуется вычислить 2
верхних
квантиля
распределения
ХИ
2
: χ
2
α/2,n-1
и
χ
2
1-
α/2,n-1
. Почему требуется вычислить два
квантиля
, не один, как при
проверке гипотез о среднем
, где используется
стандартное нормальное распределение
или
t-распределение
?
Дело в том, что в отличие от
стандартного нормального распределения
и
распределения Стьюдента
, плотность распределения
ХИ
2
не является четной (симметричной относительно оси х). У него все
квантили
больше 0, поэтому
верхний альфа-квантиль
не равен
нижнему (1-альфа)-квантилю
или по-другому:
верхний альфа-квантиль
не равен
нижнему альфа-квантилю
со знаком минус.
Чтобы вычислить
верхний
0,05/2
—
квантиль
для
ХИ
2
-распределения
с
числом степеней свободы
10, т.е.
χ
2
0,05/2,n-1
, необходимо в MS EXCEL записать формулу
=ХИ2.ОБР.ПХ(0,05/2; 10)
или
=ХИ2.ОБР(1-0,05/2; 10)
Результат равен 20,48. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике
функции распределения
.
Чтобы вычислить
верхний
(1-0,05/2)-
квантиль
при том же
числе степеней свободы
, т.е.
χ
2
1-0,05/2,n-1
и необходимо записать формулу
=ХИ2.ОБР.ПХ(1-0,05/2; 10)
или
=ХИ2.ОБР(0,05/2; 10)
Результат равен 3,25.
Квантили F-распределения
Вычислять
квантили
распределения Фишера
с
n
1
-1 и
n
2
-1 степенями свободы
требуется, если проводится
проверка гипотезы
о равенстве
дисперсий двух нормальных распределений
(см. статью
Двухвыборочный тест для дисперсии: F-тест в MS EXCEL
).
При
проверке таких гипотез
используются, как правило,
верхние квантили.
Например, при
двухсторонней гипотезе
требуется вычислить 2
верхних
квантиля
F
-распределения:
F
α/2,n1-1,
n
2
-1
и
F
1-α/2,n1-1,
n
2
-1
. Почему требуется вычислить два
квантиля
, не один, как при
проверке гипотез о среднем
? Причина та же, что и для распределения ХИ
2
– плотность
F-распределения
не является четной
.
Эти
квантили
нельзя выразить один через другой как для
стандартного нормального распределения
.
Верхний альфа-квантиль
F
-распределения
не равен
нижнему альфа-квантилю
со знаком минус.
Чтобы вычислить
верхний
0,05/2-квантиль
для
F
-распределения
с
числом степеней свободы
10 и 12, необходимо записать формулу
=F.ОБР.ПХ(0,05/2;10;12) =FРАСПОБР(0,05/2;10;12) =F.ОБР(1-0,05/2;10;12)
Результат равен 3,37. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике
функции распределения
.
Квантили распределения Вейбулла
Иногда
обратная функция распределения
может быть представлена в явном виде с помощью элементарных функций, например как для
распределения Вейбулла
. Напомним, что функция этого распределения задается следующей формулой:
После логарифмирования обеих частей выражения, выразим x через соответствующее ему значение F(x) равное P:
Примечание
: Вместо обозначения
α-квантиль
может использоваться
p
—
квантиль.
Суть от этого не меняется.
Это и есть обратная функция, которая позволяет вычислить
P
—
квантиль
(
p
—
quantile
). Для его вычисления в формуле нужно подставить известное значение вероятности P и вычислить значение х
p
(вероятность того, что случайная величина Х примет значение меньше или равное х
p
равна P).
Квантили экспоненциального распределения
Задача
:
Случайная величина имеет
экспоненциальное распределение
:
Требуется выразить
p
-квантиль
x
p
через параметр распределения λ и заданную вероятность
p
.
Примечание
: Вместо обозначения
α-квантиль
может использоваться
p-квантиль
. Суть от этого не меняется.
Решение
: Вспоминаем, что
p
-квантиль
– это такое значение x
p
случайной величины X, для которого P(X<=x
p
)=
p
. Т.е. вероятность, что случайная величина X примет значение меньше или равное x
p
равна
p
. Запишем это утверждение с помощью формулы:
По сути, мы записали
функцию вероятности экспоненциального распределения
: F(x
p
)=
p
.
Из определения
квантиля
следует, что для его нахождения нам потребуется
обратная функция распределения
.
Проинтегрировав вышеуказанное выражение, получим:
Используя это уравнение, выразим x
p
через λ и вероятность
p
.
Конечно, явно выразить
обратную функцию распределения
можно не для всех
функций распределений
.
2.4. Случайные величины и их распределения
Распределения случайных величин и функции распределения. Распределение числовой случайной величины – это функция, которая однозначно определяет вероятность того, что случайная величина принимает заданное значение или принадлежит к некоторому заданному интервалу.
Первое – если случайная величина принимает конечное число значений. Тогда распределение задается функцией 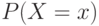


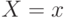
Второе – если случайная величина принимает бесконечно много значений. Это возможно лишь тогда, когда вероятностное пространство, на котором определена случайная величина, состоит из бесконечного числа элементарных событий. Тогда распределение задается набором вероятностей 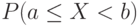


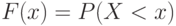


Это соотношение показывает, что как распределение может быть рассчитано по функции распределения, так и наоборот, функция распределения – по распределению.
Используемые в вероятностно-статистических методах принятия решений и других прикладных исследованиях функции распределения бывают либо дискретными, либо непрерывными, либо их комбинациями.
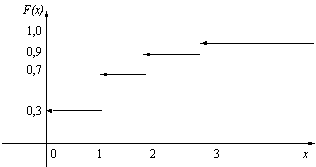
Дискретные функции распределения соответствуют дискретным случайным величинам, принимающим конечное число значений или же значения из множества, элементы которого можно перенумеровать натуральными числами (такие множества в математике называют счетными). Их график имеет вид ступенчатой лестницы (
рис.
2.1).
Пример 1. Число 

рис.
2.1.
Рис.
2.1.
График функции распределения числа дефектных изделий
Непрерывные функции распределения не имеют скачков. Они монотонно возрастают1В некоторых случаях, например, при изучении цен, объемов выпуска или суммарной наработки на отказ в задачах надежности, функции распределения постоянны на некоторых интервалах, в которые значения исследуемых случайных величин не могут попасть. при увеличении аргумента – от 0 при 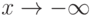
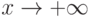
Непрерывные функции распределения, используемые в вероятностно-статистических методах принятия решений, имеют производные. Первая производная 

По плотности вероятности можно определить функцию распределения:
Для любой функции распределения
а потому
Перечисленные свойства функций распределения постоянно используются в вероятностно-статистических методах принятия решений. В частности, из последнего равенства вытекает конкретный вид констант в формулах для плотностей вероятностей, рассматриваемых ниже.
Пример 2. Часто используется следующая функция распределения:
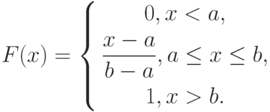 |
( 1) |
где 


(в точках 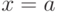


Случайная величина с функцией распределения (1) называется «равномерно распределенной на отрезке ![[a; b]](https://intuit.ru/sites/default/files/tex_cache/65c152d51ed08a1761f5a8cb653eafe5.png)
Смешанные функции распределения встречаются, в частности, тогда, когда наблюдения в какой-то момент прекращаются. Например, при анализе статистических данных, полученных при использовании планов испытаний на надежность, предусматривающих прекращение испытаний по истечении некоторого срока. Или при анализе данных о технических изделиях, потребовавших гарантийного ремонта.
Пример 3. Пусть, например, срок службы электрической лампочки – случайная величина с функцией распределения 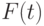
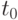
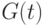
Функция 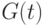
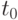
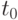
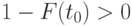
Характеристики случайных величин. В вероятностно-статистических методах принятия решений используется ряд характеристик случайных величин, выражающихся через функции распределения и плотности вероятностей.
При описании дифференциации доходов, при нахождении доверительных границ для параметров распределений случайных величин и во многих иных случаях используется такое понятие, как «квантиль порядка 
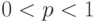
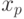




рис.
2.2). Может случиться, что это условие выполняется для всех значений 


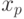

рис.
2.2), причем
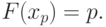 |
( 2) |
Рис.
2.2.
Пример 4. Найдем квантиль 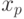


При 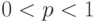
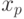
т.е. 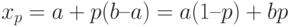



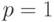
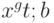
Для дискретных распределений, как правило, не существует 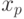
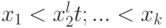
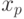


Для перечисленных 

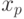
для всех 

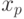
![(x_m; x_m+1]](https://intuit.ru/sites/default/files/tex_cache/fbd0f166d182a5d5000c4216d283d6d5.png)



то 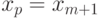
Рассмотренное свойство дискретных распределений создает значительные трудности при табулировании и использовании подобных распределений, поскольку невозможно точно выдержать типовые численные значения характеристик распределения. В частности, это так для критических значений и уровней значимости непараметрических статистических критериев (см. ниже), поскольку распределения статистик этих критериев дискретны.
Большое значение в статистике имеет квантиль порядка 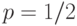



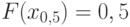
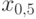
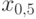
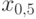
Медиана указывает «центр» распределения. С точки зрения одной из современных концепций – теории устойчивых статистических процедур – медиана является более хорошей характеристикой случайной величины, чем математическое ожидание [
[
1.15
]
,
[
2.16
]
]. При обработке результатов измерений в порядковой шкале (см. лекцию о теории измерений) медианой можно пользоваться, а математическим ожиданием – нет.
Ясный смысл имеет такая характеристика случайной величины, как мода – значение (или значения) случайной величины, соответствующее локальному максимуму плотности вероятности для непрерывной случайной величины или локальному максимуму вероятности для дискретной случайной величины.
Если 

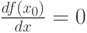
У случайной величины может быть много мод. Так, для равномерного распределения (1) каждая точка 
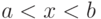
Математическое ожидание для дискретных случайных величин с конечным числом значений рассмотрено в 2.2. Для непрерывной случайной величины 
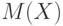
являющемуся аналогом формулы (5) из утверждения 2 
Пример 5. Математическое ожидание для равномерно распределенной случайной величины 
Для рассматриваемых в настоящем параграфе случайных величин верны все те свойства математических ожиданий и дисперсий, которые были рассмотрены ранее в 2.2 для дискретных случайных величин с конечным числом значений. Однако доказательства этих свойств не приводим, поскольку они требуют углубления в математические тонкости, не являющиеся необходимыми для понимания и квалифицированного применения вероятностно-статистических методов принятия решений.
Замечание. В настоящем учебнике сознательно обходятся математические тонкости, связанные, в частности, с понятиями измеримых множеств и измеримых функций, 
[
2.2
]
].
Каждая из трех характеристик – математическое ожидание, медиана, мода – описывает «центр» распределения вероятностей. Понятие «центр» можно определять разными способами – отсюда три разные характеристики. Однако для важного класса распределений – симметричных унимодальных – все три характеристики совпадают.
Плотность распределения 

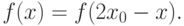 |
( 3) |
Равенство (3) означает, что график функции 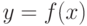
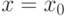
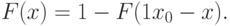 |
( 4) |
Для симметричного распределения с одной модой математическое ожидание, медиана и мода совпадают и равны 
Наиболее важен случай симметрии относительно 0, т.е. 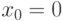
 |
( 5) |
и
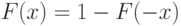 |
( 6) |
соответственно. Приведенные соотношения показывают, что симметричные распределения нет необходимости табулировать при всех 
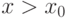
Отметим еще одно свойство симметричных распределений, постоянно используемое в вероятностно-статистических методах принятия решений и других прикладных исследованиях. Для непрерывной функции распределения
где 


Часто используют другую формулировку рассматриваемого утверждения: если
Если 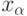
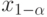

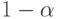
От характеристик положения – математического ожидания, медианы, моды – перейдем к характеристикам разброса случайной величины 
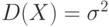


«Различные виды статистических данных»
. Для непрерывных случайных величин
Среднее квадратическое отклонение – это неотрицательное значение квадратного корня из дисперсии:
Коэффициент вариации – это отношение среднего квадратического отклонения к математическому ожиданию:
Коэффициент вариации применяется при 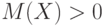
Пример 6. Для равномерно распределенной случайной величины Х найдем дисперсию, среднеквадратическое отклонение и коэффициент вариации. Дисперсия равна:
Замена переменной 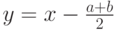
где 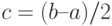
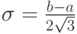

По каждой случайной величине 





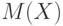


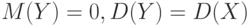
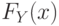



Для плотностей этих случайных величин справедливо равенство
Нормированная случайная величина 


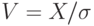


где 

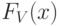
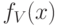

где 


Приведенная случайная величина 
Для приведенной случайной величины
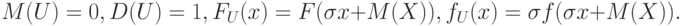 |
( 7) |
Нормированные, центрированные и приведенные случайные величины постоянно используются как в теоретических исследованиях, так и в алгоритмах, программных продуктах, нормативно-технической и инструктивно-методической документации. В частности потому, что равенства 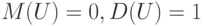
Используются преобразования случайных величин и более общего плана. Так, если 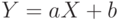


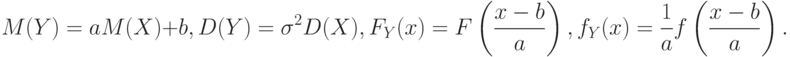 |
(
|
Пример 7. Если 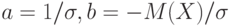

С каждой случайной величиной 

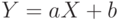
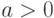


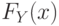

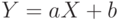
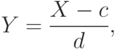 |
( 9) |
где
Число 





Для масштабно-сдвигового семейства (9) распределение 
Применяют и другие преобразования случайных величин. Например, для положительной случайной величины 
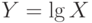
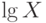

связывает функции распределения 

При обработке данных используют такие характеристики случайной величины 

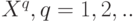

Для непрерывной случайной величины
Моменты порядка 


Так, дисперсия – это центральный момент порядка 2.
Нормальное распределение и центральная предельная теорема. В вероятностно-статистических методах принятия решений часто идет речь о нормальном распределении. Иногда его пытаются использовать для моделирования распределения исходных данных (эти попытки не всегда являются обоснованными – см. ниже). Более существенно, что многие методы обработки данных основаны на том, что расчетные величины имеют распределения, близкие к нормальному.
Пусть 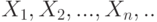
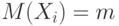
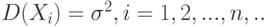
Рассмотрим приведенную случайную величину 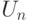

Как следует из формул (7), 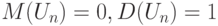
Центральная предельная теорема (для одинаково распределенных слагаемых). Пусть 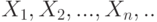
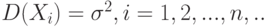

где 
Подробнее о функции 

Центральная предельная теорема (ЦПТ) носит свое название по той причине, что она является центральным, наиболее часто применяющимся математическим результатом теории вероятностей и математической статистики. История ЦПТ занимает около 200 лет – с 1730 г., когда английский математик А.Муавр (1667–1754) опубликовал первый результат, относящийся к ЦПТ (о теореме Муавра-Лапласа см. ниже), по двадцатые – тридцатые годы ХХ в., когда финн Дж. У. Линдеберг, француз Поль Леви (1886–1971), югослав В. Феллер (1906–1970), русский А.Я. Хинчин (1894–1959) и другие ученые получили необходимые и достаточные условия справедливости классической центральной предельной теоремы.
Развитие рассматриваемой тематики на этом отнюдь не прекратилось – изучали случайные величины, не имеющие дисперсии, т.е. те, для которых
(академик Б.В.Гнеденко и др.), ситуацию, когда суммируются случайные величины (точнее, случайные элементы) более сложной природы, чем числа (академики Ю.В.Прохоров, А.А.Боровков и их соратники), и т.д.
Функция распределения 
где 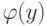
Здесь 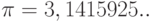

При обработке результатов наблюдений функцию нормального распределения не вычисляют по приведенным формулам, а находят с помощью специальных таблиц или компьютерных программ. Лучшие на русском языке «Таблицы математической статистики» составлены членами-корреспондентами АН СССР Л.Н. Большевым и Н.В.Смирновым [
[
2.1
]
].
Вид плотности стандартного нормального распределения 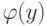
Для иллюстрации приводим небольшие таблицы функции распределения 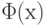
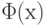
 |
 |
 |
 |
 |
 |
| -5,0 | 0,00000029 | -1,0 | 0,158655 | 2,0 | 0,9772499 |
| -4,0 | 0,00003167 | -0,5 | 0,308538 | 2,5 | 0,99379033 |
| -3,0 | 0,00134990 | 0,0 | 0,500000 | 3,0 | 0,99865010 |
| -2,5 | 0,00620967 | 0,5 | 0,691462 | 4,0 | 0,99996833 |
| -2,0 | 0,0227501 | 1,0 | 0,841345 | 5,0 | 0,99999971 |
| -1,5 | 0,0668072 | 1,5 | 0,9331928 |
 |
Квантиль порядка 
|
 |
Квантиль порядка 
|
| 0,01 | -2,326348 | 0,60 | 0,253347 |
| 0,025 | -1,959964 | 0,70 | 0,524401 |
| 0,05 | -1,644854 | 0,80 | 0,841621 |
| 0,10 | -1,281552 | 0,90 | 1,281552 |
| 0,30 | -0,524401 | 0,95 | 1,644854 |
| 0,40 | -0,253347 | 0,975 | 1,959964 |
| 0,50 | 0,000000 | 0,99 | 2,326348 |
Если случайная величина 

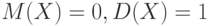
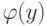













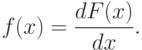
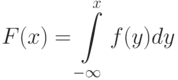
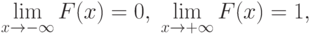
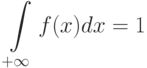
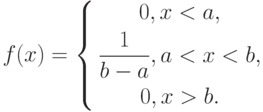


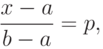
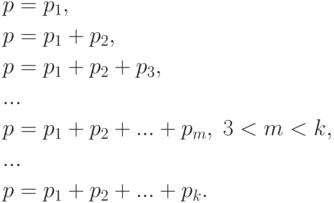
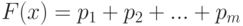
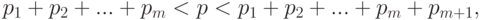
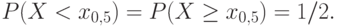
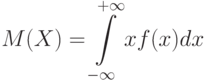
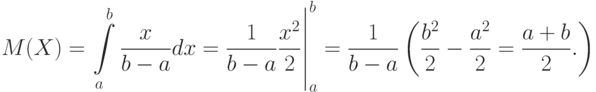
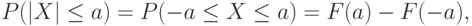



![D(X)=M[(X-M(X))^2]=intlimits_{-infty}^{+infty}(x-M(X))^2 f(x)dx.](https://intuit.ru/sites/default/files/tex_cache/a621dce410482b68ec5a69c3e1fb2517.png)
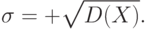
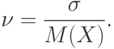
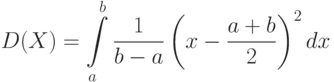
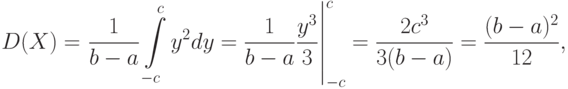
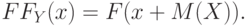
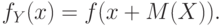
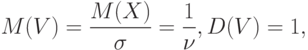

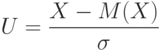
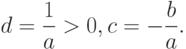

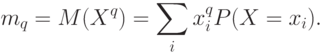
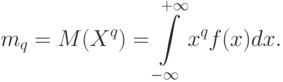
![mu_q=M[(X-M(X))^q],;q=2,3,...](https://intuit.ru/sites/default/files/tex_cache/7b7bfe61aca346f804d0c3147505d6a5.png)