Как найти квантиль статистика - Исправление недочетов и поиск решений вместе с Examum.ru

Квантиль — что это?

Определение 1. Кванти́ль в математической статистике – число x_p такое, что заданная случайная величина X превышает его лишь с фиксированной вероятностью p.

Классное определение, но годится такое определение разве что для википедии, оно не конструктивно, т.е не пригодно для практических целей. Немного терпения, и вам станет понятно данное определение. Более того, вы с легкостью сможете находить квантили любого уровня, а также сможете применять данное понятие для решения задач по статистике.

Как найти квантиль

Попытка №2 — конструктивное определение квантиля:

Определение 1*. Квантилью x_p (p-квантилью, квантилью уровня p) случайной величины X, имеющей функцию распределения F (x), называют решение x_p уравнения F (x) = p.

Следовательно, для того чтобы найти квантиль x_p необходимо найти решение уравнения F (x) = p.

Для наглядности, найдем решение графически:

1. Построим функцию распределения F(x);

2. Построим горизонтальную линию уровня p;

3. Находим точку пересечения данных линий, опускаем перпендикуляр на ось X, получаем квантиль x_p (квантиль уровня p) смотри рисунок 1.

Аналогично для дискретной случайной величины X смотри рисунок 2.

Замечание. Для дискретной случайной величины X функция распределения F(x) имеет ступенчатый вид, функция не монотонна. Поэтому решение уравнения F(x) = p в общем случае не однозначно ( в решение попадают интервалы). В таких случаях, для определенности квантилем назначают средину интервала, как показано на рис.2.

Квантили удобны для сравнения различных законов распределения вероятностей. В некоторых случаях пользуются децилями: x_0,1 , x_0,2 , x_0,3 , …, x_0,9 . Однако наибольшее распространение получили квартили. Квартилями называют квантили порядков 0,25, 0,5 и 0,75. Будем их обозначать соответственно как k₁ , k₂ , k₃ . Квартили k₁ и k₃ называют обычно нижней и верхней квартилями. Вторая квартиль k₂ совпадает с медианой распределения.

Определение 2. Децилями называют квантили уровня 0,1, 0,2, 0,3, …0,9, обозначают соответственно d₁, d₂, d₃,…d₉.

Определение 3. Квартилями называют квантили порядков 0,25, 0,5 и 0,75, обозначают соответственно k₁ , k₂ , k₃ .

Определение 4. Медианой называют квантиль уровня 0,5,

обозначают Me = x_0,5.

Ну вот, пришло время, на конкретном примере показать, как находить квантили.

Пример. Пусть имеется выборка дискретной случайной величины X:

3	0	1	5	1	2	4	5	3	4
2	4	2	0	2	3	1	3	2	1
4	3	0	2	1	0	4	2	3	2

Найти квантили уровня 0,2 и 0,3 ( x_0,2 и x_0,3 )

Решение.

1) Находим функцию распределения дискретной случайной величины:

Вариант	Частота	Частность	F(X)
0	4	0,133333	0,133333
1	5	0,166667	0,3
2	8	0,266667	0,566667
3	6	0,2	0,766667
4	5	0,166667	0,933333
5	2	0,066667	1

2) Строим график функции распределения, проводим линии уровня p = 0,2 и p = 0,3,

3) получаем квантили: x_0,2 = 1, x_0,3 = 1,5, или, можно сказать так, получаем децили d₂=1, d₃=1,5

Источник

В примерах в данной статье данные генерятся при каждой загрузке страницы. Если Вы хотите посмотреть пример с другими значениями —
обновите страницу .

Параметры дискретного закона распределения

В статье описано как найти среднее значение и стандартное отклонение. Вы узнаете, что такое квантиль и каких он бывает видов, а также,
как построить доверительный интервал.

Математическое описание

Смотря на закон распределения, мы можем понять, какова вероятность того или иного события,
можем сказать, какова вероятность, что произойдёт группа событий, а в этой статье мы рассмотрим, как наши выводы «на глаз» перевести
в математически обоснованное утверждение.

Крайне важное определение: математическое ожидание — это площадь под графиком распределения. Если мы говорим о дискретном распределении —
это сумма событий умноженных на соответсвующие вероятности, также известно как момент:

(2) E(X) = Σ(p_i•X_i) E — от английского слова Expected (ожидание)
Для математического ожидания справедливы равенства:

(3) E(X + Y) = E(X) + E(Y)
(4) E(X•Y) = E(X) • E(Y)

Момент степени k:

(5) ν_k = E(X^k)

Центральный момент степени k:

(6) μ_k = E[X — E(X)]^k

Среднее значение

Среднее значение (μ) закона распределения — это математическое ожидание случайной величины
(случайная величина — это событие), например, сколько в среднем посетителей заходит в магазин в час:

Кол-во посетителей	0	1	2	3	4	5	6
Количество наблюдений	172	107	29	13	19	24	36
Таблица 1. Количество посетителей в час

График 1. Количество посетителей в час

Чтобы найти среднее значение всех результатов необходимо сложить всё вместе и разделить на количество результатов:

μ = (172 • 0 + 107 • 1 + 29 • 2 + 13 • 3 + 19 • 4 + 24 • 5 + 36 • 6) / 400 = 616/400 = 1.54

То же самое мы можем проделать используя формулу 2:

μ = M(X) = Σ(X_i•p_i) = 0 • 0.43 + 1 • 0.27 + 2 • 0.07 + 3 • 0.03 + 4 • 0.05 + 5 • 0.06 + 6 • 0.09 = 1.54 Момент первой степени, формула (5)

Собственно, формула 2 представляет собой среднее арифметическое всех значений
Итог: в среднем, 1.54 посетителя в час

Количество посетителей	0	1	2	3	4	5	6
Вероятность (%)	43	26.8	7.3	3.3	4.8	6	9
Таблица 2. Закон распределения количества посетителей

Отклонение от среднего

Посмотрите на это распределение, можно предположить, что в среднем случайная величина равна 100±5, поскольку
кажется, что таких значений несравнимо больше чем тех, что меньше 95 или больше 105:

График 2. График функции вероятности. Распределение ≈ 100±5

Среднее значение по формуле (2): μ = 99.95, но как посчитать, насколько далеко все значения находятся от среднего? Вам должна быть
знакома запись 100±5. Что бы получить это значение ±, нам необходимо определить диапазон значений вокруг среднего. И мы могли бы
использовать в качестве меры удалённости «разность» между средним и случайными величинами:

(7) x_i — μ

но сумма таких расстояний, а следовательно и любое производное от этого числа, будет равно нулю, поэтому в качестве меры выбрали квадрат разниц
между величинами и средним значением:

(8) (x_i — μ)²

Соответственно, среднее значение удалённости — это математическое ожидание квадратов удалённости:

(9) σ² = E[(X — E(X))²]
Поскольку вероятности любой удалённости равносильны — вероятность каждого из них — 1/n, откуда:
(10) σ² = E[(X — E(X))²] = ∑[(X_i — μ)²]/n
Она же формула центрального момента (6) второй степени

σ возведена в квадрат, поскольку вместо расстояний мы взяли квадрат расстояний. σ² называется дисперсией. Корень из дисперсии
называется средним квадратическим отклонением, или среднеквадратическим отклоненим, и его используют в качестве меры разброса:

(11) μ±σ
(12) σ = √(σ²) = √[∑[(X_i — μ)²]/n]

Возвращаясь к примеру, посчитаем среднеквадратическое отклонение для графика 2:

σ = √(∑(x-μ)²/n) = √{[(90 — 99.95)² + (91 — 99.95)² + (92 — 99.95)² + (93 — 99.95)² + (94 — 99.95)² + (95 — 99.95)² + (96 — 99.95)² + (97 — 99.95)² + (98 — 99.95)² + (99 — 99.95)² + (100 — 99.95)² + (101 — 99.95)² + (102 — 99.95)² + (103 — 99.95)² + (104 — 99.95)² + (105 — 99.95)² + (106 — 99.95)² + (107 — 99.95)² + (108 — 99.95)² + (109 — 99.95)² + (110 — 99.95)²]/21} = 6.06

Итак, для графика 2 мы получили:

X = 99.95±6.06 ≈ 100±6 , что немного отличается от полученного «на глаз»

Квантиль

График 3. Функция распределения. Медиана

График 4. Функция распределения. 4-квантиль или квартиль

График 5. Функция распределения. 0.34-квантиль

Для анализа функции распределения ввели понятие квантиль. Квантиль — это случайная величина при заданном уровне вероятности, т.е.:
квантиль для уровня вероятности 50% — это случайная величина на графике плотности вероятности, которая имеет вероятность 50%.
На примере с графиком 3, квантиль уровня 0.5 = 99 (ближайшее значение, поскольку распределение дискретно и события со значением 99.3 просто не существует)

2-квантиль — медиана
4-квантиль — квартиль
10-квантиль — дециль
100-квантиль — перцентиль

То есть, если мы говорим о дециле (10-квантиле), то это означает, что мы разбили график на 10 частей, что соответствует девяти линяям,
и для каждого дециля нашли значение случайной величины.

Также, используется обозначение x-квантиль, где х — дробное число, например, 0.34-квантиль, такая запись означает значение случайной величины при
p = 0.34.

Для дискретного распределения квантиль необходимо выбирать следующим образом: квантиль гарантирует вероятность, поэтому, если рассчитанный
квантиль не совпадает с одним и значений, необходимо выбирать меньшее значение.

Построение интервалов

Квантили используют для построения доверительных интервалов, которые необходимы для исследования статистики не одного конкретного события (например,
интерес — случайное число = 98), а для группы событий (например, интерес — случайное число между 96 и 99). Доверительный интервал бывает двух видов:
односторонний и двусторонний. Параметр доверительного интервала — уровень доверия. Уровень доверия означает процент событий, которые можно считать успешными.

Двусторонний доверительный интервал

Двусторонний доверительный интервал строится следующим образом: мы задаёмся уровнем значимости, например, 10%, и выделяем область на графике так, что 90% всех
событий попадут в эту область. Поскольку интервал двусторонний, то мы отсекаем по 5% с каждой стороны, т.е. мы ищем 5й перцентиль, 95й перцентиль и значения
случайной величины между ними будут являться доверительной областью, значения за пределами доверительной области называются «критическая область»

График 6. Плотность вероятности

График 7. Функция распределения с 5 и 95 перцентилями. Цветом выделен доверительный интервал с уровнем доверия 0.9

График 8. Функция вероятности и двусторонний доверительный интервал с уровнем доверия 90%

Доверительный интервал

Левосторонний и правосторонний доверительные интервалы строятся аналогично двустороннему: для левостороннего интервала мы находим перцентиль уровня
[‘один’ минус ‘уровень значимости’]. Таким образом, для построения доверительного левостороннего интервала уровня значимости 4% нам необходимо найти четвёртый перцентиль
и всё, что справа — доверительный интервал, всё что слева — критическая область.

График 9. Левосторонний доверительный интервал с уровнем значимости 4%. Заливкой выделен доверительный интервал

График 10. Правосторонний доверительный интервал с уровнем значимости 4%. Заливкой выделен доверительный интервал

Итого

Среднее значение — математическое ожидание случайной величины, находится по формуле:

μ = E(X) = Σ(p_i•X_i)

Среднеквадратичное отклонение — математическое ожидание удалённости значений от среднего, находится по формуле:

σ = √(σ²) = √[∑[(X_i — μ)²]/n]

n-квантиль — разделение функции распределения на n равных отрезков, основные типы квантилей:

2-квантиль — медиана
4-квантиль — квартили
10-квантиль — децили
100-квантиль — перцентили

Доверительный интервал уровня α — участок функции вероятности, содержащий α всех возможных значений. Двусторонний доверительный
интервал строится отсечением (1-α)/2 справа и слева. Левосторонний и правосторонний доверительные интервалы строятся отсечением
области (1-α) слева и справа соответственно.

Построить ряд распределения

Предположим, мы имеем 100 значений и все разные, например: масса тела Сомалийских пиратов.
Такой набор данных обрабатывать неудобно, мы даже не можем представить их на обычном графике.
Поэтому нам необходимо категоризировать имеющиеся данные и для этого мы делаем следующее:

Запишем наши данные в таблицу:

111	83	96	93	76	105	66	64	91	87
94	68	96	95	65	111	78	69	75	83
77	82	110	76	98	73	72	87	94	77
74	76	75	94	65	63	83	68	63	101
82	81	94	69	86	96	97	105	102	109
65	89	64	94	77	95	88	65	75	79
104	105	68	94	77	71	95	67	75	94
109	87	110	96	80	64	84	75	65	96
94	77	94	72	69	73	95	64	112	80
89	67	96	64	105	111	73	84	108	67
Таблица 3. Вес сомалийских пиратов

Данные разобьём на группы, для начала предлагаю разбить на десять интервалов:

Узнаём максимальное и минимальное значения, вычитаем их друг из друга и делим на количество
интервалов — получили отрезки:

Максимальное значение: 112
Минимальное значение: 63
Разница: 112 — 63 = 49
Длина интервала: 49 / 10 = 4.9

Теперь посчитаем количество пиратов (весов, я имею ввиду) в каждом интервале:

#	Интервал	Количество элементов
1.	63 — 67.9	16
2.	67.9 — 72.8	9
3.	72.8 — 77.7	17
4.	77.7 — 82.6	7
5.	82.6 — 87.5	9
6.	87.5 — 92.4	4
7.	92.4 — 97.3	21
8.	97.3 — 102.2	3
9.	102.2 — 107.1	5
10.	107.1 — 112	8
Таблица 4. Количество элементов в интервалах

Вуа-ля, наше распределение на графике:

График 11. Ряд распределения массы тела сомалийских пиратов

Бонус

Интервалы лучше брать целыми числами, поэтому, если с выбранным количеством интервалов
размер выходит нецелым, то можно раздвинуть диапазон значений, пример:

Значение интервала равно 4.9, число не является целым, поэтому
отодвигаем верхнюю границу:
Остаток от деления: [(112 — 63) / 10] = 9
Подвинуть на: 1
Новый диапазон: [63;113]

Диапазон можно двигать как вверх, так и вниз, но лучше в обе стороны.

Совет

Принято делить распределение на 7-8 интервалов, но в каждой конкретной ситуации
Вы можете выбрать отличное количество интервалов, впрочем, как и сделать их
различной длины.

Список параметров

Итак, вот список основных параметров дискретного закона распределения:

Название	Символ	Формула
Математическое ожидание (среднее)	E(X)	Σ(p_i•X_i)
Центральный момент (среднеквадратичное отклонение)	σ_x	σ = √(σ²) = √[∑[(X_i — μ)²]/n]
Длина интервала	R	max(x) — min(x)
Мода	m_o	max P(x = m_o)
1й квантиль	—	F(x) = 0.25
Медиана	m_e	F(x) = 0.5
Дециль	—	F(x) = 0.1
Таблица 5. Основные параметры дискретного закона распределения

Шаблон гистограммы в OpenOffice Calc

Файл histogram_mock.ods содержит шаблон
построения гистограммы.

Вам понравилась статья?
/

Источник

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

1 Определение
2 Часто используемые квантили специальных видов
3 Терминология, принятая в математической статистике
4 Применение квантилей в задачах проверки статистических гипотез
5 Применение квантилей в задачах оценивания параметров
6 Выборочные квантили; статистическая оценка квантилей
7 Литература
8 Ссылки

alpha —кванти́ль (или квантиль порядка alpha ) — числовая характеристика закона распределения случайной величины; такое число, что данная случайная величина попадает левее его с вероятностью, не превосходящей alpha .

Определение

alpha —кванти́ль
случайной величины с функцией распределения
— это
любое число удовлетворяющее двум условиям:

Заметим, что данные условия эквивалентны следующим:

$mathbb{P}(xi<x_alpha)lealpha$ и $mathbb{P}(xi>x_alpha)le 1- alpha.$

Если F(x) — непрерывная строго монотонная функция, то
существует единственный квантиль x_alpha
любого порядка который
однозначно определяется из уравнения
и, следовательно,
выражается через функцию, обратную к функции распределения:

$x_alpha = F^{-1}(alpha).$

Кроме указанной ситуации, когда уравнение имеет единственное решение (которое и дает соответствующий квантиль), возможны также две других:

если указанное уравнение не имеет решений, то это означает, что существует единственная точка в которой функция распределения имеет разрыв, которая удовлетворяет данному определению и является квантилем порядка . Для этой точки выполнены соотношения: $mathbb{P}(xi<x_alpha)<alpha$ и $mathbb{P}(xi>x_alpha)le 1- alpha$ (первое неравенство строгое, а второе может быть как строгим, так и обращаться в равенство).
если уравнение имеет более одного решения, то все его решения образуют интервал, на котором функция распределения постоянна. В качестве квантиля порядка может быть взята любая точка этого интервала. Содержательные выводы, в которых участвует квантиль, от этого существенно не изменятся, поскольку вероятность попадания случайной величины в данный интервал равна нулю.

Часто используемые квантили специальных видов

Проценти́ль $x_{p/100}, ; p=1,ldots,99.$

Дециль $x_{p/10}, ; p=1,ldots,9.$

Квинтиль $x_{p/5}, ; p=1,2,3,4.$

Квартиль $x_{p/4}, ; p=1,2,3.$

Медиана $x_{1/2}.$

Терминология, принятая в математической статистике

В задачах математической статистики часто возникает необходимость отделить сверху, снизу или с обеих сторон области, вероятности попадания в которые малы. В связи с этим часто используется следующая терминология.

Нижний (односторонний) квантиль уровня alpha — то же, что и обычный квантиль порядка alpha :

Верхний (односторонний) квантиль уровня alpha — обычный квантиль порядка 1-alpha :

$x_alpha^+ = x_{1-alpha}$ .

Двусторонние квантили уровня alpha — пара (нижний+верхний) односторонних квантилей уровня alpha/2 . Двусторонние квантили задают интервал, в который рассматриваемая случайная величина попадает с заданной вероятностью:

$mathbb{P}left{ x_{alpha/2}^- le xi le x_{alpha/2}^+ right} ge 1-alpha$ .

Применение квантилей в задачах проверки статистических гипотез

Часто применяемая схема решения в задаче проверки статистических гипотез имеет следующий вид. Стараются найти такую статистику , чтобы:

Если статистика с указанными свойствами существует, тогда на ее основе можно получить статистический критерий для данной задачи. Для этого необходимо с помощью соответствующих квантилей выделить область (нижнюю, верхнюю или двустороннюю), попадание в которую было бы маловероятно при нулевой гипотезе (и эта вероятность известна), однако может быть объяснено тем, что на самом деле имеет место альтернатива. Многочисленные критерии принятия решения строятся именно по такой схеме.

Если в дополнение к указанным условиям, распределение будет известно также и при альтернативе H_1 , то это еще лучше, тогда можно вычислить также вероятность ошибки II рода. Но такие ситуации в реальных задачах встречаются крайне редко, поскольку альтернатива обычно гораздо сложнее нулевой гипотезы.

Применение квантилей в задачах оценивания параметров

Рассмотрим задачу построения доверительного интервала для неизвестного числового параметра theta . При этом часто применяется следующая схема. Стараются найти такую случайную величину , которая зависит и от выборки, и от неизвестного параметра (и в силу этого не является статистикой), чтобы ее закон распределения был бы известен и не зависел бы от theta . Тогда можно для заданного уровня alpha найти двусторонние квантили и записать следующее соотношение:

$mathbb{P}left{ z_{alpha/2}^- le Z le z_{alpha/2}^+ right} ge 1-alpha$ .

Далее можно попробовать разрешить неравенство, стоящее под вероятностью, относительно неизвестного параметра, и переписать его в виде:

$mathbb{P}left{ z_{alpha/2}^- le Z(theta) le z_{alpha/2}^+ right}=mathbb{P}left{ theta^- le theta letheta^+ right}$ ,

чтобы величины theta^- и theta^+ зависели бы только от выборки, т.е. являлись бы статистиками. Если это удается сделать, то мы построили доверительный интервал для неизвестного параметра.

Выборочные квантили; статистическая оценка квантилей

Пусть задана простая выборка , и её вариационный ряд есть

$x^{(1)} leq x^{(2)} leq cdots leq x^{(m)}.$

Выборочный -кванти́ль или выборочный квантиль порядка
есть статистика, равная элементу вариационного ряда с номером
(целая часть от ).

Пусть — плотность, — функция распределения случайной величины .
Тогда выборочные квантили порядка

имеют при

асимптотически k-мерное нормальное распределение с математическими ожиданиями, равными (не выборочным) квантилям
$x_{alpha_i},; i=1,ldots,k,$
и ковариациями

$frac{alpha_i(1-alpha_j)}{m fleft(x_{alpha_i}right) fleft(x_{alpha_j}right) },;; ileq j,;; i,j= 1,ldots,k.$

Таким образом, выборочные квантили являются несмещёнными оценками обычных (не выборочных) квантилей.

Асимптотическая нормальность позволяет также записать beta -процентный доверительный интервал для квантиля :

$x^{([malpha+1])}pmfrac{z_{beta/2}}{sqrt{n}} frac{sqrt{alphaleft(1-alpharight)}}{fleft(x_alpharight)}.$

Литература

Вероятность и математическая статистика: Энциклопедия / Под ред. Ю.В.Прохорова. — М.: Большая российская энциклопедия, 2003. — 912 с.

Ссылки

Quantile, Percentile, Decile — статьи в англоязычной Википедии.
Квантиль — статья в русской Википедии.

Источник

Рассмотрим вычисление квантилей для некоторых функций распределений, представленных в

MS

EXCEL

.

Понятие

Квантиля

основано на определении

Функции распределения

. Поэтому, перед изучением

Квантилей

рекомендуем освежить в памяти понятия из статьи

Функция распределения вероятности

Содержание статьи:

Определение
Квантили специальных видов
Квантили стандартного нормального распределения
Квантили распределения Стьюдента
Квантили распределения ХИ-квадрат
Квантили F-распределения
Квантили распределения Вейбулла
Квантили экспоненциального распределения

Сначала дадим формальное определение

квантиля,

затем приведем примеры их вычисления в MS EXCEL.

Определение

Пусть случайная величина

X

, имеет

функцию распределения

F

(

x

).

α-квантилем

(

альфа-

квантиль,

x
_a
,

квантиль

порядка

α, нижний

α-

квантиль

) называют решение уравнения

x
_a
=F
^-1
(α), где

α

— вероятность, что случайная величина х примет значение меньшее или равное x
_a
, т.е. Р(х<= x
_a
)=

α.

Из определения ясно, что нахождение

квантиля

распределения является обратной операцией нахождения вероятности. Т.е. если при вычислении

функции распределения

мы находим вероятность

α,

зная x
_a
, то при нахождении

квантиля

мы, наоборот, ищем

x
_a
зная

α

.

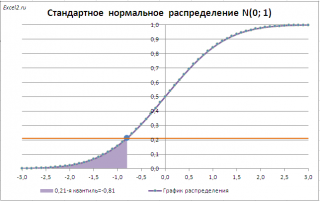
Чтобы пояснить определение, используем график функции

стандартного нормального распределения

(см.

файл примера Лист Определение

):

Примечание

: О построении графиков в MS EXCEL можно прочитать статью

Основные типы диаграмм в MS EXCEL

Например, с помощью графика вычислим 0,21-ю

квантиль

, т.е. такое значение случайной величины, что Р(X<=x
_0,21
)=0,21.

Для этого найдем точку пересечения горизонтальной линии на уровне вероятности равной 0,21 с

функцией распределения

. Абсцисса этой точки равна -0,81. Соответственно, 0,21-я

квантиль

равна -0,81. Другими словами, вероятность того, что случайная величина, распределенная

стандартному нормальному закону,

примет значение

меньше

-0,81, равна 0,21 (21%).

Примечание

: При вычислении

квантилей

в MS EXCEL используются

обратные функции распределения

:

НОРМ.СТ.ОБР()

,

ЛОГНОРМ.ОБР()

,

ХИ2.ОБР(),

ГАММА.ОБР()

и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье

Распределения случайной величины в MS EXCEL

Точное значение

квантиля

в нашем случае можно найти с помощью формулы

=НОРМ.СТ.ОБР(0,21)

СОВЕТ

: Процедура вычисления

квантилей

имеет много общего с вычислением

процентилей

выборки

(см. статью

Процентили в MS EXCEL

Квантили специальных видов

Часто используются

Квантили

специальных видов:

процентили

x
_p/100
, p=1, 2, 3, …, 99
квартили

x
_p/4
, p=1, 2, 3
медиана

x
_1/2

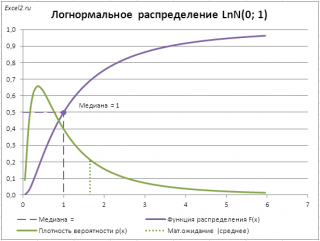
В качестве примера вычислим

медиану (0,5-квантиль)

логнормального распределения

LnN(0;1) (см.

файл примера лист Медиана

).

Это можно сделать с помощью формулы

=ЛОГНОРМ.ОБР(0,5; 0; 1)

Квантили стандартного нормального распределения

Необходимость в вычислении квантилей

стандартного нормального распределения

возникает при

проверке статистических гипотез

и при

построении доверительных интервалов.

Примечание

: Про

проверку статистических гипотез

см. статью

Проверка статистических гипотез в MS EXCEL

. Про

построение доверительных интервалов

см. статью

Доверительные интервалы в MS EXCEL

В данных задачах часто используется специальная терминология:

Нижний квантиль уровня

альфа

(

α

percentage point)

;
Верхний квантиль уровня альфа (upper

α

percentage point)

;
Двусторонние квантили уровня

альфа

.

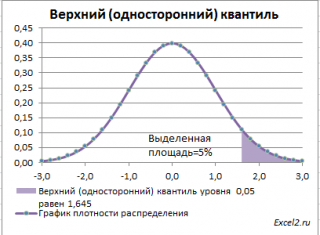
Нижний квантиль уровня альфа

— это обычный

α-квантиль.

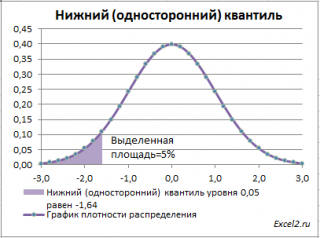
Чтобы пояснить название «

нижний» квантиль

, построим график

плотности вероятности

и

функцию вероятности

стандартного нормального

распределения

(см.

файл примера лист Квантили

).

Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение меньше

α-квантиля

. Из определения

квантиля

эта вероятность равна

α

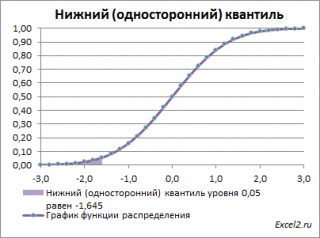
. Из графика

функции распределения

становится понятно, откуда происходит название »

нижний квантиль» —

выделенная область расположена в нижней части графика.

Для

α=0,05,

нижний 0,05-квантиль

стандартного нормального распределения

равен -1,645. Вычисления в MS EXCEL можно сделать по формуле:

=НОРМ.СТ.ОБР(0,05)

Однако, при

проверке гипотез

и построении

доверительных интервалов

чаще используется «верхний»

α-квантиль.

Покажем почему.

Верхним

α

—

квантилем

называют такое значение x
_α
, для которого вероятность, того что случайная величина X примет значение

больше или равное

x
_α
равна

альфа:

P(X>= x
_α
)=

α

. Из определения понятно, что

верхний альфа

—

квантиль

любого распределения равен

нижнему (1-

α)

—

квантилю.

А для распределений, у которых

функция плотности распределения

является четной функцией,

верхний

α

—

квантиль

равен

нижнему

α

—

квантилю

со знаком минус

.

Это следует из свойства четной функции f(-x)=f(x), в силу симметричности ее относительно оси ординат.

Действительно, для

α=0,05,

верхний 0,05-квантиль

стандартного нормального распределения

равен 1,645. Т.к.

функция плотности вероятности

стандартного нормального

распределения

является четной функцией, то вычисления в MS EXCEL

верхнего квантиля

можно сделать по двум формулам:

=НОРМ.СТ.ОБР(1-0,05)

=-НОРМ.СТ.ОБР(0,05)

Почему применяют понятие

верхний

α

—

квантиль?

Только из соображения удобства, т.к. он при

α<0,5

всегда положительный (в случае

стандартного нормального

распределения

). А при проверке гипотез

α

равно

уровню значимости

, который обычно берут равным 0,05, 0,1 или 0,01. В противном случае, в процедуре

проверки гипотез

пришлось бы записывать условие отклонения

нулевой гипотезы

μ>μ
₀
как Z
₀
>Z
_{1-

α}
, подразумевая, что Z
_{1-

α}
–

обычный

квантиль

порядка

1-

α

(или как Z
₀
>-Z
_α
). C верхнем квантилем эта запись выглядит проще Z
₀
>Z
_α
.

Примечание

: Z
₀
— значение

тестовой статистики

, вычисленное на основе

выборки

. Подробнее см. статью

Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна)

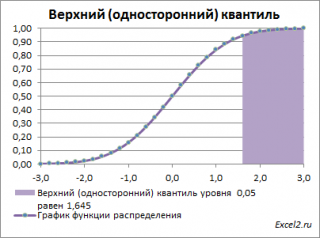
Чтобы пояснить название «

верхний»

квантиль

, построим график

плотности вероятности

и

функцию вероятности

стандартного нормального

распределения

для

α=0,05.

Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение больше

верхнего 0,05-квантиля

, т.е.

больше

значения 1,645. Эта вероятность равна 0,05.

На графике

плотности вероятности

площадь выделенной области равна 0,05 (5%) от общей площади под графиком (равна 1). Из графика

функции распределения

становится понятно, откуда происходит название «верхний»

квантиль

—

выделенная область расположена в верхней части графика. Если Z
₀
больше

верхнего квантиля

, т.е. попадает в выделенную область, то

нулевая гипотеза

отклоняется.

Также при

проверке двухсторонних гипотез

и построении соответствующих

доверительных интервалов

иногда используется понятие «двусторонний»

α-квантиль.

В этом случае условие отклонения

нулевой гипотезы

звучит как |Z
₀
|>Z
_{α

/2}
, где Z
_{α

/2}
–

верхний

α/2-квантиль

. Чтобы не писать

верхний

α/2-квантиль

, для удобства используют «двусторонний»

α-квантиль.

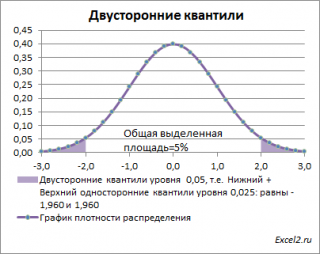
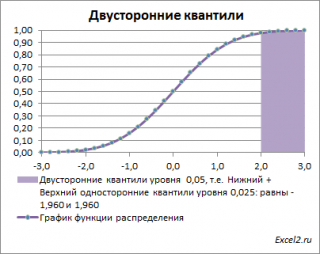
Почему двусторонний? Как и в предыдущих случаях, построим график

плотности вероятности стандартного нормального распределения

и график

функции распределения

.

Невыделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение

между

нижним квантилем уровня α

/2 и

верхним квантилем

уровня α

/2, т.е. будет между значениями -1,960 и 1,960 при α=0,05. Эта вероятность равна в нашем случае 1-(0,05/2+0,05/2)=0,95. Если Z
₀
попадает в одну из выделенных областей, то

нулевая гипотеза

отклоняется.

Вычислить

двусторонний

0,05

—

квантиль

это можно с помощью формул MS EXCEL:

=НОРМ.СТ.ОБР(1-0,05/2)

или

=-НОРМ.СТ.ОБР(0,05/2)

Другими словами,

двусторонние α-квантили

задают интервал, в который рассматриваемая случайная величина попадает с заданной вероятностью α.

Квантили распределения Стьюдента

Аналогичным образом

квантили

вычисляются и для

распределения Стьюдента

. Например, вычислять

верхний

α/2-

квантиль

распределения Стьюдента с

n

-1 степенью свободы

требуется, если проводится

проверка двухсторонней гипотезы

о

среднем значении

распределения при

неизвестной

дисперсии

(

см. эту статью

Для

верхних квантилей

распределения Стьюдента

часто используется запись t
_α/2,n-1
. Если такая запись встретилась в статье про

проверку гипотез

или про построение

доверительного интервала

, то это именно

верхний квантиль

.

Примечание

:

Функция плотности вероятности распределения Стьюдента

, как и

стандартного нормального распределения

, является четной функцией.

Чтобы вычислить в MS EXCEL

верхний

0,05/2

—

квантиль

для t-распределения с 10 степенями свободы (или тоже самое

двусторонний

0,05-квантиль

), необходимо записать формулу

=СТЬЮДЕНТ.ОБР.2Х(0,05; 10)

или

=СТЬЮДРАСПОБР(0,05; 10)

или

=СТЬЮДЕНТ.ОБР(1-0,05/2; 10)

или

=-СТЬЮДЕНТ.ОБР(0,05/2; 10)

.2X означает 2 хвоста, т.е.

двусторонний квантиль

.

Квантили распределения ХИ-квадрат

Вычислять

квантили

распределения ХИ-квадрат

с

n

-1 степенью свободы

требуется, если проводится

проверка гипотезы

о

дисперсии нормального распределения

(см. статью

Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения

При

проверке таких гипотез

также используются

верхние квантили.

Например, при

двухсторонней гипотезе

требуется вычислить 2

верхних

квантиля

распределения

ХИ
²
: χ
²_α/2,n-1
и

χ
²_1-_α/2,n-1
. Почему требуется вычислить два

квантиля

, не один, как при

проверке гипотез о среднем

, где используется

стандартное нормальное распределение

или

t-распределение

?

Дело в том, что в отличие от

стандартного нормального распределения

и

распределения Стьюдента

, плотность распределения

ХИ
²
не является четной (симметричной относительно оси х). У него все

квантили

больше 0, поэтому

верхний альфа-квантиль

не равен

нижнему (1-альфа)-квантилю

или по-другому:

верхний альфа-квантиль

не равен

нижнему альфа-квантилю

со знаком минус.

Чтобы вычислить

верхний

0,05/2

—

квантиль

для

ХИ
²
-распределения

с

числом степеней свободы

10, т.е.

χ
²_0,05/2,n-1
, необходимо в MS EXCEL записать формулу

=ХИ2.ОБР.ПХ(0,05/2; 10)

или

=ХИ2.ОБР(1-0,05/2; 10)

Результат равен 20,48. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике

функции распределения

.

Чтобы вычислить

верхний

(1-0,05/2)-

квантиль

при том же

числе степеней свободы

, т.е.

χ
²_1-0,05/2,n-1
и необходимо записать формулу

=ХИ2.ОБР.ПХ(1-0,05/2; 10)

или

=ХИ2.ОБР(0,05/2; 10)

Результат равен 3,25.

Квантили F-распределения

Вычислять

квантили

распределения Фишера

с

n
₁
-1 и

n
₂
-1 степенями свободы

требуется, если проводится

проверка гипотезы

о равенстве

дисперсий двух нормальных распределений

(см. статью

Двухвыборочный тест для дисперсии: F-тест в MS EXCEL

При

проверке таких гипотез

используются, как правило,

верхние квантили.

Например, при

двухсторонней гипотезе

требуется вычислить 2

верхних

квантиля

F

-распределения:

F
_{α/2,n1-1,

n

2

-1}
и

F
_{1-α/2,n1-1,

n

2

-1}
. Почему требуется вычислить два

квантиля

, не один, как при

проверке гипотез о среднем

? Причина та же, что и для распределения ХИ
²
– плотность

F-распределения

не является четной

.

Эти

квантили

нельзя выразить один через другой как для

стандартного нормального распределения

.

Верхний альфа-квантиль

F

-распределения

не равен

нижнему альфа-квантилю

со знаком минус.

Чтобы вычислить

верхний

0,05/2-квантиль

для

F

-распределения

с

числом степеней свободы

10 и 12, необходимо записать формулу

=F.ОБР.ПХ(0,05/2;10;12) =FРАСПОБР(0,05/2;10;12) =F.ОБР(1-0,05/2;10;12)

Результат равен 3,37. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике

функции распределения

.

Квантили распределения Вейбулла

Иногда

обратная функция распределения

может быть представлена в явном виде с помощью элементарных функций, например как для

распределения Вейбулла

. Напомним, что функция этого распределения задается следующей формулой:

После логарифмирования обеих частей выражения, выразим x через соответствующее ему значение F(x) равное P:

Примечание

: Вместо обозначения

α-квантиль

может использоваться

p

—

квантиль.

Суть от этого не меняется.

Это и есть обратная функция, которая позволяет вычислить

P

—

квантиль

(

p

—

quantile

). Для его вычисления в формуле нужно подставить известное значение вероятности P и вычислить значение х
_p
(вероятность того, что случайная величина Х примет значение меньше или равное х
_p
равна P).

Квантили экспоненциального распределения

Задача

:

Случайная величина имеет

экспоненциальное распределение

:

Требуется выразить

p

-квантиль

x
_p
через параметр распределения λ и заданную вероятность

p

.

Примечание

: Вместо обозначения

α-квантиль

может использоваться

p-квантиль

. Суть от этого не меняется.

Решение

: Вспоминаем, что

p

-квантиль

– это такое значение x
_p
случайной величины X, для которого P(X<=x
_p
)=

p

. Т.е. вероятность, что случайная величина X примет значение меньше или равное x
_p
равна

p

. Запишем это утверждение с помощью формулы:

По сути, мы записали

функцию вероятности экспоненциального распределения

: F(x
_p
)=

p

.

Из определения

квантиля

следует, что для его нахождения нам потребуется

обратная функция распределения

.

Проинтегрировав вышеуказанное выражение, получим:

Используя это уравнение, выразим x
_p
через λ и вероятность

p

.

Конечно, явно выразить

обратную функцию распределения

можно не для всех

функций распределений

.

Источник

Probability density of a normal distribution, with quartiles shown. The area below the red curve is the same in the intervals (−∞,Q₁), (Q₁,Q₂), (Q₂,Q₃), and (Q₃,+∞).

In statistics and probability, quantiles are cut points dividing the range of a probability distribution into continuous intervals with equal probabilities, or dividing the observations in a sample in the same way. There is one fewer quantile than the number of groups created. Common quantiles have special names, such as quartiles (four groups), deciles (ten groups), and percentiles (100 groups). The groups created are termed halves, thirds, quarters, etc., though sometimes the terms for the quantile are used for the groups created, rather than for the cut points.

q—quantiles are values that partition a finite set of values into q subsets of (nearly) equal sizes. There are q − 1 partitions of the q-quantiles, one for each integer k satisfying 0 < k < q. In some cases the value of a quantile may not be uniquely determined, as can be the case for the median (2-quantile) of a uniform probability distribution on a set of even size. Quantiles can also be applied to continuous distributions, providing a way to generalize rank statistics to continuous variables (see percentile rank). When the cumulative distribution function of a random variable is known, the q-quantiles are the application of the quantile function (the inverse function of the cumulative distribution function) to the values {1/q, 2/q, …, (q − 1)/q}.

Specialized quantiles[edit]

Some q-quantiles have special names:^{[citation needed]}

The only 2-quantile is called the median
The 3-quantiles are called tertiles or terciles → T
The 4-quantiles are called quartiles → Q; the difference between upper and lower quartiles is also called the interquartile range, midspread or middle fifty → IQR = Q₃ − Q₁.
The 5-quantiles are called quintiles or pentiles → QU
The 6-quantiles are called sextiles → S
The 7-quantiles are called septiles → SP
The 8-quantiles are called octiles → O
The 10-quantiles are called deciles → D
The 12-quantiles are called duo-deciles or dodeciles → DD
The 16-quantiles are called hexadeciles → H
The 20-quantiles are called ventiles, vigintiles, or demi-deciles → V
The 100-quantiles are called percentiles or centiles → P
The 1000-quantiles have been called permilles or milliles, but these are rare and largely obsolete^[1]

Quantiles of a population[edit]

As in the computation of, for example, standard deviation, the estimation of a quantile depends upon whether one is operating with a statistical population or with a sample drawn from it. For a population, of discrete values or for a continuous population density, the k-th q-quantile is the data value where the cumulative distribution function crosses k/q. That is, x is a k-th q-quantile for a variable X if

Pr[X < x] ≤ k/q or, equivalently, Pr[X ≥ x] ≥ 1 − k/q

and

Pr[X ≤ x] ≥ k/q.

For a finite population of N equally probable values indexed 1, …, N from lowest to highest, the k-th q-quantile of this population can equivalently be computed via the value of I_p = N k/q. If I_p is not an integer, then round up to the next integer to get the appropriate index; the corresponding data value is the k-th q-quantile. On the other hand, if I_p is an integer then any number from the data value at that index to the data value of the next index can be taken as the quantile, and it is conventional (though arbitrary) to take the average of those two values (see Estimating quantiles from a sample).

If, instead of using integers k and q, the «p-quantile» is based on a real number p with 0 < p < 1 then p replaces k/q in the above formulas. This broader terminology is used when quantiles are used to parameterize continuous probability distributions. Moreover, some software programs (including Microsoft Excel) regard the minimum and maximum as the 0th and 100th percentile, respectively. However, this broader terminology is an extension beyond traditional statistics definitions.

Examples[edit]

The following two examples use the Nearest Rank definition of quantile with rounding. For an explanation of this definition, see percentiles.

Even-sized population[edit]

Consider an ordered population of 10 data values [3, 6, 7, 8, 8, 10, 13, 15, 16, 20]. What are the 4-quantiles (the «quartiles») of this dataset?

Quartile	Calculation	Result
Zeroth quartile	Although not universally accepted, one can also speak of the zeroth quartile. This is the minimum value of the set, so the zeroth quartile in this example would be 3.	3
First quartile	The rank of the first quartile is 10×(1/4) = 2.5, which rounds up to 3, meaning that 3 is the rank in the population (from least to greatest values) at which approximately 1/4 of the values are less than the value of the first quartile. The third value in the population is 7.	7
Second quartile	The rank of the second quartile (same as the median) is 10×(2/4) = 5, which is an integer, while the number of values (10) is an even number, so the average of both the fifth and sixth values is taken—that is (8+10)/2 = 9, though any value from 8 through to 10 could be taken to be the median.	9
Third quartile	The rank of the third quartile is 10×(3/4) = 7.5, which rounds up to 8. The eighth value in the population is 15.	15
Fourth quartile	Although not universally accepted, one can also speak of the fourth quartile. This is the maximum value of the set, so the fourth quartile in this example would be 20. Under the Nearest Rank definition of quantile, the rank of the fourth quartile is the rank of the biggest number, so the rank of the fourth quartile would be 10.	20

So the first, second and third 4-quantiles (the «quartiles») of the dataset [3, 6, 7, 8, 8, 10, 13, 15, 16, 20] are [7, 9, 15]. If also required, the zeroth quartile is 3 and the fourth quartile is 20.

Odd-sized population[edit]

Consider an ordered population of 11 data values [3, 6, 7, 8, 8, 9, 10, 13, 15, 16, 20]. What are the 4-quantiles (the «quartiles») of this dataset?

Quartile	Calculation	Result
Zeroth quartile	Although not universally accepted, one can also speak of the zeroth quartile. This is the minimum value of the set, so the zeroth quartile in this example would be 3.	3
First quartile	The first quartile is determined by 11×(1/4) = 2.75, which rounds up to 3, meaning that 3 is the rank in the population (from least to greatest values) at which approximately 1/4 of the values are less than the value of the first quartile. The third value in the population is 7.	7
Second quartile	The second quartile value (same as the median) is determined by 11×(2/4) = 5.5, which rounds up to 6. Therefore, 6 is the rank in the population (from least to greatest values) at which approximately 2/4 of the values are less than the value of the second quartile (or median). The sixth value in the population is 9.	9
Third quartile	The third quartile value for the original example above is determined by 11×(3/4) = 8.25, which rounds up to 9. The ninth value in the population is 15.	15
Fourth quartile	Although not universally accepted, one can also speak of the fourth quartile. This is the maximum value of the set, so the fourth quartile in this example would be 20. Under the Nearest Rank definition of quantile, the rank of the fourth quartile is the rank of the biggest number, so the rank of the fourth quartile would be 11.	20

So the first, second and third 4-quantiles (the «quartiles») of the dataset [3, 6, 7, 8, 8, 9, 10, 13, 15, 16, 20] are [7, 9, 15]. If also required, the zeroth quartile is 3 and the fourth quartile is 20.

Relationship to the mean[edit]

For any population probability distribution on finitely many values, and generally for any probability distribution with a mean and variance, it is the case that

${displaystyle mu -sigma cdot {sqrt {frac {1-p}{p}}}leq Q(p)leq mu +sigma cdot {sqrt {frac {p}{1-p}}},,}$

where Q(p) is the value of the p-quantile for 0 < p < 1 (or equivalently is the k-th q-quantile for p = k/q), where μ is the distribution’s arithmetic mean, and where σ is the distribution’s standard deviation.^[2] In particular, the median (p = k/q = 1/2) is never more than one standard deviation from the mean.

The above formula can be used to bound the value μ + zσ in terms of quantiles.
When z ≥ 0, the value that is z standard deviations above the mean has a lower bound

${displaystyle mu +zsigma geq Qleft({frac {z^{2}}{1+z^{2}}}right),,mathrm {~for~} zgeq 0.}$

For example, the value that is z = 1 standard deviation above the mean is always greater than or equal to Q(p = 0.5), the median, and the value that is z = 2 standard deviations above the mean is always greater than or equal to Q(p = 0.8), the fourth quintile.

When z ≤ 0, there is instead an upper bound

${displaystyle mu +zsigma leq Qleft({frac {1}{1+z^{2}}}right),,mathrm {~for~} zleq 0.}$

For example, the value μ + zσ for z = −3 will never exceed Q(p = 0.1), the first decile.

Estimating quantiles from a sample[edit]

One problem which frequently arises is estimating a quantile of a (very large or infinite) population based on a finite sample of size N.

The asymptotic distribution of the p-th sample quantile is well-known: it is asymptotically normal around the p-th population quantile with variance equal to

${displaystyle {frac {p(1-p)}{Nf(x_{p})^{2}}}}$

where f(x_p) is the value of the distribution density at the p-th population quantile ( ${displaystyle x_{p}=F^{-1}(p)}$ ).^[3]

${displaystyle {text{Sample quantile p}}sim {mathcal {N}}(mu =p,sigma ^{2}={frac {p(1-p)}{Nf(x_{p})^{2}}})}$

However, this distribution relies on knowledge of the population distribution; which is equivalent to knowledge of the population quantiles, which we are trying to estimate! Modern statistical packages thus rely on a different technique — or selection of techniques — to estimate the quantiles.

Hyndman and Fan compiled a taxonomy of nine algorithms^[4] used by various software packages.
All methods compute Q_p, the estimate for the p-quantile (the k-th q-quantile, where p = k/q) from a sample of size N by computing a real valued index h. When h is an integer, the h-th smallest of the N values, x_h, is the quantile estimate. Otherwise a rounding or interpolation scheme is used to compute the quantile estimate from h, x_⌊h⌋, and x_⌈h⌉. (For notation, see floor and ceiling functions).

The first three are piecewise constant, changing abruptly at each data point, while the last six use linear interpolation between data points, and differ only in how the index h used to choose the point along the piecewise linear interpolation curve, is chosen.

Mathematica,^[5] Matlab,^[6] R^[7] and GNU Octave^[8] programming languages support all nine sample quantile methods. SAS includes five sample quantile methods, SciPy^[9] and Maple^[10] both include eight, EViews^[11] includes the six piecewise linear functions, Stata^[12] includes two, Python^[13] includes two, and Microsoft Excel includes two. Mathematica and SciPy support arbitrary parameters for methods which allow for other, non-standard, methods.

The estimate types and interpolation schemes used include:

Type	h	Q_p	Notes
R‑1, SAS‑3, Maple‑1	Np	x_⌈h⌉	Inverse of empirical distribution function.
R‑2, SAS‑5, Maple‑2, Stata	Np + 1/2	(x_{⌈h – 1/2⌉} + x_{⌊h + 1/2⌋}) / 2	The same as R-1, but with averaging at discontinuities.
R‑3, SAS‑2	Np − 1/2	x_⌊h⌉	The observation numbered closest to Np. Here, ⌊h⌉ indicates rounding to the nearest integer, choosing the even integer in the case of a tie.
R‑4, SAS‑1, SciPy‑(0,1), Maple‑3	Np	x_⌊h⌋ + (h − ⌊h⌋) (x_⌈h⌉ − x_⌊h⌋)	Linear interpolation of the inverse of the empirical distribution function.
R‑5, SciPy‑(1/2,1/2), Maple‑4	Np + 1/2	Piecewise linear function where the knots are the values midway through the steps of the empirical distribution function.
R‑6, Excel, Python, SAS‑4, SciPy‑(0,0), Maple‑5, Stata‑altdef	(N + 1)p	Linear interpolation of the expectations for the order statistics for the uniform distribution on [0,1]. That is, it is the linear interpolation between points (p_h, x_h), where p_h = h/(N+1) is the probability that the last of (N+1) randomly drawn values will not exceed the h-th smallest of the first N randomly drawn values.
R‑7, Excel, Python, SciPy‑(1,1), Maple‑6, NumPy, Julia	(N − 1)p + 1	Linear interpolation of the modes for the order statistics for the uniform distribution on [0,1].
R‑8, SciPy‑(1/3,1/3), Maple‑7	(N + 1/3)p + 1/3	Linear interpolation of the approximate medians for order statistics.
R‑9, SciPy‑(3/8,3/8), Maple‑8	(N + 1/4)p + 3/8	The resulting quantile estimates are approximately unbiased for the expected order statistics if x is normally distributed.

Notes:

R‑1 through R‑3 are piecewise constant, with discontinuities.
R‑4 and following are piecewise linear, without discontinuities, but differ in how h is computed.
R‑3 and R‑4 are not symmetric in that they do not give h = (N + 1) / 2 when p = 1/2.
Excel’s PERCENTILE.EXC and Python’s default «exclusive» method are equivalent to R‑6.
Excel’s PERCENTILE and PERCENTILE.INC and Python’s optional «inclusive» method are equivalent to R‑7. This is R’s default method.
Packages differ in how they estimate quantiles beyond the lowest and highest values in the sample, i.e. p < 1/N and p > (N − 1)/N. Choices include returning an error value, computing linear extrapolation, or assuming a constant value.

Of the techniques, Hyndman and Fan recommend R-8, but most statistical software packages have chosen R-6 or R-7 as the default.^[14]

The standard error of a quantile estimate can in general be estimated via the bootstrap. The Maritz–Jarrett method can also be used.^[15]

Approximate quantiles from a stream[edit]

Computing approximate quantiles from data arriving from a stream can be done efficiently using compressed data structures. The most popular methods are t-digest^[16] and KLL.^[17] These methods read a stream of values in a continuous fashion and can, at any time, be queried about the approximate value of a specified quantile.

Both algorithms are based on a similar idea: compressing the stream of values by summarizing identical or similar values with a weight. If the stream is made of a repetition of 100 times v1 and 100 times v2, there is no reason to keep a sorted list of 200 elements, it is enough to keep two elements and two counts to be able to recover the quantiles. With more values, these algorithms maintain a trade-off between the number of unique values stored and the precision of the resulting quantiles. Some values may be discarded from the stream and contribute to the weight of a nearby value without changing the quantile results too much. The t-digest maintains a data structure of bounded size using an approach motivated by k-means clustering to group similar values. The KLL algorithm uses a more sophisticated «compactor» method that leads to better control of the error bounds at the cost of requiring an unbounded size if errors must be bounded relative to p.

Both methods belong to the family of data sketches that are subsets of Streaming Algorithms with useful properties: t-digest or KLL sketches can be combined. Computing the sketch for a very large vector of values can be split into trivially parallel processes where sketches are computed for partitions of the vector in parallel and merged later.

Discussion[edit]

Standardized test results are commonly reported as a student scoring «in the 80th percentile», for example. This uses an alternative meaning of the word percentile as the interval between (in this case) the 80th and the 81st scalar percentile.^[18] This separate meaning of percentile is also used in peer-reviewed scientific research articles.^[19] The meaning used can be derived from its context.

If a distribution is symmetric, then the median is the mean (so long as the latter exists). But, in general, the median and the mean can differ. For instance, with a random variable that has an exponential distribution, any particular sample of this random variable will have roughly a 63% chance of being less than the mean. This is because the exponential distribution has a long tail for positive values but is zero for negative numbers.

Quantiles are useful measures because they are less susceptible than means to long-tailed distributions and outliers. Empirically, if the data being analyzed are not actually distributed according to an assumed distribution, or if there are other potential sources for outliers that are far removed from the mean, then quantiles may be more useful descriptive statistics than means and other moment-related statistics.

Closely related is the subject of least absolute deviations, a method of regression that is more robust to outliers than is least squares, in which the sum of the absolute value of the observed errors is used in place of the squared error. The connection is that the mean is the single estimate of a distribution that minimizes expected squared error while the median minimizes expected absolute error. Least absolute deviations shares the ability to be relatively insensitive to large deviations in outlying observations, although even better methods of robust regression are available.

The quantiles of a random variable are preserved under increasing transformations, in the sense that, for example, if m is the median of a random variable X, then 2^m is the median of 2^X, unless an arbitrary choice has been made from a range of values to specify a particular quantile. (See quantile estimation, above, for examples of such interpolation.) Quantiles can also be used in cases where only ordinal data are available.

References[edit]

^ Helen Mary Walker, Joseph Lev, Elementary Statistical Methods, 1969, [p. 60 https://books.google.com/books?id=ogYnAQAAIAAJ&dq=permille]
^ Bagui, S.; Bhaumik, D. (2004). «Glimpses of inequalities in probability and statistics» (PDF). International Journal of Statistical Sciences. 3: 9–15. ISSN 1683-5603.
^ Stuart, Alan; Ord, Keith (1994). Kendall’s Advanced Theory of Statistics. London: Arnold. ISBN 0340614307.
^ Hyndman, Rob J.; Fan, Yanan (November 1996). «Sample Quantiles in Statistical Packages». American Statistician. American Statistical Association. 50 (4): 361–365. doi:10.2307/2684934. JSTOR 2684934.
^ Mathematica Documentation See ‘Details’ section
^ «Quantile calculation». uk.mathworks.com.
^ Frohne, Ivan; Hyndman, Rob J. (2009). Sample Quantiles. R Project. ISBN 978-3-900051-07-5.
^ «Function Reference: quantile — Octave-Forge — SourceForge». Retrieved 6 September 2013.
^ «scipy.stats.mstats.mquantiles — SciPy v1.4.1 Reference Guide». docs.scipy.org.
^ «Statistics — Maple Programming Help». www.maplesoft.com.
^ «EViews 9 Help». Archived from the original on April 16, 2016. Retrieved April 4, 2016.
^ Stata documentation for the pctile and xtile commands See ‘Methods and formulas’ section.
^ «statistics — Mathematical statistics functions — Python 3.8.3rc1 documentation». docs.python.org.
^ Hyndman, Rob J. (28 March 2016). «Sample quantiles 20 years later». Hyndsignt blog. Retrieved 2020-11-30.
^ Wilcox, Rand R. (2010). Introduction to Robust Estimation and Hypothesis Testing. ISBN 978-0-12-751542-7.
^ Dunning, Ted; Ertl, Otmar (February 2019). «Computing Extremely Accurate Quantiles Using t-Digests». arXiv:1902.04023 [stat.CO].
^ Zohar Karnin; Kevin Lang; Edo Liberty (2016). «Optimal Quantile Approximation in Streams». arXiv:1603.05346 [cs.DS].
^ «percentile». Oxford Reference. Retrieved 2020-08-17.
^ Kruger, J.; Dunning, D. (December 1999). «Unskilled and unaware of it: how difficulties in recognizing one’s own incompetence lead to inflated self-assessments». Journal of Personality and Social Psychology. 77 (6): 1121–1134. doi:10.1037/0022-3514.77.6.1121. ISSN 0022-3514. PMID 10626367.
^ Stephen B. Vardeman (1992). «What about the Other Intervals?». The American Statistician. 46 (3): 193–197. doi:10.2307/2685212. JSTOR 2685212.

External links[edit]

Media related to Quantiles at Wikimedia Commons

Источник

Квантиль — что это?

Как найти квантиль

Параметры дискретного закона распределения

Математическое описание

Среднее значение

Отклонение от среднего

Квантиль

Построение интервалов

Двусторонний доверительный интервал

Доверительный интервал

Итого

Построить ряд распределения

Бонус

Совет

Список параметров

Шаблон гистограммы в OpenOffice Calc

Материал из MachineLearning.

Содержание

Определение

Часто используемые квантили специальных видов

Терминология, принятая в математической статистике

Применение квантилей в задачах проверки статистических гипотез

Применение квантилей в задачах оценивания параметров

Выборочные квантили; статистическая оценка квантилей

Литература

Ссылки

Определение

Квантили специальных видов

Квантили стандартного нормального распределения

Квантили распределения Стьюдента

Квантили распределения ХИ-квадрат

Квантили F-распределения

Квантили распределения Вейбулла

Квантили экспоненциального распределения

Specialized quantiles[edit]

Quantiles of a population[edit]

Examples[edit]

Even-sized population[edit]

Odd-sized population[edit]

Relationship to the mean[edit]

Estimating quantiles from a sample[edit]

Approximate quantiles from a stream[edit]

Discussion[edit]

See also[edit]

References[edit]

Further reading[edit]

External links[edit]