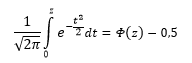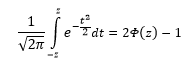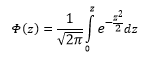Как найти квантили нормального распределения - Исправление недочетов и поиск решений вместе с Examum.ru

Рассмотренные
выборочные параметры: среднее, дисперсия
и коэффициент корреляции выборки
являются приближенными оценками
соответствующих генеральных параметров.
Погрешность этих оценок будет тем
меньше, чем больше объем выборки. Есть
способы, с помощью которых можно оценить
саму погрешность. Для этого переходят
от точечных оценок параметров к оцениванию
доверительных интервалов параметров.
При получении интервальных оценок часто
используют так называемые квантили.

Квантилем,
отвечающий заданному уровню вероятностиР, называют такое значение, при котором функция распределенияпринимает значение, равноеР, т.е.гдеР– заданный уровень вероятности.

Другими словами
квантильесть такое значение
случайной величины,
при котором

Вероятность Р, задаваемая в процентах, дает название
соответствующему квантилю, например,
называется 40%-ым квантилем.

Квантили стандартного
нормального распределения (распределение
с параметрами
)
обозначаются буквой.
Они легко находятся в соответствующих
таблицах. Если,
то подбирая такое,
для которогои находим.
Если,
то подбираем такое,
для которогои тогда.
Например, 40 % квантиль будет равен85 %, квантильи т.д.

Квантиль общего
нормального распределения
с параметрамиивыражается через квантиль:

. (2.5)

Если известны два
квантиля случайной величины
и,
то

Понятие
квантиля используется не только для
нормального , но и для большинства
встречающихся распределений.

Квантиль
называетсямедианой распределения.
Если распределение случайной величины
симметрично, то.

Например,
распределение случайных ошибок
симметрично. Поэтому для этого
распределения можно использовать как
математическое ожидание, так и медиану.

2.5. Получение интервальных оценок

Все
выборочные параметры являются случайными
величинами, а следовательно и их
отклонения от генеральных параметров,
т.е. погрешности, также будут случайными.
Поэтому оценка этих погрешностей носит
вероятностный характер. Можно лишь
указать вероятность той или иной
погрешности. Чтобы решить подобную
задачу нужно найти вероятность того,
что отклонения выборочного параметра
от исследуемого генеральногоне превосходит по абсолютной величине
некоторого заданного числа,
т.е. находятся в пределах отдо.
Обозначим отклонение через.
Поставленную задачу можно легко решить
если известна функция распределенияили плотность распределениявеличины:

(2.6)

Распределение
иногда удается точно определить по
элементам выборки. В других случаях это
распределение зависит только от объема
выборкии его можно вывести теоретически. Если
бы при этом было известно математическое
ожидание выборочного параметра,
то разность

дает точное значение
генерального параметра. К сожалению
,
как правило, не известно.

Определим генеральный
параметр. Находят по выборке одно
значение
выборочного параметраи принимают его за приближенное значение
генерального параметра.
Затем, используя выражение (2.6) оценивают
это приближение. Действительно, задаваясь
некоторым положительным числом,
мы можем найти вероятность того, что.
Но так какесть одно из допустимых значений
выборочного параметра,
то вероятность неравенстватакже равна этой вероятности. Отсюда
получаем формулу

которая
позволяет сравнивать найденное значение
выборочного параметра с неизвестным
генеральным параметром.

Неизвестный
генеральный параметр можно представить
в виде
.

Это
неравенство отличается тем, что
неизвестная величина
,
которая является неслучайной величиной,
оценивается случайными границами, т.к.
выборочный параметр является случайным.

Таким
образом, любая статистическая оценка
есть оценка вида

где
некоторые
случайные величины.

Придавая
конкретные значения, мы сможем вычислять
вероятность соответствующей оценки.

В
качестве границ
наиболее удобно брать квантили случайной
величины.
При обработке наблюдений для оценок
генерального параметра берут симметричные
квантили. В этом случае вероятностиРсоответствует оценка

Рассмотрим
как пользоваться оценками на практике.
Для этого дадим следующие определения.

Событиеназываетсяабсолютно достоверным,
если оно появляется при любом осуществлении
комплекса основных факторов. Абсолютную
достоверность нельзя установить никакой
самой длительной проверкой. Ее можно
вывести лишь теоретически , путем
логических умозаключений. Сюда относят
обычно математические истины.

Большинство
же привычных достоверных событий при
рассмотрении не является абсолютно
достоверным. Например, нельзя считать
абсолютно достоверным тот факт, что
подброшенная монета упадет гербом или
числом, т.к. у монеты есть и другие
состояния равновесия — это ребро. Однако,
в данном случае мы можем утверждать,
что монета упадет либо гербом , либо
числом. Такая достоверность называется
практической достоверностью.

Использования
принципа практической достоверности
позволяет не доводить вероятность
оценки до единицы. Принимаемый при этом
уровень вероятности называется
доверительной вероятностью. В
зависимости от конкретных обстоятельств
в качестве доверительной вероятности
берут обычно значения: 0.950.99;
реже 0.90;0.999.

Соответствующие
доверительной вероятности квантильные
границы называются доверительными
границами, а образуемый ими интервал
—доверительным интерваломили
еще называютдоверительной оценкойилиинтервальной оценкой.

Величина
называетсяуровнем значимости.
Уровень значимости соответствует
практически невозможному событию.
Уровень значимости и уровень достоверности
в сумме дают единицу. Обычно значения
уровней значимости берутся в пределах:
0.050.01
и реже 0.1; 0.001.

Соседние файлы в папке model-00ae89b6

Источник

Рассмотрим вычисление квантилей для некоторых функций распределений, представленных в

MS

EXCEL

.

Понятие

Квантиля

основано на определении

Функции распределения

. Поэтому, перед изучением

Квантилей

рекомендуем освежить в памяти понятия из статьи

Функция распределения вероятности

Содержание статьи:

Определение
Квантили специальных видов
Квантили стандартного нормального распределения
Квантили распределения Стьюдента
Квантили распределения ХИ-квадрат
Квантили F-распределения
Квантили распределения Вейбулла
Квантили экспоненциального распределения

Сначала дадим формальное определение

квантиля,

затем приведем примеры их вычисления в MS EXCEL.

Определение

Пусть случайная величина

X

, имеет

функцию распределения

F

(

x

).

α-квантилем

(

альфа-

квантиль,

x
_a
,

квантиль

порядка

α, нижний

α-

квантиль

) называют решение уравнения

x
_a
=F
^-1
(α), где

α

— вероятность, что случайная величина х примет значение меньшее или равное x
_a
, т.е. Р(х<= x
_a
)=

α.

Из определения ясно, что нахождение

квантиля

распределения является обратной операцией нахождения вероятности. Т.е. если при вычислении

функции распределения

мы находим вероятность

α,

зная x
_a
, то при нахождении

квантиля

мы, наоборот, ищем

x
_a
зная

α

.

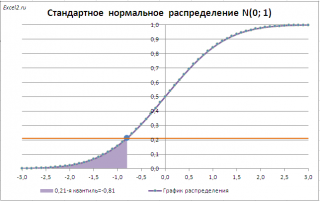
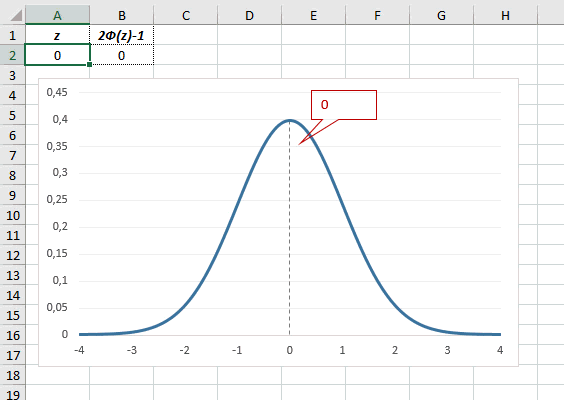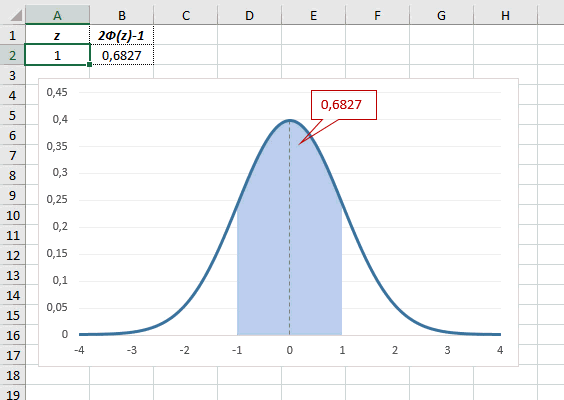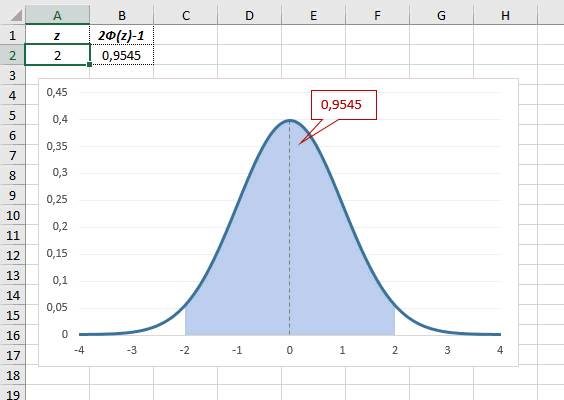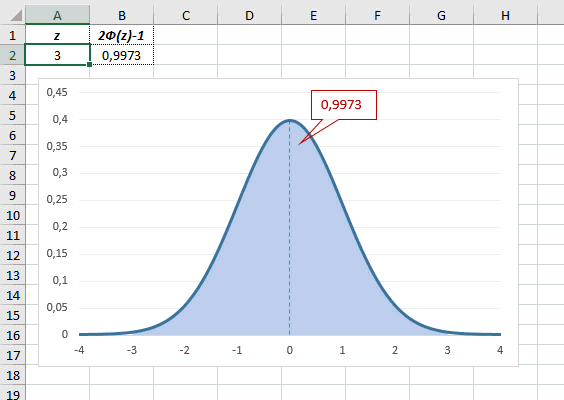
Чтобы пояснить определение, используем график функции

стандартного нормального распределения

(см.

файл примера Лист Определение

):

Примечание

: О построении графиков в MS EXCEL можно прочитать статью

Основные типы диаграмм в MS EXCEL

Например, с помощью графика вычислим 0,21-ю

квантиль

, т.е. такое значение случайной величины, что Р(X<=x
_0,21
)=0,21.

Для этого найдем точку пересечения горизонтальной линии на уровне вероятности равной 0,21 с

функцией распределения

. Абсцисса этой точки равна -0,81. Соответственно, 0,21-я

квантиль

равна -0,81. Другими словами, вероятность того, что случайная величина, распределенная

стандартному нормальному закону,

примет значение

меньше

-0,81, равна 0,21 (21%).

Примечание

: При вычислении

квантилей

в MS EXCEL используются

обратные функции распределения

:

НОРМ.СТ.ОБР()

,

ЛОГНОРМ.ОБР()

,

ХИ2.ОБР(),

ГАММА.ОБР()

и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье

Распределения случайной величины в MS EXCEL

Точное значение

квантиля

в нашем случае можно найти с помощью формулы

=НОРМ.СТ.ОБР(0,21)

СОВЕТ

: Процедура вычисления

квантилей

имеет много общего с вычислением

процентилей

выборки

(см. статью

Процентили в MS EXCEL

Квантили специальных видов

Часто используются

Квантили

специальных видов:

процентили

x
_p/100
, p=1, 2, 3, …, 99
квартили

x
_p/4
, p=1, 2, 3
медиана

x
_1/2

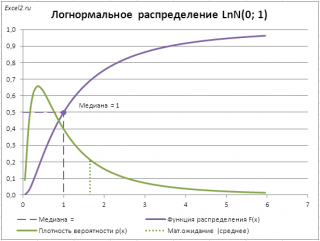
В качестве примера вычислим

медиану (0,5-квантиль)

логнормального распределения

LnN(0;1) (см.

файл примера лист Медиана

).

Это можно сделать с помощью формулы

=ЛОГНОРМ.ОБР(0,5; 0; 1)

Квантили стандартного нормального распределения

Необходимость в вычислении квантилей

стандартного нормального распределения

возникает при

проверке статистических гипотез

и при

построении доверительных интервалов.

Примечание

: Про

проверку статистических гипотез

см. статью

Проверка статистических гипотез в MS EXCEL

. Про

построение доверительных интервалов

см. статью

Доверительные интервалы в MS EXCEL

В данных задачах часто используется специальная терминология:

Нижний квантиль уровня

альфа

(

α

percentage point)

;
Верхний квантиль уровня альфа (upper

α

percentage point)

;
Двусторонние квантили уровня

альфа

.

Нижний квантиль уровня альфа

— это обычный

α-квантиль.

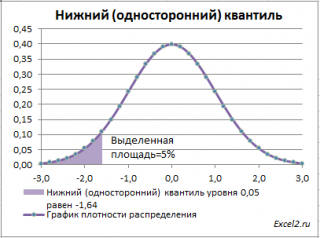
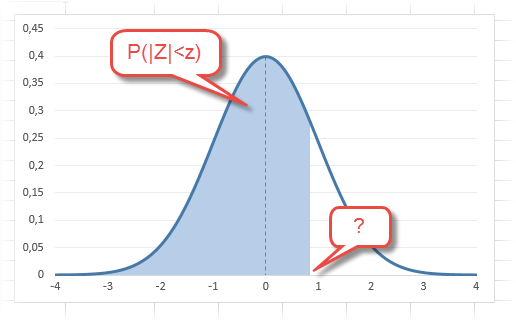
Чтобы пояснить название «

нижний» квантиль

, построим график

плотности вероятности

и

функцию вероятности

стандартного нормального

распределения

(см.

файл примера лист Квантили

).

Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение меньше

α-квантиля

. Из определения

квантиля

эта вероятность равна

α

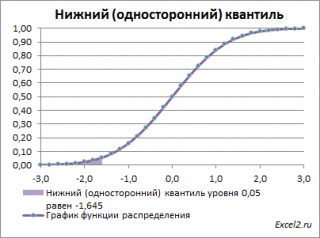
. Из графика

функции распределения

становится понятно, откуда происходит название »

нижний квантиль» —

выделенная область расположена в нижней части графика.

Для

α=0,05,

нижний 0,05-квантиль

стандартного нормального распределения

равен -1,645. Вычисления в MS EXCEL можно сделать по формуле:

=НОРМ.СТ.ОБР(0,05)

Однако, при

проверке гипотез

и построении

доверительных интервалов

чаще используется «верхний»

α-квантиль.

Покажем почему.

Верхним

α

—

квантилем

называют такое значение x
_α
, для которого вероятность, того что случайная величина X примет значение

больше или равное

x
_α
равна

альфа:

P(X>= x
_α
)=

α

. Из определения понятно, что

верхний альфа

—

квантиль

любого распределения равен

нижнему (1-

α)

—

квантилю.

А для распределений, у которых

функция плотности распределения

является четной функцией,

верхний

α

—

квантиль

равен

нижнему

α

—

квантилю

со знаком минус

.

Это следует из свойства четной функции f(-x)=f(x), в силу симметричности ее относительно оси ординат.

Действительно, для

α=0,05,

верхний 0,05-квантиль

стандартного нормального распределения

равен 1,645. Т.к.

функция плотности вероятности

стандартного нормального

распределения

является четной функцией, то вычисления в MS EXCEL

верхнего квантиля

можно сделать по двум формулам:

=НОРМ.СТ.ОБР(1-0,05)

=-НОРМ.СТ.ОБР(0,05)

Почему применяют понятие

верхний

α

—

квантиль?

Только из соображения удобства, т.к. он при

α<0,5

всегда положительный (в случае

стандартного нормального

распределения

). А при проверке гипотез

α

равно

уровню значимости

, который обычно берут равным 0,05, 0,1 или 0,01. В противном случае, в процедуре

проверки гипотез

пришлось бы записывать условие отклонения

нулевой гипотезы

μ>μ
₀
как Z
₀
>Z
_{1-

α}
, подразумевая, что Z
_{1-

α}
–

обычный

квантиль

порядка

1-

α

(или как Z
₀
>-Z
_α
). C верхнем квантилем эта запись выглядит проще Z
₀
>Z
_α
.

Примечание

: Z
₀
— значение

тестовой статистики

, вычисленное на основе

выборки

. Подробнее см. статью

Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна)

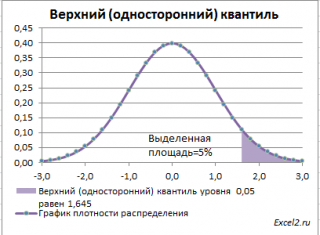
Чтобы пояснить название «

верхний»

квантиль

, построим график

плотности вероятности

и

функцию вероятности

стандартного нормального

распределения

для

α=0,05.

Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение больше

верхнего 0,05-квантиля

, т.е.

больше

значения 1,645. Эта вероятность равна 0,05.

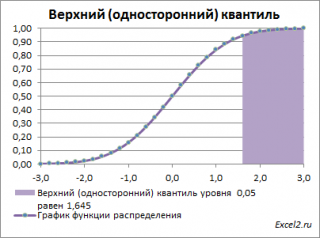
На графике

плотности вероятности

площадь выделенной области равна 0,05 (5%) от общей площади под графиком (равна 1). Из графика

функции распределения

становится понятно, откуда происходит название «верхний»

квантиль

—

выделенная область расположена в верхней части графика. Если Z
₀
больше

верхнего квантиля

, т.е. попадает в выделенную область, то

нулевая гипотеза

отклоняется.

Также при

проверке двухсторонних гипотез

и построении соответствующих

доверительных интервалов

иногда используется понятие «двусторонний»

α-квантиль.

В этом случае условие отклонения

нулевой гипотезы

звучит как |Z
₀
|>Z
_{α

/2}
, где Z
_{α

/2}
–

верхний

α/2-квантиль

. Чтобы не писать

верхний

α/2-квантиль

, для удобства используют «двусторонний»

α-квантиль.

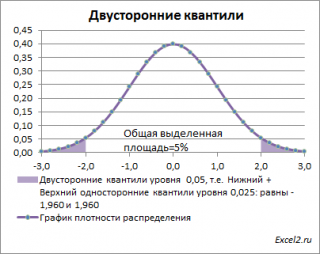
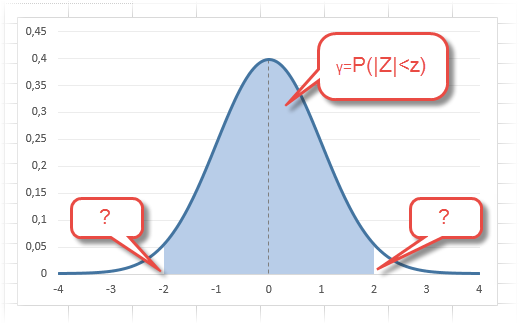
Почему двусторонний? Как и в предыдущих случаях, построим график

плотности вероятности стандартного нормального распределения

и график

функции распределения

.

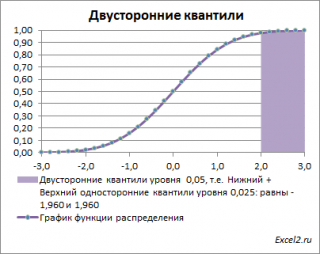
Невыделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение

между

нижним квантилем уровня α

/2 и

верхним квантилем

уровня α

/2, т.е. будет между значениями -1,960 и 1,960 при α=0,05. Эта вероятность равна в нашем случае 1-(0,05/2+0,05/2)=0,95. Если Z
₀
попадает в одну из выделенных областей, то

нулевая гипотеза

отклоняется.

Вычислить

двусторонний

0,05

—

квантиль

это можно с помощью формул MS EXCEL:

=НОРМ.СТ.ОБР(1-0,05/2)

или

=-НОРМ.СТ.ОБР(0,05/2)

Другими словами,

двусторонние α-квантили

задают интервал, в который рассматриваемая случайная величина попадает с заданной вероятностью α.

Квантили распределения Стьюдента

Аналогичным образом

квантили

вычисляются и для

распределения Стьюдента

. Например, вычислять

верхний

α/2-

квантиль

распределения Стьюдента с

n

-1 степенью свободы

требуется, если проводится

проверка двухсторонней гипотезы

о

среднем значении

распределения при

неизвестной

дисперсии

(

см. эту статью

Для

верхних квантилей

распределения Стьюдента

часто используется запись t
_α/2,n-1
. Если такая запись встретилась в статье про

проверку гипотез

или про построение

доверительного интервала

, то это именно

верхний квантиль

.

Примечание

:

Функция плотности вероятности распределения Стьюдента

, как и

стандартного нормального распределения

, является четной функцией.

Чтобы вычислить в MS EXCEL

верхний

0,05/2

—

квантиль

для t-распределения с 10 степенями свободы (или тоже самое

двусторонний

0,05-квантиль

), необходимо записать формулу

=СТЬЮДЕНТ.ОБР.2Х(0,05; 10)

или

=СТЬЮДРАСПОБР(0,05; 10)

или

=СТЬЮДЕНТ.ОБР(1-0,05/2; 10)

или

=-СТЬЮДЕНТ.ОБР(0,05/2; 10)

.2X означает 2 хвоста, т.е.

двусторонний квантиль

.

Квантили распределения ХИ-квадрат

Вычислять

квантили

распределения ХИ-квадрат

с

n

-1 степенью свободы

требуется, если проводится

проверка гипотезы

о

дисперсии нормального распределения

(см. статью

Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения

При

проверке таких гипотез

также используются

верхние квантили.

Например, при

двухсторонней гипотезе

требуется вычислить 2

верхних

квантиля

распределения

ХИ
²
: χ
²_α/2,n-1
и

χ
²_1-_α/2,n-1
. Почему требуется вычислить два

квантиля

, не один, как при

проверке гипотез о среднем

, где используется

стандартное нормальное распределение

или

t-распределение

?

Дело в том, что в отличие от

стандартного нормального распределения

и

распределения Стьюдента

, плотность распределения

ХИ
²
не является четной (симметричной относительно оси х). У него все

квантили

больше 0, поэтому

верхний альфа-квантиль

не равен

нижнему (1-альфа)-квантилю

или по-другому:

верхний альфа-квантиль

не равен

нижнему альфа-квантилю

со знаком минус.

Чтобы вычислить

верхний

0,05/2

—

квантиль

для

ХИ
²
-распределения

с

числом степеней свободы

10, т.е.

χ
²_0,05/2,n-1
, необходимо в MS EXCEL записать формулу

=ХИ2.ОБР.ПХ(0,05/2; 10)

или

=ХИ2.ОБР(1-0,05/2; 10)

Результат равен 20,48. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике

функции распределения

.

Чтобы вычислить

верхний

(1-0,05/2)-

квантиль

при том же

числе степеней свободы

, т.е.

χ
²_1-0,05/2,n-1
и необходимо записать формулу

=ХИ2.ОБР.ПХ(1-0,05/2; 10)

или

=ХИ2.ОБР(0,05/2; 10)

Результат равен 3,25.

Квантили F-распределения

Вычислять

квантили

распределения Фишера

с

n
₁
-1 и

n
₂
-1 степенями свободы

требуется, если проводится

проверка гипотезы

о равенстве

дисперсий двух нормальных распределений

(см. статью

Двухвыборочный тест для дисперсии: F-тест в MS EXCEL

При

проверке таких гипотез

используются, как правило,

верхние квантили.

Например, при

двухсторонней гипотезе

требуется вычислить 2

верхних

квантиля

F

-распределения:

F
_{α/2,n1-1,

n

2

-1}
и

F
_{1-α/2,n1-1,

n

2

-1}
. Почему требуется вычислить два

квантиля

, не один, как при

проверке гипотез о среднем

? Причина та же, что и для распределения ХИ
²
– плотность

F-распределения

не является четной

.

Эти

квантили

нельзя выразить один через другой как для

стандартного нормального распределения

.

Верхний альфа-квантиль

F

-распределения

не равен

нижнему альфа-квантилю

со знаком минус.

Чтобы вычислить

верхний

0,05/2-квантиль

для

F

-распределения

с

числом степеней свободы

10 и 12, необходимо записать формулу

=F.ОБР.ПХ(0,05/2;10;12) =FРАСПОБР(0,05/2;10;12) =F.ОБР(1-0,05/2;10;12)

Результат равен 3,37. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике

функции распределения

.

Квантили распределения Вейбулла

Иногда

обратная функция распределения

может быть представлена в явном виде с помощью элементарных функций, например как для

распределения Вейбулла

. Напомним, что функция этого распределения задается следующей формулой:

После логарифмирования обеих частей выражения, выразим x через соответствующее ему значение F(x) равное P:

Примечание

: Вместо обозначения

α-квантиль

может использоваться

p

—

квантиль.

Суть от этого не меняется.

Это и есть обратная функция, которая позволяет вычислить

P

—

квантиль

(

p

—

quantile

). Для его вычисления в формуле нужно подставить известное значение вероятности P и вычислить значение х
_p
(вероятность того, что случайная величина Х примет значение меньше или равное х
_p
равна P).

Квантили экспоненциального распределения

Задача

:

Случайная величина имеет

экспоненциальное распределение

:

Требуется выразить

p

-квантиль

x
_p
через параметр распределения λ и заданную вероятность

p

.

Примечание

: Вместо обозначения

α-квантиль

может использоваться

p-квантиль

. Суть от этого не меняется.

Решение

: Вспоминаем, что

p

-квантиль

– это такое значение x
_p
случайной величины X, для которого P(X<=x
_p
)=

p

. Т.е. вероятность, что случайная величина X примет значение меньше или равное x
_p
равна

p

. Запишем это утверждение с помощью формулы:

По сути, мы записали

функцию вероятности экспоненциального распределения

: F(x
_p
)=

p

.

Из определения

квантиля

следует, что для его нахождения нам потребуется

обратная функция распределения

.

Проинтегрировав вышеуказанное выражение, получим:

Используя это уравнение, выразим x
_p
через λ и вероятность

p

.

Конечно, явно выразить

обратную функцию распределения

можно не для всех

функций распределений

.

Источник

Пост №2 для начинающих посвящен описательным статистикам, группированию данных и нормальному распределению. Все эти сведения заложат основу для дальнейшего анализа электоральных данных. Предыдущий пост см. здесь.

Описательные статистики

Описательные статистические величины, или статистики, — это числа, которые используются для обобщения и описания данных. В целях демонстрации того, что мы имеем в виду, посмотрим на столбец с данными об электорате Electorate. Он показывает суммарное число зарегистрированных избирателей в каждом избирательном округе:

def ex_1_6():
    '''Число значений в поле "Электорат"'''
    return load_uk_scrubbed()['Electorate'].count()

Мы уже очистили столбец, отфильтровав пустые значения (nan) из набора данных, и поэтому предыдущий пример должен вернуть суммарное число избирательных округов.

Описательные статистики, так называемые сводные статистики, представляют собой разные подходы к измерению свойств последовательностей чисел. Они помогают охарактеризовать последовательность и способны выступать в качестве ориентира для дальнейшего анализа. Начнем с двух самых базовых статистик, которые мы можем вычислить из последовательности чисел — ее среднее значение и дисперсию (варианс).

Среднее значение

Наиболее распространенный способ усреднить набор данных — взять его среднее значение. Среднее значение на самом деле представляет собой один из нескольких способов измерения центра распределения данных.

$x̅=frac{1}{n}sum _{i=1}^nx_i$

Среднее значение числового ряда вычисляется на Python следующим образом:

def mean(xs): 
    '''Среднее значение числового ряда'''
    return sum(xs) / len(xs)

Мы можем воспользоваться нашей новой функцией mean для вычисления среднего числа избирателей в Великобритании:

def ex_1_7():
    '''Вернуть среднее значение поля "Электорат"'''
    return mean( load_uk_scrubbed()['Electorate'] )

70149.94

На самом деле, библиотека pandas уже содержит функцию mean, которая гораздо эффективнее вычисляет среднее значение последовательности. В нашем случае ее можно применить следующим образом:

load_uk_scrubbed()['Electorate'].mean()

Медиана

Медиана — это еще одна распространенная описательная статистика для измерения центра распределения последовательности. Если Вы упорядочили все данные от меньшего до наибольшего, то медиана — это значение, которое находится ровно по середине. Если в последовательности число точек данных четное, то медиана определяется, как полусумма двух срединных значений.

def median(xs):
    '''Медиана числового ряда'''
    n = len(xs)
    mid = n // 2
    if n % 2 == 1:
        return sorted(xs)[mid]
    else:
        return mean( sorted(xs)[mid-1:][:2] )

Медианное значение электората Великобритании составляет:

def ex_1_8():
    '''Вернуть медиану поля "Электорат"'''
    return median( load_uk_scrubbed()['Electorate'] )

70813.5

Библиотека pandas тоже располагает встроенной функцией для вычисления медианного значения, которая так и называется median.

Дисперсия

Среднее арифметическое и медиана являются двумя альтернативными способами описания среднего значения последовательности, но сами по себе они мало что говорят о содержащихся в ней значениях. Например, если известно, что среднее последовательности из девяноста девяти значений равно 50, то мы почти ничего не скажем о том, какого рода значения последовательность содержит.

Она может содержать целые числа от одного до девяноста девяти либо сорок девять нулей и пятьдесят девяносто девяток, а может быть и так, что она девяносто восемь раз содержит отрицательную единицу и одно число 5048, или же вообще все значения могут быть равны 50.

Дисперсия (варианс) последовательности чисел показывает «разброс» данных вокруг среднего значения. К примеру, данные, приведенные выше, имели бы разную дисперсию. На языке математики дисперсия обозначается следующим образом:

$s^2=frac{1}{n}sum _{i=1}^nleft(x_i-x̅right)^2$

где s² — это математический символ, который часто используют для обозначения дисперсии.

Выражение

def variance(xs):
    '''Дисперсия (варианс) числового ряда,
       несмещенная дисперсия при n <= 30'''
    mu = mean(xs)
    n = len(xs)
    n = n-1 if n in range(1, 30) else n  
    square_deviation = lambda x : (x - mu) ** 2 
    return sum( map(square_deviation, xs) ) / n

Для вычисления квадрата выражения используется оператор языка Python возведения в степень **.

Стандартное отклонение

Поскольку мы взяли средний квадрат отклонения, т.е. получили квадрат отклонения и затем его среднее, то единицы измерения дисперсии (варианса) тоже будут в квадрате, т.е. дисперсия электората Великобритании будет измеряться «людьми в квадрате». Несколько неестественно рассуждать об избирателях в таком виде. Единицу измерения можно привести к более естественному виду, снова обозначающему «людей», путем извлечения квадратного корня из дисперсии (варианса). В результате получим так называемое стандартное отклонение, или среднеквадратичное отклонение:

def standard_deviation(xs):
    '''Стандартное отклонение числового ряда'''
    return sp.sqrt( variance(xs) )
       
def ex_1_9():
    '''Стандартное отклонение поля "Электорат"'''
    return standard_deviation( load_uk_scrubbed()['Electorate'] )

7672.77

В библиотеке pandas функции для вычисления дисперсии (варианса) и стандартного отклонения имплементированы соответственно, как var и std. При этом последняя по умолчанию вычисляет несмещенное значение, поэтому, чтобы получить тот же самый результат, нужно применить именованный аргумент ddof=0, который сообщает, что требуется вычислить смещенное значение стандартного отклонения:

load_uk_scrubbed()['Electorate'].std( ddof=0 )

Квантили

Медиана представляет собой один из способов вычислить срединное значение из списка, т.е. находящееся ровно по середине, дисперсия же предоставляет способ измерить разброс данных вокруг среднего значения. Если весь разброс данных представить на шкале от 0 до 1, то значение 0.5 будет медианным.

Для примера рассмотрим следующую ниже последовательность чисел:

[10 11 15 21 22.5 28 30]

Отсортированная последовательность состоит из семи чисел, поэтому медианой является число 21 четвертое в ряду. Его также называют 0.5-квантилем. Мы можем получить более полную картину последовательности чисел, взглянув на 0.0 (нулевой), 0.25, 0.5, 0.75 и 1.0 квантили. Все вместе эти цифры не только показывают медиану, но также обобщают диапазон данных и сообщат о характере распределения чисел внутри него. Они иногда упоминаются в связи с пятичисловой сводкой.

Один из способов составления пятичисловой сводки для данных об электорате Великобритании показан ниже. Квантили можно вычислить непосредственно в pandas при помощи функции quantile. Последовательность требующихся квантилей передается в виде списка.

def ex_1_10():
    '''Вычислить квантили:
       возвращает значение в последовательности xs, 
       соответствующее p-ому проценту'''
    q = [0, 1/4, 1/2, 3/4, 1]
    return load_uk_scrubbed()['Electorate'].quantile(q=q)

0.00     21780.00
0.25     65929.25
0.50     70813.50
0.75     74948.50
1.00    109922.00
Name: Electorate, dtype: float64

Когда квантили делят диапазон на четыре равных диапазона, как показано выше, то они называются квартилями. Разница между нижним (0.25) и верхним (0.75) квартилями называется межквартильным размахом, или иногда сокращенно МКР. Аналогично дисперсии (варианса) вокруг среднего значения, межквартильный размах измеряет разброс данных вокруг медианы.

Группирование данных в корзины

В целях развития интуитивного понимания в отношении того, что именно все эти расчеты разброса значений измеряют, мы можем применить метод под названием группировка в частотные корзины (binning). Когда данные имеют непрерывный характер, использование специального словаря для подсчета частот Counter (подобно тому, как он использовался при подсчете количества пустых значений в наборе данных об электорате) становится нецелесообразным, поскольку никакие два значения не могут быть одинаковыми. Между тем, общее представление о структуре данных можно все-равно получить, сгруппировав для этого данные в частотные корзины (bins).

Процедура образования корзин заключается в разбиении диапазона значений на ряд последовательных, равноразмерных и меньших интервалов. Каждое значение в исходном ряду попадает строго в одну корзину. Подсчитав количества точек, попадающих в каждую корзину, мы можем получить представление о разбросе данных:

На приведенном выше рисунке показано 15 значений x, разбитых на 5 равноразмерных корзин. Подсчитав количество точек, попадающих в каждую корзину, мы можем четко увидеть, что большинство точек попадают в корзину по середине, а меньшинство — в корзины по краям. Следующая ниже функция Python nbin позволяет добиться того же самого результата:

def nbin(n, xs): 
    '''Разбивка данных на частотные корзины'''
    min_x, max_x = min(xs), max(xs)
    range_x = max_x - min_x
    fn = lambda x: min( int((abs(x) - min_x) / range_x * n), n-1 )
    return map(fn, xs)

Например, мы можем разбить диапазон 0-14 на 5 корзин следующим образом:

list( nbin(5, range(15)) )

[0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4]

После того, как мы разбили значения на корзины, мы можем в очередной раз воспользоваться словарем Counter, чтобы подсчитать количество точек в каждой корзине. В следующем ниже примере мы воспользуемся этим словарем для разбиения данных об электорате Великобритании на пять корзин:

def ex_1_11():
    '''Разбиmь электорат Великобритании на 5 корзин'''
    series = load_uk_scrubbed()['Electorate']
    return Counter( nbin(5, series) )

Counter({2: 450, 3: 171, 1: 26, 0: 2, 4: 1})

Количество точек в крайних корзинах (0 и 4) значительно ниже, чем в корзинах в середине — количества, судя по всему, растут по направлению к медиане, а затем снова снижаются. В следующем разделе мы займемся визуализацией формы этих количеств.

Гистограммы

Гистограмма — это один из способов визуализации распределения одной последовательности значений. Гистограммы попросту берут непрерывное распределение, разбивают его на корзины, и изображают частоты точек, попадающих в каждую корзину, в виде столбцов. Высота каждого столбца гистограммы показывает количество точек данных, которые содержатся в этой корзине.

Мы уже увидели, каким образом можно выполнить разбиение данных на корзины самостоятельно, однако в библиотеке pandas уже содержится функция hist, которая разбивает данные и визуализирует их в виде гистограммы.

def ex_1_12():
    '''Построить гистограмму частотных корзин 
       электората Великобритании'''
    load_uk_scrubbed()['Electorate'].hist()
    plt.xlabel('Электорат Великобритании')
    plt.ylabel('Частота')
    plt.show()

Приведенный выше пример сгенерирует следующий ниже график:

Число корзин, на которые данные разбиваются, можно сконфигурировать, передав в функцию при построении гистограммы именованный аргумент bins:

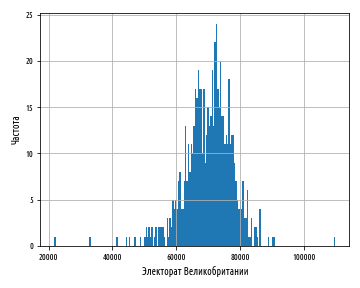
def ex_1_13():
    '''Построить гистограмму частотных корзин 
       электората Великобритании с 200 корзинами'''
    load_uk_scrubbed()['Electorate'].hist(bins=200)
    plt.xlabel('Электорат Великобритании')
    plt.ylabel('Частота')
    plt.show()

Приведенный выше график показывает единственный высокий пик, однако он выражает форму данных довольно грубо. Следующий ниже график показывает мелкие детали, но величина столбцов делает неясной форму распределения, в особенности в хвостах:

При выборе количества корзин для представления данных следует найти точку равновесия — с малым количеством корзин форма данных будет представлена лишь приблизительно, а слишком большое их число приведет к тому, что шумовые признаки могут заслонить лежащую в основании структуру.

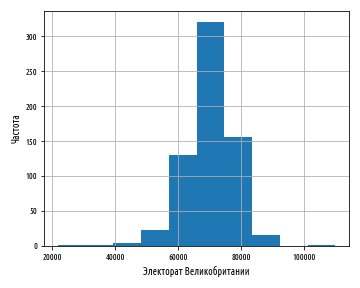
def ex_1_14():
    '''Построить гистограмму частотных корзин 
       электората Великобритании с 20 корзинами'''
    load_uk_scrubbed()['Electorate'].hist(bins=20)
    plt.xlabel('Электорат Великобритании')
    plt.ylabel('Частота')
    plt.show()

Ниже показана гистограмма теперь уже из 20 корзин:

Окончательный график, состоящий из 20 корзин, судя по всему, пока лучше всего представляет эти данные.

Наряду со средним значением и медианой, есть еще один способ измерить среднюю величину последовательности. Это мода. Мода — это значение, встречающееся в последовательности наиболее часто. Она определена исключительно только для последовательностей, имеющих по меньшей мере одно дублирующее значение; во многих статистических распределениях это не так, и поэтому для них мода не определена. Тем не менее, пик гистограммы часто называют модой, поскольку он соответствует наиболее распространенной корзине.

Из графика ясно видно, что распределение вполне симметрично относительно моды, и его значения резко падают по обе стороны от нее вдоль тонких хвостов. Эти данные приближенно подчиняются нормальному распределению.

Нормальное распределение

Гистограмма дает приблизительное представление о том, каким образом данные распределены по всему диапазону, и является визуальным средством, которое позволяет квалифицировать данные как относящиеся к одному из немногих популярных распределений. В анализе данных многие распределения встречаются часто, но ни одно не встречается также часто, как нормальное распределение, именуемое также гауссовым распределением.

^{Распределение названо нормальным распределением из-за того, что оно очень часто встречается в природе. Галилей заметил, что ошибки в его астрономических измерениях подчинялись распределению, где малые отклонения от среднего значения встречались чаще, чем большие. Вклад великого математика Гаусса в описание математической формы этих ошибок привел к тому, что это распределение стали называть в его честь распределением Гаусса.}

Любое распределение похоже на алгоритм сжатия: оно позволяет очень эффективно резюмировать потенциально большой объем данных. Нормальное распределение требует только два параметра, исходя из которых можно аппроксимировать остальные данные. Это среднее значение и стандартное отклонение.

Центральная предельная теорема

Высокая встречаемость нормального распределения отчасти объясняется центральной предельной теоремой. Дело в том, что значения, полученные из разнообразных статистических распределений, при определенных обстоятельствах имеют тенденцию сходиться к нормальному распределению, и мы это покажем далее.

В программировании типичным распределением является равномерное распределение. Оно представлено распределением чисел, генерируемых функцией библиотеки scipy stats.uniform.rvs: в справедливом генераторе случайных чисел все числа имеют равные шансы быть сгенерированными. Мы можем увидеть это на гистограмме, многократно генерируя серию случайных чисел между 0 и 1 и затем построив график с результатами.

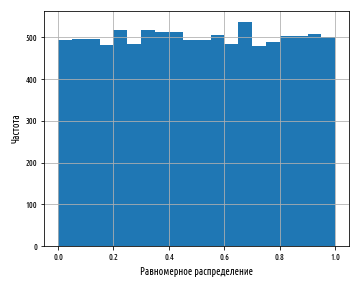
def ex_1_15():
    '''Показать гистограмму равномерного распределения 
       синтетического набора данных'''
    xs = stats.uniform.rvs(0, 1, 10000)
    pd.Series(xs).hist(bins=20)
    plt.xlabel('Равномерное распределение')
    plt.ylabel('Частота')
    plt.show()

Обратите внимание, что в этом примере мы впервые использовали тип Series библиотеки pandas для числового ряда данных.

Приведенный выше пример создаст следующую гистограмму:

Каждый столбец гистограммы имеет примерно одинаковую высоту, что соответствует равновероятности генерирования числа, которое попадает в каждую корзину. Столбцы имеют не совсем одинаковую высоту, потому что равномерное распределение описывает теоретический результат, который наша случайная выборка не может отразить в точности. Раздел инференциальной статистики, посвященный проверке статистических гипотез, изучает способы точной количественной оценки расхождения между теорией и практикой, чтобы определить, являются ли расхождения достаточно большими, чтобы обратить на это внимание. В данном случае они таковыми не являются.

Если напротив сгенерировать гистограмму средних значений последовательностей чисел, то в результате получится распределение, которое выглядит совсем непохоже.

def bootstrap(xs, n, replace=True): 
    '''Вернуть список массивов меньших размеров 
       по n элементов каждый'''
    return np.random.choice(xs, (len(xs), n), replace=replace) 

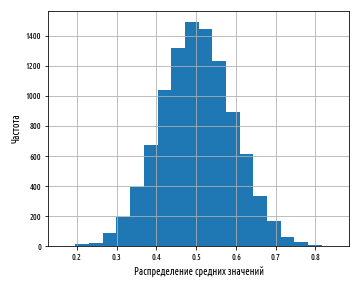
def ex_1_16():
    '''Построить гистограмму средних значений'''
    xs = stats.uniform.rvs(loc=0, scale=1, size=10000)
    pd.Series( map(sp.mean, bootstrap(xs, 10)) ).hist(bins=20)
    plt.xlabel('Распределение средних значений') 
    plt.ylabel('Частота')
    plt.show()

Приведенный выше пример сгенерирует результат, аналогичный следующей ниже гистограмме:

Хотя величина среднего значения близкая к 0 или 1 не является невозможной, она является чрезвычайно невероятной и становится менее вероятной по мере роста числа усредненных чисел и числа выборочных средних. Фактически, на выходе получается результат очень близкий к нормальному распределению.

Этот результат, когда средний эффект множества мелких случайных колебаний в итоге приводит к нормальному распределению, называется центральной предельной теоремой, иногда сокращенно ЦПТ, и играет важную роль для объяснения, почему нормальное распределение встречается так часто в природных явлениях.

До 20-ого века самого термина еще не существовало, хотя этот эффект был зафиксирован еще в 1733 г. французским математиком Абрахамом де Mуавром, который использовал нормальное распределение, чтобы аппроксимировать число орлов в результате бросания уравновешенной монеты. Исход бросков монеты лучше всего моделировать при помощи биномиального распределения. В отличие от центральной предельной теоремы, которая позволяет получать выборки из приближенно нормального распределения, библиотека scipy содержит функции для эффективного генерирования выборок из самых разнообразных статистических распределений, включая нормальное:

def ex_1_17():
    '''Показать гистограмму нормального распределения 
       синтетического набора данных'''
    xs = stats.norm.rvs(loc=0, scale=1, size=10000)
    pd.Series(xs).hist(bins=20)
    plt.xlabel('Нормальное распределение')
    plt.ylabel('Частота')
    plt.show()

Отметим, что в функции sp.random.normal параметр loc – это среднее значение, scale – дисперсия и size – размер выборки. Приведенный выше пример сгенерирует следующую гистограмму нормального распределения:

По умолчанию среднее значение и стандартное отклонение для получения нормального распределения равны соответственно 0 и 1.

Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.

Следующая часть, часть 3, серии постов «Python, исследование данных и выборы» посвящена генерированию распределений, их свойствам, а также графикам для их сопоставительного анализа

Источник

В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.

Нормальное распределение в статистике

История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.

Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.

Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.

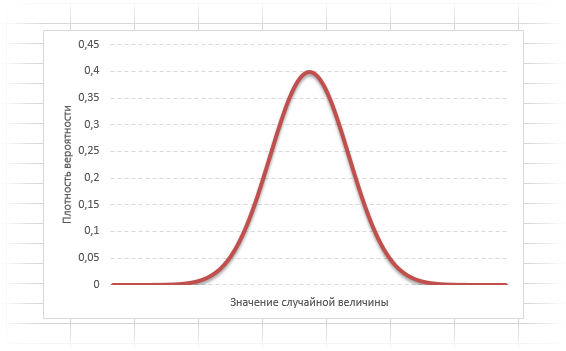
Кривая нормального распределения Гаусса имеет следующий вид.

График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.

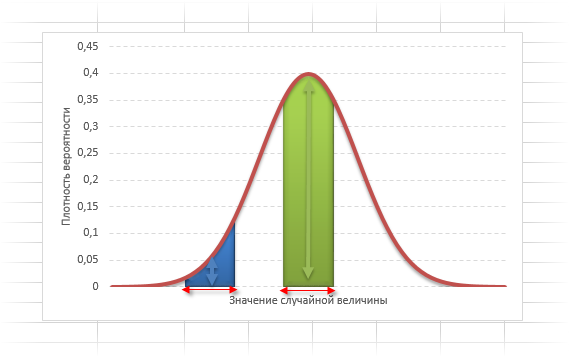
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.

Формула нормального распределения (плотности) следующая.

Формула состоит из двух математических констант:

π – число пи 3,142;

е – основание натурального логарифма 2,718;

двух изменяемых параметров, которые задают форму конкретной кривой:

m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);

σ² – дисперсия;

ну и сама переменная x, для которой высчитывается плотность вероятности.

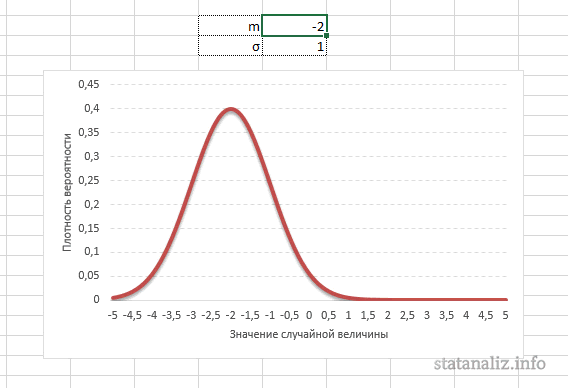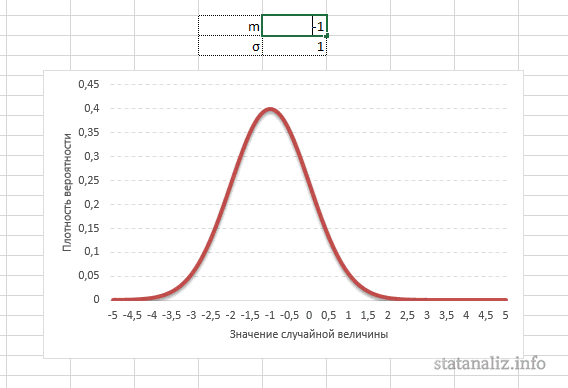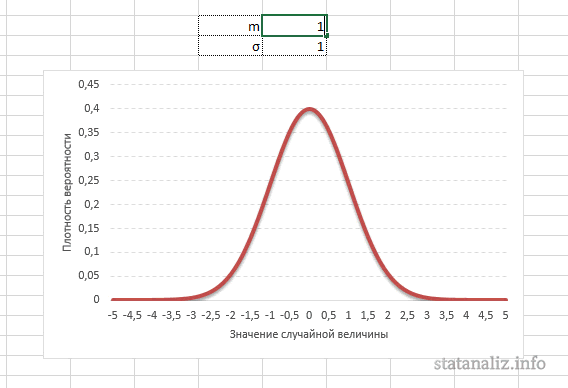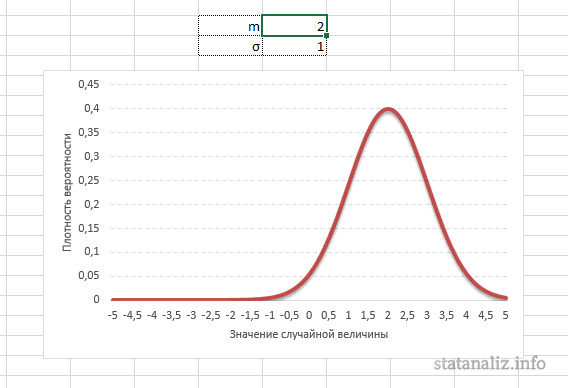
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ²). Кратко обозначается N(m, σ²) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ² характеризует размах вариации, то есть «размазанность» данных.

Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.

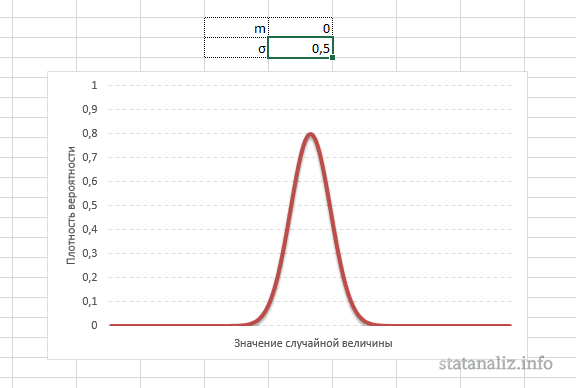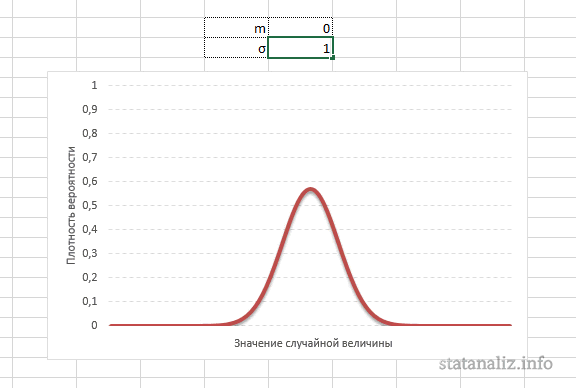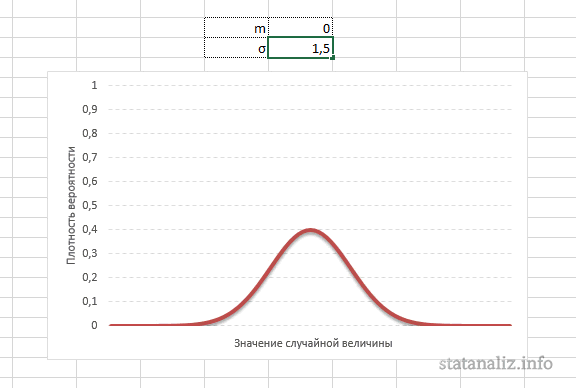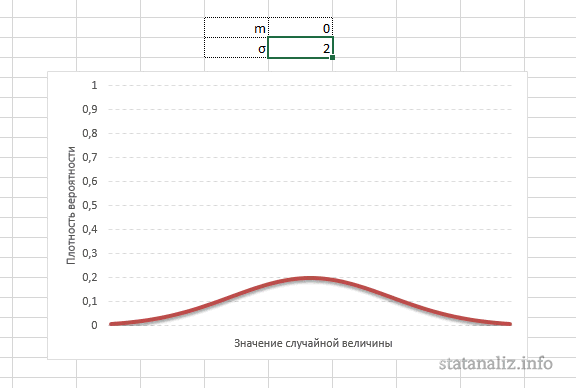
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.

Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.

Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:

Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как

P(a ≤ X < b) = Ф(b) – Ф(a)

Стандартное нормальное распределение

Нормальное распределение зависит от параметров средней и дисперсии, из-за чего плохо видны его свойства. Хорошо бы иметь некоторый эталон распределения, не зависящий от масштаба данных. И он существует. Называется стандартным нормальным распределением. На самом деле это обычное нормальное нормальное распределение, только с параметрами математического ожидания 0, а дисперсией – 1, кратко записывается N(0, 1).

Любое нормальное распределение легко превращается в стандартное путем нормирования:

где z – новая переменная, которая используется вместо x;
m – математическое ожидание;
σ – стандартное отклонение.

Для выборочных данных берутся оценки:

Среднее арифметическое и дисперсия новой переменной z теперь также равны 0 и 1 соответственно. В этом легко убедиться с помощью элементарных алгебраических преобразований.

В литературе встречается название z-оценка. Это оно самое – нормированные данные. Z-оценку можно напрямую сравнивать с теоретическими вероятностями, т.к. ее масштаб совпадает с эталоном.

Посмотрим теперь, как выглядит плотность стандартного нормального распределения (для z-оценок). Напомню, что функция Гаусса имеет вид:

Подставим вместо (x-m)/σ букву z, а вместо σ – единицу, получим функцию плотности стандартного нормального распределения:

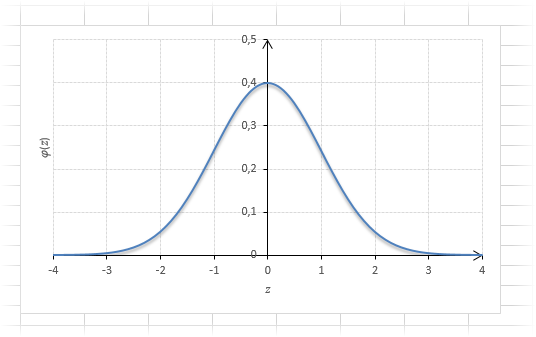
График плотности:

Центр, как и ожидалось, находится в точке 0. В этой же точке функция Гаусса достигает своего максимума, что соответствует принятию случайной величиной своего среднего значения (т.е. x-m=0). Плотность в этой точке равна 0,3989, что можно посчитать даже в уме, т.к. e⁰=1 и остается рассчитать только соотношение 1 на корень из 2 пи.

Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.

Функция стандартного нормального распределения позволяет рассчитывать вероятности.

Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.

Таблица нормального распределения

Таблицы нормального распределения встречаются двух типов:

— таблица плотности;

— таблица функции (интеграла от плотности).

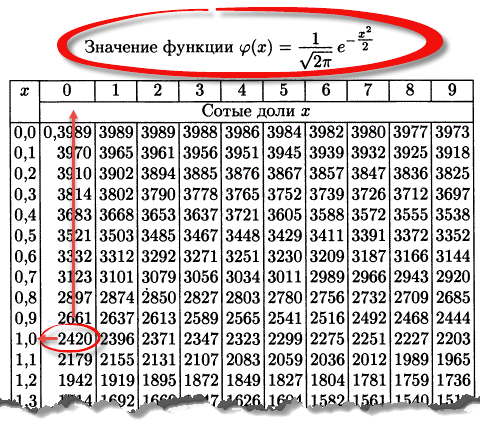
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.

В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).

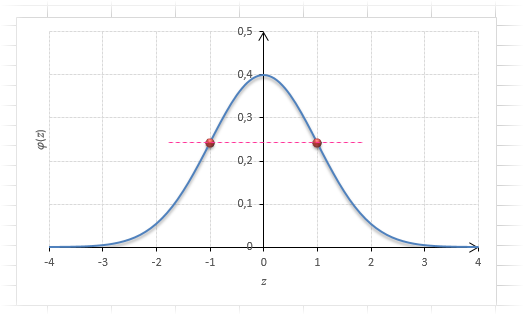
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.

Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.

На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.

В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.

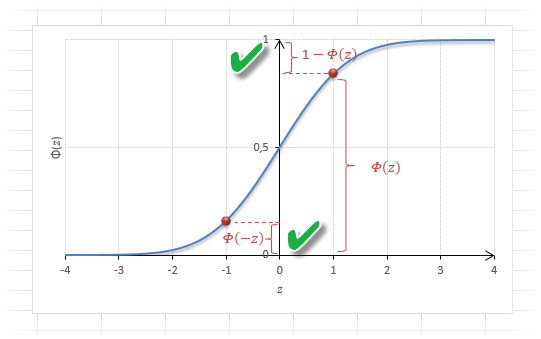
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:

Это факт показан на картинке:

Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.

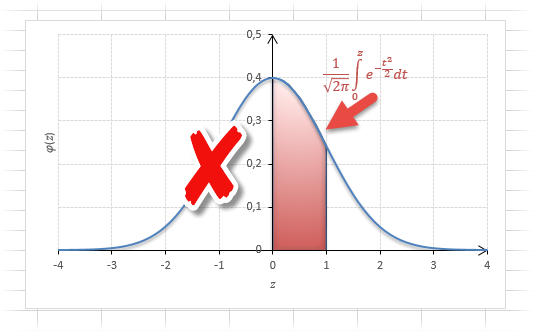
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:

Для наглядности можно взглянуть на рисунок.

На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.

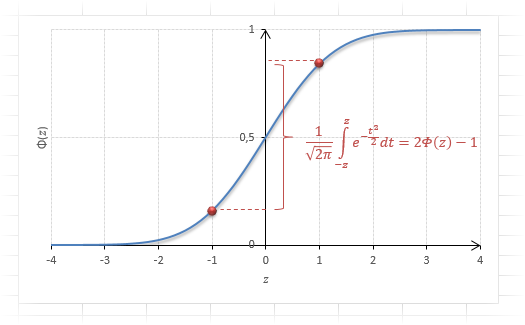
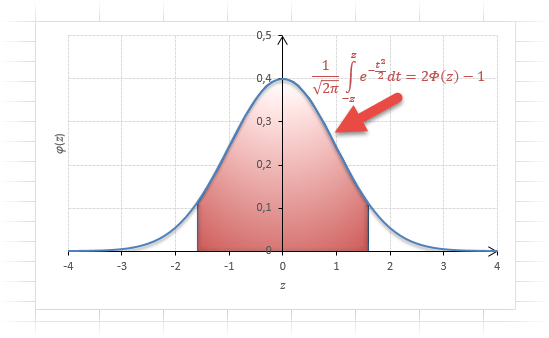
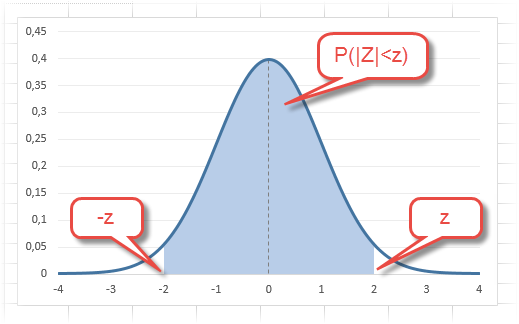
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:

Рисунок ниже.

Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.

Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.

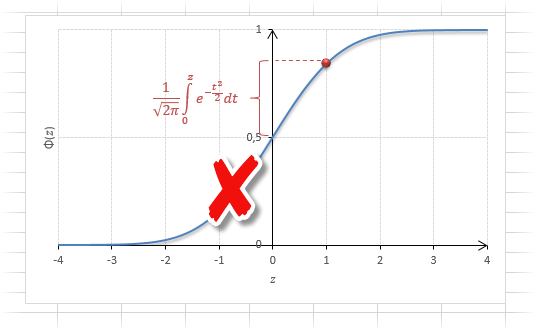
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:

Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.

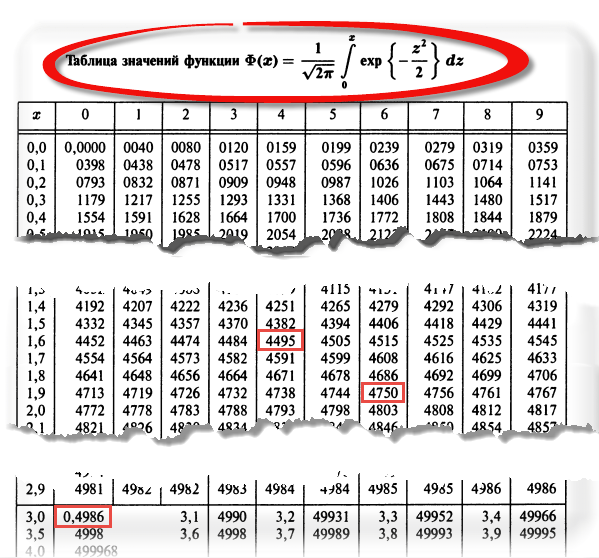
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.

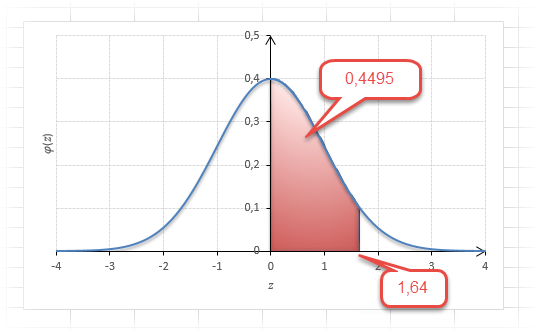
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.

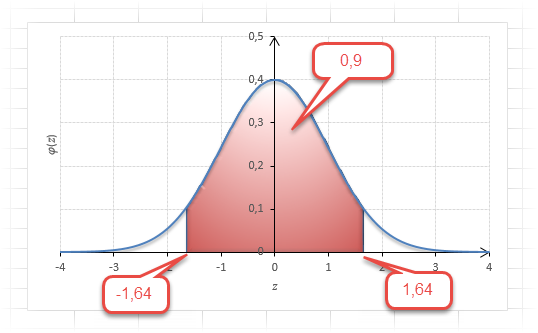
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.

Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).

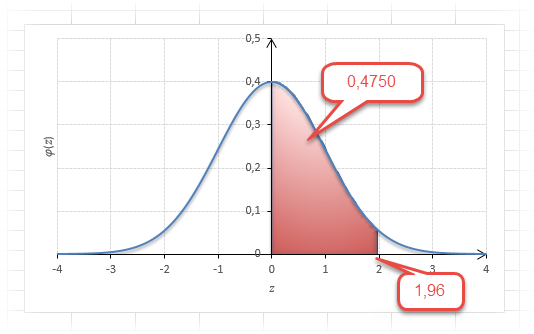
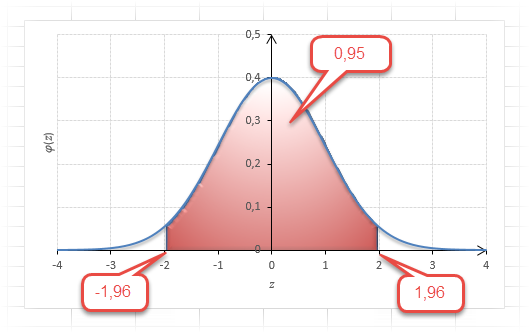
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).

Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.

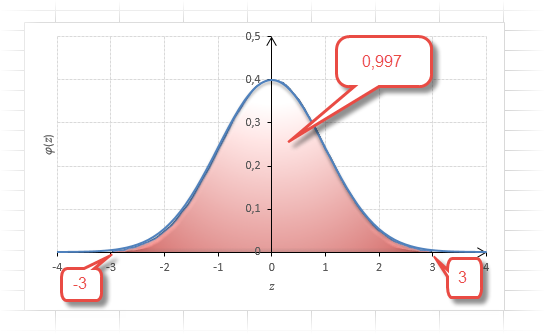
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.

Так выглядит правило 3 сигм для нормального распределения на диаграмме.

С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.

В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.

Функция НОРМ.СТ.РАСП

Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ(z) или вероятности Φ(z) по нормированным данным (z).

=НОРМ.СТ.РАСП(z;интегральная)

z – значение стандартизованной переменной

интегральная – если 0, то рассчитывается плотность ϕ(z), если 1 – значение функции Ф(z), т.е. вероятность P(Z<z).

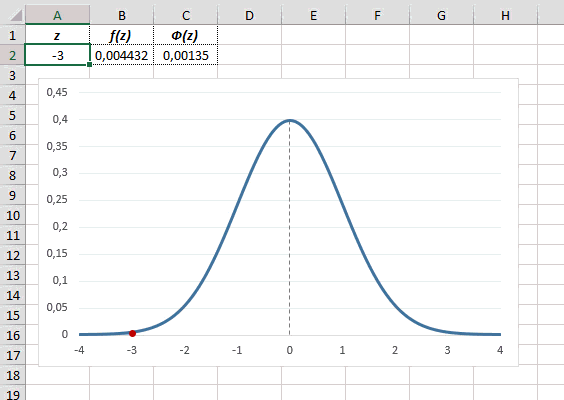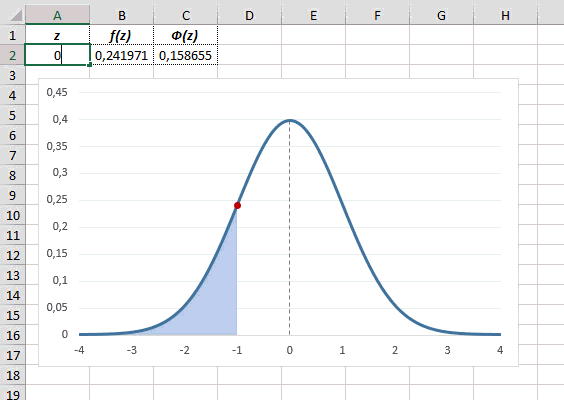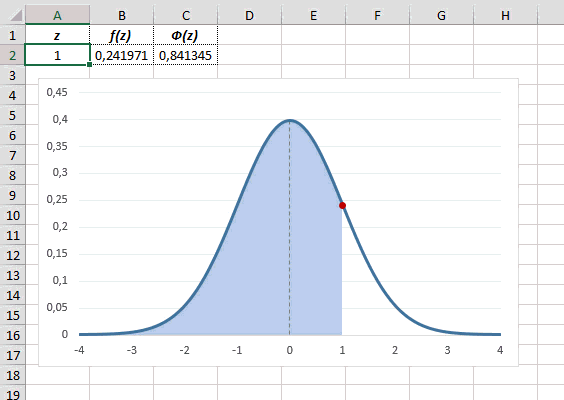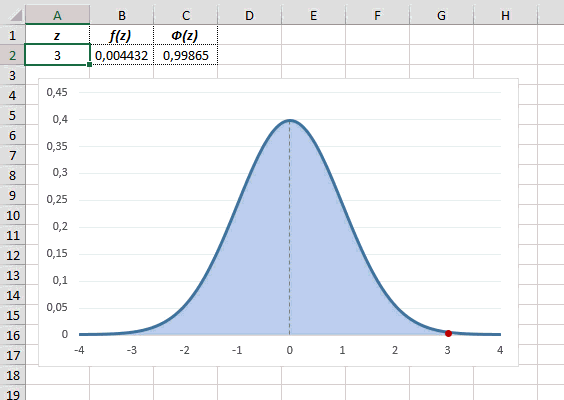
Рассчитаем плотность и значение функции для различных z: -3, -2, -1, 0, 1, 2, 3 (их укажем в ячейке А2).

Для расчета плотности потребуется формула =НОРМ.СТ.РАСП(A2;0). На диаграмме ниже – это красная точка.

Для расчета значения функции =НОРМ.СТ.РАСП(A2;1). На диаграмме – закрашенная площадь под нормальной кривой.

В реальности чаще приходится рассчитывать вероятность того, что случайная величина не выйдет за некоторые пределы от средней (в среднеквадратичных отклонениях, соответствующих переменной z), т.е. P(|Z|<z).

Определим, чему равна вероятность попадания случайной величины в пределы ±1z, ±2z и ±3z от нуля. Потребуется формула 2Ф(z)-1, в Excel =2*НОРМ.СТ.РАСП(A2;1)-1.

На диаграмме отлично видны основные основные свойства нормального распределения, включая правило трех сигм. Функция НОРМ.СТ.РАСП – это автоматическая таблица значений функции нормального распределения в Excel.

Может стоять и обратная задача: по имеющейся вероятности P(Z<z) найти стандартизованную величину z ,то есть квантиль стандартного нормального распределения.

Функция НОРМ.СТ.ОБР

НОРМ.СТ.ОБР рассчитывает обратное значение функции стандартного нормального распределения. Синтаксис состоит из одного параметра:

=НОРМ.СТ.ОБР(вероятность)

вероятность – это вероятность.

Данная формула используется так же часто, как и предыдущая, ведь по тем же таблицам искать приходится не только вероятности, но и квантили.

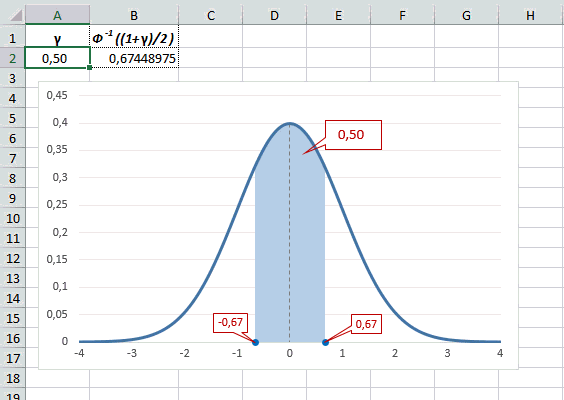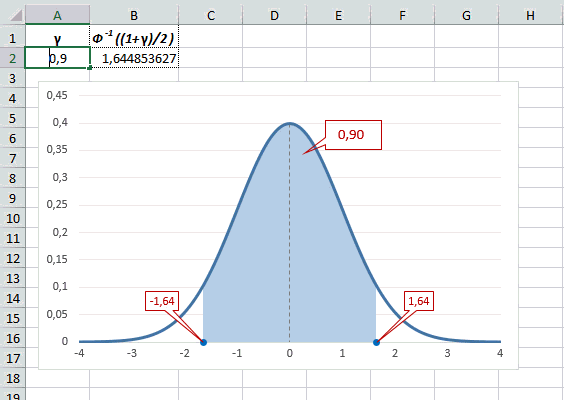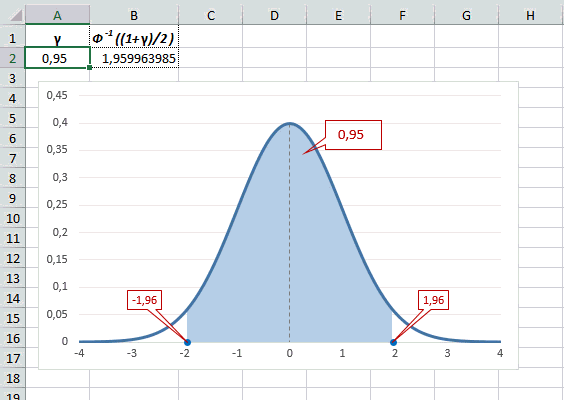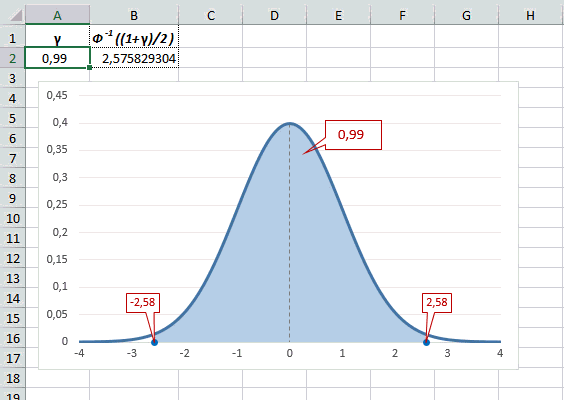
Например, при расчете доверительных интервалов задается доверительная вероятность, по которой нужно рассчитать величину z.

Учитывая то, что доверительный интервал состоит из верхней и нижней границы и то, что нормальное распределение симметрично относительно нуля, достаточно получить верхнюю границу (положительное отклонение). Нижняя граница берется с отрицательным знаком. Обозначим доверительную вероятность как γ (гамма), тогда верхняя граница доверительного интервала рассчитывается по следующей формуле.

Рассчитаем в Excel значения z (что соответствует отклонению от средней в сигмах) для нескольких вероятностей, включая те, которые наизусть знает любой статистик: 90%, 95% и 99%. В ячейке B2 укажем формулу: =НОРМ.СТ.ОБР((1+A2)/2). Меняя значение переменной (вероятности в ячейке А2) получим различные границы интервалов.

Доверительный интервал для 95% равен 1,96, то есть почти 2 среднеквадратичных отклонения. Отсюда легко даже в уме оценить возможный разброс нормальной случайной величины. В общем, доверительным вероятностям 90%, 95% и 99% соответствуют доверительные интервалы ±1,64, ±1,96 и ±2,58 σ.

В целом функции НОРМ.СТ.РАСП и НОРМ.СТ.ОБР позволяют произвести любой расчет, связанный с нормальным распределением. Но, чтобы облегчить и уменьшить количество действий, в Excel есть несколько других функций. Например, для расчета доверительных интервалов средней можно использовать ДОВЕРИТ.НОРМ. Для проверки статистической гипотезы о средней арифметической есть формула Z.ТЕСТ.

Рассмотрим еще пару полезных формул с примерами.

Функция НОРМ.РАСП

Функция НОРМ.РАСП отличается от НОРМ.СТ.РАСП лишь тем, что ее используют для обработки данных любого масштаба, а не только нормированных. Параметры нормального распределения указываются в синтаксисе.

=НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)

x – значение (или ссылка на ячейку), для которого рассчитывается плотность или значение функции нормального распределения

среднее – математическое ожидание, используемое в качестве первого параметра модели нормального распределения

стандартное_откл – среднеквадратичное отклонение – второй параметр модели

интегральная – если 0, то рассчитывается плотность, если 1 – то значение функции, т.е. P(X<x).

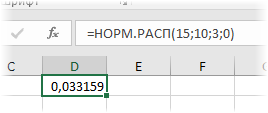
Например, плотность для значения 15, которое извлекли из нормальной выборки с матожиданием 10, стандартным отклонением 3, рассчитывается так:

Если последний параметр поставить 1, то получим вероятность того, что нормальная случайная величина окажется меньше 15 при заданных параметрах распределения. Таким образом, вероятности можно рассчитывать напрямую по исходным данным.

Функция НОРМ.ОБР

Это квантиль нормального распределения, т.е. значение обратной функции. Синтаксис следующий.

=НОРМ.ОБР(вероятность;среднее;стандартное_откл)

вероятность – вероятность

среднее – матожидание

стандартное_откл – среднеквадратичное отклонение

Назначение то же, что и у НОРМ.СТ.ОБР, только функция работает с данными любого масштаба.

Пример показан в ролике в конце статьи.

Моделирование нормального распределения

Для некоторых задач требуется генерация нормальных случайных чисел. Готовой функции для этого нет. Однако В Excel есть две функции, которые возвращают случайные числа: СЛУЧМЕЖДУ и СЛЧИС. Первая выдает случайные равномерно распределенные целые числа в указанных пределах. Вторая функция генерирует равномерно распределенные случайные числа между 0 и 1. Чтобы сделать искусственную выборку с любым заданным распределением, нужна функция СЛЧИС.

Допустим, для проведения эксперимента необходимо получить выборку из нормально распределенной генеральной совокупности с матожиданием 10 и стандартным отклонением 3. Для одного случайного значения напишем формулу в Excel.

=НОРМ.ОБР(СЛЧИС();10;3)

Протянем ее на необходимое количество ячеек и нормальная выборка готова.

Для моделирования стандартизованных данных следует воспользоваться НОРМ.СТ.ОБР.

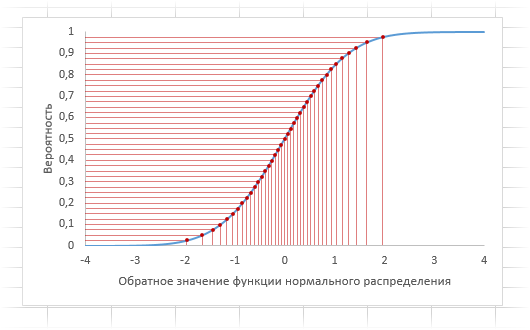
Процесс преобразования равномерных чисел в нормальные можно показать на следующей диаграмме. От равномерных вероятностей, которые генерируются формулой СЛЧИС, проведены горизонтальные линии до графика функции нормального распределения. Затем от точек пересечения вероятностей с графиком опущены проекции на горизонтальную ось.

На выходе получаются значения с характерной концентрацией около центра. Вот так обратный прогон через функцию нормального распределения превращает равномерные числа в нормальные. Excel позволяет за несколько секунд воспроизвести любое количество выборок любого размера.

Как обычно, прилагаю ролик, где все вышеописанное показывается в действии.

Скачать файл с примером.

Поделиться в социальных сетях:

Источник