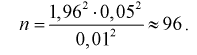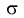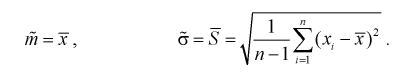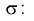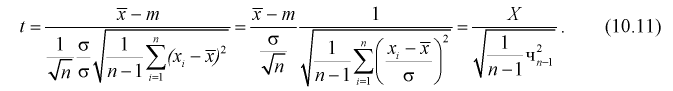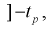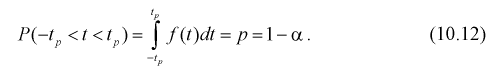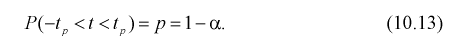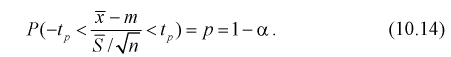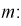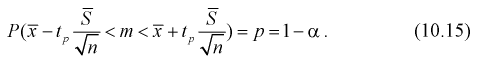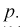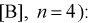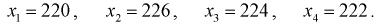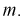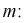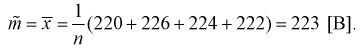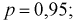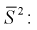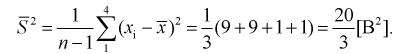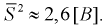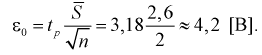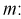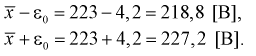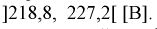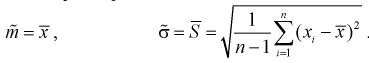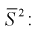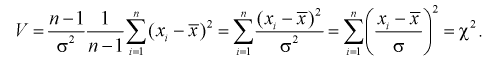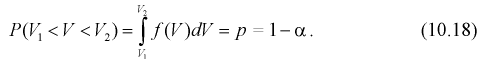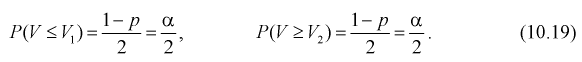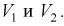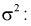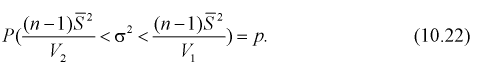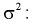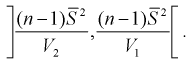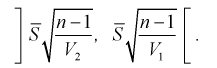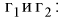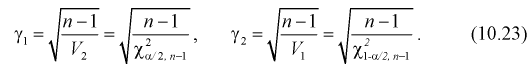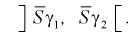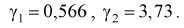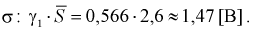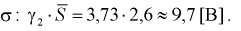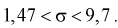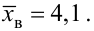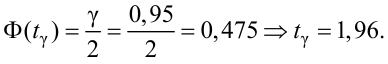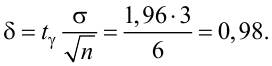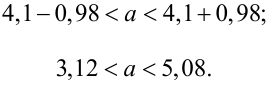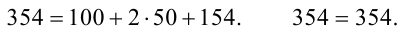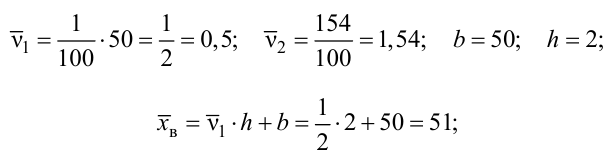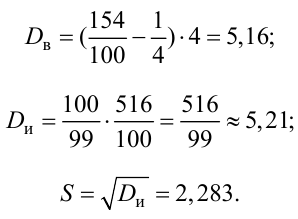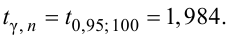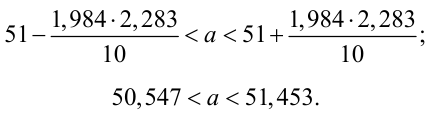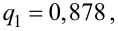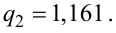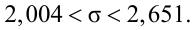Функция ДОВЕРИТ в Excel предназначена для определения доверительного интервала для среднего значения, найденного для генеральной совокупности, которая имеет нормальное распределение.
Другими словами, рассматриваемая функция позволяет определить допустимые отклонения для найденного среднего значения с учетом известных уровня значимости (заданная вероятность того, что некоторое значение находится в доверительном интервале) и стандартного отклонения (меры степени разброса значений относительно среднего значения для генеральной совокупности).
Как построить доверительный интервал нормального распределения в Excel
Поскольку интервал значений, в котором находится некоторая неизвестная величина, совпадает с областью, в которой могут изменяться значения этой величины, то вероятность правильности оценки данной величины стремится к нулю. Поэтому, принято устанавливать определенное значение вероятности для нахождения границ изменения некоторой величины. Значения, находящиеся между этими границами, называют доверительным интервалом.
Примечание:
Рассматриваемая функция была заменена функцией ДОВЕРИТ.НОРМ с версии Excel 2010. Функция ДОВЕРИТ была оставлена для обеспечения совместимости с документами, созданными в более ранних версиях табличного редактора.
Пример расчета доверительного интервала в Excel
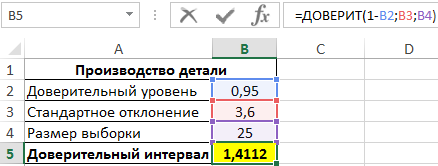
Пример 1. В заводском цехе производят деталь, длина которой должна составлять 200 мм. Стандартное отклонение от длины – 3,6 мм. Для контроля качества деталей из партии (генеральная совокупность) делают выборку из 25 деталей. Определить интервал с доверительный уровнем 95%.
Вид таблицы данных:
Для определения доверительного интервала используем функцию:
=ДОВЕРИТ(1-B2;B3;B4)
Описание параметров:
- 1-B2 – уровень значимости (рассчитан с учетом зависимости от доверительного уровня);
- B3 – значение стандартного отклонения;
- B4 – количество деталей в выборке.
Полученный результат:
То есть, границы доверительного интервала соответствуют: (Xср-1,4112;Xср+1,4112). Допустим, было определено среднее значение выборки – 199,5 мм. Тогда доверительный интервал примерно определяется как (198,1;200,9), при этом номинальная длина детали (200 мм) находится в доверительном диапазоне, то есть производственный процесс не нарушен.
Как найти границы доверительного интервала в Excel
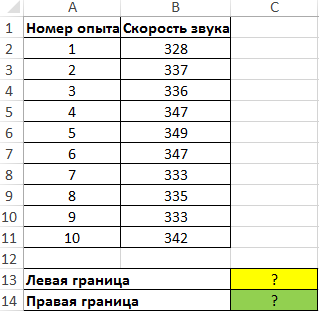
Пример 2. Были проведены опыты по определению скорости распространения звуковой волны в воздухе. Результаты 10 опытов записаны в таблицу. Определить левую и правую границы доверительного интервала для среднего значения.
Вид таблицы данных:
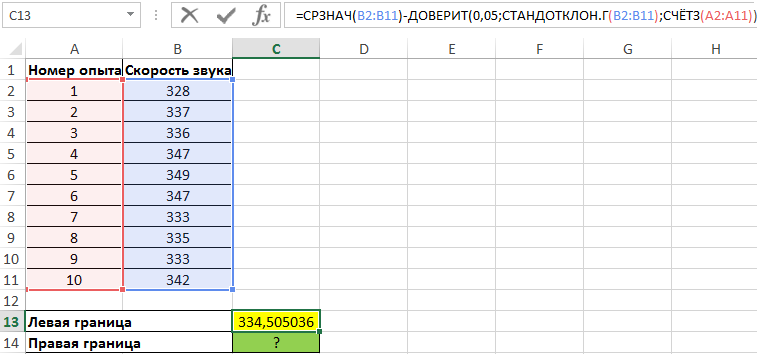
Для нахождения левой границы используем формулу:
В данном случае выборка и генеральная совокупность приняты как имеющиеся данные для 10 проведенных опытов. Среднее выборочное значение рассчитано с помощью функции СРЗНАЧ. Для получения левой границы доверительного интервала из данного значения вычитаем число, полученное в результате выполнения функции ДОВЕРИТ, в которой значение второго аргумента определено с помощью функции СТАНДОТКЛОН.Г, а число опытов – подсчетом количества ячеек функцией СЧЁТЗ.
Поскольку уровень значимости не задан, используем стандартное значение – 0,05.
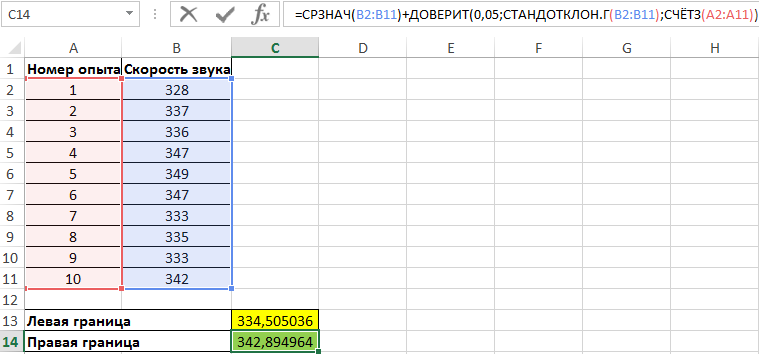
Правая граница определяется аналогично с разницей в том, что к среднему значению выборки прибавляется результат расчета функции ДОВЕРИТ:
Полученные значения:
Как посчитать доверительный интервал по функции ДОВЕРИТ в Excel
Функция имеет следующую синтаксическую запись:
=ДОВЕРИТ(альфа;стандартное_откл;размер)
Описание аргументов:
- альфа – обязательный, принимает числовое значение, характеризующее уровень значимости – вероятность отклонения нулевой (неверной) гипотезы в том случае, когда она на самом деле верна. Определяется как 1-, где — уровень доверия (вероятность нахождения истинного значения некоторой оцениваемой величины в определенном интервале, называемом доверительным).
- стандартное_откл – обязательный, принимает значение стандартного отклонения величины для генеральной совокупности значений (в Excel предусмотрена функция для определения этой величины — СТАНДОТКЛОН.Г).
- размер – обязательный, принимает числовое значение, характеризующее количество точек данных в анализируемой выборке (ее размер).
Примечания:
- Все аргументы функции должны указываться в виде числовых значений или данных, которые могут быть преобразованы в числа (например, текстовые строки с числами, логические ИСТИНА, ЛОЖЬ). В противном случае результатом выполнения функции ДОВЕРИТ будет код ошибки #ЧИСЛО!
- Аргумент альфа должен быть указан числовым значением из диапазона от 0 до 1 (оба включительно). Иначе функция ДОВЕРИТ вернет код ошибки #ЧИСЛО! Аналогичная ошибка возникает в случаях, когда аргумент стандартное_откл задан числом, взятым из диапазона отрицательных значений или нулем.
- Диапазон допустимых значений для аргумента размер – от 1 до бесконечности со знаком плюс.
Программа Эксель используется для выполнения различных статистических задач, одной из которых является вычисление доверительного интервала, который применяется как наиболее подходящая замена точечной оценки при малом объеме выборки.
Хотим сразу заметить, что сама процедура вычисления доверительного интервала довольно непростая, однако, в Excel существует ряд инструментов, призванных облегчить выполнение данной задачи. Давайте рассмотрим их.
Содержание
- Вычисление доверительного интервала
- Метод 1: оператор ДОВЕРИТ.НОРМ
- Метод 2: оператор ДОВЕРИТ.СТЬЮДЕНТ
- Заключение
Вычисление доверительного интервала
Доверительный интервал нужен для того, чтобы дать интервальную оценку каким-либо статическим данным. Основная цель этой операции – убрать неопределенности точечной оценки.
В Microsoft Excel существует два метода выполнения данной задачи:
- Оператор ДОВЕРИТ.НОРМ – применяется в случаях, когда дисперсия известна;
- Оператор ДОВЕРИТ.СТЬЮДЕНТ– когда дисперсия неизвестна.
Ниже мы пошагово разберем оба метода на практике.
Метод 1: оператора ДОВЕРИТ.НОРМ
Данная функция впервые была внедрена в арсенал программы в редакции Эксель 2010 года (до этой версии ее заменял оператор “ДОВЕРИТ”). Оператор входит в категорию “статистические”.
Формула функции ДОВЕРИТ.НОРМ выглядит так:
=ДОВЕРИТ.НОРМ(Альфа;Станд_откл;Размер)
Как мы видим, у функции есть три аргумента:
- “Альфа” – это показатель уровня значимости, который берется за основу при расчете. Доверительный уровень считается так:
1-"Альфа". Это выражение применимо в случае, если значение “Альфа” представлено в виде коэффициента. Например, 1-0,7=0,3, где 0,7=70%/100%.(100-"Альфа")/100. Применятся это выражение, если мы считаем доверительным уровень со значением “Альфа” в процентах. Например, (100-70)/100=0,3.
- “Стандартное отклонение” — соответственно, стандартное отклонение анализируемой выборки данных.
- “Размер” – объем выборки данных.
Примечание: У данной функции наличие всех трех аргументов является обязательным условием.
Оператор “ДОВЕРИТ”, который применялся в более ранних редакциях программы, содержит такие же аргументы и выполняет те же самые функции.
Формула функции ДОВЕРИТ выглядит следующим образом:
=ДОВЕРИТ(Альфа;Станд_откл;Размер)
Отличий в самой формуле нет никаких, лишь название оператора иное. В редакциях приложения Эксель 2010 года и последующих этот оператор находится в категории “Совместимость”. В более же старых версиях программы он находится в разделе статических функций.
Граница доверительного интервала определяется следующей формулой:
X+(-)ДОВЕРИТ.НОРМ
где Х – это среднее значение по заданному диапазону.
Теперь давайте разберемся, как применять эти формулы на практике. Итак, у нас есть таблица с различными данными 10-ти проведенных замеров. При этом, стандартное отклонение совокупности данных равняется 8.
Перед нами стоит задача – получить значение доверительного интервала с 95%-ым уровнем доверия.
- Первым делом выбираем ячейку для вывода результата. Затем кликаем по кнопке “Вставить функцию” (слева от строки формул).
- Откроется окно Мастера функций. Кликнув по текущей категории функций, раскрываем список и щелкаем в нем по строке “Статистические”.
- В предложенном перечне кликаем по оператору “ДОВЕРИТ.НОРМ”, затем жмем OK.
- Перед нами появится окно с настройками аргументов функции, заполнив которые нажимаем кнопку OK.
- в поле “Альфа” указываем уровень значимости. В нашей задаче предполагается 95%-ый уровень доверия. Подставив данное значение в формулу расчета, которую мы рассматривали выше, получаем выражение:
(100-95)/100. Пишем его в поле аргумента (или можно сразу написать результат вычисления, равный 0,05). - в поле “Станд_откл” согласно нашим условия, пишем цифру 8.
- в поле “Размер” указываем количество исследуемых элементов. В нашем случае было проведено 10 замеров, значит пишем цифру 10.
- в поле “Альфа” указываем уровень значимости. В нашей задаче предполагается 95%-ый уровень доверия. Подставив данное значение в формулу расчета, которую мы рассматривали выше, получаем выражение:
- Чтобы при изменении данных не пришлось заново настраивать функцию, можно автоматизировать ее. Для это применим функцию “СЧЁТ”. Ставим указатель в область ввода информации аргумента “Размер”, затем щелкаем по значку треугольника с левой стороны от строки формул и кликаем по пункту “Другие функции…”.
- В результате откроется еще одно окно Мастера функций. Выбрав категорию “Статистические”, кликаем по функции “СЧЕТ”, затем – OK.
- На экране отобразится еще одно окно с настройками аргументов функции, которая применяется для определения числа ячеек в заданном диапазоне, в которых находятся числовые данные.
Формула функции СЧЕТ пишется так:=СЧЁТ(Значение1;Значение2;...).
Количество доступных аргументов этой функции может достигать 255 штук. Здесь можно прописать, либо конкретные числа, либо адреса ячеек, либо диапазоны ячеек. Мы воспользуемся последним вариантом. Для этого кликаем по области ввода информации для первого аргумента, затем зажав левую кнопку мыши выделяем все ячейки одного из столбцов нашей таблицы (не считая шапки), после чего жмем кнопку OK. - В результате проделанных действий в выбранной ячейке будет выведено результат расчетов по оператору ДОВЕРИТ.НОРМ. В нашей задаче его значение оказалось равным 4,9583603.
- Но это еще не конечный результат в нашей задаче. Далее требуется рассчитать среднее значение по заданному интервалу. Для этого потребуется применить функцию “СРЗНАЧ”, которая выполняет задачу по вычислению среднего значения в пределах указанного диапазона данных.
Формула оператора пишется так:=СРЗНАЧ(число1;число2;...).
Выделяем ячейку, куда планируем вставить функцию и жмем кнопку “Вставить функцию”. - В категории “Статистические” выбираем нудный оператор “СРЗНАЧ” и кликаем OK.
- В аргументах функции в значении аргумента “Число” указываем диапазон, в который входят все ячейки со значениями всех замеров. Затем кликаем OK.
- В результате проделанных действий среднее значение будет автоматически подсчитано и выведено в ячейку с только что вставленной функцией.
- Теперь нам нужно рассчитать границы ДИ (доверительного интервала). Начнем с расчета значения правой границы. Выбираем ячейку, куда хотим вывести результат, и выполняем в ней сложение результатов, полученных с помощью операторов “СРЗНАЧ” и “ДОВЕРИТ.НОРМ”. В нашем случае формула выглядит так:
A14+A16. После ее набора жмем Enter. - В результате будет произведен расчет и результат немедленно отобразится в ячейке с формулой.
- Затем аналогичным способом выполняем расчет для получения значения левой границы ДИ. Только в этом случае значение результата “ДОВЕРИТ.НОРМ” нужно не прибавлять, а вычитать из результата, полученного при помощи оператора “СРЗНАЧ”. В нашем случае формула выглядит так:
=A16-A14. - После нажатия Enter мы получим результат в заданной ячейке с формулой.
Примечание: В пунктах выше мы постарались максимально подробно расписать все шаги и каждую применяемую функцию. Однако все прописанные формулы можно записать вместе, в составе одной большой:
- Для определения правой границы ДИ общая формула будет выглядеть так:
=СРЗНАЧ(B2:B11)+ДОВЕРИТ.НОРМ(0,05;8;СЧЁТ(B2:B11)). - Точно также и для левой границы, только вместо плюса нужно поставить минус:
=СРЗНАЧ(B2:B11)-ДОВЕРИТ.НОРМ(0,05;8;СЧЁТ(B2:B11)).
Метод 2: оператор ДОВЕРИТ.СТЬЮДЕНТ
Теперь давайте познакомимся со вторым оператором для определения доверительного интервала – ДОВЕРИТ.СТЬЮДЕНТ. Данная функция была внедрена в программу относительно недавно, начиная с версии Эксель 2010, и направлена на определение ДИ выбранной совокупности данных с применением распределения Стьюдента, при неизвестной дисперсии.
Формула функции ДОВЕРИТ.СТЬЮДЕНТ выглядит следующим образом:
=ДОВЕРИТ.СТЬЮДЕНТ(Альфа;Cтанд_откл;Размер)
Давайте разберем применение данного оператора на примере все той же таблицы. Только теперь стандартное отклонение по условиям задачи нам неизвестно.
- Сначала выбираем ячейку, куда планируем вывести результат. Затем кликаем по значку “Вставить функцию” (слева от строки формул).
- Откроется уже хорошо знакомое окно Мастера функций. Выбираем категорию “Статистические”, затем из предложенного списка функций щелкаем по оператору “ДОВЕРИТ.СТЬЮДЕНТ”, после чего – OK.
- В следующем окне нам нужно настроить аргументы функции:.
- В выбранной ячейке отобразится значение доверительного интервала согласно заданным нами параметрам.
- Далее нам нужно рассчитать значения границ ДИ. А для этого потребуется получить среднее значение по выбранному диапазону. Для этого снова применим функцию “СРЗНАЧ”. Алгоритм действий аналогичен тому, что был описан в первом методе.
- Получив значение “СРЗНАЧ”, можно приступать к расчетам границ ДИ. Сами формулы ничем не отличаются от тех, что использовались с оператором “ДОВЕРИТ.НОРМ”:
- Правая граница ДИ=СРЗНАЧ+ДОВЕРИТ.СТЬЮДЕНТ
- Левая граница ДИ=СРЗНАЧ-ДОВЕРИТ.СТЬЮДЕНТ
Заключение
Арсенал инструментов Excel невероятно большой, и наряду с распространенными функциями, программа предлагает большое разнообразие специальных функций, которые помогут существенно облегчить работу с данными. Возможно, описанные выше шаги некоторым пользователям, на первый взгляд, могут показаться сложными. Но после детального изучения вопроса и последовательности действий, все станет намного проще.
Содержание:
Интервальные оценки параметров распределения. Непрерывное и дискретное распределения признаков:
В материалах сегодняшней лекции мы рассмотрим интервальные оценки параметров распределения, а именно непрерывное и дискретное распределения признаков генеральной и выборочной совокупности.
Статистические ряды и их геометрическое изображение дают представление о распределении наблюдаемой случайной величины X по данным выборки. Во многих задачах вид распределения случайной величины X известен, необходимо получить приближённое значение неизвестных параметров этого распределения: m,
Пусть
Точечной оценкой 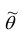
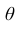
Очевидно, что 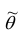
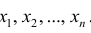
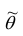
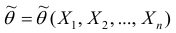
Точечная оценка 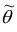
1. Состоятельность. Оценка 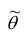
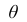
состоятельной, если 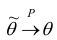
Состоятельность оценки можно установить с помощью теоремы: если 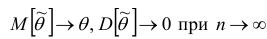
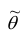
2. Несмещённость. Оценка 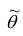
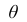
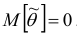
Для оценки параметра 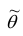
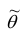
Отсюда вытекает третье свойство.
3. Эффективность. Несмещённая оценка 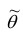
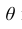
Запишем точечные оценки числовых характеристик случайной величины X.
1. Точечная оценка 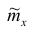
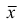
Проверим свойства оценки:
а) состоятельность следует из теоремы Чебышева: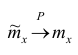
б) несмещённость:
в)эффективность:
так как
2. Точечная оценка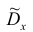
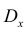
она обладает свойствами: состоятельность, несмещённость,
эффективность.
3. Точечная оценка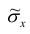
Интервальные оценки
При статистической обработке результатов наблюдений необходимо знать не только точечную оценку 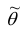
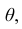
Характеристики вариационного ряда
В материалах сегодняшней лекции мы рассмотрим характеристики вариационного ряда.
Вариационные ряды
Установление закономерностей, которым подчиняются массовые случайные явления, основано на изучении статистических данных — сведений о том, какие значения принял в результате наблюдений интересующий исследователя признак.
Пример:
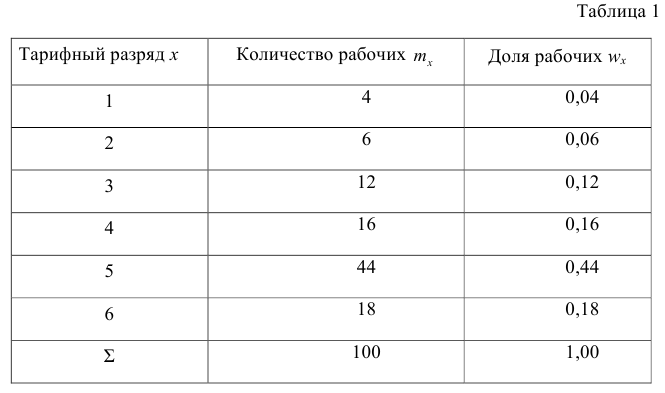
Исследователь, интересующийся тарифным разрядом рабочих механического цеха, в результате опроса 100 рабочих получил следующие сведения:
Здесь признаком является тарифный разряд, а полученные о нём сведения образуют статистические данные. Для изучения данных прежде всего необходимо их сгруппировать. Расположим наблюдавшиеся значения признака в порядке возрастания. Эта операция называется ранжированием статистических данных. В результате получим следующий ряд, который называется ранжированным:
(1, 1, 1, 1) — 4 раза; (2, 2, 2, 2, 2, 2) — 6 раз; (3, 3, …, 3) — 12 раз; (4, 4, …, 4) —
16 раз; (5, 5, …, 5) — 44 раза; (6, 6, …, 6) — 18 раз.
Из ранжированного ряда следует, что признак (тарифный разряд) принял шесть различных значений: первый, второй и т.д. до шестого разряда.
В дальнейшем различные значения признака условимся называть вариантами, а под варьированием — понимать изменение значений признака. Если признак по своей сущности таков, что различные его значения не могут отличаться друг от друга меньше чем на некоторую конечную величину, то говорят, что это дискретно варьирующий признак.
Тарифный разряд — дискретно варьирующий признак: его различные значения не могут отличаться друг от друга меньше, чем на единицу. В примере этот признак принял 6 различных значений — 6 вариантов: вариант 1 повторился 4 раза, вариант 2-6 раз и т.д. Число, показывающее. сколько раз встречается вариант л* в ряде наблюдений, называется частотой варианта 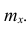
Вместо частоты варианта x можно рассматривать её отношение к общему числу наблюдений n, которое называется частостью варианта х и обозначается 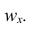
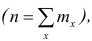
Таблица, позволяющая судить о распределении частот (или частостей) между вариантами, называется дискретным вариационным рядом.
В примере 1 была поставлена задача изучить результаты наблюдений. Если просмотр первичных данных не позволил составить представление о варьировании значений признака, то, рассматривая вариационный, ряд, можно сделать следующие выводы: тарифный разряд колеблется от 1-го до 6-го; наиболее часто встречается 5-й тарифный разряд; с ростом тарифного разряда (до 5-го разряда) растёт число рабочих, имеющих соответствующий разряд.
Наряду с понятием частоты используют понятие накопленной частоты, которую обозначают 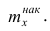
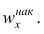
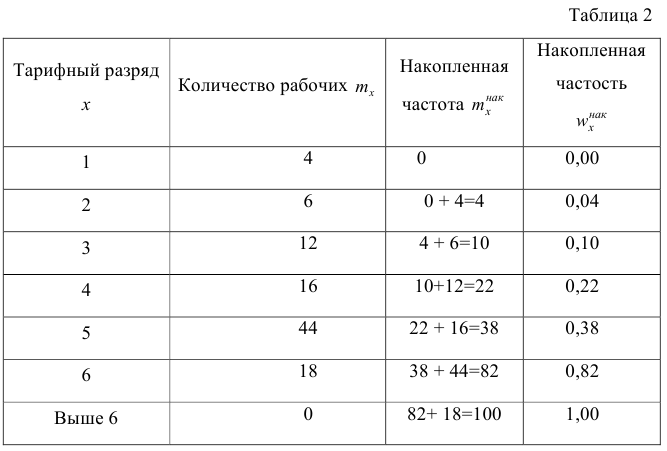
В дискретном вариационном ряду накопленные частоты (частости) вычисляются для каждого варианта и являются результатом последовательного суммирования частот (частостей). Накопленные частоты (частости) для вариационного ряда, заданного в табл. 1, вычислены в табл. 2.
Например, варианту 1 соответствует накопленная частота, равная нулю, так как среди опрошенных рабочих не было таких, у которых тарифный разряд был бы меньше 1-го; варианту 5 соответствует накопленная частота 38, так как было 4+6+12+16 рабочих с тарифным разрядом, меньшим 5-го, накопленная частость для этого варианта равна 0,38 (38: 100); если тарифный разряд выше 6-го, то ему соответствует накопленная частота 100, так как тарифный разряд всех опрошенных рабочих не выше 6-го.
Пример:
Исследователь, изучающий выработку на одного рабочего-станочника механического цеха в отчётном году в процентах к предыдущему году, получил следующие данные (в целых процентах) по 117 рабочим:
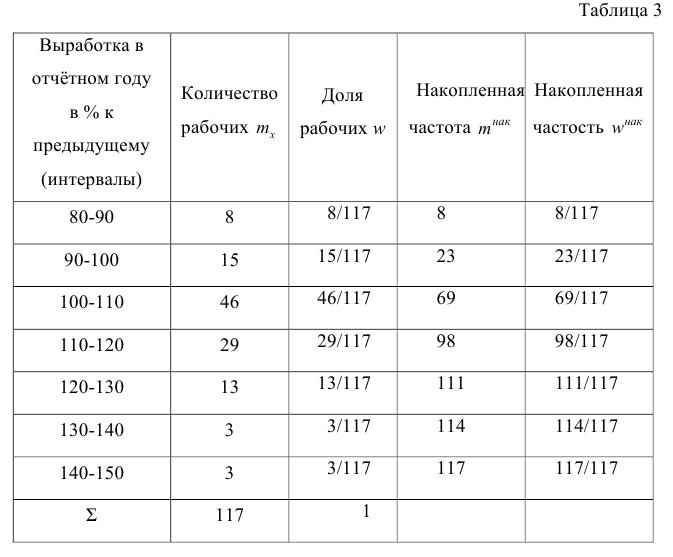
В этом примере признаком является выработка в отчётном году в процентах к предыдущему. Очевидно, что значения, принимаемые этим признаком, могут отличаться одно от другого на сколь угодно малую величину, т. е. признак может принять любое значение в некотором числовом интервале (только для упрощения дальнейших расчетов полученные данные округлены до целых процентов). Такой признак называют непрерывно варьирующим. По приведенным данным трудно выявить характерные черты варьирования значений признака. Построение дискретного вариационного ряда также не даст желаемых результатов (слишком велико число различных наблюдавшихся значений признака). Для получения ясной картины объединим в группы рабочих, у которых величина выработки колеблется, например, в пределах 10%. Сгруппированные данные представим в табл. 3.
В табл. 3 частоты m показывают, во скольких наблюдениях признак принял значения, принадлежащие тому или иному интервалу. Такую частоту называют интервальной, а отношение её к общему числу наблюдений — интервальной частостью w. Таблицу, позволяющую судить о распределении частот (или частостей) между интервалами варьирования значений признака, называют интервальным вариационным рядом.
Интервальный вариационный ряд, представленный в табл. 3, позволяет выявить закономерности распределения рабочих по интервалам выработки. В табл. 3 для верхних границ интервалов приведены накопленные частоты (частости) (они получены последовательным суммированием интервальных частот (частостей), начиная с частоты (частости) первого интервала). Например, для верхней границы третьего интервала, равной 110, накопленная частота равна 69; так как 8+15+46 рабочих имели выработку меньше 110%, накопленная частость равна 69/117.
Интервальный вариационный ряд строят по данным наблюдений за непрерывно варьирующим признаком, а также за дискретно варьирующим, если велико число наблюдавшихся вариантов. Дискретный вариационный ряд строят только для дискретно варьирующего признака.
Иногда интервальный вариационный ряд условно заменяют дискретным. Тогда серединное значение интервала принимают за вариант х, а соответствующую интервальную частоту — за
Построение интервального вариационного ряда
Для построения интервального вариационного ряда необходимо определить величину интервала, установить полную шкалу интервалов, в соответствии с ней сгруппировать результаты наблюдений. В примере 2 при выборе величины интервала учитывались требования наибольшего удобства отсчётов. Интервал был принят равным 10% и оказался удачным. Построенный интервальный ряд позволил выявить закономерности варьирования значений признака. Для определения оптимального интервала h, т.е. такого, при котором построенный интервальный ряд не был бы слишком громоздким и в то же время позволял выявить характерные черты рассматриваемого явления, можно использовать формулу Стэрджеса
где 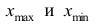
За начало первого интервала рекомендуется принимать величину
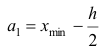
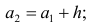
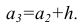
После установления шкалы интервалов следует сгруппировать результаты наблюдений. Границы последовательных интервалов записывают в столбец слева, а затем, просматривая статистические данные в том порядке, в каком они были получены, проставляют чёрточки справа от соответствующего интервала. В интервал включается данные, большие или равные нижней границе интервала и меньшие верхней границы. Целесообразно каждые пятое и шестое наблюдения отмечать диагональными черточками, пересекающими квадрат из четырёх предшествующих. Общее количество чёрточек, проставленных против какого-либо интервала, определяет его частоту.
Графическое изображение вариационных рядов
Графическое изображение вариационного ряда позволяет представить в наглядной форме закономерности варьирования значений признака. Наиболее широко используются следующие виды графического изображения вариационных рядов: полигон, гистограмма, кумулятивная
кривая.
Полигон, как правило, служит для изображения дискретного вариационного ряда. Для его построения в прямоугольной системе координат наносят точки с координатами 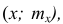
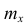
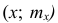
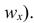
Гистограмма служит для изображения только интервального вариационного ряда. Для её построения в прямоугольной системе координат по оси абсцисс откладывают отрезки, изображающие интервалы варьирования, и на этих отрезках, как на основании, строят прямоугольники с высотами, равными частотам (или частостям) соответствующего интервала. В результате получают ступенчатую фигуру, состоящую из прямоугольников, которую и называют гистограммой.
Если по оси абсцисс выбрать такой масштаб, чтобы ширина интервала была равна единице, и считать, что по оси ординат единица масштаба соответствует одному наблюдению, то площадь гистограммы равна общему числу наблюдений, если по оси ординат откладывались частоты, и эта площадь равна единице, если откладывались частости.
Иногда интервальный ряд изображают с помощью полигона. В этом случае интервалы заменяют их серединными значениями и к ним относят интервальные частоты. Для полученного дискретного ряда строят полигон.
Кумулятивная кривая (кривая накопленных частот или накопленных частостей) строится следующим образом. Если вариационный ряд дискретный, то в прямоугольной системе координат строят точки с координатами 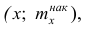
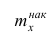
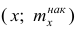
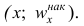
Если вариационный ряд интервальный, то по оси абсцисс откладывают интервалы. Верхним границам интервалов соответствуют накопленные частоты (или накопленные частости); нижней границе первого интервала — накопленная частота, равная нулю. Построив кумулятивную кривую, можно приблизительно установить число наблюдений (или их долю в общем количестве наблюдений), в которых признак принял значения, меньшие заданного.
Построение вариационного ряда — первый шаг к осмысливанию ряда наблюдений. Однако на практике этого недостаточно, особенно когда необходимо сравнить два ряда или более. Сравнению подлежат только так называемые однотипные вариационные ряды, т. е. ряды, которые построены по результатам обработки сходных статистических данных. Например, можно сравнивать распределения рабочих по возрасту на двух заводах или распределения времени простоев станков одного вида. Однотипные вариационные ряды обычно имеют похожую форму при графическом изображении, однако могут отличаться друг от друга, а именно: иметь различные значения признака, вокруг которых концентрируются наблюдения (меры этой качественной особенности называется средними величинами); различаться рассеянием наблюдений вокруг средних величин (меры этой особенности получили название показателей вариации).
Средние величины и показатели вариации позволяют судить о характерных особенностях вариационного ряда и называются статистическими характеристиками. К статистическим характеристикам относятся также показатели, характеризующие различия в скошенности полигонов и различия в их островершинности.
Средние величины
Средние величины являются как бы «представителями» всего ряда наблюдений, поскольку вокруг них концентрируются наблюдавшиеся значения признака. Заметим, что только для качественно однородных наблюдений имеет смысл вычислять средние величины.
Различают несколько видов средних величин: средняя арифметическая, средняя геометрическая, средняя гармоническая, средняя квадратическая, средняя кубическая и т.д. При выборе вида средней величины необходимо прежде всего ответить на вопрос: какое свойство ряда мы хотим представить средней величиной или, иначе говоря, какая цель преследуется при вычислении средней? Это свойство, получившее название определяющего, и определяет вид средней. Понятие определяющего свойства впервые введено советским статистиком А. Я. Боярским.
Наиболее распространенной средней величиной является средняя арифметическая. Пусть 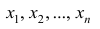
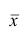
Так как 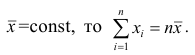
вычисления средней арифметической по данным наблюдений:
Если по наблюдениям построен вариационный ряд, то средняя арифметическая
где x- — вариант, если ряд дискретный, и центр интервала, если ряд интервальный;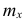
Частоты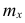
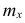
Очевидно, что если по данным наблюдений построен дискретный вариационный ряд, то формулы (3) и (4) дают одинаковые значения средней арифметической. Если же по наблюдениям построен интервальный ряд, то средние арифметические, вычисленные по формулам
(3) и (4), могут не совпадать, так как в формуле (4) значения признака внутри каждого интервала принимаются равными центрам интервалов. Ошибка, возникающая в результате такой замены, вообще говоря, очень мала, если наблюдения, распределены равномерно вдоль каждого интервала, а не скапливаются к одноименным границам интервалов (т.е. либо все к нижним границам, либо все к верхним границам).
Среднюю арифметическую для вариационного ряда можно вычислять по формуле
которая является следствием формулы (4). Действительно,
Свойство, определяющее среднюю арифметическую, сводилось к требованию неизменности суммы наблюдений при замене каждого из них средней арифметической. При решении практических задач может оказаться необходимым вычислить такую среднюю 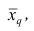
где q — положительное или отрицательное число. Среднюю 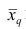
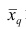
Сравнивая формулы (7) и (3), можно сделать вывод, что степенная средняя первого порядка есть не что иное, как средняя арифметическая, т.е.
При q=-l из формулы (7) получаем выражение для средней гармонической, при q=2 — для среднеквадратической, при q=3 — для средней кубической и т.д.
Средней геометрической 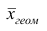
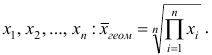
Рассмотрим основные свойства средней арифметической.
1°. Сумма отклонений результатов наблюдений от средней арифметической равна нулю.
Доказательство. Исходя из определяющего свойства (2) средней арифметической, получаем
Если по результатам наблюдений построен вариационный ряд и средняя арифметическая взвешенная, то свойство 1° формулируется так: сумма произведений отклонений вариантов от средней арифметической на соответствующие частоты равна нулю. Действительно, на основании формулы (4) получаем
или
2°. Если все результаты наблюдений уменьшить (увеличить) на одно и то же число, то средняя арифметическая уменьшится (увеличится) на то же число. (Доказательство свойств 2° и 3° проведём в предположении, что по результатам наблюдений построен вариационный ряд и средняя арифметическая — взвешенная).
Доказательство. Очевидно, что при уменьшении вариантов на одно и то же число с соответствующие им частоты останутся прежними. Поэтому взвешенная средняя арифметическая для изменённого вариационного ряда такова:
Аналогично можно показать, что 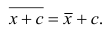
3°. Если все результаты наблюдений уменьшить (увеличить) в одно и то же число раз, то средняя арифметическая уменьшится (увеличится) во столько же раз.
Доказательство. Очевидно, что при уменьшении вариантов в k раз их частоты останутся прежними. Поэтому средняя арифметическая для изменённого ряда
Аналогично можно доказать, что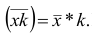
(уменьшить) в k раз, то получим среднюю арифметическую для первоначального вариационного ряда.
4°. Если ряд наблюдений состоит из двух групп наблюдений, то средняя арифметическая всего ряда равна взвешенной средней арифметической групповых средних, причём весами являются объёмы групп.
Пусть 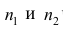
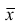
средняя арифметическая для всего ряда 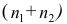
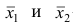
Доказательство. Исходя из определяющего свойству средней арифметической, имеем: произведение 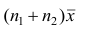
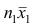
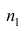
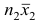
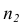
Следовательно,
Следствие. Если ряд наблюдений состоит из k групп наблюдений, то средняя арифметическая всего ряда 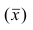
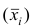
5°. Средняя арифметическая для сумм (разностей) взаимно соответствующих значений признака двух рядов наблюдений с одинаковым числом наблюдений равна сумме (разности) средних арифметических этих рядов.
Пусть 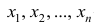
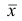
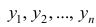
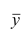
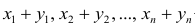
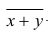
Доказательство. Имеем
Аналогично можно показать, что
Следствие. Средняя арифметическая алгебраической суммы соответствующих значений признака нескольких рядов наблюдений с одинаковым числом наблюдений равна алгебраической сумме средних арифметических этих рядов.
Вычисление средней арифметической вариационного ряда непосредственно по формуле (4) приводит к громоздким расчётам, если числовые значения вариантов и соответствующие им частоты велики. Поэтому часто используют следующий способ, основанный на свойствах 3° и 2° средней арифметической: среднюю вычисляют не по первоначальным вариантам л-, а по уменьшенным на не которое число с, а затем разделённым на некоторое число k т.е. для вариантов 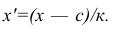
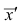
Действительно, принимая во внимание свойства 3° и 2° средней арифметической, получаем
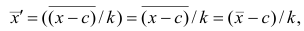
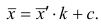
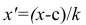
Медиана и мода
Наряду со средними величинами в качестве описательных характеристик вариационного ряда применяют медиану и моду.
Медианой 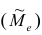
Пусть проведено нечётное число наблюдений, т.е. n=2q—1, и результаты наблюдений проранжированы и выписаны в следующий ряд:
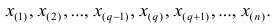
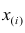
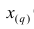
Если проведено чётное число наблюдений, т.е. n=2q, то на середину ранжированного ряда 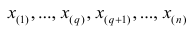
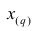
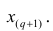
, т.е.
Покажем на примерах на практическом занятии, как определяется медиана дискретного и интервального вариационных рядов.
В общем случае медиана для интервального вариационного ряда определяется по формуле
или по следующей формуле, полученной из формулы (9) в результате деления числителя и знаменателя входящей в неё дроби на n:
где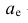
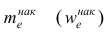
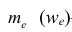
Модой 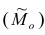
В случае интервального вариационного ряда мода вычисляется по следующей формуле (вывод формулы можно найти в кн.: Венецкий И. Г Кильдишев Г. С. Теория вероятностей и математическая статистика. М., 1975.):
или по тождественной формуле:
где 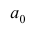
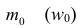
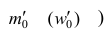
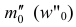
Моду используют в случаях, когда нужно ответить на вопрос, какой товар имеет наибольший спрос, каковы преобладающие в данный момент уровни производительности труда, себестоимости и т. д. Модальная производительность, себестоимость и т.д. помогают вскрыть ресурсы, имеющиеся в экономике.
Показатели вариации
Средние величины, характеризуя вариационный ряд числом, не отражают изменчивости наблюдавшихся значений признака, т.е. вариацию. Простейшим показателем вариации является вариационный размах 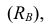
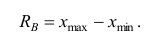
Вариационный размах — приближённый показатель вариации, так как почти не зависит от изменения вариантов, а крайние варианты, которые используются для его вычисления, как правило, ненадёжны.
Более содержательными являются меры рассеяния наблюдений вокруг средних величин. Средняя арифметическая является основным видом средних, поэтому ограничимся рассмотрением мер рассеяния наблюдений вокруг средней арифметической.
Сумма отклонений результатов наблюдений 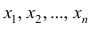
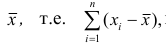
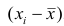
Средним линейным отклонением (d) называют среднюю арифметическую абсолютных величин отклонений результатов наблюдений от их средней ар и ф метической:
Эмпирической дисперсией 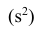
Если по результатам наблюдений построен вариационный ряд, то эмпирическая дисперсия
Вместо эмпирической дисперсии в качестве меры рассеяния наблюдений вокруг средней арифметической часто используют эмпирическое среднеквадратическое отклонение, равное арифметическому значению корня квадратного из дисперсии и имеющее ту же размерность, что и значения признака.
где x — вариант (если ряд дискретный) и центр интервала (если ряд интервальный); 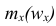
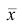
Для краткости величину 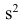
Приведем свойство минимальности эмпирической дисперсии: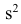
если
Доказательство. Найдём экстремум функции 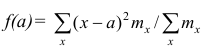
этого решим уравнение 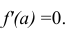
Так как 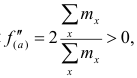
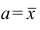
Можно показать, что среднее линейное отклонение не обладает свойством минимальности. Поэтому наиболее употребительными мерами рассеяния
Для вариационного ряда среднеквадратическое отклонение наблюдений вокруг средней арифметической являются эмпирическая дисперсия и эмпирическое среднеквадратическое отклонение.
Итальянский статистик Коррадо Джинни предложил в качестве показателя вариации использовать величину 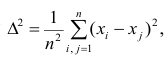
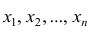
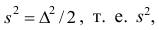
Свойства эмпирической дисперсии
Рассмотрим основные свойства эмпирической дисперсии, знание которых позволит упростить её вычисление.
1 °. Дисперсия постоянной величины равна нулю.
Доказательство этого свойства очевидно вытекает из того, что дисперсия является показателем рассеяния наблюдений вокруг средней арифметической, а средняя арифметическая постоянной равна этой постоянной.
2°. Если все результаты наблюдений уменьшить (увеличить) на одно и то же число с, то дисперсия не изменится.
Доказательство свойств 2° и 3° проведём в предположении, что по результатам наблюдений построен вариационный ряд.
Доказательство. Если все варианты уменьшить на число с, то в соответствии со свойством 2° средней арифметической средняя для измененного вариационного ряда равна 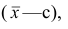
,т.е. совпадает с дисперсией первоначального вариационного ряда. Аналогично можно показать, что
Доказанное свойство позволяет вычислять дисперсию не по данным вариантам, а по уменьшенным, (увеличенным) на одно и то же число с, так как дисперсия, вычисленная для измененного ряда, равна первоначальной.
3°. Если все результаты наблюдений уменьшить (увеличить) в одно и то же число k раз, то дисперсия уменьшится (увеличится) в 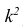
Доказательство. Если все варианты уменьшить в k раз, то, согласно свойству 3 средней арифметической, средняя для измененного вариационного ряда равна 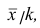
Аналогично можно показать, что
Это свойство позволяет эмпирическую дисперсию вычислять не по данным вариантам, а по уменьшенным (увеличенным) в одно и то же число k раз. Если дисперсию, вычисленную для измененного ряда, увеличить (уменьшить) в 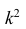
Следствие. Если все варианты уменьшить (увеличить) в k раз, то среднеквадратическое отклонение уменьшится (увеличится) в число раз, равное k.
Следствие очевидно вытекает из определения среднеквадратического
отклонения.
Прежде чем рассматривать следующее свойство дисперсии, докажем теорему.
Теорема. Эмпирическая дисперсия равна разности между средней
арифметической квадратов наблюдений и квадратом средней
арифметической, т.е.
Доказательство проведём для случая взвешенных средних арифметических, т.е.
Доказательство. Тождественно преобразуя выражения для дисперсии, имеем
4°, Если ряд наблюдений состоит из двух групп наблюдений, то дисперсия всего ряда равна сумме средней арифметической групповых дисперсий и средней арифметической квадратов отклонений групповых средних от средней всего ряда, причем ‘ при вычислении средних арифметических весами являются объемы групп.
Пусть 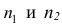
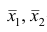
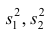
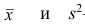
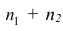
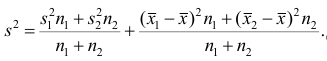
Пусть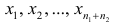
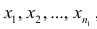
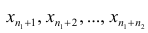
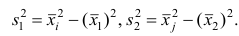
В соответствии со свойством 4° средней арифметической можно записать 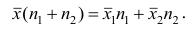
Используя найденные выражения для слагаемых, получаем
Свойство 4° можно обобщить на случай, когда ряд наблюдений состоит из любого количества 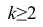
Если ряд наблюдений состоит из k групп наблюдений, то межгрупповой дисперсией 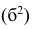
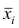
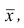
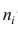
Средней групповых дисперсий или внутригрупповой дисперсией 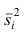
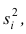
Следствие (свойства 4°). Если ряд наблюдений состоит из k групп наблюдений, то дисперсия всего ряда s2 равна сумме внутригрупповой и межгрупповой дисперсий, т.е.
Вычисление дисперсии вариационного ряда непосредственно по формуле (16) приводит к громоздким расчётам, если числовые значения вариантов и соответствующие им частоты велики. Поэтому часто дисперсию вычисляют не по первоначальным вариантам х, а по вариантам 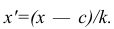
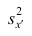
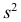
Действительно, принимая во внимание свойства 3° и 2° дисперсии, получаем
откуда следует, что
Требования к с и k предъявляют те же, что и в упрощенном способе вычисления средней арифметической.
Эмпирические центральные и начальные моменты
Средняя арифметическая и дисперсия вариационного ряда являются частными случаями более общего понятия о моментах вариационного ряда.
Эмпирическим начальным моментом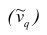
Эмпирический начальный момент нулевого порядка
Эмпирический начальный момент первого порядка
Эмпирический начальный момент второго порядка 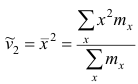
Эмпирическим центральным моментом 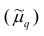
Эмпирический центральный момент нулевого порядка
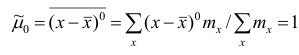
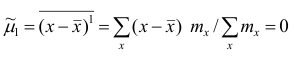
Эмпирический центральный момент второго порядка
В дальнейшем для краткости величину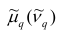
Используя формулу бинома Ньютона, разложим в ряд выражение для центрального момента q-го порядка:
В проведенных тождественных преобразованиях использованы свойства 5° и 3° средней арифметической; 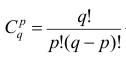
Итак, центральный момент q-го порядка выражается через начальные моменты следующим образом:
Полагая q = 0, 1, 2,…, можно получить выражения центральных моментов различных порядков через начальные моменты:
и т.д.
Заметим, что формула (23) для центрального момента второго порядка, как и следовало ожидать, аналогична формуле (18) для дисперсии.
Рассмотрим свойства центральных моментов, которые позволят значительно упростить их вычисление.
1°. Если все варианты уменьшить (увеличить) на одно и то же число с, то центральный момент q-го порядка не изменится.
Доказательство. Если все варианты уменьшить на число с, то средняя арифметическая для измененного ряда равна 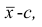
Аналогично можно показать, что
2°. Если все варианты уменьшить (увеличить) в одно и то же число k раз, то центральный момент q-го порядка уменьшится (увеличится) в 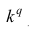
то средняя арифметическая для измененного вариационного ряда равна
поэтому центральный момент q-го порядка
Аналогично можно показать, что
Для облегчения расчётов центральные моменты вычисляют не по первоначальным вариантам х, а по вариантам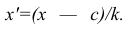
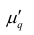
внимание свойства центрального момента, получаем
откуда следует, что
Эмпирические асимметрия и эксцесс
Эмпирическим коэффициентом асимметрии 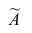
Если полигон вариационного ряда скошен, т.е. одна из его ветвей, начиная от вершины, зримо длиннее другой, то такой ряд называют асимметричным. Из формулы (27) следует, что если в вариационном ряду преобладают варианты, меньшие 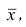
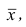
Эмпирическим эксцессом или коэффициентом крутости 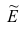
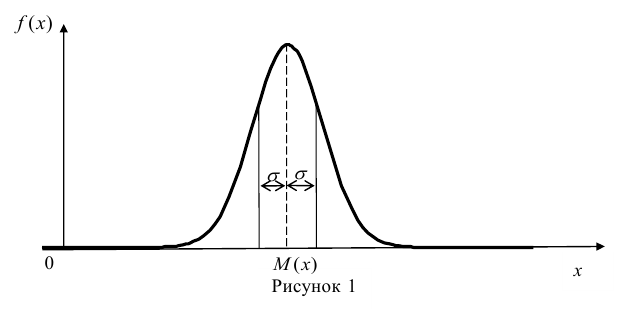
За стандартное значение эксцесса принимают нуль-эксцесс так называемой нормальной кривой (см. рис. 1).
Кривые, у которых эксцесс отрицательный, по сравнению с нормальной менее крутые, имеют, более плоскую вершину и называются «плосковершинными» Кривые с положительным эксцессом более крутые по сравнению с нормальной кривой, имеют более острую вершину и называются «островершинными».
Интервальные оценки параметров распределений
Доверительный интервал, доверительная вероятность:
Точечная оценка неизвестного параметра 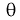
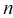
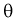
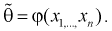
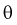
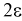
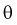
Чем меньше разность 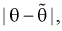
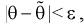
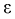
Доверительной вероятностью оценки называется вероятность 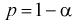
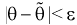
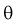
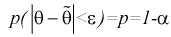
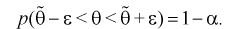
Из (10.1) видно, что неизвестный параметр 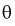
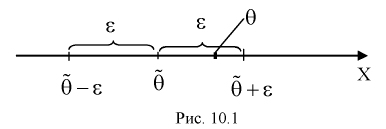
Доверительным интервалом называется интервал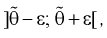
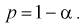
Длина его (см. рис. 10.1) 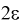
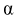
Доверительный интервал для математического ожидания случайной величины X при известной дисперсии
Доверительный интервал для математического ожидания случайной величины X при известной дисперсии (или 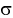
Пусть эксперимент Е описывается нормальной случайной величиной X.
Плотность распределения 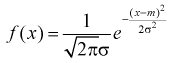
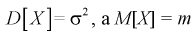
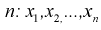
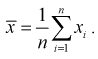
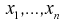
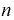
откуда получим
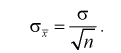
Для определения доверительного интервала рассмотрим разность между оценкой и параметром: 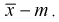
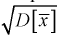
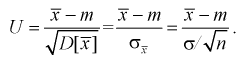
Покажем, что случайная величина U имеет нормированный нормальный закон распределения. Найдем ее числовые характеристики:
Таким образом 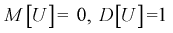
Зная плотность распределения случайной величины U, легко найти вероятность попадания случайной величины U в интервал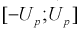
Левая часть этого уравнения представляет собой доверительную вероятность
Тогда из (10.4) и (10.5) следует уравнение
Решая уравнение (10.6), по таблицам функции Лапласа для заданной доверительной вероятности 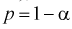
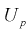
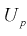
Считая, что 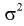
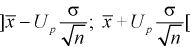
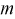
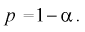
Замечания по формуле (10.8):
- при увеличении объема выборки
из (10.8) видим, что е уменьшается, значит, уменьшается длина доверительного интервала, а точность оценки увеличивается;
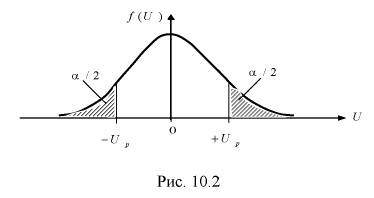
- увеличение доверительной вероятности
приводит к увеличению длины доверительного интервала (см. рис. 10.2, где квантили
увеличиваются), т. е. е увеличивается, а точность оценки падает;
- если задать точность е и доверительную вероятность
, то можно найти объем выборки, который обеспечит заданную точность:
Пример №1
Сколько конденсаторов одного номинала надо измерить, чтобы с вероятностью 0,95 можно было утверждать, что мы с точностью 1 % определили их среднее значение — математическое ожидание.
Обозначим 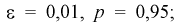
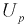
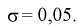
Доверительный интервал для математического ожидания нормальной случайной величины X при НЕизвестной дисперсии
Доверительный интервал для математического ожидания нормальной случайной величины X при неизвестной дисперсии или
Пусть эксперимент описывается случайной величиной X с нормальным распределением с неизвестными параметрами 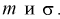
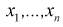
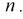
Здесь использовали для оценки дисперсии 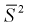
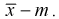
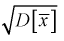
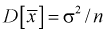
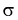
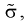
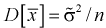
Умножим числитель и знаменатель в (10.10) на
Здесь X — нормированная нормальная случайная величина, знаменатель — распределение 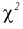
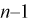
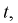
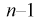
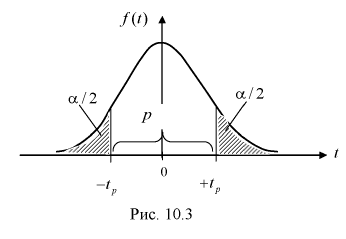
Зная закон распределения случайной величины t и задавая доверительную вероятность 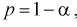
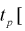
Из таблиц распределений Стьюдента по заданной доверительной вероятности 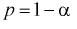
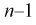
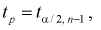
Подставляя в (10.13) вместо t равенство (10.10), получаем
Разрешим неравенство в левой части формулы (10.14) относительно
Отсюда непосредственно следует, что доверительный интервал 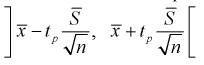
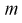
Интервал (10.15) несколько шире интервала (10.7), определенного для той же выборки и той же доверительной вероятности. Зато в (10.15) используется меньшая априорная информация — 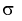
Можно обозначить ширину доверительного интервала или точность через 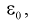
Все замечания, сделанные по формуле (10.8), справедливы и для формулы (10.16).
Пример №2
Даны результаты четырех измерений напряжения сети (значения приведены в
Считаем, что X — напряжение сети — является нормальной случайной величиной. Построить доверительный интервал с вероятностью 0,95 для истинного напряжения сети —
Найдем точечную оценку
Из таблиц распределения Стьюдента для 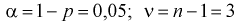
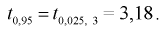
Тогда
Полученные значения подставим в формулу (10.16):
Найдем левую и правую границы доверительного интервала для
Таким образом, истинное напряжение сети с вероятностью 0,95 накрывается доверительным интервалом
Найдем минимальное число измерений, чтобы с вероятностью 0,95 точ ность определения истинного напряжения сети не превышала 0,5 В, т. е. 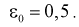
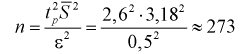
Видим, что число измерений 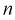
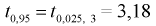
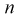
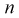
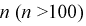
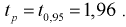
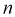
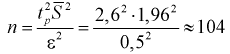
Доверительный интервал для дисперсии или ст нормальной случайной величины X
Рассмотрим вероятностный эксперимент с нормальной моделью, где параметры 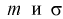
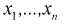
Составим вспомогательную случайную величину
Эта случайная величина имеет распределение 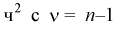
Это и есть распределение хи-квадрат с 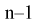
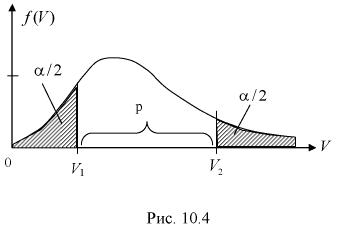
Зная закон распределения случайной величины У, определим вероятность того, что случайная величина 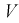
Здесь 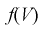
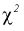
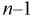
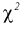
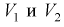
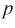
Это означает, что площади заштрихованных фигур равны. Задавая доверительную вероятность 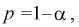
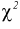
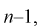
Считая 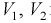
Подставим в (10.20) значение 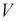
Решаем неравенство в левой части (10.21) относительно
Из (10.22) записываем доверительный интервал для
Для среднего квадратического отклонения 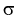
Можно ввести коэффициенты
Тогда доверительный интервал для о определится следующим образом:
Коэффициенты 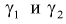
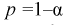
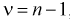

Пример №3
В предыдущем разделе (10.3) приведен пример для измеренных значений напряжения сети. Продолжим и найдем доверительный интервал для среднего квадратического отклонения 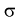
Найдена точечная оценка для 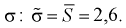
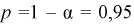
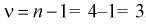
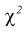
Тогда нижняя граница для
Верхняя граница для
И окончательно:
Пример №4
Случайная величина 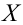
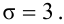
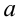
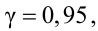
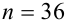
Решение. Определим значение 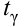
Точность оценки
Подставим в неравенство (4.1):
Смысл полученного результата: если произведено достаточно большое число выборок по 36 в каждой, то 95 % из них определяют такие доверительные
интервалы, в которых 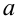
Пример №5
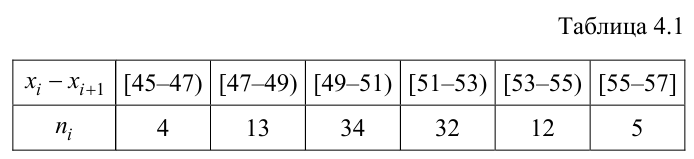
Для исследования нормального распределения 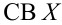
Найти с надежностью 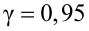
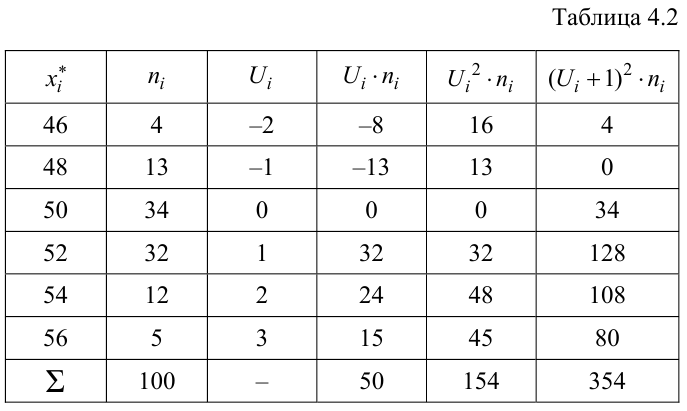
Решение. Найдем несмещенные оценки для математического ожидания и дисперсии, используя метод произведений (табл. 4.2).
Контроль:
По табл. П3 по данным 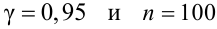
Для определения доверительного интервала для математического ожидания используем неравенство (4.2):
Таким образом, интервал (50, 547; 51, 453) накрывает точку 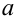
Для определения доверительного интервала для среднего квадратического отклонения используем неравенство (4.3). По табл. П4 по заданным 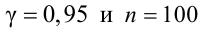
С вероятностью 0,95 неизвестное значение 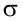
- Алгебра событий — определение и вычисление
- Свойства вероятности
- Многомерные случайные величины
- Случайные события — определение и вычисление
- Основные законы распределения дискретных случайных величин
- Непрерывные случайные величины
- Закон больших чисел
- Генеральная и выборочная совокупности
Построим в MS EXCEL доверительный интервал для оценки среднего значения распределения в случае известного значения дисперсии.
В статье
Статистики, выборочное распределение и точечные оценки в MS EXCEL
дано определение
точечной оценки
параметра распределения (point estimator). Однако, в силу случайности выборки,
точечная оценка
не совпадает с оцениваемым параметром и более разумно было бы указывать интервал, в котором может находиться неизвестный параметр при наблюденной выборке х
1
, x
2
, …, х
n
. Поэтому цель использования
доверительных интервалов
состоит в том, чтобы по возможности избавиться от неопределенности и сделать как можно более полезный
статистический вывод
.
Примечание
: Процесс обобщения данных
выборки
, который приводит к
вероятностным
утверждениям обо всей
генеральной совокупности
, называют
статистическим выводом
(statistical inference).
СОВЕТ
: Для построения
Доверительного интервала
нам потребуется знание следующих понятий:
-
дисперсия и стандартное отклонение
,
-
выборочное распределение статистики
,
-
уровень доверия/ уровень значимости
,
-
стандартное нормальное распределение
и
его квантили
.
К сожалению, интервал, в котором
может
находиться неизвестный параметр, совпадает со всей возможной областью изменения этого параметра, поскольку соответствующую
выборку
, а значит и
оценку параметра
, можно получить с ненулевой вероятностью. Поэтому приходится ограничиваться нахождением границ изменения неизвестного параметра с некоторой заданной наперед вероятностью.
Определение
:
Доверительным интервалом
называют такой интервал изменения случайной величины
,
которыйс заданной вероятностью
,
накроет истинное значение оцениваемого параметра распределения.
Эту заданную вероятность называют
уровнем доверия
(или
доверительной вероятностью
).
Обычно используют значения
уровня доверия
90%; 95%; 99%, реже 99,9% и т.д. Например,
уровень
доверия
95% означает, что дополнительное событие, вероятность которого 1-0,95=5%, исследователь считает маловероятным или невозможным.
Примечание
:
Вероятность этого дополнительного события называется
уровень значимости
или
ошибка первого рода
. Подробнее см. статью
Уровень значимости и уровень надежности в MS EXCEL
.
Разумеется, выбор
уровня доверия
полностью зависит от решаемой задачи. Так, степень доверия авиапассажира к надежности самолета, несомненно, должна быть выше степени доверия покупателя к надежности электрической лампочки.
Примечание
:
Построение
доверительного интервала
в случае, когда
стандартное отклонение
неизвестно, приведено в статье
Доверительный интервал для оценки среднего (дисперсия неизвестна) в MS EXCEL
. О построении других
доверительных интервалов
см. статью
Доверительные интервалы в MS EXCEL
.
Формулировка задачи
Предположим, что из
генеральной совокупности
имеющей
нормальное распределение
взята
выборка
размера n. Предполагается, что
стандартное отклонение
этого распределения известно. Необходимо на основании этой
выборки
оценить неизвестное
среднее значение распределения
(μ,
математическое ожидание
) и построить соответствующий
двухсторонний
доверительный интервал
.
Точечная оценка
Как известно из
Центральной предельной теоремы
,
статистика
(обозначим ее
Х
ср
) является
несмещенной оценкой среднего
этой
генеральной совокупности
и имеет распределение N(μ;σ
2
/n).
Примечание
:
Что делать, если требуется построить
доверительный интервал
в случае распределения, которое
не является
нормальным?
В этом случае на помощь приходит
Центральная предельная теорема
, которая гласит, что при достаточно большом размере
выборки
n из распределения
не являющемся
нормальным
,
выборочное распределение статистики Х
ср
будет
приблизительно
соответствовать
нормальному распределению
с параметрами N(μ;σ
2
/n).
Итак,
точечная оценка
среднего
значения распределения
у нас есть – это
среднее значение выборки
, т.е.
Х
ср
. Теперь займемся
доверительным интервалом.
Построение доверительного интервала
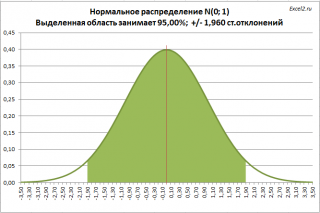
Обычно, зная распределение и его параметры, мы можем вычислить вероятность того, что случайная величина примет значение из заданного нами интервала. Сейчас поступим наоборот: найдем интервал, в который случайная величина попадет с заданной вероятностью. Например, из свойств
нормального распределения
известно, что с вероятностью 95%, случайная величина, распределенная по
нормальному закону
, попадет в интервал примерно +/- 2
стандартных отклонения
от
среднего значения
(см. статью про
нормальное распределение
). Этот интервал, послужит нам прототипом для
доверительного интервала
.
Теперь разберемся,знаем ли мы распределение
,
чтобы вычислить этот интервал? Для ответа на вопрос мы должны указать форму распределения и его параметры.
Форму распределения мы знаем – это
нормальное распределение
(напомним, что речь идет о
выборочном распределении
статистики
Х
ср
).
Параметр μ нам неизвестен (его как раз нужно оценить с помощью
доверительного интервала
), но у нас есть его оценка
Х
ср
,
вычисленная на основе
выборки,
которую можно использовать.
Второй параметр –
стандартное отклонение выборочного среднего
будем считать известным
, он равен σ/√n.
Т.к. мы не знаем μ, то будем строить интервал +/- 2
стандартных отклонения
не от
среднего значения
, а от известной его оценки
Х
ср
. Т.е. при расчете
доверительного интервала
мы НЕ будем считать, что
Х
ср
попадет в интервал +/- 2
стандартных отклонения
от μ с вероятностью 95%, а будем считать, что интервал +/- 2
стандартных отклонения
от
Х
ср
с вероятностью 95% накроет μ
– среднее генеральной совокупности,
из которого взята
выборка
. Эти два утверждения эквивалентны, но второе утверждение нам позволяет построить
доверительный интервал
.
Кроме того, уточним интервал: случайная величина, распределенная по
нормальному закону
, с вероятностью 95% попадает в интервал +/- 1,960
стандартных отклонений,
а не+/- 2
стандартных отклонения
. Это можно рассчитать с помощью формулы
=НОРМ.СТ.ОБР((1+0,95)/2)
, см.
файл примера Лист Интервал
.
Теперь мы можем сформулировать вероятностное утверждение, которое послужит нам для формирования
доверительного интервала
: «Вероятность того, что
среднее генеральной совокупности
находится от
среднего выборки
в пределах 1,960 «
стандартных отклонений выборочного среднего»
, равна 95%».
Значение вероятности, упомянутое в утверждении, имеет специальное название
уровень доверия
, который связан с
уровнем значимости α (альфа) простым выражением
уровень доверия
=
1
-α
.
В нашем случае
уровень значимости
α
=1-0,95=0,05
.
Теперь на основе этого вероятностного утверждения запишем выражение для вычисления
доверительного интервала
:
где Z
α/2
–
верхний α/2-квантиль
стандартного
нормального распределения
(такое значение случайной величины
z
,
что
P
(
z
>=
Z
α/2
)=α/2
).
Примечание
:
Верхний α/2-квантиль
определяет ширину
доверительного интервала
в
стандартных отклонениях
выборочного среднего.
Верхний α/2-квантиль
стандартного
нормального распределения
всегда больше 0, что очень удобно.
В нашем случае при α=0,05,
верхний α/2-квантиль
равен 1,960. Для других уровней значимости α (10%; 1%)
верхний α/2-квантиль
Z
α/2
можно вычислить с помощью формулы
=НОРМ.СТ.ОБР(1-α/2)
или, если известен
уровень доверия
,
=НОРМ.СТ.ОБР((1+ур.доверия)/2)
.
Обычно при построении
доверительных интервалов для оценки среднего
используют только
верхний α
/2-
квантиль
и не используют
нижний α
/2-
квантиль
. Это возможно потому, что
стандартное
нормальное распределение
симметрично относительно оси х (
плотность его распределения
симметрична относительно
среднего, т.е. 0
)
.
Поэтому, нет нужды вычислять
нижний α/2-квантиль
(его называют просто α
/2-квантиль
), т.к. он равен
верхнему α
/2-
квантилю
со знаком минус.
Напомним, что, не смотря на форму распределения величины х, соответствующая случайная величина
Х
ср
распределена
приблизительно
нормально
N(μ;σ
2
/n) (см. статью про
ЦПТ
). Следовательно, в общем случае, вышеуказанное выражение для
доверительного интервала
является лишь приближенным. Если величина х распределена по
нормальному закону
N(μ;σ
2
/n), то выражение для
доверительного интервала
является точным.
Расчет доверительного интервала в MS EXCEL
Решим задачу.
Время отклика электронного компонента на входной сигнал является важной характеристикой устройства. Инженер хочет построить доверительный интервал для среднего времени отклика при уровне доверия 95%. Из предыдущего опыта инженер знает, что стандартное отклонение время отклика составляет 8 мсек. Известно, что для оценки времени отклика инженер сделал 25 измерений, среднее значение составило 78 мсек.
Решение
: Инженер хочет знать время отклика электронного устройства, но он понимает, что время отклика является не фиксированной, а случайной величиной, которая имеет свое распределение. Так что, лучшее, на что он может рассчитывать, это определить параметры и форму этого распределения.
К сожалению, из условия задачи форма распределения времени отклика нам не известна (оно не обязательно должно быть
нормальным
).
Среднее, т.е. математическое ожидание
, этого распределения также неизвестно. Известно только его
стандартное отклонение
σ=8. Поэтому, пока мы не можем посчитать вероятности и построить
доверительный интервал
.
Однако, не смотря на то, что мы не знаем распределение
времени
отдельного отклика
, мы знаем, что согласно
ЦПТ
,
выборочное распределение
среднего времени отклика
является приблизительно
нормальным
(будем считать, что условия
ЦПТ
выполняются, т.к. размер
выборки
достаточно велик (n=25))
.
Более того,
среднее
этого распределения равно
среднему значению
распределения единичного отклика, т.е. μ. А
стандартное отклонение
этого распределения (σ/√n) можно вычислить по формуле
=8/КОРЕНЬ(25)
.
Также известно, что инженером была получена
точечная оценка
параметра μ равная 78 мсек (Х
ср
). Поэтому, теперь мы можем вычислять вероятности, т.к. нам известна форма распределения (
нормальное
) и его параметры (Х
ср
и σ/√n).
Инженер хочет знать
математическое ожидание
μ распределения времени отклика. Как было сказано выше, это μ равно
математическому ожиданию выборочного распределения среднего времени отклика
. Если мы воспользуемся
нормальным распределением
N(Х
ср
; σ/√n), то искомое μ будет находиться в интервале +/-2*σ/√n с вероятностью примерно 95%.
Уровень значимости
равен 1-0,95=0,05.
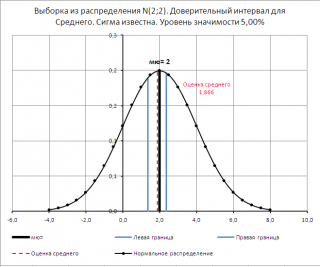
Наконец, найдем левую и правую границу
доверительного интервала
. Левая граница:
=78-НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25)
=
74,864
Правая граница:
=78+НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25)=81,136
или так
Левая граница:
=НОРМ.ОБР(0,05/2; 78; 8/КОРЕНЬ(25))
Правая граница:
=НОРМ.ОБР(1-0,05/2; 78; 8/КОРЕНЬ(25))
Ответ
:
доверительный интервал
при
уровне доверия 95% и σ
=8
мсек
равен
78+/-3,136 мсек.
В
файле примера на листе Сигма
известна создана форма для расчета и построения
двухстороннего
доверительного интервала
для произвольных
выборок
с заданным σ и
уровнем значимости
.
Функция
ДОВЕРИТ.НОРМ()
Если значения
выборки
находятся в диапазоне
B20:B79
, а
уровень значимости
равен 0,05; то формула MS EXCEL:
=СРЗНАЧ(B20:B79)-ДОВЕРИТ.НОРМ(0,05;σ; СЧЁТ(B20:B79))
вернет левую границу
доверительного интервала
.
Эту же границу можно вычислить с помощью формулы:
=СРЗНАЧ(B20:B79)-НОРМ.СТ.ОБР(1-0,05/2)*σ/КОРЕНЬ(СЧЁТ(B20:B79))
Примечание
: Функция
ДОВЕРИТ.НОРМ()
появилась в MS EXCEL 2010. В более ранних версиях MS EXCEL использовалась функция
ДОВЕРИТ()
.
Интервальный ряд.
Так как первая часть задачи решалась
по пяти группам, то и вторая часть задачи
должна решаться по пяти группам.
Подвергнем обследованию возрастные
характеристики рабочих.
Исходные данные: 24 19 26
42 25 28 36 34 35 18 40 18 22 33 42 21 22 23 43 40 29 38 31 27
Однако возраст рабочих имеет более
широкий диапазон поэтому применим
интервальный ряд.
I=Xmax-Xmin / nгрупп
При расчёте интервала необходимо
пользоваться правилом интервала. При
получении дробных значений округляем
до целых в большую сторону (даже 2,1
округляем до 3)
I=5
1) 18-23
2) 23-28
3) 28-33
4) 33-38
5) 38-43 – границы интервалов вариант. 43 –
правая граница последней группы>=Xmax
В интервальном ряду необходимо ввести
дополнительные интервалы: от левого
края влево, от правого края вправо на 1
интервал. (13-18 и 43-48)
Для облегчения расчётов необходимо
рассчитать середину интервала (центр
распределения)
x’=Xmax+Xmin/ 2
В интервальном ряду подсчёт частоты
определяется по ПЛОЦ
|
X |
X’ |
F |
X’f |
S |
ПЛОЦ |
d |
|d|f |
d^2f |
d^4f |
Y% |
C (градус сектора) |
|
13-18 |
15.5 |
0 |
0 |
||||||||
|
18-23 |
20.5 |
6 |
123 |
6 |
(1-5) |
-9,791 |
58,746 |
575,182 |
55138,68 |
25 |
90 |
|
23-28 |
25.5 |
5 |
127.5 |
11 |
(6-10) |
-4,791 |
23,955 |
114,768 |
2634,28 |
21 |
76 |
|
28-33 |
30.5 |
3 |
91.5 |
14 |
(11-13) |
0,209 |
0,627 |
0,131 |
0,006 |
12 |
43 |
|
33-38 |
35.5 |
4 |
142 |
18 |
(14-17) |
5,209 |
20,836 |
108,535 |
2944,95 |
17 |
61 |
|
38-43 |
40.5 |
6 |
243 |
24 |
(18-24) |
10,209 |
61,254 |
625,342 |
65175,454 |
25 |
90 |
|
43-48 |
45.5 |
0 |
0 |
||||||||
|
∑ |
24 |
1,045 |
165,418 |
1423,96 |
125893,37 |
100 |
360 |
Полигон: по оси Х откладываются
интервалы границ варианты, по осиY– частоты, но точки наносятся в системе
(Х’:f) (см «График №1» в
тетради).
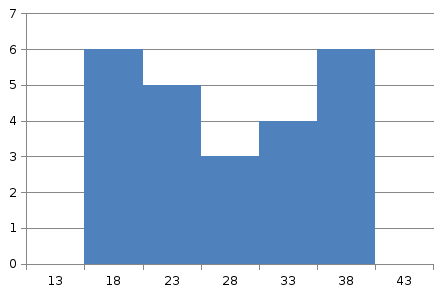
Гистограмма– система прямоугольников,
основания которых располагаются на
границах интервалов вариант, а высота
соответствует частоте (деления все те
же самые).
С помощью гистограммы можно определить
приближённое значение графической
моды. Правую вершину модального
прямоугольника соединить с правой
вершиной предыдущего прямоугольника,
левую вершину модального прямоугольника
соединить с левой вершиной последующего
прямоугольника. Через точку пересечения
этих отрезков опустить перпендикуляр
на ось абсцисс – это и будет приближённое
значение графической моды. (см тетр.
«График №2»)
Модальный прямоугольник– самый
высокий. Данное распределение получило
название «Бимодальное» (2 частоты). При
совпадении 3 частот распределение модой
не обладает.
Кумулята: По оси Х откладываются
интервалы границ варианты без
дополнительных интервалов. По оси
ординат откладываются накопленные
частотыS.
Методика нанесения точек: Левая граница
первого интервала (18:0) является точкой
начала графика. В ней накопленные частоты
равны нулю. Все правые границы остальных
интервалов равны накопленным частотам
соответствующих рядов.
С помощью кумуляты можно определить
приблизительное значение графической
медианы.
Методика: Последнюю ординату разделить
пополам. Через полученную точку провести
прямую параллельную оси Х до пересечения
с кумулятой. Через точку пересечения
опустить перпендикуляр на ось Х – это
и будет приближённое значение графической
медианы. (см тетр. «График №3)
Вычислить показатели центра
распределения.
1. Среднее арифметическое
Xср.= ∑x’f/ ∑f(x’ –
середина интервала)=727/24=30,291
2. Мо= X(Мо)+I*f(мо)-f(мо-1)
/( (f(мо)-f(мо-1))+(fмо
-f(мо+1))
Xмо — левая граница
модального интервала. Модальный интервал
определяется по максимальной частоте.
I=интервал распределения
f(мо) – модальная или
максимальная частота
f(мо-1) – частота предшествующая
модальной частоте
f(мо+1) – частота последующая
за модальной частоте
Мо(1)=18+5 *
6-0 / 6-0 + 5=22,286 (22,5)
Мо(2)=38+5 *
6-4 / 6-4 + 6-0=39,25 (39)
Ме=Xме + I *(n+1 /2)
– Sме-1 / fме)=28+5
*(12,5-11/3) =30,5
Хме – медианная варианта, левая граница
медианного интервала
N(ме)=n+1/2=24+1/2=12,5
(принадлежностьSплоц
11-13)=>X(28-33)=>Xme=28
Fme– частота медианного
интервала
Sme-1 – накопленная частота
предшествующая накопленной частоте
медианного интервала
Me=30,5
Вычислить
показатели вариации.
D=x’-xср.
D1=20,5-30,291=-9,791
D2=25,5-30,291=-4,791
D3=-
Dср.=∑
|x-xср|f/ ∑f= ∑|d|f/ ∑f
D^2=∑(x’-xср.)^2f/∑f=∑(d^2f)/∑f=59,332
δ=(D^2)^1/2=7,703
V=δ/xср.*100=25,43
5. вычислить
показатели формы распределения
As(1)=Xср.-Mo(1)/δ=1,039
As(2)=Xср.-Mo(2)/δ=-1,163
Эксцесс
Ex=M/δ^4
– 3= 5245,56/3520,79 – 3= -1,51
M=∑(x’-xср.)^4f/∑f=∑d^4f/∑f=125839,37/24=5245,56
Ex=
— плоско
Ex=
+ остро вершины распределения
Мажор
Левая
асимметрия Правая асимметрия
As=-1,163As=
левая асимметрия не получается
Mo>Me>Xср Mo<Me<xср.
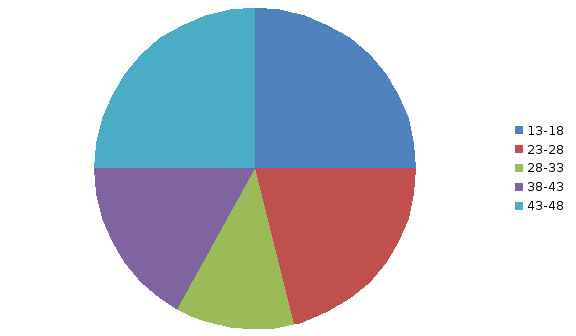
7. Сектор
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
























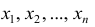
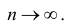
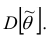
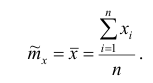
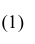
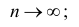
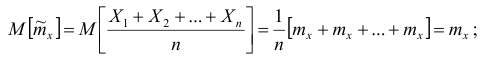
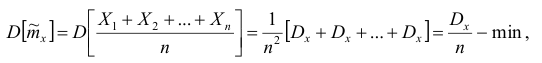
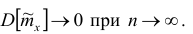



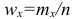
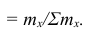
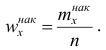

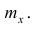
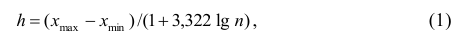
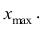




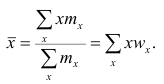


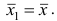
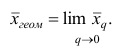
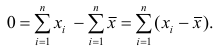
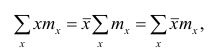
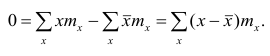
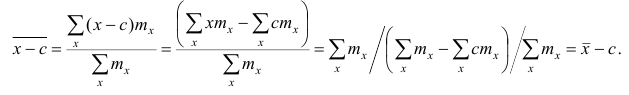
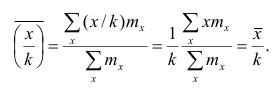
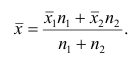
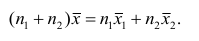
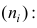
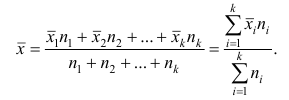
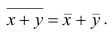
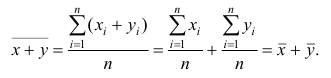
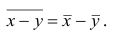

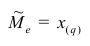
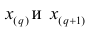
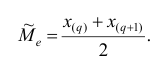
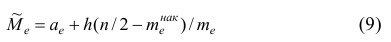
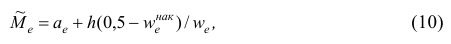
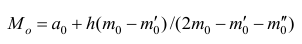
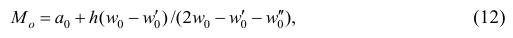


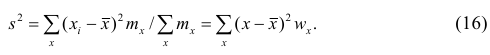
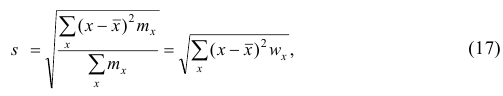
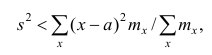
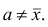
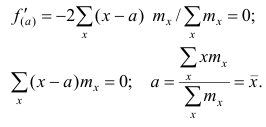
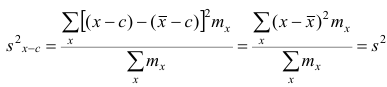
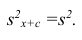

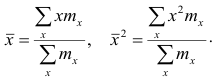
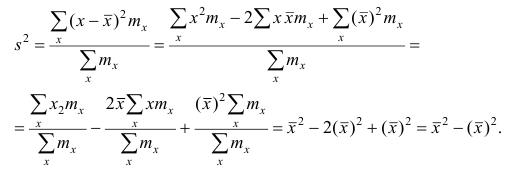
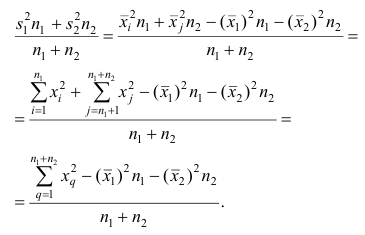
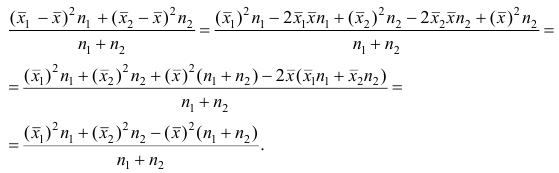
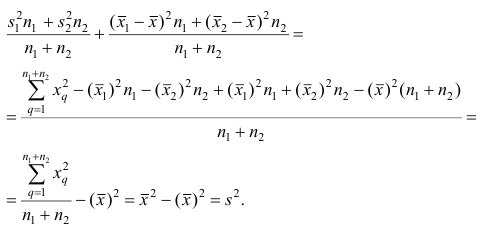
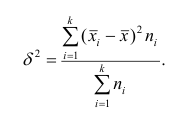
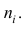
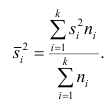
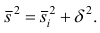

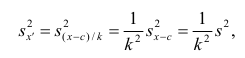

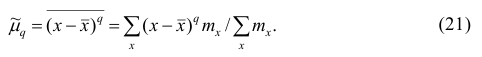
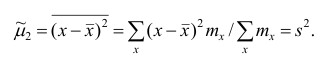
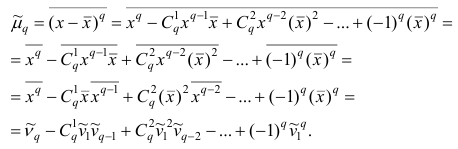

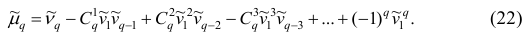
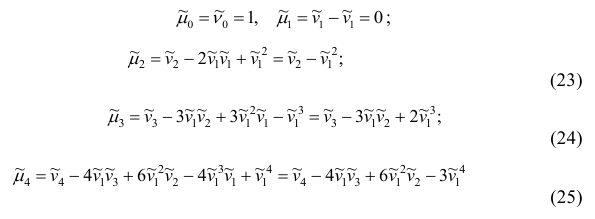
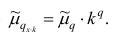

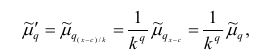
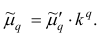
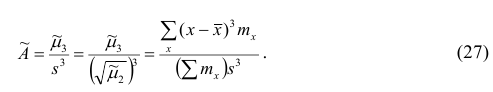

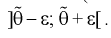
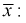
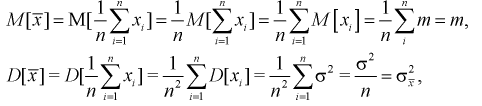
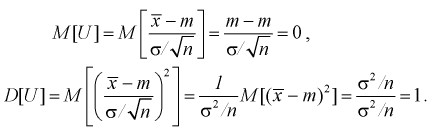
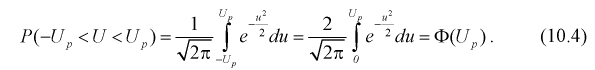
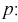
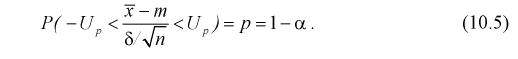

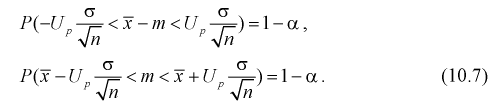

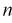 из (10.8) видим, что е уменьшается, значит, уменьшается длина доверительного интервала, а точность оценки увеличивается;
из (10.8) видим, что е уменьшается, значит, уменьшается длина доверительного интервала, а точность оценки увеличивается;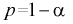 приводит к увеличению длины доверительного интервала (см. рис. 10.2, где квантили
приводит к увеличению длины доверительного интервала (см. рис. 10.2, где квантили 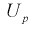 увеличиваются), т. е. е увеличивается, а точность оценки падает;
увеличиваются), т. е. е увеличивается, а точность оценки падает;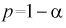 , то можно найти объем выборки, который обеспечит заданную точность:
, то можно найти объем выборки, который обеспечит заданную точность: