Определение. Пусть даны два пространства и
. Если по закону
каждому вектору
поставлен в соответствие вектор
, то говорят, что задан оператор
(функция, отображение), отображающий
в
и пишут
.
Обозначение: ;
– образ,
– прообраз.
Определение. Если для любых и
из
и любых вещественных чисел
и
имеет место
, то оператор
называется линейным.
Произвольные отображения линейных пространств изучаются в курсе математического анализа. В курсе линейной алгебры изучаются лишь линейные отображения.
Пример 6. Оператор действует из
в
по закону
, где
, и
– фиксированный вектор, например,
. Оператор
переводит вектор из
в другой вектор из
. Докажем, что он линейный:
. Здесь воспользовались свойствами векторного произведения.
Пример 7. Линеен ли оператор , где
произвольный вектор, а вектор
– фиксированный?
Решение. , так как
,
. Следовательно, оператор
– нелинейный.
Пусть даны два пространства и
и оператор
, действующий из
в
. Пусть в
есть базис
, а в
– базис
.
Подействовав оператором на базисные векторы пространства
, получим векторы из
, которые можно разложить по базису
с коэффициентами линейных комбинаций
:
Строим матрицу таким образом, чтобы в ее столбцах стояли координаты образов базисных векторов пространства
относительно базисных векторов пространства
:

Матрица называется матрицей линейного оператора
, действующего из
в
. Таким образом, если оператор
, то матрица этого оператора имеет размер
, то есть у нее
строк и
столбцов.
Замечание. Если в и
выбрать другие базисы, то в этих базисах матрица линейного оператора будет иметь другой вид.
Из определения матрицы линейного оператора следует, что, зная закон (оператор), по которому вектору сопоставляется вектор
, можно построить матрицу, и наоборот, любой матрице соответствует некоторый линейный оператор.
Пример 8. Построить матрицу линейного оператора, действующего из в
по закону
, где векторы
и
заданы относительно канонического базиса.
Решение. Подействуем оператором на базисные векторы :



Таким, образом, 
Пример 9. Пусть в выбран базис
,
,
, а в
выбран базис
,
. Найти матрицу линейного оператора, действующего из
в
по закону
, где
.
Решение. ;
;
;

Пример 10. Дана матрица 
Решение. Матрица – это матрица линейного оператора, действующего из
в
. Пусть в
базис
, в
базис
. Так как в столбцах матрицы
стоят координаты векторов
относительно базиса
, то

Пусть произвольный вектор из
, где
– координаты этого вектора в базисе
, тогда
. Действуя оператором
на вектор
и учитывая линейность оператора, получим:
.
Учитывая (1), имеем:
.
Таким образом, оператор действует по закону
.
Зная матрицу оператора , результат его действия на вектор
можно найти в матричной форме. Пусть известна матрица оператора
размера
с элементами
. В этом случае оператор с такой матрицей действует из
в
. Если
– любой вектор из
, то результат действия оператора
на вектор
можно найти по формуле:

Где – координаты вектора
.
Пример 11. Операторы и
действуют в пространстве
по законам
,
, где
;
(
– скалярное произведение векторов
и
). Найти координаты вектора
в каноническом базисе.
Решение. Координаты вектора можно найти двумя способами:
А) найдем матрицу .
Строим матрицу в каноническом базисе:
;
;
.

Строим матрицу в каноническом базисе:
;
;
.



Этот способ решения называется матричным;
Б) операторный способ.
. Подействуем оператором
на вектор
:
, теперь на полученный вектор подействуем оператором
:

Для самостоятельной работы.
1. Оператор действует по закону:
.
Найти его матрицу в каноническом базисе.
Ответ: 
2. Оператор действует в плоскости
и осуществляет зеркальное отражение относительно прямой
. Доказать, что он линейный и найти его матрицу в каноническом базисе.
Ответ: 
3. Дана матрица 
А) Найти оператор, матрицей которого является матрица .
Б) Найти образ вектора .
Ответ: .
| < Предыдущая | Следующая > |
|---|
Упражнение 1
Проверить является ли оператор линейным
Проверить, является ли оператор линейным в
Решение:
Проверим оператор на линейность:
Если выполняются условия:
,
-
Проверим условие 1:
Проверим условие 2:
Так как оба условия выполняются, то оператор линейный.
Упражнение 2
Найти значение выражения
.
— линейные операторы из
,
,
Решение:
Ответ:
Упражнение 3
Найти значение выражения
.
— линейные операторы из
,
,
Решение:
Ответ:
Упражнение 4
Найти значение выражения
.
— линейные операторы из
,
,
Решение:
=
Ответ:
Список использованной литературы :
- Личный конспект, составленный на основе лекций Г.С. Белозерова
Линейные операторы
1. Понятие линейного оператора
Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 
Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x1 и x2 пространства R и любого λ из числового поля K выполняются соотношения
- A(x1+x2)=Ax1+Ax2.
- A(λx)=λAx.
Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.
Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы 

где A — m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:
Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов 

Пусть x − произвольный элемент в R. Тогда
 |
(3) |
является разложением x в по базису 
Применим оператор A к базисным векторам 
 |
(4) |
где aij − координаты полученного вектора в базисе 
Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем
|
|
(5) |
Сделаем следующее обозначение:
 |
(6) |
Тогда равенство (5) примет следующий вид:
 |
(7) |
Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе 
Построим матрицу A с элементами aij:
 |
(8) |
Тогда выражение (6) можно записать в матричном виде:
Матрица A называется матрицей линейного оператора в заданных базисах 

2. Сложение линейных операторов
Пусть A и B два линейных оператора действующих из R в S и пусть A и B — mxn − матрицы соответствующие этим операторам.
Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством
где x∈R означает, что x принадлежит пространстве R.
Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.
Применим оператор C к базисному вектору ej, тогда:
| Cej=Aej+Bej= | n | (aij+bij)ej |
| ∑ | ||
| j=1 |
Следовательно оператору C отвечает матрица 
3. Умножение линейных операторов
Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.
Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:
Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.
Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C
можно записать в виде матричных равенств
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
Учитывая произвольность х, получим
Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.
4. Умножение линейного оператора на число
Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.
Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:
Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства
можно записать в виде матричных равенств
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
Учитывая произвольность х, получим
Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.
5. Нулевой оператор
Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:
6. Противоположный оператор
Противоположным оператору A называется оператор −A удовлетворяющий равенству:
7. Ядро линейного оператора
Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.
Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.
8. Образ линейного оператора
Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.
Образ линейного оператора обозначается символом im A.
9. Ранг линейного оператора
Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).
Одно
из фундаментальных понятий матричной
алгебры — понятие линейного оператора.
Рассмотрим
два линейных пространства: Rn
размерности n
и Rm
размерности m.
Определение
1.
Если задан закон (правило), по которому
каждому вектору х
пространства
Rn
ставится
в соответствие единственный вектор
у
пространства Rm,
то говорят, что задан оператор
(преобразование, отображение) А(х),
действующий из Rn
в Rm,
и записывают у
= А (х).
Определение
2. Оператор
(преобразование) называется
линейным, если
для любых векторов
х
и
у
пространства
Rn
и
любого числа
выполняются
соотношения:
-
А(х
+ у) = А(х) + А(у)
— свойство аддитивности оператора; -
А(х)
= А(x)
— свойство однородности оператора.
Определение
3. Вектор
у
= А(х)
называется образом вектора x,
а сам вектор х
—
прообразом вектора у.
Если
пространства Rn
и Rm
совпадают, то оператор А
отображает пространство Rn
в себя. Именно такие операторы мы будем
рассматривать в дальнейшем.
Связь
между вектором х
и
его образом у
=
А(х)
можно
выразить
в матричной форме уравнением
Y
= А∙Х,
где
А
— матрица
линейного оператора, X
= (х1,х2,…,хn)Т,
Y
= (y1,
y2,…,
yn)Т
— матрицы-столбцы из координат векторов
х
и
у.
Пример
1.
Пусть
Являются ли линейными следующие
преобразования?
Решение.
Преобразование
будет линейным, если все координаты
образов векторов будут линейными
комбинациями координат вектора
.
Здесь в преобразованиивторая координата равная
не является линейной комбинацией, в
преобразовании,
аналогично, кроме того, третья координата
имеет вид,
что так же не является линейной комбинацией
координат вектора.
Значит, эти преобразования не являются
линейными. Преобразованиеявляется линейным.
Пример
2.
Пусть в пространстве R3
линейный
оператор А,
в
базисе е1,
е2,
е 3
задан
матрицей A
=

Найти
образ у
=
А(х)
вектора
х
= 4е1
—
Зе2
+ е3.
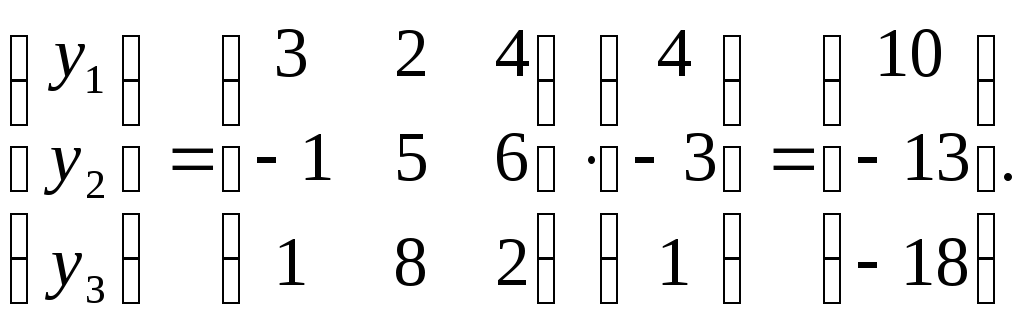
Решение.
По формуле Y
= А∙Х
имеем
Следовательно,
у
= 10el
— 13e2
—
18е3.
►
2. Действия над линейными операторами.
Определение
4. Суммой
двух линейных операторов А
и
В
называется
оператор (А
+ В),
определяемый равенством: (А
+ В)(х) = А(х) + В(х).
Определение
5. Произведением
линейного оператора А
на число
называется
оператор
А
, определяемый
равенством (А)(х)
= (А(х)).
Определение
6. Произведением
линейных операторов А
и
В
называется
оператор
АВ,
определяемый
равенством: (АВ)(х)
= А(В(х)).
Можно
убедиться в том, что операторы (А
+ В), А,
АВ
полученные
в результате этих действий, удовлетворяют
отмеченным
выше
свойствам аддитивности и однородности,
т.е. являются линейными.
Определим
нулевой
оператор О,
переводящий
все векторы пространства
Rn
в
нулевые векторы 0(х)
=
0,
и тождественный
оператор
Е,
действующий по правилу: Е(х)
= х.
Пример
3. Выяснить,
какие из заданных отображений в себя
пространства арифметических векторов
R3
являются линейными операторами. Выписать
их матрицы в каноническом базисе:
-
А(х)=(х1,
х2+1,
х3+2)
– не является линейным оператором; -
А(х)=(х2
+х3
,2х1
+х2
, 3х1
– х2
+х3)
– является линейным оператором с
матрицей
.
Пример
3.
В пространстве заданы два линейных
оператора А
и В.
Найти матрицу С
линейного оператора С=АВ
и его явный вид в каноническом базисе:
А(х)=(2х2,
-2х1
+3х2
+2х3
, 4х1
– х2
+5х3
), В(х)=(-3х1
+х3
, 2х2
+х3
, -х2
+3х3
).
Решение:
Составим матрицы операторов
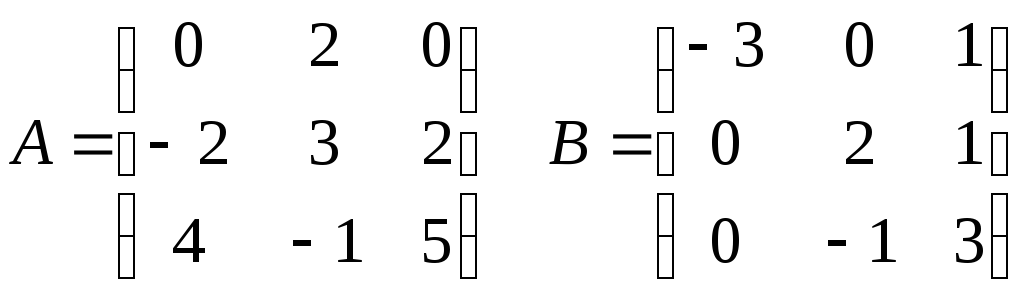
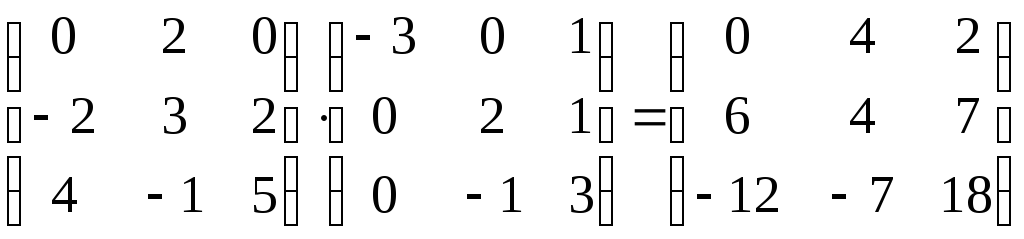
Следовательно
С(х)
=(4х2
+2х3,
6х1
+4х2
+7х3
, -12х1
-7х2
+18х3
).
Пример
4. Пусть
Найти
ψ(х)=
Решение.
Матрицы
преобразований
будут соответственно
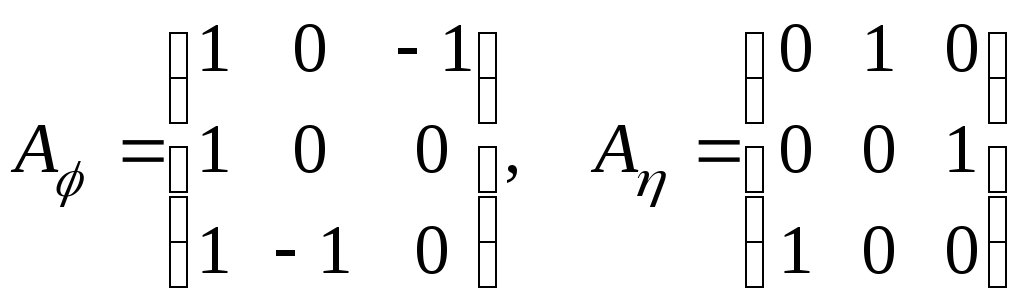
Пусть
– матрица преобразования
,
тогда

.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
$begingroup$
Let $Tcolonmathbb{R}^2tomathbb{R}^2$ be given
by $T(x,y) = (x + 2y, 3x + y)$.
I’m not sure if I plugged the values in the right place.
Ax. 1:
$T(x + y) = T(x) + T(y)$
$[(x+2y) + 2(3x + y) + 3(x + 2y) — (3x — y)] = [(x+2y) + 2(3x + y)] + [3(x + 2y) — (3x — y)]$
Is that right?
asked Apr 15, 2011 at 1:39
$endgroup$
1
$begingroup$
You can write $T(x,y)$ in matrix form:
$$ begin{bmatrix} 1 & 2 \ 3 & 1 end{bmatrix} begin{bmatrix} x \ y end{bmatrix} $$
Now it’s clear that it’s linear.
answered Apr 15, 2011 at 1:47
Yuval FilmusYuval Filmus
56.3k5 gold badges90 silver badges162 bronze badges
$endgroup$
1
$begingroup$
In your «Ax 1», $x$ and $y$ are supposed to elements of $mathbb{R}^2$. So $x=(x_1,x_2)$, and $y=(y_1,y_2)$. Then $x+y = (x_1+y_1, x_2+y_2)$. That is:
$$T(x+y) = T(x_1+y_1,x_2+y_2) = Bigl( (x_1+y_1)+2(x_2+y_2), 3(x_1+y_1)+(x_2+y_2)Bigr).$$
Then you should evaluate $T(x) = T(x_1,x_2)$ and $T(y)=T(y_1,y_2)$, add the results, and compare the answers.
Ross Millikan
369k27 gold badges252 silver badges444 bronze badges
answered Apr 15, 2011 at 3:02
Arturo MagidinArturo Magidin
377k55 gold badges787 silver badges1103 bronze badges
$endgroup$
$begingroup$
HINT $ $ One easily verifies that these maps are linear: $rm A:(x,y) = (x,0):;: $ $rm B:(x,y) = (y,0):.: $
Thus so too is $rm (A+2:B):(x,y) := A:(x,y) + 2:B:(x,y) = (x,0) + (2:y,0) = (x+2:y,0):.$
answered Apr 19, 2011 at 20:43
Bill DubuqueBill Dubuque
265k37 gold badges278 silver badges906 bronze badges
$endgroup$


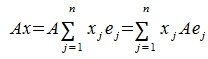
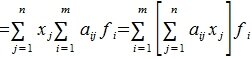
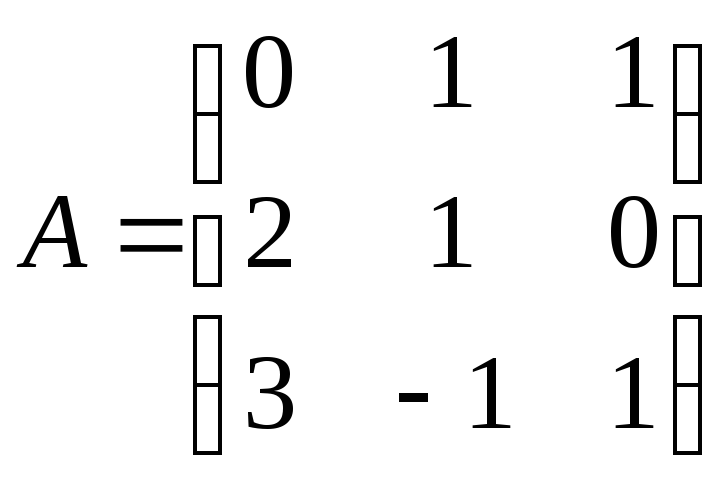 .
.