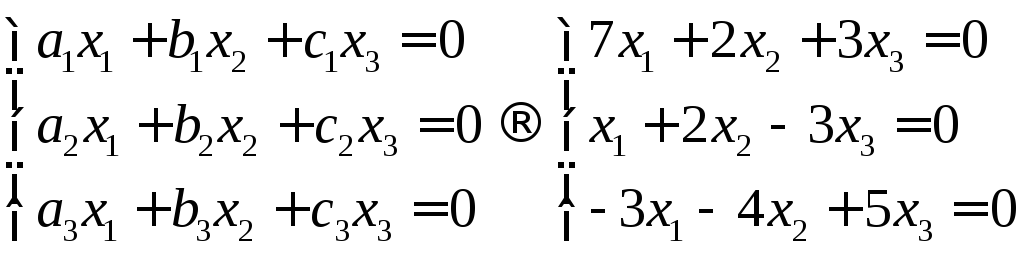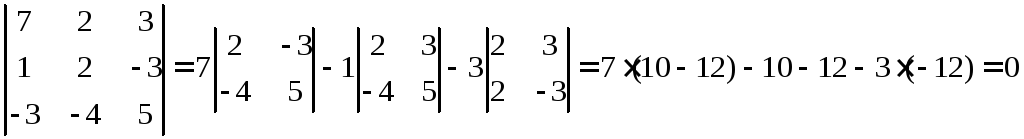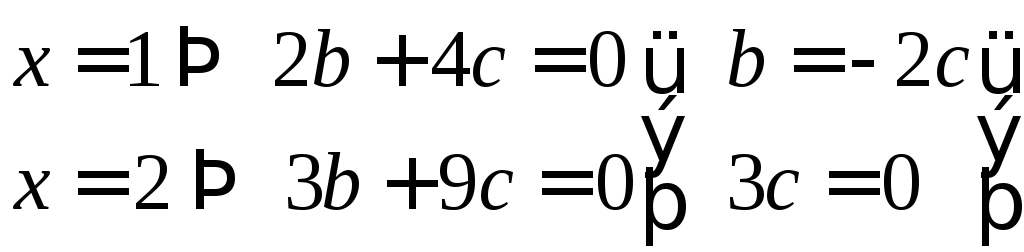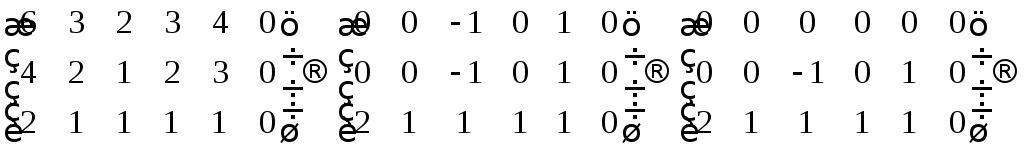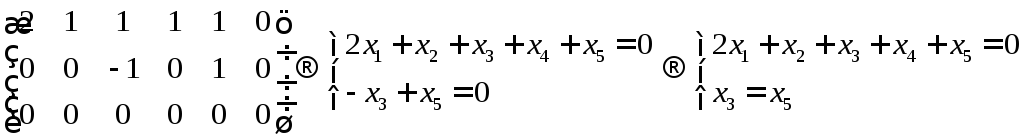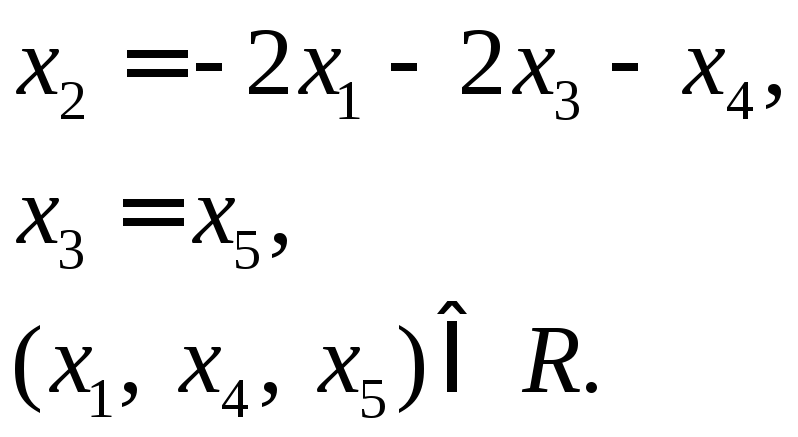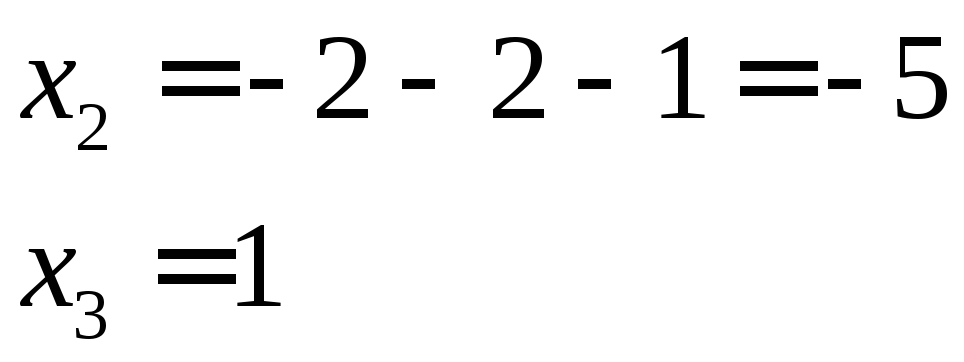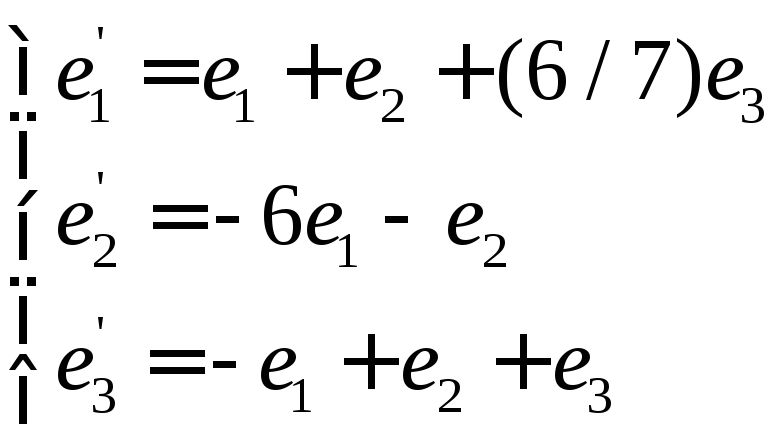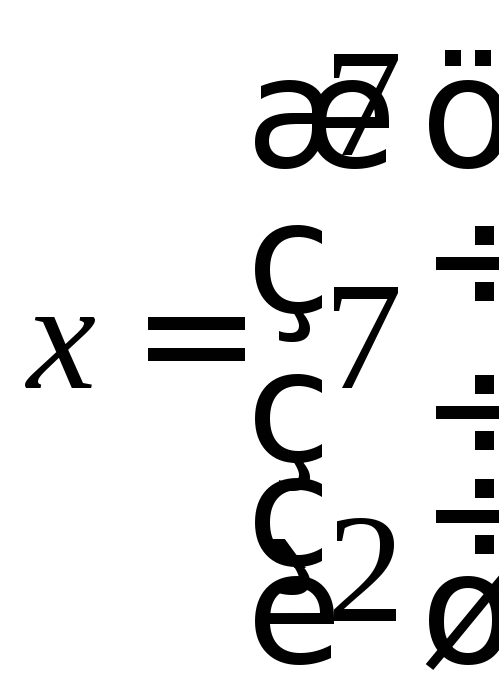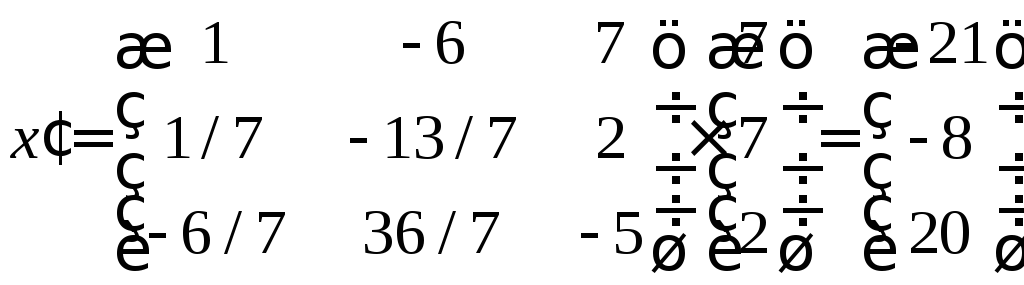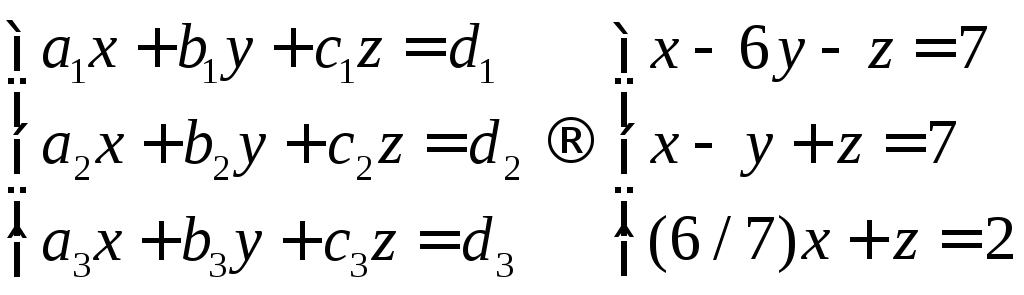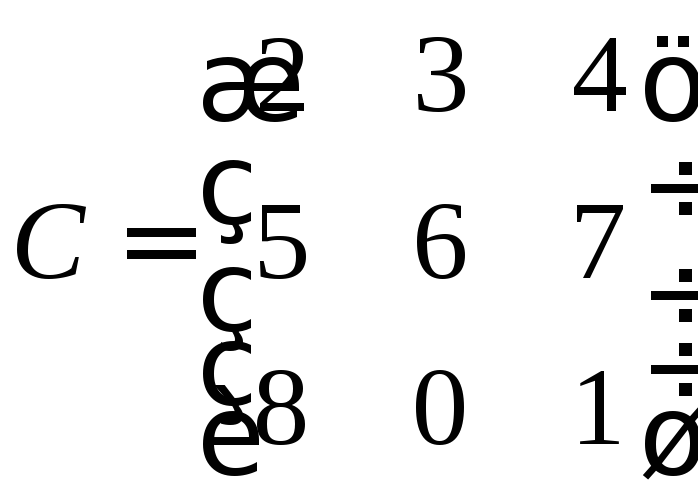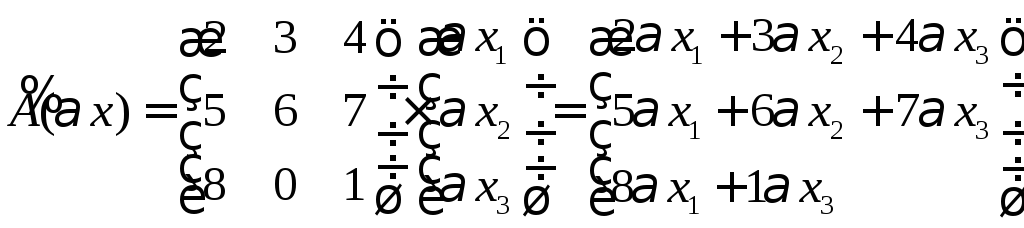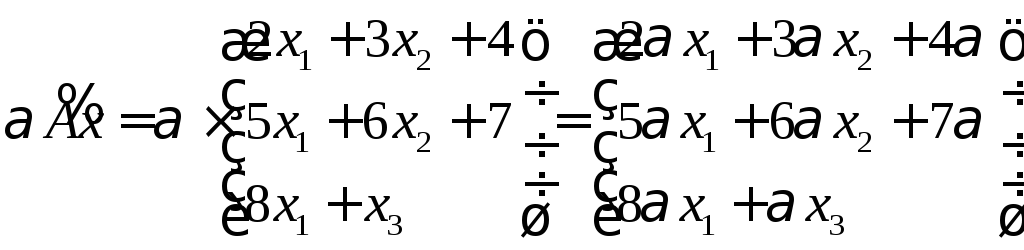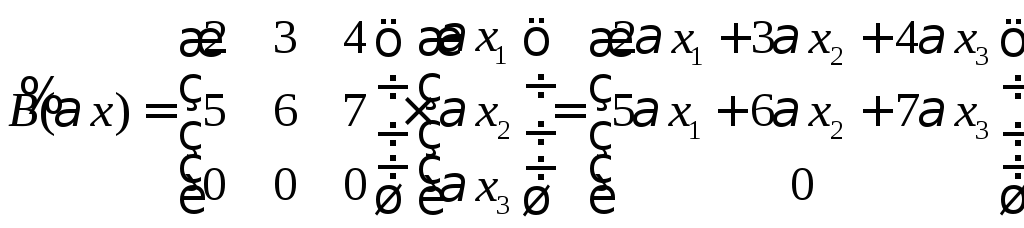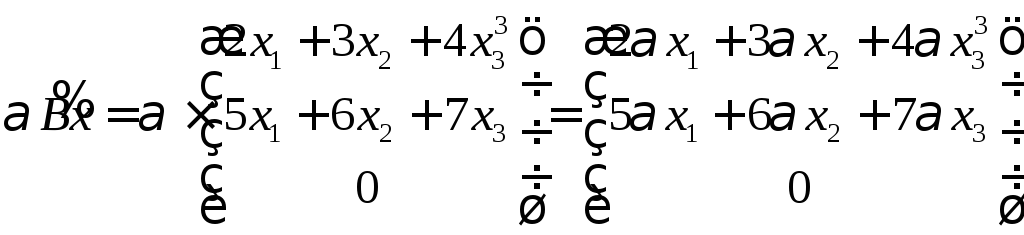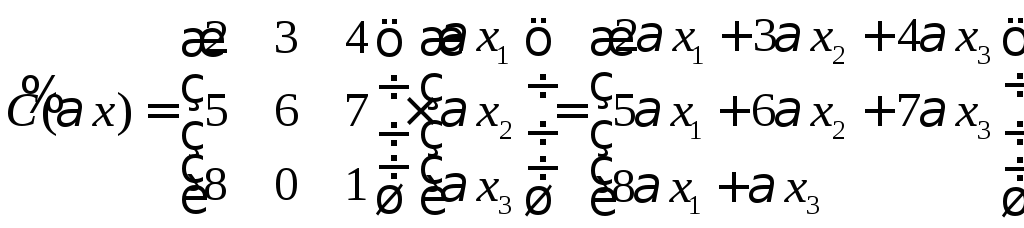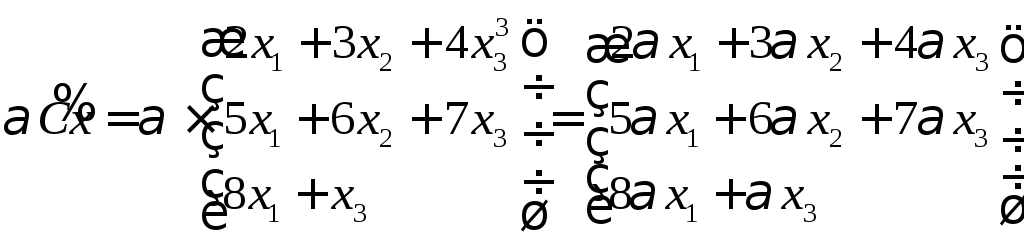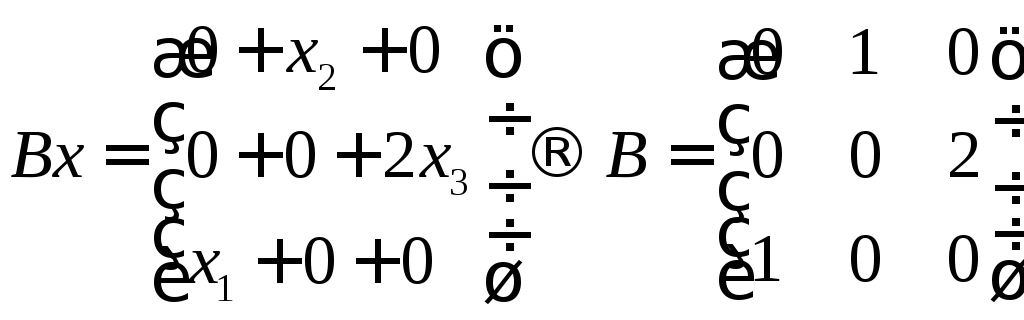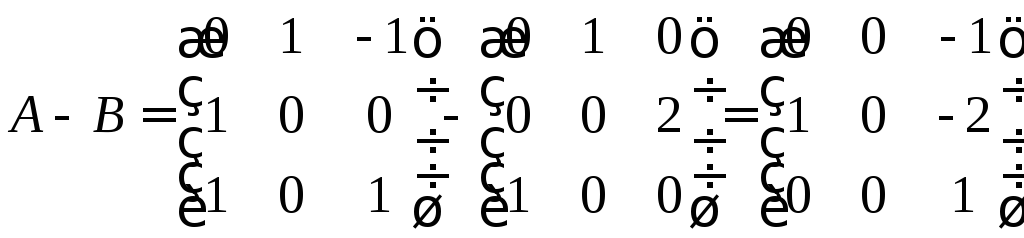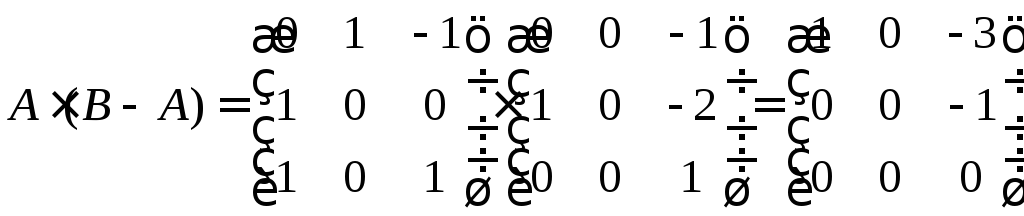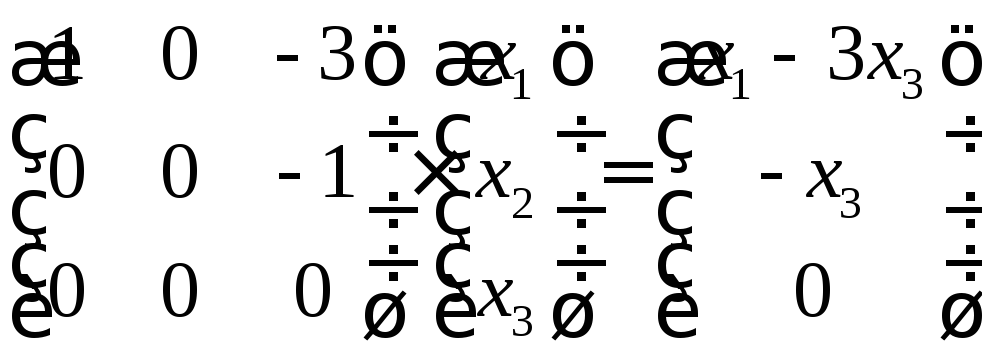Как найти линейно зависимы вектора или нет - Исправление недочетов и поиск решений вместе с Examum.ru

Линейно зависимые и линейно независимые вектора.

Навигация по странице:

Определение линейной комбинации векторов
Определение линейно независимой комбинации векторов
Определение линейно зависимой комбинации векторов
Свойства линейно зависимых векторов
Примеры задач на линейную зависимость и линейную независимость векторов

Определение. Линейной комбинацией векторов a₁, …, a_n с коэффициентами x₁, …, x_n называется вектор

x₁a₁ + … + x_na_n.

Определение. Линейная комбинация x₁a₁ + … + x_na_n называется тривиальной, если все коэффициенты x₁, …, x_n равны нулю.

Определение. Линейная комбинация x₁a₁ + … + x_na_n называется нетривиальной, если хотя быбы один из коэффициентов x₁, …, x_n не равен нулю.

Определение. Вектора a₁, …, a_n называются линейно независимыми, если не существует нетривиальной комбинации этих векторов равной нулевому вектору.

То есть вектора a₁, …, a_n линейно независимы если x₁a₁ + … + x_na_n = 0 тогда и только тогда, когда x₁ = 0, …, x_n = 0.

Определение. Вектора a₁, …, a_n называются линейно зависимыми, если существует нетривиальная комбинация этих векторов равная нулевому вектору.

Свойства линейно зависимых векторов:

Для 2-х и 3-х мерных векторов.

Два линейно зависимые вектора — коллинеарные. (Коллинеарные вектора — линейно зависимы.)
.
Для 3-х мерных векторов.

Три линейно зависимые вектора — компланарные. (Три компланарные вектора — линейно зависимы.)
Для n -мерных векторов.

n + 1 вектор всегда линейно зависимы.

Примеры задач на линейную зависимость и линейную независимость векторов:

Пример 1. Проверить будут ли вектора a = {3; 4; 5}, b = {-3; 0; 5}, c = {4; 4; 4}, d = {3; 4; 0} линейно независимыми.

Решение:

Вектора будут линейно зависимыми, так как размерность векторов меньше количества векторов.

Пример 2. Проверить будут ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 1} линейно независимыми.

Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.

x₁a + x₂b + x₃c₁ = 0

Это векторное уравнение можно записать в виде системы линейных уравнений

	x₁ + x₂ = 0
x₁ + 2x₂ — x₃ = 0
x₁ + x₃ = 0

Решим эту систему используя метод Гаусса

1100
12-10
1010

из второй строки вычтем первую; из третей строки вычтем первую:

1100
1 — 12 — 1-1 — 00 — 0
1 — 10 — 11 — 00 — 0

1100
01-10
0-110

из первой строки вычтем вторую; к третей строке добавим вторую:

1 — 01 — 10 — (-1)0 — 0
01-10
0 + 0-1 + 11 + (-1)0 + 0

1010
01-10
0000

Данное решение показывает, что система имеет множество решений, то есть существует не нулевая комбинация значений чисел x₁, x₂, x₃ таких, что линейная комбинация векторов a, b, c равна нулевому вектору, например:

—a + b + c = 0

а это значит вектора a, b, c линейно зависимы.

Ответ: вектора a, b, c линейно зависимы.

Пример 3. Проверить будут ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 2} линейно независимыми.

x₁a + x₂b + x₃c₁ = 0

Это векторное уравнение можно записать в виде системы линейных уравнений

	x₁ + x₂ = 0
x₁ + 2x₂ — x₃ = 0
x₁ + 2x₃ = 0

Решим эту систему используя метод Гаусса

1100
12-10
1020

из второй строки вычтем первую; из третей строки вычтем первую:

1100
1 — 12 — 1-1 — 00 — 0
1 — 10 — 12 — 00 — 0

1100
01-10
0-120

из первой строки вычтем вторую; к третей строке добавим вторую:

1 — 01 — 10 — (-1)0 — 0
01-10
0 + 0-1 + 12 + (-1)0 + 0

1010
01-10
0010

из первой строки вычтем третью; к второй строке добавим третью:

1 — 00 — 01 — 10 — 0
0 + 01 + 0-1 + 10 + 0
0010

1010
0100
0010

Данное решение показывает, что система имеет единственное решение x₁ = 0, x₂ = 0, x₃ = 0, а это значит вектора a, b, c линейно независимые.

Ответ: вектора a, b, c линейно независимые.

Источник

Чтобы проверить
является ли система векторов
линейно-зависимой, необходимо составить
линейную комбинацию этих векторов
,
и проверить, может ли она быть рана нулю,
если хот один коэффициент равен нулю.

Случай 1. Система
векторов заданна векторами

Составляем линейную
комбинацию

Мы получили
однородную систему уравнений. Если она
имеет ненулевое решение, то определитель
должен быть равен нулю. Составим
определитель и найдём его значение.

Определитель равен
нулю, следовательно, вектора линейно
зависимы.

Случай 2. Система
векторов заданна аналитическими
функциями:

a)
,
если тождество верно, значит система
линейно зависима.

Составим линейную
комбинацию.

Необходимо
проверить, существуют ли такие a,
b,
c
(хотя бы одна из которых не равна нулю)
при которых данное выражение равно
нулю.

Запишем гиперболические
функции

,
,
тогда

тогда линейная
комбинация векторов примет вид:

,
откуда
,
возьмём, например,,
тогда линейная комбинацияравна нулю, следовательно, система
линейно зависима.

Ответ: система
линейно зависима.

b)
,
составим линейную комбинацию

Линейная комбинация
векторов, должна быть равна нулю для
любых значений x.

Проверим для
частных случаев.

Линейная комбинация
векторов равна нулю, только если все
коэффициенты равны нулю.

Следовательно,
система линейно не зависима.

Ответ: система
линейно не зависима.

5.3. Найти какой-нибудь базис и определить размерность линейного пространства решений.

Сформируем
расширенную матрицу и приведём её к
виду трапеции методом Гаусса.

Получим

Чтоб
получить какой-нибудь базис подставим
произвольные значения:

Получим
остальные координаты

Ответ:

5.4. Найти координаты вектора X в базисе , если он задан в базисе .

Нахождение координат
вектора в новом базисе сводится к решению
системы уравнений

Способ 1.
Нахождение при помощи матрицы перехода

Составим матрицу
перехода

Найдём вектор в
новом базисе по формуле

Найдём обратную
матрицу и выполним умножение

Способ 2.
Нахождение путем составления системы
уравнений.

Составим базисные
вектора из коэффициентов базиса

,
,

Нахождение вектора
в новом базисе имеет вид

,
где d
это заданный вектор x.

Полученное уравнение
можно решить любым способом, ответ будет
аналогичным.

Ответ: вектор в
новом базисе
.

5.5. Пусть x = (
x₁,
x₂,
x₃
).
Являются ли линейными следующие
преобразования.

Составим матрицы
линейных операторов из коэффициентов
заданных векторов.

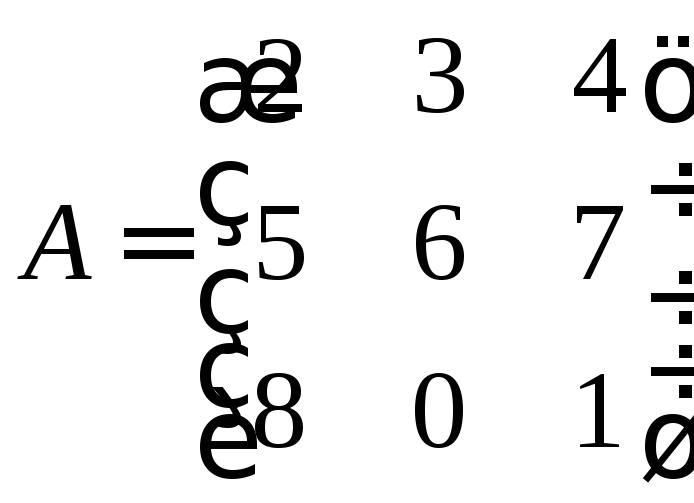
Проверим свойство
линейных операций для каждой матрицы
линейного оператора.

Левую часть найдём
умножением матрицы А
на вектор

Правую часть
найдем, умножив заданный вектор на
скаляр
.

Мы видим, что
значит, преобразование не является
линейным.

Проверим другие
вектора.

,
преобразование не является линейным.

,
преобразование является линейным.

Ответ: Ах
– не линейное преобразование, Вх
– не линейное, Сх
– линейное.

Примечание.
Можно выполнить данное задание гораздо
проще, внимательно посмотрев на заданные
вектора. В Ах
мы видим, что есть слагаемые которые не
содержат элементы х,
что не могло быть получено в результате
линейной операции. В Вх
есть элемент х
в третьей степени, что также не могло
быть получено умножением на вектор х.

5.6. Дано x
= {
x₁,
x₂,
x₃
},
Ax
= {
x₂
–
x₃,
x₁,
x₁
+ x₃
},
Bx
= {
x₂,
2x₃,
x₁
}.
Выполнить заданную операцию: (
A(
B
– A
))x
.

Выпишем матрицы
линейных операторов.

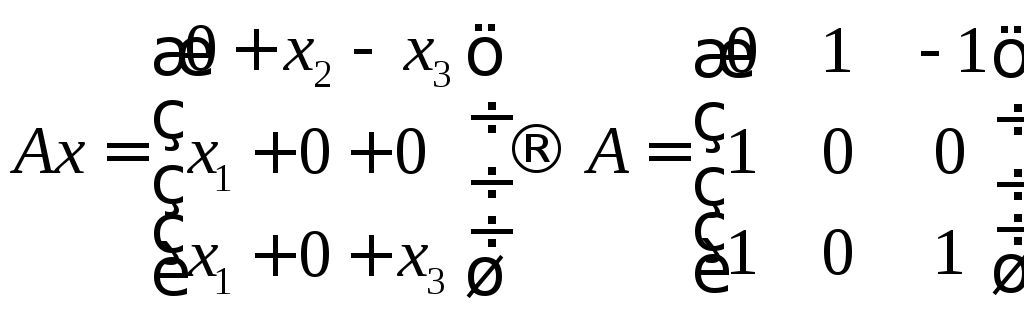
Выполним операцию
над матрицами

При умножении
полученной матрицы на Х, получим

Ответ:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
#
#
#
03.03.2016959.94 Кб5PT.pdf
#

Источник

Понятия и определения

По сути, под вектором в математике понимают отрезок с определённой длиной и направлением. Его принято изображать в виде прямой линии, ограниченной двумя точками. Одна из них является началом, а другая концом. Подписывается вектор с помощью двух больших латинских букв или одной маленькой. Числовое значение, соответствующее длине отрезка, является модулем вектора. Изображается модульность двумя вертикальными линиями слева и справа.

Когда начальная и конечная точка отрезка совпадают, вектор называется нулевым. Соответственно, его длина равняется нулю. Кроме этого, векторы, в зависимости от расположения, разделяют на следующие виды:

коллинеарные — отрезки, располагающиеся в пространстве на одной прямой или параллельные одной линии;
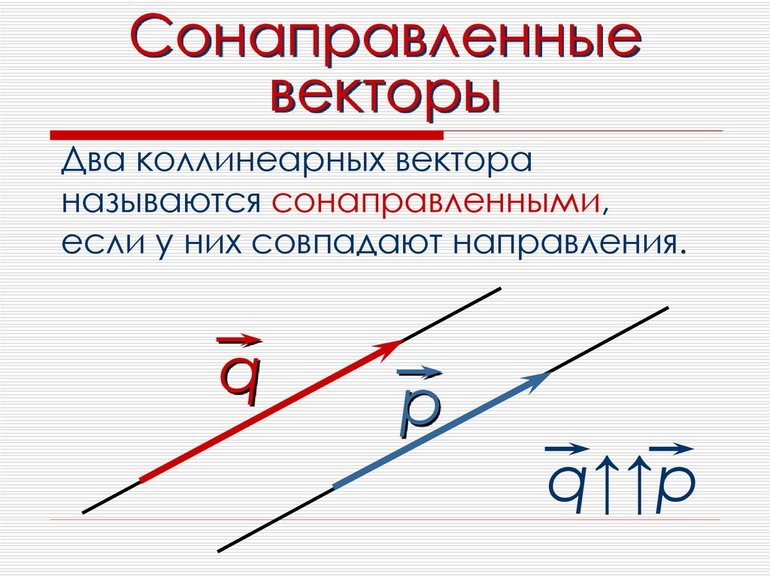
сонаправленные — векторы, совпадающие по направлению;
противоположные — ограниченные линии, у которых направление является обратным по отношению друг к другу;
ортогональными — прямые расположены на плоскости так, что создают угол 90 градусов;
компланарные — отрезки, располагающиеся на одной плоскости, или параллельные;
равные — прямые, совпадающие по направлению и длине.

Чтобы два вектора можно было назвать коллинеарными, должно выполняться любое из следующих условий:

для двух отрезков существует число, при котором выполняется равенство a = c * b, где b может быть любым числом;
координаты векторов равны.

Ортогональность предполагает выполнение условия, при котором выполняется равенство a = {ax; ay} и b = {bx; by}. При этом справедливо выражение a * b = ax * bx + ay * by = 0.

Над векторами можно выполнять арифметические действия. Их можно складывать, вычитать или перемножать. Произведение может быть скалярным, векторным или смешанным. Под первым понимается произведение модулей отрезков на косинус угла, ими образованного, под вторым — площадь параллелограмма, выстроенного на перемножаемых векторах, под третьим — умножение скалярного произведения на векторное.

Зависимость векторов и свойства

В линейной алгебре вводится такое понятие, как векторная система. Под ней понимают заданный набор вида a1, a2, …, an. Если в это множество вести свободные коэффициенты, а векторные элементы системы сложить между собой, то получится выражение, являющееся линейной комбинацией рассматриваемого пространства: Ya1 + Ya2 + … + Yan.

Когда все свободные члены системы одновременно равняются нулю, то комбинация называется тривиальной. Но если хотя бы один из коэффициентов отличен от нуля, то множество уже будет нетривиальным. Например, система 0 * a1 + 0 * a2 — тривиальная, a 12 * a1 + 0 * a2 — нетривиальная. Разобравшись в этих терминах, можно дать определение зависимости системы. Так, она может быть двух типов:

линейно независимая — когда тривиальная комбинация совпадает с нулевым отрезком;
линейно зависимая — когда одна из нетривиальных комбинаций равняется нулевому отрезку.

Определение зависимости важно в векторной алгебре. Опираясь на него, исследуют размерность и базис пространства. Пусть имеется упорядоченная совокупность действительных или комплексных чисел a1, a2, … ap. Линейная комбинация будет выглядеть следующим образом: u * a1 + u * a2 + … + u * ap. Используя правила сложения и произведения векторов, а также понятие n-мерного массива, справедливо утверждать, что рассматриваемая линейная совокупность будет равняться некому отрезку: u * a1 + u * a2 + … + u * ap = b.

При исследовании системы на зависимость необходимо выполнить её проверку на достаточность признаков. Для этого вначале следует убедиться в том, что число векторов не превышает величины координат (в ином случае делается вывод о линейности), затем проверить систему на содержание нулевых отрезков. Если их нет, то необходимо составить матрицу, строками которой будут уравнения системы. При ранге составленной матрицы меньше p — система линейно зависима.

Свойства зависимых и независимых линейных отрезков:

Система, содержащая нулевую линию, является линейно зависимой.
Два одинаковых вектора в системе приводят её к линейной зависимости.
Если в пространстве существуют два пропорциональных отрезка, то она считается линейно зависимой.
Система из ограниченных прямых будет только тогда линейно зависимой, когда хотя бы один из отрезков является линейной комбинацией остальных.
Когда к линейно независимой системе присоединяется отрезок и она превращается в линейно зависимую, то добавляемый вектор можно разложить по существующим прямым системы и только единственным образом.

Операции над отрезками

При нахождении результата в векторной математике часто приходится выполнять различные действия, основанные на свойствах линейных операций над векторами. Самые элементарные из них — это сложение отрезков и умножение их на число.

Пусть имеются две ограниченные линии A и С. Перенеся первую из них к точке O, получится А = AO, а приложив к отрезку A вторую, — С = AC. Соединив две свободные точки, можно построить отрезок OC. Это и будет векторная сумма. Произведение же на число представляет операцию, соответствующую правилу: полученный отрезок, коллинеарный начальному, сонаправлен при n > 0 или противоположно направлен при n < 0, где n — число, на которое выполняется умножение.

Существуют следующие свойства линейных операций:

Коммутативное сложение. При нём выполняется условие a + b = b + a. То есть перестановка значений отрезков на результат не влияет.
Ассоциативное сложение. В этом случае будет верным следующее равенство: (a + b) + с = a + (b + c).
К любому вектору можно прибавить нулевой без изменения ответа: a + 0 = a. Это очевидно, если изобразить на рисунке нулевой отрезок ОА и добавить к нему линию произвольной длины.
Для любой ограниченной прямой AB имеется такой вектор -AB = BA, при котором сложение приведёт к нулю: AB + (-AB) = 0. То есть AB + BA = AA = 0.
Произведение отрезка и числа ассоциативно: (mn) * a = m * (an).
Перемножение вектора и числа является дистрибутивной операцией относительно сложения чисел: (m + n) * a = am * an.
Умножение на единичный отрезок не изменяет исходного результата: 1 * a = a.

В алгебре работают чаще всего с алгебраическими структурами. По сути, это множества, состоящие из математических объектов с известными для них операциями, не противоречащими системным аксиомам. В качестве примера такой структуры можно привести линейное пространство.

В линейной математике исследуются общие свойства таких множеств. При этом их абстрактные векторы необязательно являются геометрическими отрезками. Если же говорить об аналитической геометрии, то векторы используются для обозначения системы координат. Их обычно достаточно, чтобы можно было описать фигуры, используя аналитические формулы.

Разложение по базису

Ограниченная линия является элементом пространства. Так как коллинеарные отрезки могут принадлежать одной прямой или иметь параллельность с другими линиями, то они могут быть как противоположно направленными, так и сонаправленными. Из любой выбранной точки в пространстве можно построить отрезок лишь одним способом.

Под базисом плоскости понимают неколлинеарные векторы (линейно независимые). Произвольная прямая, имеющая ограничения, представляет линейную комбинацию базисных отрезков. Когда имеются два определённых неколлинеарных вектора, любой другой, находящийся на рассматриваемой плоскости, возможно разложить по ним. То есть, как говорят в математике, разложить по базису.

Таким образом, существует теорема, которая гласит, что три вектора называются базисом в декартовой системе координат геометрических отрезков P, если любой из них можно выразить в виде выражения x = j * a + k * c + y * n, где j, k, c — координаты вектора икс в базисе векторов.

Базис записывают в виде (a; b). Упорядоченная пара из неколлинеарных прямых y1 и y2 считается базисом при компланарных векторах определённой плоскости. Любой ненулевой отрезок k будет образовывать базис B = (k) в рассматриваемом множестве геометрических отрезков, коллинеарных некому направлению.

Существует три теоремы:

Если совокупность отрезков принадлежит одному пространству и они соответствуют критерию линейной зависимости векторов, то хотя бы один из них будет являться комбинацией других. Иными словами, любая прямая, имеющая начало и конец, может быть выражена в пространстве с помощью линейных операций. Представление вектора AB как суммы ni + mj + ly называют разложением вектора по базису i, j, y. Коэффициенты, стоящие возле элементов, носят название «составляющие».
Любой вектор AB всегда можно преобразовать по базису, то есть представить в виде равенства AB = Xi + Yi + Zy. При этом коэффициенты выражения можно определить в виде проекций на оси координат. Три вектора всегда будут базисом пространства, если определитель матрицы, составленный из координат, не будет равняться нулю.
Вектор AB можно представить как линейную комбинацию AB1, AB2, AB3, то есть разложить по базису AB1, AB2, AB3: AB = iAB1 + jAB2 + yAB3.

Для доказательства этих теорем используют свойства некомпланарных отрезков и определение линейной комбинации, то есть такого набора, при котором линии пространства R являются скалярами: x = c1x1 + c2x2 + … + CxXn.

Решение примеров

На практических занятиях в школе учащимся для закрепления курса учитель предлагает решить несколько типовых заданий. Школьники, решая их, выходят на достаточный уровень понимания темы и видят практическое применение знаниям. Вот некоторые из таких заданий:

В пространстве размещены четыре вектора: a = {7; 9; 0}, b = {-8; 9; 4}, c = {2; 1; 6}, d = {-1; 8; 5}. Нужно проверить их линейную зависимость. Зная определение, можно утверждать, что отрезки будут линейно зависимыми, так как размерность линий не превышает их число.
Установить линейную зависимость или доказать, что её нет для ограниченных прямых с координатами a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 1}. Чтобы решить это задание, нужно показать соответствие системы на критерии линейности или установить несоответствие. Для этого необходимо вначале найти значения свободных членов, при которых комбинация отрезков будет равняться нулевому вектору. Уравнение следует представить в виде матрицы. Решить ее проще поможет метод Гаусса. После решения матрицы можно будет установить, что система имеет множество корней. Отсюда следует, что имеется ненулевая комбинация коэффициентов, равная нулевому отрезку, например, a — b + c = 0. А это и подтверждает линейную зависимость.
Проверить отрезки a = {1; -1; 3}, b = 2; -1; 4}, c = {2; 0; 2} на линейную зависимость. Для решения примера из заданных координат необходимо построить матрицу. Её ранг можно вычислить методом Гаусса. В ответе получится, что её размерность равняется двум. Так как 2 < 3, то заданная система соответствует линейности.

Простые школьные задания довольно просто решать самостоятельно. Но на практике часто исследование векторной системы занимает много времени и требует внимательности при анализе. Всё дело в том, что координатами могут быть дробные числа, работать с которыми не всегда удобно. В таких случаях есть резон использовать так называемые онлайн-калькуляторы.

С их помощью можно быстро и безошибочно проверить набор базисов на линейную зависимость. При этом от пользователя никаких особых знаний не требуется. Необходимо лишь иметь устройство с доступом в интернет, на котором установлен веб-обозреватель. Все действия сводятся к заполнению предложенной формы данными из задачи и нажатием кнопки «Проверить».

Из бесплатных популярных сайтов можно отметить onlinemschool, mathforyou, matematikam. Эти сервисы имеют интуитивно понятный интерфейс и предоставляют свои услуги бесплатно.

Источник

Линейные системы векторов – зависимые и независимые системы (определение и примеры)

Линейные системы векторов бывают как зависимые, так и независимые. Линейно зависимые системы могут быть тогда, когда из векторов можно составить нулевую линейную комбинацию, а линейно независимая система – когда любая линейная комбинация не равняется нулевому вектору.

Помощь в написании работы

Линейно зависимая система векторов

Система векторов $l_{1}, l_{2},...l_{n}$ называется линейно зависимой, если их линейная комбинация равняется нулевому вектору:

$lambda_{1}overrightarrow{l}_{1} + lambda_{2}overrightarrow{l}_{2} + ... + lambda_{n}overrightarrow{l}_n$ =

(1)

при условии, если хотя бы один из коэффициентов $lambda_{k}(k = 1, 2, 3,..., n)$ не равен нулю.

Если система векторов линейно зависимая, то хотя бы один из них можно преподнести в виде линейной комбинации других. Действительно, если, например, , тогда согласно формуле (1) получается:

$overrightarrow{l}_{1}$ = – $lambda_{2}over{lambda_1}$ x $overrightarrow{l_2}$ -… – $lambda{n}over{lambda_1}$ x $overrightarrow{l_n}$

Наоборот, если $overrightarrow{l_1}$ линейная комбинация векторов $overrightarrow{l_2}, overrightarrow{l_3}, overrightarrow{l_n}$ , то есть

$overrightarrow{l_1} = lambda_{2}overrightarrow{l_2} + ... + lambda_{n}overrightarrow {l_n}$ ,

тогда вся система $overrightarrow{l_1}, overrightarrow{l_2}, ..., overrightarrow{l_n}$ – линейно зависимая, так как:

x $overrightarrow{l_1}$ + $(-lambda_{2})overrightarrow{l_2} + ... + (- lambda_{n})overrightarrow{l}_{n} = 0$

где

Линейно независимая система векторов

Линейные системы векторов – это не только зависимые системы, но и независимые.

Так вот, линейно независимая система векторов $overrightarrow{l_1}, overrightarrow {l_2},...,overrightarrow{l_n}$ называется тогда, когда их линейная комбинация равняется нулевому вектору:

$lambda_{1}overrightarrow{l_1} + lambda_{2}overrightarrow {l_2} + ... + lambda{n}overrightarrow{l_n} = overrightarrow{0}$

только при условии равенства нулю всех коэффициентов: $lambda_{1} = lambda_{2} = ... = lambda_{n} = 0$ .

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Доказательства линейной зависимости и линейной независимости

Понятие линейной зависимости векторов позволяет характеризовать их взаимное положение в пространстве.

Два вектора линейно зависимы тогда и только тогда, когда они коллинеарные.

Произвольные три вектора линейно зависимые тогда и только тогда, когда они компланарные.

Действительно, если предположить , что существует ещё одно решение:

$overrightarrow{a} = alpha_{1}overrightarrow{l_1} + beta_{1}overrightarrow{l_2} + gamma_{1}overrightarrow{l_3}$ .

Тогда, отнимая из (2) последнее равенство, получим:

= $(alpha - alpha_{1})$ x $overrightarrow{l_1}$ + $(beta - beta_{1})$ x $overrightarrow{l_2}$ + $(gamma - gamma_{1})$ x $overrightarrow{l_3}$ .

Как видим, $overrightarrow{l_1}, overrightarrow{l_2}, overrightarrow{l_3}$ – линейно независимы (они не компланарные), тогда решение возможно при условии:

$alpha - alpha_{1}$ = $beta - beta_{1}$ = $gamma - gamma_{1}$ = = $alpha_{1}$ , $beta = beta_{1}$ , $gamma = gamma_{1}$

Примеры задач

Задача

Проверить будут ли вектора = , , , линейно независимыми.

Решение

Вектора будут линейно зависимыми, так как размерность векторов меньше количества векторов.

Задача

Проверить будут ли вектора = , = , = линейно независимыми.

Решение

Найти значение коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору:

$x_{1}overline {a} + x_{2}overline {b} x_{3}c_{1} = overline {0}$

Это векторное уравнение можно записать в виде системы линейных уравнений:

$left{ begin{aligned} x_{1} + x_{2} = 0\ x_{1} + 2x_{2} - x_{3} = 0\ x_{1} + x{3} = 0 end{aligned} right$

Решим эту систему используя метод Гаусса:

$begin{pmatrix} 1&1&0\ 1&2&-1\ 1&0&1 end{pmatrix} right$

Везде получаются нули. Теперь из второй строки вычтем первую; из третьей строки вычтем первую:

$begin{pmatrix} 1&1&0\ 1-1&2-1&-1-0\ 1-1&0-1&1-0 end{pmatrix} to begin{pmatrix} 1&1&0\ 0&1&-1\ 0&-1&1 end{pmatrix} right$

из первой строки вычтем вторую; к третьей строке добавим вторую:

$begin{pmatrix} 1-0&1-1&0-(-1)\ 0&1&-1\ 0+0&-1+1&1+(-1) end{pmatrix}to begin{pmatrix} 1&0&1&\ 0&1&-1\ 0&0&0& end{pmatrix} right$

Данное решение показывает, что система имеет множество решений, то есть существует не нулевая комбинация значений чисел $x_{1}, x_{2}, x_{3}$ таких, что линейная комбинация векторов , , равна нулевому вектору, например

+ + = .

А это значит, что вектора , , линейно зависимы.

Ответ: вектора , , линейно зависимы.

Источник