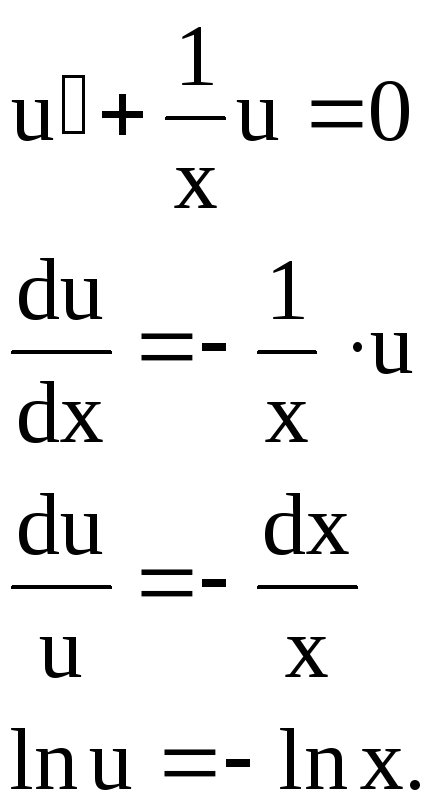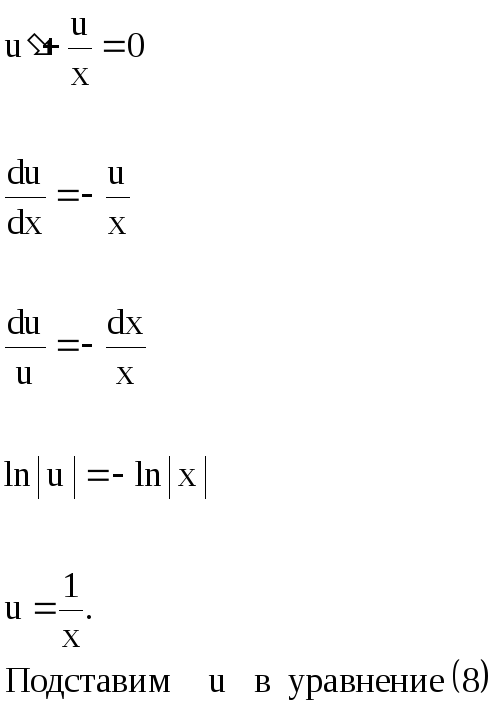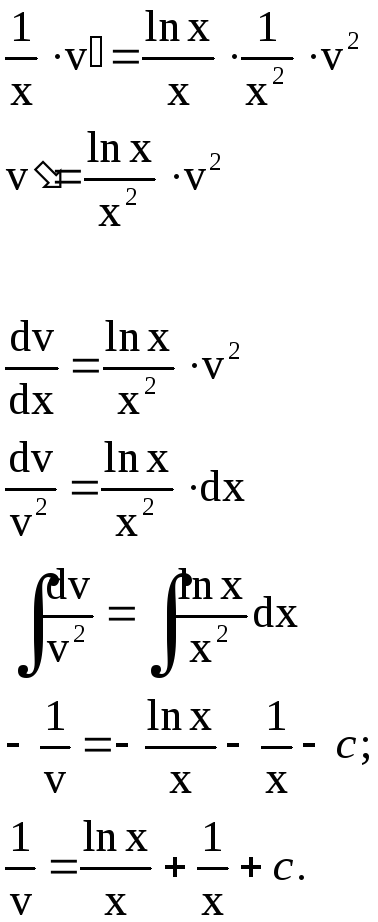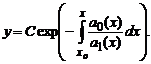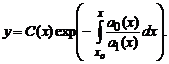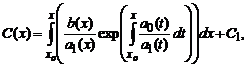Заказать задачи по любым предметам можно здесь от 10 минут
Как найти общее и частное решение линейных дифференциальных уравнений
СОДЕРЖАНИЕ ТЕКУЩЕЙ СТАТЬИ
- Линейное ДУ первого порядка
-
- Метод Бернулли
- Метод Лагранжа (вариация произвольной постоянной)
- Линейное ДУ второго порядка
-
- Метод подбора по правой части
- Метод Лагранжа (вариация произвольной постоянной)
Линейное дифференциальное уравнение — это уравнение, в котором все $y$ и его производные, входят только в первой степени и не перемножаются между собой.
В этой статье рассмотрим решение таких уравнений первого и второго порядка с неоднородной правой частью. В зависимости от порядка диффура выбирается метод его решения. Хотя есть универсальный метод вариации произвольных постоянных. Разберем все методы.
Линейное ДУ первого порядка
Линейные дифференциальные уравнения первого порядка имеют следующий вид $$y’+g(x)y=f(x),$$ где $g(x)$ и $f(x)$ некоторые функции. Для решения такого типа уравнений можно применить метод Бернулли, либо метод Лагранжа (вариация произвольной постоянной).
Метод Бернулли
- Выполняем подстановку $y=uv, y’=u’v+uv’$, где $u(x),v(x)$ некоторые функции
- Строим систему уравнений, чтобы найти $u(x)$ и $v(x)$
- Подставляем $u(x), v(x)$ в $y=uv$, чтобы получить общее решение.
| Пример 1 |
| Найти частное решение линейного дифференциального уравнения первого порядка $$y’-y tg x=frac{1}{cos x}, y(0)=0.$$ |
| Решение |
|
Первым шагом делаем подстановку $y=uv, y’=u’v+uv’$ и получаем $$u’v+uv’-uv tg x=frac{1}{cos x}.$$ Теперь выносим за скобки функцию $u$ и составляем систему уравнений: $$u’v+u(v’-v tg x)=frac{1}{cos x}$$ $$begin{cases} v’-v tg x = 0 \ u’v=frac{1}{cos x} end{cases}.$$ Сначала решаем первое уравнение методом разделяющихся переменных, чтобы из него получить $v(x)$: $$begin{cases} frac{dv}{v} = tg x dx \ u’v=frac{1}{cos x} end{cases} Rightarrow begin{cases} ln|v| = -int frac{d(cos x)}{cos x} \ u’v = frac{1}{cos x} end{cases}$$ $$begin{cases} ln|v| = -ln|cos x| \ u’v=frac{1}{cos x} end{cases} Rightarrow begin{cases} v=frac{1}{cos x} \ u’ = 1 end{cases} Rightarrow begin{cases} v=frac{1}{cos x} \ u=x+C end{cases}.$$ Таким образом подставляем найденные $u$ и $v$ в подстановку $y=uv$, чтобы получить общее решение линейного дифференциального уравнения $$y=frac{x+C}{cos x}.$$ Но по условию требуется найти частное решение, поэтому используя дополнительное условие $y(0)=0$ находим константу $C$ $$frac{0+C}{cos 0} = 0 Rightarrow C = 1.$$ Теперь зная значение $C=1$ подставляем его в общее решение и получаем ответ в виде частного решения линейного дифференциального уравнения $$y = frac{x}{cos x}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = frac{x}{cos x}$$ |
Метод Лагранжа (вариация произвольной постоянной)
- Находим общее решение однородного уравнения
- В общем решении заменяем постоянную $C$ на функцию $C(x)$
- Находим $y’$ и подставляем его вместе с $y$ в исходное уравнение
- Получаем чему равно $C(x)$ из последнего равенства
- Подставляем $C(x)$ в ранее полученное общее решение и записываем ответ
| Пример 2 |
| Решить линейное дифференциальное уравнение первого порядка $$y’ cos^2 x + y = tg x, quad y(0)=0.$$ |
| Решение |
|
Сначала приведем уравнение к виду $y’+g(x)=f(x)$ путем деления обеих частей диффура на квадрат косинуса $$y’ + frac{y}{cos^2 x} = frac{sin x}{cos^3 x}.$$ Теперь находим общее решение однородного дифференциального уравнения $$y’+frac{y}{cos^2 x} = 0.$$ Разделяем переменные по разные стороны и интегрируем обе части: $$frac{dy}{dx}=-frac{y}{cos^2 x}$$ $$int frac{dy}{y}=-int frac{dx}{cos^2 x}$$ $$ln|y|=-tg x + C$$ $$y = Ce^{-tg x}.$$ Теперь найдем частное решение неоднородного уравнения методом Лагранжа варьируя произвольную постоянную. А именно, заменяем в полученном общем решении константу $C$ на функцию $C(x)$ $$y = C(x)e^{-tg x}.$$ Находим производную функции $$y’ = C'(x)e^{-tg x} — C(x)e^{-tg x} frac{1}{cos^2 x}.$$ Подставляем общее решение и его производную в исходное линейное дифференциальное уравнение, чтобы получить $C'(x)$ $$(C'(x)e^{-tg x} — C(x)e^{-tg x} frac{1}{cos^2 x}) cos^2 x + C(x)e^{-tg x} = tg x.$$ После упрощения получаем, что $$C'(x)e^{-tg x} cos^2 x = tg x.$$ Умножаем уравнение на $e^{tg x}$ и делим на $cos^2 x$ $$C'(x) = frac{tg x}{cos^2 x} e^{tg x}.$$ Теперь, можно получить $C(x)$, просто проинтегрировав правую часть уравнения $$C(x) = int frac{tg x}{cos^2 x} e^{tg x} dx. $$ Выполняем подведение под знак дифференциала $frac{1}{cos^2 x}$ $$C(x) = int tg x e^{tg x} d(tg x).$$ Для комфорта взятия интеграла сделаем замену $tg x = t$, а затем применяя метод интегрирования по частям найдем решение интеграла $$C(x)=int t e^t dt = begin{vmatrix} u = t qquad du=dt \ dv=e^t qquad v=e^t end{vmatrix} = te^t — int e^t dt = te^t — e^t + C.$$ Возвращаемся назад к иксам $$C(x) = te^t — e^t + C = tg x e^{tg x} — e^{tg x} + C.$$ Итак, теперь можно записать общее решение линейного дифференциального уравнения неоднородного $$ytext{о.н.} = ( tg x e^{tg x} — e^{tg x} + C)e^{-tg x} = tg x — 1 + Ce^{-tg x}.$$ По условию задачи требуется найти частное решение, значит применяем условие $y(0)=0$ и находим значение постоянной $C$ $$0 — 1 + C = 0 Rightarrow C=1.$$ Теперь можно записать окончательный ответ $$y = e^{-tg x} + tg x — 1.$$ |
| Ответ |
| $$y = e^{-tg x} + tg x — 1$$ |
Линейное ДУ второго порядка
Обычно в контрольных работах дают задачи на решение линейных дифференциальных уравнений второго порядка с постоянными коэффициентами. Поэтому разберем как решать именно такие уравнения $$y»+py’+qy=f(x).$$
Метод подбора по правой части
Общее решение линейного неоднородного уравнения складывается из общего решения однородного и частного решения неоднородного уравнений $$y_text{о.н.} = y_text{о.о.}+y_text{ч.н.}.$$ Поэтому первым делом нужно решить однородное уравнение (т.е. f(x)=0), а затем найти частное решение подобрав правую часть по таблице.
Для того, чтобы найти общее решение линейного однородного уравнения, требуется составить характеристический многочлен и найти его корни $$lambda^2 + plambda + q = 0.$$ В зависимости от получившихся корней общее решение однородного уравнения выглядит следующим образом:
- $lambda_1 neq lambda_2$, то $y_text{о.о.} = C_1 e^{lambda_1 x} + C_2 e^{lambda_2 x}$
- $lambda_1 = lambda_2$, то $y_text{о.о.} = C_1 e^{lambda_1 x} + C_2 xe^{lambda_1 x}$
- $lambda_{1,2} = alpha pm beta i$, то $y_text{о.о.} = C_1e^{alpha x}cos beta x + C_2 e^{alpha x} sin beta x$.
Далее необходимо по виду правой части подобрать частное решение $y_text{ч.н.}$. Для этого нужно воспользоваться таблицей.
| № | Правая часть | Корни характеристического многочлена | Вид частного решения |
| 1 | $$P_n (x)$$ | Число 0 не является корнем характеристического уравнения. | $$tilde{P_n}(x)$$ |
| Число 0 – корень характеристического уравнения кратности $S$. | $$x^s tilde{P_n}(x)$$ | ||
| 2 | $$P_n (x) e^{alpha x}$$ | Число $alpha$ не является корнем характеристического уравнения. | $$tilde{P_n} (x) e^{alpha x}$$ |
| Число $alpha$ является корнем характеристического уравнения кратности $S$. | $$x^s tilde{P_n} (x) e^{alpha x}$$ | ||
| 3 | $$P_n (x) cos beta x + Q_m (x) sin beta x$$ | Число $pm ibeta$ не является корнем характеристического уравнения. | $$tilde {P_n} cos beta x + tilde{Q_m} sin beta x$$ |
| Число $pm ibeta$ является корнем характеристического уравнения кратности $S$. | $$x^s (tilde {P_n} cos beta x + tilde{Q_m} sin beta x)$$ | ||
| 4 | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ | Число $alpha pm ibeta$ не является корнем характеристического уравнения. | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
| Число $alpha pm ibeta$ является корнем характеристического уравнения. | $$x^s e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
Где $P_n(x)$ и $Q_m(x)$ многочлены.
| Пример 3 |
| Найти общее решение линейного дифференциального уравнения второго порядка $$y»+y’-2y=8sin 2x.$$ |
| Решение |
|
Первым делом находим общее решение однородного дифференциального уравнения $$y»+y’-2y=0.$$ Для этого составляем характеристический многочлен и находим его корни по общей формуле решения квадратных уравнений: $$lambda^2+lambda-2=0$$ $$lambda_{1,2} = frac{-1pm sqrt{1^2-4cdot 1 cdot (-2)}}{2} = frac{-1pm 3}{2}$$ $$lambda_1 = -2, quad lambda_2 = 1.$$ Теперь, используя корни, записывам $$y_text{о.о.} = C_1e^{-2 x} + C_2e^{x}.$$ Теперь нужно найти частное решение неоднородного уравнения $y_text{ч.н.}$ методом подбора правой части. Смотрим на неё и видим, что в нее входит произведение многочлена нулевой степени на косинус. Значит, частное решение будет подбирать в виде $$y_text{ч.н.} = Acos 2x + Bsin 2x,$$ где $A$ и $B$ неизвестные коэффициенты, которые требуется найти на следующем этапе решения. Найдем первую и вторую производную от частного решения: $$y’_text{ч.н.} = -2Asin 2x + 2Bcos 2x$$ $$y»_text{ч.н.} = -4Acos 2x — 4Bsin 2x$$ Теперь подставим полученные производные от $y_text{ч.н.}$ и его само в исходное дифференциальное уравнение, чтобы получить значения $A$ и $B$ методом неопределенных коэффициентов: $$-4Acos 2x — 4Bsin 2x -2Asin 2x + 2Bcos 2x — 2Acos 2x -2Bsin 2x = 8sin 2x$$ $$(2B — 6A)cos 2x + (-6B — 2A)sin 2x = 8sin 2x.$$ Теперь необходимо составить систему уравнений. Справа видим только синус, значит все что перед косинусом слева равно нулю. А всё что перед синусом равно восьми $$begin{cases} 2B-6A = 0 \ -6B-2A = 8 end{cases} Leftrightarrow begin{cases} B-3A=0 \ 3B+A=-4 end{cases} Leftrightarrow begin{cases} B = frac{6}{5} \ A=-frac{2}{5} end{cases}$$ Теперь частное решение неоднородного уравнения выглядит следующим образом $$y_text{ч.н.} = -frac{2}{5} cos 2x — frac{6}{5}sin 2x.$$ Подставляем все найденные данные в окончательную формулу, чтобы записать ответ $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.} = C_1e^{-2 x} + C_2e^{x} -frac{2}{5} cos 2x — frac{6}{5}sin 2x.$$ |
| Ответ |
| $$y = C_1e^{-2 x} + C_2e^{x} -frac{2}{5} cos 2x — frac{6}{5}sin 2x$$ |
| Пример 4 |
| Решить линейное дифференциальное уравнение $$y»-4y=e^{2x}sin 2x.$$ |
| Решение |
|
Сначала получим общее решение однородного уравнения $$y»-4y=0.$$ Составляем характеристическое уравнение и найдем его корни: $$lambda^2 — 4 = 0$$ $$(lambda — 2)(lambda + 2) = 0$$ $$lambda_1 = -2, quad lambda_2 = 2.$$ Записываем теперь решение $$y_text{о.о.} = C_1 e^{2x} + C_2 e^{-2x}.$$ Теперь выполним подбор частного решения неоднородного уравнения, основываясь на типе правой части. Она состоит из произведение экспоненты на синус, перед которым многочлен. По таблице находим, что частное решение нужно искать в виде $$y_text{ч.н.} = Ae^{2x}cos 2x + Be^{2x}sin 2x.$$ Необходимо найти коэффициенты $A$ и $B$. Для этого нужно найти вторую производную частного решения и подставить в исходное уравнение $$y’_text{ч.н.} = 2Ae^{2x}cos 2x — 2Ae^{2x}sin 2x + 2Be^{2x}sin 2x + 2Be^{2x}cos 2x = $$ $$ = (2A+2B)e^{2x}cos 2x + (2B-2A)e^{2x}sin 2x$$ $$y»_text{ч.н.} = 2(2A+2B)e^{2x}cos 2x — 2(2A+2B)e^{2x}sin 2x + 2(2B-2A)e^{2x}sin 2x + 2(2B-2A)e^{2x}cos 2x = $$ $$ = 8Be^{2x}cos 2x — 8Ae^{2x}sin 2x.$$ Подставляем в исходное ДУ: $$8Be^{2x}cos 2x — 8Ae^{2x}sin 2x — 4Ae^{2x}cos 2x — 4Be^{2x}sin 2x = e^{2x} sin 2x$$ $$(8B-4A)e^{2x}cos 2x + (-8A-4B)e^{2x}sin 2x = e^{2x}sin 2x.$$ Теперь составляем систему уравнений путем сопоставления левой и правой части. То, что слева перед синусом приравниваем к тому, что справа перед синусом. А справа косинуса нет, значит там ноль. Поэтому приравниваем скобки перед косинусом слева к нулю $$begin{cases} 8B-4A=0 \ -8A-4B = 1 end{cases} Rightarrow begin{cases} 2B-A=0 \ -8A-4B=1 end{cases} Rightarrow begin{cases} A = -frac{1}{10} \ B = -frac{1}{20} end{cases}.$$ Теперь частное решение приобретает вид $$y_text{ч.н.} = -frac{1}{10}e^{2x}cos 2x — frac{1}{20} e^{2x} sin 2x,$$ и можно записать окончательный ответ к задаче $$y_text{о.н.} = y_text{о.о.}+y_text{ч.н.} = C_1 e^{2x} + C_2 e^{-2x}-frac{1}{10}e^{2x}cos 2x — frac{1}{20} e^{2x} sin 2x.$$ |
| Ответ |
| $$y = C_1 e^{2x} + C_2 e^{-2x}-frac{1}{10}e^{2x}cos 2x — frac{1}{20} e^{2x} sin 2x$$ |
Метод Лагранжа (вариация произвольной постоянной)
Данный метод удобно применять тогда, когда правая часть не подходит под формулы из таблицы. Таким образом, метод Лагранжа становится универсальной палочкой-выручалочкой при решении данного типа задач. Алгоритм следующий:
- Находим общее решение однородного уравнения $y_text{о.о.} = C_1 y_1 + C_2 y_2$
- Заменяем константы $C_1,C_2$ на функции $C_1(x)$ и $C_2(x)$
- Решаем систему методом Крамера $begin{cases} C_1 ‘(x)y_1 + C_2 ‘(x)y_2 = 0 \ C_2 ‘(x)y’_1 + C_2 ‘(x) y’_2 = f(x) end{cases}$
- Интегрируем полученные $C’_1 (x)$ и $C’_2 (x)$
- Подставляем $C_1(x)$ и $C_2(x)$ в общее решение $y_text{о.о.}$
| Пример 5 |
| Найти общее решение линейного дифференциального уравнения второго порядка $$y»+y=frac{1}{sin x}.$$ |
| Решение |
|
Первым делом находим общее решение однородного уравнения $$y»+y=0, $$ составив характериcтический многочлен $$lambda^2 + 1 = 0, $$ и вычислив его корни $$lambda_{1,2} = pm i.$$ Записываем решение $$y_text{о.о.} = C_1 cos x + C_2 sin x.$$ Далее заменяем в нём постоянные $C_1$ и $C_2$ на функции $C_1(x)$ и соответственно $C_2(x)$. И сразу замечаем, что $y_1 = cos x$ и $y_2 = sin x$. Это пригодится для дальнейшего решения задачи при построении системы уравнений. А сейчас записываем, что $$y_text{о.о.} = C_1 (x) cos x + C_2(x) sin x.$$ Перед тем как составим систему уравнений найдем производные: $$y’_1 = -sin x$$ $$y’_2 = cos x.$$ Теперь получаем систему и решаем её методом Крамера $$begin{cases} C_1 ‘(x)cos x+C_2(x)sin x = 0 \ -C’_1 (x)sin x + C’_2(x) cos x = frac{1}{sin x} end{cases}.$$ Находим значение главного определителя $$Delta = begin{vmatrix} cos x & sin x \ -sin x & cos x end{vmatrix} = cos^2 x + sin^2 x = 1.$$ Найдем значение первого дополнительного определителя $$Delta_1 = begin{vmatrix} 0 & sin x \ frac{1}{sin x} & cos x end{vmatrix} = -1 .$$ Найдем значение второго дополнительного определителя $$Delta_2 = begin{vmatrix} cos x & 0 \ -sin x & frac{1}{sin x} end{vmatrix} = frac{cos x}{sin x}.$$ Теперь можно получить производные от искомых функций: $$C’_1(x) = frac{Delta_1}{Delta} = -1$$ $$C’_2(x) = frac{Delta_2}{Delta} = frac{cos x}{sin x}.$$ А затем путем интегрирования находим первообразные последних функций: $$C_1(x)=int (-1) dx = -x + tilde{C_1}$$ $$C_2(x)=int frac{cos x}{sin x} dx = int frac{d(sin x)}{sin x} = ln|sin x| + tilde{C_2}.$$ Теперь получим общее решение неоднородного линейного дифференциального уравнения путем подстановки найденных $C_1(x)$ и $C_2(x)$ в $y_text{о.о.}$ $$y_text{о.о.} = (-x + tilde{C_1})cos x + (ln|sin x|+tilde{C_2})sin x.$$ |
| Ответ |
| $$y = (-x + tilde{C_1})cos x + (ln|sin x|+tilde{C_2})sin x$$ |
Линейные дифференциальные уравнения первого порядка
Определение.
Линейным уравнением первого порядка
называется уравнение, линейное
относительно искомой функции и ее
производной. Общий вид линейного д.у.1:
непрерывные функции или постоянные.
Если,
то уравнениерешается как дифференциальное уравнение
с разделяющимися переменными.
Рассмотрим
уравнения:
1)
Это уравнение является линейным по
определению
,но лучше рассматривать
его как уравнение с разделяющимися
переменными:
2)
Это
уравнение не является линейным, т. к.
функцияy
в уравнении имеет не первую степень,
а выше
3)
Уравнение является
линейным по определению. Но проще
рассматривать его как однородное д.у.1:
где
– однородная функция нулевого измерения.
4)
Запишем уравнение в виде
.
Это линейное д.у.1.
Решение линейного дифференциального уравнения первого порядка
Общее решение
ищется в виде
где
некоторые функции.
Покажем на
примере, что любую функцию
можно представить в виде произведения
двух функций, одна из которых выбирается
произвольно, а вторая зависит от этого
выбора.
Пусть
.
Можнопредставить в виде различных пар
множителей:
где первый множитель
выбирается произвольно.
Указанная подстановка
приводит линейное д.у.1 к решению двух
д.у. с разделяющимися переменными.
Покажем это в общем виде. В линейное
уравнениеподставим
Получим
или
.
(4)
Выберем функцию
u
такой, чтобы
(5)
Уравнение (5) –
дифференциальное уравнение с разделяющимися
переменными:
Интегрируя, найдем
функцию
без
учета произвольной
постоянной. Подставим найденную функцию
в уравнение (4) и получим
дифференциальное уравнение с разделяющимися
переменными (3). Его общее решение
позволит получить второй множитель
Тогда
общее решение линейного д. у. 1.
Пример 1.
Найти общее решение уравнения
Решаем подстановкой
(6)
подставим в (6).
Общее решение:
Пример 2. Найти
частное решение дифференциального
уравнения
Подстановка:
.
(7)
Подставим найденную
функцию u
в уравнение (7):
Таким образом,
общее решение данного уравнения будет
иметь вид
или
Найдем частное
решение дифференциального решения,
удовлетворяющее начальному условию
Следовательно,
искомое частное решение такое:
Уравнения, приводящиеся к линейным (уравнения Бернулли)
Уравнение вида
называется
уравнением Бернулли.
Здесь n
– действительное число, причем при n
= 0 получим линейное уравнение; при
получим уравнение с разделяющимися
переменными. Приуравнение Бернулли приводится к
линейному, поэтому решается подстановкой
Пример. Найти
общее решение уравнения
Разделив левую и
правую части уравнения на
х, представим
его в виде
.
Можно утверждать, что это уравнение
имеет общий вид
т. е. является
уравнением Бернулли. Решаем его
подстановкой
где
– вспомогательные функции.
Подставим
в исходное уравнение:
(8)
Для получения
общего интеграла найдем
или
.
Замечание.
Неопределенный интеграл
найден с применением
формулы интегрирования
по частям:
Производим
подстановку
;
.
Тогда
Соседние файлы в папке ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Линейные уравнения первого порядка
Уравнение первого порядка вида a1(x)y' + a0(x)y = b(x) называется линейным дифференциальным уравнением. Если b(x) ≡ 0 то уравнение называется однородным, в противном случае — неоднородным. Для линейного дифференциального уравнения теорема существования и единственности имеет более конкретный вид.
Назначение сервиса. Онлайн калькулятор можно использовать для проверки решения однородных и неоднородных линейных дифференциальных уравнений вида y'+y=b(x).
- Решение онлайн
- Видеоинструкция
Для получения решения исходное выражение необходимо привести к виду: a1(x)y' + a0(x)y = b(x). Например, для y'-exp(x)=2*y это будет y'-2*y=exp(x).
Теорема. Пусть a1(x), a0(x), b(x) непрерывны на отрезке [α,β], a1≠0 для ∀x∈[α,β]. Тогда для любой точки (x0, y0), x0∈[α,β], существует единственное решение уравнения, удовлетворяющее условию y(x0) = y0 и определенное на всем интервале [α,β].
Рассмотрим однородное линейное дифференциальное уравнение a1(x)y'+a0(x)y=0.
Разделяя переменные, получаем , или, интегрируя обе части,
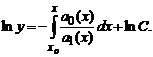
Попытаемся теперь найти решение уравнения в указанном виде, в котором вместо константы C подставлена функция C(x) то есть в виде
Подставив это решение в исходное, после необходимых преобразований получаем 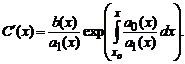
где C1— некоторая новая константа. Подставляя полученное выражение для C(x), окончательно получаем решение исходного линейного уравнения
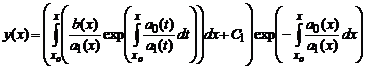
Описанный метод решения называется методом Лагранжа или методом вариации произвольной постоянной (см. также Метод вариации произвольной постоянной решения линейных неоднородных уравнений).
Пример. Решить уравнение y' + 2y = 4x. Рассмотрим соответствующее однородное уравнение y' + 2y = 0. Решая его, получаем y = Ce-2x. Ищем теперь решение исходного уравнения в виде y = C(x)e-2x. Подставляя y и y’ = C'(x)e-2x — 2C(x)e-2x
в исходное уравнение, имеем C'(x) = 4xe2x, откуда C(x) = 2xe2x — e2x + C1 и y(x) = (2xe2x — e2x + C1)e-2x = 2x — 1 + C1e-2x — общее решение исходного уравнения. В этом решении y1(x) = 2x-1 — движение
объекта под действием силы b(x) = 4x, y2(x) = C1e-2x -собственное движение объекта.
Пример №2. Найти общее решение дифференциального уравнения первого порядка y’+3 y tan(3x)=2 cos(3x)/sin22x.
Это неоднородное уравнение. Сделаем замену переменных: y=u•v, y’ = u’v + uv’.
3u v tg(3x)+u v’+u’ v = 2cos(3x)/sin22x или u(3v tg(3x)+v’) + u’ v= 2cos(3x)/sin22x
Решение состоит из двух этапов:
1. u(3v tg(3x)+v’) = 0
2. u’v = 2cos(3x)/sin22x
1. Приравниваем u=0, находим решение для 3v tg(3x)+v’ = 0
Представим в виде: v’ = -3v tg(3x)
Интегирируя, получаем:
ln(v) = ln(cos(3x))
v = cos(3x)
2. Зная v, Находим u из условия: u’v = 2cos(3x)/sin22x
u’ cos(3x) = 2cos(3x)/sin22x
u’ = 2/sin22x
Интегирируя, получаем:
Из условия y=u•v, получаем:
y = u•v = (C-cos(2x)/sin(2x)) cos(3x) или y = C cos(3x)-cos(2x) ctg(3x)
Общий вид дифференциального уравнения первого порядка:
$Fleft( {x,y,y’} right) = 0$.
Его общее решение имеет вид:
$y = fleft( {x,c} right)$.
Простейшие дифференциальные уравнения первого порядка.
- Дифференциальные уравнения с разделёнными перемеными: [{f_1}left( x right)dx = {f_2}left( y right)dy,] где множителем при $dx$ является функция, зависящая только от $x$, а множителем при $dy$ является функция, зависящая только от $y$. Решение находится методом интегрирования обеих частей.[int {{f_1}left( x right)dx} = int {{f_2}left( y right)dy} + C]
- Дифференциальные уравнения вида [y’ = {f_1}left( x right){f_2}left( y right)dy,] где правая часть представляет собой произведение двух функций, из которых одна не зависит от $x$, а вторая не зависит от $y$, называется уравнением с разделяющимися переменными. Метод решения:[int {frac{{dy}}{{{f_2}left( x right)}}} = int {{f_1}left( x right)dx} + C]
- Дифференциальные уравнения с разделяющимися переменными, записанные в форме дифференциалов: [{f_1}left( x right) cdot {f_2}left( y right)dx + {f_3}left( x right) cdot {f_4}left( y right)dy = 0] для решения таких дифференциальных уравнений их надо привести к уравнениям с разделёнными переменными.[int {frac{{{f_1}left( x right)}}{{{f_3}left( x right)}}} dx + int {frac{{{f_4}left( y right)}}{{{f_2}left( y right)}}dy} = C]
Функция $fleft( {x,y} right)$ называется однородной функцией n-го измерения, если при замене в ней переменных $x$ и $y$ соответственно на $tx$ и $ty$, где $t$ — произвольная величина (параметр) получается та же функция, умноженная на ${t^n}$, т.е. если выполняется условие: [fleft( {tx,ty} right) = {t^n} cdot fleft( {x,y} right)] n- степень однородности уравнения.
Однородная функция степени $n$ представима в виде [fleft( {x,y} right) = {x^n} cdot varphi left( {frac{y}{x}} right)]
Однородная функция нулевой степени может быть записана в виде [fleft( {x,y} right) = varphi left( {frac{y}{x}} right)]
Если функции $Mleft( {x,y} right)$ и $Nleft( {x,y} right)$ однородные одной и той же степени $n$, то дифференциальное уравнение [Mleft( {x,y} right)dx + Nleft( {x,y} right)dy = 0] называется однородным.
Уравнение $y’ = fleft( {x,y} right)$ называется однородным, если оно имеет вид: [y’ = varphi left( {frac{y}{x}} right)]
Очевидно, что $fleft( {x,y} right)$ однородная функция нулевого измерения.
Однородные уравнения приводятся к уравнению с разделяющимися перемеными при помощи подстановки.
$t = frac{y}{x}$ т.е. $y = tx$ и $y’ = t’x + t$ или в дифференциалах $dy = tdx + xdt$.
Линейные уравнения первого порядка.
Линейным дифференциальным уравнением первого порядка называется такое дифференциальное уравнение, в которое неизвестные функции $y$ и ${y’}$ входят в первых степенях и не перемножаются между собой.
Общий вид линейного уравнения первого порядка: [y’ + Pleft( x right) cdot y = Qleft( x right)]
Если $Qleft( x right) = 0$, то это линейное однородное уравнение с разделяющимися переменными.
Методы решения:метод Бернулли и метод Лагранжа.
Метод Бернулли
- Будем искать решение в виде $y = U cdot V$, тогда $y’ = U’V + V’U$ или $dy = Vdu + Udv$ (это подстановка Бернулли, где $v$ — вспомогательная функция.) Пример. [begin{gathered}
xy’ — 2y = 2{x^4} hfill \
xleft( {U’V + V’U} right) — 2UV = 2{x^4} hfill \
xU’V + xV’U — 2UV = 2{x^4} hfill \
end{gathered} ] - $xU’V + Uleft( {xV’ — 2V} right) = 2{x^4}$ найдём функцию $V$ таким образом, чтобы выражение в скобках было равно нулю. [begin{gathered}
xV’ — 2V = 0 hfill \
xfrac{{dV}}{{dx}} = 2V hfill \
int {frac{{dV}}{{dx}} = 2int {frac{{dx}}{x}} } hfill \
end{gathered} ] Интегрируя уравнение, получим $ln V = ln {x^2} Rightarrow V = {x^2}.$ Поскольку функция $V$ выбрана, чтобы удовлетворять определённому условию мы опускаем постоянную $С$. Полученное выражение подставляем в исходное уравнение [begin{gathered}
x cdot frac{{dU}}{{dx}} cdot {x^2} = 2{x^4} hfill \
frac{{dU}}{{dx}} = x Rightarrow U = int {xdx = {x^2}} + C hfill \
end{gathered} ] Объединив полученные выражения для $V$ $U$ в подстановке Бернулли, получим окончательное общее решение уравнения $y = {x^2}left( {{x^2} + C} right).$
Метод вариации произвольной постоянной. (Метод Лагранжа)
Покажем применение метода на том же примере.
[xy’ — 2y = 2{x^4}] Сначала решаем данное уравнение без правой части:[begin{gathered}
xy’ — 2y = 2{x^4} hfill \
xfrac{{dy}}{{dx}} = 2y hfill \
xy’ — 2y = 0 hfill \
frac{{dy}}{y} = 2frac{{dx}}{x} hfill \
ln y = 2ln x + ln C hfill \
y = C cdot {x^2} hfill \
end{gathered} ] Пусть $C = Cleft( x right)$ — некоторая неизвестная функция в исходном уравнении, тогда [begin{gathered}
y = {x^2} cdot Cleft( x right) hfill \
y’ = 2x cdot Cleft( x right) + {x^2} cdot C’left( x right) hfill \
end{gathered} ] Подставляем в исходное уравнение[begin{gathered}
x cdot 2x cdot Cleft( x right) + x cdot {x^2} cdot C’left( x right) — 2{x^2} cdot Cleft( x right) = 2{x^4}left| { div left( {{x^2}} right)} right. hfill \
2Cleft( x right) + x cdot C’left( x right) — 2Cleft( x right) = 2{x^2} hfill \
C’left( x right) = 2x Rightarrow Cleft( x right) = int {2xdx = {x^2}} + C hfill \
end{gathered} ] Подставляем полученное выражение в $y = {x^2} cdot Cleft( x right)$ и получает окончательное решение $y = {x^2} cdot left( {{x^2} + C} right).$
Уравнение Бернулли.
Общий вид уравнения:[y’ + Pleft( x right)y = Qleft( x right){y^n}] слева линейное выражение, а справа присутсвует множитель ${y^n}left( {n = const} right)$. Умножим обе части на $frac{1}{{{y^n}}}$ [frac{1}{{{y^n}}}frac{{dy}}{{dx}} + Pleft( x right)frac{1}{{{y^{n — 1}}}} = Qleft( x right)] Применим подстановку
$zleft( x right) = frac{1}{{{y^{n — 1}}}}$ и $frac{{dz}}{{dx}} = z’ = left( {1 — n} right) cdot frac{1}{{{y^n}}} cdot y’$ $frac{1}{{{y^n}}} cdot y’ = frac{{z’}}{{left( {1 — n} right)}}$ получим дифференциальное уравнение вида:[begin{gathered}
frac{{z’}}{{left( {1 — n} right)}} + Pleft( x right)zleft( x right) = Qleft( x right) hfill \
frac{{dz}}{{dx}} + left( {1 — n} right)Pleft( x right)zleft( x right) = Qleft( x right)left( {1 — n} right) hfill \
end{gathered} ]Это линейное уравнение I-го порядка, для его решения применяем, например, подстановку Бернулли.