Как найти линейное ускорение точки

Что такое линейное ускорение при движении по окружности?

Если материальная точка M движется по окружности, то рассматривается угловое ускорение и линейное ускорение.

Линейное ускорение при движении по окружности определение

Определение линейного ускорения:

линейное ускорение – это производная от скорости по времени.

Линейное ускорение при движении по окружности формула

Формула линейного ускорения:

a = dv/dt = d²s/dt²

где s – путь, пройденный материальной точкой М по дуге окружности, начиная от точки X:

Путь s можно выразить через радиус окружности и его угол поворота:

s = rφ

Подставим это значение пути s в формулу линейного ускорения:

v = d²s/dt²= d²(rφ)/dt² = r * d²φ/dt²

радиус окружности r является константой, поэтому мы вынесли его за знак производной.

Вторая производная d²φ/dt² – это угловое ускорение:

β = dω/dt = d²φ/dt²

Учитывая это, получаем формулу линейного ускорения при движении по окружности:

a = βr

Линейное ускорение — векторная физическая величина, показывающая быстроту изменения скорости со временем. В школьной физике для всех типов задач постоянно, чаще всего используется в задачах на равномепеременное движение/падение.

Исходя из определения ускорения и учитывая, что оно всегда постоянно, можно математизировать наше определение, итак, определение вектора среднего ускорения:

 (1)

• где

Исходя из определения любого изменения физического параметра, изменение вектора скорости можно расписать как:

(2)

• где

Тогда, подставив определение изменения вектора скорости в определение ускорения, получим: .

Т.к. в школе рассматривается движение с постоянным ускорением, мы имеем право заменить среднее ускорение обычным (или мгновенным): . Кроме того, можем заменить диапазон времени  на текущее время , т.к. действия задачи обычно начинается с нулевого начального времени.

Таким образом, выделяя конечную скорость, мы получим известное выражение для скорости равнопеременного движения: .

Вывод: соотношения, определяющие линейное ускорение во всём курсе физики, — это (1) и (2).

Линейные скорости и ускорения точек вращающегося тела

• Линейная скорость и ускорение точки ротатора-произвольная точка ротатора на расстоянии R от оси вращения, описывающая окружность радиуса/?. Центр этого круга находится на оси вращения, а плоскость, на которой он расположен, Q, перпендикулярна оси вращения(рис. 11.5). Скорость и ускорение любой точки

вращающегося тела называют линейными. Для их определения достаточно одной точки М(рис. 11.5). Как уже указывалось, траектория его движения представляет собой дугу окружности. В первый момент точка м находится в положении Л40, и время с позиции Афи. Возьмем начало координат в точке Mo,

так что положительное направление координаты кривизны s совпадает с
Людмила Фирмаль

направлением увеличения угла поворота тела. Тогда координаты s будут равны длине дуги M0L1|, но из геометрии видно, что длина дуги окружности равна радиусу, умноженному на соответствующий центральный угол. s=/?Р. (1 1 1. 1 4 ) Мы различаем результирующее равенство во времени: ds__ _ _ d(/?< p)_ _ d y dt=dt «R dt’ Или u=/? c o (1 1. 1 5 ) Таким образом, величина линейной скорости любой точки

ротатора равна произведению расстояния от этой точки до оси вращения на угол поворота. От этого тем дальше от оси вращения, что линейная скорость увеличивается. Линейная скорость направлена по касательной и окружности. Поскольку вращение тела заставляет его точку двигаться по криволинейной траектории, вектор линейного ускорения равен векторной сумме векторов нормального и

• тангенциального ускорения (11.6): a=at -} — an. Для определения положительного ускорения по формуле (9.28) подставим соотношение (11.15): d (Ro)) 7t (1 1 1. 1-6. ) 1 0 3 0. Рис. 11.5. 11.6 Аналогично находим значение нормального ускорения в формулах (9.31) и (11.15): AP=v* / R=(/?2//? = / ?СО2 (11.17)) Модуль Полного Ускорения А2 п — — $ = ] L? 2e2+/?2-й>2=/? ] / Е2+П2. (11.18) Из Формулы (11.18) следует, что чем дальше точка удаляется от оси вращения, тем больше ускорение.

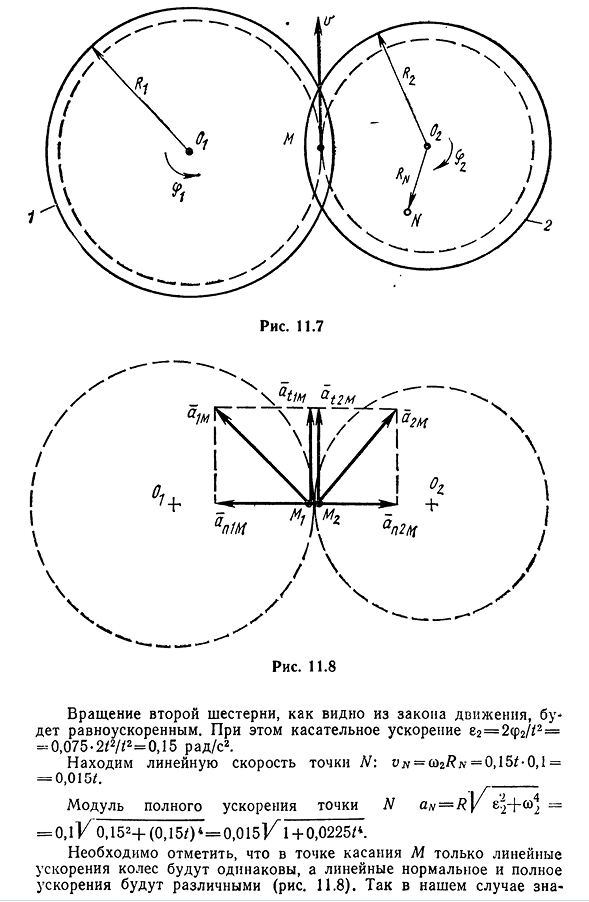
Например. Шестерня / Шестерня 2 (Рис. 11.7) из оставшегося состояния начинает вращаться равномерно ускоренно с угловым ускорением 81=0,1 Радиана / сек. Решение. Так как начальная угловая скорость первой передачи равна нулю(Oi=ei/+0, l-T. Закон равного вращения первой шестерни равен= < Ro».^2/ 2 = 8^ /2/ 2 = 0 ,05/2 . Так как шестерни находятся в зацеплении, то вращение точек соприкосновения этих шестерен M будет иметь одинаковую линейную скорость V. 1=0, а -0.3=0.03/. Поскольку та же линейная скорость имеет точку, принадлежащую второй передаче, y=CO2/?2, где (O2=и/#2 = 0,03//0,2 = = 0,15/.

Учитывая, что CO2= (/() / d t, мы имеем dcp2=(o)/ =0.15/ ( / / . Если мы интегрируем левую и правую части
Людмила Фирмаль

последнего уравнения, то получим закон вращения шестерни 2CP2=f в первый раз(P2=0,15/(// = 0,15-/2/2-=0,075/2. б Вращение 104-й шестерни равномерно ускоряется, как видно из законов движения. В этом случае тангенциальное ускорение E2=2(p2l2= = 0,075 -2/2//2=0,15 Радиан / С2. Найти линейную скорость точки N: Y нет. (O2/?л=0.15/-0.1= = 0.015/. Суммарный коэффициент ускорения для точки N=e24′(Y1= = 0,11/ 0,152+(0,150 4 = 0,015 К1 + 0,0225/. Следует отметить, что в точке контакта м только линейное ускорение колеса остается одинаковым, а линейное нормальное и полное ускорения различны(рис. 11.8). Итак, в нашем случае знание- 105чения тангенциального

ускорения будут равны: с м=/?iei=0,3-0, l= = 0,03 м / с2; agmg=/?2B2=0,2-0,15 = 0,3 м/с2. Так как линейное нормальное ускорение зависит от расстояния точки до оси вращения, то имеем (0,0302 °»W== — O3 7=0.003 / 2 , Отчет / (0.03/) 2 P2m= ^ 2 = — 0> 2 = 0,045/2. Нормальное ускорение имеет не только различные значения, но и направления-нормальное ускорение первой точки передачи направлено к центру 01, а нормальное ускорение а » 2 м-к центру О2. Модуль ускорения рассчитывается по формуле (12.18): A1M=+=0, 3K O. 1 2+(0, K)4 = 0 ,0 3 ^ 1 + 0 , 01/4 , am= 0 ,2 ]/0 ,1 5 2 + (0,15/)4 = 0 ,0 3 ]/1 + 0,0225/*.

Смотрите также:

Решение задач по технической механике

Если вам потребуется заказать решение по технической механике вы всегда можете написать мне в whatsapp.

Ускорение точки
— это пространственно-временная мера
измене­ния движения точки (быстрота
изменения движения — по величине и
направлению скорости). Ускорение точки
равно первой производной по времени от
скорости этой точки в рассматриваемой
системе отсчета:

Ускорение точки
определяется по изменению ее скорости
во времени. Ускорение — величина
векторная, характеризующая быс­троту
изменения скорости по ее величине и
направлению в данный момент (мгновенное
ускорение)¹
.

Вектор ускорения
можно разложить на составляющие: а)
каса­тельное ускорение, направленное
вдоль касательной к траектории в данной
точке: а_τ
= ─ или а_τ
= ─ , б) нормальное ускорение, на­правленное
перпендикулярно к вектору скорости
внутрь кривизны: а_н
= ─, где R — радиус кривизны в этой же
точке. Касательное ускорение будет
положительным, когда скорость точки
увеличивается, и отрицатель­ным, когда
она уменьшается. Если касательное
ускорение равно нулю, то скорость по
величине постоянная. Если нормальное
ускорение равно нулю, то направление
скорости постоянное.

Угловое ускорение
тела определяется как мера быстроты
изменения его угловой скорости. Оно
равно первой производной по времени от
угловой скорости тела:

Различают ускорение
тела линейное (в поступательном движении)
и угловое (во вращательном движении).
Отношение ли­нейного ускорения каждой
точки вращающегося тела к ее радиусу
равно угловому ускорению (е) в радианах
в секунду в квадрате. Оно одинаково для
всех точек вращающегося тела, кроме
лежащих на оси:

Значит, линейное
ускорение любой точки вращающегося
тела равно по величине его угловому
ускорению, умноженному на радиус вращения
этой точки:

Ускорение системы
тел, изменяющей свою конфигу­рацию,
определяется еще сложнее, чем скорость.
Ускорение служит хорошим показателем
качества приложенных усилий (рис. 6).

1. Среднее ускорение
   за время движения, особенно в тех
   случаях, когда оно меняет знак, обычно
   не определяют, поскольку оно не
   характеризует достаточно подробности
   (детали) движения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Линейное ускорение при движении по окружности

Что такое линейное ускорение при движении по окружности?

Если материальная точка M движется по окружности, то рассматривается угловое ускорение и линейное ускорение.

Линейное ускорение при движении по окружности определение

Определение линейного ускорения:

Линейное ускорение при движении по окружности формула

Формула линейного ускорения:

где s – путь, пройденный материальной точкой М по дуге окружности, начиная от точки X:

Путь s можно выразить через радиус окружности и его угол поворота:

Подставим это значение пути s в формулу линейного ускорения:

радиус окружности r является константой, поэтому мы вынесли его за знак производной.

Вторая производная d 2 φ/dt 2 – это угловое ускорение:

Учитывая это, получаем формулу линейного ускорения при движении по окружности:

Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.

Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.

Если угол поворота мал, то ∆ l ≈ ∆ s .

Угловая скорость

При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.

Определение. Угловая скорость

Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .

ω = ∆ φ ∆ t , ∆ t → 0 .

Единица измерения угловой скорости — радиан в секунду ( р а д с ).

Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:

Нормальное ускорение

При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.

При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.

a n = ∆ v → ∆ t , ∆ t → 0

Модуль центростремительного ускорения можно вычислить по формуле:

a n = v 2 R = ω 2 R

Докажем эти соотношения.

Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .

В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.

По определению ускорения:

a → = ∆ v → ∆ t , ∆ t → 0

Взглянем на рисунок:

Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .

Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:

R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R

При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:

a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .

При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.

Запись центростремительного ускорения в векторной форме выглядит следующим образом:

Здесь R → — радиус вектор точки на окружности с началом в ее центре.

Тангенциальное ускорение

В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.

Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.

a τ = ∆ v τ ∆ t ; ∆ t → 0

Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t

Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.

Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .

Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω

Движение по окружности с постоянной по модулю скоростью

теория по физике 🧲 кинематика

Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:

1. Траектория движения тела есть окружность.
2. Вектор скорости всегда направлен по касательной к окружности.
3. Направление скорости постоянно меняется под действием центростремительного ускорения.
4. Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости

Линейная скорость

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

• У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂.
• У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
• Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Центростремительное ускорение

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_ц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Алгоритм решения

1. Записать исходные данные.
2. Записать формулу для определения искомой величины.
3. Подставить известные данные в формулу и произвести вычисления.

Решение

Записываем исходные данные:

• Радиус окружности, по которой движется автомобиль: R = 100 м.
• Скорость автомобиля во время движения по окружности: v = 20 м/с.

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?

а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза

Алгоритм решения

1. Записать исходные данные.
2. Определить, что нужно найти.
3. Записать формулу зависимости центростремительного ускорения от частоты.
4. Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
5. Приравнять правые части формул и найти искомую величину.

Решение

Запишем исходные данные:

Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».

pазбирался: Алиса Никитина | обсудить разбор | оценить