Как найти линейность функции

Полином Жегалкина у булевой функции от трёх переменных x₁, x₂ и x₃ будет иметь вид:
f(x₁, x₂, x₃) = a₀ + a₁x + a₂x₂ + a₃x₃ + a₁₂x₁x₂ + a₁₃x₁x₃ + a₂₃x₂x₃ + a₁₂₃x₁x₂x₃, где:
коэффициенты a₀, a₁, a₂, a₃, a₁₂, a₁₃, a₂₃, a₁₂₃ ∈ {0; 1}.

Чтобы найти эти коэффициенты, нужно подставить в полином Жегалкина (написанный выше) значения функции на различных наборах переменных и решить систему уравнений. Далее, подставив найденные коэффициенты в полином, убеждаемся в его линейности.

f(000) = 1 → a₀ = 1
f(001) = 1 → a₀ + a₃ = 1 → 1 + a₃ = 1 → a₃ = 0
f(010) = 0 → a₀ + a₂ = 0 → 1 + a₂ = 0 → a₂ = 1
f(011) = 0 → a₀ + a₂ + a₃ + a₂₃ = 0 → 1 + 1 + 0 + a₂₃ = 0 → a₂₃ = 0
f(100) = 0 → a₀ + a₁ = 0 → 1 + a₁ = 0 → a₁ = 1
f(101) = 0 → a₀ + a₁ + a₃ + a₁₃ = 0 → 1 + 1 + 0 + a₁₃ = 0 → a₁₃ = 0
f(110) = 1 → a₀ + a₁ + a₂ + a₁₂ = 1 → 1 + 1 + 1 + a₁₂ = 1 → a₁₂ = 0
f(111) = 1 → a₀ + a₁ + a₂ + a₃ + a₁₂ + a₁₃ + a₂₃ + a₁₂₃ = 1 → 1 + 1 + 1 + 0 + 0 + 0 + 0 + a₁₂₃ = 1 → a₁₂₃ = 0

{a₀ = 1
{a₁ = 1
{a₂ = 1
{a₃ = 0
{a₁₂ = 0
{a₁₃ = 0
{a₂₃ = 0
{a₁₂₃ = 0

Тогда f(x₁, x₂, x₃) = 1 + x₁ + x₂ — линейный.

ЛИНЕЙНЫЕ БУЛЕВЫ ФУНКЦИИ 1. Полиномы Жегалкина. 2. Класс линейных функций.

Вопрос 1. Полиномы Жегалкина Рассмотрим кольцевую сумму (операцию сложения по модулю 2 или сумму Жегалкина), которая обозначается х у и задается таблицей истинности:

О. 1. 1. Полиномом (многочленом) Жегалкина называется многочлен, являющийся суммой константы (0 или 1) и различных одночленов, в которых все переменные входят не выше, чем в первой степени: (1) причем на каждом наборе (i 1, i 2, …, ik) все ij (j = 1, 2, …, k) различны, а

Пример 1. 1. Полином Жегалкина константы равен самой этой константе. 2. Полином Жегалкина булевой функции одной переменной f(х) имеет вид f(х) = а 0 а 1 х. 3. Полином Жегалкина булевой функции двух переменных f(х1, х2) имеет вид f(х1, х2) = а 0 а 1 х1 а 2 х2 а 12 х1 х2. 4. Полином Жегалкина булевой функции трех переменных f(х1, х2, х3) имеет вид f(х1, х2, х3) = а 0 а 1 х1 а 2 х2 а 3 х3 а 12 х1 х2 а 13 х1 х3 а 23 х2 х3 а 123 х1 х2 х3.

Во всех приведенных формулах коэффициенты и свободный член а 0 принимают значения 0 или 1; число слагаемых в формуле равно 2 n (где n – число переменных). Можно показать, что число полиномов Жегалкина от n переменных х1, х2, …, хn, т. е. число выражений вида (1), равно Так как число булевых функций от n переменных так же равно то каждая булева функция может быть представлена полиномом Жегалкина.

T. 1. 1. (теорема Жегалкина) Каждая булева функция f(х1, х2, …, хn) может быть представлена в виде полинома Жегалкина и притом единственным образом (с точностью до порядка слагаемых). Пример 2. С помощью таблицы истинности найдем полином Жегалкина для функции х. х = х 1.

Алгоритмы построения полинома Жегалкина Известно, что любую булеву функцию, отличную от константы 0, можно представить в виде СДНФ. Сравним таблицы истинности дизъюнкции и кольцевой суммы:

Мы видим, что они отличаются только последней строкой, т. е. на наборе (11). Так как в СДНФ на каждом наборе только одна конъюнкция равна 1, то все дизъюнкции можно заменить суммами по модулю 2. Кроме того, х = х 1. На этом основан следующий алгоритм построения полинома Жегалкина.

Первый алгоритм построения полинома Жегалкина (на основе СДНФ) 1. Находим множество тех двоичных наборов, на которых функция принимает значение 1. 2. Составляем СДНФ. 3. В СДНФ каждый знак дизъюнкции заменяем знаком суммы Жегалкина. 4. Упрощаем, если можно, полученное выражение, используя тождество

5. В полученной формуле каждое отрицание заменяем на хi 1. 6. Раскрываем скобки в полученной формуле, содержащей только функции , и константу 1. 7. Приводим подобные члены, используя тождество хi = 0.

Пример 3. На основе СДНФ построить полином Жегалкина для функции Решение Данная функция представлена в форме СДНФ. Таким образом, имеет место представление

Второй алгоритм построения полинома Жегалкина (с помощью метода неопределенных коэффициентов) 1. Запишем предполагаемый результат в виде выражения общего вида с неопределенными коэффициентами. 2. Составляем систему линейных уравнений относительно 2 n неизвестных коэффициентов, содержащую 2 n уравнений, решением которой являются коэффициенты полинома Жегалкина.

Пример 4. С помощью метода неопределенных коэффициентов построить полином Жегалкина для функции Решение Запишем предполагаемый результат в виде выражения общего вида с неопределёнными коэффициентами:

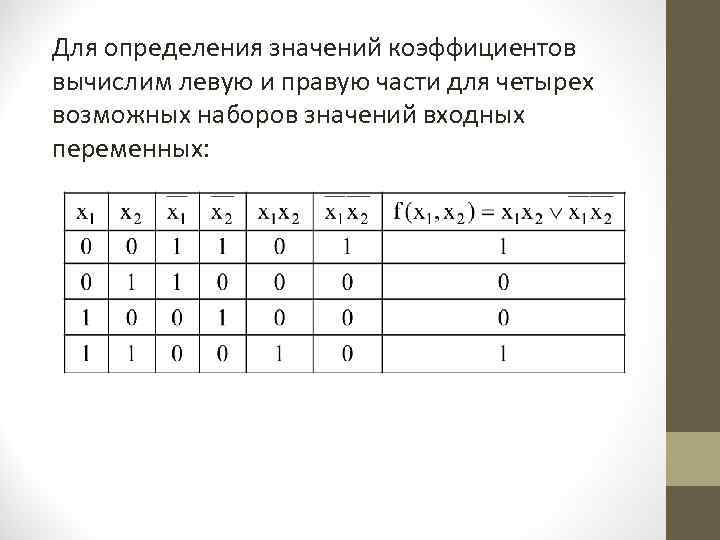
Для определения значений коэффициентов вычислим левую и правую части для четырех возможных наборов значений входных переменных:

f(0, 0) = 1 = a 0 0 0 = a a = 1. f(0, 1) = 0 = 1 0 c 0 1 c = 0 c = 1. f(1, 0) = 0 = 1 b 0 0 1 b = 0 b = 1. f(1, 1) = 1 1 1 d = 1 d = 0. Таким образом, имеет место представление f(x 1, x 2) = 1 x 2.

Вопрос 2. Класс линейных функций О. 2. 1. Полином Жегалкина называется линейным (нелинейным), если он не содержит (содержит) конъюнкции переменных. О. 2. 2. Булева функция f(х1, х2, …, хn) называется линейной (нелинейной), если ее полином Жегалкина является линейным (нелинейным).

Полином Жегалкина линейной функции f(х1, х2, …, хn) имеет вид a 0 a 1 x 1 a 2 x 2 …. anxn. Из определения полинома Жегалкина следует, что для любой булевой функции коэффициенты при переменных х1, х2, …, хn и свободный член выражаются по формулам: а 0 = f(0, 0, …, 0), а 1 = а 0 f(1, 0, …, 0), а 2 = а 0 f(0, 1, …, 0), …, аn = а 0 f(0, 0, …, 1).

Алгоритм определения линейности (нелинейности) булевой функции 1. По таблице истинности указанной функции f(х1, х2, …, хn) и выше указанным формулам находим коэффициенты a 0, a 1, …, an. 2. Выписываем полином Ф(х1, х2, …, хn) = a 0 a 1 x 1 a 2 x 2 …. anxn и проверяем, задает ли он эту функцию. Для этого строим таблицу истинности полинома Ф(х1, х2, …, хn) и сравниваем ее с таблицей истинности функции f(х1, х2, …, хn).

3. Если результирующие столбцы таблиц истинности совпадают, то функция f(х1, х2, …, хn) линейная и Ф(х1, х2, …, хn) – ее полином Жегалкина. , т. е. f(х1, х2, …, хn) = Ф(х1, х2, …, хn). В противном случае функция f(х1, х2, …, хn) нелинейная.

Пример 5. Докажите, что булева функция f(х1, х2, х3), заданная таблицей истинности, линейна:

Решение 1. Вычислим коэффициенты а 0, а 1, а 2, а 3 полинома Жегалкина функции f(х1, х2, х3): а 0 = f(0, 0, 0) = 1, а 1 = а 0 f(1, 0, 0) = 1 1 = 0, а 2 = а 0 f(0, 1, 0) = 1 0 = 1, а 3 = а 0 f(0, 0, 1) = 1 0 = 1. 2. Запишем многочлен Ф(х1, х2, х3) = a 0 a 1 x 1 a 2 x 2 a 3 x 3 = =1 0 x 1 1 x 2 1 x 3. Таким образом, Ф(х1, х2, х3) = 1 x 2 х3.

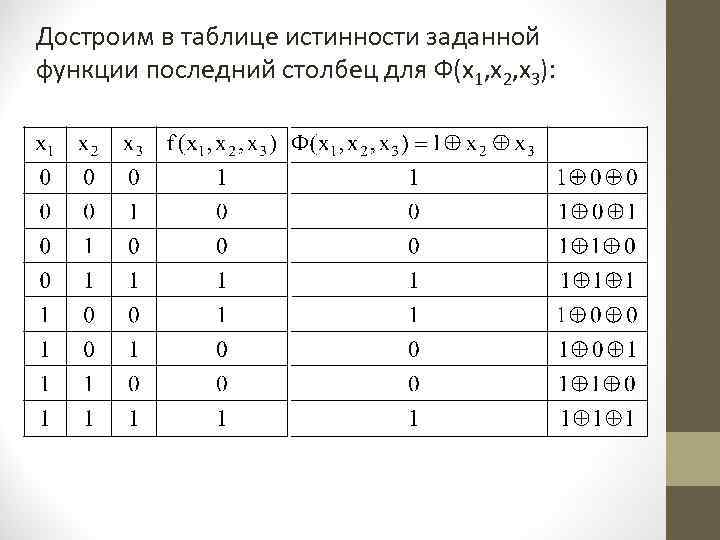
Достроим в таблице истинности заданной функции последний столбец для Ф(х1, х2, х3):

3. Из расширенной таблицы истинности видно, что столбцы для Ф(х1, х2, х3) и f(х1, х2, х3) совпадают. Следовательно, данная функция f(х1, х2, х3) линейна и представима в виде линейного полинома Жегалкина: f(х1, х2, х3) = 1 x 2 х3. Класс линейных булевых функций обозначается L. Пример 6. 1. К классу линейных булевых функций относятся константы 0 и 1, тождественная функция х, функции х и х1 х2. 2. Функции х1 х2 не принадлежат классу L.

Определение.
Арифметические функции в
алгебре логики это сложение по модулю
два и умножение (конъюнкция).

Определение.
Многочленом Жегалкина
называется многочлен, являющийся суммой
константы 0 или 1 и различных одночленов,
в которые все переменные входят не выше,
чем в первой степени:
,
причем на каждом наборе <i₁,
…, i_k>
все а_ij (j
= 1, …, k) различны,
a_j
 {0, 1}.

Теорема.
Всякую булеву функцию можно представить
единственным полиномом Жегалкина.

Многочлен Жегалкина можно получить
различными способами. Остановимся на
рассмотрении построения многочлена
Жегалкина с помощью треугольника
Паскаля. Рассмотрим алгоритм на примере.

Пример 46.

Построить
многочлен Жегалкина для функции
f=10011110.

Решение.

Алгоритм
построения многочлена Жегалкина:

Шаг 1. Строим таблицу (табл. 57). Первый
столбец содержит возможные слагаемые
полинома Жегалкина. Нулевому набору
всегда соответствует слагаемое 1.
Остальным наборам соответствует
слагаемое, представляющее собой
конъюнкцию переменных, которые на данном
наборе принимают значение 1. Следующие
n столбцов – всевозможные
наборы из 0 и 1, соответствующие переменным.
Далее столбец значений функции f.
Функция g является
вспомогательной, поэтому изначально
этот столбец не заполнен.

Таблица 57

Шаг 2. Построение треугольника
Паскаля. Верхняя сторона треугольника
есть функция f. Любой
другой элемент треугольника есть сумма
по модулю два двух соседних элементов
предыдущей строки. Левая сторона
треугольника представляет собой значение
вспомогательной функции g
(табл. 58).

Таблица 58

Шаг 3. Построение полинома Жегалкина.
В полином войдут только те слагаемые,
которым соответствует единица во
вспомогательной функции g.

Для данной функции многочлен Жегалкина
имеет вид:

f
= 1 + x₃
+ x₂
+ x₁
x₃
+ x₁
x₂
+ x₁
x₂
x₃.

Определение.
Функция f(x₁,
x₂, …,
x_n)
называется линейной, если
многочлен Жегалкина для нее имеет
следующий линейный относительно
переменных вид:

f(x₁,
x₂, …,
x_n)
= a₁x₁
+ … + a_nx_n
+ a_n+1,
где каждое a_i
равно 0 или 1.

Булева функция из рассмотренного выше
примера не является линейной.

Теорема. Класс
L = {f
| f = a₀+a₁x₁+…+a_nx_n,
a_i{0,
1}} линейных функций замкнут относительно
суперпозиций.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #