Как найти линейную аппроксимирующую функцию - Исправление недочетов и поиск решений вместе с Examum.ru

При обработке экспериментальных данных часто возникает необходимость аппроксимировать их линейной функцией.

Аппроксимацией (приближением) функции f(x) называется нахождение такой функции (аппроксимирующей функции) g(x), которая была бы близка заданной. Критерии близости функций могут быть различные.

В случае если приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной.

В случае если аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной. Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.

Наиболее часто встречающим видом точечной аппроксимации является интерполяция – нахождение промежуточных значений величины по имеющемуся дискретному набору известных значений.

Пусть задан дискретный набор точек, называемых узлами интерполяции, а также значения функции в этих точках. Требуется построить функцию g(x), проходящую наиболее близко ко всем заданным узлам. Таким образом, критерием близости функции является g(xi)=yi.

В качестве функции g(x) обычно выбирается полином, который называют интерполяционным полиномом.

В случае если полином един для всей области интерполяции, говорят, что интерполяция глобальная.

В случае если между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции.

Найдя интерполяционный полином, мы можем вычислить значения функции между узлами, а также определить значение функции даже за пределами заданного интервала (провести экстраполяцию).

Аппроксимация линейной функцией

Пример реализации

Для примера реализации воспользуемся набором значений, полученных в соответствии с уравнением прямой

y = 8 · x — 3

Рассчитаем указанные коэффициенты по методу наименьших квадратов.
Результат сохраняем в форме двумерного массива, состоящего из 2 столбцов.
При следующем запуске программы добавим случайную составляющую к указанному набору значений и снова рассчитаем коэффициенты.

Реализация на Си

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
// Задание начального набора значений
double ** getData(int n) {
  double **f;
  f = new double*[2];
  f[0] = new double[n];
  f[1] = new double[n];
  for (int i = 0; i<n; i++) {
    f[0][i] = (double)i;
    f[1][i] = 8 * (double)i — 3;
    // Добавление случайной составляющей
    f[1][i] = 8*(double)i — 3 + ((rand()%100)-50)*0.05;
  }
  return f;
}
// Вычисление коэффициентов аппроксимирующей прямой
void getApprox(double **x, double *a, double *b, int n) {
  double sumx = 0;
  double sumy = 0;
  double sumx2 = 0;
  double sumxy = 0;
  for (int i = 0; i<n; i++) {
    sumx += x[0][i];
    sumy += x[1][i];
    sumx2 += x[0][i] * x[0][i];
    sumxy += x[0][i] * x[1][i];
  }
  *a = (n*sumxy — (sumx*sumy)) / (n*sumx2 — sumx*sumx);
  *b = (sumy — *a*sumx) / n;
  return;
}
int main() {
  double **x, a, b;
  int n;
  system(«chcp 1251»);
  system(«cls»);
  printf(«Введите количество точек: «);
  scanf(«%d», &n);
  x = getData(n);
  for (int i = 0; i<n; i++)
    printf(«%5.1lf — %7.3lfn», x[0][i], x[1][i]);
  getApprox(x, &a, &b, n);
  printf(«a = %lfnb = %lf», a, b);
  getchar(); getchar();
  return 0;
}

Результат выполнения
Запуск без случайной составляющей

Запуск со случайной составляющей

Построение графика функции

Для наглядности построим график функции, полученный аппроксимацией по методу наименьших квадратов. Подробнее о построении графика функции описано здесь.

Реализация на Си

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149

#include <windows.h>
const int NUM = 70; // количество точек
LONG WINAPI WndProc(HWND, UINT, WPARAM, LPARAM);
double **x; // массив данных
      // Определение коэффициентов линейной аппроксимации по МНК
void getApprox(double **m, double *a, double *b, int n) {
  double sumx = 0;
  double sumy = 0;
  double sumx2 = 0;
  double sumxy = 0;
  for (int i = 0; i<n; i++) {
    sumx += m[0][i];
    sumy += m[1][i];
    sumx2 += m[0][i] * m[0][i];
    sumxy += m[0][i] * m[1][i];
  }
  *a = (n*sumxy — (sumx*sumy)) / (n*sumx2 — sumx*sumx);
  *b = (sumy — *a*sumx) / n;
  return;
}
// Задание исходных данных для графика
// (двумерный массив, может содержать несколько рядов данных)
double ** getData(int n) {
  double **f;
  double a, b;
  f = new double*[3];
  f[0] = new double[n];
  f[1] = new double[n];
  f[2] = new double[n];
  for (int i = 0; i<n; i++) {
    double x = (double)i * 0.1;
    f[0][i] = x;
    f[1][i] = 8 * x — 3 + ((rand() % 100) — 50)*0.05;
  }
  getApprox(f, &a, &b, n); // аппроксимация
  for (int i = 0; i<n; i++) {
    double x = (double)i * 0.1;
    f[2][i] = a*x + b;
  }
  return f;
}
// Функция рисования графика
void DrawGraph(HDC hdc, RECT rectClient, double **x, int n, int numrow = 1) {
  double OffsetY, OffsetX;
  double MAX_X = 0;
  double MAX_Y = 0;
  double ScaleX, ScaleY;
  double min, max;
  int height, width;
  int X, Y;    // координаты в окне (в px)
  HPEN hpen;
  height = rectClient.bottom — rectClient.top;
  width = rectClient.right — rectClient.left;
  // Область допустимых значений X
  min = x[0][0];
  max = x[0][0];
  for (int i = 0; i<n; i++) {
    if (x[0][i] < min)
      min = x[0][i];
    if (x[0][i] > max)
      max = x[0][i];
  }
  double temp = max — min;
  MAX_X = max — min;
  OffsetX = min*width / MAX_X;  // смещение X
  ScaleX = (double)width / MAX_X; // масштабный коэффициент X
                  // Область допустимых значений Y
  min = x[1][0];
  max = x[1][0];
  for (int i = 0; i<n; i++) {
    for (int j = 1; j <= numrow; j++) {
      if (x[j][i] < min)
        min = x[j][i];
      if (x[j][i] > max)
        max = x[j][i];
    }
  }
  MAX_Y = max — min;
  OffsetY = max*height / (MAX_Y);  // смещение Y
  ScaleY = (double)height / MAX_Y; // масштабный коэффициент Y
                   // Отрисовка осей координат
  hpen = CreatePen(PS_SOLID, 0, 0); // черное перо 1px
  SelectObject(hdc, hpen);
  MoveToEx(hdc, 0, OffsetY, 0);  // перемещение в точку (0;OffsetY)
  LineTo(hdc, width, OffsetY);   // рисование горизонтальной оси
  MoveToEx(hdc, OffsetX, 0, 0);  // перемещение в точку (OffsetX;0)
  LineTo(hdc, OffsetX, height);  // рисование вертикальной оси
  DeleteObject(hpen);  // удаление черного пера
             // Отрисовка графика функции
  int color = 0xFF; // красное перо для первого ряда данных
  for (int j = 1; j <= numrow; j++) {
    hpen = CreatePen(PS_SOLID, 2, color); // формирование пера 2px
    SelectObject(hdc, hpen);
    X = (int)(OffsetX + x[0][0] * ScaleX);    // координаты начальной точки графика
    Y = (int)(OffsetY — x[j][0] * ScaleY);
    MoveToEx(hdc, X, Y, 0);  // перемещение в начальную точку
    for (int i = 0; i<n; i++) {
      X = OffsetX + x[0][i] * ScaleX;
      Y = OffsetY — x[j][i] * ScaleY;
      LineTo(hdc, X, Y);
    }
    color = color << 8; // изменение цвета пера для следующего ряда
    DeleteObject(hpen); // удаление текущего пера
  }
}
// Главная функция
int  WINAPI  WinMain(HINSTANCE  hInstance,
  HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow) {
  HWND hwnd;
  MSG msg;
  WNDCLASS w;
  x = getData(NUM); // задание исходных данных
  memset(&w, 0, sizeof(WNDCLASS));
  w.style = CS_HREDRAW | CS_VREDRAW;
  w.lpfnWndProc = WndProc;
  w.hInstance = hInstance;
  w.hbrBackground = CreateSolidBrush(0x00FFFFFF);
  w.lpszClassName = «My Class»;
  RegisterClass(&w);
  hwnd = CreateWindow(«My Class», «График функции»,
    WS_OVERLAPPEDWINDOW, 500, 300, 500, 380, NULL, NULL,
    hInstance, NULL);
  ShowWindow(hwnd, nCmdShow);
  UpdateWindow(hwnd);
  while (GetMessage(&msg, NULL, 0, 0)) {
    TranslateMessage(&msg);
    DispatchMessage(&msg);
  }
  return msg.wParam;
}
// Оконная функция
LONG WINAPI WndProc(HWND hwnd, UINT Message,
  WPARAM wparam, LPARAM lparam) {
  HDC hdc;
  PAINTSTRUCT ps;
  switch (Message) {
  case WM_PAINT:
    hdc = BeginPaint(hwnd, &ps);
    DrawGraph(hdc, ps.rcPaint, x, NUM, 2); // построение графика
    EndPaint(hwnd, &ps);
    break;
  case WM_DESTROY:
    PostQuitMessage(0);
    break;
  default:
    return DefWindowProc(hwnd, Message, wparam, lparam);
  }
  return 0;
}

Результат выполнения

Аппроксимация с фиксированной точкой пересечения с осью y

В случае если в задаче заранее известна точка пересечения искомой прямой с осью y, в решении задачи останется только одна частная производная для вычисления коэффициента a.

В этом случае текст программы для поиска коэффициента угла наклона аппроксимирующей прямой будет следующий (имя функции getApprox() заменено на getApproxA() во избежание путаницы).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
// Задание начального набора значений
double ** getData(int n) {
  double **f;
  f = new double*[2];
  f[0] = new double[n];
  f[1] = new double[n];
  for (int i = 0; i<n; i++) {
    f[0][i] = (double)i;
    f[1][i] = 8 * (double)i — 3;
    // Добавление случайной составляющей
    //f[1][i] = 8 * (double)i — 3 + ((rand() % 100) — 50)*0.05;
  }
  return f;
}
// Вычисление коэффициентов аппроксимирующей прямой
void getApproxA(double **x, double *a, double b, int n) {
  double sumx = 0;
  double sumx2 = 0;
  double sumxy = 0;
  for (int i = 0; i<n; i++) {
    sumx += x[0][i];
    sumx2 += x[0][i] * x[0][i];
    sumxy += x[0][i] * x[1][i];
  }
  *a = (sumxy — b*sumx) / sumx2;
  return;
}
int main() {
  double **x, a, b;
  int n;
  system(«chcp 1251»);
  system(«cls»);
  printf(«Введите количество точек: «);
  scanf(«%d», &n);
  x = getData(n);
  for (int i = 0; i<n; i++)
    printf(«%5.1lf — %7.3lfn», x[0][i], x[1][i]);
  b = 0;
  getApproxA(x, &a, b, n);
  printf(«a = %lfnb = %lf», a, b);
  getchar(); getchar();
  return 0;
}

Результат выполнения программы поиска коэффициента угла наклона аппроксимирующей прямой при фиксированном значении b=0:

Назад: Алгоритмизация

Источник

A linear approximation is a mathematical term that refers to the use of a linear function to approximate a generic function. It is commonly used in the finite difference method to create first-order methods for solving or approximating equations. The linear approximation formula is used to get the closest estimate of a function for any given value.

Linear Approximation Formula

The linear approximation of a function is defined as using a line to approximate the function’s value at a given position. The concept of the tangent line is linked with the curve of a function with a point on it. The value of the function at any point that is very close to the provided point can be approximated using the equation of the tangent line if the equation of the tangent line is found at a given point. This notion is known as linear approximation, and it is also known as tangent line approximation because it is done using the tangent line.

Formula

Suppose a tangent line is drawn to the curve y = f(x) at the point (a, f(a)).

The equation of tangent is the required linear approximation formula. It can be derived by using the point-slope form as its slope is the derivative of function f(x) at x = a, that is, f ‘(a).

L(x) = f(a) + f ‘(a) (x – a)

where,

L(x) is the linear approximation of the function f(x) for x = a,

f'(a) is the first derivative of f(x) for x = a.

Sample Problems

Problem 1. Find the linear approximation of the function f(x) = x³ if the value of x is approaching 2.

Solution:

We have, f(x) = x³.

Now, f'(x) = d(f(x))/dx

= 3x²

For a = 2,

f(a) = 2³ = 8

f'(a) = 3 (2)² = 3 (4) = 12

Using the formula we have,

L(x) = f(a) + f ‘(a) (x – a)

= 8 + 12 (x – 2)

= 8 + 12x – 24

= 12x – 16

Problem 2. Find the linear approximation of the function f(x) = √x if the value of x is approaching 4.

Solution:

We have, f(x) = √x.

Now, f'(x) = d(f(x))/dx

= 1/(2√x)

For a = 4,

f(a) = √4 = 2

f'(a) = 1/(2√4) = 1/4

Using the formula we have,

L(x) = f(a) + f ‘(a) (x – a)

= 2 + (1/4) (x – 4)

= 2 + (x – 4)/4

= (x + 4)/4

Problem 3. Find the linear approximation of the function f(x) = sin x if the value of x is approaching π/3.

Solution:

We have, f(x) = sin x.

Now, f'(x) = d(f(x))/dx

= cos x

For a = π/3,

f(a) = sin π/3 = √3/2

f'(a) = cos π/3 = 1/2

Using the formula we have,

L(x) = f(a) + f ‘(a) (x – a)

= √3/2 + (1/2) (x – π/3)

= (3 (√3 + x) – π)/6

Problem 4. Find the linear approximation of the function f(x) = log x if the value of x is approaching 1.

Solution:

We have, f(x) = log x.

Now, f'(x) = d(f(x))/dx

= 1/x

For a = 1,

f(a) = log 1 = 0

f'(a) = 1/1 = 1

Using the formula we have,

L(x) = f(a) + f ‘(a) (x – a)

= 0 + 1 (x – 1)

= x – 1

Problem 5. Find the linear approximation of the function f(x) = tan x if the value of x is approaching π/3.

Solution:

We have, f(x) = tan x.

Now, f'(x) = d(f(x))/dx

= sec² x

For a = π/3,

f(a) = tan π/3 = √3

f'(a) = sec² π/3 = 4

Using the formula we have,

L(x) = f(a) + f ‘(a) (x – a)

= √3 + (4) (x – π/3)

= (3 (√3 + 4x) – 4π)/3

Last Updated :
26 Apr, 2022

Like Article

Save Article

Источник

Применим метод наименьших квадратов
для аппроксимации экспериментальных
данных.

Читаем данные из файлов datax и datay

При использовании
MathCAD 2000имя файла следует
заключать в кавычки и записывать его
по правиламMS DOS, например,READPRN(«c:mylibdatax.prn»).

Определяем количество прочитанных
данных (число экспериментальных точек).

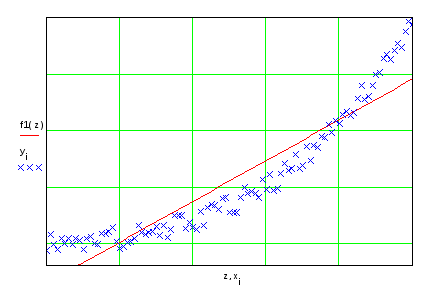
Используем встроенные
функции slope
и intercept
для определения коэффициентов линейной
регрессии (аппроксимация данных прямой
линией). Функция slope
определяет угловой
коэффициент прямой, а функция intercept –
точку пересечения графика с вертикальной
осью.

Определяем аппроксимирующую
функцию:

Коэффициенты линейной регрессии –

Mathcad
2000 предлагает для этих же целей
использовать функцию line

Вычислим стандартное отклонение.

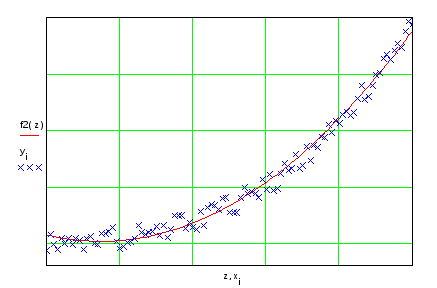
3.3.2. Аппроксимация полиномами

Теперь попытаемся подобрать
полиномы второй и третьей степени, в
качестве аппроксимирующей функции.
Для этих целей служат встроенные функции
regress
и уже знакомая нам функция interp.
(Очевидно, что если в качестве
аппроксимирующей функции брать полином
степени на единицу меньше числа точек,
то задача сведется к задаче глобальной
интерполяции и полученный полином
будет точно проходить через все заданные
узлы.)

Вводим степени
полиномов:

Функция regress
является вспомогательной, она
подготавливает данные, необходимые
для работы функции interp.
Вектор vs
содержит, в том числе, и коэффициенты
полинома

Функция interp
возвращает значение полинома в точке
z.
Определив новые функции f2,
f3,
мы получили возможность находить
значение полинома в любой заданной
точке.

Коэффициенты:

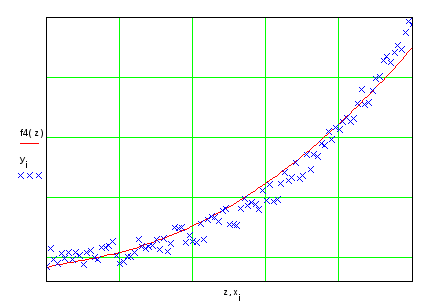
Стандартные отклонения
почти не отличают друг от друга,
коэффициент при четвертой степени z
невелик, поэтому дальнейшее увеличение
степени полинома нецелесообразно и
достаточно ограничиться только второй
степенью.

К сожалению, функция regress
имеется далеко не во всех версиях
Matcad‘а.
Однако, провести полиномиальную
регрессию можно и без использования
этой функции. Для этого нужно определить
коэффициенты нормальной системы и
решить полученную систему уравнений,
например, матричным методом.

Теперь попытаемся
аппроксимировать экспериментальные
данные полиномами степени m
и m1, не
прибегая к помощи встроенной функции
regress
.

Вычисляем элементы матрицы коэффициентов
нормальной системы

и столбец свободных членов

Находим коэффициенты полинома, решая
систему матричным методом,

Определяем аппроксимирующие функции

Коэффициенты полиномов следующие:

Вычислим стандартное отклонение

3.3.3. Аппроксимация линейной комбинацией функций

Mathcad
предоставляет пользователям встроенную
функцию linfit для
аппроксимации данных по методу наименьших
квадратов линейной комбинацией
произвольных функций.

Функция linfit
имеет три аргумента:

вектор x –
x–координаты
заданных точек,
вектор y –
y–координаты
заданных точек,
функция F –
содержит набор функций, который будет
использоваться для построения линейной
комбинации.

Задаем функцию F
(аппроксимирующая функция ищется в
виде
:

Определяем аппроксимирующую
функцию:

Вычисляем дисперсию:

Соседние файлы в папке 2010

Источник

Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.

Если не ввести значения x, калькулятор примет, что значение x меняется от 0 с шагом 1.

Аппроксимация функции одной переменной

Квадратичная аппроксимация

Аппроксимация степенной функцией

Показательная аппроксимация

Логарифмическая аппроксимация

Гиперболическая аппроксимация

Экспоненциальная аппроксимация

Точность вычисления

Знаков после запятой: 4

Коэффициент линейной парной корреляции

Средняя ошибка аппроксимации, %

Логарифмическая регрессия

Средняя ошибка аппроксимации, %

Гиперболическая регрессия

Средняя ошибка аппроксимации, %

Экспоненциальная регрессия

Средняя ошибка аппроксимации, %

Результат

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Линейная регрессия

Уравнение регрессии:

Коэффициент a:
$a&=frac{sum x_i sum y_i- nsum x_iy_i}{left(sum x_iright)^2-nsum x_i^2}$

Коэффициент b:
$b&=frac{sum x_i sum x_iy_i-sum x_i^2sum y_i}{left(sum x_iright)^2-nsum x_i^2}$

Коэффициент линейной парной корреляции:
$r_{xy}&=frac{nsum x_iy_i-sum x_isum y_i}{sqrt{left(nsum x_i^2-left(sum x_iright)^2right)!!left(nsum y_i^2-left(sum y_iright)^2 right)}}$

Коэффициент детерминации:
$R^2=r_{xy}^2$

Средняя ошибка аппроксимации:
$overline{A}=dfrac{1}{n}sumleft|dfrac{y_i-widehat{y}_i}{y_i}right|cdot100%$

Квадратичная регрессия

Уравнение регрессии:
$widehat{y}=ax^2+bx+c$

Система уравнений для нахождения коэффициентов a, b и c:
$begin{cases}asum x_i^2+bsum x_i+nc=sum y_i,,\[2pt] asum x_i^3+bsum x_i^2+csum x_i=sum x_iy_i,,\[2pt] asum x_i^4+bsum x_i^3+csum x_i^2=sum x_i^2y_i,;end{cases}$

Коэффициент корреляции:
$R= sqrt{1-frac{sum(y_i-widehat{y}_i)^2}{sum(y_i-overline{y})^2}}$ ,
где
$overline{y}= dfrac{1}{n}sum y_i$

Коэффициент детерминации:
R^2

Средняя ошибка аппроксимации:
$overline{A}=dfrac{1}{n}sumleft|dfrac{y_i-widehat{y}_i}{y_i}right|cdot100%$

Кубическая регрессия

Уравнение регрессии:
$widehat{y}=ax^3+bx^2+cx+d$

Система уравнений для нахождения коэффициентов a, b, c и d:
$begin{cases}asum x_i^3+bsum x_i^2+csum x_i+nd=sum y_i,,\[2pt] asum x_i^4+bsum x_i^3+csum x_i^2+dsum x_i=sum x_iy_i,,\[2pt] asum x_i^5+bsum x_i^4+csum x_i^3+dsum x_i^2=sum x_i^2y_i,,\[2pt] asum x_i^6+bsum x_i^5+csum x_i^4+dsum x_i^3=sum x_i^3y_i,;end{cases}$

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Степенная регрессия

Уравнение регрессии:
$widehat{y}=acdot x^b$

Коэффициент b:
$b=dfrac{nsum(ln x_icdotln y_i)-sumln x_icdotsumln y_i }{nsumln^2x_i-left(sumln x_iright)^2 }$

Коэффициент a:
$a=exp!left(dfrac{1}{n}sumln y_i-dfrac{b}{n}sumln x_iright)$

Показательная регрессия

Уравнение регрессии:
$widehat{y}=acdot b^x$

Коэффициент b:
$b=expdfrac{nsum x_iln y_i-sum x_icdotsumln y_i }{nsum x_i^2-left(sum x_iright)^2 }$

Коэффициент a:
$a=exp!left(dfrac{1}{n}sumln y_i-dfrac{ln b}{n}sum x_iright)$

Гиперболическая регрессия

Уравнение регрессии:
$widehat{y}=a + frac{b}{x}$

Коэффициент b:
$b=dfrac{nsumdfrac{y_i}{x_i}-sumdfrac{1}{x_i}sum y_i }{nsumdfrac{1}{x_i^2}-left(sumdfrac{1}{x_i}right)^2 }$

Коэффициент a:
$a=dfrac{1}{n}sum y_i-dfrac{b}{n}sumdfrac{1}{x_i}$

Логарифмическая регрессия

Уравнение регрессии:

Коэффициент b:
$b=dfrac{nsum(y_iln x_i)-sumln x_icdot sum y_i }{nsumln^2x_i-left(sumln x_iright)^2 }$

Коэффициент a:
$a=dfrac{1}{n}sum y_i-dfrac{b}{n}sumln x_i$

Экспоненциальная регрессия

Уравнение регрессии:
$widehat{y}=e^{a+bx}$

Коэффициент b:
$b=dfrac{nsum x_iln y_i-sum x_icdotsumln y_i }{nsum x_i^2-left(sum x_iright)^2 }$

Коэффициент a:
$a=dfrac{1}{n}sumln y_i-dfrac{b}{n}sum x_i$

Вывод формул

Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.

Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.

Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.

Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:

Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.

Используя формулу производной сложной функции, получим следующую систему уравнений:
$begin{cases} sum [y_i - F(x_i, a, b)]cdot F^prime_a(x_i, a, b)=0 \ sum [y_i - F(x_i, a, b)]cdot F^prime_b(x_i, a, b)=0 end{cases}$

Для функции вида частные производные равны:
,

Подставив производные, получим:
$begin{cases} sum (y_i - ax_i-b)cdot x_i=0 \ sum (y_i - ax_i-b)=0 end{cases}$

Далее:
$begin{cases} sum y_ix_i - a sum x_i^2-bsum x_i=0 \ sum y_i - asum x_i - nb=0 end{cases}$

Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.

Источник