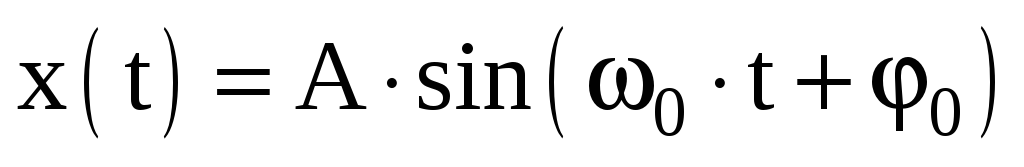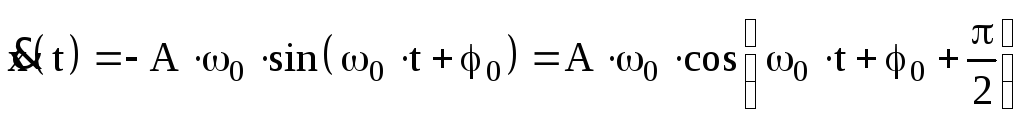Периодическое движение — это повторяющееся и непрерывное движение объекта через равные промежутки времени. Простое гармоническое движение — это разновидность периодического движения.
Линейная частота — это количество колебаний, повторений или колебаний, совершаемых объектом или телом за единицу секунды. Величина, обратная периоду времени, дает частоту. Слово линейная частота используется, чтобы отличить ее от пространственной частоты и угловой частоты.
Время, которое требуется объекту для покрытия полного цикла, — это период времени. Например: если камертон вибрирует 5 раз в секунду, то линейная частота будет 5 Гц. Частота играет жизненно важную роль в физике, чтобы рассказать о скорости колебаний и вибраций, таких как звуковые сигналы, радиоволны и свет.
Линейное частотное уравнение
Под линейной частотой обычно понимают время, необходимое для завершения одного колебания или вибрации. Период времени определяет время, затрачиваемое объектом на выполнение одного цикла. Частота и период взаимосвязаны следующим образом:
f = 1 / T
Для волнового уравнения линейная частота вычисляется из уравнения:
f=с/λ
Здесь,
c равна скорости волны
λ — длина волны.
Линейная частота рассчитывается из соотношения:
ω = 2πf
Линейные единицы измерения частоты
Для колебаний, волн и простая гармоника движения, частота – это количество колебаний в одну секунду. Единица частоты названа в честь известного физика Генриха Герца. Его единицей СИ является Герц (Гц). До этого единицей измерения частоты был cps, то есть количество циклов в секунду. Так как единица периода для всех систем секундная, то для вращательных и циркуляционных устройств частоту называют оборотами в минуту, сокращенно об/мин. Здесь 60 об/мин равны одному герцу. Для линейной частоты другая единица: с-1
Линейный символ частоты
Частота говорит о колебаниях или циклах, совершенных за единицу времени. Жизненно важно определить природу и характер многих важных физических понятий, таких как колебания, периодическое движение, волны, свет и изменение тока и напряжения.
Стандартный символ, который используется для представления линейной частоты, — f. Обычно для колебания и SHM используется f. Но для света и волн есть другой символ, обозначающий частоту. Это греческий символ ν.
Угловая частота против линейной частоты
Угловая частота колебания и его линейная частота — это два разных понятия. Для колеблющегося объекта угловая частота говорит об изменении фазы, которое представляет собой угловое смещение. В то же время частота говорит о совершении колебания за единицу времени.
Он дает соотношение между частотой и угловая частота колебания. Для простого гармонического движения или просто колебаний формула угловой частоты получается путем умножения линейной частоты на угол, который покрывают колеблющиеся частицы. Для одного полного цикла угол равен 2π.
Например, мяч колеблется и совершает 5 оборотов за 1 секунду. Тогда частота будет 5 Гц, а угловая частота будет 10π рад / с.
| Угловая частота | Линейная частота |
|---|---|
| Изменение угла колеблющегося тела или просто угловое смещение известно как угловая частота. | Колебания или колебания, завершенные за одну секунду, — это частота объекта или частицы. |
| Угловая частота обозначается символом ω. | Линейная частота обозначается буквой ν. |
| Его стандартная единица измерения — радиан в секунду (рад / с). | Единица измерения частоты в системе СИ — герц (Гц). |
| The formula for angular frequency is ω =2πf or ω=2π/T | The equation for the linear frequency is: f =1/T |
Как найти линейную частоту
To find the linear frequency of any vibratory object, or oscillatory body the formulas that are used are: f=1/T
f — частота, а T — период
Or
f=с/λ
c — скорость волны, а λ — длина волны.
Например, маятник колеблется с периодом 0.5 секунды. Тогда частота маятника будет:
f=1/Т
f=1/0.5
f=10/5
f=2 Гц
Во втором случае, если скорость волны задана как 320 м / с, а соответствующая длина волны задана как 8 м, то частота будет:
f=с/λ
f=320/8
f=4 Гц
При расчете частоты важно сохранять все величины в их стандартных единицах измерения, например, секунды для времени, для длины это должен быть метр.
Теперь предположим, что мяч делает 360 циклов за одну минуту, тогда частота будет:
f=360/1min
f=360/60sec
f=6 Гц
Часто задаваемые вопросы (FAQ)
Объясните частоту простыми словами.
В физике линейная частота определяется как количество колебания или колебания завершаются за одну секунду.
Частота в простейшем понимании — это количество появлений какого-либо явления. Предположим, мяч отскакивает 8 раз, тогда частота прыгающего мяча составляет 8 Гц.
Угловая частота совпадает с линейной частотой?
Нет, угловая частота и линейная частота — это два разных физических понятия.
Угловая частота говорит об угловом смещении или изменении фазы объекта. В то же время линейная частота говорит о количестве колебаний или вибраций, которые объект покрывает за единицу времени.
Как связаны линейная частота и угловая частота?
Угловая частота и линейная частота связаны формулой:
ω = 2πf
ω — угловая частота
f — линейная частота
Символ частоты ν или f?
Оба ν и f используются для представления частоты. Для волновой системы используется ν, тогда как для других колеблющихся тел, таких как маятник и пружина, используется символ f.
Какое общее правило частоты?
Частота дает представление о циклах, совершаемых колеблющимся телом за одну секунду.
Общая формула или правило для определения значения частоты дается как:
f=1/Т
Т представляет период. Он показывает время, необходимое для завершения одного полного колебания. Единица измерения частоты — герц (Гц).
Как рассчитать частоту?
Для расчета частоты используется формула f = 1 / T и f = c / λ.
Во-первых, чтобы вычислить частоту, все значения времени или длины волны и скорости должны быть в их стандартных единицах измерения после того, как преобразование заменяет значения в соответствующих уравнениях и выполняет упрощения.
Т=1/2 мин
Например, тело совершает одно колебание за ½ минуты. Тогда первым шагом будет преобразование периода в секунды, то есть:
T=1/2 X 60 seconds
T= 30seconds
Теперь подставляя значение T в формулу, получаем:
f=1/Т
f=1/30
f=0.03 Гц
Содержание
- 1 Гармонические колебания
- 2 Тестирование онлайн
- 3 Угловая скорость
- 4 Период и частота
- 5 Линейная скорость
- 6 Центростремительное ускорение
- 7 Вращение Земли
- 8 Связь со вторым законом Ньютона
- 9 Как вывести формулу центростремительного ускорения
- 10 Движение по циклоиде*
- 11 Понятие скорости
- 12 Линейная скорость
- 13 Связь между линейной и угловой скоростями
Колебательные процессы весьма часто встречаются в окружающей нас природе и технике. Значительная часть механических движений – движение машин, работающих циклически; почти все акустические явления; переменный ток, применяющийся в быту и в разнообразных технических устройствах; радиотехника и часть электроники; вся волновая оптика; волновые свойства частиц – вот далеко не полный перечень явлений и технических приложений, описываемых на языке колебательных и волновых процессов. В конце концов, наши сердца бьются; наши легкие колеблются при дыхании; мы дрожим, когда нам холодно; мы можем слышать и разговаривать благодаря колебаниям барабанных перепонок и голосовых связок. Световые волны, которые позволяют нам видеть, имеют колебательную природу. Когда мы ходим, наши ноги совершают колебания. Колеблются даже атомы, из которых мы состоим. Если расширенно толковать термин «колебания», то сразу становится очевидным, что многие события повседневной жизни обладают необычайной цикличностью. Мир, в котором мы живем, удивительно склонен к колебаниям. Именно поэтому колебательному движению уделяется особое внимание в физике и технике.
Кроме того, периодическое негармоническое движение можно свести к сумме гармонических движений, причем эти составные движения доступны непосредственному наблюдению при помощи современной аппаратуры. Более того, существует аппаратура, позволяющая складывать заданные гармонические движения и получать, таким образом, периодические движения сложного характера.
В процессе развития науки создан мощный и удобный математический аппарат для описания и исследования периодических движений различной физической природы.
Колебаниями называются движения, процессы, изменения состояния, которые характеризуются определенной повторяемостью во времени значений физических величин, определяющих это движение, процесс или состояние.
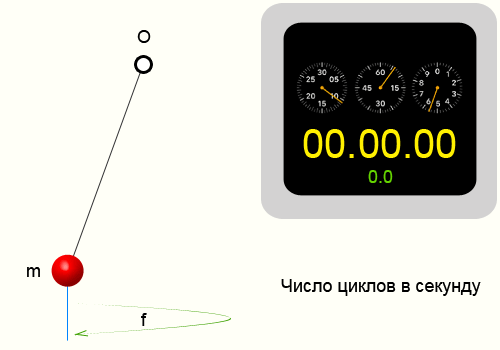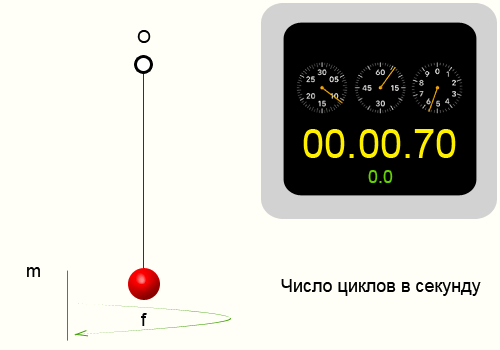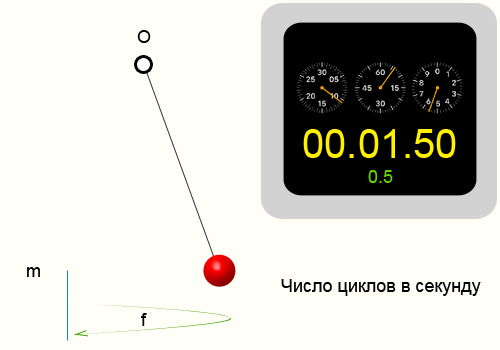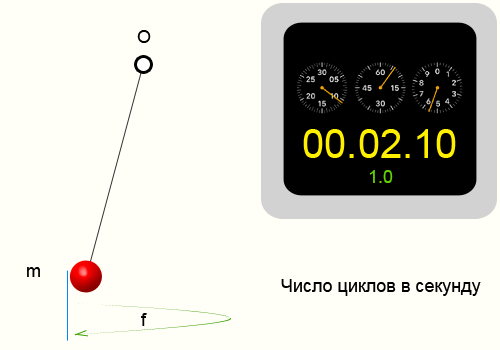
Колебание называют периодическим, если значения величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени. Период колебания Т – это минимальный промежуток времени через который повторяются определенные состояния системы (время, за которое совершается одно полное колебание). Период измеряется в секундах.
Частота колебаний 
Если за какое-то время t система совершает N колебаний, то 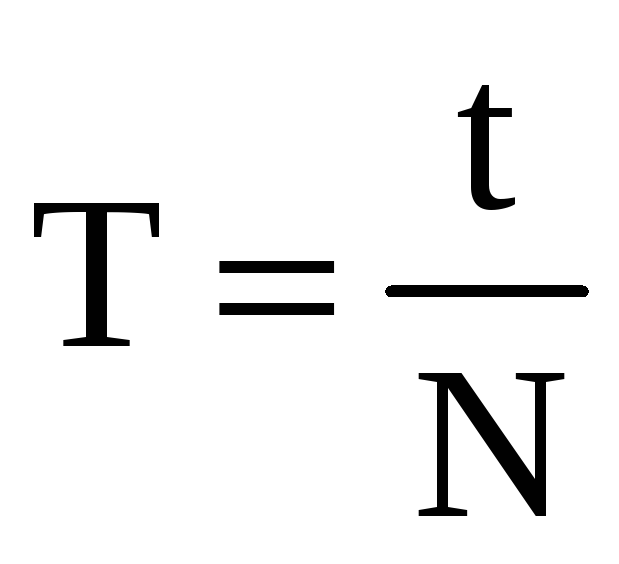

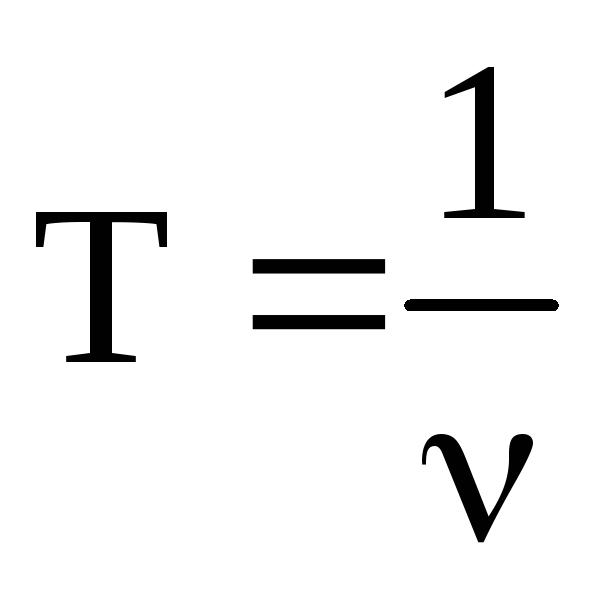
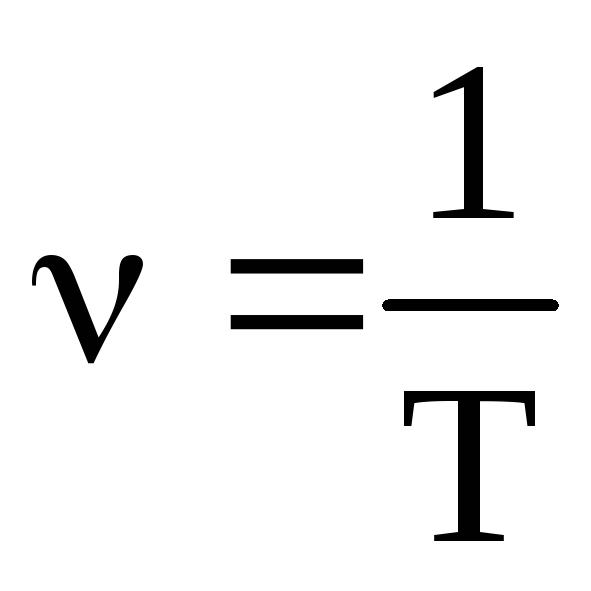
Гармонические колебания
Среди разнообразных периодических движений особое место занимает гармоническое колебательное движение. Гармоническими называют колебания, в которых интересующая нас величина х (например, линейное или угловое смещение из положения равновесия, скорость, ускорение, заряд, напряжение и т.д.) изменяется со временем t по закону косинуса или синуса, то есть
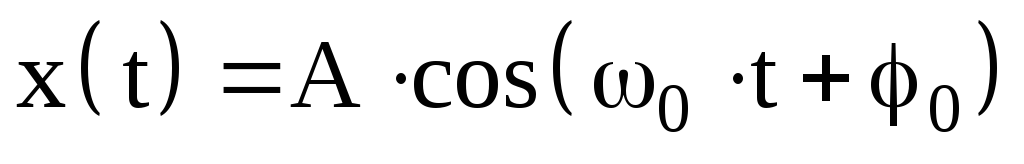
А – амплитуда (максимальное значение величины х). Определяется начальными условиями. Измеряется в единицах величины х.
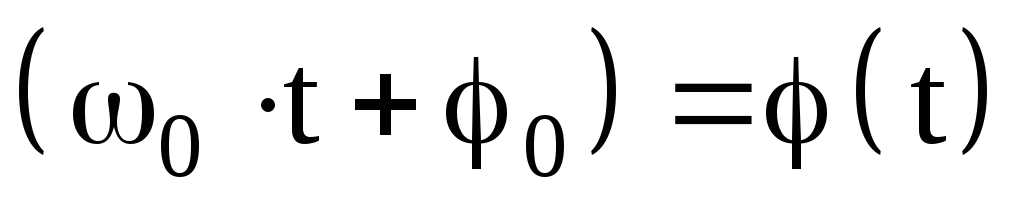



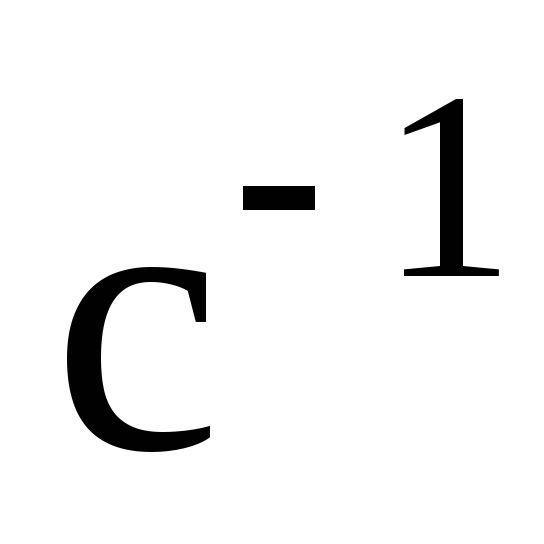
Циклическая частота связана с линейной частотой и периодом следующими соотношениями 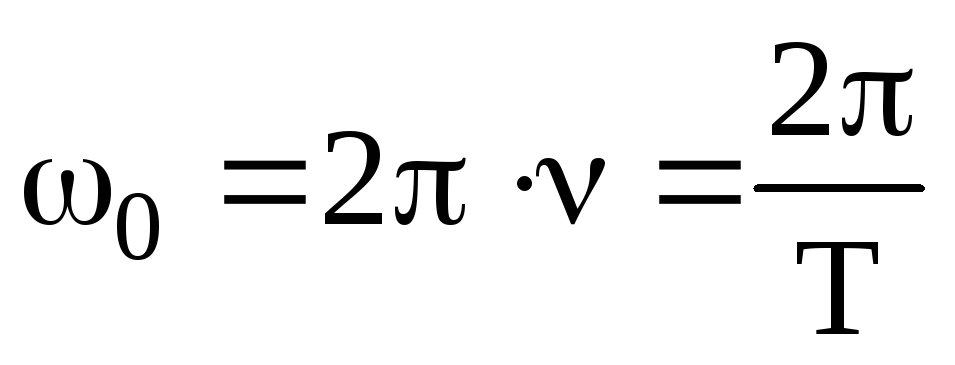
С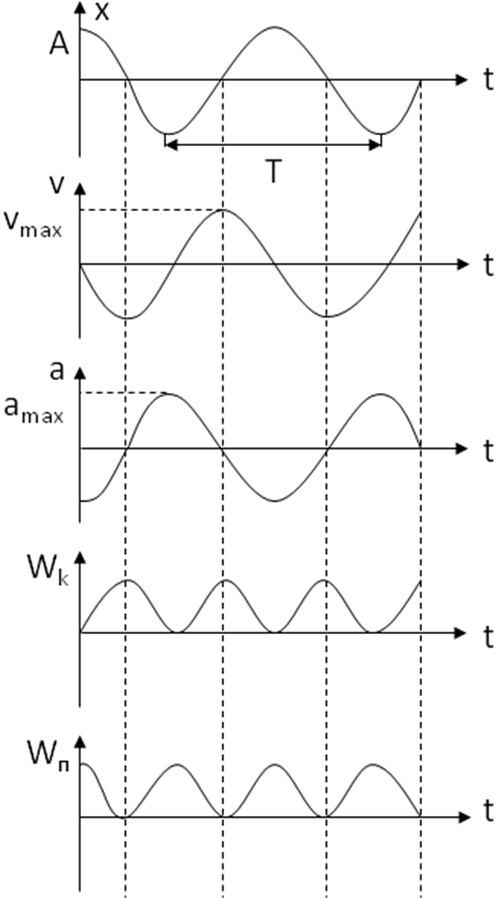
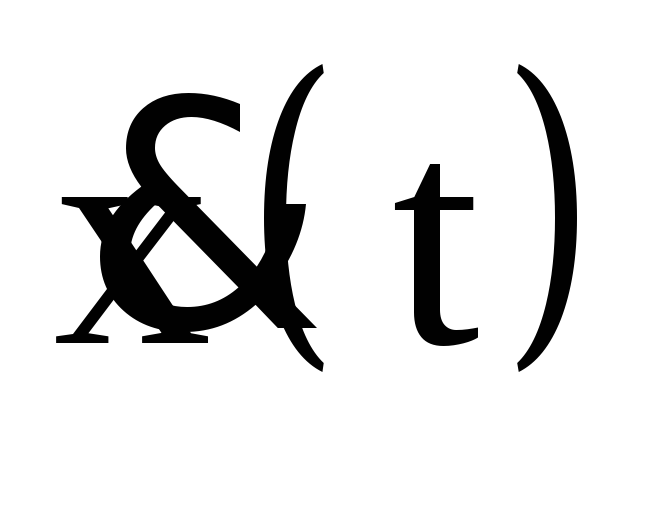
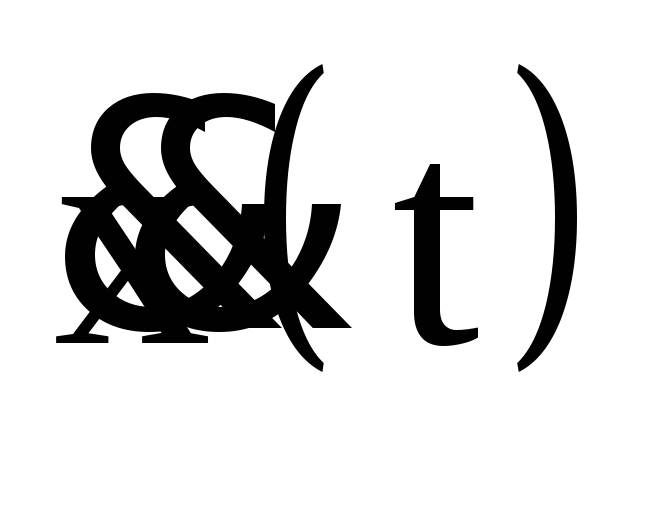
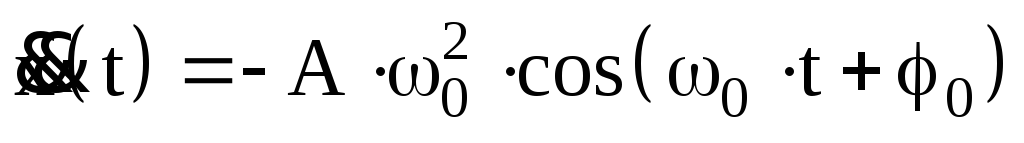
При этом максимальное значение скорости колеблющегося тела Vmax = Aω, максимальное значение модуля ускорения amax = Aω 2 .
Кинетическая энергия колеблющегося тела Wk = ½mv 2 = ½mA 2 ω 2 sin 2 (ωt+φ).
Потенциальная энергия (учитывая, что сила квазиупругая) Wп = ½ kx 2 = ½ kA 2 cos 2 (ωt+φ).
Полная энергия системы при гармонических колебаниях W= Wk + Wп =½ kA 2 = ½ mω 2 A 2 .
На рисунке приведены графики зависимости от времени смещения х, скорости V, ускорения а, кинетической Wk и потенциальной Wп энергии гармонических колебаний при начальной фазе φ = 0. Из рисунка видно, частота изменения кинетической Wk и потенциальной Wп энергии при гармонических колебаниях вдвое больше частоты изменения смещения, скорости и ускорения.
Сопоставив уравнения (1) и (2), видим, что 
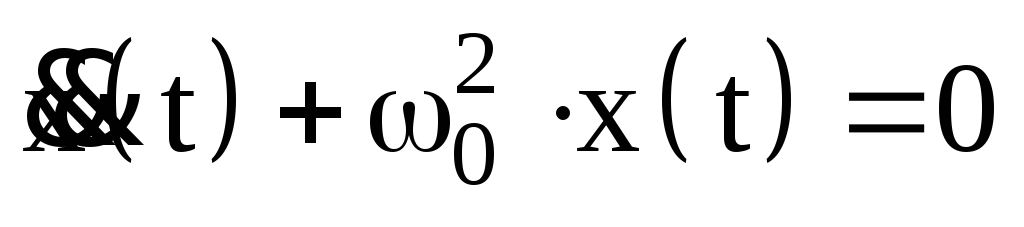
Это линейное однородное дифференциальное уравнение второго порядка называют уравнением гармонических колебаний.
Колебательная система, совершающая гармонические колебания, называется гармоническим осциллятором. Если колебательная система, совершающая гармонические колебания, обладает одной степенью свободы (для характеристики положения достаточно одной координаты), то такая система называется линейным гармоническим осциллятором.
Для определения характера движения механической системы составляют уравнение движения системы (исходя из законов динамики или закона сохранения энергии). Если уравнение при этом приводится к виду (3), то можно однозначно утверждать, что данная система совершает гармоническое колебание, собственная частота 
Рассмотрим сначала пружинный маятник (рис 1 б). Пусть подвешенное к пружине тело оттянуто от положения равновесия на расстояние х (рис.1.в), а затем предоставлено самому себе. На тело действуют сила тяжести и сила упругости. Под действием этих сил тело движется с ускорением. Запишем уравнение второго закона Ньютона для этого случая (рис.1.в)
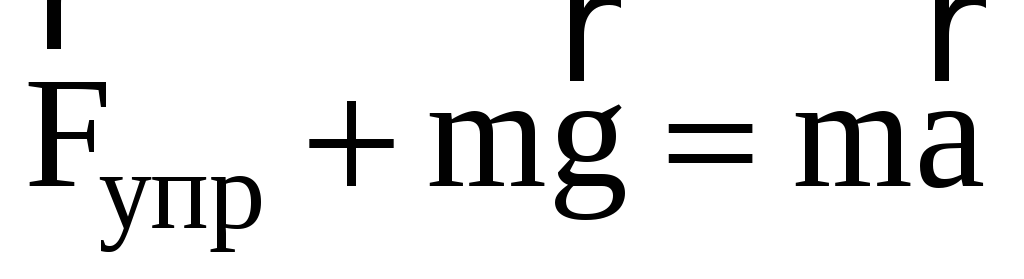
Это уравнение в проекции на ось ОХ и с учетом того, что для одномерного движения ускорение – это вторая производная от координаты по времени, то есть 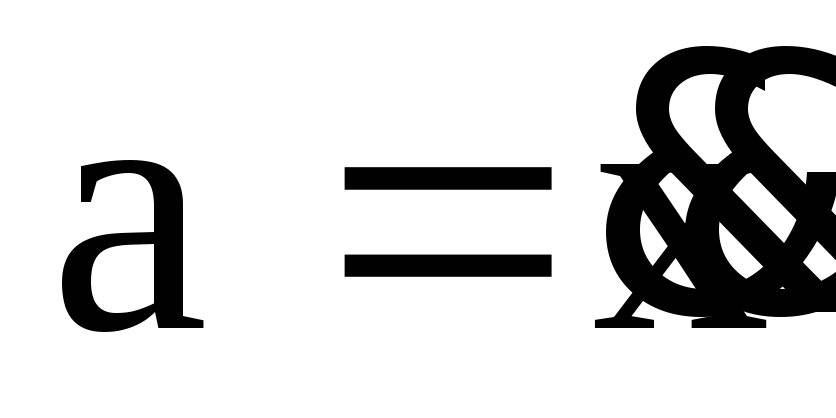
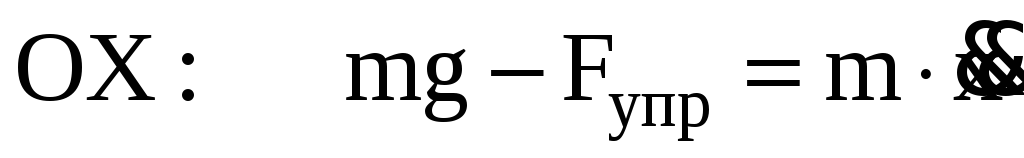
Величину силы упругости 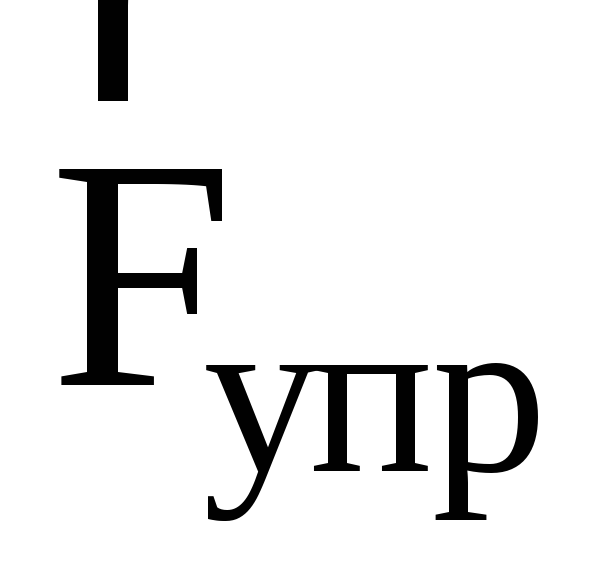
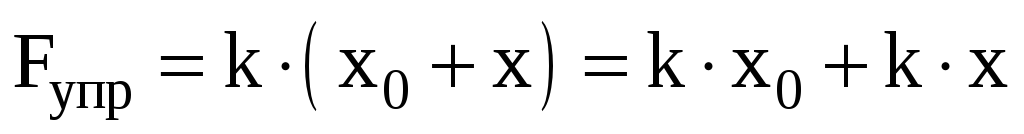
После подстановки (5) в (4) получим
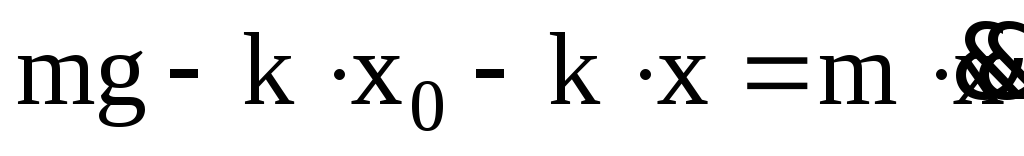
Величину растяжения пружины в положении равновесия 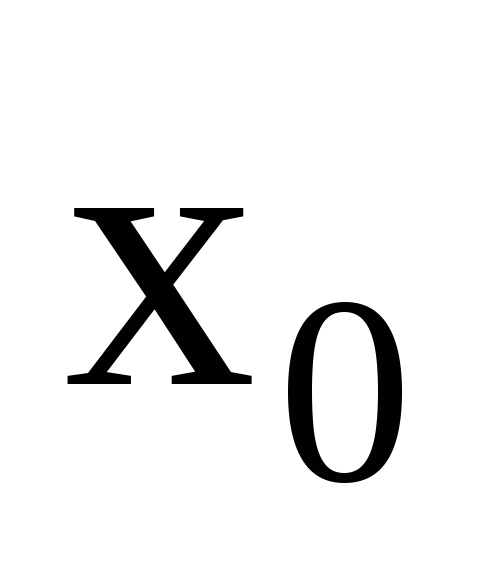

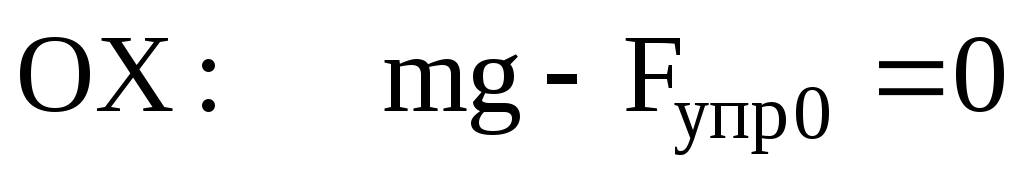
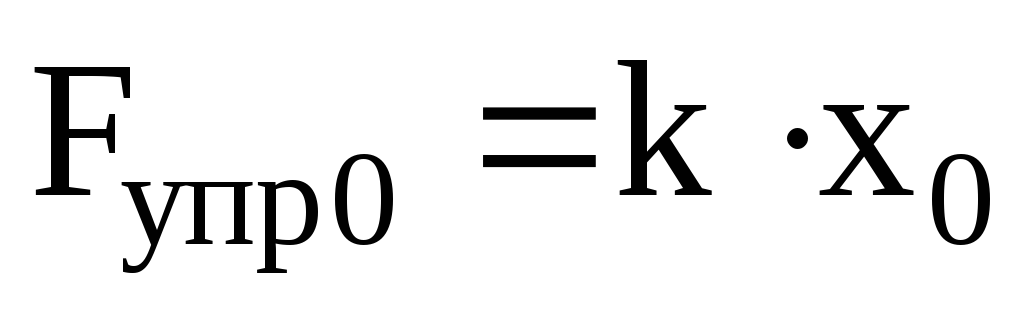
Из (7) и (8) следует, что
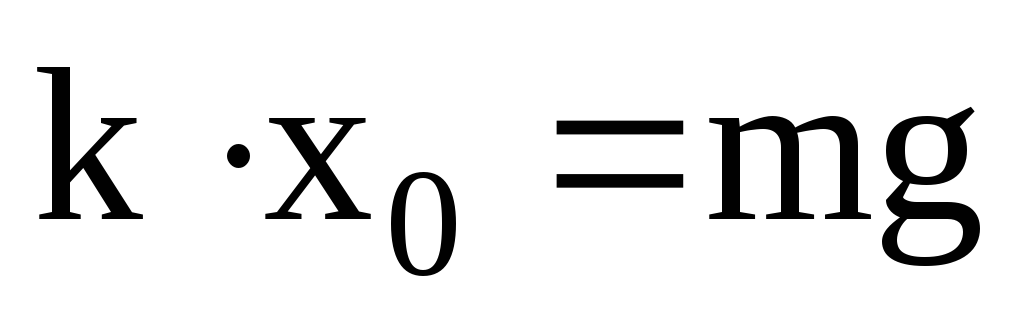
После подстановки (9) в (6) и приведения подобных слагаемых получаем: 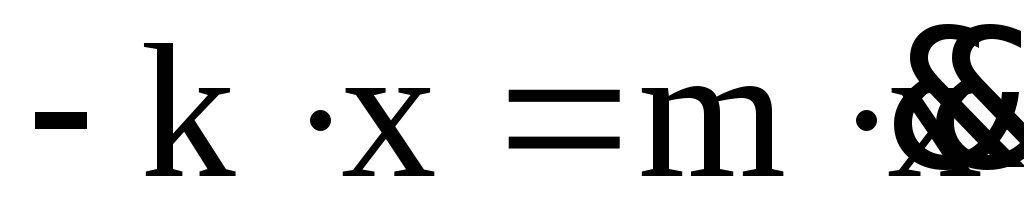

Сравнив уравнения (3) и (10), получим, что для пружинного маятника 
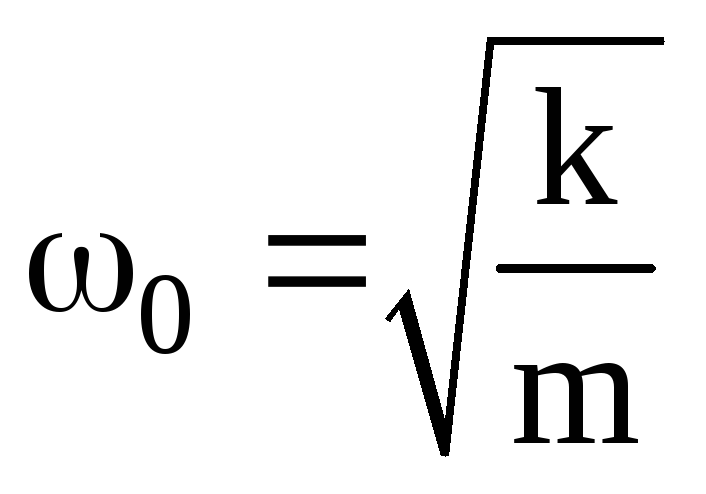
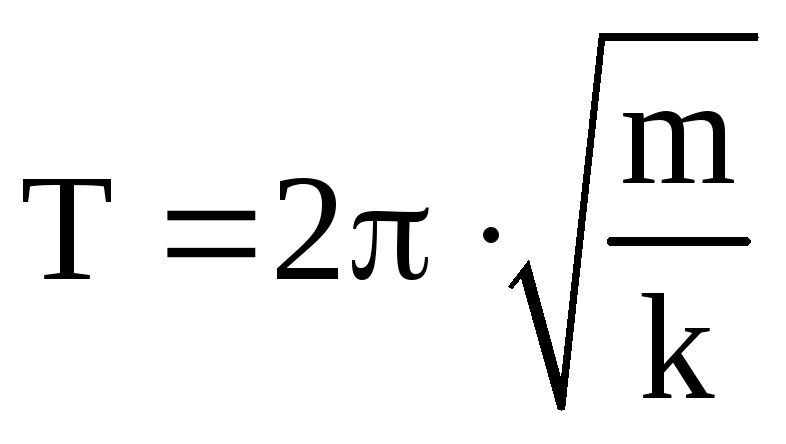
Похожие рассуждения можно провести для математического маятника (рис.2) и показать, что 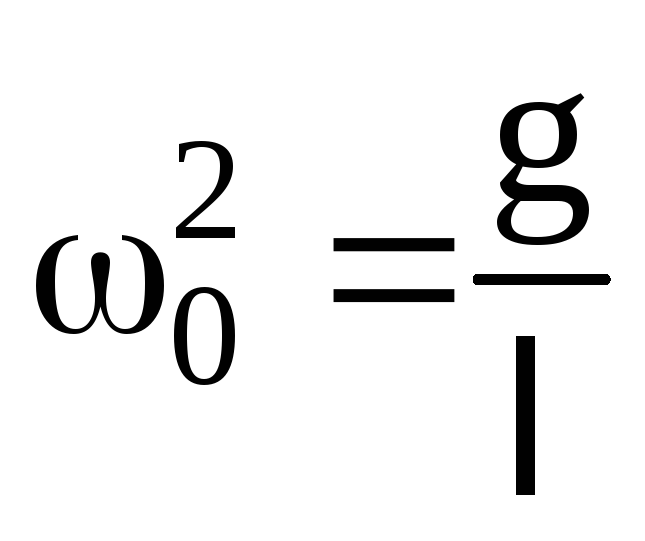
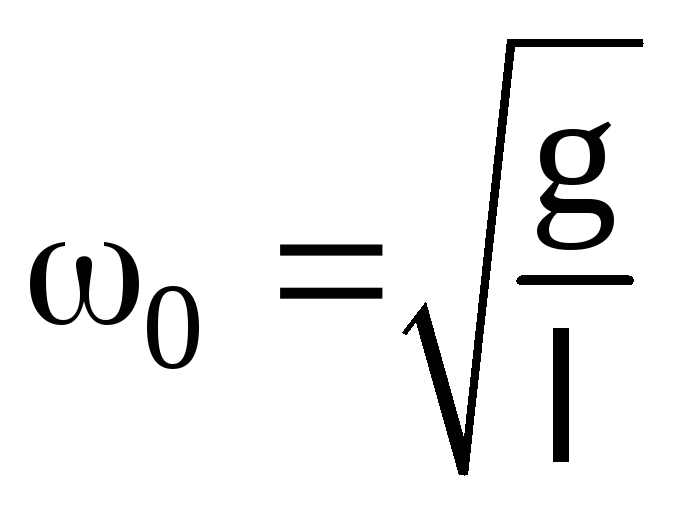
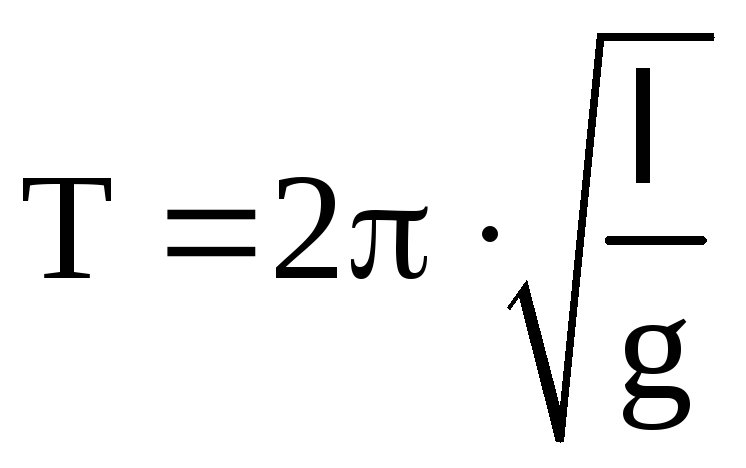
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть 

Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью 
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Понятие скорости
Когда мы сравниваем движение каких-либо тел, то говорим, что одни тела двигаются быстрее, а другие — медленнее. Такую простую терминологию мы используем в повседневной жизни, говоря, например, о движении транспорта. В физике быстрота движения тел характеризуется определенной величиной. Эта величина называется скоростью. Общее определение скорости (в случае, если тело движется равномерно):
Скорость при равномерном движении тела — это физическая величина, показывающая, какой путь прошло тело за единицу времени.
Под равномерным движением тела подразумевается, что скорость тела постоянна. Формула нахождения скорости: $v=frac$, $s$ — это пройденный телом путь (то есть длина линии), $t$ — время (то есть промежуток времени, за который пройден путь).
Согласно международной системе СИ, единица измерения линейной скорости является производной от двух основных единиц — метра и секунды, то есть измеряется в метрах в секунду (м/с). Это значит, что под единицей скорости понимается скорость такого равномерного движения, при котором путь в один метр тело проходит за одну секунду.
Попробуй обратиться за помощью к преподавателям
Также скорость часто измеряют в км/ч, км/с, см/с.
Рассмотрим простой пример задачи на вычисление скорости.
Задача. Двигаясь равномерно, поезд за 4 ч проходит 219 км. Найти его скорость движения.
Решение. $v=frac<219 км><4 ч>=54,75frac<км><ч>$. Переведём километры в метры и часы в секунды: $54,75frac<км><ч>=frac<54750 м><3600c>approx 15,2frac<м>$.
Из примера мы видим, что числовое значение скорости отличается в зависимости от выбранной единицы измерения.
Кроме числового значения, скорость имеет направление. Числовое значение величины в физике называют модулем. Когда у физической величины есть и направление, то эту величину называют векторной. То есть скорость — это векторная физическая величина.
На письме модуль скорости обозначается $v$, а вектор скорости — $vec v$.
В свою очередь, такие величины как путь, время, длина и другие характеризуются только числовым значением. Тогда говорят, что это скалярные физические величины.
Задай вопрос специалистам и получи
ответ уже через 15 минут!
В случае, когда движение является неравномерным, используют понятие средней скорости. Формула средней скорости: $v_<ср>=frac$, где $s$ — это весь пройденный телом путь, $t$ — всё время движения. Рассмотрим пример задачи на среднюю скорость, чтобы понять разницу.
Задача. Некоторый транспорт за 2,5 часа преодолевает путь в 213 км. Найти его $v_<ср>$.
Ответ. $85,2 frac<км><ч>$ или $23,7frac<м> <с>$.
Линейная скорость
Определение линейной скорости относится к разделу физики о механике и подразделу о кинематике в рамках вопроса движения по окружности. В измерении скорости движения по окружности выделяют угловую скорость и линейную скорость.
Дадим определение линейной скорости.
Линейная скорость $V$ — это физическая величина, показывающая путь, который прошло тело за единицу времени.
Формула линейной скорости:
$V=frac$, где $S$ — путь, $t$ — время, за которое точка прошла путь $S$.
Также существует иной вариант этой формулы:
$V=frac$, где $l$ — путь, $t$ — время, за которое точка прошла по дуге $l$.
В некоторых учебниках линейная скорость также обозначается маленькой буквой $v$.
Есть ещё одна формула, по которой можно найти линейную скорость:
$2pi$ соответствует полной окружности (360 угловым градусам).
$vec V$ направленена по касательной к тракетории.
Связь между линейной и угловой скоростями
Чтобы проследить связь между линейной и угловой скоростями, нужно дать определение угловой скорости.
Угловая скорость — это величина, которая равна отношению угла поворота отрезка, соединяющего точку с центром окружности, к промежутку времени, за который этот поворот произошёл.
Записывается эта формула следующим образом:
$omega = frac<phi>$, где $phi$ — это угловое перемещение (или угол поворота, измеряется в радианах), $t$ — промежуток времени, за которое соврешено угловое перемещение.
В системе СИ угловая скорость измеряется в рад/с.
Угловую скорость также называют циклической частотой вращения, потому что при вращении твёрдого тела угловая скорость всех его точек одинакова.
Связь между $V$ и $omega$: $V=omega R$.
Эта формула выводится из определения модуля центростремительного ускорения.
Центростремительное ускорение $a$ — это ускорение точки при равномерном движении по окружности.
С помощью элементарных математических действий из этих двух формул выводится связь между $V$ и $omega$.
Таким образом, в данной статье мы разобрали следующие понятия:
- скорость;
- линейная и угловая скорость;
- связь между линейной и угловой скоростями.
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
Формула частоты в физике
Формула частоты
Определение
Частота — это физический параметр, которые используют для характеристики периодических процессов.
Частота равна количеству повторений или свершения событий в единицу времени.
Чаще всего в физике частоту обозначают буквой $nu ,$ иногда встречаются другие обозначения частоты, например $f$ или $F$.
Частота (наряду со временем) является самой точно измеряемой величиной.
Формула частоты колебаний
При помощи частоты характеризуют колебания. В этом случае частота является физической величиной обратной периоду колебаний $(T).$
[nu =frac{1}{T}left(1right).]
Частота, в этом случае — это число полных колебаний ($N$), совершающихся за единицу времени:
[nu =frac{N}{Delta t}left(2right),]
где $Delta t$ — время за которое происходят $N$ колебаний.
Единицей измерения частоты в Международной системе единиц (СИ) служат в герцы или обратные секунды:
[left[nu right]=с^{-1}=Гц.]
Герц — это единица измерения частоты периодического процесса, при которой за время равное одной секунде происходит один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.
Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами (${nu }_1 и {nu }_2$) равна:
[{nu =nu }_1- {nu }_2left(3right).]
Еще одно величиной характеризующей колебательный процесс является циклическая частота (${omega }_0$), связанная с частотой как:
[{omega }_0=2pi nu left(4right).]
Циклическая частота измеряется в радианах, деленных на секунду:
[left[{omega }_0right]=frac{рад}{с}.]
Частота колебаний тела, имеющего массу$ m,$ подвешенного на пружине с коэффициентом упругости $k$ равна:
[nu =frac{1}{2pi sqrt{{m}/{k}}}left(5right).]
Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.
Для математического маятника частоту колебаний вычисляют как: длина нити:
[nu =frac{1}{2pi sqrt{{l}/{g}}}left(6right),]
где $g$ — ускорение свободного падения; $ l$ — длина нити (длина подвеса) маятника.
Физический маятник совершает колебания с частотой:
[nu =frac{1}{2pi sqrt{{J}/{mgd}}}left(7right),]
где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.
Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, вычисляемых с их помощью.
Формулы для вычисления частоты дискретных событий, частота вращения
дискретных колебаний ($n$) — называют физическую величину, равную числу действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $tau $, то частота дискретных событий равна:
[n=frac{1}{tau }left(8right).]
Единицей измерения частоты дискретных событий является обратная секунда:
[left[nright]=frac{1}{с}.]
Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $tau $ — время, затрачиваемое на один полный оборот, то:
[n=frac{1}{tau }left(9right).]
Примеры задач с решением
Пример 1
Задание. Колебательная система совершила за время равное одной минуте ($Delta t=1 мин$) 600 колебаний. Какова частота этих колебаний?
Решение. Для решения задачи воспользуемся определением частоты колебаний: Частота, в этом случае — это число полных колебаний, совершающихся за единицу времени.
[nu =frac{N}{Delta t}left(1.1right).]
Прежде чем переходить к вычислениям, переведем время в единицы системы СИ: $Delta t=1 мин=60 с$. Вычислим частоту:
[nu =frac{600}{60}=10 left(Гцright).]
Ответ. $nu =10Гц$
Пример 2
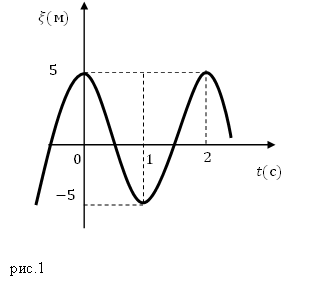
Задание. На рис.1 изображен график колебаний некоторого параметра $xi (t)$, Какова амплитуда и частота колебаний этой величины?
Решение. Из рис.1 видно, что амплитуда величины $xi left(tright)={xi }_{max}=5 (м)$. Из графика получаем, что одно полное колебание происходит за время, равное 2 с, следовательно, период колебаний равен:
[T=2 left(cright).]
Частота — величина обратная периоду колебаний, значит:
[nu =frac{1}{T}=0,5 left(Гцright).]
Ответ. 1) ${xi }_{max}=5 (м)$. 2) $nu =0,5$ Гц
Читать дальше: формулы математического маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Колебательные
процессы весьма часто встречаются в
окружающей нас природе и технике.
Значительная часть механических движений
– движение машин, работающих циклически;
почти все акустические явления; переменный
ток, применяющийся в быту и в разнообразных
технических устройствах; радиотехника
и часть электроники; вся волновая оптика;
волновые свойства частиц – вот далеко
не полный перечень явлений и технических
приложений, описываемых на языке
колебательных и волновых процессов. В
конце концов, наши сердца бьются; наши
легкие колеблются при дыхании; мы дрожим,
когда нам холодно; мы можем слышать и
разговаривать благодаря колебаниям
барабанных перепонок и голосовых связок.
Световые волны, которые позволяют нам
видеть, имеют колебательную природу.
Когда мы ходим, наши ноги совершают
колебания. Колеблются даже атомы, из
которых мы состоим. Если расширенно
толковать термин «колебания», то сразу
становится очевидным, что многие события
повседневной жизни обладают необычайной
цикличностью. Мир, в котором мы живем,
удивительно склонен к колебаниям. Именно
поэтому колебательному движению
уделяется особое внимание в физике и
технике.
Кроме того,
периодическое негармоническое движение
можно свести к сумме гармонических
движений, причем эти составные движения
доступны непосредственному наблюдению
при помощи современной аппаратуры.
Более того, существует аппаратура,
позволяющая складывать заданные
гармонические движения и получать,
таким образом, периодические движения
сложного характера.
В процессе развития
науки создан мощный и удобный математический
аппарат для описания и исследования
периодических движений различной
физической природы.
Колебаниями
называются движения, процессы, изменения
состояния, которые характеризуются
определенной повторяемостью во времени
значений физических величин, определяющих
это движение, процесс или состояние.
Колебание называют
периодическим,
если значения величин, изменяющихся в
процессе колебаний, повторяются через
равные промежутки времени. Период
колебания Т
– это минимальный промежуток времени
через который повторяются определенные
состояния системы (время, за которое
совершается одно полное колебание).
Период измеряется в секундах.
Частота
колебаний
(линейная частота) – это скалярная
физическая величина равная числу
колебаний, совершаемых системой за
единицу времени. Частота колебаний
измеряется в Герцах (Гц).
Если
за какое-то время t
система совершает N
колебаний, то
и
.
Отсюда следует, что
и
.
Гармонические колебания
Среди разнообразных
периодических движений особое место
занимает гармоническое колебательное
движение.
Гармоническими
называют колебания, в которых интересующая
нас величина х (например, линейное или
угловое смещение из положения равновесия,
скорость, ускорение, заряд, напряжение
и т.д.) изменяется со временем t
по закону косинуса или синуса, то есть
, (1)
или
Здесь:
-
А
– амплитуда (максимальное значение
величины х). Определяется начальными
условиями. Измеряется в единицах
величины х. -
– фаза
колебания. Определяет мгновенное
значение величины х в момент времени
t.
За период фаза получает приращение
.
-
– начальная
фаза колебания. Определяется значением
величины х в момент времени t=0. -
– собственная
циклическая (круговая) частота колебаний.
Определяется
параметрами колебательной системы.
Измеряется
в
.
Циклическая частота
связана с линейной частотой и периодом
следующими соотношениями
.
С
и ускорение тела также изменяются по
гармоническому закону. Продифференцировав
по времени уравнение (1) найдем скорость
изменения величины х —
и ускорение
:
.
(2)
При этом максимальное
значение скорости колеблющегося тела
Vmax
= Aω0,
максимальное значение модуля ускорения
amax
= Aω02.
Кинетическая
энергия колеблющегося тела Wk
= ½mv2
= ½mA2ω02
sin2
(ω0t+φ).
Потенциальная
энергия (учитывая, что сила квазиупругая)
Wп
= ½ kx2
= ½ kA2
cos2
(ω0t+φ).
Полная энергия
системы при гармонических колебаниях
W=
Wk
+ Wп
=½ kA2
= ½ mω02
A2.
На рисунке приведены
графики зависимости от времени смещения
х, скорости V,
ускорения а, кинетической Wk
и потенциальной Wп
энергии гармонических колебаний при
начальной фазе φ = 0. Из рисунка видно,
частота изменения кинетической Wk
и
потенциальной Wп
энергии при гармонических колебаниях
вдвое больше частоты изменения смещения,
скорости и ускорения.
Сопоставив уравнения
(1) и (2), видим, что
,
или
. (3)
Это линейное
однородное дифференциальное уравнение
второго порядка называют уравнением
гармонических колебаний.
Колебательная
система, совершающая гармонические
колебания, называется гармоническим
осциллятором. Если колебательная
система, совершающая гармонические
колебания, обладает одной степенью
свободы (для характеристики положения
достаточно одной координаты), то такая
система называется линейным гармоническим
осциллятором.
Для определения
характера движения механической системы
составляют уравнение движения системы
(исходя из законов динамики или закона
сохранения энергии). Если уравнение при
этом приводится к виду (3), то можно
однозначно утверждать, что данная
система совершает гармоническое
колебание, собственная частота
которого равна корню квадратному из
коэффициента при х(t).
Воспользуемся этим методом для определения
циклических частот и периодов колебаний
пружинного и математического маятников.
Рассмотрим сначала
пружинный маятник (рис 1 б). Пусть
подвешенное к пружине тело оттянуто от
положения равновесия на расстояние х
(рис.1.в), а затем предоставлено самому
себе. На тело действуют сила тяжести и
сила упругости. Под действием этих сил
тело движется с ускорением. Запишем
уравнение второго закона Ньютона для
этого случая (рис.1.в)
.
Это уравнение в
проекции на ось ОХ и с учетом того, что
для одномерного движения ускорение –
это вторая производная от координаты
по времени, то есть
,
запишется
. (4)
Величину силы
упругости
,
действующей на тело массой m,
найдем по формуле закона Гука
.
(5)
После подстановки
(5) в (4) получим
(6)
Величину растяжения
пружины в положении равновесия
(рис.1.а и 1.б) найдем из уравнения второго
закона Ньютона для неподвижного тела,
подвешенного к пружине
,
, (7)
,
(8)
Из (7) и (8) следует,
что
.
(9)
После подстановки
(9) в (6) и приведения подобных слагаемых
получаем:
,
или
(10)
Сравнив уравнения
(3) и (10), получим, что для пружинного
маятника
.
.
(11)
Похожие рассуждения
можно провести для математического
маятника (рис.2) и показать, что
.
.
(12)
Математический
маятник – это материальная точка на
невесомой и нерастяжимой нити длиной.
При гармонических колебаниях смещение
маятника от положения равновесия х
много меньше длины нити х <<
,
поэтому для угла отклонения нити от
вертикали
имеет место соотношение
Следовательно,
второй закон Ньютона для материальной
точки массы m:
ma
= F
можно записать в виде
,
где — ускорение точки, F
= mg
sin=mg
— возвращающая сила. Знак минус в правой
части означает, что возвращающая сила
направлена противоположно смещению х.
Таким
образом, дифференциальное уравнение
гармонических колебаний математического
маятника
Сравнивая
это уравнение с уравнением (3), получаем
формулы для собственной частоты и
периода колебаний математического
маятника
и
.
Физический
маятник – это абсолютно твёрдое тело,
совершающее колебания относительно
горизонтальной оси О, не проходящей
через центр масс маятника С. Основное
уравнение динамики вращательного
движения для маятника Jε
= M,
где J
– момент инерции маятника относительно
горизонтальной оси проходящей через
точку О. Угловое ускорение маятника ε
.
Момент силы тяжести маятника относительно
горизонтальной оси, проходящей через
точку О M
= mgd
sinφ,
где m
– масса маятника, d
= CO
– расстояние от оси до центра масс
маятника С. При малых углах отклонения
маятника от вертикали можно считать,
что
Подставляя
всё в уравнение второго закона Ньютона,
получаем
.
Минус
означает, что момент возвращающей силы
противоположен угловому перемещению.
Отсюда получаем
Это
дифференциальное уравнение гармонических
колебаний физического маятника. Из
сравнения этого уравнения с уравнением
(3), находим период колебаний физического
маятника
Приведенная
длина физического маятника
— это длина нити математического маятника,
у которого период колебаний совпадает
с периодом данного физического маятника.
Колебания называются
собственными,
если они совершаются за счет первоначально
сообщенной энергии при последующем
отсутствии внешних воздействий на
колебательную систему.
Соседние файлы в папке Лекции по физике
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Частота колебаний, формула
Частота колебаний — это число циклов периодического процесса совершенных за одну секунду. Обозначается буквой f.
Единица измерения частоты:
[ 1 enspace [цикл enspace в enspace секунду] = 1 enspace [Герц] ]
Свое название данная единица измерения получила в честь немецкого физика Генриха Рудольфа Герца, который производил опыты с электрическими колебаниями.
Частота колебаний, формула
Чтобы определить частоту колебаний необходимо взять известный временной интервал и подсчитать количество циклов которые совершит система за это время.
Если
| ∆t | определенный временной интервал, | секунд |
|---|---|---|
| N | количество циклов, | шт. |
| T | период колебаний, | секунд |
то
[ f = frac{N}{∆t} = frac{1}{T} ]
Пример определения частоты колебаний
Повторим опыт описанный в периоде колебаний. Тогда у нас получились следующие цифры: N = 10 циклов, ∆t = 14.35 секунд,
соответственно приблизительная частота колебаний нити 0.697 Герц.
Вычислить, найти частоту колебаний по формуле 1
Как найти частоту колебаний через период
Частота колебаний, формула |
стр. 534 |
|---|