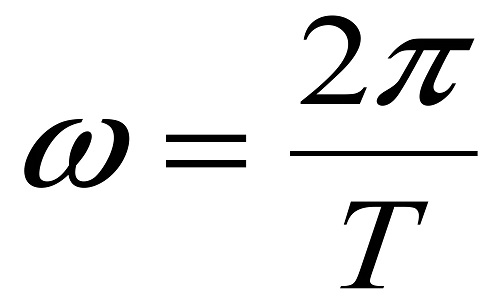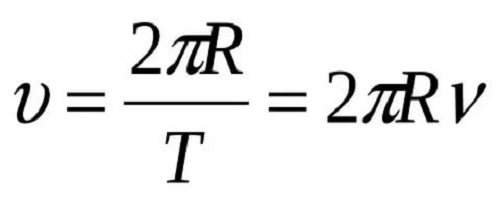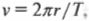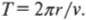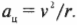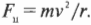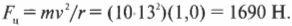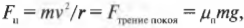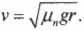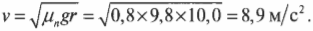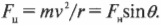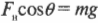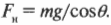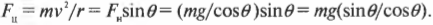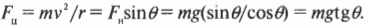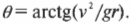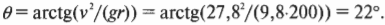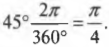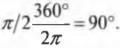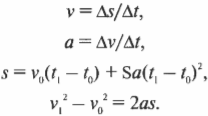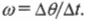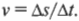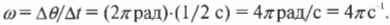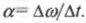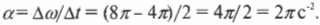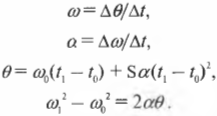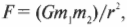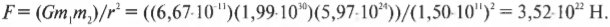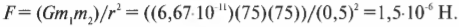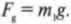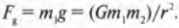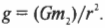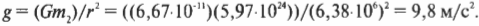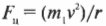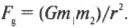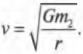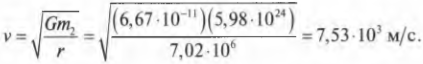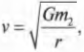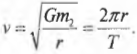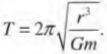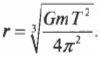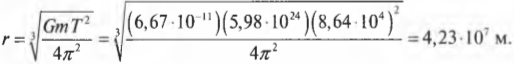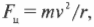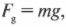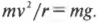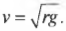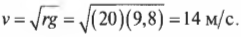поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,985 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
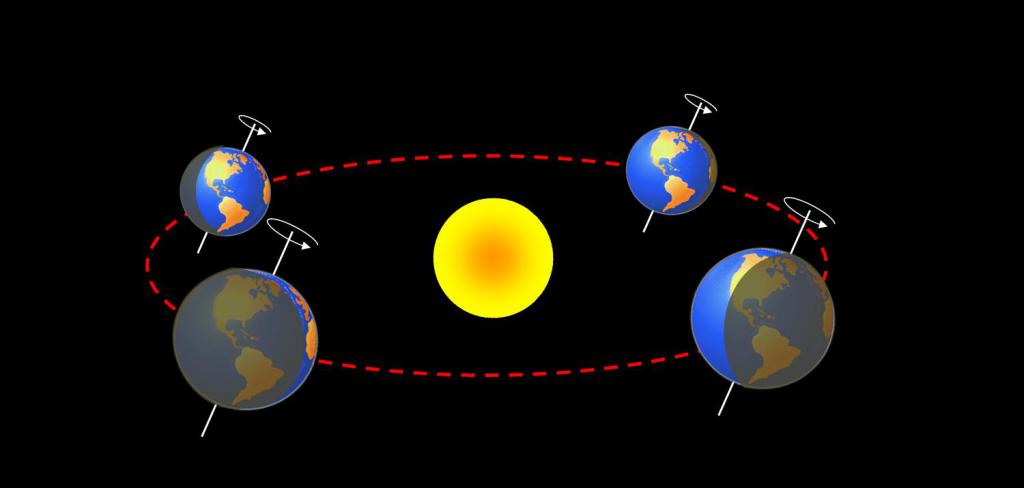
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Исследовательская работа «Определение линейной и угловой скоростей точки, равномерно движущейся по окружности»
ОГЭ 2021 по физике ›
1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.
При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.
2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности ( T ) — время, в течение которого тело совершает один полный оборот. Единица периода — ( [,T,] ) = 1 с.
Частота обращения ( (n) ) — число полных оборотов тела за одну секунду: ( n=N/t ). Единица частоты обращения — ( [,n,] ) = 1 с-1 = 1 Гц (герц). Один герц — это такая частота, при которой тело совершает один оборот за одну секунду.
Связь между частотой и периодом обращения выражается формулой: ( n=1/T ).
Пусть некоторое тело, движущееся по окружности, за время ( t ) переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол ( varphi ).
Быстроту обращения тела характеризуют угловая и линейная скорости.
Угловая скорость ( omega ) — физическая величина, равная отношению угла поворота ( varphi ) радиуса-вектора к промежутку времени, за которое этот поворот произошел: ( omega=varphi/t ). Единица угловой скорости — радиан в секунду, т.е. ( [,omega,] ) = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен ( 2pi ). Поэтому ( omega=2pi/T ).
Линейная скорость тела ( v ) — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.
Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: ( vec=l/t ). За один оборот точка проходит путь, равный длине окружности. Поэтому ( vec=2pi!R/T ). Связь между линейной и угловой скоростью выражается формулой: ( v=omega R ).
Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.
4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: ( vec=frac<Deltavec> ) и направлено так же, как вектор изменения скорости. Это ускорение называется центростремительным ускорением.
Центростремительное ускорение при равномерном движении тела по окружности — физическая величина, равная отношению квадрата линейной скорости к радиусу окружности: ( a=frac ). Так как ( v=omega R ), то ( a=omega^2R ).
При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности.
Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T
. Путь, который преодолевает точка — это есть длина окружности.
Общие понятия
Кинематика, входящая в состав механики, занимается изучением закономерностей движения. Под этим понятием понимается изменение положения тела относительно других объектов. Основная задача науки состоит в определении координат рассматриваемого предмета в любой момент. Кинематика изучает перемещение без учёта воздействия его вызвавшего. Любое движение считается относительным. Поэтому для его описания используют систему координат с начальной и конечной точкой отсчёта.
Для облегчения понимания процессов размерами исследуемого тела пренебрегают. Считая, что любой объект представляет собой совокупность материальных точек, повторяющих одинаковое движение при сравнении с друг другом. Существует несколько видов изменения положения. Различают их по траектории — воображаемой линии, повторяющей путь прохождения объекта. Сравнивая виды движения, выделяют два типа перемещения: прямолинейное и криволинейное.
Кроме этого, если рассматривать изменение положения во времени, движение можно различать по равномерности. При перемещении с постоянной скоростью движение называют равномерным, а при изменении её — неравномерным.
Более узкая классификация разделяет перемещение по характеру на следующие виды:
- равноускоренное — это перемещение, обусловленное движением тела, при котором ускорение будет постоянным по направлению;
- равнозамедленное — движение, при котором происходит отрицательное ускорение, до полного замедления объекта;
- равнопеременное — при таком виде перемещения скорость изменяется на одинаковое значение в любом промежутке времени;
- поступательное — если на перемещаемое тело нанести линии, они будут перемещаться параллельно сами себе;
- вращательное — это периодическое движение, при котором материальная точка описывает окружность.
Частным случаем криволинейного движения, то есть по траектории, отличной от прямой линии, является равномерное движение по окружности. Определение понятия включает в себя центростремительное ускорение и постоянную по модулю скорость. Под этим видом понимают изменение положения, при котором изменяется только направление скорости.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение тел
Под вращением понимают тип движения, при котором траектория перемещающегося тела представляет собой окружность. Вращение может происходить вокруг оси или вокруг фиксированной точки. Вращение колеса, планет по своим орбитам, спортсменов во время соревнований по фигурному катанию — все это примеры указанного типа движения.
По аналогии с линейным перемещением, главной формулой динамики вращения является следующая:
Здесь M и I — моменты силы и инерции, соответственно, α — ускорение угловое.
Для описания вращения удобно пользоваться не линейной, а угловой скоростью. Она определяется так:
Где θ — угол, на который тело повернулось за время t. С записанным ускорением α скорость ω связана следующим равенством:
Для измерения всех угловых величин используются радианы.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Основные понятия и законы динамики
Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой
Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано. Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется
инертностью.
Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией.
Инерциальными системами отсчёта
называют системы, в которых выполняется первый закон Ньютона.
Принцип относительности Галилея:
во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законам
Масса
— это мера инертности тела
Сила
— это количественная мера взаимодействия тел.
Второй закон Ньютона:
Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой: $F↖ <→>= m⋅a↖<→>$
Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.
Третий закон Ньютона:
Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению: $F_1↖ <→>= -F_2↖ <→>$
III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело A (см. рис.).
Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места. Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости
записывают в виде где k — жёсткость пружины, x — деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.
При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения.
Различают трение покоя и трение скольжения.
Сила трения скольжения
подсчитывается по формуле где N — сила реакции опоры, µ — коэффициент трения. Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.
возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значения
называют силы, с которыми любые два тела притягиваются друг к другу.
Закон всемирного тяготения:
любые два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
Здесь R — расстояние между телами. Закон всемирного тяготения в таком виде справедлив либо для материальных точек, либо для тел шарообразной формы.
называют силу, с которой тело давит на горизонтальную опору или растягивает подвес.
— это сила, с которой все тела притягиваются к Земле: При неподвижной опоре вес тела равен по модулю силе тяжести: Если тело движется по вертикали с ускорением, то его вес будет изменяться. При движении тела с ускорением, направленным вверх, его вес Видно, что вес тела больше веса покоящегося тела.
При движении тела с ускорением, направленным вниз, его вес В этом случае вес тела меньше веса покоящегося тела.
называется такое движение тела, при котором его ускорение равно ускорению свободного падения, т.е. a = g. Это возможно в том случае, если на тело действует только одна сила — сила тяжести.
Искусственный спутник Земли
— это тело, имеющее скорость V1, достаточную для того, чтобы двигаться по окружности вокруг Земли На спутник Земли действует только одна сила — сила тяжести, направленная к центру Земли
Первая космическая скорость
— это скорость, которую надо сообщить телу, чтобы оно обращалось вокруг планеты по круговой орбите. где R — расстояние от центра планеты до спутника. Для Земли, вблизи её поверхности, первая космическая скорость равна
1.3. Основные понятия и законы статики и гидростатики
Тело (материальная точка) находится в состоянии равновесия, если векторная сумма сил, действующих на него, равна нулю. Различают 3 вида равновесия: устойчивое, неустойчивое и безразличное.
Если при выведении тела из положения равновесия возникают силы, стремящиеся вернуть это тело обратно, это
устойчивое равновесие.
Если возникают силы, стремящиеся увести тело ещё дальше из положения равновесия, это
неустойчивое положение
; если никаких сил не возникает —
безразличное
(см. рис. 3). Когда речь идёт не о материальной точке, а о теле, которое может иметь ось вращения, то для достижения положения равновесия помимо равенства нулю суммы сил, действующих на тело, необходимо, чтобы алгебраическая сумма моментов всех сил, действующих на тело, была равна нулю. Здесь d —плечо силы.
Плечом силы
d называют расстояние от оси вращения до линии действия силы.
Условие равновесия рычага:
алгебраическая сумма моментов всех вращающих тело сил равна нулю.
Давлением
называют физическую величину, равную отношению силы, действующей на площадку, перпендикулярную этой силе, к площади площадки:
Для жидкостей и газов справедлив закон Паскаля:
давление распространяется по всем направлениям без изменений. Если жидкость или газ находятся в поле силы тяжести, то каждый вышерасположенный слой давит на нижерасположенные и по мере погружения внутрь жидкости или газа давление растёт. Для жидкостей где ρ — плотность жидкости, h — глубина проникновения в жидкость.
Однородная жидкость в сообщающихся сосудах устанавливается на одном уровне. Если в колена сообщающихся сосудов залить жидкость с разными плотностями, то жидкость с большей плотностью устанавливается на меньшей высоте. В этом случае Высоты столбов жидкости обратно пропорциональны плотностям:
представляет собой сосуд, заполненный маслом или иной жидкостью, в котором прорезаны два отверстия, закрытые поршнями. Поршни имеют разную площадь. Если к одному поршню приложить некоторую силу, то сила, приложенная ко второму поршню, оказывается другой. Таким образом, гидравлический пресс служит для преобразования величины силы. Поскольку давление под поршнями должно быть одинаковым, то
На тело, погружённое в жидкость или газ, со стороны этой жидкости или газа действует направленная вверх выталкивающая сила, которую называют
силой Архимеда
Величину выталкивающей силы устанавливает
закон Архимеда
: на тело, погружённое в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости или газа, вытесненного телом: где ρжидк — плотность жидкости, в которую погружено тело; Vпогр — объём погружённой части тела.
Условие плавания тела
— тело плавает в жидкости или газе, когда выталкивающая сила,действующая на тело, равна силе тяжести, действующей на тело.
1.4. Законы сохранения
Импульсом тела
называют физическую величину, равную произведению массы тела на его скорость:
Импульс — векторная величина.
=кг·м/с. Наряду с импульсом тела часто пользуются импульсом силы.
Это произведение силы на время её действия Изменение импульса тела равно импульсу действующей на это тело силы. Для изолированной системы тел (система, тела которой взаимодействуют только друг с другом) выполняется
закон сохранения импульса
: сумма импульсов тел изолированной системы до взаимодействия равна сумме импульсов этих же тел после взаимодействия.
Механической работой
называют физическую величину, которая равна произведению силы, действующей на тело, на перемещение тела и на косинус угла между направлением силы и перемещения:
— это работа, совершённая в единицу времени:
Способность тела совершать работу характеризуют величиной, которую называют энергией.
Механическую энергию делят на
кинетическую и потенциальную.
Если тело может совершать работу за счёт своего движения, говорят, что оно обладает
кинетической энергией.
Кинетическая энергия поступательного движения материальной точки подсчитывается по формуле Если тело может совершать работу за счёт изменения своего положения относительно других тел или за счёт изменения положения частей тела, оно обладает
потенциальной энергией.
Пример потенциальной энергии: тело, поднятое над землёй, его энергия подсчитывается по формуле где h — высота подъёма
Энергия сжатой пружины:
где k — коэффициент жёсткости пружины, x — абсолютная деформация пружины.
Сумма потенциальной и кинетической энергии составляет механическую энергию.
Для изолированной системы тел в механике справедлив
закон сохранения механической энергии
: если между телами изолированной системы не действуют силы трения (или другие силы, приводящие к рассеянию энергии), то сумма механических энергий тел этой системы не изменяется (закон сохранения энергии в механике). Если же силы трения между телами изолированной системы есть, то при взаимодействии часть механической энергии тел переходит во внутреннюю энергию.
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
При равномерном движении по окружности вектор скорости тела меняется (скорость направлена по касательным к окружности), а модуль скорости тела (числовое значение) остается постоянным. Поэтому если один полный оборот тела по окружности обозначить как s (пройденный путь), а время, за которое он был совершен, как t, то найдем модуль скорости тела, движущегося равномерно по окружности:





Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости — радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Мгновенная и средняя скорости
Как найти линейную скорость? Формулу, согласно определению величины, можно записать следующую:
Где dl¯ — вектор перемещения тела за время dt. Эта скорость называется мгновенной, поскольку рассчитывается за чрезвычайно короткий промежуток времени dt. Мгновенная скорость в действительности является величиной не стабильной и постоянно меняющейся. Например, представим, что по дороге движется автомобиль. На первый взгляд можно полагать, что в любой момент времени его мгновенная скорость будет постоянной, однако, это не так. Мгновенная скорость испытывает колебания. Если спидометр автомобиля достаточно чувствителен, то он фиксирует эти колебания.
Формула линейной скорости средней ничем не отличается от таковой для мгновенной, однако, измеряется она за более длительный промежуток времени Δt:
В примере с автомобилем выше, хотя мгновенная скорость испытывает колебания, средняя скорость остается постоянной с определенной точностью на всем участке пути Δl¯.
При решении задач, как правило, используют среднюю скорость. Мгновенная же величина имеет смысл только в случае движения с ускорением.
Занимательный пример
Пусть имеется некая планета, которая совершила полтора оборота за сорок два часа, при этом метеостанция, располагающаяся на её экваторе, прошла путь равный 50 тыс. километров, делённых на час. Нужно определить линейную и угловую скорости планеты при её вращении вокруг собственной оси. Кроме этого, вычислить, чему равны сутки, и найти радиус планеты. При этом считать, что форма космического тела — идеальный шар.
Для решения задачи следует обозначить буквой эн число оборотов: n = 1,5, а t — время, за которое планета их совершила. Путь же, который прошла станция, можно представить в виде материальной точки и принять за l = 50 000 км. Найти же будет нужно линейную и угловую скорости. Кроме этого, по условию задачи нужно найти сутки, длина которых равняется периоду — полному обороту планеты вокруг оси.
В такой задаче необязательно переводить данные в систему СИ. Можно использовать километры и часы, так как в задании не требуется дать ответ в соответствии с СИ, тем более что метры и секунды использовать неудобно.
Первое, что можно найти, это линейную скорость, равную отношению пройденного пути ко времени: v = l / t = 50000 / 42. Решив дробь, примерный результат будет равняться 1190 км /ч. Теперь можно найти скорость угла поворота. Нужно разделить угол, на который изменилось положение точки, на время. Так как один полный оборот — это 2p, то полтора оборота будут составлять 3p. Тогда искомая скорость будет равняться: w = φ / t = 3p / 42 = 0,22 рад/ч.
Сутки, то есть период обращения, будут определяться как полный период вращения, который можно разделить на число оборотов за это время. Формула для расчёта будет выглядеть следующим образом: T = t / N. Подставив значения, можно найти искомый период. Он будет составлять: T = 42 / 1,5 = 28 часов.
Осталось вычислить радиус, который равняется отношению линейной скорости к угловой: R = v / w. Так как в качестве ответов записывались примерные значения, то для предотвращения арифметической ошибки подставлять уже найденные числа не следует. Поэтому лучше подставить алгебраические выражения. Тогда: R = (l /t) / (φ / t) = l / φ = 50000 / 3p = 5305 км. Задача решена.
http://svet202.ru/teoriya/formula-skorosti-cherez-radius.html
Мы уже рассчитывали линейную и угловую скорости вращения Земли вокруг своей собственной оси. Давайте сегодня рассмотрим движение Земли вокруг Солнца, и найдем скорость этого движения. Ну, и заодно, рассмотрим три закона Кеплера. Куда без них.
Первый способ
С какой скоростью вращается Земля вокруг Солнца? Первое что приходит в голову, это воспользоваться уже знакомым уравнением для нахождения линейной скорости:
Расстояние от Земли до Солнца одна астрономическая единица или 149 597 870 700 м. Период обращения составляет один год. Если перевести это в секунды мы получим 31 536 000 с.
Подставляем это все в наше уравнение и считаем.
м/с
Второй способ
Но можно и пойти другим путем. Скорость движения Земли будет являться первой космической скоростью в поле тяготения Солнца. По этому, вспоминаем уравнение для нахождения первой космической скорости.
Где G -это гравитационная постоянная, R — расстояние от Земли до Солнца, ну и M — масса самого Солнца. Остается только взвесить Солнце и произвести расчет:
м/с
Часто для удобства скорость округляют и представляют как 30 км/с или 108 000 км/ч. Последний вариант, кстати, очень любят индусы. Так как в индуизме число 108 считается священным. Они даже число Пи, в свое время, определяли как отношение 339/108. Но вернемся к скорости.
Первый закон Кеплера
В наших расчетах мы принимали что Земля равномерно движется по окружности. Хотя в реальности это не совсем так.
Еще в начале XVII века немецкий астроном Иоганн Кеплер, опираясь на данные многолетних наблюдений за планетой Марс, полученные его учителем — датским астрономом Тихо Браге, заключил, что все планеты солнечной системы движутся не по окружности, а по эллипсу, в одном из фокусов которого находится Солнце. Этот закон называют первым законом Кеплера.
Все планеты Солнечной Системы движутся по эллипсу, в одном из фокусов которого находится Солнце.
Так что давайте разобраться что такое такое эллипс, и в чем его фокус.. или фокусы.
Что такое эллипс?
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами.
Рассмотрим все на простом примере. Берем шнурок с канцелярскими кнопками-гвоздиками на концах. Втыкаем кнопки в кусок гипсокартонна, который завалялся в гараже после ремонта.
Далее карандашом, опираясь на шнурок рисуем линии. Получившаяся фигура и есть эллипс, а точки куда мы втыкали кнопки называются фокусами.
Большая и малая полуось
Важными характеристиками эллипса являются его полуоси. Большая ее обычно обозначают латинской буквой «a», и малая, которую обозначают буквой «b». Тоже латинской.
Большая полуось — это расстояния от центра эллипса до самой дальней его точки. Соответственно, малая полуось — это расстояние от центра до самой ближней точки эллипса.
Эксцентриситет
Еще одна важная характеристика эллипса носит шикарное название — эксцентриситет. Его обычно обозначают буквой «е» и определяют как отношение фокусного расстояния эллипса (c) к большой полуоси (a).
Эллипс иногда называют сплющенной окружностью. Так вот эксцентриситет как раз показывает насколько эта окружность сплющена.
Для эллипса:
Чем ближе эксцентриситет к единице, тем более вытянутый эллипс мы получим. И наоборот эксцентриситет близкий к 0, будет иметь эллипс ну очень похожий на окружность. В принципе можно сказать что окружность это эллипс с е=0.
В солнечной системе самый маленький эксцентриситет у Венеры всего 0,007, то есть траектория ее движения это практически окружность. Эксцентриситет близкий к единице имеют кометы. К примеру у кометы Галея е=0,967.
Что же касается Земли, то эксцентриситет земной орбиты тоже очень близок к нулю, всего 0,017. Но тем не менее это не ноль. А это значит что расстояние от Земли до Солнца величина отнюдь не постоянная.
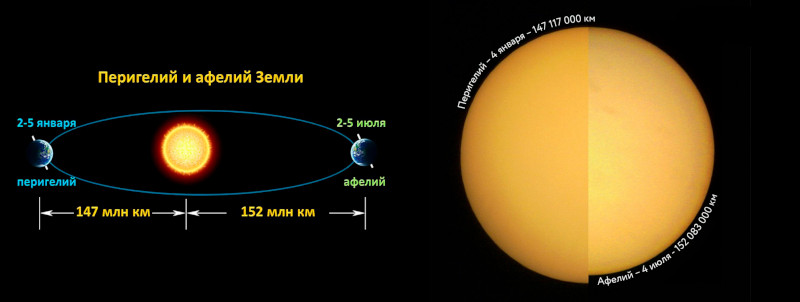
Афелий и перигелий
Точка в которой планета находится ближе всего к Солнцу называется перигелий. От греческого perihelion, “peri“ — рядом и “helios“ — Солнце. Противоположная перигелию точка называется афелий. Соответственно это точка где планета максимально удалена от светила.
Земля находится перигелии, начале января. Она приближается к Солнцу на расстояние в 147,1 миллионов километров. Афелий она проходит в начале июля, когда удаляется на 152,1 миллионов километров. Разница выходит около 5 миллионов километров.
Этим иногда объясняют то что зимы в северном полушарии менее суровые, нежели в южном. Все таки зимой мы чуть ближе к солнцу. С другой стороны так как земля получает меньше солнечной энергии в июле, лето в северном полушарии более прохладное.
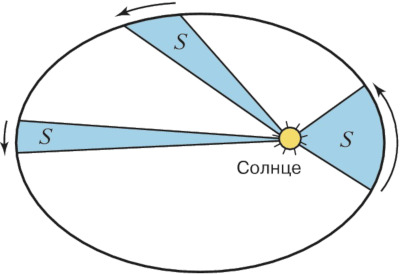
Второй закон Кеплера
Итак, мы сказали что согласно первому закону Кеплера Земля движется не по круговой, а по эллиптической орбите. Что же касается ее скорости, то она возрастает при приближении к Солнцу, и убывает при удалении от него.
Кеплер сформулировал это следующим образом:
За одинаковые промежутки времени радиус-вектор планеты описывает одинаковые площади.
Это так называемый закон площадей или второй закон Кеплера, пожалуй в самой бесполезной его формулировке. Но фактически мы имеем дело с законом сохранения момента импульса. И куда больший интерес для нас будет иметь следующее уравнение:
Произведение линейной скорости и радиус-вектора в перигелии, равно произведению скорости и радиус-вектора афелии. Это частный случай второго закона Кеплера, соответственно для максимального и минимального значений скорости движения планеты.
Максимальная и минимальная скорость движения Земли
Зная это можно, рассчитать с какими скоростями движется Земля перигелии и афелии. То есть найти ее максимальную и минимальную скорости. Но здесь нам понадобится закон сохранения энергии.
А так же, формулы для определения расстояний от солнца до афелия и перигелия, через эксцентриситет и большую полуось:
Ну и пожалуй уравнение для нахождения первой космической скорости.
Единственное в формуле расстояние R мы заменим на a, то есть на большую полуось. Большая полуось земной орбиты — это среднее расстояние от Земли до Солнца, и именно значение большой полуоси мы использовали в расчетах в самом начале. А значит скорость которую мы рассчитывали в самом начале есть средняя орбитальная. Она нам пригодится.
Составляем небольшую систему уравнения и с точки зрения физики задача решена. Остается только математика.
Начнем с того, что сократим массу Земли в законе сохранения энергии, а так же заменим радиус векторы на, соответственно,
,
.
Если внимательно посмотреть, то можно увидеть что в отношениях , и
,
, это квадрат средней орбитальной скорости
. А ее мы уже рассчитали в самом начале. Так что здесь удобно будет выполнить замену.
Теперь из первого уравнения выражаем , и подставляем это все во второе. Делаем все необходимые преобразования и выражаем
:
Ну и теперь так же выражаем :
Остается только подставить значения, и посчитать.
м/с
м/с
Третий закон Кеплера
Опубликовав в 1609 г. два своих закона Иоганн Кеплер так и не остался удовлетворен, и продолжил поиски, которые спустя десять лет привели его к открытию третьего закона.
Квадраты звездных периодов обращений планет относятся между собой как кубы больших полуосей их орбит.
Но это уже совсем другая история…
Как известно, наша планета движется, и не только вокруг Солнца, но и вокруг своей оси. Вдобавок, мы знаем, что для любого движения характерна определённая скорость, которая может зависеть (как и само движение) от различных факторов. Следовательно, вращение Земли также имеет свою скорость.
Скорость — это векторная физическая величина, характеризующая быстроту перемещения материальной точки за любой отрезок времени относительно величины промежутка.
Скорость вращения Земли
Правда, земная скорость — вещь относительна. Так как для её расчёта нужна определённая точка отсчёта. Например, для того, чтобы вычислить с какой скоростью движется Земля вокруг своей оси, такой точкой является центр планеты.
Однако, говоря о подобном параметре земельного кружения, важно знать, что скорость разделяют на угловую и линейную.
Угловая скорость
Это величина, которая равна отношению угла тела к отрезку времени, затраченному на этот поворот. Можно сказать, что это быстрота изменения угла тела за промежуток времени. Выражается она в радианах в секунду, и для всех точек имеет постоянное значение.
Как выяснилось, на полный оборот нашей планеты вокруг своей оси требуется 23 часа 56 минут 4,09053 секунды. Проще говоря, одни звездные сутки.
Формула угловой скорости: отношение изменения угла за время.
Так как земной оборот равен 360 градусов или 2π (2*3,14=6,28), а время этого оборота в секундах 86344, то угловая скорость вращения Земли вокруг своей оси приблизительно равна 7,26851851851-5с-1.
Линейная скорость
Такую характеристику применяют для того, чтобы выразить темп движения по окружности. Как известно, при круговом вращении тела его разные точки имеют разные скорости. Хотя угловая величина перемещения для них остаётся неизменной.
А это значит, что скорость вращения Земли равна примерно 465 м/сек. То есть расчет производится путём деления окружности на время, затраченное на весь оборот.
Однако скорость движения Земли изменяется, потому как её окружность также меняется относительно широты. Ведь радиус планеты уменьшается к полюсам. Соответственно, на разных широтах разный темп вращения. Другими словами, где меньший радиус медленнее и скорость. К примеру, на полюсах она почти нулевая, а на экваторе составляет 1674 км/час.
Для того, чтобы рассчитать скорость вращения Земли на другой широте, необходимо косинус выбранной широты умножить на экваторную скорость. Например, быстроту движения планеты на широте 30 градусов мы вычислим, если косинус 30 градусов, который равен 0,866, умножим на 1674. Таким образом, получаем 1449,7 км/час.
С какой скоростью Земля движется относительно Солнца
Поскольку наша планета, как и другие планеты звездной группы, движутся вокруг Солнца, у данного движение также есть своя скоростная величина.
На полный оборот вокруг главного светила уходит 365 дней 5 часов 48 минут и 46 секунд. Хотя мы привыкли округлять и говорить просто один год. Между прочим за каждый такой год накапливается по пять часов, так сказать, лишних. Но и им нашли место, их объединяют и каждому следующему четвертому году добавляют один день. Наверняка вы догадались, что такие года называются високосными.
На основании данных о времени полного оборота планеты вокруг Солнца, не трудно вычислить с какой быстротой она движется относительно него. Следует учитывать, что двигаемся мы по орбите. А значит определяем с какой скоростью Земля летит именно по орбите.
Как рассчитать темп земного движения вокруг Солнца
Для этого необходимо радиус орбиты или расстояние до Солнца (≈150 млн км) умножить на 2π (23,14=6,28), что составляет 942 млн км. Все это разделим на время, затраченное на этот промежуток (365 дней 24 часа*3600 секунд=31 536 000 секунд). В итоге получаем 29,87 км в секунду.
Принято считать, что средняя скорость Земли по орбите (по окружности Солнца) равна 30 км/сек.
По данным учёных, скорость вращения Земли вокруг своей оси постепенно уменьшается. Причем наблюдаются пятилетние циклы то ускорения, то замедления движения планеты. Но объяснить по какой причине происходят такие изменения пока не получается. Поэтому за движением нашей планеты ведётся постоянное наблюдение и мониторинг. Возможно, отыщется какая-либо взаимосвязь данного явления.
В этой главе. . .
- Постигаем равномерное вращательное движение
- Изучаем угловое ускорение
- Испытываем влияние центростремительной силы
- Учитываем перемещение, скорость и ускорение
- Движемся по орбите под действием законов Ньютона и силы гравитационного притяжения
- Поддерживаем вращение в вертикальной плоскости
Вращательное движение выполняют искусственные спутники вокруг планет, гоночные автомобили по трекам и даже пчелы вокруг ульев. В предыдущих разделах рассматривались такие характеристики прямолинейного движения, как перемещение, скорость и ускорение. В этой главе мы снова рассмотрим их, но теперь уже для вращательного движения.
Для перечисленных выше характеристик прямолинейного движения есть аналоги, характеризующие вращательное движение, а именно: угловое перемещение, угловая скорость и угловое ускорение. Как видно из их названия, роль перемещения во вращательном движении играет угол. Угловая скорость обозначает величину угла поворота за единицу времени, а угловое ускорение — изменение угловой скорости за единицу времени. Все, что нужно сделать, чтобы освоить премудрости вращательного движения, это взять уравнения прямолинейного движения и заменить в них одни характеристики другими: перемещение поменять на угол, скорость — на угловую скорость и ускорение — на угловое ускорение.
Содержание
- Держим курс: равномерное вращательное движение
- Меняем направление: центростремительное ускорение
- Управляем скоростью с помощью центростремительного ускорения
- Определяем величину центростремительного ускорения
- Стремимся к центру: центростремительная сила
- Вписываемся в повороты: учитываем радиус и наклон
- Вращательное движение: перемещение, скорость и ускорение
- Бросаем яблоко: закон всемирного тяготения Ньютона
- Вычисляем силу гравитационного притяжения на поверхности Земли
- Исследуем орбитальное движение с помощью закона всемирного тяготения
- Вычисляем скорость спутника
- Вычисляем период обращения спутника
- Вращаемся вдоль вертикальной плоскости
Держим курс: равномерное вращательное движение
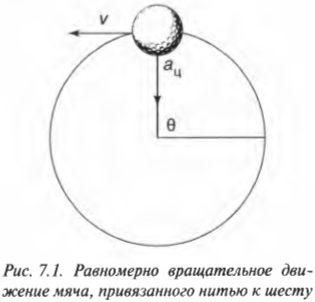
Если объект движется с постоянной по величине скоростью по окружности, то такое движение называется равномерным вращательным движением. Примерами такого движения являются движение гоночного автомобиля по круглому треку и стрелки на циферблате часов. На рис. 7.1 показан мяч для игры в гольф, привязанный нитью к шесту и совершающий движение по окружности. Мяч совершает движение с одинаковой по величине скоростью, но с изменяющимся направлением. Потому такое движение мяча называется равномерным вращательным движением.
Время, которое требуется мячику (или какому-либо другому объекту), чтобы полностью обогнуть окружность, называется периодом и обозначается символом ( T ). Период и линейную скорость можно легко связать, если известно пройденное расстояние, т.е. длина окружности ( 2pi r ), а точнее ее радиус ( r ). Итак, линейная скорость мячика ( v ) равна:
а период вращения ( T ) равен:
Допустим, что длина нити равна 1 м, а период вращения равен 0,5 с. Чему в таком случае будет равна линейная скорость мячика? Подставим численные значения в одно из предыдущих соотношений и получим:
Итак, мячик вращается с линейной скоростью 13 м/с!
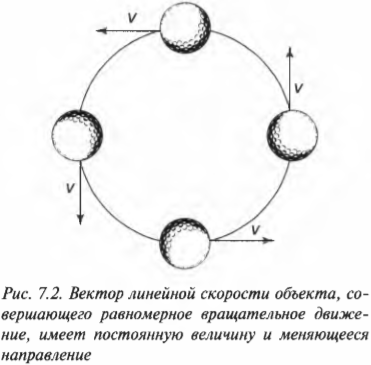
Меняем направление: центростремительное ускорение
При вращательном движении по окружности линейная скорость мячика постоянно меняет направление, как показано на рис. 7.2. Ускорение, характеризующее такое изменение скорости, называется центростремительным (или центробежным). В любой точке вращательного движения с постоянной величиной и меняющимся направлением вектор линейной скорости перпендикулярен радиусу.
Это правило справедливо для всех объектов: вектор линейной скорости объекта, равномерно вращающегося по окружности, всегда перпендикулярен радиусу окружности.
Если в показанных на рис. 7.2 положениях нить, удерживающая мяч, оборвется, то куда полетит мяч? Если в этот момент вектор линейной скорости направлен влево, то мяч полетит влево, а если этот вектор направлен вправо, то мяч полетит вправо, и т.д. Этот, казалось бы, простой и интуитивно понятный момент часто вызывает трудности у тех, кто впервые постигает физику.
Всегда следует помнить, что вектор линейной скорости объекта, выполняющего равномерное вращательное движение, всегда направлен под прямым углом к радиусу вращения в текущей точке траектории. (В общем случае неравномерного криволинейного движения эта компонента вектора скорости, перпендикулярная радиусу вращения и касательная к траектории движения, называется тангенциальной компонентой, а перпендикулярная ей компонента — нормальной компонентой. — Примеч. ред.)
Управляем скоростью с помощью центростремительного ускорения
Особенностью равномерного вращательного движения является постоянство величины линейной скорости. Это значит, что вектор ускорения не имеет компоненты, параллельной вектору линейной скорости, поскольку в противном случае величина линейной скорости менялась бы. Однако при равномерном вращательном движении меняется только направление линейной скорости. Такое изменение линейной скорости поддерживается центростремительным ускорением, направленным к центру окружности вращения и перпендикулярно вектору линейной скорости.
В примерах на рис. 7.1 и 7.2 на мяч со стороны нити действует сила натяжения нити, которая поддерживает его движение по окружности. Именно эта сила сообщает мячу центростремительное ускорение ( a_ц ), вектор которого показан на рис. 7.1. (Попробуйте раскрутить мяч с помощью привязанной к нему нити, и вы сразу же почувствуете действие этой силы со стороны нити.)
Часто возникает вопрос: если вектор ускорения мяча направлен к центру окружности, то почему мяч не движется к центру? Дело в том, что при равномерном вращательном движении это ускорение меняет только направление, а не величину линейной скорости.
Определяем величину центростремительного ускорения
Нам уже известно направление вектора центростремительного ускорения, а чему же равна его величина? Итак, величина центростремительного ускорения объекта, равномерно движущегося с линейной скоростью ( v ) по окружности с радиусом ( r ), равна:
Как видите, величина центростремительного ускорения обратно пропорциональна радиусу окружности ( r ) и прямо пропорциональна квадрату скорости ( v ). Поэтому не удивительно, что автомобиль на более крутых поворотах испытывает более сильное центростремительное ускорение.
Стремимся к центру: центростремительная сила
На крутых поворотах действие центростремительного ускорения обеспечивается трением шин по дороге. Какую силу нужно приложить, чтобы удержать движущийся со скоростью ( v ) автомобиль на повороте с радиусом кривизны ( r )?
Допустим, что в примере на рис. 7.1 легкий мяч заменили на тяжелое пушечное ядро. Теперь, чтобы поддерживать движение ядра по окружности с тем же радиусом и периодом вращения, потребуется гораздо большая сила.
Дело в том, что сила ( F=ma ) равна произведению ускорения ( a ) и массы ( m ), а значит, увеличение массы объекта (замена мяча на ядро) неизбежно приводит к необходимости увеличения силы для обеспечения прежнего ускорения.
Центростремительная сила ( F_ц ), необходимая для равномерного вращения по окружности с радиусом ( r ) объекта массой ( m ) с постоянной скоростью ( v ), равна:
С помощью этого уравнения можно легко определить силу, необходимую для равномерного вращения объекта по окружности с известной массой, скоростью и радиусом окружности.
Обратите внимание, что если объект движется по той же окружности, но с разной скоростью, то он будет испытывать разную центростремительную силу.
В примерах на рис. 7.1 и 7.2 мяч движется со скоростью ( v ) = 13 м/с и удерживается нитью длиной 1,0 м, т.е. в данном случае радиус окружности ( r ) = 1 м. Какая сила потребуется, чтобы поддерживать такое же движение для пушечного ядра с массой 10 кг? Подставляя численные значения в уже известную нам формулу, получим:
Приличная сила! Остается только надеяться, что ваши руки достаточно сильны, чтобы удержать ядро.
Является ли центростремительная сила реальной силой?
Центростремительная сила не является каким-то особым типом взаимодействия. Она имеет отношение только к объекту, движущемуся по криволинейной траектории, и необходима для удержания объекта на данной траектории. Поэтому ее часто называют центростремительно-необходимой силой. Довольно часто новички считают центростремительную силу каким-то новым фундаментальным типом взаимодействия. И это понятно, поскольку известные нам силы (например, сила гравитации и сила трения) имеют вполне определенный источник, который не зависит от траектории движения. Но это совсем не так для центростремительной силы. Центростремительная сила возникает из необходимости удержания объекта на криволинейной траектории. Сумма всех остальных сил, действующих на объект, который движется по криволинейной траектории, должна быть равна центростремительной силе. (Если объект движется по прямолинейной траектории, а затем ему нужно изменить направление движения, то для этого придется приложить силу, равную центростремительной силе. — Примеч. ред.)
Вписываемся в повороты: учитываем радиус и наклон
Если вам приходилось ехать на автомобиле или велосипеде или даже бежать трусцой, то наверняка вы заметили, что в крутой поворот проще вписаться, если поверхность дороги немного наклонена внутрь поворота. Из опыта известно, что чем больше наклон, тем проще вписаться в поворот. Это объясняется тем, что в таком случае на вас действует меньшая центростремительная сила. Центростремительная сила обеспечивается силой трения о поверхность дороги. Если поверхность дороги покрыта льдом, то сила трения становится меньше и потому часто не удается вписаться в поворот на обледеневшей дороге на большой скорости.
Представьте, что автомобилю с массой 1000 кг нужно вписаться в поворот с радиусом Юм, а коэффициент трения покоя (подробнее о нем см. главу6) равен 0,8. (Здесь используется коэффициент трения покоя, поскольку предполагается, что шины по поверхности дороги.) Какую максимальную скорость может развить этот автомобиль без риска не вписаться в поворот. Итак, сила трения покоя шин о поверхность дороги ( F_{трение,покоя} ) должна обеспечивать центростремительную силу:
где ( m ) — это масса автомобиля, ( v ) — его скорость, ( r ) — радиус, ( mu_п ) — коэффициент трения покоя, a ( g ) = 9,8 м/с2 — ускорение свободного падения под действием силы гравитации. Отсюда легко находим скорость:
(Обратите внимание, что максимальная безопасная скорость прохождения поворота не зависит от массы автомобиля. — Примеч. ред.)
Это выражение выглядит очень просто, а после подстановки в него численных значений получим:
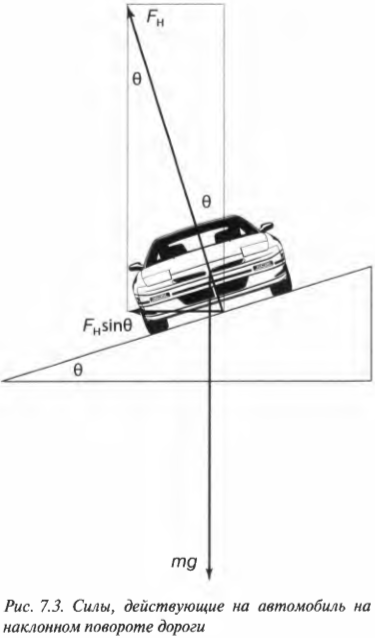
Итак, максимальная скорость безопасного проезда при таком повороте равна 8,9 м/с. Пересчитаем в единицы “км/ч”, в которых скорость указана на спидометре, и сравним. Получается, что 8,9 м/с = 32 км/ч, а на спидометре всего 29 км/ч. Прекрасно, но далеко не все водители умеют так быстро рассчитывать безопасную скорость прохождения поворотов. Поэтому конструкторы дорог часто строят повороты с наклоном внутрь, чтобы обеспечить центростремительное ускорение не только за счет силы трения, но и за счет горизонтальной компоненты силы гравитации.
На рис. 7.3 показан пример поворота дороги с некоторым наклоном под углом ( theta ) к горизонтали. Предположим, что конструкторы решили полностью обеспечить центростремительное ускорение только за счет горизонтальной компоненты силы гравитации (т.е. без учета силы трения) ( F_нsintheta ), где ( F_н ) — это нормальная сила (подробнее о ней см. в главе 6). Тогда:
В вертикальном направлении на автомобиль действует сила гравитации ( mg ), которая уравновешивается вертикальной компонентой нормальной силы ( F_нcostheta ):
или, иначе выражая это соотношение, получим:
Подставляя это выражение в прежнее соотношение между центростремительной силой и нормальной силой, получим:
Поскольку ( sintheta/!costheta=tg,theta ) в то
Отсюда легко получаем, что угол наклона поворота дороги ( theta ) равен:
Именно это уравнение используют инженеры при проектировании дорог. Обратите внимание, что масса автомобиля не влияет на величину угла, при котором центростремительная сила полностью обеспечивается только горизонтальной компонентой нормальной силы. Попробуем теперь определить величину угла наклона поворота с радиусом 200 м для автомобиля, движущегося со скоростью 100 км/ч или 27,8 м/с:
Для обеспечения безопасного движения автомобиля со скоростью 100 км/ч в повороте с радиусом 200 м без учета силы трения, инженеры должны создать наклон около 22°. Отлично, из вас может получиться неплохой инженер-конструктор автомагистралей!
Вращательное движение: перемещение, скорость и ускорение
Если вы привыкли решать задачи о прямолинейном движении типа “некто движется из пункта А в пункт Б”, то задачи о вращательном движении можно формулировать аналогично, но для этого нужно приобрести некоторый опыт. На рис. 7.1 мяч движется криволинейно по окружности, а не прямолинейно по линии. Это движение можно было бы описать как комбинацию прямолинейных движений с координатами X и Y. Однако гораздо удобнее характеризовать его иначе, а именно как вращательное движение с одной координатой ( theta ). В данном примере вращательного движения перемещение можно характеризовать углом ( theta ) так же, как в прямолинейном движении перемещение характеризуется расстоянием ( s ). (Более подробно перемещение при прямолинейном движении описывается в главе 3.)
Стандартной единицей измерения перемещения при вращательном движении является радиан (рад), а не градус. Полная окружность охватывает угол величиной ( 2pi ) радиан, что равно 360°. Соответственно, половина окружности охватывает угол величиной ( pi ) радиан, а четверть окружности — ( pi/2 ).
Как преобразуются величины углов из градусов в радианы и обратно? Достаточно определить, сколько радиан приходится на один градус, т.е. вычислить отношение ( 2pi )/360°. Например, величина угла 45° в радианах равна:
Аналогично, для преобразования величины угла из радианов в градусы следует определить, сколько градусов приходится на один радиан, т.е. вычислить отношение 360°/( 2pi ). Например, величина угла ( pi/2 ) в градусах равна:
Формулировка вращательного движения в терминах прямолинейного движения очень удобна. Напомним основные формулы прямолинейного движения, которые подробно описываются в главе 3:
Теперь для вывода аналогичных основных формул вращательного движения достаточно в формулах прямолинейного движения вместо расстояния ( s ), которое характеризует прямолинейное перемещение, подставить угол ( theta ), который характеризует угловое перемещение. А как определяется угловая скорость? Очень просто. Угловая скорость ( omega ) определяется аналогично, как изменение угла за единицу времени, и равна количеству радианов, пройденных за секунду:
Обратите внимание, как похоже это выражение для угловой скорости на выражение для линейной скорости:
Давайте теперь вычислим угловую скорость мяча на рис. 7.1. Он совершает полный круг, охватывающий ( 2pi ) радиан, за 1/2 с, а значит, его угловая скорость равна:
(Величина угла, выраженная в радианах, равна отношению длины дуги окружности к длине ее радиуса. Поэтому радиан — это безразмерная величина, и ее обозначение (рад) часто опускается. Соответственно, угловую скорость принято указывать “в обратных секундах” как с-1, т.е. без указания единицы измерения углов. — Примеч. ред.)
Угловое ускорение ( alpha ) определяется аналогично линейному ускорению:
Оно определяется как изменение угловой скорости за единицу времени и измеряется в радианах на секунду в квадрате. Если скорость за 2 с изменилась от величины ( 4pi c^{-1} ) до величины ( 8pi c^{-1} ), то чему равно угловое ускорение? Подставим эти численные значения в предыдущую формулу и получим:
Итак, для описания вращательного движения у нас есть следующие аналоги: для линейного перемещения ( s ) — угловое перемещение ( theta ), для линейной скорости ( v ) — угловая скорость ( omega ) и для линейного ускорения ( a ) — угловое ускорение ( alpha ).
На основании этой аналогии можно легко вывести основные формулы вращательного движения (подобно основным формулам прямолинейного движения, которые подробно описываются в главе 3):
Более подробно эти выражения рассматриваются далее в главе 10 при описании момента импульса и момента силы.
Бросаем яблоко: закон всемирного тяготения Ньютона
Чтобы проводить опыты с вращательным движением, необязательно привязывать мячики к нитям и вращать их вокруг себя. Например, Луне совсем не нужны никакие нити, чтобы вращаться вокруг Земли. А дело в том, что необходимую центростремительную силу, вместо силы натяжения нити, обеспечивает сила гравитационного притяжения.
Один из важнейших законов физики, а именно закон всемирного тяготения, вывел еще сэр Исаак Ньютон. Согласно этому закону любые два тела притягиваются друг к другу с некоторой силой. Величина этой силы притяжения между телами с массами ( m_1 ) и ( m_2 ), которые находятся на расстоянии ( r ) друг от друга, равна:
где ( G ) — это константа, равная 6,67·10-11 Н·м2/кг2.
Благодаря этому уравнению можно легко вычислить силу гравитационного притяжения между двумя телами. Например, какова сила гравитационного притяжения между Землей и Солнцем? Солнце имеет массу около 1,99·1030 кг, Земля — 5,97·1024 кг, а расстояние между ними равно 1,50·1011 м. Подставляя эти числа в закон всемирного тяготения Ньютона, получим:
Историческая яблоня
Как известно, яблоко упало на голову Исаака Ньютона, и он открыл закон всемирного тяготения. Неужели это так и было? Правда ли, что какое-то падающее яблоко натолкнуло его на верную мысль или, по крайней мере, привлекло внимание Ньютона к данной теме? Согласно последним историческим исследованиям, весьма маловероятно, что именно падение яблока на голову великого ученого вдохновило его. Скорее всего, глядя в окно на падающие яблоки в саду, он нашел еще один пример всемирного тяготения. Историки до сих пор спорят, какое именно дерево является “яблоней Ньютона”. Сотрудники поместья матери Ньютона в Вулсторпе возле Грантхэма в Линкольншире (Великобритания) утверждают, в ее семейном саду до сих пор сохранились потомки “яблони Ньютона”.
Возвращаясь с небес на грешную землю, давайте вычислим силу притяжения между двумя влюбленными на парковой скамейке. Какой величины может быть сила гравитационного притяжения между ними, если, едва встретившись, они обнимают друг друга все сильнее и сильнее? Допустим, что они весят по 75 кг и находятся на расстоянии не больше полуметра. Подставляя эти значения в уже известную нам формулу, получим:
Ничтожная сила в несколько миллионных долей ньютона!
Вычисляем силу гравитационного притяжения на поверхности Земли
Описанное выше уравнение ( F=(Gm_1m_2)/r^2 ) для силы гравитационного притяжения справедливо независимо от расстояния между двумя массивными телами. В обыденных ситуациях часто приходится иметь дело с небольшими (по сравнению с размерами Земли) объектами на поверхности Земли, т.е. на фиксированном расстоянии между центром Земли и центром небольшого объекта. Силу гравитационного притяжения (или силу тяжести), действующую на небольшой объект, часто называют весом. Вес ( F_g ) равен произведению массы ( m ) на ускорение свободного падения ( g ), т.е. ( F_g = mg ). Массу измеряют в граммах, килограммах, центнерах, каратах и т.д., а вес — в динах, ньютонах и даже фунт-силах.
Попробуем вычислить ускорение свободного падения на поверхности Земли, пользуясь законом всемирного тяготения. Формула веса тела с массой ( m_1 ) нам известна:
Она создается силой гравитационного притяжения между этим телом и Землей и равна этой силе:
Здесь ( r ) — это радиус Земли, равный 6,38·106 м, а ( m_2 ) — ее масса, равная 5,97·1024 кг.
Сокращая массу тела ( m_1 ) в обеих половинах предыдущего равенства, получим:
Подставляя численные значения, получим:
Так, благодаря закону всемирного тяготения Ньютона мы смогли вычислить значение ускорения свободного падения, уже известное нам из прежних глав. Как видите, для этого нам потребовались значения константы всемирного тяготения ( G ), радиуса Земли ( r ) и ее массы ( m_2 ). (Конечно, значение ускорения свободного падения ( g ) можно определить экспериментально, измеряя время падения предмета с известной высоты. Но, согласитесь, гораздо интересней использовать последнюю формулу, для применения которой потребуется экспериментально измерить… радиус и массу Земли. Шутка!)
Исследуем орбитальное движение с помощью закона всемирного тяготения
Небесные тела в космическом пространстве из-за силы гравитационного притяжения вращаются друг относительно друга: спутники — вокруг своих планет (как Луна — вокруг Земли), планеты — вокруг звезд (как Земля — вокруг Солнца в Солнечной системе), а звезды — вокруг центра Галактики (как Солнце — вокруг центра нашей галактики, т.е. Млечного пути), а Галактика — вокруг местной группы галактик (как Млечный путь — вокруг нашей Местной группы галактик). Во всех этих случаях тела удерживаются центростремительной силой, которую обеспечивает сила гравитации. Как показано ниже, такая центростремительная сила несколько отличается от той, которая известна нам по прежнему примеру с вращающимся на нитке мячом для игры в гольф. В следующих разделах рассматриваются широко известные законы вращения тел под действием силы гравитационного притяжения, так называемые законы Кеплера, т.е. соотношения между параметрами вращательного движения: периодами вращения, радиусами и площадями орбит вращения.
Вычисляем скорость спутника
Чему равна скорость спутника, вращающегося вокруг планеты по орбите с постоянным радиусом? Ее можно легко определить, приравнивая центростремительную силу:
и силу гравитации:
В итоге получаем:
После простых алгебраических операций получим следующее выражение для скорости вращения:
Это уравнение определяет скорость вращения спутника по постоянной орбите независимо от его происхождения, будь-то искусственный спутник Земли, как рукотворный космический корабль на постоянной орбите, или естественный спутник Земли, как Луна.
Подсчитаем скорость вращения искусственного спутника Земли, вращающегося вокруг Земли. Для этого нужно в предыдущую формулу подставить массу Земли и расстояние от космического орбитального спутника до центра Земли.
Рукотворные спутники Земли обычно вращаются на высоте около 640 км, а радиус Земли, как известно, равен 6,38·106 м. Можно считать, что искусственные спутники вращаются на круговой орбите с радиусом около 7,02·106 м. Подставляя это и другие известные нам численные значения в предыдущую формулу, получим:
В этом месте нужно сделать несколько важных замечаний.
Значение 7,02·106 м в знаменателе обозначает расстояние от спутника до центра Земли, а не расстояние от спутника до поверхности Земли, равное 640 км. Помните, что в законе всемирного тяготения под расстоянием между телами подразумевается расстояние между их центрами масс, а не между их поверхностями.
В данном примере предполагается, что космический корабль находится достаточно высоко и не испытывает влияние атмосферы, например силу трения от соприкосновения с ней. На самом деле это не так. Даже на такой большой высоте как 640 км, космический корабль теряет скорость, вследствие трения в разреженных слоях атмосферы. В результате его скорость уменьшается, а сам корабль постепенно снижается. (Более подробно об этом рассказывается ниже.)
Движение искусственного спутника вокруг Земли можно рассматривать как “вечное” падение. От фактического падения его “удерживает” только то, что вектор скорости всегда направлен перпендикулярно радиусу окружности вращения. Действительно, именно из-за такого “вечного” падения космонавты испытывают чувство невесомости. Дело в том, что космонавты и их космический корабль “вечно” падают по касательной к орбите вращения вокруг Земли, но при этом нисколько не приближаются к Земле.
В практических целях часто важнее знать период обращения искусственного спутника, а не его скорость. Это нужно, например, в ситуации, когда требуется определить момент выхода на связь с космическим кораблем.
Вычисляем период обращения спутника
Периодом обращения спутника называется время, которое необходимо ему, чтобы совершить полный цикл вращательного движения по орбите. Если нам известна орбитальная скорость движения ( v ) спутника по окружности с радиусом ( r ) (см. предыдущий раздел), то можно легко и просто вычислить период обращения ( T ). За период обращения спутник преодолевает расстояние, равное длине окружности ( 2pi r ). Это значит, что орбитальная скорость ( v ) спутника равна ( 2pi r/T ). Приравнивая это соотношение и полученное ранее выражение для орбитальной скорости
где ( m ) — масса Земли, получим:
Отсюда легко получить следующее выражение для периода обращения спутника:
А на какой высоте должен находиться спутник, чтобы вращаться с периодом обращения Земли вокруг своей оси, равным 24 часам или 86400 с? Это вовсе не праздный вопрос. Такие спутники действительно существуют и используются для обеспечения непрерывной связи в данном регионе. Действительно, ведь, обращаясь вокруг Земли с тем же периодом, что и Земля, спутник на такой геостационарной орбите постоянно находится над одной и той же точкой поверхности Земли. Несколько таких спутников образуют систему глобального позиционирования. Итак, с помощью предыдущей формулы вычислим радиус окружности вращения спутника на стационарной орбите:
Подставляя численные значения, получим:
Отнимая от этой величины 4,23·107 м, значение радиуса Земли, равное 6,38·106 м, получим приблизительно 3,59·107 м, т.е. около 35900 км. Именно на таком расстоянии от Земли вращаются спутники глобальной системы позиционирования.
На практике спутники на геостационарной орбите все же теряют скорость из- за взаимодействия с магнитным полем Земли (подробнее о магнитном поле рассказывается в следующих главах). Поэтому спутники оборудованы небольшими двигателями для корректировки их положения на геостационарной орбите.
Вращаемся вдоль вертикальной плоскости
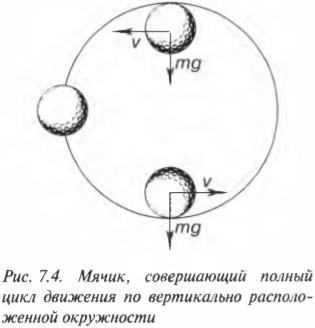
Наверняка вам приходилось наблюдать, как отважные мотоциклисты, велосипедисты или скейтбордисты вращаются внутри круглого трека, расположенного в вертикальной плоскости. Почему сила тяжести не опрокидывает их в самой верхней точке, где они находятся вверх ногами? Как быстро им нужно двигаться, чтобы сила гравитации не превышала центростремительной силы?
Рассмотрим эту ситуацию подробнее с помощью схемы на рис. 7.4. Для простоты предположим, что вместо отважных спортсменов маленький мячик совершает движение по окружности, расположенной в вертикальной плоскости. Итак, предыдущий вопрос формулируется следующим образом: “Какой минимальной скоростью должен обладать мячик, чтобы совершить полный цикл движения по вертикально расположенной окружности?”. Какому основному условию должно отвечать движение мячика, чтобы он совершил полный цикл движения по такой окружности и не упал в самой верхней точке?
Для прохождения самой верхней точки без падения мячик должен обладать минимальной скоростью, достаточной для создания такой центростремительной силы, которая была бы не меньше силы гравитации.
При таких условиях нормальная сила со стороны трека будет равна нулю, а единственной силой, которая будет удерживать объект на окружности, является сила гравитации. Поскольку центростремительная сила равна:
а сила гравитации равна:
то, приравнивая их, получим:
Отсюда получим выражение для минимально необходимой скорости для безопасного движения по окружности, расположенной в вертикальной плоскости:
Обратите внимание, что на величину минимально необходимой скорости для безопасного движения объекта по окружности, расположенной в вертикальной плоскости, не влияет масса объекта, будь-то мячик, мотоцикл или гоночный автомобиль.
Любой объект, движущийся с меньшей скоростью, в самой верхней точке трека неизбежно отклонится от траектории движения по окружности и упадет. Давайте вычислим величину минимально необходимой скорости для безопасного движения по окружности с радиусом 20 м. Подставляя численные значения в предыдущую формулу, получим:
Итак, для безопасного движения по окружности с радиусом 20 м объект (мячик, мотоцикл или гоночный автомобиль) должен иметь скорость не менее 14 м/с, т.е. около 50 км/ч.
Учтите, что для безопасного движения по окружности такую минимальную скорость объект должен иметь в самой верхней точке! Для того чтобы развить такую скорость в верхней точке, объекту в нижней точке нужно иметь гораздо большую скорость. Действительно, ведь чтобы добраться до верхней точки объекту придется какое-то время преодолевать силу гравитации с неизбежной потерей скорости.
Возникает вопрос: какую минимальную скорость в нижней точке должен иметь объект для безопасного движения по такой окружности? Подробный ответ на этот вопрос будет дан в части III этой книги, в которой рассматриваются такие понятия, как “кинетическая энергия”, “потенциальная энергия” и “преобразование энергии из одной формы в другую”.
Глава 7. Движемся по орбитам
2.9 (58.71%) 31 votes

































![Rendered by QuickLaTeX.com [begin{cases} upsilon_1cdot r_1 =upsilon_2cdot r_2\ frac {mupsilon_1^2}{2} - G frac { M_c cdot m}{r_1} = frac {mupsilon_2^2}{2} - G frac {M_c cdot m}{r_2}\ r_1 = a(1-e)\ r_2 = a(1+e)\ upsilon =sqrt{frac {G*M_c}{a}} end{cases}]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-5dfe79c27e647523efa6949a61b647e7_l3.png)
![Rendered by QuickLaTeX.com [begin{cases} upsilon_1cdot a(1-e) =upsilon_2cdot a(1+e)\ frac {upsilon_1^2}{2} - G frac { M_c}{a(1-e)} = frac {upsilon_2^2}{2} - G frac {M_c}{a(1+e)}\ upsilon =sqrt{frac {G*M_c}{a}} end{cases}]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-78225b3bcdc0b1a4ae3d2e0cb0bdf948_l3.png)
![Rendered by QuickLaTeX.com [begin{cases} upsilon_1cdot a(1-e) =upsilon_2cdot a(1+e)\ frac {upsilon_1^2}{2} - frac { upsilon ^2}{1-e} = frac {upsilon_2^2}{2} - G frac {upsilon ^2}{1+e}]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-373db51e8d047756949f29f18d3595e5_l3.png)