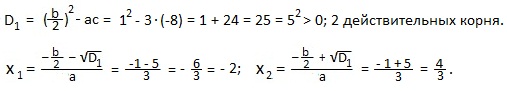Как найти линейные множители - Исправление недочетов и поиск решений вместе с Examum.ru

На чтение 3 мин. Просмотров 42k.

Квадратный трехчлен ax²+bx+c можно разложить на линейные множители по формуле:

ax²+bx+c=a (x-x₁)(x-x₂), где x_1,x₂ — корни квадратного уравнения ax²+bx+c=0.

Разложить квадратный трехчлен на линейные множители:

Пример 1). 2x²-7x-15.

Решение. Найдем корни квадратного уравнения: 2x²-7x-15=0.

a=2; b=-7; c=-15. Это общий случай для полного квадратного уравнения. Находим дискриминант D.

D=b²-4ac=(-7)²-4∙2∙(-15)=49+120=169=13²>0; 2 действительных корня.

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

2x²-7x-15=2 (х+1,5)(х-5)=(2х+3)(х-5). Мы представили данный трехчлен 2x²-7x-15 в виде произведения двучленов 2х+3 и х-5.

Ответ: 2x²-7x-15=(2х+3)(х-5).

Пример 2). 3x²+2x-8.

Решение. Найдем корни квадратного уравнения:

3x²+2x-8=0.

a=3; b=2; c=-8. Это частный случай для полного квадратного уравнения с четным вторым коэффициентом (b=2). Находим дискриминант D₁.

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

Мы представили трехчлен 3x²+2x-8 в виде произведения двучленов х+2 и 3х-4.

Ответ: 3x²+2x-8=(х+2)(3х-4).

Пример 3). 5x²-3x-2.

Решение. Найдем корни квадратного уравнения:

5x²-3x-2=0.

a=5; b=-3; c=-2. Это частный случай для полного квадратного уравнения с выполненным условием: a+b+c=0 (5-3-2=0). В таких случаях первый корень всегда равен единице, а второй корень равен частному от деления свободного члена на первый коэффициент:

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

5x²-3x-2=5 (х-1)(х+0,4)=(х-1)(5х+2). Мы представили трехчлен 5x²-3x-2 в виде произведения двучленов х-1 и 5х+2.

Ответ: 5x²-3x-2=(х-1)(5х+2).

Пример 4). 6x²+x-5.

Решение. Найдем корни квадратного уравнения:

6x²+x-5=0.

a=6; b=1; c=-5. Это частный случай для полного квадратного уравнения с выполненным условием: a-b+c=0 (6-1-5=0). В таких случаях первый корень всегда равен минус единице, а второй корень равен минус частному от деления свободного члена на первый коэффициент:

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

Мы представили трехчлен 6x²+x-5 в виде произведения двучленов х+1 и 6х-5.

Ответ: 6x²+x-5=(х+1)(6х-5).

Пример 5). x²-13x+12.

Решение. Найдем корни приведенного квадратного уравнения:

x²-13x+12=0. Проверим, можно ли применить теорему Виета. Для этого найдем дискриминант и убедимся, что он является полным квадратом целого числа.

a=1; b=-13; c=12. Находим дискриминант D.

D=b²-4ac=13²-4∙1∙12=169-48=121=11².

Применим теорему Виета: сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, а произведение корней должно быть равно свободному члену:

x₁+x₂=13; x₁∙x₂=12. Очевидно, что x₁=1; x₂=12.

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

x²-13x+12=(х-1)(х-12).

Ответ: x²-13x+12=(х-1)(х-12).

Пример 6). x²-4x-6.

Решение. Найдем корни приведенного квадратного уравнения:

x²-4x-6=0.

a=1; b=-4; c=-6. Второй коэффициент — четное число. Находим дискриминант D₁.

Дискриминант не является полным квадратом целого числа, поэтому, теорема Виета нам не поможет, и мы найдем корни по формулам для четного второго коэффициента:

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂) и запишем ответ:

Друзья, для того, чтобы разложить квадратные трехчлены на множители, мы решали каждое квадратное уравнение рациональным способом. Все эти способы мы рассмотрели ранее в теме: «Решение полных квадратных уравнений».

Источник

На чтение 3 мин Просмотров 3.6к. Опубликовано 21 октября, 2020

Что такое квадратный трехчлен и как разложить на множители квадратный трехчлен.

Содержание

Квадратный трехчлен
Разложение на множители квадратного трехчлена
Краткая схема разложения на множители квадратного трехчлена

Квадратный трехчлен

Квадратным трехчленом называют выражение вида

Разложить на множители квадратный трехчлен — это значит, записать его в виде произведения.

Разложение на множители квадратного трехчлена

Чтобы разложить на множители квадратный трехчлен используем следующее правило:

, где , где x_1 и — корни уравнения — корни уравнения .

Таким образом, нам нужно решить квадратное уравнение и затем найденные корни подставить сюда: и затем найденные корни подставить сюда:

Рассмотрим на примере: требуется разложить на множители квадратный трехчлен:

Решим уравнение: , находим дискриминант , находим дискриминант , тогда корни уравнения: и и , тогда по формуле разложения на множители получаем:

Давайте еще рассмотрим один пример: пусть требуется разложить на линейные множители квадратный трехчлен . Находим корни этого уравнения . Находим корни этого уравнения .

Находим дискриминант уравнения. Если вы забыли как найти дискриминант посмотрите здесь.

, отсюда корни уравнения , отсюда корни уравнения и . И разложение квадратного трехчлена на множители мы запишем так: . И разложение квадратного трехчлена на множители мы запишем так: .

Краткая схема разложения на множители квадратного трехчлена

Приравнять квадратный трехчлен к нулю. Получим квадратное уравнение.
Решим квадратное уравнение, найдем два корня.
Подставим корни в формулу

Схема не сложная. Но иногда могут встречаться затруднения. Например — что если корень получился один, а не два. На самом деле в квадратном уравнении всегда два корня. Об этом нам «говорит» степень 2, над . Это означает, что если у вас дискриминант равен нулю, вы получаете не один корень, а два совпадающих друг с другом корня. И разложение на множители будет выглядеть так:

Например: квадратный трехчлен при равенстве нулю имеет два совпадающих корня при равенстве нулю имеет два совпадающих корня и раскладывать на множители мы будем его так

В дальнейшем, следует помнить — что в кубическом уравнении 3 корня, в биквадратном — 4. Сколько степеней в уравнении, столько и корней у него должно быть. Другое дело, что некоторые из них, и даже все, могут совпадать в значении. Геометрический смысл такого совпадения в том, что график кривой, которая описывается уравнением, будет лишь касаться оси .

Итак, давайте выполним следующее задание: нужно разложить на множители квадратных трехчлен .

Найдем корни уравнения . Для этого сначала найдем дискриминант . Для этого сначала найдем дискриминант .

Тогда корни уравнения: $x_1=frac{-b-sqrt{D}}{2a}=frac{-3-7}{4}=frac{-10}{4}=-2,5$ . И $x_2=frac{-b+sqrt{D}}{2a}=frac{-3+7}{4}=frac{4}{4}=1$ . И $x_2=frac{-b+sqrt{D}}{2a}=frac{-3+7}{4}=frac{4}{4}=1$ .

Итак, получили и и x_2=1 . Подставляя в формулу разложения на множители квадратного трехчлена, получим:

Теперь вы знаете как разложить на множители квадратный трехчлен. Успехов в учебе!

Источник

Теорема о разложении многочлена на линейные множители

Всякий
многочлен n –
ой степени разлагается на n линейных
множителей вида х
– а и
множитель, равный коэффициенту при
старшей степени xⁿ.

Доказательство.
Пусть f (x)
= A₀xⁿ +
A₁xⁿ^—

1 +
… + A_n —
многочлен n –
ой степени. Этот многочлен в силу основной
теоремы алгебры имеет один корень а₁.
Тогда из следствия теоремы Безу будем
иметь f (x)
= (х
– а₁)·f₁ (x),
где f₁ (x)
— многочлен степени n —
1. Многочлен f₁ (x)
тоже имеет корень а₂.

Тогда f₁ (x)
= (х
– а₂ )·f₂ (x),
где f₂ (x)
— многочлен степени n – 2.
Аналогично f₂ (x)
= (х
– а₃)·f₃ (x).
Продолжая процесс выделения линейных
множителей, дойдём до соотношения f_n(x)
= (х
– а_n )·f_n,
где f_n —
число (многочлен нулевой степени), и это
число равно коэффициенту при хⁿ,
то есть f_n =
А₀.
На основании всех этих равенств можно
записать

f (x)
= А₀·( х
– а₁)·( х
– а₂)·
… ·( х
– а_n).

17.Разложение
многочлена с действительными коэффицентами
на неприводимые множетели

Неприводимый
многочлен — многочлен,
неразложимый на нетривиальные
(неконстантные) многочлены. Неприводимые
многочлены являются неприводимыми
элементами кольца
многочленов.

Определение

Неприводимый
многочлен над полем
― многочлен
от
переменных
над полем
является
простым элементом кольца
,
то есть, непредставим в виде произведения
,
где
и
―
многочлены с коэффициентами из
,
отличные от констант.

Многочлен
называется абсолютно
неприводимым,
если он неприводим над алгебраическим
замыканием поля коэффициентов. Абсолютно
неприводимые многочлены одной переменной
― это многочлены 1-й степени и только
они. В случае нескольких переменных
существуют абсолютно неприводимые
многочлены сколь угодно высокой степени
— например, любой многочлен вида

абсолютно
неприводим.

Примеры

Следующие
пять многочленов демонстрируют некоторые
элементарные свойства неприводимых
многочленов:

Над
кольцом
целых
чисел,
первые два многочлена — приводимые,
последние два — неприводимые. (Третий
вообще не является многочленом над
целыми числами).

Над
полем
рациональных
чисел,
первые три многочлена являются
приводимыми, двое других — неприводимыми.

Над
полем
действительных
чисел,
первые четыре многочлена — приводимые,
но
является
неприводимым. В поле действительных
чисел неприводимыми являются линейные
многочлены и квадратичные многочлены
без действительных корней. Например
разложение многочлена
в
поле действительных чисел имеет вид
.
Оба множителя в данном разложении
являются неприводимыми многочленами.

Над
полем
комплексных
чисел,
все пять многочленов — приводимые.
Фактически, каждый отличный от константы
многочлен
над
может
быть разложен на множители вида:

где
— степень
многочлена,
—
старший коэффициент,
— корни
.
Поэтому единственными неприводимыми
многочленами над
являются
линейные многочлены (основная
теорема алгебры).

[Править]Конечные поля

Многочлены
с целочисленными коэффициентами, которые
являются неприводимыми над полем
могут
быть приводимыми над конечным
полем.
Например, многочлен
является
неприводимым над
,
но над полем
из
двух элементов мы имеем:

18.Интегрирование
по частям.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Разложение на линейные множители некоторых квадратных трехчленов

Прежде всего укажем на некоторые употребительные названия. Станем рассматривать многочлены, в состав которых входит лишь одна какая-нибудь буква, напр., буква x. Тогда самым простым является многочлен, в котором два члена, причем в одном из них имеется буква x в первой степени, а в другом вовсе буквы x не имеется, напр., 3x – 5 или 15 – 7x или 8z + 7 (здесь уже вместо буквы x взята буква z) и т. д. Такие многочлены называются линейными двучленами.

Далее, усложняя дело, составим многочлен из трех членов: в одном буква x пусть входит во второй степени, в другом – в первой, а третий член вовсе этой буквы не содержит, напр.:

3x² – 5x + 7 или x² + 2x – 1
или 5y² + 7y + 8 или z² – 5z – 2 и т. д.

Такие многочлены называются квадратными трехчленами.

Затем, мы можем составить кубический четырехчлен, напр.:

x³ + 2x² – x + 1 или 3x³ – 5x² – 2x – 3 и т. д.,

многочлен четвертой степени, напр.:

x⁴ – 2x³ – 3x² + 4x – 5 и т. д.

Возможно обозначать коэффициенты при x, при x², при x³ и т. д. также буквами, напр., буквами a, b, c и т. д. Тогда получим:

1) общий вид линейного относительно x двучлена ax + b,

2) общий вид квадратного трехчлена (относительно x): ax² + bx + c,

3) общий вид кубического трехчлена (относительно x): ax³ + bx² + cx + d и т. д.

Заменяя в этих формулах буквы a, b, c, d … различными числами, получим всевозможные линейные двучлены, квадратные трехчлены и т. д. Напр., в формуле ax² + bx + c, выражающей общий вид квадратного трехчлена, заменим букву a числом +3, букву b числом –2 и букву c числом –1, получим квадратный трехчлен 3x² – 2x – 1. В частном случае возможно получить и двучлен, заменяя одну из букв нулем, напр., если a = +1, b = 0 и c = –3, то получим квадратный двучлен x² – 3.

Можно научиться раскладывать некоторые квадратные трехчлены довольно быстро на линейные множители. Ограничимся, однако, рассмотрением только таких квадратных трехчленов, которые удовлетворяют следующим условиям:

1) коэффициентом при старшем члене (при x²) служит +1,

2) можно подыскать такие два целых числа (со знаками, или два относительных целых числа), чтобы их сумма равнялась коэффициенту при x в первой степени и их произведение равнялось члену, свободному от x (где буквы x вовсе нет).

Примеры. 1. x² + 5x + 6; легко в уме подыскать два числа (со знаками), чтобы их сумма равнялась +5 (коэффициенту при x) и чтобы их произведение = +6 (члену, свободному от x), – эти числа суть: +2 и +3 [в самом деле, +2 + 3 = +5 и (+2) ∙ (+3) = +6]. При помощи этих двух чисел заменим член +5x двумя членами, а именно: +2x + 3x (конечно, +2x + 3x = +5x); тогда наш техчлен искусственно будет обращен в четырехчлен x² + 2x + 3x + 6. Применим теперь к нему прием группировки, относя первые два члена в одну группу и последние два – в другую:

x² + 5x + 6 = x² + 2x + 3x + 6 = x (x + 2) + 3 (x + 2) = (x + 2) (x + 3).

В первой группе мы вынесли за скобку x и во второй +3, получили два члена, у которых оказался общий множитель (x + 2), который также вынесли за скобку, и наш трехчлен x² + 5x + 6 разложился на 2 линейных множителя: x + 2 и x + 3.

2. x² – x – 12. Здесь надо подыскать два числа (относительных), чтобы их сумма равнялась –1 и чтобы их произведение равнялось –12. Такие числа суть: –4 и +3.

Проверка: –4 + 3 = –1; (–4) (+3) = –12. При помощи этих чисел заменим член –x двумя членами: –x = –4x + 3x, – получим:

x² – x – 12 = x² – 4x + 3x – 12 = x (x – 4) + 3 (x – 4) = (x – 4) (x + 3).

3. x² – 7x + 6; здесь нужные числа суть: –6 и –1. [Проверка: –6 + (–1) = –7; (–6) (–1) = +6].

Тогда:

x² – 7x + 6 = x² – 6x – x + 6 = x (x – 6) – (x – 6) = (x – 6) (x – 1).

Здесь члены второй группы –x + 6 пришлось заключить в скобки, со знаком минус перед ними.

4. x² + 8x – 48. Здесь нужно подыскать два числа, чтобы их сумма равнялась +8 и чтобы их произведение равнялось –48. Так как произведение должно иметь знак минус, то искомые числа должны быть с разными знаками, так как сумма наших чисел имеет знак +, то абсолютная величина положительного числа должна быть больше. Раскладывая арифметическое число 48 на два множителя (а это можно сделать по-разному), получим: 48 = 1 ∙ 48 = 2 ∙ 24 = 3 ∙ 16 = 4 ∙ 12 = 6 ∙ 8. Из этих разложений легко выбрать подходящее к нашим требованиям, а именно: 48 = 4 ∙ 12. Тогда наши числа суть: +12 и –4. Дальнейшее просто:

x² + 8x – 48 = x² + 12x – 4x – 48 = x (x + 12) – 4 (x + 12) = (x + 12) (x – 4).

5. x² + 7x – 12. Здесь надо найти 2 числа, чтобы их сумма равнялась +7 и произведение = –12; 12 = 1 ∙ 12 = 2 ∙ 6 = 3 ∙ 4. По-видимому, подходящими числами являлись бы 3 и 4, но их надо взять с разными знаками, чтобы их произведение равнялось –12, а тогда их сумма ни в коем случае не может равняться +7 [–3 + (+4) = +1, +3 + (–4) = –1]. Другие разложения на множители также не дают требуемых чисел; поэтому мы приходим к заключению, что данных квадратных трехчлен мы еще не умеем разложить на линейные множители, так как к нему наш прием не применим (он не удовлетворяет второму из условий, какие были установлены вначале).

Источник

Алгоритм разложения квадратного трёхчлена на множители с помощью дискриминанта
Алгоритм разложения квадратного трёхчлена на множители по теореме Виета
Примеры

Алгоритм разложения квадратного трёхчлена на множители с помощью дискриминанта

Данный алгоритм является универсальным.

На входе: квадратный трёхчлен $ax^2+bx+c$

Задача: разложить трёхчлен на множители

Шаг 1. Находим дискриминант $D = b^2-4ac$

Шаг 2. Если $D gt 0, x_1,2 = frac{-b pm sqrt{D}}{2a} $ и $ax^2+bx+c = a(x-x_1 )(x-x_2 )$

Если D = 0, $x_0 = — frac{b}{2a}$ и $ax^2+bx+c = a(x-x_0 )^2$

Если $D lt 0$, разложение на множители невозможно.

Шаг 3. Работа завершена.

Алгоритм разложения квадратного трёхчлена на множители по теореме Виета

Данный алгоритм применяется в частных случаях.

Если один (или оба) корня квадратного уравнения целые, то полезным навыком становится разложение на множители «в уме», с помощью теоремы Виета.

Навык этот не простой, и если у вас сразу не получится, не расстраивайтесь.

Рассмотрим следующий трёхчлен: $x^2+8x+15$

b = 8, c = 15

Если корни трёхчлена существуют, то их произведение равно 15.

Прикинем «в уме» соответствующие пары натуральных чисел:

(1;15),(3;5)

В трёхчлене $c gt 0$, значит корни одного знака, и в построении b участвует сумма этих корней. Из пары (1;15) сумма 8 не выходит, а вот из пары (3;5) — получается.

Для выбранной пары (3;5) запишем разложение, пока без знаков:

$$ (x…3)(x…5) = x^2+8x+15 $$

Теперь видно, что знаки в скобках – два плюса:

$$ (x+3)(x+5) = x^2+8x+15 $$

Разложение найдено.

Рассмотрим другой трёхчлен: $x^2+2x-35$

b = 2, c = -35

Пары натуральных чисел, дающие произведение 35:

(1;35),(5;7)

В трёхчлене $c lt 0$, значит корни разных знаков, и в построении b участвует разность этих корней. Из пары (1;35) разность 2 не выходит, а вот из пары (5;7) — получается.

Для выбранной пары (5;7) запишем разложение, пока без знаков:

$$ (x…5)(x…7) = x^2+2x-35 $$

Теперь видно, что 7 должно быть с плюсом, а 5 – с минусом:

$$ (x-5)(x+7) = x^2+2x-35 $$

Разложение найдено.

Обобщим алгоритм разложения по теореме Виета.

На входе: приведенный квадратный трёхчлен $x^2+bx+c$

Задача: разложить трёхчлен на множители при гипотезе, что корни — целочисленные

Шаг 1. Записать все пары натуральных чисел (m;n), дающих в произведении c.

Шаг 2. Если $c gt 0$, то из всех пар выбрать ту, сумма которой даёт b.

Если $c lt 0$, то из всех пар выбрать ту, разность которой даёт b.

Если выбрать пару не удаётся, данный алгоритм не подходит, и нужно приступить к разложению с помощью дискриминанта.

Шаг 3. Для выбранной пары записать разложение без знаков в виде:

$$ (x…m)(x…n) = x^2+bx+c $$

Сопоставляя левую и правую части, окончательно расставить знаки в скобках.

Шаг 4. Работа завершена.

Внимание!

Предложенный алгоритм позволяет не только раскладывать на линейные множители трёхчлены, но и находить их корни, т.е. решать соответствующие квадратные уравнения.

Не забывайте менять знаки при записи решений уравнения!

Например:

Решаем $x^2+8x+15 = 0$. Получаем (x+3)(x+5) = 0. Корни $x_1 = -3, x_2 = -5$.

Решаем $x^2+2x-35 = 0$. Получаем (x-5)(x+7) = 0. Корни $x_1 = 5, x_2 = -7$.

При некотором опыте, можно наловчиться раскладывать не только приведенные трёхчлены, например:

$$ 5x^2-14x-3 = (5x+1)(x-3), 3x^2+13x-10 = (3x-2)(x+5), $$

$$ 6x^2+7x-3 = (3x-1)(2x+3) $$

В этих случаях алгоритм усложняется за счёт дополнительных вариантов расстановки коэффициентов при переменной в скобках.

Примеры

Пример 1. Разложите квадратный трёхчлен с помощью дискриминанта:

$а) 2x^2+7x-4$

$ D = 7^2-4 cdot 2 cdot (-4) = 49+32 = 81 = 9^2 $

$ x = frac{-7 pm 9}{4} = left[ begin{array}{cc} x_1 = -4 \ x_2 = frac{1}{2} end{array} right. $

Получаем: $2x^2+7x-4 = 2(x+4) left(x- frac{1}{2} right)$

Можно также записать: $2x^2+7x-4 = (x+4)(2x-1)$

$б) 3x^2+20x-7$

$ D = 20^2-4 cdot 3 cdot (-7) = 400+84 = 484 = 22^2 $

$x = frac{-20 pm 22}{6} = left[ begin{array}{cc} x_1 = -7 \ x_2 = frac{1}{3} end{array} right.$

Получаем: $3x^2+20x-7 = 3(x+7) left(x-frac{1}{3} right)$

Можно также записать: $3x^2+20x-7 = (x+7)(3x-1)$

$в) 4x^2-19x-5$

$D = 19^2-4 cdot 4 cdot (-5) = 361+80 = 441 = 21^2$

$ x = frac{19 pm 21}{8} = left[ begin{array}{cc} x_1 = -frac{1}{4} \ x_2 = 5 end{array} right.$

Получаем: $4x^2-19x-5 = 4 left(x+ frac{1}{4} right)(x-5)$

Можно также записать: $4x^2-19x-5 = (4x+1)(x-5)$

$г*) x^2- sqrt{2}x+ frac{1}{2}$

$ D = (sqrt{2})^2-4 cdot frac{1}{2} = 2-2 = 0, x = frac{sqrt{2}}{2} $

Получаем: $x^2-sqrt{2} x+ frac{1}{2} = left(x- frac{sqrt{2}}{2} right)^2 $

Пример 2*. Разложите трёхчлены на множители подбором по теореме Виета:

$а) x^2+7x+12$

Пары множителей: (1;12),(2;6),(3;4)

$c = 12 gt 0 Rightarrow$ выбираем из пар ту, что в сумме дает b = 7. Это пара (3;4).

Записываем разложение без знаков: $(x…3)(x…4) = x^2+7x+12$

Расставляем знаки, результат: $x^2+7x+12 = (x+3)(x+4)$

$б) x^2+3x-18$

Пары множителей: (1;18),(2;9),(3;6)

$c = -18 lt 0 Rightarrow$ выбираем из пар ту, разность которой дает b = 3. Это пара (3;6).

Записываем разложение без знаков: $(x…3)(x…6) = x^2+3x-18$

Расставляем знаки, результат: $x^2+3x-18 = (x-3)(x+6)$

в) x+4x-77

Пары множителей: (1;77),(7;11)

$c = -18 lt 0 Rightarrow$ выбираем из пар ту, разность которой дает b=4. Это пара (7;11).

Записываем разложение без знаков: $(x…7)(x…11) = x^2+4x-77$

Расставляем знаки, результат: $x^2+4x-77 = (x-7)(x+11)$

$г*) 2x^2-x-3$

Одна пара множителей (1;3)

Возможные разложения с коэффициентом:

$$ (2x…1)(x…3) = 2x^2-x-3, (2x…3)(x…1) = 2x^2-x-3 $$

$c = -3 lt 0$, в скобках разные знаки.

Перебираем четыре возможных варианта и получаем:

$$2x^2-x-3 = (2x+3)(x-1) = 2 left(x+ frac{3}{2} right)(x-1)$$

Пример 3. Сократите дробь.

Разложение на множители проводим по формулам сокращенного умножения, с помощью дискриминанта или по теореме Виета.

а) $$ frac{x^2-16}{x^2+11x+28} = frac{(x-4)(x+4)}{(x+4)(x+7)} = frac{x-4}{x+7}$$

б) $$ frac{x^2-2x-15}{x^2-10x+25} = frac{(x-5)(x+3)}{(x-5)^2} = frac{x+3}{x-5}$$

в) $$ frac{3y^2-5y+2}{3y^2-y-2} = frac{(3y-2)(y-1)}{(3y+2)(y-1)} = frac{3y-2}{3y+2}$$

г)$$ frac{2y^2-3y+1}{3y^2-4y+1} = frac{(2y-1)(y-1)}{(3y-1)(y-1)} = frac{2y-1}{3y-1}$$

Пример 4. Упростите выражение:

$$ frac{x-16}{(x+2)^2} ∶ left(frac{3x+11}{(3x^2+17x+22)} — frac{2}{x+2} right) = frac{x-16}{(x+2)^2} ∶ left(frac{3x+11}{(3x+11)(x+2)} — frac{2}{x+2} right) = $$

$$ = frac{x-16}{(x+2)^2} ∶ left(frac{1}{x+2} — frac{2}{x+2}right) = frac{x-16}{(x+2)^2} ∶ left(-frac{1}{x+2}right) = -frac{(x-16)(x+2)}{(x+2)^2} = $$

$$ =-frac{x-16}{x+2} = frac{16-x}{x+2}$$

Источник