Как найти угол между плоскостями?
Найти угол между плоскостями можно двумя способами: геометрическим и алгебраическим.
Геометрический способ
При геометрическом способе нужно сначала построить угол двугранного угла, а потом искать этот линейный угол с помощью знаний из планиметрии.
Алгебраический способ
Алгебраический способ – это применение метода координат – там есть формула для нахождения угла между плоскостями.
Вот такая:
( displaystyle cos gamma =frac{{{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}}{sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}})
Здесь ( displaystyle {{A}_{1}},{{B}_{1}},{{C}_{1}},{{A}_{2}},{{B}_{2}},{{C}_{2}}) — коэффициенты уравнений плоскостей ( displaystyle alpha ) и ( displaystyle beta ) соответственно.
Подробнее про уравнение плоскости ты можешь прочитать в статье «Расстояние от точки до плоскости»!
( displaystyle alpha ): ( displaystyle {{A}_{1}}x+{{B}_{1}}y+{{C}_{1}}z+D=0)
( displaystyle beta ): ( displaystyle {{A}_{2}}x+{{B}_{2}}y+{{C}_{2}}z+D=0).
Какой же способ лучше? Зависит от задачи.
Если нужно найти, скажем, двугранный угол при основании правильной , то проще использовать геометрический способ.
А если линейный угол двугранного угла никак не хочет проходить ни через какие удобные точки, то можно использовать метод координат как палочку выручалочку.
Но тогда нужно очень твёрдо знать формулы и не делать арифметических ошибок при многочисленных подсчётах – ведь придётся искать ( displaystyle {{A}_{1}},{{B}_{1}},{{C}_{1}},{{A}_{2}},{{B}_{2}},{{C}_{2}}), а потом ещё и ( displaystyle cos gamma ).
Давай разберём несложную задачу для примера. Мы применим оба метода к одной и той же задаче.
Рис. (1). Ноутбук.
Двугранный угол — это часть пространства, заключённая между двумя полуплоскостями, имеющими одну общую границу.
Рис. (2). Две пересекающиеся плоскости.
Если в пространстве пересекаются две плоскости, получаются четыре двугранных угла (аналогично как при пересечении двух прямых получаются четыре угла). Рассмотрим один из них.
Рис. (3). Двугранный угол.
Полуплоскости
α
и
β
, образующие двугранный угол, называются его гранями.
Общая прямая (a) этих граней называется ребром двугранного угла.
Выберем на ребре (a) двугранного угла произвольную точку (C) и проведём две пересекающиеся прямые
AC⊥a
и
BC⊥a
, а через эти прямые — плоскость
γ
перпендикулярно ребру (a).
Рис. (4). Линейный угол двугранного угла.
Линии пересечения (AC) и (BC) полуплоскостей
α
и
β
с плоскостью
γ
образуют некоторый угол
∠ACB
. Этот угол называется линейным углом двугранного угла. Величина линейного угла не зависит от выбора точки (C) на ребре (a).
Обрати внимание!
Величина двугранного угла (0° <)
∠ACB
(< 180°).
Если плоскости параллельны, то угол между ними равен (0°) по определению.
Если при пересечении плоскостей один из двугранных углов составляет (90°), то три остальных угла — тоже (90°). Эти плоскости называют перпендикулярными.
Следующие теоремы, которые здесь приведём без доказательств, могут пригодиться при решении задач.
1. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
2. Плоскость, перпендикулярная прямой, по которой пересекаются две плоскости, перпендикулярна каждой из этих плоскостей.
3. Если две плоскости перпендикулярны, и в одной из них прямая проведена перпендикулярно линии пересечения плоскостей, то эта прямая перпендикулярна второй плоскости.
Многогранные углы
Объясним понятие многогранных углов.
Представим несколько лучей в пространстве с общим началом. Их можно представить тоже как часть линий пересечения плоскостей — трёх, четырёх или больше — и назвать рёбрами многогранного угла.

Рис. (5). Трёхгранный угол.

Рис. (6). Четырёхгранный угол.
Рис. (7). Пятигранный угол.
Каждые два луча образуют угол, который называют плоским углом многогранного угла.
Обрати внимание!
Каждый плоский угол трёхгранного угла меньше суммы двух других плоских углов.
Сумма плоских углов многогранного угла меньше (360°).
Источники:
Рисунки 2-7. Плоскости, углы, © ЯКласс.
§ 14.Двугранные углы. Угол между двумя плоскостями
14.1. Двугранный угол и его измерение
Рассмотрим два полупространства, образованные непараллельными плоскостями. Пересечение этих полупространств назовём двугранным углом.
Прямую, по которой пересекаются плоскости — границы полупространств, называют ребром двугранного угла, а полуплоскости этих плоскостей, образующие двугранный угол, — гранями двугранного угла.
Двугранный угол с гранями α, β и ребром a обозначают αaβ. Можно использовать и такие обозначения двугранного угла, как K(AB)T; α(AB)β (рис. 94, 95).
Рис. 94
Рис. 95
Рис. 96
Замечание. Иногда говорят, что двугранный угол αaβ образован двумя полуплоскостями α и β, имеющими общую граничную прямую a.
Фигуры, образованные двумя страницами одной книги, двумя соседними гранями куба, — модели двугранного угла.
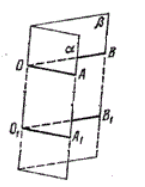
Для измерения двугранного угла введём понятие его линейного угла. На ребре a двугранного угла αaβ отметим произвольную точку O и в гранях α и β проведём из точки O соответственно лучи OA и OB, перпендикулярные ребру a (рис. 96, а). Угол AOB, образованный этими лучами, называется линейным углом двугранного угла αaβ.
Так как OA ⊥ a и OB ⊥ a, то плоскость AOB перпендикулярна прямой a. Это означает, что линейный угол двугранного угла есть пересечение данного двугранного угла и плоскости, перпендикулярной его ребру.
Вследствие произвольного выбора точки O на ребре двугранного угла заключаем, что двугранный угол имеет бесконечное множество линейных углов. Докажем, что все они равны. Действительно, рассмотрим два линейных угла AOB и A1O1B1 двугранного угла αaβ (рис. 96, б). Лучи OA и O1A1 лежат в одной грани α и перпендикулярны прямой a — ребру двугранного угла, поэтому они сонаправлены. Аналогично получаем, что сонаправлены лучи OB и O1B1. Тогда ∠ AOB = ∠ A1O1B1 (как углы с сонаправленными сторонами).
Таким образом, нами доказана теорема.

Иначе говоря, все линейные углы данного двугранного угла равны между собой.
Это позволяет ввести следующее определение.
Определение. Величиной двугранного угла называется величина его линейного угла.
Рис. 97
Величина двугранного угла, измеренная в градусах, принадлежит промежутку (0°; 180°).
На рисунке 97 изображён двугранный угол, градусная мера (величина) которого равна 30°. В этом случае также говорят, что двугранный угол равен тридцати градусам.
Двугранный угол является острым (рис. 98, а), прямым (рис. 98, б) или тупым (рис. 98, в), если его линейный угол соответственно острый, прямой или тупой.
Рис. 98
Заметим, что аналогично тому, как и на плоскости, в пространстве определяются смежные (рис. 99, а) и вертикальные (рис. 99, б) двугранные углы. При этом справедливы и аналогичные теоремы о величинах этих углов.
Попробуйте доказать самостоятельно следующие два утверждения, важные для решения задач.
На гранях двугранного угла величины α взяты точки A и B; A1 и B1 — проекции этих точек на ребро двугранного угла; AA1 = a; BB1 = b; A1B1 = h. Тогда
AB = 
Рис. 99
Если внутри двугранного угла величины α взята точка на расстояниях a и b от граней двугранного угла, то её расстояние от ребра двугранного угла равно 
14.2. Угол между двумя плоскостями
Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром (рис. 100). Если величина одного из них равна ϕ, то величины трёх остальных равны соответственно 180° – ϕ, ϕ, 180° – ϕ (почему?). Наименьшая из этих величин принимается за величину угла между данными пересекающимися плоскостями.
Определение. Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных при их пересечении.
Угол между параллельными или совпадающими плоскостями полагается считать равным нулю.
Если величина угла между плоскостями α и β равна ϕ, то пишут: 
Рис. 100
Так как двугранный угол измеряется своим линейным углом, то из выше приведённого определения следует, что угол между пересекающимися плоскостями равен углу между пересекающимися прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения (см. рис. 100). Это означает, что величина угла между плоскостями принадлежит промежутку [0°; 90°].
Рис. 101
ЗАДаЧа. Отрезок DM длиной 3,2 перпендикулярен плоскости ромба ABCD (∠ ADC — тупой). Диагонали ромба равны 12 и 16. Найти углы между плоскостями:
а) ABC и MBC; б) AMD и CMD.
Решение. а) Пусть DE — высота ромба ABCD (рис. 101). Тогда по теореме о трёх перпендикулярах ME ⊥ BC и ∠ DEM = ϕ — линейный угол двугранного угла, образованного плоскостями ABC и MBC. Найдём величину этого угла.
По условию задачи DM ⊥ (ABC), поэтому ⧌ MDE — прямоугольный, значит, tg ϕ = 



Учитывая, что S = 






б) Так как отрезок DM — перпендикуляр к плоскости ромба ABCD, то AD ⊥ DM, CD ⊥ DM, значит, ∠ ADC = ψ — линейный угол двугранного угла, образованного пересекающимися плоскостями ADM и CDM. Найдём этот угол.
В треугольнике ACD по теореме косинусов находим
cos ψ = 


откуда ψ = arccos 
Ответ: а) arctg 

Двугранным углом называется фигура, образованная двумя не принадлежащими одной плоскости полуплоскостями, имеющими общую границу – прямую а. Полуплоскости, образующие двугранный угол, называются его гранями, а общая граница этих плоскостей – ребром двугранного угла.
В реальности мы встречаемся с предметами, которые имеют форму двугранного угла: двускатные крыши домов, приоткрытая дверь, полураскрытая папка и т. п.
Линейным углом двугранного угла называется угол, сторонами которого являются лучи, по которым грани двугранного угла пересекаются плоскостью, перпендикулярной ребру двугранного угла.
У каждого двугранного угла сколько угодно линейных углов: через каждую точку ребра можно провести плоскость, перпендикулярную этому ребру; лучи, по которым эта плоскость пересекает грани двугранного угла, и образуют линейные углы.
Все линейные углы двугранного угла равны между собой.
Пример.
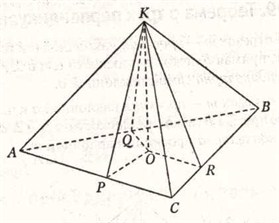
Доказательство. Прежде всего, построим линейные углы равных двугранных углов.
По определению, плоскость линейного угла должна быть перпендикулярна ребру двухгранного угла.
Следовательно, ребро двугранного угла должно быть перпендикулярно сторонам линейного угла. Если КО перпендикуляр к плоскости основания, то можно провести ОР перпендикулярно АС, ОR перпендикулярно CB, OQ перпендикулярно АВ, а затем соединить точки Р, Q, R с точкой К. Тем самым, мы построим проекции наклонных РК, QК, RК так, что рёбра АС, СВ, АВ перпендикулярны этим проекциям. Следовательно, эти рёбра перпендикулярны и самим наклонным. И потому плоскости треугольников РОQ, QOК, RОК перпендикулярны соответствующим рёбрам двугранного угла и образуют те равные линейные углы, о которых сказано в условии.
Прямоугольные треугольники РОК, QOК, RОК равны (так как у них общий катет ОК и равны противолежащие этому катету углы). Следовательно, ОР = ОR = OQ. Если провести окружность с центром О и радиусом ОР, то стороны треугольника АВС перпендикулярны радиусам ОР, OR, OQ, а потому являются касательными к этой окружности.
Остались вопросы? Не знаете, как доказать теорему?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Двугранный угол
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Понятие двугранного угла
Для введения понятия двугранного угла, для начала вспомним одну из аксиом стереометрии.
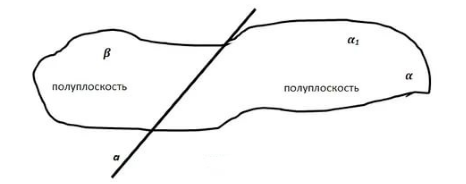
Любую плоскость можно разделить на две полуплоскости прямой $a$, лежащей в этой плоскости. При этом, точки, лежащие в одной полуплоскости находятся с одной стороны от прямой $a$, а точки, лежащие в разных полуплоскостях — по разные стороны от прямой $a$ (рис. 1).
Рисунок 1.
На этой аксиоме основан принцип построение двугранного угла.
Определение 1
Фигура называется двугранным углом, если она состоит из прямой и двух полуплоскостей этой прямой, не принадлежащих одной плоскости.
При этом полуплоскости двугранного угла называются гранями, а прямая, разделяющая полуплоскости — ребром двугранного угла (рис. 1).
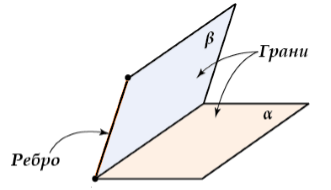
Рисунок 2. Двугранный угол
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Градусная мера двугранного угла
Определение 2
Выберем на ребре произвольную точку $A$. Угол между двумя прямыми, лежащими в разных полуплоскостях, перпендикулярных ребру и пересекающихся в точке $A$ называется линейным углом двугранного угла (рис. 3).
Рисунок 3.
Очевидно, что каждый двугранный угол имеет бесконечное число линейных углов.
Все линейные углы одного двугранного угла равняются между собой.
Доказательство.
Рассмотрим два линейных угла $AOB$ и $A_1{OB}_1$ (рис. 4).
Рисунок 4.
Так как лучи $OA$ и ${OA}_1$ лежат в одной полуплоскости $alpha $ и перпендикулярны одной прямой, то они являются сонаправленными. Так как лучи $OB$ и ${OB}_1$ лежат в одной полуплоскости $beta $ и перпендикулярны одной прямой, то они являются сонаправленными. Следовательно
[angle AOB=angle A_1{OB}_1]
В силу произвольности выборов линейных углов. Все линейные углы одного двугранного угла равны между собой.
Теорема доказана.
«Двугранный угол» 👇
Определение 3
Градусной мерой двугранного угла называется градусная мера линейного угла двугранного угла.
Примеры задач
Пример 1
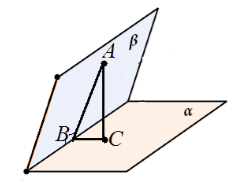
Пусть нам даны две неперпендикулярные плоскости $alpha $ и $beta $ которые пересекаются по прямой $m$. Точка $A$ принадлежит плоскости $beta $. $AB$ — перпендикуляр к прямой $m$. $AC$ перпендикуляр к плоскости $alpha $ (точка $C$ принадлежит $alpha $). Доказать, что угол $ABC$ является линейным углом двугранного угла.
Доказательство.
Изобразим рисунок по условию задачи (рис. 5).
Рисунок 5.
Для доказательства вспомним следующую теорему
Теорема 2: Прямая, проходящая через основание наклонной, перпендикулярно ей, перпендикулярна её проекции.
Так как $AC$ — перпендикуляр к плоскости $alpha $, то точка $C$ — проекция точки $A$ на плоскость $alpha $. Следовательно, $BC$ — проекция наклонной $AB$. По теореме 2, $BC$ перпендикулярна ребру двугранного угла.
Тогда, угол $ABC$ удовлетворяет всем требованиям определения линейного угла двугранного угла.
ч. т. д.
Пример 2
Двугранный угол равен $30^circ$. На одной из граней лежит точка $A$, которая удалена от другой грани на расстояние $4$ см. Найти расстояние от точки $A$ до ребра двугранного угла.
Решение.
Будем рассматривать рисунок 5.
По условию, имеем $AC=4 см$.
По определению градусной меры двугранного угла, имеем, что угол $ABC$ равен $30^circ$.
Треугольник $ABC$ является прямоугольным треугольником. По определению синуса острого угла
[frac{AC}{AB}=sin{30}^0] [frac{5}{AB}=frac{1}{2}] [AB=10]
Ответ: $10$ см.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 27.04.2023