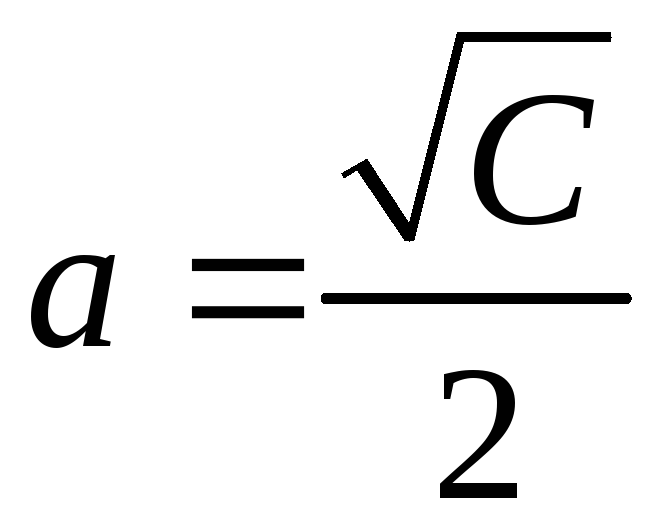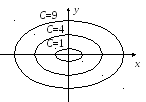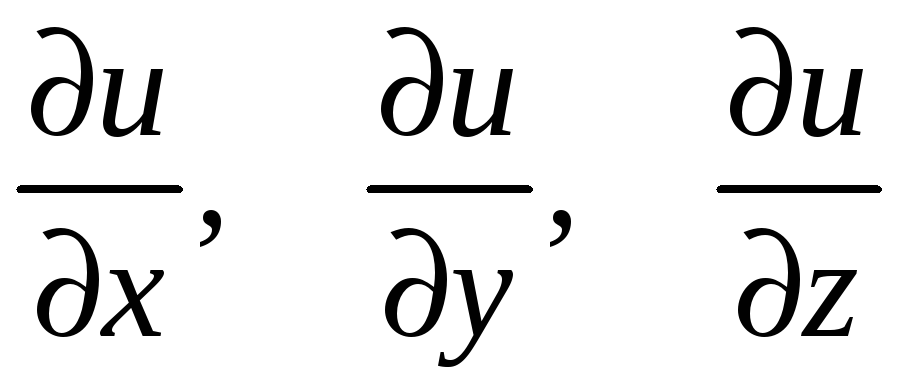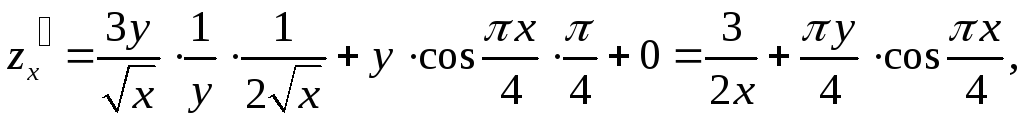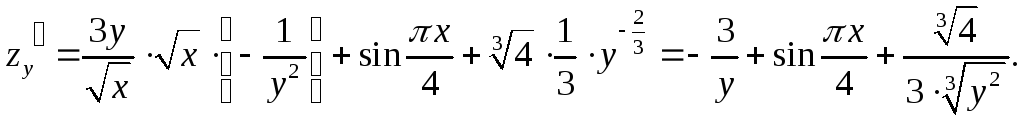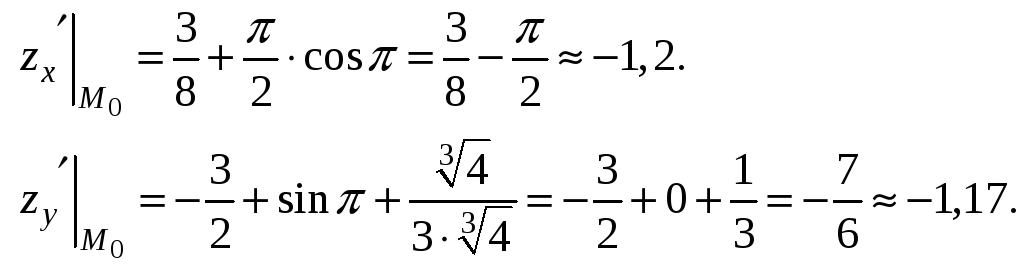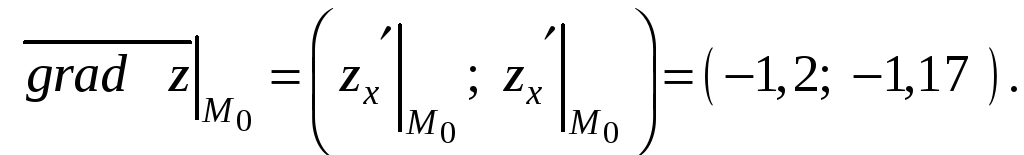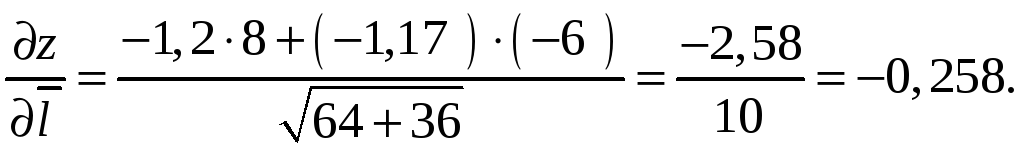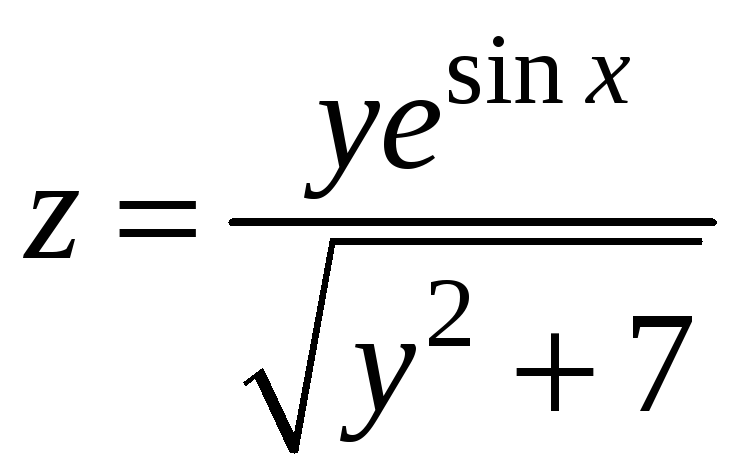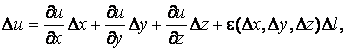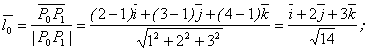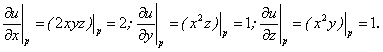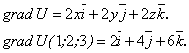Как найти линии равного уровня

Линии и поверхности уровня

Содержание:

Линии и поверхности уровня

Понятие линии и поверхности уровня:

Для характеристики функций двух переменных вводится понятие линий уровня.

Определение 2. Линией уровня функции z = f (x, y) называется совокупность всех точек на плоскости Oxy, для которых выполняется условие f (x, y) = C.

Линии уровня можно получить, пересекая поверхность z = f (x, y) плоскостями z = C, где С = соnst.

Пример 1. Найти линии уровня функции z = x 2 + y 2 .

Решение.
Пусть z = C. x 2 + y 2 = C (C ≥ 0),

В этом случае линиями уровня является множество концентрических окружностей с центром в начале координат и радиусом С (рис. 2) .Аналогично вводится понятие поверхности уровня для функции трех переменных u = f (x, y, z), (f (x, y, z) = C).

Пример 2. Найти поверхности уровня функции u = x 2 + y 2 + z 2 .

Решение. Пусть u = C. Тогда x 2 + y 2 + z 2 = C (C ≥ 0) — это множество сфер с центром в точке O(0; 0; 0) и радиусом C.

Поверхности второго порядка

Наиболее изучены поверхности в курсе аналитической геометрии — поверхности второго порядка. В общем случае уравнение такой поверхности имеет вид:
a₁₁ x 2 + 2a₁₂ xy + a₂₂ y 2 + 2a₁₃ xz + 2a₂₃ yz + a₃₃ z 2 + 2a₁₄ x + 2a₂₄ y + 2a₃₄ z + a₄₄ = 0.

В зависимости от значений коэффициентов получают различные поверхности второго порядка.

Например:
1) — конус;

2) — полусфера;

Рис. 4.

3) — эллиптический параболоид;

Рис. 5.

4) — гиперболический параболоид;

рис.6

5) — трехосный эллипсоид.

Рис. 7.

Для изучения поверхностей в трехмерном пространстве применяется метод сечений. Суть этого метода такова: пересекаем заданную поверхность плоскостями x = C₁, y = C₂, z = C₃. В результате получим некоторые кривые, характеризующие поверхность.

Пример 3. z = x 2 + y 2 . Пусть z = C₁ (C₁ ≥ 0). Получим уравнение x 2 + y 2 = C₁ (уравнение окружности). Положим y = C₂ , тогда — уравнение параболы в плоскости Оxz, которая смещена на единиц вверх по оси Oz. Положим x = C₃ , получим уравнение
Получили уравнение параболы в плоскости Оyz, которая смещена на единиц вверх по оси Оz. Из этих исследований вытекает, что графиком функции z = x 2 + y 2 является параболоид вращения вокруг оси Оz.

Гиперповерхности уровня

Пусть задана функция от n переменных u = f (x₁, x₂, . x_n) . Если положить u = C, то получим уравнение f (x₁, x₂, . x_n) = C, которое называется уравнением гиперповерхности уровня в пространстве R n . Например: Если u = C, то уравнение является уравнением гиперсферы в R n с центром в точке O (0,0, . 0) и радиусом .

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Электронная библиотека

Полем называется область пространства, каждой точке Р которой поставлена в однозначное соответствие некоторая величина Q(p).

Если величина Q(p) является физической, то поле называется физическим. В зависимости от природы функции Q(p), поля разделяются на скалярные и векторные. Примерами скалярных физических полей могут быть поля температуры, атмосферного давления, плотности воздуха, электрического потенциала, массы и т.д. К векторным величинам относятся: поля силы тяжести, скорости частиц текущей жидкости (газа), сдвига точек упругого тела, магнитной индукции и др.

Если функция Q(p) не изменяется с течением времени, то поле называется стационарным или установившимся, в противном случае – нестационарным.

Для получения общих результатов, справедливых для любых конкретных физических полей, всякому полю ставится в соответствие его математическая модель. Математическая теория поля изучает свойства векторных и скалярных полей, которые выявляются практическими задачами из физики, электротехники, математики и других наук.

Для успешного овладения теорией поля необходим математический аппарат, в который входит векторная алгебра и векторный анализ, элементы дифференциального и интегрального исчисления. Отметим, что в перспективе обобщением теории скалярных и векторных полей является теория тензорных полей, которая играют важную роль в теории упругости, теории относительности и др.

Для задания скалярного поля надо задать скалярную функцию . Введем понятие поверхности (линии) равного уровня скалярного поля.

Определение. Поверхностью равного уровня скалярного поля называется такая поверхность, на которой функция имеет постоянное значение.

Уравнение поверхности уровня:

где С – постоянная. Если функция , то говорят о линии равного уровня: .

При различных значениях С получаем семейство поверхностей (линий) уровня. Примерами поверхностей уровня являются поверхности: равных температур в некотором теле; равного потенциала V в электрическом поле .

Совокупность поверхностей (линий) уровня дает наглядное представление конкретного поля, что облегчает его изучение.

Найти поверхность уровня поля , проходящую через точку .

Решение. Уравнение поверхности уровня: U = C:

Очевидно, . Поверхностями уровня служит семейство сфер с центром в начале координат. Чтобы выбрать нужную сферу, проходящую через , требуется подставить координаты этой точки в уравнение поверхностей уровня:

Уравнение искомой поверхности уровня:

описывает сферу радиуса R = 3 с центром в начале координат.

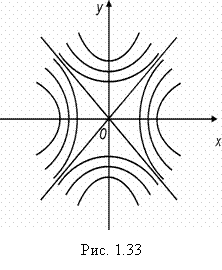
Найти линии уровня поля .

При С > 0 линии уровня есть равнобочные гиперболы с вершинами на оси Ох; при С = 0 – прямые – асимптоты этих гипербол (сопряженных) (рис. 1.33).

Понятие скалярного поля тесно связано с важным понятием производной скалярной функции по заданному направлению (в математическом анализе этого не было).

Теорема: если функция дифференцируема в точке Р, то производная в точке Р по любому направлению существует и равна (обозначается ):

Доказательство. Как известно из математического анализа [6], если функция дифференцируема, то её приращение (рис.

Разделим на обе части последнего равенства, получим:

Переходя к пределу при , и учитывая, что

получим формулу (1.91). Если , то поле возрастает; при – убывает и – дает скорость изменения поля в направлении .

Найти производную от функции по направлению от точки Р(1; 1; 1) к точке Р₁(2; 3; 4).

Формула (1.91) ставит задачу: найти то направление, которое доставляет максимальное значение для . Оказывается, такое направление дается понятием градиента скалярного поля.

Определение. Градиентом скалярного поля (обозначается grad U) называется вектор, проекции которого на оси декартовой системы координат есть , , , т.е.

Вывод: градиент скалярного поля есть вектор.

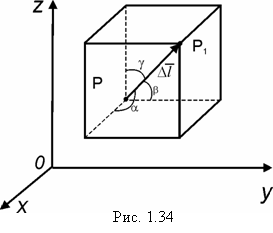
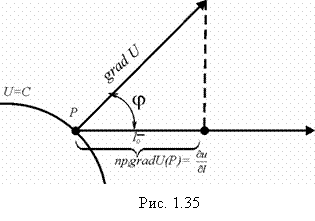
Имеется связь между производной по направлению и градиентом (рис. 1.35).

Найдем скалярное произведение :

.

Таким образом, левая часть полученного равенства есть .

При изменении будет меняться и . Очевидно, эта проекция будет максимальной, когда направление совпадает с . Учитывая физический смысл производной по направлению и формулу (1.94) убеждаемся в том, что: вектор grad U по величине и направлению есть наибольшая скорость возрастания . В этом состоит физический смысл градиента. Это широко используется в практике.

Покажем, что направлен по нормали к поверхности (линии) уровня скалярного поля , проходящей через точку Р.

Уравнение поверхности уровня: . Уравнение нормали к поверхности уровня:

где X, Y, Z – текущие координаты нормали; x, y, z – координаты поверхности, в которой проведена нормаль. Видим, что проекции направляющего вектора нормали те же, что и градиента.

Найти наибольшую скорость возрастания скалярного поля в точке Р(1; 2; 3).

Решение. Согласно (1.92) имеем:

Поверхность уровня поля U, проходящая через точку Р(1; 2; 3) – сфера: . Наибольшая скорость возрастания функции U будет в направлении радиуса этой сферы, проходящего через данную точку Р(1; 2; 3).

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Тема 5 Поверхность уровня

Поверхностью уровня называется такая поверхность, все точки которой имеют одно и то же значение рассматриваемой функции: например, поверхность равной температуры (изотермическая поверхность), поверхность равного потенциала и т.д. Для рассмотрения задач гидрогазодинамики особое значение имеет поверхность равного давления, которую кратко будем называть поверхностью уровня.

Поверхность, во всех точках которой давление жидкости одинаково называется поверхностью равного давления (или поверхностью уровня).

Так как во всех точках поверхности уровня гидростатическое давление одинаково р = const, то изменение давления dp = 0. Из основного уравнения гидростатики (4.6) dp = r × (X × dx + Y × dy + Z × dz) получим

r × (X × dx + Y × dy + Z × dz) = 0.

Так как плотность r ¹ 0, то

X × dx + Y × dy + Z × dz = 0. (5.1)

где X, Y и Z – проекции ускорения массовой (объёмной при r = const) силы на координатные оси.

Уравнение (5.1) представляет собой дифференциальное уравнение поверхности равного давления, то есть уравнение поверхности уровня.

Свойства поверхности уровня

1. Две поверхности уровня не пересекаются между собой.

Действительно, допустим, что поверхность давления р₁ пересекается с поверхностью давления р₂. Тогда в точках линии пересечения этих поверхностей давление должно быть одновременно равным и р₁ и р₂, что невозможно, так как р₁ ¹ р₂. Следовательно, пересечение этих поверхностей невозможно.

2. Внешние массовые (объёмные) силы направлены нормально к поверхности уровня.

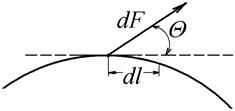
Доказать это положение можно следующим образом. Работа силы dF на элементарном пути dl равна: dА = r × (X × dx + Y × dy + Z × dz). Но для поверхности уровня трёхчлен в скобках равен нулю, поэтому работа силы dF на пути dl вдоль поверхности уровня равна нулю (dА = 0).

С другой стороны, согласно рис. 8 работа силы dF равна dА = dF × cosQ × dl. Поскольку dА = 0, а dF ¹ 0 и dl = 0, то cosQ должен быть равен нулю, то есть угол Q = .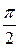

Рассмотрим равновесие капельной и газообразной жидкости в поле земного тяготения в пределах небольшой ограниченной области. Ускорения свободного падения в различных точках этого пространства будут параллельны и направлены вертикально вниз. Расположим координатную ось 0z вертикально вверх. При этом ускорение свободного падения g = 9,81 м/с 2 будет направлено параллельно оси 0z.

Составим уравнение поверхности уровня, учитывая, что для данного случая равновесия жидкости величины X, Y и Z будут равны соответственно:

Подставляя эти значения в дифференциальное уравнение поверхности уровня (5.1) X × dx + Y × dy + Z × dz = 0 получим дифференциальное уравнение поверхности уровня для рассматриваемых условий:

– g × dz = 0 или dz = 0. (5.2)

Интегрируя это уравнение, находим

Так как С = const – произвольная постоянная, то это уравнение (5.3) будет уравнением семейства горизонтальных плоскостей, параллельным осям 0x и 0y,

Итак, ели на жидкость действует только сила тяжести, поверхность уровня есть горизонтальная плоскость.

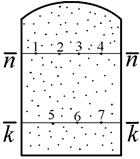
Следовательно, в пределах любой горизонтальной плоскости, проведенной через область, занятую покоящимся газом, давление остаётся неизменным (рис. 9). При равновесии газа гидростатическое давление в точке р изменяется только с высотой расположения этой точки р = f(z).

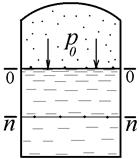
Если закрытый резервуар заполнен капельной жидкостью, то во всех точках свободной поверхности гидростатическое давление одинаково р₀ (рис. 10). Свободная поверхность воды в открытом резервуаре испытывает одно и то же атмосферное давление р_бар. Свободная поверхность в этих случаях является поверхностью уровня и, следовательно, горизонтальной плоскостью. В условиях равновесия поверхность уровня неподвижна.

Рисунок 9 Рисунок 10

Волновая поверхность водоёма также есть поверхность уровня р_бар, но волновая поверхность изменяется во времени, то есть подвижна.

Проведём произвольную горизонтальную плоскость n – n (рис. 10). Эта плоскость также будет поверхностью уровня. Во всех точках этой плоскости давление будет одинаковым.

Так как плоскости n – n и свободной поверхности параллельны между собой, то все точки плоскости n – n находятся на одной и той же глубине. Следовательно, величина гидростатического давления зависит только от глубины погружения точки под уровень свободной поверхности и на одинаковой глубине гидростатическое давление в любой точке будет одним и тем же.

Этот вывод является выражением следствия из закона Паскаля.

Следствие из закона Паскаля: на данном горизонтальном уровне внутри покоящейся жидкости давление во всех точках одинаково.

Тема 6 Распределение гидростатического давления (Интегрирование уравнения Эйлера)

Воспользуемся основным дифференциальным уравнением гидростатики (4.6)

dp = r × (X × dx + Y × dy + Z × dz).

В случае равновесия несжимаемой жидкости в поле земного тяготения проекции ускорения массовой силы (силы тяжести) X, Y и Z на координатные оси 0x, 0y и 0z (ось 0z направлена вертикально вверх) равны соответственно:

Тогда из основного дифференциального уравнения гидростатики (4.6) имеем:

dp = – r × g × dz

+ dz = 0. (6.1)

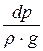
Интегрируя (6.1) при r = const, имеем

+ z = С, (6.2)

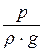
где С – постоянная интегрирования.

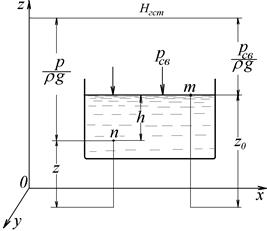
Для определения постоянной интегрирования С рассмотрим резервуар, заполненный жидкостью (рис. 12).

Для точки m, лежащей на свободной поверхности жидкости р = р_св и z = z₀. Подставляя эти значения в (6.2) находим, что

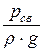
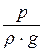
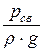
С = + z₀.

+ z = + z₀

где h – глубина погружения рассматриваемой точки под уровень свободной поверхности жидкости.

Окончательно основное уравнение гидростатики (в интегральной форме) имеет вид:

где р – полное (или абсолютное) давление в рассматриваемой точке;

р_св – давление на свободную поверхность жидкости (внешнее давление). Часто обозначается р₀;

r × g × h – относительное (или весовое) давление. Эта величина равна весу столба жидкости при единичной площади и высоте h.

Общий гидростатический закон может быть сформулирован следующим образом: давление в любой точке покоящейся жидкости равно внешнему давлению, сложенному с весом столба жидкости высотой от поверхности до данной точки с площадью основания, равной единице.

Иначе можно сказать, что абсолютное (полное) давление в рассматриваемой точке равно внешнему давлению, сложенному с давлением столба жидкости над точкой.

Если абсолютное давление в рассматриваемой точке р больше атмосферного р_бар, то разность (р – р_бар) представляет собой превышение полного давления над атмосферным и называется манометрическим или избыточным давлением в данной точке:

Если давление на свободной поверхности жидкости равно атмосферному (р_св = р_бар), то

В этом случае избыточное и весовое давление совпадают.

Если абсолютное давление в точке меньше атмосферного, то недостача абсолютного давления до атмосферного называется вакуумом или разрежением:

 Линии на плоскости xOy,
заданные уравнениями
,
где С – произвольная константа,
называются линиями уровня функции
.

Линии уровня являются линиями пересечения
поверхности, заданной функцией

и плоскости z = C,
параллельной плоскости xOy.
С помощью линий уровня можно изучать
форму поверхности, заданной функцией
.

Пример 9.2. Найти линии уровня и
определить форму поверхности, заданной
уравнением
.

Решение. Уравнения линий уровня в
данном случае имеют вид
.
При C < 0 уравнение

дает пустое множество решений
(следовательно, вся поверхность
расположена выше плоскости xOy).
При C = 0 уравнению
линии уровня удовлетворяет только одна
точка x = 0, y
= 0 (с плоскостью xOy
поверхность пересекается только вначале
координат). При C >
0 линии уровня являются эллипсами
,
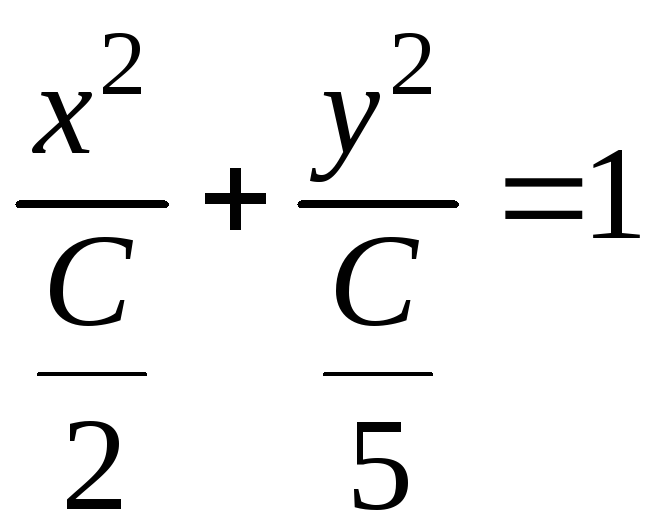
с полуосями

и
.
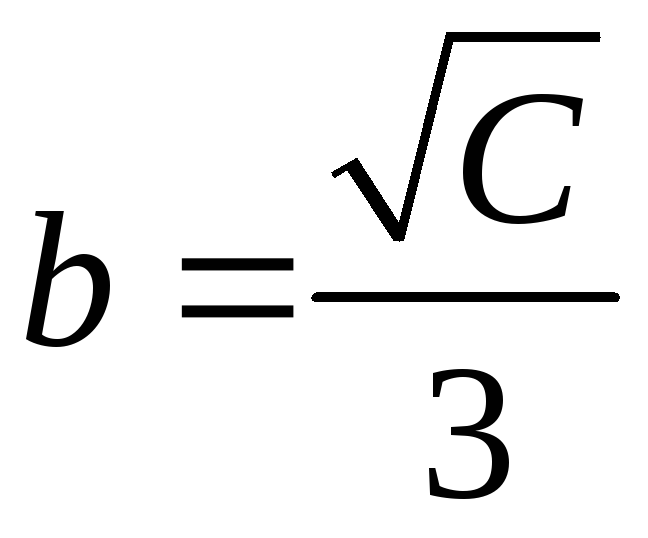
Линии уровня, соответствующие различным
значениям С, изображены на рис.
9.3. Поверхность, заданная уравнением
,
называется эллиптическим параболоидом
(рис. 9.4).

Рис.9.3 Рис. 9.4

§9.3. Частные производные первого порядка

Пусть в некоторой области D
плоскости xOy задана
функция
,
и пусть

– некоторая точка области D.

 Частной производной функции

в точке

по переменной x
(обозначается

или
)
называется

,
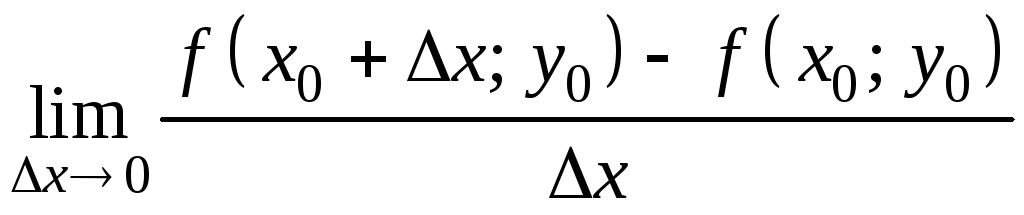
(9.1)

если данный
предел существует и конечен.

 Частной производной функции

в точке

по переменной y
(обозначается

или
)
называется

,
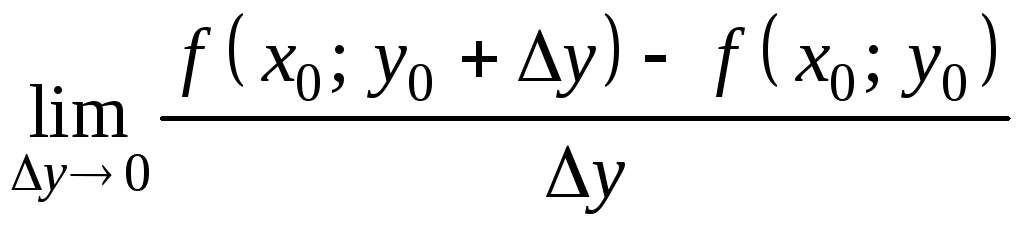
(9.2)

если данный
предел существует и конечен.

 Частной производной функции n
переменных

в точке

по переменной x_i
называется

,
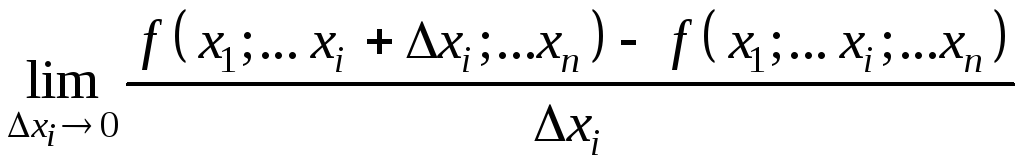
(9.3)

если данный
предел существует и конечен.

Как видно из формул (9.1) – (9.3), частные
производные определяются аналогично
тому, как определялась производная
функции одной переменной. При вычислении
предела приращение получает только
одна из переменных, остальные переменные
приращения не получают и остаются
постоянными. Следовательно, частные
производные можно вычислять по тем же
правилам, что и обычные производные,
обращаясь со всеми свободными переменными
(кроме той, по которой производится
дифференцирование) как с константами.

Пример 9.3. Найти частные производные
функции

.

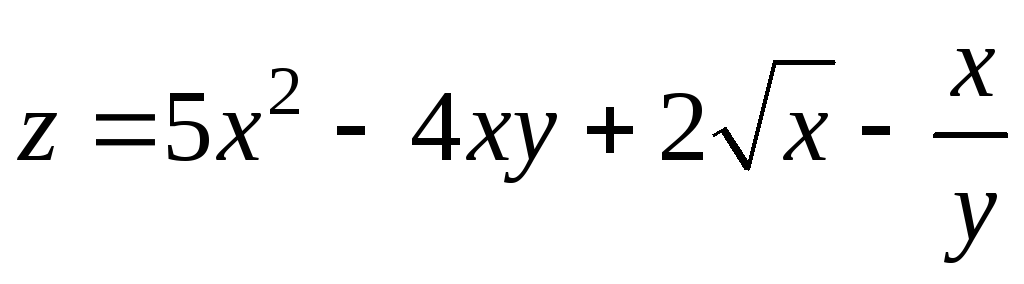
Решение.
.

.

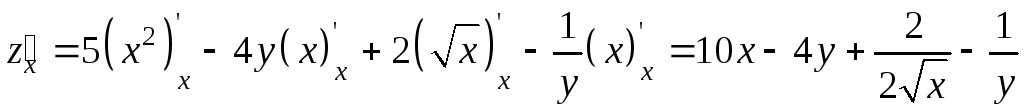
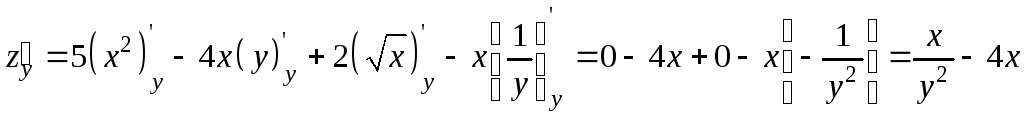
Пример 9.4. Найти частные производные
функции
.

Решение. При дифференцировании
данной функции по переменной x
мы пользуемся правилом дифференцирования
степенной функции, а при нахождении
частной производной по переменной y
– правилом дифференцирования показательной
функции:

,

.

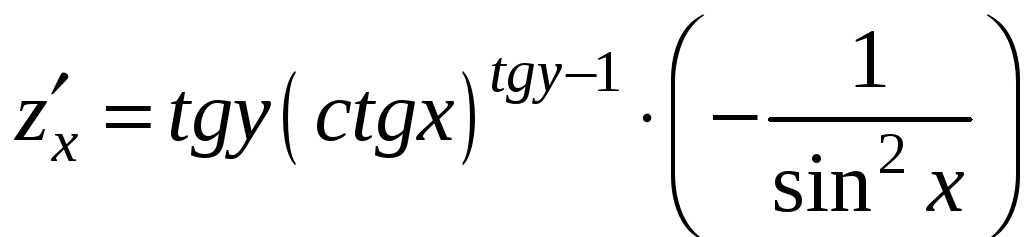
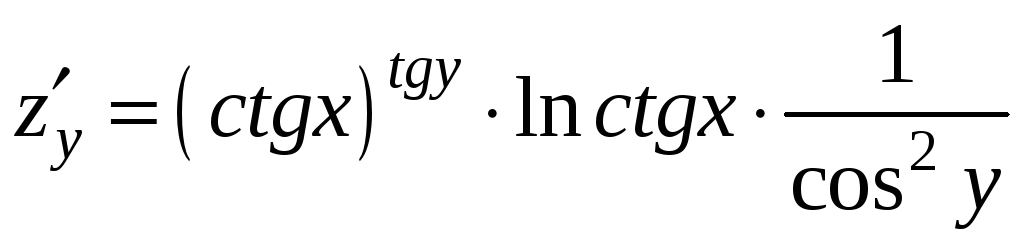
Пример 9.5. Вычислить частные
производные

функции

в точке
.

Решение. Применяя правило
дифференцирования сложной функции,
найдем частные производные

,

,

.

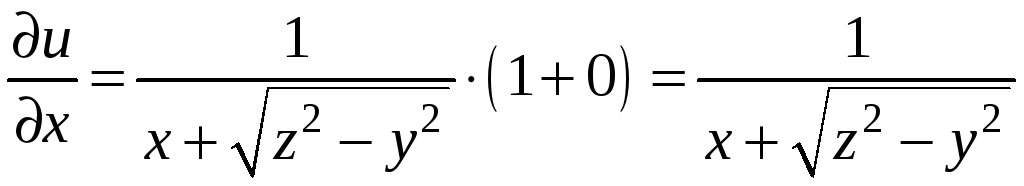
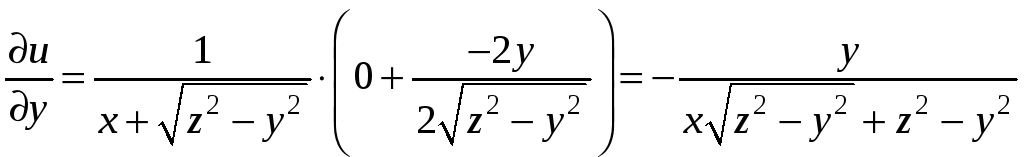
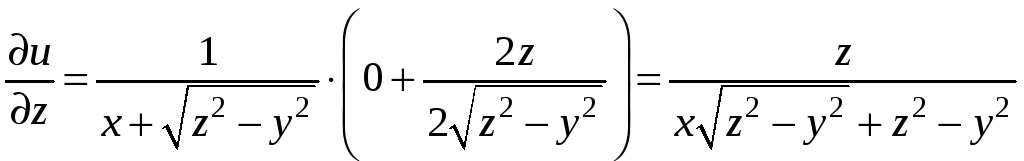
Подставляя в частные производные
координаты точки М, получим

,

,

.

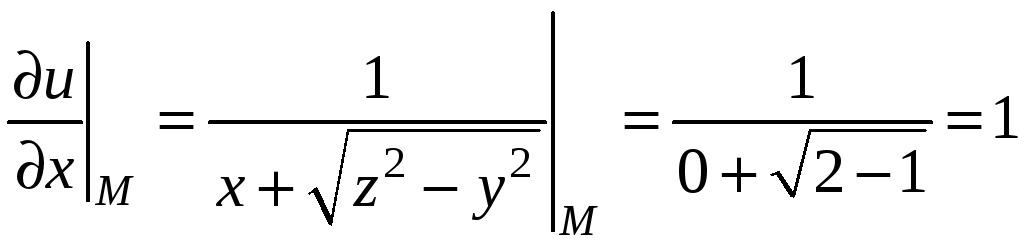
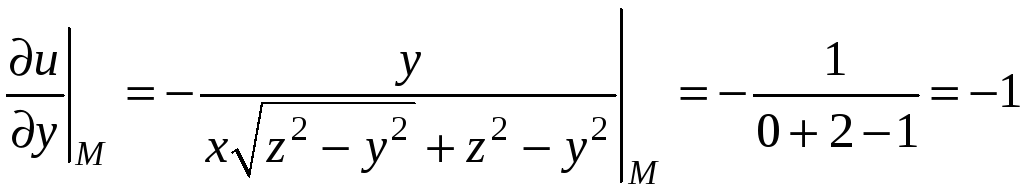
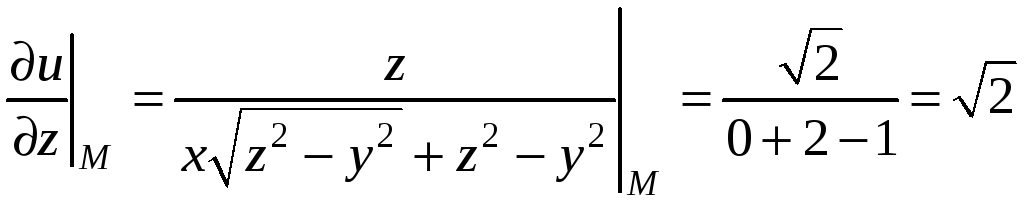
§9.4. Градиент функции нескольких переменных. Производная по направлению

 Градиентом функции

в точке

называется вектор, составленный из
частных производных данной функции,
вычисленных в данной точке:

.
(9.4)

 Если в точке

градиент функции

отличен от нулевого вектора, то он
направлен в сторону наибольшего
возрастания данной функции в точке М₀.
Это означает, что существует такое
достаточно малое число 
> 0, что в точке
,
находящейся от точки

на расстоянии r < 
(),
приращение функции

будет максимальным, если направление
вектора

совпадает с направлением вектора
.

 Производной функции

в точке

по направлению вектора

называется проекция вектора градиента
данной функции, вычисленного в точке
М₀, на данное направление

.
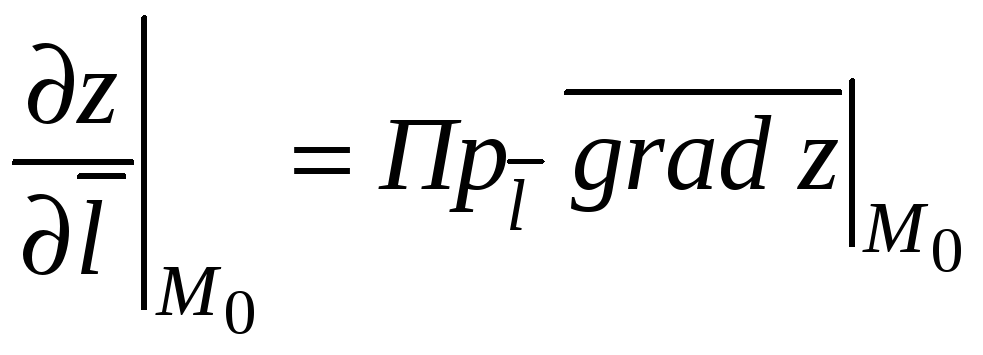
(9.5)

Из формулы (9.5) следует, что по знаку
производной по направлению в точке М₀
можно определить поведение функции
(возрастание или убывание) в данной
точке и в данном направлении. Угол между
векторами

и

острый (функция в данном направлении
возрастает), тогда и только тогда, когда
производная по направлению вектора

в точке М₀ больше нуля. Угол
между векторами

и

тупой (функция в данном направлении
убывает), тогда и только тогда, когда
производная по направлению вектора

в точке М₀ меньше нуля.

Вычисляя проекцию вектора на вектор в
соответствие с формулой (2.6) первой
части пособия, получим

.
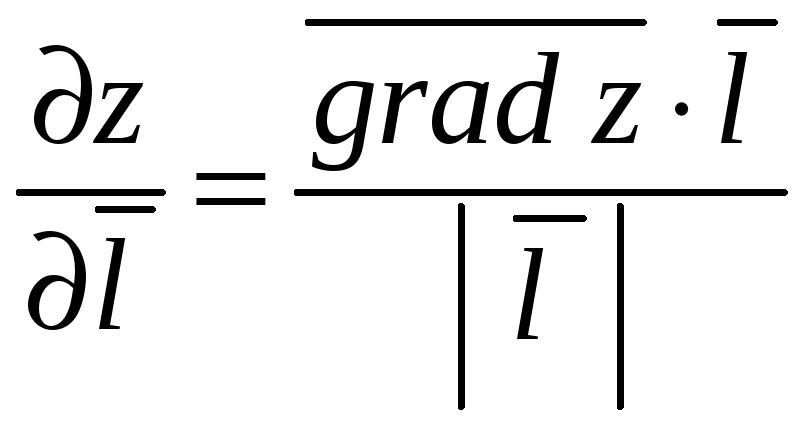
(9.6)

Замечая, что
,
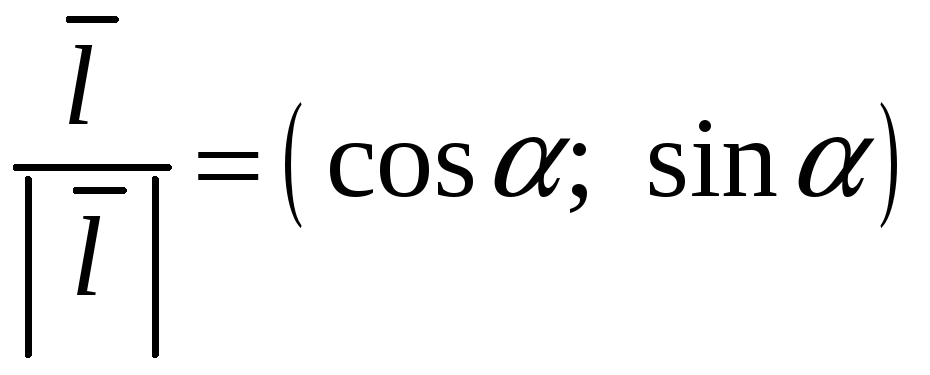
где 
– угол, который вектор

образует с осью OX,
получим еще одну формулу для вычисления
производной по направлению вектора

. (9.7)

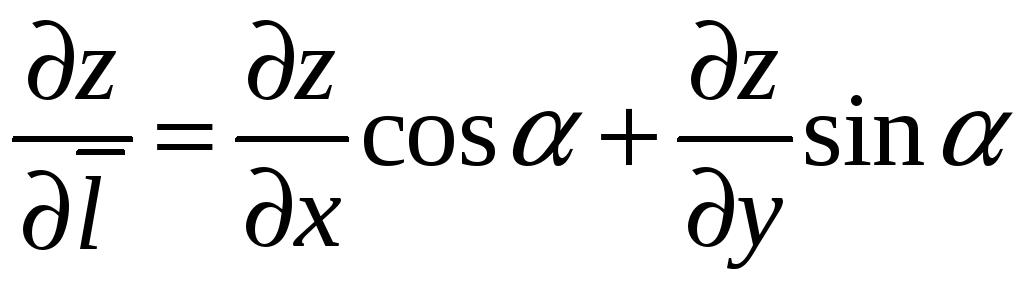
Пример 9.6. Найти градиент функции

в точке М₀(4; 2) и производную
по направлению вектора

Решение. Найдем частные производные

Вычислим значения частных производных
в точке М₀:

Градиент функции в точке М₀
найдем по формуле (9.4):

Производную функции в точке М₀
по направлению вектора

найдем по формуле (9.6):

Пример 9.7. В точке М₀(0; 1)
вычислить производную функции

по направлению биссектрисы второго
координатного угла и сделать вывод о
поведении функции в данном направлении.

Решение. Найдем частные производные
функции
:

,

.

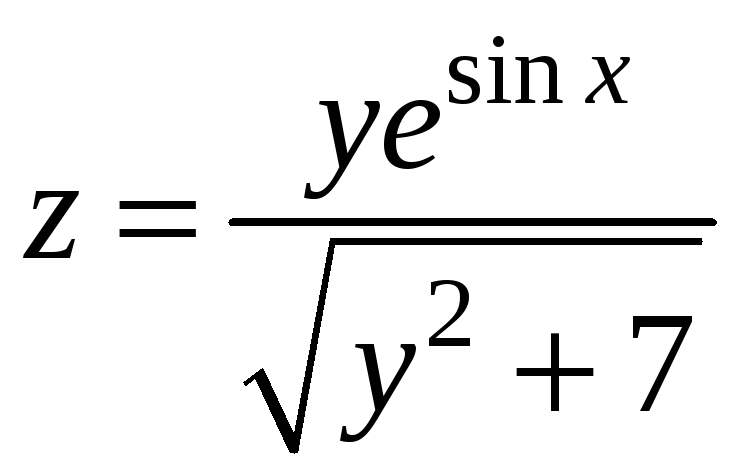
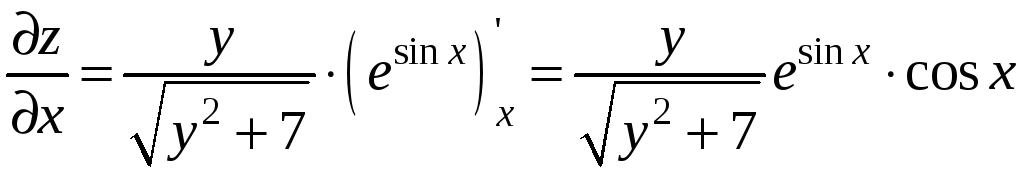
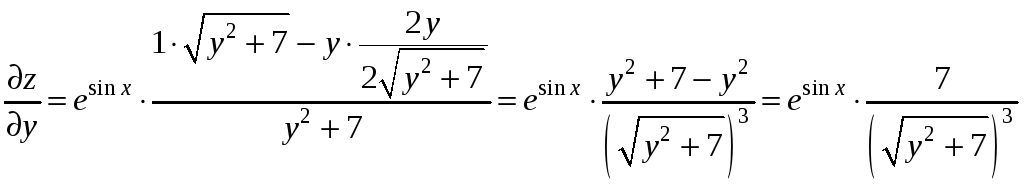
Вычислим значения частных производных
и градиент функции в точке М₀:

,

,

.

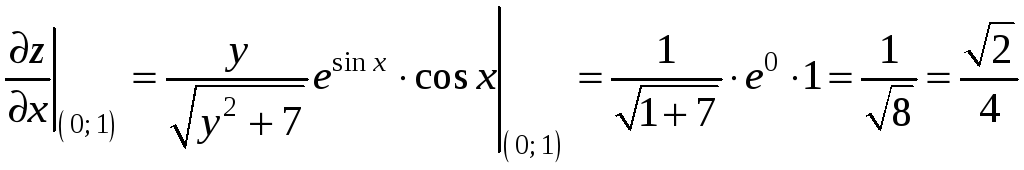
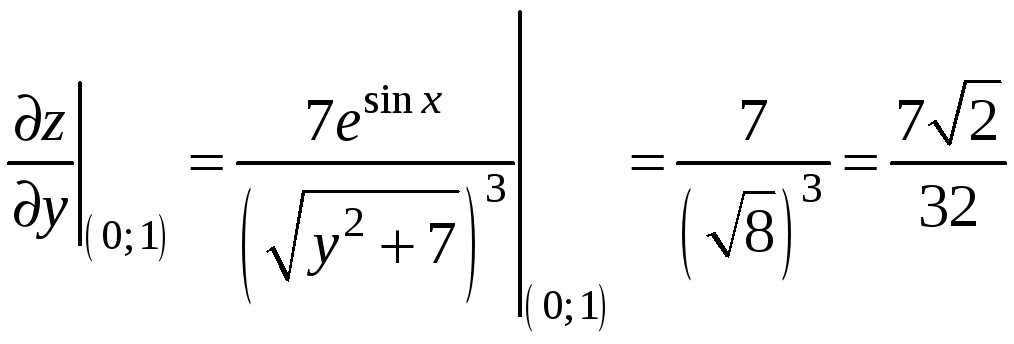
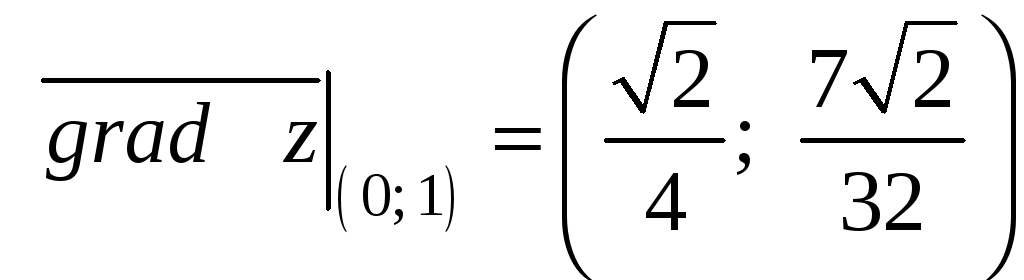
Производную функции в точке М₀
по направлению биссектрисы второго
координатного угла (данное направление
составляет с осью OX
угол 
= 135)
найдем по формуле (9.7):

.

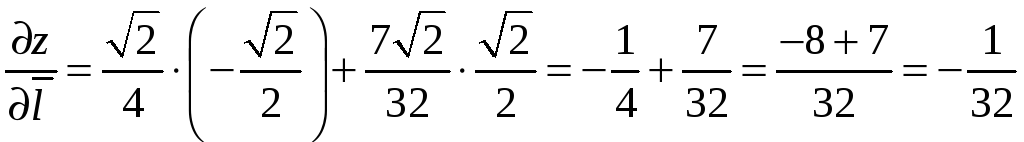
Так как прозиводная по данному
направлению отрицательна, то, следовательно,
в точке М₀ по выбранному
направлению функция убывает.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Линии и поверхности уровня

Полем называется область пространства, каждой точке Р которой поставлена в однозначное соответствие некоторая величина Q(p).

Если величина  Q(p)  является физической, то поле называется физическим. В зависимости от природы функции Q(p), поля разделяются на скалярные  и  векторные. Примерами скалярных физических полей могут быть поля температуры, атмосферного давления, плотности воздуха, электрического потенциала, массы и т.д. К векторным величинам относятся: поля силы тяжести, скорости частиц текущей жидкости (газа), сдвига точек упругого тела, магнитной индукции и др.

Если функция Q(p) не изменяется с течением времени, то поле называется стационарным или установившимся, в противном случае – нестационарным.

Для получения общих результатов, справедливых для любых конкретных физических полей, всякому полю ставится в соответствие его математическая модель. Математическая теория поля изучает свойства векторных и скалярных полей, которые выявляются практическими задачами из физики, электротехники, математики и других наук.

Для успешного овладения теорией поля необходим математический аппарат, в который входит векторная алгебра и векторный анализ, элементы дифференциального и интегрального исчисления. Отметим, что в перспективе обобщением теории скалярных и векторных полей является теория тензорных полей, которая играют важную роль в теории упругости, теории относительности и др.

Для задания скалярного поля надо задать скалярную функцию . Введем понятие поверхности (линии) равного уровня скалярного поля.

Определение. Поверхностью равного уровня скалярного поля  называется такая поверхность, на которой функция имеет постоянное значение.

Уравнение поверхности уровня:

,                                                             (1.90)

где       С – постоянная. Если функция , то говорят о линии равного уровня: .

При различных значениях С получаем семейство поверхностей (линий) уровня. Примерами поверхностей уровня являются поверхности: равных температур в некотором теле; равного потенциала V в электрическом поле .

Совокупность поверхностей (линий) уровня дает наглядное представление конкретного поля, что облегчает его изучение.

Пример 1

Найти поверхность уровня поля , проходящую через точку .

Решение. Уравнение поверхности уровня: U = C:

Очевидно, . Поверхностями уровня служит семейство сфер с центром в начале координат. Чтобы выбрать нужную сферу, проходящую через , требуется подставить координаты этой точки в уравнение поверхностей уровня:

Уравнение искомой поверхности уровня:

описывает сферу радиуса R = 3 с центром в начале координат.

Пример 2

Найти линии уровня поля .

Решение. Положим ; .

При С > 0 линии уровня есть равнобочные гиперболы с вершинами на оси Ох; при С = 0 – прямые  – асимптоты этих гипербол (сопряженных) (рис. 1.33).

Понятие скалярного поля тесно связано с важным понятием производной скалярной функции  по заданному направлению (в математическом анализе этого не было).

Теорема: если функция  дифференцируема в точке Р, то производная  в точке Р по любому направлению  существует и равна (обозначается ):

                                     (1.91)

Доказательство. Как известно из математического анализа [6], если функция дифференцируема, то её приращение (рис.

1.34) равно:

где       , когда .

Разделим на  обе части последнего равенства, получим:

Переходя к пределу при , и учитывая, что

получим формулу (1.91). Если , то поле возрастает; при  – убывает и  – дает скорость изменения поля в направлении .

Пример 3

Найти производную от функции  по направлению  от точки Р(1; 1; 1) к точке Р₁(2; 3; 4).

Решение. Найдем:

Следовательно,

Формула (1.91) ставит задачу: найти то направление, которое доставляет максимальное значение для . Оказывается, такое направление дается понятием градиента скалярного поля.

Определение. Градиентом скалярного поля (обозначается grad U) называется вектор, проекции которого на оси декартовой системы координат есть , , , т.е.

                                           (1.92)

                                           1.93)

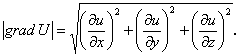
Вывод: градиент скалярного поля есть вектор.

Имеется связь между производной по направлению и градиентом (рис. 1.35).

Найдем скалярное произведение :

.

Таким образом, левая часть полученного равенства есть .

Итак,

           (1.94)

При изменении  будет меняться и . Очевидно, эта проекция будет максимальной, когда направление  совпадает с . Учитывая физический смысл производной по направлению и формулу (1.94) убеждаемся в том, что: вектор grad U по величине  и направлению есть наибольшая скорость возрастания . В этом состоит физический смысл градиента. Это широко используется в практике.

Покажем, что  направлен по нормали к поверхности (линии) уровня скалярного поля , проходящей через точку Р.

Уравнение поверхности уровня: . Уравнение нормали к поверхности уровня:

,

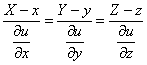
где       X, Y, Z –  текущие координаты нормали; x, y, z – координаты поверхности, в которой проведена нормаль. Видим, что проекции направляющего вектора  нормали те же, что и градиента.

Пример 4

Найти наибольшую скорость возрастания скалярного поля  в точке Р(1; 2; 3).

Решение. Согласно (1.92) имеем:

Согласно (1.93):

Значит,                                      

Поверхность уровня поля U, проходящая через точку Р(1; 2; 3) – сфера: . Наибольшая скорость возрастания функции U будет в направлении радиуса этой сферы, проходящего через данную точку Р(1; 2; 3).