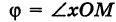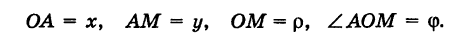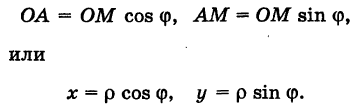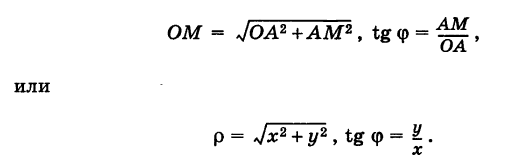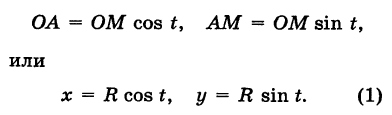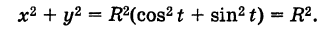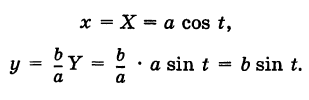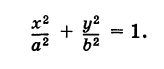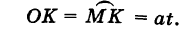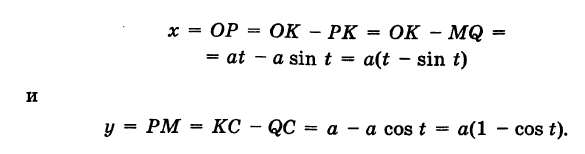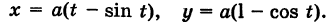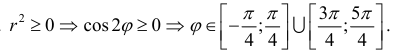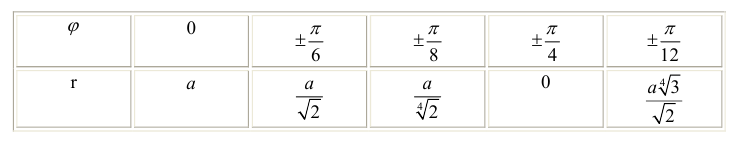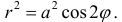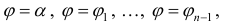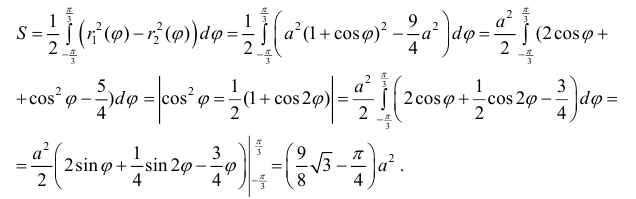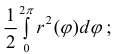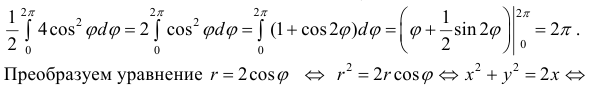4.6. Как построить линию в полярных координатах?
Собственно:
– Сначала нужно построить полярную систему координат: отметить полюс, изобразить полярную ось и указать
масштаб. Впрочем, этот пункт можно выполнить позже.
– Определяем область определения функции – угловые секторы, в которых линия существует, и в которых нет. Тонко прочерчиваем
соответствующие угловые направления (прямые и / или лучи, разграничивающие эти секторы). Лучше пунктиром.
– В большинстве случаев потребуется найти десяток-другой точек, принадлежащих линии. Но иногда можно обойтись меньшим количеством, а то и вовсе
отделаться схематическим чертежом.
– На следующем шаге следует прочертить угловые направления точек (тонкие прямые) и отметить на них найденные точки. Как это сделать с помощью
каменного топора транспортира, циркуля и линейки, я подробнейшим образом объяснил выше.
– И, наконец, отложенные точки нужно аккуратно-аккуратно соединить линией (линиями).
Отработаем алгоритм на более основательных типовых задачах:
Задача 120
Построить по точкам линию, заданную в полярной системе координат уравнением ,
рассматривая значения угла с интервалом в рад. Найти уравнение линии в
прямоугольной системе координат.
Решение: найдём область определения. Поскольку полярный радиус неотрицателен, то:
Неравенство опять же удобно решить графически. Мысленно либо на черновике изобразите график косинуса (см. Приложение
Тригонометрия) и прямой . Что означает неравенство
? Оно означает, что нас
устраивает та часть косинусоиды, которая не ниже прямой .
График косинуса полностью удовлетворяет этому условию, поэтому может принимать
любые значения, и нам предстоит «перепахать» весь круг от 0 до , причём, по
условию сделать это требуется строго с интервалом в рад. (22,5 градусов).
Ложку в зубы, калькулятор в руки:
и так далее, пока не будет пройден весь оборот до «двух пи»…., но хочется ли вам сидеть с калькулятором… и ложкой? J Используйте Приложение
Геометрический Калькулятор, который позволит буквально в пару щелчков вычислить все значения !
Вычисления, как правило, не расписывают подробно, а сразу заносят их результаты в таблицу:
Изобразим на чертеже полярную систему координат и угловые направления – тонкие прямые, соответствующие
вышеуказанным углам. Здесь можно опять воспользоваться Геометрическим Калькулятором, где все направления уже прочерчены,
но вы должны быть готовы к самым суровым обстоятельствам 
Если у вас под рукой нет ни программы, ни транспортира, ни даже линейки, то используйте мой handmade-продукт – выполните этот чертёж,
ориентируясь по клеточкам:
(углы проставлены для удобства, и на чистовике их записывать не надо)
До сих пор бережно храню этот листок бумаги, чтобы лет через 10-20 продать его антикварном аукционе J
… Шутки шутками, а оперативная память моего первого компьютера ZX Spectrum составляла 32 килобайта. КИЛОбайта. При этом программисты умудрялись
заталкивать туда аркадные игры с сотнями экранов и отличной графикой (по меркам 8-разрядных машин, конечно). …А ведь с той поры прошло немногим
больше двух десятилетий.
После ностальгических воспоминаний отметим найденные точки на чертеже и аккуратно соединим их линией:
Напоминаю, что одинаковые значения радиуса эффективнее засекать циркулем,
а слишком малые значения для углов допустимо отметить и «на глазок».
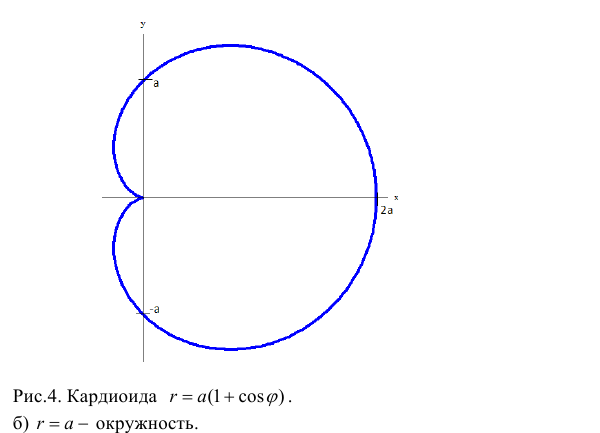
Данная кривая называется кардиоидой. Найдём её уравнение в декартовой системе координат. Для этого используем знакомый приём – домножим обе части
уравнения на «эр»:
И по формулам перехода к прямоугольным координатам ,
получим:
Перенесём «икс» налево и возведём обе части в квадрат:
Дальнейшее возведение левой части в квадрат только усложнит запись, поэтому результат целесообразнее оставить в таком виде.
Из полученного уравнения следует, что кардиоида – это алгебраическая линия 4-го порядка, и обратите
внимание, насколько сложной получилась её формула по сравнению с полярной системой координат. Алгебраическим линиям 3-го, 4-го, 5-го, 6-го и высших
порядков посвящены серьёзные исследования, и желающие без труда могут отыскать море информации по данной теме. Хорошая тема для курсовика, кстати,
или реферата. Ну а я, как обычно, предлагаю полезную и здоровую пищу на каждый день:
Задача 121
Линия задана уравнением в полярной системе координат. Треба:
1) построить линию по точкам, придавая значения через интервал
, начиная
с и заканчивая
;
2) найти уравнение линии в декартовой системе координат;
3) определить вид кривой.
Типовая формулировка, предвещающая час (а то и больше) усердного пыхтения,
а нередко и чертыханья студента. Но только не того, кто прочитал эту книгу! Примерный образец оформления задачи в конце урока.
Рассмотрим ряд других важных особенностей решения:
Задача 122
Линия задана уравнением в полярной системе координат. Требуется:
1) построить линию по точкам, начиная от до
и придавая
значения через
промежуток ;
2) найти уравнение данной линии в прямоугольной системе координат;
3) назвать линию, найти координаты фокусов и эксцентриситет.
Решение: 1) найдём область определения: .
Заметьте, что ноль в знаменателе нас тоже не устраивает, и поэтому неравенство строгое. Перенесём косинус направо: и развернём избушку – к нам передом, а к лесу задом:
Неравенство несложно решить аналитически, но для лучшего
понимания я опять воспользуюсь графическим методом. Мысленно или на черновике изобразим графики , при этом нас будет интересовать только один период – от
до
:
Условию удовлетворяет та часть синусоиды, которая расположена ПОД прямой
.
То есть, в нашем распоряжении оказываются почти все значения угла за исключением «макушки», расположенной на симметричном отрезке .
Таким образом, . Арккосинус
составляет примерно
, поэтому из
рассмотрения исключаем углы и
. Заполним расчётную таблицу с прочерками в соответствующих ячейках:
Изобразим полярную систему координат и лучи , между которыми нет точек линии. Прочертим угловые направления найденных точек и с помощью циркуля сделаем засечки. Аккуратно соединим отмеченные
точки линией (точки, соответствующие углам , не вместились на
чертёж):

системе координат. Судя по всему должна получиться гипербола. Избавляемся от дроби:
Используем формулы перехода
и дальнейшее знакомо из задач с линиями второго порядка:

– искомое
уравнение.
3) Данная линия представляется собой гиперболу с центром симметрии в точке , действительной полуосью
, мнимой полуосью
.
Вы спрОсите: «но в полярной же системе координат прорисовалась только одна ветвь гиперболы, поэтому не ошибочно ли сейчас говорить
о целой гиперболе?». Не ошибочно! И вот по какой причине: если подразумевать обобщённую полярную систему координат с отрицательными значениями «эр», то при значениях угла из интервала прорисуется левая ветвь! Желающие могут провести самостоятельную проверку и анализ этого факта. Я не сторонник и даже
противник обобщенных полярных координат, но в данном случае всё получается ловко и очень хитро – можно как бы и не оговариваться о том, что на
чертеже только одна ветвь гиперболы.
Вычислим координаты фокусов и эксцентриситет. По условию уравнение не нужно приводить к каноническому виду, а значит, требуемые вещи проще найти напрямую – с учётом параллельного переноса гиперболы, к тому же, она не повёрнута.
Вычислим значение и поправкой на параллельный перенос в точку
найдём фокусы:
Эксцентриситет:
Готово. Педантичные люди могут ещё записать развёрнутый ответ.
Заключительное задание для самостоятельного решения:
Задача 123
Линия задана уравнением в полярной системе координат. Требуется:
1) построить линию по точкам, начиная от до
и придавая
значения через
промежуток ;
2) найти уравнение данной линии в прямоугольной системе координат и определить её вид;
3) привести уравнение к каноническому виду и выполнить чертёж в прямоугольной системе координат. Найти фокусы кривой и её эксцентриситет.
Внимательно проанализируйте, что и в каком порядке требуется выполнить по условию. Сам много раз «налетал» – краем
глаза показалось одно, а нужно совсем другое. В образце решения приведение уравнения линии 2-го порядка к
каноническому виду выполнено строгим академическим способом.
Когда удобно использовать полярные координаты? Ну, конечно, когда мы имеем дело со всевозможными окружностям, дугами, кругами, эллипсами, спиралями
и т.д. А причина простА – уравнения получаются простые.
На основе полярных координат плоскости базируются цилиндрические и сферические координаты пространства. В частности, угловые
величины широко используются в воздушной навигации и астрономии. Действительно, представьте земной шар (а если строго, эллипсоид),
эллиптические орбиты планет и вы поймёте, что «распиаренная» прямоугольная система координат как-то здесь совсем «не в тему».


| Оглавление |
Автор: Aлeксaндр Eмeлин
Линия в полярной системе координат
Краткая теория
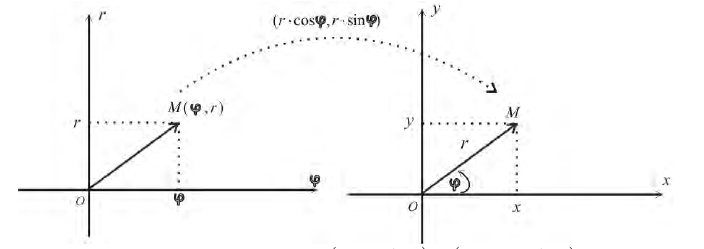
В полярной системе координат точка задается полярным углом φ и полярным радиусом r.
φ — угол, отсчитываемый от полярной оси в положительном направлении (против часовой стрелки)
r — расстояние от заданной точки до полюса
Если совместить начало декартовых координат с полюсом, а ось абсцисс с полярной осью, то между полярной и декартовой системой координат может быть установлена однозначная связь.
Пример решения задачи
Задача
Линия задана
уравнением
в полярной
системе координат. Требуется:
Решение
Построение линии по точкам
Построим линию по
точкам, предварительно заполнив таблицу значений r и j:
|
|
|
|
|
|
| 1 | 0 | 1 | 9 | 0,556 |
| 2 |
|
0,924 | 8,772 | 0,570 |
| 3 |
|
0,707 | 8,121 | 0,616 |
| 4 |
|
0,383 | 7,148 | 0,699 |
| 5 |
|
0,000 | 6,000 | 0,833 |
| 6 |
|
-0,383 | 4,852 | 1,031 |
| 7 |
|
-0,707 | 3,879 | 1,289 |
| 8 |
|
-0,924 | 3,228 | 1,549 |
| 9 |
|
-1 | 3 | 1,667 |
| 10 |
|
-0,924 | 3,228 | 1,549 |
| 11 |
|
-0,707 | 3,879 | 1,289 |
| 12 |
|
-0,383 | 4,852 | 1,031 |
| 13 |
|
0,000 | 6,000 | 0,833 |
| 14 |
|
0,383 | 7,148 | 0,699 |
| 15 |
|
0,707 | 8,121 | 0,616 |
| 16 |
|
0,924 | 8,772 | 0,570 |
| 17 |
|
1 | 9 | 0,556 |
Используя данные
таблицы, строим линию.
- Отмечаем полюс и указываем масштаб.
- С помощью транспортира прочерчиваем
угловые направления - Циркулем и линейкой отмечаем найденные
точки - Отложенные точки соединяем линией
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
График в полярной
системе координат имеет вид:
Уравнение линии в декартовой прямоугольной системе координат
Найдем уравнение
данной линии в декартовой системе координат:
Подставляя в исходное
уравнение в полярных координатах, получаем:
Полученная линия
-эллипс
Полярная система
координат на плоскости определяется
заданием некоторой точки О, луча ОР,
исходящего из этой точки, и единицы
масштаба. Точка О называется полюсом,
а луч ОР – полярной осью.

– произвольная точка плоскости. Обозначим
через r
и
ее расстояние от полюса и угол,
отсчитываемый от полярной оси против
часовой стрелки до направления ОМ. Эти
числа называются полярными координатами
точки М, причем величинаr
называется полярным радиусом, а
— полярным углом точки М. По определению
величинаЗадание пары чисел
однозначно
определяет точку М на плоскости.
Если ограничить
изменение угла
пределами
то и обратно каждой точке плоскости
однозначно соответствует пара чисел
(r,).Исключение
составляет только полюс О, для которого
r
= 0, а угол неопределенный.
На практике обычно
обобщают понятие полярных координат.
Для этого углы ,отсчитываемые от
полярной оси по часовой стрелке, считают
отрицательными и допускают, что —
При этом, правда,
различным парам чисел
будут
соответствовать одни и те же точки
плоскости (здесьn
– любое целое число). Однако это не
приводит к каким-либо противоречиям.
Если выбрать
декартову систему координат так, чтобы
ее начало О совпадало с полюсом полярной
системы, а ось ox
шла по полярной оси ОР, то между полярными
координатами (r,
)
и декартовыми координатами (x,y)
для каждой точки М будет осуществляться
следующая связь:
(6.1.1)
(6.1.2)
Из этих формул
следует, что
(6.1.3)
Замечание:
Формула
определяет два угла
(в пределах от 0 до
Формулы (6.1.3) уточняют, какой из этих
углов следует выбрать. Из формулы
вытекает, что надо брать тот угол
для которого
имеет тот же знак, что иx.
Пример 1.
Построить точки, заданные своими
полярными координатами:
A(3;
—
D(2;0).
Решение:
Для построения точек A,
B
и С из полюса О проведем лучи под углом

и на них откладываем отрезки длины 3, 2,
1 соответственно. ТочкуD
откладываем на полярной оси на расстоянии
2 от полюса.
Пример 2.
Построить линию
в полярной системе координат.
Решение:
Построим
эту линию по точкам, задавая углу
определенные значения и получая значенияr
из уравнения .
Если
Если далее
рассматривать углы из промежутка
то значенияr
будут отрицательными, так как в этом
промежутке
Это означает, что в области нет точек
данной линии.
Если
Запишем полученные
данные в таблицу
З
что последние четыре значенияr
в таблице можно было получить, если
рассмотреть отрицательные значения
угла
,
соответственно,—
;
—
—
—
.
Далее из полюса проводим лучи и откладываем
на них соответствующие значенияr.
Соединяя полученные точки плавной
линией, строим заданную кривую. Построенная
кривая является окружностью радиуса 1
с центром в точке (1,0), лежащей на полярной
оси.
Пример 3.
Построить
линию, заданную уравнением
перейдя в полярную систему координат.
Решение:
Преобразуем данное уравнение, используя
формулы (6.1.1):
,получим:
Построим эту линию
по точкам. Так как
то
Для вычисления
значений r
составляем таблицу:
Далее из полюса
проводим лучи и откладываем на них
соответствующие значения r.
Соединим полученные точки плавной
линией. Построенная кривая (см. рис.40)
также является окружностью радиуса 2 с
центром в точке
Соседние файлы в предмете Математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.20154.96 Кб8Содержание OneNote.onetoc2
- #
Download Article
Download Article
The familiar rectangular grid is an easy system to learn, but it is not convenient in all situations. What if you want to plot the spokes on a wheel, or the movement of water down a drain? In these cases, a circular coordinate system is a more natural fit. In fact, you’ve already used the basic idea of polar coordinates in everyday life.[1]
If you’re locating the source of a siren, for example, you need two piece of information: how far away it is, and which direction the sound is coming from. The polar coordinate system maps points the same way, describing the distance 

-
1
Set up the polar plane. You’ve probably graphed points with Cartesian coordinates before, using
notation to mark locations on a rectangular grid. Polar coordinates use a different kind of graph instead, based on circles:
- The center point of the graph (or «origin» in a rectangular grid) is the pole. You can label this with the letter O.
- Starting from the pole, draw a horizontal line to the right. This is the polar axis. Label the axis with units as you would the positive x-axis on a rectangular grid.
- If you have special polar graph paper, it will include many circles of different sizes, all centered on the pole. You do not have to draw these yourself if using blank paper.
-
2
Understand polar coordinates. On the polar plane, a point is represented by a coordinate in the form
:
Advertisement
-
3
Advertisement
-
1
-
2
Measure an angle of
from the polar axis. Place a protractor so the center is on the pole, and the edge runs along the polar axis. Measure the angle
from this axis. If the angle is in radians and your protractor only shows degrees, you can convert the units or refer to the unit circle for help.
-
3
Draw a line based on the sign of
. The next step will be to draw a line along the angle you measured. Before you can do this, however, you need to know which way to draw the line. Refer back to the polar coordinates
to find out:
-
4
Label the point where the line and circle meet. This is the point
.
- The point
is located on a circle with radius 5 centered on the pole, ¼ of the way along the circle’s circumference in a counter-clockwise direction from the polar axis. (This point is equivalent to (0, 5) in rectangular coordinates.)
- The point
Advertisement
First Example
Plot the point P located at 
-
1
Construct a circle with radius
. Use the pole as its centre.
-
2
Measure the angle
radians. Measure this angle from the polar axis (equivalent to the positive x-axis). Since the angle
is negative, measure this angle in a clockwise direction.
-
3
Draw a line at this angle. Start at the pole (origin). Since the radius is positive, move forward from the pole through the angle you measured. The point where the line intersects the circle is
.
Advertisement
Second Example
Plot the point Q located at 
-
1
Construct a circle with radius
. Use the pole as its centre. Although the radius is actually -2, the sign is not important for this step.
-
2
Measure the angle
radians. Since the angle
is positive, you must go counter-clockwise from the polar axis.
-
3
Construct a line opposite that angle. Since the radius
is negative, you must go from the pole in the opposite direction of the given angle. The point where the line intersects the circle is
.
Advertisement
-
1
Consider the point
in the Cartesian plane. Starting at the origin, draw a line segment 2 units along the positive x-axis. Draw a second line segment from that point 1 unit in the positive y direction. You are now at point (2, 1), so label this point P.
-
2
-
3
Find the angle between
and the positive x-axis. Use trigonometry to find this value:
-
4
Write down the polar coordinates. You now have the values of
and
. The rectangular coordinates (2, 1) convert to approximate polar coordinates of (2.24, 26.6º), or exact coordinates of
.
Advertisement
Add New Question
-
Question
How can I calculate a vector in 3D?
Vectors in 3D are represented using the x, y, and z axes. You can find their intersections and lengths just like you would in 2D vectors.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
Unlike the rectangular coordinate system, a point has infinite polar coordinates. For example, the point (1, 2π) is the same as the point (-1, π). It is also the same as the points (1, 4π), (1, 6π), (1, 8π), and so on. Each one instructs you to «circle around» a different number of times, but they all end up in the same place.[2]
Thanks for submitting a tip for review!
Advertisement
Things You’ll Need
- Paper
- Pencil
- Drawing compass
- Protractor
References
About This Article
Article SummaryX
To plot polar coordinates, set up the polar plane by drawing a dot labeled “O” on your graph at your point of origin. Draw a horizontal line to the right to set up the polar axis. When you look at the polar coordinate, the first number is the radius of a circle. To plot the coordinate, draw a circle centered on point O with that radius. The second coordinate is an angle. Use a protractor to draw a line that intersects point O at that angle. The point where the circle and the angled line meet is the polar coordinate. To learn what direction to draw your line, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 58,896 times.
Did this article help you?
Содержание:
Полярные координаты. параметрические уравнения линии
Полярные координаты
Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.
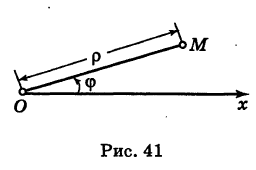
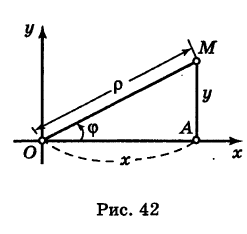
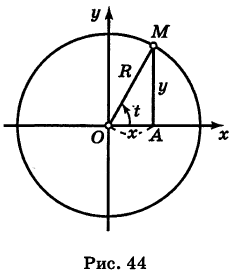
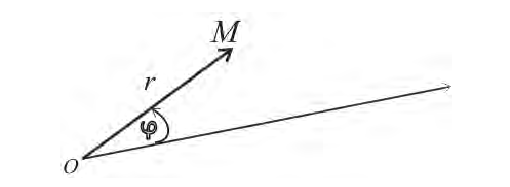
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).
Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол
Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.
Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до 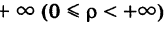
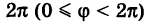
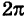
Связь между прямоугольными и полярными координатами
Рассмотрим переход от полярных координат к прямоугольным и обратно.
Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).
Тогда для произвольной точки М имеем
Считая угол ф острым, из прямоугольного треугольника АОМ находим
Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты. Далее, из этого же прямоугольного треугольника АОМ получаем
Так выражаются полярные координаты точки через ее прямоугольные координаты.
Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.
Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.
Пример:
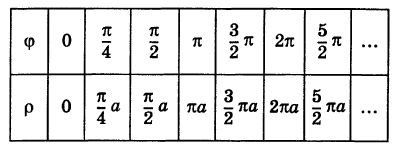
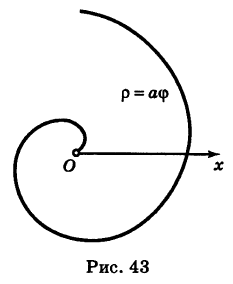
Рассмотрим кривую 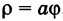
По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).
Параметрические уравнения линии
Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты 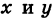
Пример:
Выведем параметрические уравнения окружности.
Пусть М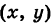
Это и есть параметрические уравнения окружности.
Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:
Пример:
Выведем параметрические уравнения эллипса.
Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где
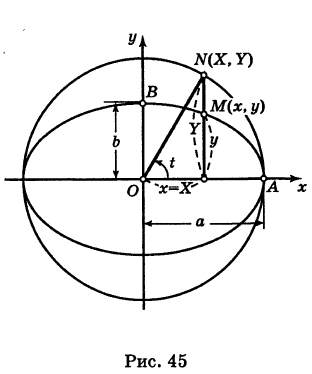
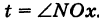
Таким образом, параметрические уравнения эллипса с полуосями а и b есть
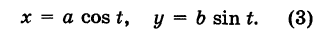
Имея параметрические уравнения линии, можно по точкам построить ее.
Пример:
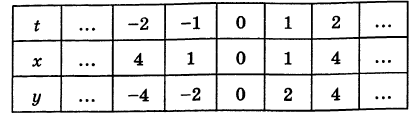
Построить кривую
Решение:
Составляем таблицу значений:
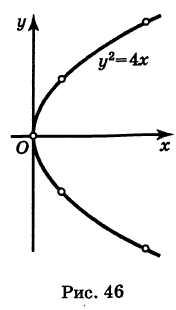
Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим 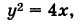
Параметрические уравнения циклоиды
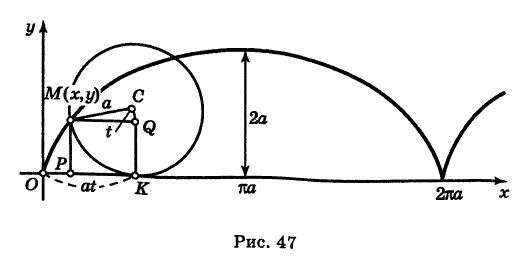
Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).
Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем
Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:
Таким образом, параметрические уравнения циклоиды есть
——-
Полярная система координат
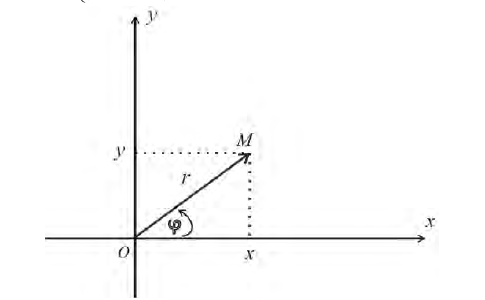
Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат Оху . Пусть М(х, у) – точка на плоскости, M ≠ 0. Полярными координатами точки М называются числа r − длина ее радиус-вектора (полярный
радиус) и ϕ − угол, образованный радиус-вектором с положительным направлением оси Ох (полярный угол), 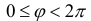
полюсом, а полуось Ох – полярной осью.
Замечание. Зависимость между прямоугольными (х, у) и полярными ( , ) r ϕ
координатами точки М задается в виде: 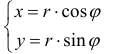
Рис.1. Полярные координаты точки.
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:
Пример 1.
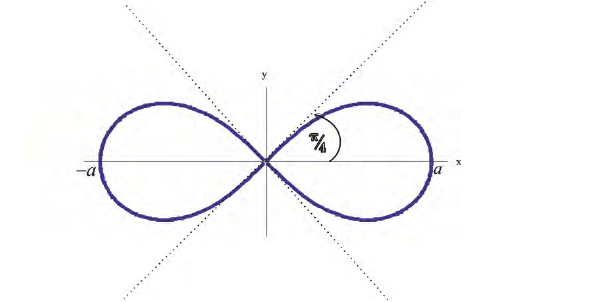
Построим на плоскости линию, заданную уравнением:
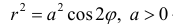
Решение.
Вычислим значения r при различных значениях ϕ :
Проводим лучи из начала координат под углами ϕ к оси Ох и на них откладываем
отрезки длины r , получим :
Рис.3. Лемниската
- Заказать решение задач по высшей математике
Пример 2.
а) Построим кривую 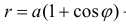
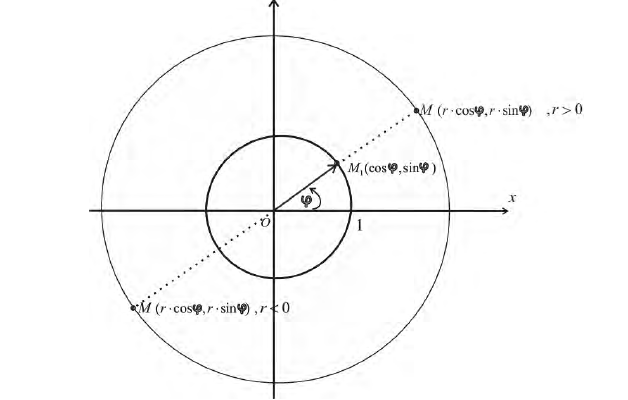
Замечание. Если в определении 1 отбросить требование 0 ≤ ϕ < 2π и не требовать r > 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).
При этом, если r > 0, то векторы 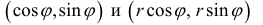
Тогда, с учетом (1), кривую r= r(ϕ) можно рассматривать как заданную параметрически в виде:
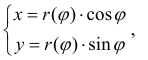
В этом случае на кривой 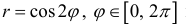
лепестка, когда 
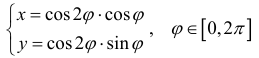
На кривой 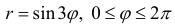
задается параметрически формулами:
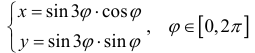
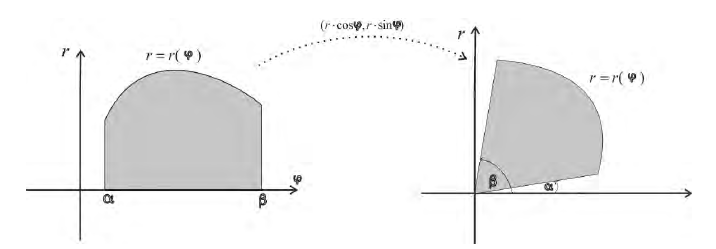
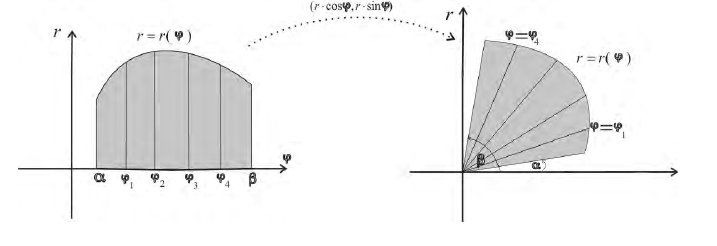
Пусть r = r(ϕ) – кривая в полярной системе координат, r (ϕ) – непрерывна при 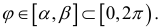
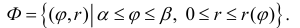
соответствует обычная криволинейная трапеция на плоскости (O, r, ϕ)
Разобьем фигуру Ф на n частичных фигур лучами 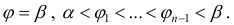
трапеции:
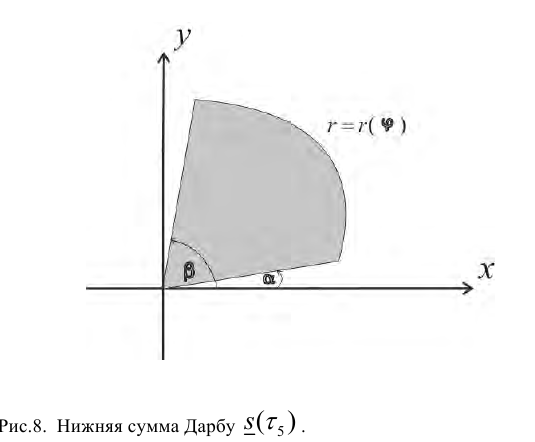
Рассмотрим, например, нижние суммы Дарбу:
Каждое слагаемое в нижней сумме 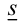
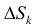
сектора радиуса 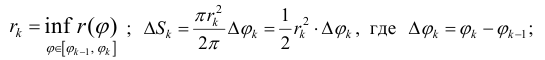
таким образом,
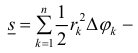
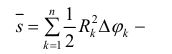
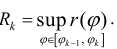
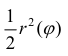
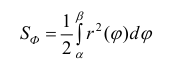
Пример 3.
Найти площадь ограниченную лемнискатой 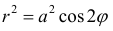
Решение.
По формуле (4):
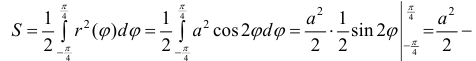
Поэтому
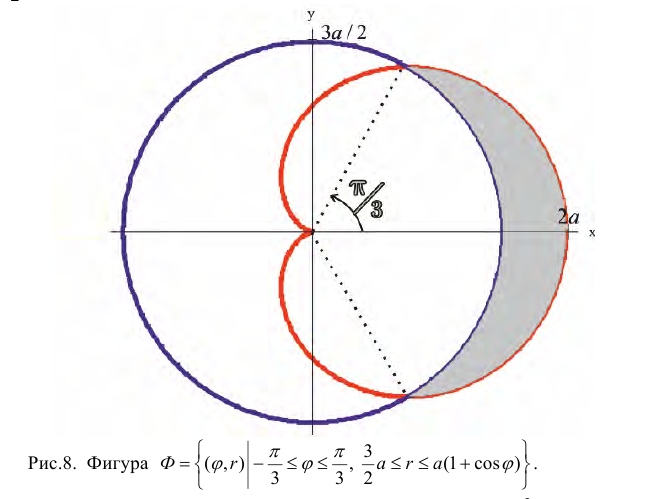
Пример 4.
Найти площадь фигуры ограниченной линиями: 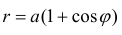
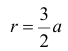
Решение. Найдем точки пересечения кривых: 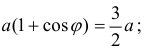
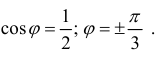
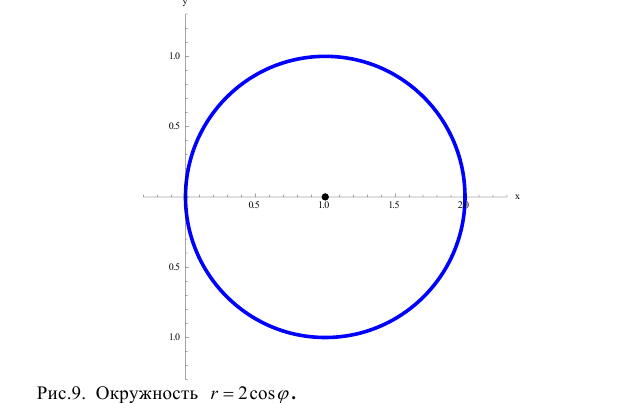
Пример 3.
r=2cosϕ. Вычислим
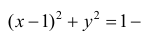
При изменении ϕ от 0 до 2 π окружность проходится дважды и оба раза против
часовой стрелки, поэтому (см. § 30) найденное значение интеграла задает
удвоенную площадь круга.
- Непрерывность функции
- Уравнения поверхности и линии в пространстве
- Общее уравнение плоскости
- Угол между плоскостями
- Интегрирование тригонометрических выражений
- Интегрирование иррациональных функций
- Прямоугольная система координат на плоскости и ее применение
- Линии второго порядка