С древовидными графами работает механизм индукции — это значит, что по каждому дереву с
вершинами можно перемещаться с шагом
ребро.
Для этого нам понадобится лист в дереве — вершина, которая находится на концах каждого дерева.
Разберем следующую теорему: у каждого дерева с хотя бы двумя вершинами есть хотя бы два листа. Докажем это утверждение.
Рассмотрим любой путь максимальной длины в дереве. Поскольку у дерева две вершины и оно связное, этот путь должен существовать. У обеих конечных точек этого пути степень
в дереве. Их единственные соседи — вершины, которые располагаются перед ними на пути.
Обсудим, почему это работает именно так:
-
У конечных точек не может быть других соседей на пути, поскольку это создало бы цикл, что невозможно в дереве
-
У конечных точек не может быть других соседей вне пути, поскольку тогда мы могли бы использовать такого соседа для расширения пути. Только это невозможно, так как у пути уже максимальная длина
Воспользуемся индукцией, чтобы доказать, что каждое дерево с
вершинами имеет
ребро.
Предположим, что все деревья на
вершинах содержат
ребро. Пусть
— дерево на
вершинах. У
есть лист
. У графа
вершин. При этом он является деревом, потому что удаление вершины не может создать цикл, а удаление листа не может разорвать граф.
По гипотезе индукции
имеет
ребер. Чтобы получить
из
было удалено одно ребро, у
должно быть
ребер. Таким образом, результат индукции верен. Такую же технику можно использовать в доказательствах с участием других деревьев.
| ВНИМАНИЕ | Для заказа программы на двоичное дерево поиска пишите на мой электронный адрес proglabs@mail.ru |
Иногда мне приходится находить количество листьев в поисковом двоичном дереве. Решил ( в первую очередь для себя ) написать эту заметку-шпаргалку, чтобы при необходимости быстро вспомнить алгоритм.
Хочу рассмотреть следующее анонимное двоичное дерево поиска:
Рисунок — стандартное анонимное бинарное дерево поиска
➡ Очевидно, чтобы найти количество листьев в бинарном дереве, необходимо знать определения термина «лист», чтобы понимать, а что, собственно, ищем-то.
Лист — узел поискового двоичного дерева, который не имеет потомков.
Тогда я отмечу все листовые узлы на рассматриваемом анонимном дереве красным цветом:
Рисунок — двоичное дерево поиска, у которого листовые вершины закрашены красным цветом
Моя задача — понять, каким образом найти все эти «красные» вершины, являющиеся листьями. То есть мне нужна функция, которая в качестве результата вернет количество листьев двоичного дерева.
Я хочу посмотреть на это анонимное поисковое бинарное дерево со всеми связями, на котором выделены красным цветом все листовые узлы с их связями:
Рисунок — бинарное дерево поиска со всеми связями его вершин
Внимательно изучив топологию этого дерева стало понятно, что листовые узлы прекращают порождение новых узлов, так как у них нет потомков ( кстати, в соответствии с их определением ). Следовательно, если встретился лист, то сразу можно делать возврат. Нет никакого смысла спускаться ниже, доходя до NULL-указателей.
Поскольку искомая программная функция должна в качестве результата возвращать количество листьев в бинарном дереве поиска, то я буду возвращать «$+1$», когда встретится лист. Понятно, что мне потребуется запустить обход вершин всего поискового дерева.
В итоге я написал следующую мощную функцию, которая считает количество листов:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
//—————————————————————————— // нахождение количества листьев в двоичном дереве поиска //—————————————————————————— int Get_leafs_count( const Node* const node ) { Node_status status = Get_status_node( node ); if ( status == NONE ) { return 0; } if ( status == LEAF ) { return 1; } return Get_leafs_count( node -> left ) + Get_leafs_count( node -> right ); } //—————————————————————————— |
Также напомню, что собой представляет пользовательский тип данных Node_status:
|
//—————————————————————————— // статус узла бинарного дерева поиска //—————————————————————————— typedef enum Node_status { NONE, // нет узла ( NULL-указатель ) LEAF, // пустой узел ( лист — не имеет сыновей ) HALF, // половинчатый ( имеет одного сына: левого или правого ) FULL // полный ( имеет обоих сыновей ) } Node_status; //—————————————————————————— |
Функция Get_leafs_count является максимально универсальной. Даже, если на вход этой функции передать пустое дерево, то она корректно обработает такую ситуацию и в качестве ответа вернет $0$. При этом данная функция является достаточно сложной для понимания, так как использует каскадную рекурсию.
➡ Думаю, что теперь я легко смогу брать алгоритм и программную функцию для своих проектов, связанных с обработкой бинарного дерева поиска.
В комментариях пишите, что непонятно в рамках этой функции. Если непонятно, что это за функция Get_status_node, которая вызывается внутри функции Get_leafs_count, то попробуйте реализовать ее самостоятельно. Цель этой функции — определение статуса узла поискового дерева. Кстати, в одной из своих заметок, я детально рассказываю об этой функции и привожу ее программную реализацию.
| ВНИМАНИЕ | Для заказа программы на двоичное дерево поиска пишите на мой электронный адрес proglabs@mail.ru |
-
Основные
определения
Дерево
– связный граф без циклов. Лес
(или ациклический
граф) – неограф без циклов. Компонентами
леса являются деревья.
Теорема 14.1.
Для неографа G
с n
вершинами без петель следующие условия
эквивалентны:
-
G
– дерево; -
G
– связной граф, содержащий n
– 1
ребро; -
G
– ациклический граф, содержащий n
– 1
ребро; -
Любые две
несовпадающие вершины графа G
соединяет единственная цепь; -
G
– ациклический граф, такой, что если в
него добавить одно ребро, то в нем
появится ровно один цикл.
Теорема 14.2.
Неограф G
является лесом тогда и только тогда,
когда коранг графа v(G)=0.
Висячая вершина
в дереве – вершина степени 1. Висячие
вершины называются листьями,
все остальные – внутренними
вершинами.
Если в дереве особо
выделена одна вершина, называемая
корнем,
то такое дерево называется корневым,
иначе – свободным.
Корневое дерево
можно считать орграфом с ориентацией
дуг из корня или в корень. Очевидно, что
для любой вершины корневого дерева,
кроме корня,
.
Для корня,
для листьев.
Вершины дерева,
удаленные на расстояние k
(в числе дуг) от корня, образуют k-й
ярус (уровень) дерева. Наибольшее значение
k
называется высотой
дерева.
Если из какой-либо
вершины корневого дерева выходят дуги,
то вершины на концах этих дуг называют
сыновьями
(в английской литературе – дочери
(daughter)).
-
Центроид дерева
Ветвь
к вершине v
дерева – это максимальный подграф,
содержащий v
в качестве висячей вершины. Вес
вершиныk
– наибольший размер ее ветвей. Центроид
(или центр масс) дерева C
– множество вершин с наименьшим весом:
C
= {v|
c(v)
=
}.
Вес любого листа
дерева равен размеру дерева. Высота
дерева с корнем, расположенным в
центроиде, не больше наименьшего веса
его вершин.
Свободное дерево
порядка n
с двумя центроидами имеет четное
количество вершин, а вес каждого центроида
равен n/2.
Теорема 14.3
(Жордана).
Каждое дерево имеет центроид, состоящий
из одной или двух смежных вершин.
Пример 14.1.
Найти наименьший вес вершин дерева,
изображенного на рис. 14.1, и его центроид.
Рис. 14.1
Решение.
Очевидно, что вес каждой висячей вершины
дерева порядка n
равен n
– 1. Висячие вершины не могут составить
центроид дерева, поэтому исключим из
рассмотрения вершины 1, 2, 4, 6, 12, 13 и 16. Для
всех остальных вершин найдем их вес,
вычисляя длину (размер) их ветвей.
Число ветвей
вершины равно ее степени. Вершины 3, 5 и
8 имеют по две ветви, размеры которых
равны 1 и 14. К вершине 7 подходят четыре
ветви размером 1, 2, 2 и 10. Таким образом,
ее вес
.
Аналогично вычисляются веса других
вершин:,
,
.
Минимальный вес вершин равен 8,
следовательно, центроид дерева образуют
две вершины с таким весом: 11 и 15.
-
Десятичная
кодировка
Деревья представляют
собой важный вид графов. С помощью
деревьев описываются базы данных,
деревья моделируют алгоритмы и программы,
их используют в электротехнике, химии.
Одной из актуальных задач в эпоху
компьютерных и телекоммуникационных
сетей является задача сжатия информации.
Сюда входит и кодировка деревьев.
Компактная запись дерева, полностью
описывающая его структуру, может
существенно упростить как передачу
информации о дереве, так и работу с ним.
Существует множество
способов кодировки деревьев. Рассмотрим
одну из простейших кодировок помеченных
деревьев с выделенным корнем – десятичную.
Кодируя дерево,
придерживаемся следующих правил.
-
Кодировка начинается
с корня и заканчивается в корне. -
Каждый шаг на одну
дугу от корня кодируется единицей. -
В узле выбираем
направление на вершину с меньшим
номером. -
Достигнув листа,
идем назад, кодируя каждый шаг нулем. -
При движении назад
в узле всегда выбираем направление на
непройденную вершину с меньшим номером.
Кодировка в такой
форме получается достаточно компактной,
однако она не несет в себе информации
о номерах вершин дерева. Существуют
аналогичные кодировки, где вместо единиц
в таком же порядке проставляются номера
или названия вершин.
Есть деревья, для
которых несложно вывести формулу
десятичной кодировки. Рассмотрим,
например, графы-звезды
,
являющиеся полными двудольными графами,
одна из долей которых состоит из одной
вершины. Другое обозначение звезд –.
На рис. 14.2 показаны
звезды, а также приведены их двоичные
и десятичные кодировки. Корень дерева
располагается в центральной вершине
звезды. Легко получить общую формулу:
. (14.1)
Рис. 14.2
Если корень
поместить в любой из висячих вершин, то
код
такого дерева будет выражаться большим
числом. Более того, существует зависимость.
Аналогично рассматриваются и цепи (рис.
14.3). Цепи обозначаются как.
Рис. 14.3
В звездах только
два варианта расположения корня с
различными десятичными кодировками. В
цепи же число вариантов кодировок в
зависимости от положения корня растет
с увеличением n.
Рассмотрим самый простой вариант,
расположив корень в концевой вершине
(листе). Для
получим двоичную кодировку 10 и десятичную
2, для– 1100 и 12, для
– 111000 и 56, для
– 11110000 и 240. Общая формула для десятичной
кодировки цепи с корнем в концевой
вершине имеет вид
. (14.2)
Пример
14.2. Записать
десятичный код дерева, изображенного
на рис. 14.4, с корнем в вершине 3.
Рис. 14.4
Решение.
На основании правила кодировки, двигаясь
по дереву, проставим в код единицы и
нули. При движении из корня 3 к вершине
7 проходим четыре ребра. В код записываем
четыре единицы: 1111. Возвращаясь от
вершины 7 к вершине 2 (до ближайшей
развилки), проходим три ребра. Записываем
в код три нуля: 000. От вершины 2 к 5 и далее
к 8 (меньший номер): 11; от 8 назад к 5 и от
5 к 9: 01; от 9 к корню 3: 000.
И, наконец, от 3 к
6 и обратно: 10. В итоге, собирая все вместе,
получим двоичный код дерева:
1 111 000 110 100 010.
Разбивая число
на тройки, переводим полученное двоичное
представление в восьмеричное. Получаем
.
Затем переводим это число в десятичное:.
Соседние файлы в предмете Дискретная математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
Использование графа, как основы для создания рубрикатора
Время на прочтение
6 мин
Количество просмотров 10K
Определения
В этой статье я опишу способы создания, и использования рубрикаторов, в основе которых лежит структура графа.
Рубрикатор, категоризатор, каталог категорий, предметный указатель, индекс. Для удобства будем считать, что все эти термины описывают примерно одно и то же. А там, где будут существенные отличия, мы будем явно на них указывать.
Информационный элемент – чаще всего файл, но в общем случае любая информация представленная как единое целое.
Введение
Рубрикаторы используются для решения самых разнообразных задач:
- Для ускорения поиска и облегчения навигации по большим массивам информации.
- Для пометки (тегирования) информации с целью организации выборок по определенным рубрикам
- Для сортировки информации по:
областям знаний (физика, математика, биология)
способам использования (Книги — читать, музыка — слушать, фильмы — смотреть)
принадлежности (папки мои и общие документы)
важности (папки inbox и spam) и т.п.
Как правило, классические рубрикаторы основаны на древовидной структуре. Основное достоинство такой организации рубрикатора – это простота и распространенность. В каждой книге есть оглавление – это пример классической структуры в виде дерева. В книге есть разделы, которые в свою очередь делятся на части, главы и так далее. Глубина рубрикатора при этом хорошо отображает сложность структуры книги. Но книга, в классическом понимании это поток информации со свойством «Forward Only». Т.е. оглавление позволяет легко найти конкретное место в книге, а далее мы открываем книгу и последовательно читаем страница за страницей.
Сложности начинаются тогда, когда в качестве книги выступает справочник, и когда при помощи рубрикатора делается попытка организовать выборочный доступ к контенту вида команд «SELECT * FROM BOOK WHERE TOPIC = ‘Something Interesting’».

Рис. 1Предметный указатель
Результатом таких попыток становится – предметный указатель. Это, очень удобный вид указателя. По нему мы можем легко и просто найти в тексте книги разделы, в которых встречается интересная нам тема. Но вот как раз тут и кроется одно из неудобств этого вида рубрикатора – невозможно сразу сгруппировать результаты, разбросанные по всей книге.
Пример: «Имитация материальной поверхности» встречается на 4 страницах. Эти страницы идут не подряд. То есть, можно предположить, что, все эти страницы относятся к разным рубрикам. Но для того, чтобы найти название соответствующей рубрики требуется проделать отдельную работу: перелистать книгу на нужную страницу и прочитать название рубрики в колонтитуле, если он есть.
Построение рубрикатора в виде графа (не дерева)
Начнем с небольшого теоретического отступления: «Дерево является связанным графом, не содержащим циклы»
Из этого определения следует, что классический рубрикатор, построенный в виде дерева, является «урезанной» версией полноценного рубрикатора, основанного на неориентированном графе.
Пример построения рубрикатора в виде графа
Для построения примера рубрикатора на основе графа возьмем близкую многим новосёлам область – строительства ремонта.
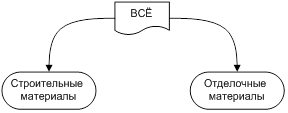
Корневой узел
Несмотря на то, что в графе не существует ярко выраженного «корня», для создания рубрикатора, в основе которого будет лежать граф – мы нарисуем/назначим один из узлов корневым. В примере – это будет узел «всё».
«Всё» — это одна из вершин графа, которая имеет специальное предназначение. Эта вершина представляет собой корневой узел дерева рубрикатора. (Так как любое дерево можно представить графом, то такая интерпретация особого назначения вполне допустима).
Необходимость наличия корневого узла рубрикатора обусловлена «привычностью» его наличия. Этот узел добавляет удобства при использовании рубрикатора человеком. Любой разговор, любое описание строения рубрикатора всегда начинается с выбора основных разделов. Так же, наличие этого узла позволяет реализовать такую удобную функцию как «хлебные крошки».
Связи
Связи – это самое ценное, что может предложить рубрикатор, составленный по принципу графа. В отличие от классического древовидного рубрикатора граф позволяет легко задать связи, наличие которых необходимо для полноты описания предметной области, но которые невозможно задать в рамках древовидной структуры.
Рассмотрим организацию связей в рубрикаторе-графе на примере более подробно.
Рис. 2 Циклы в рубрикаторе-графе
На Рис. 2 (выше) изображено подмножество рубрикатора, взятого со строительного портала stroika.ru
На примере выделена рубрика с названием «Клей паркетный». Если проследить путь, по которому можно добраться до этого раздела, то можно отметить, что узел «Клей паркетный» достижим из узла «всё» через две различные ветки рубрикатора. Узел «Клей паркетный» в равной мере относится как к разделу «Клей» так и к разделу «Паркет». Причем задание такого отношения является естественным для рубрикатора, основанного на графе.
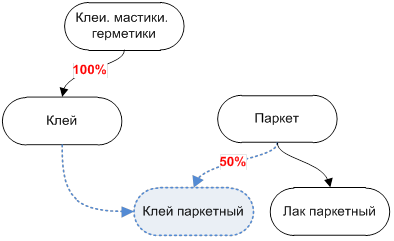
При желании данную схему можно расширить, задав для каждой дуги графа приоритет (вес). И тогда можно будет указать что «Клей паркетный» это больше клей, нежели паркет. Например, так:
Рис. 3 Приоритет связей
Возможность создавать в рубрикаторе циклы является очень важной при работе с категориями, которые:
- нельзя четко, на 100%. отнести к какой-то одной основной рубрике.
- имеют особенный смысл только при нахождении в пограничной области. Как раз, пример с клеем для паркета. Без паркета этот вид клея не имеет никакой ценности. Ценность паркетного клея именно в его применимости к паркету.
- являются ортогональными существующей структуре рубрикатора. Например, разделение товары и услуги аренды. Автокран можно как продать, так взять в аренду.
- Конкретный компьютерный вирус может быть отнесен к Email-Worm, к P2P-Worm и к Trojan Mailfinder, если он одновременно и распространяется по электронной почте, и является червём, да еще и собирает адреса email.
Приведем примеры, когда наличие множественных связей существенно упрощает рубрицирование:
- Клей паркетный (Это и клей и для паркета)
- Макро-Вирус блокер (Это и макровирус и блокер)
- Аренда автокрана (Это и аренда автотехники и автокран)
- Благотворительный концерт (И концерты и благотворительность)
- Цвет светло-зелёный металлик (И оттенки зеленого и металлики)
Вершины графа. Промежуточные рубрики
Граф-рубрикатор состоит из корневого узла «Всё», рёбер графа обозначающих подчинённость одной рубрики другой, вершин (промежуточных рубрик) и листьев (просто рубрик).
Для создания строго описанного рубрикатора требуется обязательно ответить на вопрос о физическом смысле вершин графа. Т.е. на вопрос о том, как будет трактоваться принадлежность определенной информации в вершине графа. Возможно, в некоторых случаях, будет проще вообще отказаться от использования вершин графа (не листьев!) в качестве рубрик, чем определять смысл отнесения рубрики к вершине графа.
Рассмотрим этот вопрос более детально на примере:
Рис. 4 Отнесение информации к листу и вершине графа
Информационный элемент «письмо» отнесен к рубрике «Клей паркетный». Здесь имеет место отнесение информации к листу графа. И это однозначное соответствие, которое прямо говорит нам о том, что в письме речь идет о паркетном клее. Вариант прямого, однозначного соответствия рубрике является наиболее простым и распространенным.
Более сложный вариант – элемент «Информационная статья» отнесен к рубрике «Клей». Здесь могут появиться разночтения.
Например, отнесение к рубрике «Клей» может означать, что статья носит чисто информационный характер и описывает такое вещество, как клей, в общем. Возможно, даже без упоминания таких деталей как «Клей обойный», «Клей резиновый» и «Клей паркетный».
Другой вариант – когда в статье будет описан не один конкретный «Клей паркетный» а еще и «клей резиновый». В таком случае, отнесение элемента «информационное письмо» к какой либо одной рубрике (листу графа) не будет полностью корректным.
Итого, при использовании любого древовидного рубрикатора надо обязательно определиться, будут ли вершины графа (промежуточные рубрики) использоваться для пометки информации, или же они будут использоваться только для облегчения составления и навигации по рубрикатору безотносительно рубрицируемых информационных элементов.
В случае, когда принято решение использовать в качестве рубрик не только листья, но и вершины графа, то стоит подумать о множественной рубрикации информации.
Листья. Конечные рубрики
Листья графа – это вершины графа, которые соединены с другими элементами графа только одним ребром. Применительно к графу-рубрикатору это конечные рубрики. Т.е. рубрики, которые не делятся на подрубрики.
Листья графа-рубрикатора могут содержать дополнительную информацию, которая может помочь в выборе именно этого раздела рубрикатора. В качестве такой информации могут выступать наборы ключевых слов.
Одним из интересных вариантов использования вершин и листьев графа-рубрикатора может быть вариант, когда и вершины и листья по сути сами являются ключевыми словами. В таком случае в качестве рубрик могут использоваться вершины графа, а листья будут играть роль ключевых слов. Этот вариант построения рубрикатора и алгоритм автоматического рубрицирования будет рассмотрен в следующей статье.
Содержание
- 1 Диаметр дерева
- 1.1 Алгоритм
- 1.2 Реализация
- 1.3 Обоснование корректности
- 1.4 Оценка времени работы
- 2 Центр дерева
- 2.1 Определения
- 2.2 Алгоритм
- 2.2.1 Наивный алгоритм
- 2.2.2 Алгоритм для дерева за O(n)
- 3 См. также
- 4 Источники информации
Диаметр дерева
| Определение: |
| Диаметр дерева (англ. diameter of a tree) — максимальная длина (в рёбрах) кратчайшего пути в дереве между любыми двумя вершинами. |
Пусть дан граф . Тогда диаметром называется , где — кратчайшее расстояние между вершинами.
Алгоритм
- Возьмём любую вершину и найдём расстояния до всех других вершин.
- Возьмём вершину такую, что для любого . Снова найдём расстояние от до всех остальных вершин. Самое большое расстояние — диаметр дерева.
Расстояние до остальных вершин будем искать алгоритмом .
Реализация
//граф g представлен списком смежности
int diameterTree(list<list<int>> g):
v = u = w = 0
d = bfs(g, v)
for i = 0, i < n, i++
if d[i] > d[u]
u = i
d = bfs(g, u)
for i = 0, i < n, i++
if d[i] > d[w]
w = i
return d[w]
Обоснование корректности
Будем пользоваться свойством, что в любом дереве больше одного листа. Исключительный случай — дерево из одной вершины, но алгоритм сработает верно и в этом случае.
| Теорема: |
|
Искомое расстояние — расстояние между двумя листами. |
| Доказательство: |
| Пусть искомое расстояние — расстояние между вершинами , где не является листом. Так как не является листом, то её степень больше единицы, следовательно, из неё существует ребро в непосещённую вершину (дважды посетить вершину мы не можем). |
После запуска алгоритма получим дерево .
| Теорема: |
|
В дереве не существует ребер между вершинами из разных поддеревьев некоторого их общего предка. |
| Доказательство: |
|
Предположим, существует ребро между соседними поддеревьями: Рассмотрим первую вершину, в которую приведет наш алгоритм, пусть это вершина , тогда в ходе рассмотрения всех смежных вершин мы добавим в список вершину , тем самым исключив возможность попадания их в разные поддеревья. |
Мы свели задачу к нахождению вершины , такой что сумма глубин поддеревьев максимальна.
Докажем, что одно из искомых поддеревьев содержит самый глубокий лист.
Пусть нет, тогда, взяв расстояние от до глубочайшего листа, мы можем улучшить ответ.
Таким образом мы доказали, что нам нужно взять вершину с наибольшей глубиной после первого , очевидно, что ей в пару надо сопоставить вершину , такую что максимально. Вершину можно найти запуском из .
Оценка времени работы
Все операции кроме — .
работает за линейное время, запускаем мы его два раза. Получаем .
Центр дерева
Определения
| Определение: |
| Эксцентриситет вершины (англ. eccentricity of a vertex) — , где — множество вершин связного графа . |
| Определение: |
| Радиус (англ. radius) — наименьший из эксцентриситетов вершин графа . |
| Определение: |
| Центральная вершина (англ. central vertex) — вершина графа , такая что |
| Определение: |
| Центр графа (англ. center of a graph) — множество всех центральных вершин графа . |
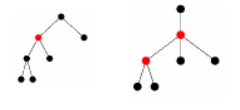
Примеры деревьев с одной и двумя центральными вершинами
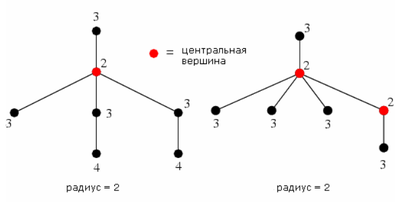
Графы, у которых показан эксцентриситет каждой вершины
Алгоритм
Наивный алгоритм
Найдём центр графа исходя из его определения.
- Построим матрицу ( — мощность множества ), где , то есть матрицу кратчайших путей. Для её построения можно воспользоваться алгоритмом Флойда-Уоршелла или Дейкстры.
- Подсчитаем максимум в каждой строчке матрицы . Таким образом, получим массив длины .
- Найдём наименьший элемент в этом массиве. Эта вершина и есть центр графа. В том случае, когда вершин несколько, все они являются центрами.
Асимптотика зависит от используемого способа подсчета кратчайших путей. При Флойде это будет , а при Дейкстре — максимум из асимптотики конкретной реализации Дейкстры и , за которую мы находим максимумы в матрице.
Алгоритм для дерева за O(n)
| Теорема: |
|
Каждое дерево имеет центр, состоящий из одной вершины или из двух смежных вершин. |
| Доказательство: |
| Утверждение очевидно для деревьев с одной и двумя вершинами. Покажем, что у любого другого дерева те же центральные вершины, что и у дерева , полученного из удалением всех его висячих вершин. Расстояние от данной вершины дерева до любой другой вершины достигает наибольшего значения, когда – висячая вершина. Таким образом, эксцентриситет каждой вершины дерева точно на единицу меньше эксцентриситета этой же вершины в дереве , следовательно, центры этих деревьев совпадают. Продолжим процесс удаления и получим требуемое. |
Собственно, алгоритм нахождения центра описан в доказательстве теоремы.
- Пройдёмся по дереву обходом в глубину и пометим все висячие вершины числом .
- Обрежем помеченные вершины.
- Образовавшиеся листья пометим числом и тоже обрежем.
- Будем повторять, пока на текущей глубине не окажется не более двух листьев, и при этом в дереве будет тоже не более двух листьев.
Оставшиеся листья являются центром дерева.
Для того, чтобы алгоритм работал за , нужно обрабатывать листья по одному, поддерживая в очереди два последовательных по глубине слоя.
См. также
- Дерево, эквивалентные определения
- Дополнительный, самодополнительный граф
Источники информации
- Wikipedia — Distance (graph theory)
- Ф. Харари: Теория графов
- А. Клебанов: Центры графов(нерабочая ссылка)