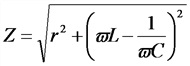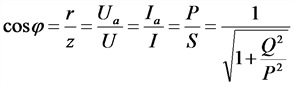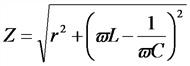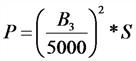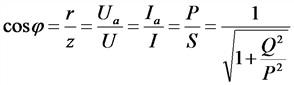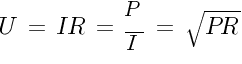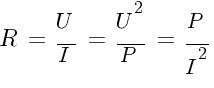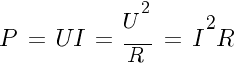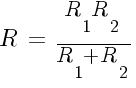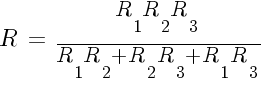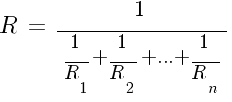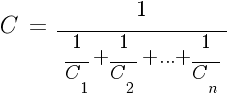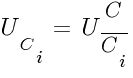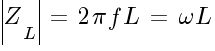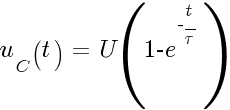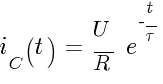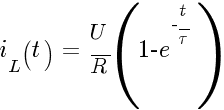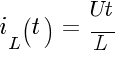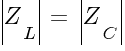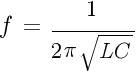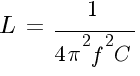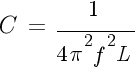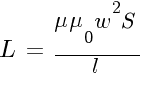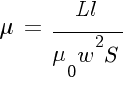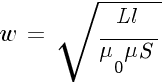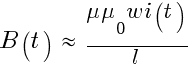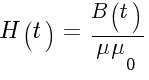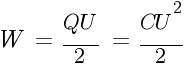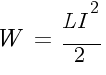Формулы, примеры решения задач: ТОЭ | Электрические машины | Высшая математика | Теоретическая механика
- Электрический ток, плотность тока, электрическое напряжение, энергия при протекании тока, мощность электрического тока
- Электрический ток
Электрический ток — это явление упорядоченного движения электрических зарядов. За направление электрического тока принимается направление движения положительных зарядов.
Формула электрического тока:
Электрический ток измеряется в амперах. СИ: А.
Электрический ток обозначается латинскими буквами i или I. Символом i(t) обозначается «мгновенное» значение тока, т.е. ток произвольного вида в любой момент времени. В частном случае он может быть постоянным или переменным.
Прописной латинской буквой I обозначается, как правило, постоянное значение тока.
В любом участке неразветвленной электрической цепи протекает одинаковый по величине ток, который прямо пропорционален напряжению на концах участка и обратно пропорционален его сопротивлению. Величина тока определяется по закону Ома:
1) для цепи постоянного тока
2) для цепи переменного тока,
где U — напряжение, В;
R — омическое сопротивление, Ом;
Z — полное сопротивление, Ом.
Омическое сопротивление проводника:
,
где l — длина проводника, м;
s — поперечное сечение, мм2;
ρ — удельное сопротивление, (Ом · мм2) / м.
Зависимость омического сопротивления от температуры:
Rt = R20 [1 + α(t — 20°)],
где R20 — сопротивление при 20°C, Ом;
Rt — сопротивление при t°C, Ом;
α — температурный коэффициент сопротивления.
Полное сопротивление цепи переменного тока:
,
где— активное сопротивление, Ом;
— индуктивное сопротивление, Ом;
— индуктивность, Гн;
— емкостное сопротивление, Ом;
— ёмкость, Ф.
Активное сопротивление больше омического сопротивления R:
,
где— коэффициент, учитывающий увеличение сопротивления при переменном токе, зависящий от: частоты тока; магнитных свойств, проводимости и диаметра проводника.
При промышленной частоте, для нестальных проводников, принимаюти считают
.
- Плотность тока
Плотность тока (j) — это сила тока, рассчитанная на единицу площади поперечного сечения (s).
Для равномерного распределения плотности тока и сонаправленности её с нормалью к поверхности, через которую протекает ток, формула плотности тока принимает вид:,
где I — сила тока через поперечное сечение проводника площадью s.
СИ: А/м2 - Электрическое напряжение
При протекании тока, как и при всяком перемещении зарядов, происходит процесс преобразования энергии. Электрическое напряжение — количество энергии, которое необходимо затратить на перемещение единицы заряда из одной точки в другую.
Формула электрического напряжения:
Электрическое напряжение обозначается латинской буквой u. Символом u(t) обозначается «мгновенное» значение напряжения, а прописной латинской буквой U обозначается, как правило, постоянное напряжение.
Электрическое напряжение измеряется в вольтах. СИ: В. - Энергия при протекании электрического тока
Формула энергии, при протекании электрического тока:
СИ: Дж - Мощность при протекании электрического тока
Формула мощности, при протекании электрического тока:
СИ: Вт.
- Электрическая цепь
- Электрическая цепь — это совокупность устройств, предназначенных для протекания по ним электрического тока.
Эти устройства называются элементами цепи. - Источники электрической энергии — устройства, преобразующие различные виды энергии, например механическую или химическую, в энергию электрического тока.
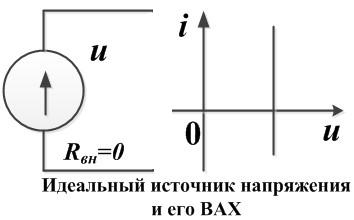
- Идеальный источник напряжения — источник, напряжение на зажимах которого не зависит от величины протекающего через него тока.
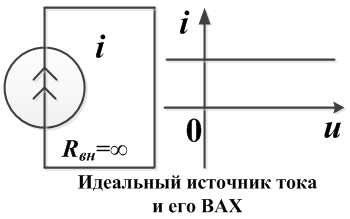
Внутреннее сопротивление идеального источника напряжения можно условно принять равным нулю. - Идеальный источник тока — источник, величина протекающего тока через который не зависит от напряжения на его зажимах.
Внутреннее сопротивление такого источника можно условно принять равным бесконечности. - Приемник — это устройство, потребляющее энергию или преобразующее электрическую энергию в другие виды энергии.
- Двухполюсник — это цепь, имеющая два зажима для подключения (полюса).
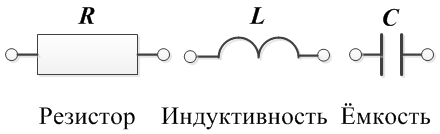
- Идеальный R-элемент (резистивный элемент, резистор) — это такой пассивный элемент цепи, в котором происходит необратимый процесс преобразования электрической энергии в тепловую.
Основной параметр резистора — это его сопротивление.
Сопротивление измеряется в омах. СИ: Ом
Проводимость — это обратная величина по отношению к сопротивлению..
Измеряется проводимость в сименсах. СИ: См.
Формула мощности R-элемента:.
Формула энергии R-элемента:
.
- Идеальный С-элемент (емкостной элемент, или конденсатор) — это такой пассивный элемент цепи, в котором происходит процесс преобразования энергии электрического тока в энергию электрического поля и наоборот. В идеальном C-элементе потери энергии отсутствуют.
Формула ёмкости:
. Примеры: задача 1, задача 2.
Ток в ёмкости:
Напряжения на ёмкости:
.
Закон коммутации для емкостного элемента. При токе конечной амплитуды заряд на C-элементе не может измениться скачком:.
.
При неизменной ёмкости, напряжение на емкостном элементе не может измениться скачком:.
Мощность C-элемента:.
При p > 0 — энергия запасается, при p < 0 — энергия возвращается в источник.
Энергия C-элемента:
, или
.
Если к моменту времени, энергия равна 0, то
Емкость измеряется в фарадах. СИ: Ф. - Идеальный L-элемент (индуктивный элемент или катушка индуктивности) — это такой пассивный элемент цени, в котором происходит процесс преобразования энергии электрического тока в энергию магнитного поля и наоборот. В идеальном L-элементе потери энергии отсутствуют.
Для линейного L-элемента формула индуктивности (L) имеет вид:
,
где— потокосцепление.
Индуктивность обозначается буквойи играет роль коэффициента пропорциональности между потоком
и током
.
Напряжение на индуктивном элементе:
.
Ток в индуктивном элементе:
.
Закон коммутации для индуктивного элемента. При напряжении конечной амплитуды, потокосцепление не может измениться скачком:.
.
При неизменной индуктивности ток в индуктивном элементе не может измениться скачком:.
Мощность L-элемента:.
При p > 0 — энергия запасается, при p < 0 — энергия возвращается в источник.
Энергия L-элемента:
, или
.
Если к моменту времени, энергия равна 0, то
Индуктивность измеряется в генри. СИ: Гн
Пример: задача 3. - R, L, C — основные пассивные двухполюсные элементы электрических цепей.
- Основные законы электрических цепей
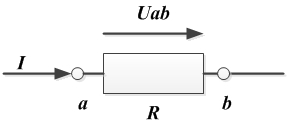
- Закон Ома для участка цепи, не содержащего источник ЭДС.
Закон Ома для участка цепи, не содержащего источник ЭДС, устанавливает связь между током и напряжением на этом участке.
Применительно к данному рисунку, математическое выражение закона Ома имеет вид:
, или
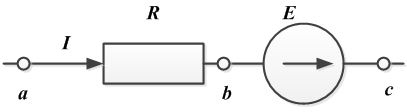
Формулируется это равенство так: при неизменном сопротивлении проводника напряжение на нем пропорционально току в проводнике. - Закон Ома для участка цепи, содержащего источник ЭДС
Для схемы
.
Для схемы
.
В общем случае
.
- Закон Джоуля-Ленца. Энергия, выделяемая на сопротивлении R при протекании по нему тока I, пропорциональна произведению квадрата силы тока и величины сопротивления:
- Законы Кирхгофа.
Топология (строение) цепи.
Электрическая схема — графическое изображение электрической цепи.
Ветвь ‐ участок цепи, содержащий один или несколько последовательно соединенных элементов и заключенный между двумя узлами.
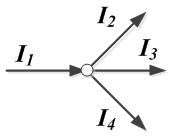
Узел ‐ точка цепи, где сходится не менее трех ветвей. Узлы нумеруют произвольно, как правило, арабской цифрой. На схеме узел может быть обозначен точкой, а может и не быть обозначен. Как правило, не обозначают те узлы, расположение которых очевидно (т‐образные соединения). Если пересекающиеся ветви образуют узел, то он обозначается точкой. Если в месте пересечения ветвей точки нет, то и узла нет (провода лежат друг на друге).
Контур – замкнутый путь, проходящий по нескольким ветвям. Контуры независимы, если отличаются хотя бы одной ветвью. Контура обозначают стрелкой с указанным направлением обхода и римской цифрой. Направление обхода выбирают произвольно. Независимых контуров в схеме может быть много, при этом не все эти контура необходимы для составления достаточного для решения задачи количества уравнений.
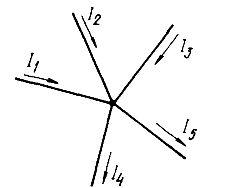
Первый закон Кирхгофа:
1) алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю:
;
2) сумма подтекающих к любому узлу токов равна сумме утекающих от узла токов:
. Пример 1. Первый закон Кирхгофа.
Второй закон Кирхгофа:
1) алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура:
2) алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю:
. Пример 2. Второй закон Кирхгофа.
- Матричная форма записи уравнений Кирхгофа:
,
где А, В — квадратные матрицы коэффициентов при токах и напряжениях порядка p х p (p — число ветвей схемы; q — число узлов схемы);
I, E — матрицы-столбцы неизвестных токов и заданных ЭДС
Элементами матрицы А являются коэффициенты при токах в левой части уравнений, составленных по первому и второму законам Кирхгофа. Первыестроки матрицы А содержат коэффициенты при токах в уравнениях, составленных по первому закону Кирхгофа, и имеют элементы +1, -1, 0 в зависимости от того, с каким знаком входит данный ток в уравнение.
Элементы следующихстрок матрицы А равны значениям сопротивлении при соответствующих токах в уравнениях, составленных по второму закону Кирхгофа, с соответствующим знаком. Элементы матрицы В равны коэффициентам при ЭДС в правой части уравнений, составленных по законам Кирхгофа. Первые
строки матрицы имеют нулевые элементы, так как ЭДС в правой части уравнений, записанных по первому закону Кирхгофа, отсутствуют. Остальные
строки содержат элементы +1, -1 в зависимости от того, с каким знаком входит ЭДС в уравнение, и 0, если ЭДС в уравнения не входит.
Общее решение уравнений, составленных по законам Кирхгофа:
,
где— матрица проводимостей.
.
Токи в каждой ветви:
;
;
.
- Режимы работы электрических цепей
- Номинальный режим работы элемента электрической цепи — это режим, при котором он работает с номинальными параметрами.
- Согласованный режим — это режим, при котором мощность, отдаваемая источником или потребляемая приемником, имеет максимальное значение. Такое значение получается при определенном соотношении (согласовании) параметров электрической цепи.
- Режим холостого хода — это такой режим, при котором через источник или приемник не протекает электрический ток. При этом источник не отдает энергию во внешнюю часть цепи, а приемник не потребляет ее. Для двигателя это будет режим без механической нагрузки навалу.
- Режим короткого замыкания — это режим, возникающий при соединении между собой разноименных зажимов источника или пассивного элемента, а также участка электрической цепи, находящегося под напряжением.
- Электрические цепи постоянного тока
- Если ток постоянный, то отсутствует явление самоиндукции и напряжение на катушке индуктивности равно нулю:
, так как
- Постоянный ток через емкость не проходит.
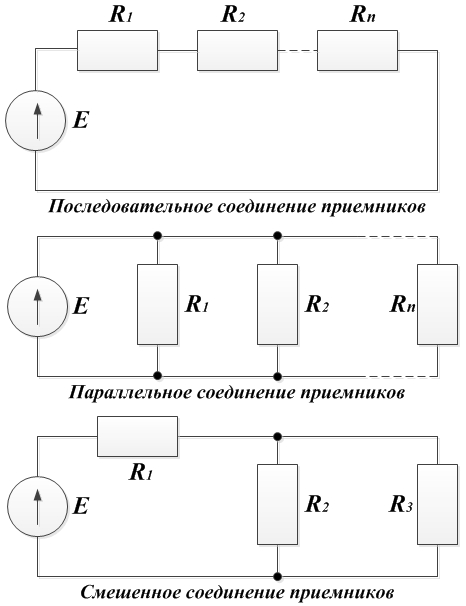
- Простая цепь постоянного тока — это цепь с одним источником при последовательном, параллельном или смешанном соединение приемников.
При последовательном соединении приемников:
I×Rэкв;
Rэкв=ΣRi.
При параллельном соединении приемников напряжение на всех приемниках одинаково.
По закону Ома токи в каждой ветви:
.
По первому закону Кирхгофа общий ток:
E×Gэкв;
Gэкв=G1+G2+…+Gn; Rэкв=1/Gэкв.
При смешанном соединении:
Rэкв=.
- Метод контурных токов.
Метод основан на применении второго закона Кирхгофа и позволяет сократить при расчете сложных систем число решаемых уравнений.
Во взаимно независимых контурах, где для каждого контура хотя бы одна ветвь входит только в этот контур, рассматривают условные контурные токи во всех ветвях контура.
Контурные токи, в отличие от токов ветвей, имеют следующие индексы:или
Уравнения составляют по второму закону Кирхгофа для контурных токов.
Токи ветвей выражают через контурные токи по первому закону Кирхгофа.
Число выбираемых контуров и число решаемых уравнений равно числу уравнений, составляемых по второму закону Кирхгофа:.
Сумма сопротивлений всех резистивных элементов каждого контура со знаком плюс является коэффициентом при токе контура, имеет следующие индексы:или
Знак коэффициента при токе смежных контуров зависит от совпадения или несовпадения направления смежных контурных токов. ЭДС входят в уравнение со знаком плюс, если направления ЭДС и направление тока контура совпадают. Пример 3. Метод контурных токов. - Метод узловых потенциалов.
Метод основан на применении первого закона Кирхгофа и позволяет сократить число решаемых уравнений при нахождении неизвестных токов до. При составлении уравнений потенциал одного из узлов схемы принимают равным нулю, а токи ветвей выражают через неизвестные потенциалы остальных
узлов схемы и для них записывают уравнения по первому закону Кирхгофа. Решение системы
уравнений позволяет определить неизвестные потенциалы, а через них найти токи ветвей.
Приследует отдавать предпочтение методу узловых потенциалов.
- Формула двух узлов:
.
Пример 4. Метод узловых потенциалов. - Метод пропорциональных величии.
Метод применяют для нахождения неизвестных токов при цепочечном соединении резистивных элементов в электрических цепях с одним источником. Токи и напряжения, а также и известную ЭДС цепи выражают через ток самой удаленной от источника ветви. Задача сводится к решению одного уравнения с одним неизвестным. - Баланс мощностей
На основании закона сохранения энергии мощность, развиваемая источниками электрической энергии, должна быть равна мощности преобразования в цепи электрической энергии в другие виды энергии:
.
— сумма мощностей, развиваемых источниками;
— сумма мощностей всех приемников и необратимых преобразований энергии внутри источников.
Баланс мощностей составляют, чтобы проверить правильность найденного решения. При этом сравнивают мощность, внесенную в цепь источниками энергии с мощностью, затрачиваемой потребителями.
Формула мощности для одного резистора:
Суммарная мощность потребителей:
PП=
Мощность источников:
Pист = PE + PJ,
где PE = ±EI — мощность источника ЭДС (определятся умножением его ЭДС на ток, протекающий в данной ветви. Ток берут со знаком, полученным в результате расчета. Минус перед произведением ставят, если направление тока и ЭДС не совпадают на схеме);
PJ = JUJ — мощность источника тока (определятся умножением тока источника на падение напряжения на нем).
Для определения UJ выбирают любой контур, который включал бы в себя источник тока. Обозначают падение UJ на схеме против тока источника, и записывают контурное уравнение. Все величины, кроме UJ, в данном уравнении уже известны, что позволяет рассчитать падение напряжения UJ.
Сравнение мощностей: Pист = PП. Если равенство соблюдено, значит, баланс сошелся и расчет токов верен. - Алгоритм расчета цепи по законам Кирхгофа
- Топология цепи.
- Определяем общее число ветвей p*.
- Определяем число ветвей с источниками тока pит. Токи в данных ветвях считаем известными и равными токам источников.
- Определяем число ветвей с неизвестными токами: p*‐pит
- Находим количество узлов q.
- Находим число уравнений, составляемых по первому закону Кирхгофа:
.
- Находим число уравнений, составляемых по второму закону Кирхгофа:
.
- Произвольно наносим на схему номера и направления неизвестных токов.
- Произвольно наносим на схему номера узлов.
- Составляем узловые уравнения для произвольно выбранных узлов (по первому закону).
- Обозначаем на схеме контура и выбираем направления их обхода.
- Количество обозначаемых контуров равно количеству уравнений, составляемых по второму закону Кирхгофа. При этом ни один из контуров не должен включать в себя ветвь с источником тока.
- Составляем контурные уравнения для выбранных контуров (по второму закону).
- Объединяем составленные уравнения в систему. Известные величины переносим в правую часть уравнений. Коэффициенты при искомых токах вносим в матрицу А (левые части уравнений)(о матрицах читаем здесь). Заполняем матрицу F, занося в нее правые части уравнений.
- Решаем полученную систему уравнений (примеры решения систем уравнений).
- Проверяем правильность решения составлением баланса мощностей.
Пример: задача 4.
- Электрические цепи переменного тока
- Электрическая цепь синусоидального тока — это электрическая цепь, в которой ЭДС, напряжения и и токи, изменяющиеся по синусоидальному закону:
- Переменный ток — это ток, периодически меняющийся по величине и направлению и характеризующийся амплитудой, периодом, частотой и фазой.
- Амплитуда переменного тока — это наибольшее значение, положительное или отрицательное, принимаемое переменным током.
- Период — это время, в течение которого происходит полное колебание тока в проводнике.
- Частота — это величина, обратная периоду.
- Фаза — это угол
или
, стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной.
- Периодический режим:
. К такому режиму может быть отнесен и синусоидальный:
,
где— амплитуда;
— начальная фаза;
— угловая скорость вращения ротора генератора.
При f = 50 Гцрад/с.
- Синусоидальный ток — это ток изменяющийся во времени по синусоидальному закону:
.
- Среднее значение синусоидального тока (ЭДС, напряжение), формула:
,
то есть среднее значение синусоидального тока составляетот амплитудного. Аналогично,
.
- Действующее значение синусоидального тока (ЭДС, напряжение), формула:
. Аналогично,
.
- Количество теплоты, выделенное за один период синусоидальным током, формула:
.
Действующее значение синусоидального тока I численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты,что и синусоидальный ток.
=R×Iпост2×T или Iпост=I=
- Коэффициент амплитуды синусоидального тока (κa) — это отношение амплитуды синусоидального тока к действующему значению синусоидального тока:
.
- Коэффициент формы синусоидального тока (κф) — это отношение действующего значения синусоидального тока к среднему за пол периода значению синусоидального тока:
κф=.
Для несинусоидальных периодических токов κa≠, κф≠1,11. Это отклонение косвенно свидетельствует о том, насколько несинусоидальный ток отличается от синусоидального.
- Резонансные явления в электрических цепях
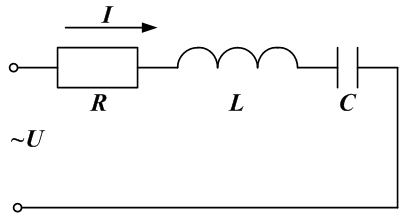
- Резонанс напряжений.
Резонансом в электрических цепях называется режим участка электрической цепи, содержащей индуктивный и емкостной элементы, при котором разность фаз между напряжением и током равна нулю.
Режим резонанса может быть получен при изменении частоты ω питающего напряжения или изменением параметров L и C.
При последовательном соединении возникает резонанс напряжения.
Ток в схеме равен:
При совпадении вектора тока с вектором напряжения по фазе:
где— резонансная частота напряжения, определяемая из условия
Тогда
Волновое или характеристическое сопротивление последовательного контура:
Добротность контура — это отношение напряжения на индуктивности или емкости к напряжению на входе в режиме резонанса:
Добротность контура представляет собой коэффициент усиления по напряжению:
ULрез=IрезXрез=
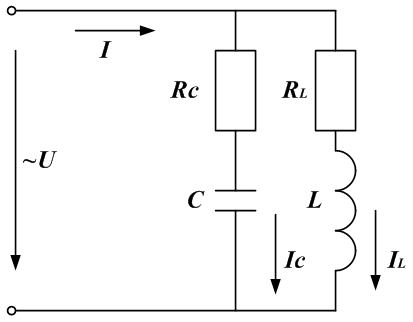
В промышленных сетях резонанс напряжений является аварийным режимом, так как увеличение напряжения на конденсаторе может привести к его пробою, а рост тока — к нагреву проводов и изоляции. - Резонанс токов.
Резонанс токов может возникнуть при параллельном соединении реактивных элементов в цепях переменного тока. В этом случае:где
тогда
При резонансной частоте реактивные составляющие проводимости могут сравниться по модулю и суммарная проводимость будет минимальной. При этом общее сопротивление становится максимальным, общий ток минимальным, вектор тока совпадает с вектором напряжения. Такое явление называется резонансом токов.
Волновая проводимость:.
При g << bL ток в ветви с индуктивностью значительно больше общего тока, поэтому такое явление называется резонансом токов.
Резонансная частота:
ω*=
Из формулы следует:
1) резонансная частота зависит от параметров не только реактивных сопротивлений, но и активных;
2) резонанс возможен, если RL и RC больше или меньше ρ, в противном случае частота будет мнимой величиной и резонанс не возможен;
3) если RL = RC = ρ, то частота будет иметь неопределенное значение, что означает возможность существования резонанса на любой частоте при совпадении фаз напряжения питания и общего тока;
4) при RL = RC << ρ резонансная частота напряжения равна резонансной частоте тока.
Энергетические процессы в цепи при резонансе токов аналогичны процессам при резонансе напряжений.
Реактивная мощность при резонансе токов равна нулю. Подробно, реактивная мощность рассмотрена здесь.
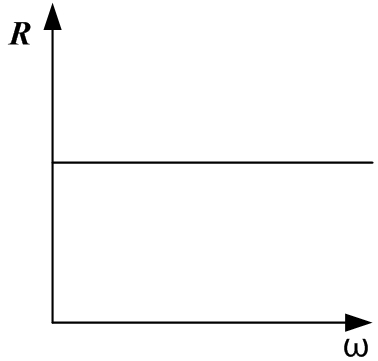
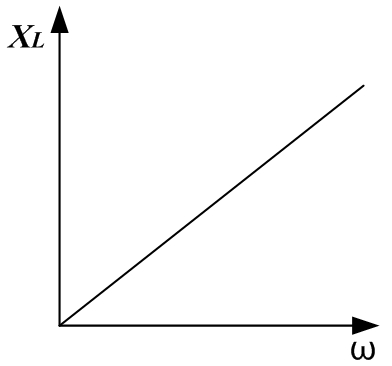
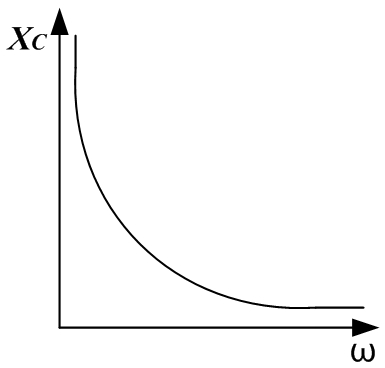
Идеальное активное сопротивление не зависит от частоты, индуктивное сопротивление линейно зависит от частоты, емкостное сопротивление зависит от частоты по гиперболическому закону:

силовая электротехника——автор Книжников ВВ
Основоположник силовой электротехники английский ученый Фарадей придумавший первый рамочный электродвигатель!!!
Электротехника это подраздел общей физики электромагнетизма или прикладной электродинамики!
Принцип действия любого электромотора основан всего на двух фундаментальных уравнениях электротехники ——
1) закон Ампера описывает момент силы М(Нм) как произведение плотности магнитного потока или индукция B(Тесла=вб/м2) , на длину проводника фазы L(м), на диаметр статора d(м), на силу тока I(А) !!!
M=(BLd)I=Ki I
На практике, чем сильней магнит—больше боковая площадь статора—-больше витков на зубе—-больше диаметр железного статора—-сильнее ток, тем выше момент силы вращения!
2) закон самоиндукции Фарадея это ЭДС наведенная как произведение полного магнитного потока Ф(Вольт с)=BS=BLd на круговую частоту изменения w=2пиf (считай кол-во переключений фаз в секунду)!!!
ЭДС=Uинд=dФ/dt=Фw=(BLd) х 2пиf
При торможении ротора нагрузочным моментом,чем больше ток, тем меньше частота переключений фаз при которой наведенная эдс запирает напряжение питания ——разница или дельта между питанием и ЭДС деленная на активное электросопротивления обмоток и есть потребляемая сила тока мотором!
Pмех=Mw=(BLd I) x (Uинд/Ф)=IUинд-----мощность электромотора прямо пропорциональна напряжению питания и силе потребляемого тока
то есть в теории любой электромотор можно форсировать по напряжению бесконечно много не превышая максимальный ток ограниченный тепловой мощностью омических потерь сопротивления обмоток Pтеп=RI2 не более 1вт на 1г массы мотора при интенсивном охлаждении, тогда Iмах=(Pтеп/R)^0.5, но на практике повышая удельную мощность мотора с 3-4 вт/г до 6-8 вт/г можно увеличить напряжение питания от номинала всего 1.5-2раза из-за возможности пробоя лаковой изоляции проводов обмоток соседних фаз!!!
моментность Ki=M/I=U/w=1/2пиf/U=0.16/Кхх----обратно пропорциональна оборотистости Кхх=f/U
Электрический заряд является носителем энергии, которую можно преобразовать в механическую мощность движения тела!
Все преобразования энергии возможны лишь через гармоническое уравнение Фурье или возвратно-поступательную функцию вращения—-то есть любая трансформация электроэнергии требует наличие переменного тока желательно формы синусоиды !
За это отвечают генераторы переменного напряжения ——постоянной частоты для трансформаторов и асинхронных электродвигателей и переменной частоты для синхронных силовых приводов ——например модельные эд! Основоположник передачи электроэнергии на большие расстояния по принципу переменного напряжения сербский ученый Тесла!
Чем выше частота переключений в фазах эд или частота питающего переменного напряжения, тем выше удельная мощность электро-потребителя по закону насыщения линий гистерезиса магнитного потока в железе статора трансформатора или эд!
Для питания синхронных эд через БУМ типа регулятора хода справедливо закономерность— чем выше напряжение, тем выше частота вращения и больше мощность, которую можно снять с эму при тойже силе тока, ограниченной омическими тепловыми потерями на обмотках!
Для оптимизация полной электроцепи типа —аккумулятор—регулятор хода—-электромотор применима эмпирическая зависимость ——корень квадратный из потребляемой мощности на полном газу и есть напряжения акку в вольтах и ток в амперах!!!
например для ВМГ электросамолёта Рпотр=340вт ,тогда корень получается по напряжению 18,3В и ток 18,3А!!!то есть достаточно липо акку на 5 банок и регулятор хода на 20А, провода сечением 2мм2 и разъём силовой на диаметр в 2 мм типа бананов
На практике оптимальная сила тока протекающая через обмотки электромотора на полном газу при максимальном КПД электродвигателя равна корню квадратному из произведения тока холостого хода на напряжение питания и делённого на электро сопротивление мотора
Iопт=(Рхх/Rэд)0.5=(Iхх Uакку/Rэд)^0.5 это очень красивая формула!!!
например—-например при омическом сопротивлении обмоток R=0.1ом —-Iопт=(1а х 11в/0.1ом)^0.5=10.5а!
Математика следующая—-
1) Ртеп = Rэд (I)^2 —-тепловые омические потери в обмотках эд в ваттах
2) Рпер = U Iхх—- электромагнитные потери на перемагничевание железа статора в вт
3) Рпотерь = Ртеп + Рпер—-общая мощность потерь в вт
4) Рэл = U I—-входная потребляемая электрическая мощность в вт
5) Рмех = Рэл − Рпотерь—-механическая мощность на валу или полезная мощность эд
6) КПДэд = Efficiency = Pмех/ Pэл—- Коэффициент Полезного Действия эд или эффективность
7) Ki = 1/Ku = 1/(2пи Кхх)—-электромеханическая постоянная эд нм/а по моменту (моментность электромотора)

9) Кхх= Ku/6.28 = fхх/Uакку —-электромеханическая характеристика эд гц/в по частоте вращения (оборотистость электромотора)
10) Iопт=(Iхх Iкз )^0.5= (Iхх Uакку/Rэд)^0.5—— сила тока электромотора на максимальном КПД (среднеквадратичное значение)
Pмех(Вт)=2пи M(Нм) f(Гц)=Рэл-(Ртеп+Рпер)=Uакку(В) Iэд(А)-Iэд(А)2 Rобм(Ом)-Uакку(В) Iхх(А)
например для бк эд массой 100 г——— Рмех=15в х 30а -30а х 30а х 0.05ом -15в х 2а= 450вт-45вт-30вт= 375 вт!
и КПДэд= 375вт / 450вт = 0.83 = 83% , Kхх=300гц/15в=20гц/в=1200 оборотов в минуту на вольт!
подробно об электродвигателях смотри статью «силовые электроприводы»
общие закономерности расчёта электро-цепей для компонентов а и в
наименование компонента ——— параллельное соединение ——— последовательное соединение
сопротивление резистора ————- Rобщ=(Rа Rв)/(Rа+Rв)———————Rобщ=Rа+Rв
индуктивность катушки ——————Lобщ=(Lа Lв)/(Lа+Lв)————————Lобщ=Lа+Lв
емкость конденсатора——————-Cобщ=Cа+Cв——————————Cобщ=(Cа Cв)/(Cа+Cв)
реактивное сопротивление катушки индуктивности----- R=6.28f L
реактивное сопротивление емкостного конденсатора----- R=1/(6.28f C)
частота резонанса контура в Гц=1/с-------f=0.16/(LС)^0.5
В таблице представлены основные расчетные формулы по электротехнике для расчета тока, напряжения, сопротивления, мощности и других парметров электрических схем.
|
Измеряемые величины |
Формулы |
Обозначение и единицы измерения |
|
Сопротивление проводника омическое (при постоянном токе) |
|
s — сечение, мм2 |
|
Активное сопротивление при переменном токе |
|
r — активное сопротивление, Ом; k — коэффициент, учитывающий поверхностный эффект, а в магнитных проводниках — также явление намагничивания |
|
Зависимость омического сопротивления проводника от температуры |
|
|
|
Индуктивное (реактивное) сопротивление |
|
сопротивление, Ом; f— частота, Гц; L — коэффициент самоиндукции (индуктивность), Гц; С — емкость, Ф; Z — полное сопротивление, Ом |
|
Емкостное (реактивное) сопротивление |
|
|
|
Полное реактивное сопротивление |
|
|
|
Полное сопротивление переменному току |
|
|
|
Емкость пластинчатого конденсатора |
|
С — емкость, Ф; S — площадь между двумя электродами, см n — число пластин; b — толщина слоя диэлектрика, см |
|
Общая емкость цепи: а) при последовательном соединении емкостей б) при параллельном соединении емкостей |
|
|
|
Закон Ома; цепь переменного тока с реактивным сопротивлением |
|
I — ток в цепи, А; U — напряжение цепи, В; |
|
1-й закон Кирхгофа (для узла) |
|
точке, А; i = 1, 2… n; Е — ЭДС, действующая в контуре, В; r — сопротивление отдельных участков, Ом |
|
2-й закон Кирхгофа (для замкнутого контура) |
|
|
|
Распределение тока в двух параллельных ветвях цепи переменного тока |
|
|
|
Закон электромагнитного индукции для синусоидального тока |
|
f — частота, Гц; w — число витков обмотки; В — индукция магнитного поля в стали, Тс; S — сечение магнитопровода, см2 |
|
Электродинамический эффект тока для двух параллельных проводников |
|
F — сила, действующая на 1 (см) длины проводника, кГ; а — расстояние между проводниками, си; |
|
Подъемная сила электромагнита |
|
Р — подъемная сила, кГ; В3 — индукция в воздушном зазоре; В3 = 1000 Гс (электромагниты для подъема стружки и мелких деталей); В3 = 8000 — 10 000 Гс (электромагниты для подъема крупных деталей) S — сечение стального сердечника, см2 |
|
Тепловой эффект тока |
|
тепла, кал; t— время протекания тока, сек; r — сопротивление, Ом; А — количество вещества, от- ложившегося на электроде, мг; α — электрохимический эквивалент вещества |
|
Химический эффект тока |
|
|
|
Зависимости в цепи переменного тока при частоте 50 Гц: а) период изменения тока б) угловая скорость |
|
Т — период изменения тока, сек; f — частота тока, Гц; |
|
Зависимости токов и напряжений в цепи переменного тока: а) ток в цепи б) напряжение в цепи |
|
I — полный ток в цепи, А; тока, А; U— напряжение в цепи, В; напряжения, В; |
|
Соотношения токов и напряжений в трехфазной системе: а) соединение в звезду б) соединение в треугольник |
|
|
|
Коэффициент мощности |
|
Р — активная мощность, Вт; Q — реактивная мощность, нар; S —полная мощность, B*А; r — активное сопротивление, z — полное сопротивление, Ом |
|
Мощность в цепи постоянного тока |
|
|
|
Мощность в цепи переменного тока: а) цепь однофазно тока б) цепь трехфазного тока |
|
|
|
Энергия в цепи постоянного тока |
|
t —время ч |
|
Энергия в цепи переменного тока: а) цепь однофазного тока б) цепь трехфазного тока |
|
Способы нахождения общего сопротивления цепи
Содержание
- 1 Определение сопротивления
- 2 Соединение параллельным и последовательным способом
- 2.1 Сопротивление при подключении проводников последовательно
- 2.2 Напряжение при подключении проводников последовательно
- 2.3 Параллельное подключение потребителей
- 2.4 Сопротивление при подключении проводников параллельно
- 2.5 Напряжение при подключении проводников параллельно
- 2.6 Сила тока при подключении проводников параллельно
- 3 Практическое применение
- 4 Комбинированное соединение
- 5 Видео по теме
Нередко при использовании электрооборудования бывает необходимо найти общее сопротивление цепи. С помощью данной величины определяют противодействие перемещению электричества в цепи или проводнике. В первый раз ее обосновали в законе Ома – трудах физика из Германии, ставившего опыты, связанные электричеством. По его имени и получила название единица сопротивления – Ом.
Определение сопротивления
Есть 2 вида напряжения – переменное и постоянное, а сопротивление электрической цепи может быть активным и реактивным. Дополнительно оно подразделяется на емкостное и индуктивное. Частоты в электросети не влияют на активное сопротивление. Этому параметру совершенно неважно, какой вид электроэнергии перемещается по проводам. А вот реактивная разновидность, наоборот, способна изменяться при перемене частоты. Дополнительно емкостные показатели в конденсаторах, а также индуктивные в трансформаторах проявляют себя по-разному.
Кроме сопротивления электрических приборов, работающих от сети, на ее общее состояние воздействуют промежуточные проводники, также способные сопротивляться электронапряжению. Чтобы правильно определить параметры электроцепи, необходимо понимать, что такое общее сопротивление, и по каким формулам осуществляется его расчет.
Необходимо учитывать, что индуктивный вид сопротивления при увеличении частоты электротока в сети также увеличивается. Его находят по формуле:
Емкостное сопротивление конденсатора с увеличением частоты электротока, наоборот, снижается. По этой причине принимается, что конденсатор при использовании постоянного тока имеет бесконечно большое сопротивление. Чтобы рассчитать емкостное сопротивление участка цепи, следует воспользоваться формулой:
Полное сопротивление включает в себя активную и реактивную составляющие. Графически оно выражается гипотенузой прямоугольного треугольника, катеты которого – активное и реактивное сопротивление.
Чтобы посчитать общее активное сопротивление, достаточно знать значение тока и напряжения в цепи, подключенной к определенному источнику питания. В данной ситуации достаточно воспользоваться законом Ома.
Но значение общего сопротивления в электроцепи зависит не только от используемых радиоэлементов и присутствующего в схеме вида сопротивления. Особое влияние в этом случае оказывает метод сборки электроцепи из отдельных элементов. На практике используется 2 способа подключения потребителей:
- Параллельный;
- Последовательный.
Соединение параллельным и последовательным способом
Эти способы часто используются в электротехнике и электронике, во многих случаях без них невозможна правильная работа оборудования или узла электроники. В первую очередь нужно понять, как функционируют простейшие цепи радиоэлектронных устройств — проводники.
По существу, проводник — особый материал, хорошо передающий электрический ток. Каждый из них обладает собственным сопротивлением. Вычисляют этот параметр для какого-либо проводника по следующей формуле:
По факту каждый проводник – это простейший резистор, имеющий собственное сопротивление.
Сопротивление при подключении проводников последовательно
При таком соединении к одному из проводников подключается следующий и таким образом соединяется цепочка из отдельных элементов. Подобная сборка электроцепи называется последовательной. Допустимо соединять в одну систему необходимое количество резисторов и прочих компонентов.
Узнать общее сопротивление схемы с последовательным подключением элементов совсем несложно. Для этого найдем, чему равна сумма сопротивлений всех использованных проводников. В результате получается формула для определения общего сопротивления цепи с последовательным подключением:
Например, соединяют последовательно в одну цепь 3 проводника. Один из них имеет сопротивление 3 Ома, следующий 4 Ома и последний 2 Ома. Для подсчета общего сопротивления нужно суммировать значение всех установленных элементов:
R цепи = R1 + R2 + R3 = 3 + 4 + 2 = 9 Ом.
Напряжение при подключении проводников последовательно
При соединении элементов цепи последовательно, через каждый из них проходит одинаковая сила тока. Но нужно понять, как определить напряжение и что с ним происходит на каждом участке цепи.
Следует вспомнить закон Ома и станет просто находить, чему равно реальное напряжение на каждом резисторе. Например, есть собранная система элементов с такими характеристиками как на рисунке:
В этой цепи, как выяснили выше, везде присутствует одинаковая сила тока. Но как узнать ее номинальное напряжение? Сперва нужно модифицировать систему, изменив ее как на изображении, представленном ниже. При этом принимаем сумму сопротивлений всех элементов системы, как RАВ:
В результате выходит по расчетам, что:
RАВ = R1 + R2 + R3 = 2 + 3 + 4 = 9 Ом.
По вычисленному RАВ с учетом закона Ома определяется сила тока, имеющаяся в цепи:
I = U/R = 9/9 = 1 Ампер.
После этого нужно найти напряжение на всех установленных резисторах. Точнее говоря, требуется вычислить значения, соответствующие UR1, UR2, UR3. Для их нахождения также следует воспользоваться законом Ома, согласно которому U = IR.
В результате выходит, что:
- UR1 = IR1= 1×2 = 2 В.
- UR2= IR2 = 1×3 = 3 В.
- UR3= IR3 = 1×4 = 4 В.
После этих вычислений если суммировать все найденные напряжения на отдельных участках, то в результате получится характеристика, равная 10 Вольтам. С учетом этого выходит, что U = UR1 + UR2 + UR3. В результате мы получили элементарный делитель напряжения.
Следовательно, при последовательном подключении сумма изменения напряжения на отдельных участках соответствует общему напряжению источника питания.
Параллельное подключение потребителей
Это соединение выполняется по-другому, пример показан на рисунке:
Сопротивление при подключении проводников параллельно
Общее сопротивление считают по формуле:
Если подсоединены параллельно только 2 компонента, то формулу можно сделать проще. Выглядеть она должна таким образом:
Напряжение при подключении проводников параллельно
С этим все просто. Благодаря тому, что все потребители подключаются параллельно, то они имеют равное напряжение. По этой причине выходит, что напряжение, которое можно получить на R1 не станет отличаться от показаний на всех других участках.
Сила тока при подключении проводников параллельно
Если все было просто с напряжением, то появляются сложности с силой тока. При соединении последовательным способом на всех проводниках одинаковая сила тока, а при параллельном все происходит наоборот. На установленные потребители будет поступать разная сила тока. Чтобы ее определить, придется еще раз воспользоваться законом Ома.
Проще разобраться в принципе работы и расчетов, на реальном примере. На изображении, расположенном ниже, 3 резистора соединены параллельно, и запитаны от источника U.
В любом из установленных устройств напряжение отличаться не будет, как выяснили ранее. Но на разных участках цепи будет собственная сила тока. Для каждого потребителя ее определяют по закону Ома, используя для этой цели соотношение I=U/R.
Таким образом получается:
- I1 = U/R1
- I2 = U/R2
- I3 = U/R3
Если в системе присутствуют другие подключенные параллельно приборы, для них используют: In = U/Rn
В результате сила тока всей цепи определяется по формуле:
В электронике способ параллельного подсоединения потребителей называют дополнительно «делителем тока», причина в том, что в схемах резисторы поступающий ток делят между установленными элементами.
Практическое применение
Попробуем решить следующую задачу: найти проходящую через каждый резистор силу тока и определить общую силу тока при известных номиналах резисторов и напряжении питания.
Решение
Расчет проводится с помощью выше приведенных формул:
- I1 = U/R1
- I2 = U/R2
- I3 = U/R3
В результате получается:
- I1 = U/R1 = 10/2=5 Ампер
- I2 = U/R2 = 10/5=2 Ампера
- I3 = U/R3 = 10/10=1 Ампер
После этого используется формула расчета общего сопротивления цепи, позволяющая определить силу тока, проходящую по ней.
Следовательно, Iобщ = 5 + 2 + 1 = 8 Ампер.
В результате получается I=I1 + I2 + I3 = 5+2+1=8 Ампер
Комбинированное соединение
На практике используются довольно сложные электроцепи, состоящие и из последовательно подключенных сопротивлений, и из параллельно. Такую цепь следует разбить на отдельные участки, включающие элементы, соединенные только последовательным способом или только параллельным.
Расчет следует начинать с того участка цепи, который является наиболее удаленным от двух конечных выводов, выступающих в роли контактов общего сопротивления. Схему соединения элементов, называемую «треугольником» можно трансформировать в «звезду» и обратно.
Чтобы не напрягаться с различными расчетами, на практике очень часто используют онлайн-калькуляторы.
Видео по теме
|
Измеряемые |
Формулы |
Обозначение |
|
Сопротивление |
|
s |
|
Активное |
|
r k |
|
Зависимость |
|
|
|
Индуктивное |
|
сопротивление,
f— L С Z |
|
Емкостное |
|
|
|
Полное |
|
|
|
Полное |
|
|
|
Емкость |
|
С S электродами, n
b |
|
Общая а) б) |
|
|
|
Закон |
|
I U |
|
1-й |
|
точке, Е r участков,
|
|
2-й |
|
|
|
Распределение |
|
|
|
Закон |
|
f w В S |
|
Электродинамический |
|
F
а
|
|
Подъемная |
|
Р В3 зазоре; S |
|
Тепловой |
|
тепла, t— r А ложившегося α |
|
Химический |
|
|
|
Зависимости а) б) |
|
Т f
|
|
Зависимости а) б) |
|
I
тока,
U—
напряжения,
|
|
Соотношения а) б) |
|
|
|
Коэффициент |
|
Р Q S r z |
|
Мощность |
|
|
|
Мощность а) б) |
|
|
|
Энергия |
|
t |
|
Энергия а) б) |
|
Закон
Ома и электрическая мощность:
где
-
U
— напряжение [В] -
I
— ток [А] -
R
— сопротивление [Ом] -
P
— мощность [Вт]
Параллельное
включение резисторов:
Последовательное
включение резисторов:
Параллельное
включение конденсаторов:
Последовательное
включение конденсаторов:
Модуль
сопротивления конденсатора в цепи
переменного синусоидального
тока:
Модуль
сопротивления индуктивности в цепи
переменного синусоидального
тока:
где
-
C
— ёмкость конденсатора [Ф] -
L
— индуктивность катушки [Гн] -
ƒ
— частота [Гц] -
ω
— круговая частота [рад/с]
Напряжение
на конденсаторе и ток при заряде через
резистор (при начальном условии uC(0)=0):
где
-
U
— входное напряжение [В] -
—
постоянная времени RC-цепи [с]
Ток
в индуктивности (при начальном условии
iL(0)=0):
Ток
в индуктивности (упрощенная формула
для R→0):
где
-
—
постоянная времени RL-цепи [с]
Условие
резонанса:
Резонансная
частота:
Параметры
LC контура при заданной резонансной
частоте:
Индуктивность
катушки с замкнутым магнитопроводом:
Магнитная
проницаемость магнитопровода:
Количество
витков:
Магнитная
индукция в дросселе с замкнутым
магнитопроводом:
Знак
приблизительно равно стоит из-за
предположения:
не
учитывающего гистерезис.
где
-
L
— индуктивность Генри [Гн] -
B
— магнитная индукция Тесла [Тл] -
ω
— количество витков -
S
— площадь поперечного сечения
магнитопровода [м2] -
l
— длина средней линии магнитопровода
[м] -
μ
— относительная магнитная проницаемость
магнитопровода -
μ0
— магнитная постоянная [Гн/м]
Заряд
конденсатора:
Энергия
конденсатора:
Энергия
индуктивности:
Мощность
которую способен перенести конденсатор
заряжаясь от источника до напряжения
U и разряжаясь на нагрузку до напряжения
0 с частотой f:
Мощность
выделяемая на резисторе снаббера
(резистор последовательно включенный
с конденсатором) с частотой коммутации
f напряжения от 0 до U:
Мощность
выделяемая на резисторе снаббера
(резистор последовательно включенный
с конденсатором) с частотой коммутации
f напряжения от -U до U:
где
-
Q
— электрический заряд Кулон [Кл] -
W
— электрическая энергия Джоуль [Дж] -
P
— электрическая мощность Ватт [Вт] -
ƒ
— частота [Гц]
Преобразования
величин
1
дюйм = 25,4 мм
1
мм ≈ 0,03937 дюйма
крутящий
момент:
1
Н·м = 10,2 кгс·см
1
кгс·см = 0,098 Н·м
энергия:
1
Дж = 1 Вт·с ≈ 0,238846 калории
1
кВт·ч = 3600000 Дж ≈ 859,845 ккалории
1
калория = 4,1868 Дж
Скорость:
1
м/с = 3,6 км/ч
Константы
Число
ПИ:
π
= 3,14159265359
Число
e:
e
= 2,71828182846
Магнитная
постоянная (абсолютная магнитная
проницаемость вакуума):
μ0
= 1,25663706·10-6
Гн/м или Н/А2
или м·кг·с-2·А-2
(численно равна 4π·10-7)
Ускорение
свободного падения (средняя величина,
может отличаться на ±0,27% и более в
зависимости от расположения и высоты
над уровнем моря):
g
= 9,80665 м/с2
Скорость
света в вакууме:
C
= 299792458 м/с = 1079252848,8 км/ч
Скорость
звука в воздухе (при 0°C и давлении 101325
Па):
331
м/с = 1191,6 км/ч
Скорость
звука в воде:
1348
м/с = 4852,8 км/ч
ЗАКОН
ОМА
(по имени немецкого физика Г. Ома
(1787-1854)) – единица электрического
сопротивления. Обозначение Ом. Ом –
сопротивление проводника, между концами
которого при силе тока 1 А возникает
напряжение 1 В. Определяющее уравнение
для электрического сопротивления R= U /
I.
Закон
Ома является основным законом
электротехники, без которого нельзя
обойтись при расчете электрических
цепей. Взаимосвязь между падением
напряжения на проводнике, его сопротивлением
и силой тока легко запоминается в виде
треугольника, в вершинах которого
расположены символы U, I, R.
К
закону Ома
Самый
главный закон электротехники — закон
Ома
ЗАКОН
ДЖОУЛЯ-ЛЕНЦА
(по имени английского физика Дж.П.Джоуля
и русского физика Э.Х.Ленца) – закон,
характеризующий тепловое действие
электрического тока.
Согласно
закону, количество теплоты Q (в джоулях),
выделяющейся в проводнике при прохождении
по нему постоянного электрического
тока, зависит от силы тока I (в амперах),
сопротивления
проводника
R (в омах) и времени его прохождения t (в
секундах): Q = I2Rt.
Преобразование
электрической энергии в тепловую широко
используется в электрических печах и
различных электронагревательных
приборах. Тот же эффект в электрических
машинах и аппаратах приводит к
непроизвольным затратам энергии (потере
энергии и снижении КПД). Тепло, вызывая
нагрев этих устройств, ограничивает их
нагрузку. При перегрузке повышение
температуры может вызвать повреждение
изоляции или сокращение срока службы
установки.
Как
провод нагревается электрическим током
Как
влияет нагрев на величину сопротивления
ЗАКОН
КИРХГОФА
(по имени немецкого физика Г.Р.Кирхгофа
(1824-1887)) – два основных закона электрических
цепей. Первый закон устанавливает связь
между суммой токов, направленных к узлу
соединения (положительные), и суммой
токов, направленных от узла (отрицательные).
Алгебраическая
сумма сил токов In, сходящихся в любой
точке разветвления проводников (узле),
равна нулю, т.е. SUMM(In)= 0. Например, для
узла A можно записать: I1 + I2 = I3 + I4 или I1 +
I2 – I3 – I4 = 0.
Узел
тока
Второй
закон устанавливает связь между суммой
электродвижущих сил и суммой падений
напряжений на сопротивлениях замкнутого
контура электрической цепи. Токи,
совпадающие с произвольно выбранным
направлением обхода контура, считаются
положительными, а не совпадающие –
отрицательными.
Контур
тока
Алгебраическая
сумма мгновенных значений ЭДС всех
источников напряжения в любом контуре
электрической цепи равна алгебраической
сумме мгновенных значений падений
напряжений на всех сопротивлениях того
же контура SUMM(En)=SUMM(InRn). Переставив
SUMM(InRn) в левую часть уравнения, получим
SUMM(En) – SUMM(InRn) = 0. Алгебраическая сумма
мгновенных значений напряжений на всех
элементах замкнутого контура электрической
цепи равна нулю.
Законы
Кирхгофа
ЗАКОН
ПОЛНОГО ТОКА
один из основных законов электромагнитного
поля. Устанавливает взаимосвязь между
магнитной силой и величиной тока,
проходящего через поверхность. Под
полным током понимается алгебраическая
сумма токов, пронизывающих поверхность,
ограниченную замкнутым контуром.
Намагничивающая
сила вдоль контура равна полному току,
проходящему сквозь поверхность,
ограниченную этим контуром. В общем
случае напряженность поля на различных
участках магнитной линии может иметь
разные значения, и тогда намагничивающая
сила будет равна сумме намагничивающих
сил каждой линии.
ЗАКОН
ЛЕНЦА
— основное правило, охватывающее все
случаи электромагнитной
индукции
и позволяющее установить направление
возникающей э.д.с. индукции.
Согласно
закону Ленца это направление во всех
случаях таково, что ток, созданный
возникшей э.д.с., препятствует тем
изменениям, которые вызвали появление
э.д.с. индукции. Этот закон является
качественной формулировкой закона
сохранения энергии в применении к
электромагнитной индукции.
ЗАКОН
ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ,
закон Фарадея – закон, устанавливающий
взаимосвязь между магнитными и
электрическими явлениями. ЭДС
электромагнитной индукции в контуре
численно равна и противоположна по
знаку скорости изменения магнитного
потока сквозь поверхность, ограниченную
этим контуром. Величина ЭДС поля зависит
от скорости изменения магнитного потока.
ЗАКОНЫ
ФАРАДЕЯ
(по имени английского физика М.Фарадея
(1791-1867)) – основные законы электролиза.
Устанавливают
взаимосвязь между количеством
электричества, проходящего через
электропроводящий раствор (электролит),
и количеством вещества, выделяющегося
на электродах.
При
пропускании через электролит постоянного
тока I в течение секунды q = It, m = kIt.
Второй
закон ФАРАДЕЯ: электрохимические
эквиваленты элементов прямо пропорциональны
их химическим эквивалентам.
ПРАВИЛО
БУРАВЧИКА
— правило, позволяющее определить
направление магнитного поля, зависящее
от направления электрического тока.
При совпадении поступательного движения
буравчика с протекающим током направление
вращения его рукоятки указывает
направление магнитных линий. Или при
совпадении направления вращения рукоятки
буравчика с направлением тока в контуре
поступательное движение буравчика
указывает направление магнитных линий,
пронизывающих поверхность, ограниченную
контуром.
Правило
буравчика
ПРАВИЛО
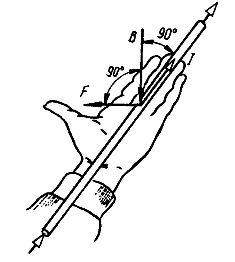
ЛЕВОЙ РУКИ
— правило, позволяющее определить
направление электромагнитной силы.
Если ладонь левой руки расположена так,
что вектор магнитной индукции входит
в нее (вытянутые четыре пальца совпадают
с направлением тока), то отогнутый под
прямым углом большой палец левой руки
показывает направление электромагнитной
силы.
Правило
левой руки
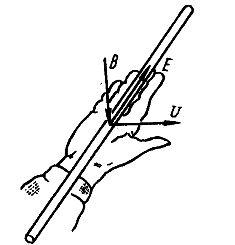
ПРАВИЛО
ПРАВОЙ РУКИ
— правило, позволяющее определить
направление наведенной эдс электромагнитной
индукции. Ладонь правой руки располагают
так, чтобы магнитные линии входили в
нее. Отогнутый под прямым углом большой
палец совмещают с направлением движения
проводника. Вытянутые четыре пальца
укажут направление индуктированной
эдс.
Правило
правой руки
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #



 ,
, ,
, ,
, — активное сопротивление, Ом;
— активное сопротивление, Ом; — индуктивное сопротивление, Ом;
— индуктивное сопротивление, Ом; — индуктивность, Гн;
— индуктивность, Гн; — емкостное сопротивление, Ом;
— емкостное сопротивление, Ом; — ёмкость, Ф.
— ёмкость, Ф. ,
, — коэффициент, учитывающий увеличение сопротивления при переменном токе, зависящий от: частоты тока; магнитных свойств, проводимости и диаметра проводника.
— коэффициент, учитывающий увеличение сопротивления при переменном токе, зависящий от: частоты тока; магнитных свойств, проводимости и диаметра проводника. и считают
и считают  .
. .
. ,
,



 .
. .
. .
. . Примеры: задача 1, задача 2.
. Примеры: задача 1, задача 2.
 .
. .
. .
. .
. .
. , или
, или .
. , энергия равна 0, то
, энергия равна 0, то
 ,
, — потокосцепление.
— потокосцепление. .
. .
. .
. .
. .
. .
.
 , или
, или 
 .
.
 .
. .
.
 ;
;
 . Пример 1. Первый закон Кирхгофа.
. Пример 1. Первый закон Кирхгофа.
 . Пример 2. Второй закон Кирхгофа.
. Пример 2. Второй закон Кирхгофа. ,
, строки матрицы А содержат коэффициенты при токах в уравнениях, составленных по первому закону Кирхгофа, и имеют элементы +1, -1, 0 в зависимости от того, с каким знаком входит данный ток в уравнение.
строки матрицы А содержат коэффициенты при токах в уравнениях, составленных по первому закону Кирхгофа, и имеют элементы +1, -1, 0 в зависимости от того, с каким знаком входит данный ток в уравнение. строк матрицы А равны значениям сопротивлении при соответствующих токах в уравнениях, составленных по второму закону Кирхгофа, с соответствующим знаком. Элементы матрицы В равны коэффициентам при ЭДС в правой части уравнений, составленных по законам Кирхгофа. Первые
строк матрицы А равны значениям сопротивлении при соответствующих токах в уравнениях, составленных по второму закону Кирхгофа, с соответствующим знаком. Элементы матрицы В равны коэффициентам при ЭДС в правой части уравнений, составленных по законам Кирхгофа. Первые  ,
, — матрица проводимостей.
— матрица проводимостей. .
. ;
; ;
;
 .
. , так как
, так как 
 I×Rэкв;
I×Rэкв; .
. E×Gэкв;
E×Gэкв; .
. или
или 
 .
. или
или 
 следует отдавать предпочтение методу узловых потенциалов.
следует отдавать предпочтение методу узловых потенциалов. .
. .
. — сумма мощностей, развиваемых источниками;
— сумма мощностей, развиваемых источниками; — сумма мощностей всех приемников и необратимых преобразований энергии внутри источников.
— сумма мощностей всех приемников и необратимых преобразований энергии внутри источников.

 .
.
 или
или  , стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной.
, стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной. . К такому режиму может быть отнесен и синусоидальный:
. К такому режиму может быть отнесен и синусоидальный: ,
, — амплитуда;
— амплитуда; — начальная фаза;
— начальная фаза; — угловая скорость вращения ротора генератора.
— угловая скорость вращения ротора генератора. рад/с.
рад/с. .
. ,
, от амплитудного. Аналогично,
от амплитудного. Аналогично, .
. . Аналогично,
. Аналогично, .
. .
. =R×Iпост2×T или Iпост=I=
=R×Iпост2×T или Iпост=I=
 .
. .
. , κф≠1,11. Это отклонение косвенно свидетельствует о том, насколько несинусоидальный ток отличается от синусоидального.
, κф≠1,11. Это отклонение косвенно свидетельствует о том, насколько несинусоидальный ток отличается от синусоидального. .
.




 — резонансная частота напряжения, определяемая из условия
— резонансная частота напряжения, определяемая из условия




 где
где


 .
.