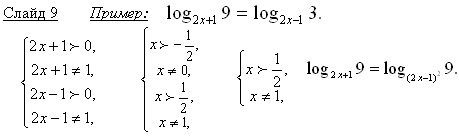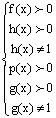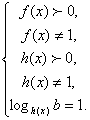Цели урока:
- обучающие: закрепить основные способы решения логарифмических уравнений: по определению логарифма с учётом области определения, на основании свойств монотонности (потенцирование) с учётом равносильности перехода, переход к новому основанию, введение новой переменной; рассмотреть некоторые приемы быстрого решения уравнений рассматриваемого типа;
- развивающие: содействовать развитию логического мышления учащихся; развивать умения рассуждать, сравнивать, осмысливать материал; развивать у учащихся умения анализа условия задачи перед выбором способа ее решения; развивать навыки исследовательской деятельности; учить видеть задачу целиком, логически мыслить при переходе от частного к общему; развивать навыки обобщения;
- воспитывающие: воспитание познавательного интереса, элементов культуры общения; побуждение учащихся к преодолению трудностей в процессе умственной деятельности; воспитание у учащихся уверенности в себе, веры в свои силы в нестандартной ситуации.
Тип урока: урок комплексного применения знаний и навыков.
Ход урока:
1. Организационный момент
(сообщить учащимся тему урока, поставить перед ними задачи урока), (на партах у каждого раздаточный материал см. Приложение 1).
Изучив основные свойства логарифмической функции, правила вычисления логарифмов, овладев основными приемами решения логарифмических уравнений и неравенств, наша основная задача на сегодняшний урок – обобщить методы решения логарифмических уравнений, содержащих переменную в основании логарифма.
2. Активизация знаний учащихся.
Устная работа:
- Найдите область определения функций:
Ответ: (0;1) U (1;∞)
(- 4; — 3) U (- 3; — 1) U (1;∞)
(-∞; — 2) U (- 2; 2)
- Каким способом решается уравнение:
. Ответ: по определению логарифма. Решений нет!!
- При каком значении параметра а функция
определена на множестве (1; ∞); если изменить основание, значение параметра изменится?
Ответ: а ≥ 1
Ответ: а ≥ 1
Ответ: а > 1
3. Основная часть урока.
Слайд 2. Виды уравнений и методы решения
слайд 3.
На области определения 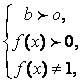
Или
слайд 4.
Пример Решение:

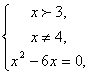
слайд 5.
На области определения 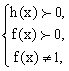
слайд 6.
Пример:
Решение: 7x-14=3-2x; 9x=17; x=17/9; НО!!! 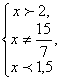
слайд 7.
Пример:Каким способом решается уравнение?
предполагаемый ответ учащихся: решаем, применяя определение логарифма (решение учеником письменно на доске и в тетрадях)
Решение: 
при х= 6 верно. Ответ: 6
Слайд 8
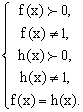
Слайд 10. На найденной области определения
решим уравнение: ,
, х = 0 или х = 1,5
Ответ: 1,5
Слайд 11 Следующий вид уравнения:
Одна и та же функция в основании логарифма
Вопрос: Каким способом решать?
Один из вариантов ответов: область определения достаточно объёмная, поэтому переходим к следствию
Найдём корни этого уравнения и подстановкой в первоначальное логарифмическое, проверим.
Слайд 12. Одна и та же функция является подлогарифмическим выражением
Вопрос: Каким способом решать? Один из вариантов ответов: область определения достаточно объёмная, поэтому переходим к совокупности уравнений
Найдём корни этого уравнения и подстановкой в первоначальное логарифмическое, проверим.
Слайд 13 .Пример
Решение:
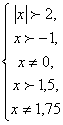
Слайд 14. На промежутке решаем совокупность уравнений:
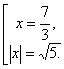
Слайд 15. Проверяем на принадлежность этих чисел области определения, делаем вывод: решением уравнения являются числа: ;
. Ответ:
;
.
Слайд 16 Следующий вид уравнений:
Область определения достаточно объёмная
Найдём корни этого уравнения и подстановкой в первоначальное логарифмическое, проверим.
Слайд 17. Как вы думаете, каким способом лучше решать это уравнение?
Один из вариантов ответов: переход к новому основанию (числовому)
Слайд 18. или к буквенному
Слайд 19. Пример:
(решение с подробным комментарием письменно на доске и в тетрадях).
Решение: Очевидно . Выполним преобразования основания и подлогарифмического выражения правой части уравнения
,
Перейдём в правой части уравнения к новому основанию х, применяя свойство: логарифм произведения равен сумме логарифмов множителей по такому же основанию
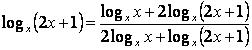
Выполним замену переменных
Получим уравнение ,
,
Выполнив обратную замену, получим
Х= — 1.
Очевидно – 1 не входит в область определения заданного уравнения.
Или ,
,
.
По свойству: если коэффициенты квадратного уравнения таковы, что
a + c – b =0, то Х= — 1, Х= ½. Ответ: ½
Слайд 20
Следующий тип уравнений
Слайд 21. Пример
Решение:
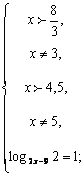
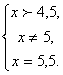
Слайд 22 «Комбинированные» виды уравнений
Пример
Решение: очевидно
Слайд 23 ,
,
(очевидно, последнее уравнение решений не имеет)
Слайд 24 ,
. Ответ:
Слайд 25 Уравнения, левая часть которых – сумма взаимно обратных слагаемых
Пример: (*)
Очевидно, каждое слагаемое равно 1.
Получим систему, равносильную уравнению (*)
Слайд 26
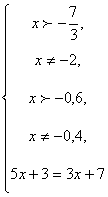
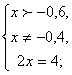
Слайд 27. В чём отличие в решении следующего уравнения?
(*)
Равенство взаимно обратных слагаемых верно при условии х > 0,5, х ≠ 1,5.
На рассматриваемом промежутке уравнение (*) равносильно совокупности
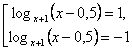
Слайд 28 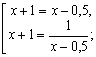
Слайд 29
с учётом области определения: Ответ: 1
Подведение итогов урока
4. Домашнее задание.
Слайд 30. Решите уравнения: ,
P. S. Урок проведён в 10 классе физико-химического профиля. Уложились за урок за счёт экономии времени: на партах лежали у каждого ученика листы с напечатанными типами уравнений, учащиеся записывали только метод решения (без области определения и решения). Эти листы ученики забрали с собой и вклеили в тетрадь.
В слабом классе лучше потратить на эту тему сдвоенный урок.
P. S. S. В кабинете один компьютер с выходом на экран телевизора. В связи с этим, на слайдах текст печатается очень крупно.
Список используемой литературы:
- Балаян Э. Н. ЕГЭ по математике: Новейшие тесты. Пособие для учащихся старших классов и абитуриентов вузов. — М: ИКЦ «МарТ»; Ростов-на-Дону: Издательский центр «МарТ», 2004.
- Балаян Э. Н. Математика. Серия «Единый госэкзамен». — Ростов н/Д: Феникс, 2004.
- Математика. Интенсивный курс подготовки к Единому государственному экзамену. — М.: Айрис-пресс, 2004.
- Математика: Варианты задач для вступительных испытаний в НГУЭУ. — Новосибирск: НГУЭУ, 2005.
- Математика: Учебное пособие для поступающих в вузы и старшеклассников / М. К. Потапов, С. Н. Олехник, Ю. В. Нестеренко. — М.: ООО «Издательство АСТ»: ООО «Издательство Астрель», 2004.
- Уравнения и неравенства: Учеб. пособие / А. Г. Калашникова и др.— Новосибирск: Изд-во НГТУ, 2003.
Презентация.
Как решать логарифмические уравнения
Уравнения, содержащие в том или ином виде логарифмы от некоторого выражения, зависящего от (х), называются логарифмическими.
Давайте сразу же рассмотрим пример, так будет легче всего разобраться.
Пример 1
$$ log_{2}(x)=log_{2}(5)$$
Мы видим слева и справа логарифмы с одинаковыми основаниями, равными (2). Вполне логично предположить, что логарифмы будут равны, если будут равны выражения, стоящие под логарифмом (их называют аргументами) — то есть (х=5). Мы только что решили логарифмическое уравнение!
На самом деле, абсолютно такая же логика применима при решении почти всех логарифмических уравнений — если у нас сравниваются два логарифма с одинаковыми основаниями, то мы можем избавиться от логарифмов, приравнять их аргументы и решить получившееся уравнение.
Пример 2
$$ log_{3}(2x+5)=log_{3}(11) $$
Опять имеем два логарифма с одинаковым основанием (3). Избавляемся от логарифмов, приравнивая аргументы:
$$ 2x+5=11,$$
$$ 2x=6,$$
$$ x=3.$$
Кажется, что все очень просто. Но есть несколько непростых нюансов, которые необходимо обсудить. Давайте посмотрим еще один пример:
Пример 3
$$ log_{2}(1+3x)=log_{2}(2x-3) $$
Смотрим на основания — они одинаковые, значит убираем логарифмы и решаем уравнение:
$$1+3x=2x-3,$$
$$3x-2x=-3-1,$$
$$x=-4.$$
Мы решили уравнение, но я хочу позанудствовать и проверить, действительно ли получившийся корень является корнем исходного уравнения. Для этого подставим его в логарифмическое уравнение:
$$ log_{2}(1+3*(-4))=log_{2}(2*(-4)-3),$$
$$log_{2}(-11)=log_{2}(-11).$$
Мы получили слева и справа два одинаковых логарифма, вот только эти логарифмы НЕ СУЩЕСТВУЮТ, потому что нельзя взять логарифм от отрицательного числа.
Действительно, давайте вспомним определение логарифма (log_{a}b) — это в какую степень нужно возвести (a), чтобы получить (b). При этом определение справедливо не для всех (a) и (b), а только для (a>0), (b>0), (a neq 1). Подробнее про логарифм и его свойства можно почитать здесь.
Значит, с нашим решением что-то не так — мы нашли корень, подставили его в уравнение, но получили логарифм от отрицательного числа, который не существует!
Тут самое время вспомнить про область допустимых значений (ОДЗ). В логарифмах нужно всегда внимательно следить за тем, чтобы не нарушались ограничения, которые вытекают из определения логарифма. Рассмотрим логарифм от некоторой функции:
$$log_{a}f(x)$$
Область допустимых значений (ОДЗ) для него будет задаваться системой неравенств:
$$ begin{cases}
f(x)>0, \
a>0, \
a neq 1.
end{cases}$$
И при решении любых логарифмических уравнений или неравенств всегда первым делом записываем ОДЗ для каждого логарифма в уравнении.
В нашем примере 3, ОДЗ будет выглядеть вот так:
$$ begin{cases}
1+3x>0, \
2x-3>0. \
end{cases}$$
Решаем получившуюся систему
$$ begin{cases}
x>-frac{1}{3}, \
x>frac{3}{2}. \
end{cases}$$
Находим (х), удовлетворяющие одновременно обоим неравенствам, и получаем в итоге ОДЗ:
$$x>frac{3}{2}.$$
Вспоминаем, что решая это уравнение мы получили корень (x=-4), который нашему ОДЗ не удовлетворяет. Поэтому в примере 3 корней нет.
И так, всегда пишем ОДЗ!
Следующая трудность при решении логарифмических уравнений возникает, когда у нас сравниваются логарифмы с разными основаниями:
Пример 4
$$ log_{2}(x)=log_{4}(9).$$
Запишем ОДЗ: (x>0).
У логарифма слева основание (2), а у логарифма справа основание (4). Чтобы воспользоваться способом решения, аналогичным первым трем примерам, необходимо привести логарифмы к одинаковому основанию.
$$ log_{2}(x)=log_{2}(3).$$
Ого, как я такое получил?
Просто воспользовался формулой возведения в степень основания и аргумента логарифма — если возвести в одинаковую степень, то логарифм от этого не поменяется:
$$ log_{a}(b)=log_{a^n}(b^n).$$
В нашем примере возведем основание и аргумент в степень (frac{1}{2}):
$$ log_{4}(9)=log_{4^{frac{1}{2}}}(9^{frac{1}{2}})=log_{2}(3).$$
$$ log_{2}(x)=log_{2}(3).$$
Ну теперь основании у логарифмов одинаковые и можно с чистым сердцем приравнять аргументы, как мы делали до этого.
$$x=3.$$
Кстати, решить уравнение (log_{2}(x)=log_{4}(9))
можно было и по-другому — привести к основанию (4) логарифм, стоящий слева в уравнении:
Опять воспользуемся свойством логарифма:
$$ log_{a}(b)=log_{a^n}(b^n);$$
$$log_{2}(x)=log_{2^2}(x^2)=log_{4}(x^2);$$
Подставим в исходное уравнение наши преобразования:
$$ log_{4}(x^2)=log_{4}(9);$$
Ура, у нас слева и справа логарифмы с одинаковым основанием — вычеркиваем логарифмы:
$$x^2=9;$$
Решаем аккуратно простейшее квадратное уравнение. Не забываем, что у него будет 2 корня!
$$x=pm3;$$
Опа, у нас получилось два корня. А когда мы решали первым способом был один корень! Что за дела?
Вспоминаем, что в самом начале к уравнению мы записывали ОДЗ (х>0). Тогда корень (x=-3) не удовлетворяет ОДЗ. Обратите внимание, что без учета ОДЗ в этом случае, мы бы получили неправильный ответ.
Ответ: (x=3.)
Подробнее про свойства логарифмов можно посмотреть тут. Логарифмические уравнения с разными основаниями встречаются в ЕГЭ регулярно, поэтому важно уметь применять все свойства логарифмов.
Рассмотрим еще один пример.
Пример 5
$$log_{5}(x)=2$$
Как видим, в примере есть только логарифм в левой части равенства, а справа стоит просто число 2. Давайте постараемся привести к такому же виду, как и в прошлых примерах. То есть сделаем так, чтобы справа появился логарифм с основанием 5.
Оказывается, любое число (a) можно представить в виде логарифма с нужным вам основанием (b) по формуле:
$$a=log_{b}(b^a);$$
Эту формулу можно просто запомнить. А въедливым читателям, я бы рекомендовал посидеть и подумать откуда берется данное выражение. Подсказка — оно напрямую вытекает из определения логарифма. Задайте себе вопрос — «В какую степень нужно возвести основание, чтобы получить аргумент?»
И так, воспользуемся формулой и распишем 2-ку:
$$2=log_{5}(5^2);$$
Подставим в уравнение:
$$log_{5}(x)=log_{5}(5^2);$$
Ура, у нас два логарифма с одинаковыми основаниями, теперь можно приравнять подлогарифмические выражения.
$$x=5^2;$$
$$x=25.$$
Пример 6
$$log_{3}(x+2)=0$$
Начинаем с ОДЗ:
$$x+2>0;$$
$$x>-2.$$
Приступаем к решению уравнения. Что делать в случае, когда справа стоит (0)? Ничего страшного в этом нет, действуем по прежнему плану — представим (0) в виде логарифма по нашей формуле:
$$a=log_{b}(b^a);$$
$$log_{3}(x+2)=log_{3}(3^0);$$
Вспоминаем, что любое число в нулевой степени это единица.
$$log_{3}(x+2)=log_{3}(1);$$
$$x+2=1;$$
$$x=-1.$$
Корень удовлетворяет ОДЗ — записываем ответ.
Ответ: (x=-1).
Подведем итоги. В большинстве случаев, для того, чтобы решить простейшее логарифмическое уравнение, необходимо привести логарифмы слева и справа к одинаковому основанию. Затем приравнять подлогарифмические выражения и решить получившееся уравнения. При этом ни в коем случае не забываем про ОДЗ. На ЕГЭ, если вы вдруг запишите в ответ хотя бы один корень, не удовлетворяющий ОДЗ, то вам поставят за это задание 0 баллов.
В общем виде формула для решения логарифмов выглядит так:
$$ log_{a}(f(x))=log_{a}(g(x)) qquad (*)$$
где (a>0) — основание логарифмов, а (f(x)) и (g(x)) — какие-то выражения, зависящие от (x).
$$ begin{cases}
f(x)>0, или \
g(x)>0. \
end{cases}$$
$$f(x)=g(x).$$
Обратите внимание на «или» в ОДЗ. Оказывается можно накладывать условие больше нуля только на одную функцию: либо на f(x), либо на g(x) — смотря какое неравенство вам кажется легче для решения. Дело в том, что если одна из функций будет больше нуля, то и другая автоматически тоже будет будет больше, ведь мы ищем корни, при которых (f(x)=g(x)).
Для того, чтобы закрепить материал, решим еще одно логарифмическое уравнение:
Пример 7
$$2*log_{4}(4+x)=4-log_{2}(x-2);$$
Здесь все несколько сложнее, чем в предыдущих примерах. Для того чтобы представить наше уравнение в виде (*), нужно избавиться от множителя (2) перед первым логарифмом, кроме этого, нам мешается отдельное слагаемое (4), и в придачу ко всем этим неприятностям у логарифмов разные основания!
Но перед тем как решать, запишем ОДЗ:
$$ begin{cases}
4+x>0, \
x-2>0. \
end{cases}$$
$$ begin{cases}
x>-4, \
x>2. \
end{cases}$$
Находим пересечение и в итоге ОДЗ получается:
$$ x>2.$$
Приступаем непосредственно к решению уравнения. Самое главное, нам необходимо привести все логарифмы к одинаковому основанию, и, по возможности, привести к виду (log_{a}f(x)=log_{a}g(x)).
Здесь не обойтись без свойств логарифмов.
Воспользуемся формулой вынесения степени из основания логарифма:
$$log_{a^n}(b)=frac{1}{n}*log_{a}(b)$$
$$log_{4}(4+x)=log_{2^2}(4+x)=frac{1}{2}*log_{2}(4+x)$$
Подставим в уравнение
$$2*frac{1}{2}*log_{2}(4+x)=4-log_{2}(x-2);$$
$$log_{2}(4+x)=4-log_{2}(x-2);$$
Теперь у нас хотя бы логарифмы с одинаковым основанием. Далее преобразуем левую часть уравнения, воспользовавшись формулами:
$$ a=log_{b}(b^a);$$
$$log_{a}(b)-log_{a}(c)=log_{a}(frac{b}{c})$$
$$4-log_{2}(x-2)=log_{2}(2^4)-log_{2}(2-x)=log_{2}(16)-log_{2}(2-x)=log_{2}(frac{16}{2-x});$$
Подставим получившееся выражение в уравнение:
$$log_{2}(4+x)=log_{2}(frac{16}{2-x});$$
Ура, теперь у нас слева и справа в уравнении логарифмы с одинаковым основанием (2).
Избавляемся от логарифмов и решаем:
$$4+x=frac{16}{x-2};$$
Перекинем все налево и приведем к общему знаменателю
$$4+x-frac{16}{x-2}=0;$$
$$frac{(4+x)(x-2)}{x-2}—frac{16}{x-2}=0;$$
$$frac{4x-8+x^2-2x–16}{x-2}=0;$$
$$frac{x^2+2x-24}{x-2}=0;$$
Дробь равна 0, когда числитель равен 0
$$x^2+2x-24=0;$$
$$D=(2^2-4*(-24)=4+96=100;$$
$${x}_{1,2}=frac{-2pm 10}{2};$$
$${x}_{1}=4;$$
$${x}_{2}=-6;$$
Мы получили два корня. Но не забываем про ОДЗ. Выше мы его посчитали и получилось, что (x>2). Значит второй корень не подходит.
Ответ: (x=4).
Логарифмические уравнения с переменным основанием
Рассмотри теперь уравнение, в котором есть, так называемый, логарифм с переменным основанием. То есть логарифм, у которого в основании стоит какое-то выражение, зависящее от (х).
Пример 8
$$log_{1-x}(x^2+3x+1)=1;$$
В основании логарифма стоит ((1-х)), это переменное основание, потому что я могу подставлять различные значения (х) и каждый раз основание логарифма будет разным. Ничего страшного в этом нет, начинаем решать, руководствуясь тем же принципом, что и в предыдущих примерах — стараемся привести обе части уравнения к виду двух логарифмов с одинаковым основанием. Для этого нужно представить (1) справа в виде логарифма с основанием ((1-х)).
Но первым делом выпишем ОДЗ, не забывая накладывать условия и на основание логарифма, так как оно зависит от (х):
$$ begin{cases}
x^2+3x+1>0, \
1-x>0, \
1-xneq1.\
end{cases} qquad (**)$$
Теперь приступаем к решению самого уравнения. Выпишем еще раз формулу, по которой преобразуем правую часть:
$$a=log_{b}(b^a);$$
Где (а=1), а (b=1-x):
$$1=log_{1-x}(1-x)^1=log_{1-x}(1-x);$$
Подставим в уравнение
$$log_{1-x}(x^2+3x+1)=log_{1-x}(1-x);$$
Два логарифма с одинаковым основанием — можем приравнять аргументы:
$$x^2+3x+1=1-x;$$
$$x^2+4x=0;$$
$$x(x+4)=0;$$
$$x=0;$$
$$x=-4.$$
Получили два корня, проверим удовлетворяют ли они ОДЗ, подставив их в (**). Корень (0) не удовлетворяет последнему неравенству в ОДЗ, а ((-4)) удовлетворяет всем условиям.
Ответ: x=-4.
Замена переменной в уравнениях с логарифмами
Разберем еще один частый тип логарифмических уравнений — это уравнения с заменой переменной. Общий принцип заключается в том, чтобы привести все логарифмы в уравнении к одинаковому основанию и одинаковому аргументу, а потом сделать замену.
Проще разобрать на примерах:
Пример 9
$$log^2_{2}(x)+6=5*log_{2}(x)$$
Как и любой пример на логарифмы, начинаем с ОДЗ:
$$x>0.$$
В уравнении один из логарифмов в квадрате, поэтому представить в виде равенства двух логарифмов, как мы делали в предыдущих примерах, не получится. Кроме этого, замечаем, что у нас оба логарифма абсолютно одинаковые (у них одинаковые основания, и одинаковые аргументы).
Попробуем сделать замену:
$$t=log_{2}(x)$$
Тогда наше уравнение после замены примет вид:
$$t^2-5t+6=0;$$
$$D=25-24=1;$$
$$t_{1}=frac{5+1}{2}=3;$$
$$t_{2}=frac{5-1}{2}=1;$$
И сделаем обратную замену, получив два простых логарифмических уравнения:
$$t_{1}=log_{2}(x)=3;$$
$$log_{2}(x)=log_{2}(2^3);$$
$$x=8.$$
$$t_{2}=log_{2}(x)=1;$$
$$log_{2}(x)=log_{2}(2^1);$$
$$x=2.$$
Обязательно, не забываем проверить, удовлетворяют ли корни ОДЗ ((x>0)). Оба корня подходят, записываем ответ.
Ответ: (x=8; , x=2.)
Пример 10
$$ log_{2}left(frac{8}{x}right)-frac{10}{log_{2}(16x)} = 0;$$
Как обычно, начинаем с ОДЗ:
$$ begin{cases}
frac{8}{x}>0, \
log_{2}(16x)neq0,\
16x>0.\
end{cases}$$
Решаем каждое из получившихся неравенств в системе:
$$ begin{cases}
x>0, \
xneqfrac{1}{16},\
x>0.\
end{cases}$$
В итоге ОДЗ будет: (xin(0;frac{1}{16})cup(frac{1}{16};infty)).
Посмотрим теперь на сам пример. Видим два логарифма, у них одинаковые основания, что хорошо. Но функции, стоящие под логарифмами, разные. Постараемся при помощи свойств логарифма сделать одинаковые аргументы, чтобы потом сделать замену.
Воспользуемся формулами суммы и разности логарифмов с одинаковыми основаниями:
$$log_{a}(b*c)=log_{a}(b)+log_{a}(c);$$
$$log_{a}(frac{b}{c})=log_{a}(b)-log_{a}(c);$$
$$log_{2}left(frac{8}{x}right)=log_{2}(8)-log_{2}(x)=3-log_{2}(x);$$
$$log_{2}(16x)=log_{2}(16)+log_{2}(x)=4+log_{2}(x);$$
Подставим наши преобразования в исходное уравнение
$$3-log_{2}(x)-frac{10}{4+log_{2}(x)}=0;$$
Теперь в уравнении все логарифмы одинаковые, модем сделать замену. Пусть (t=log_{2}(x)).
$$3-t-frac{10}{4+t}=0;$$
Приводим к общему знаменателю
$$frac{(3-t)(4+t)-10}{4+t}=0;$$
$$frac{-t^2-t+2}{4+t}=0;$$
Дробь равна нулю, когда числитель равен нулю:
$$-t^2-t+2=0;$$
$$t_{1}=1;$$
$$t_{2}=-2;$$
Делаем обратную замену:
$$t_{1}=log_{2}(x)=1;$$
$$log_{2}(x)=log_{2}(2^1);$$
$$x=2.$$
$$t_{2}=log_{2}(x)=-2;$$
$$log_{2}(x)=log_{2}({2}^{-2});$$
$$x=frac{1}{4}.$$
Сверяем с ОДЗ, видим, что оба корня подходят, записываем ответ.
Ответ: (x=2; , x=frac{1}{4}.)
Пример 11
$$log_{2}(x^2+4x)+log_{0,5}(frac{x}{4})+2=log_{2}(x^2+3x-4)$$
Область допустимых значений:
$$ begin{cases}
x^2+4x>0, \
x^2+3x-4>0,\
x>0.\
end{cases}$$
$$ begin{cases}
x(x+4)>0, \
x>0,\
(x-1)(x+4)>0.\
end{cases}$$
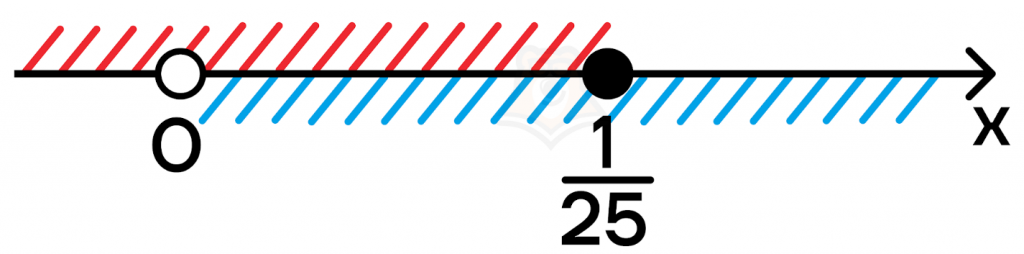
Зеденым цветом показано решение первого неравенства в системе, синим — второго и фиолетовым третьего. Область, которая находится на пересечении сразу всех трех промежутков заштрихована бордовым.
Решаем методом интервалов, и находим пересечение решений всех неравенств в системе:
В итоге получаем ОДЗ: (x>1).
Приступаем к решению самого уравнения. Первым делом приведем все логарифмы к одинаковому основанию (2). Для этого нужно преобразовать только второе слагаемое в уравнении:
$$0,5=frac{1}{2}=2^{-1};$$
$$log_{2}(x^2+4x)+log_{2^{-1}}(frac{x}{4})+2=log_{2}(x^2+3x-4);$$
Вынесем степень из основания, воспользовавшись формулой (log_{a^n}(b)=frac{1}{n}log_{a}(b)).
$$log_{2}(x^2+4x)-log_{2}(frac{x}{4})+2=log_{2}(x^2+3x-4);$$
В первом слагаемом под логарифмом вынесем общий множитель (х). А квадратный многочлен под логарифмом справа разложим на множители при помощи дискриминанта:
$$log_{2}(x(x+4))-log_{2}(frac{x}{4})+2=log_{2}((x-1)(x+4));$$
И опять воспользуемся формулами суммыразности логарифмов:
$$log_{a}(b*c)=log_{a}(b)+log_{a}(c);$$
$$log_{a}left(frac{b}{c}right)=log_{a}(b)-log_{a}(c);$$
$$log_{2}(x)+log_{2}(x+4)-log_{2}(x)+log_{2}(4)+2=log_{2}(x-1)+log_{2}(x+4);$$
Сократим подобные слагаемые и посчитаем (log_{2}(4)=2):
$$4=log_{2}(x-1);$$
$$log_{2}(x-1)=4;$$
$$log_{2}(x-1)=log_{2}(2^4);$$
$$x-1=16;$$
$$x=17.$$
Сверяем корень с ОДЗ — подходит. Записываем ответ.
Ответ: (x=17).
Логарифмическое уравнение: решение на примерах
Как решить логарифмическое уравнение? Этим вопросом задаются многие школьники, особенно в преддверии сдачи ЕГЭ по математике. Ведь в задании С1 профильного ЕГЭ могут встретиться именно логарифмические уравнения.
Уравнение, в котором неизвестное находится внутри логарифмов, называется логарифмическим. Причем неизвестное может находится как в аргументе логарифма, так и в его основании.
Способов решения таких уравнений существует несколько. В этой статье мы разберем способ, который легко понять и запомнить.
Как решать уравнения с логарифмами: 2 способа с примерами
Решить логарифмическое уравнение можно разными способами. Чаще всего в школе учат решать логарифмическое уравнение с помощью определения логарифма. То есть мы имеем уравнение вида:Вспоминаем определение логарифма и получаем следующее:Таким образом мы получаем простое уравнение, которое сможем легко решить.
При решении логарифмических уравнений важно помнить об области определения логарифма, т.к. аргумент f(x) должен быть больше ноля. Поэтому после решения логарифмического уравнения мы всегда делаем проверку!
Давайте посмотрим, как это работает на примере:
Воспользуемся определением логарифма и получим:
Теперь перед нами простейшее уравнение, решить которое не составит труда:
Сделаем проверку. Подставим найденный Х в исходное уравнение:Так как 3 2 = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
Основной минус данного метода решения логарифмических уравнений в том, что многие ребята путают, что именно нужно возводить в степень. То есть при преобразовании logaf(x) = b, многие возводят не a в степень b, а наоборот b в степень a. Такая досадная ошибка может лишить вас драгоценных баллов на ЕГЭ.
Поэтому мы покажем еще один способ решения логарифмических уравнений.
Чтобы решить логарифмическое уравнение, нам нужно привести его к такому виду, когда и в правой, и в левой части уравнения будут стоять логарифмы с одинаковыми основаниями. Это выглядит вот так:
Когда уравнение приведено к такому виду, то мы можем «зачеркнуть» логарифмы и решить простое уравнение. Давайте разбираться на примере.
Решим еще раз то же самое уравнение, но теперь этим способом:В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2.
Для этого вспоминаем свойства логарифмов. Первое свойство, которое нам здесь понадобится – это логарифмическая единица. Напомним его:То есть в нашем случае:Возьмем правую часть нашего уравнения и начнем ее преобразовывать:Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:
Воспользуемся этим свойством в нашем случае, получим:Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили:Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение:
Да, действий в этом способе больше, чем при решении с помощью определения логарифма. Но все действия логичны и последовательны, в результате чего шансов ошибиться меньше. К тому же данный способ дает больше возможностей для решения более сложных логарифмических уравнений.
Разберем другой пример:Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:После преобразования правой части наше уравнение принимает следующий вид:Теперь можно зачеркнуть логарифмы и тогда получим:Вспоминаем свойства степеней:
Теперь делаем проверку:то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
Еще один пример решения логарифмического уравнения:Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:Теперь преобразуем правую часть уравнения:Выполнив преобразования правой и левой частей уравнения, мы получили:Теперь мы можем зачеркнуть логарифмы:
Решим данное квадратное уравнение, найдем дискриминант:
Сделаем проверку, подставим х1 = 1 в исходное уравнение:Верно, следовательно, х1 = 1 является корнем уравнения.
Теперь подставим х2 = -5 в исходное уравнение:Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х2 = -5 – посторонний корень.
Пример решения логарифмического уравнения с разными основаниями
Выше мы решали логарифмические уравнения, в которых участвовали логарифмы с одинаковыми основаниями. А что же делать, если основания у логарифмов разные? Например,
Правильно, нужно привести логарифмы в правой и левой части к одному основанию!
Итак, разберем наш пример:Преобразуем правую часть нашего уравнения:
Мы знаем, что 1/3 = 3 -1 . Еще мы знаем свойство логарифма, а именно вынесение показателя степени из логарифма:Применяем эти знания и получаем:Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:
Тогда получим:Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:Делаем проверку:Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим:Верно, следовательно, х = 4 является корнем уравнения.
Пример решения логарифмического уравнения с переменными основаниями
Выше мы разобрали примеры решения логарифмических уравнений, основания которых были постоянными, т.е. определенным значением – 2, 3, ½ … Но в основании логарифма может содержаться Х, тогда такое основание будет называться переменным. Например, logx+1(х 2 +5х-5) = 2. Мы видим, что основание логарифма в данном уравнении – х+1. Как же решать уравнение такого вида? Решать мы его будем по тому же принципу, что и предыдущие. Т.е. мы будем преобразовывать наше уравнение таким образом, чтобы слева и справа были логарифмы с одинаковым основанием.Преобразуем правую часть уравнения:Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:Теперь мы можем зачеркнуть логарифмы:Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:
1. Аргумент логарифма должен быть больше ноля, следовательно:
2. Основание логарифма должно быть больше 0 и не должно равняться единице, следовательно:
Сведем все требования в систему:
Данную систему требований мы можем упростить. Смотрите х 2 +5х-5 больше ноля, при этом оно приравнивается к (х + 1) 2 , которую в свою очередь так же больше ноля. Следовательно, требование х 2 +5х-5 > 0 выполняется автоматически и мы можем его не решать. Тогда наша система будет сведена к следующему:Перепишем нашу систему:Следовательно, наша система примет следующий вид:Теперь решаем наше уравнение:Справа у нас квадрат суммы:Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.
Для полной уверенности можем выполнить проверку, подставим х = 2 в исходное уравнение:
Т.к. 3 2 =9, то последнее выражение верно.
Как сделать проверку
Еще раз обращаем ваше внимание, что при решении логарифмических уравнений необходимо учитывать область допустимых значений. Так, основание логарифма должно быть больше ноля и не должно равняться единице. А его аргумент должен быть положительным, т.е. больше ноля.
Если наше уравнение имеет вид loga (f(x)) = loga (g(x)), то должны выполняться следующие ограничения:
После решения логарифмического уравнения нужно обязательно сделать проверку. Для этого вам необходимо подставить получившееся значения в исходное уравнение и посчитать его. Времени это займет немного, зато позволит не записать в ответ посторонние корни. Ведь так обидно правильно решить уравнение и при этом неправильно записать ответ!
Итак, теперь вы знаете, как решить логарифмическое уравнение с помощью определения логарифма и с помощью преобразования уравнения, когда в обеих его частях стоят логарифмы с одинаковыми основаниями, которые мы можем «зачеркнуть». Отличное знание свойств логарифма, учет области определения, выполнение проверки – залог успеха при решении логарифмических уравнений.
Решение уравнений, содержащих неизвестную в основании логарифма
Разделы: Математика
Цели урока:
- обучающие: закрепить основные способы решения логарифмических уравнений: по определению логарифма с учётом области определения, на основании свойств монотонности (потенцирование) с учётом равносильности перехода, переход к новому основанию, введение новой переменной; рассмотреть некоторые приемы быстрого решения уравнений рассматриваемого типа;
- развивающие: содействовать развитию логического мышления учащихся; развивать умения рассуждать, сравнивать, осмысливать материал; развивать у учащихся умения анализа условия задачи перед выбором способа ее решения; развивать навыки исследовательской деятельности; учить видеть задачу целиком, логически мыслить при переходе от частного к общему; развивать навыки обобщения;
- воспитывающие: воспитание познавательного интереса, элементов культуры общения; побуждение учащихся к преодолению трудностей в процессе умственной деятельности; воспитание у учащихся уверенности в себе, веры в свои силы в нестандартной ситуации.
Тип урока: урок комплексного применения знаний и навыков.
Ход урока:
1. Организационный момент
(сообщить учащимся тему урока, поставить перед ними задачи урока), (на партах у каждого раздаточный материал см. Приложение 1).
Изучив основные свойства логарифмической функции, правила вычисления логарифмов, овладев основными приемами решения логарифмических уравнений и неравенств, наша основная задача на сегодняшний урок – обобщить методы решения логарифмических уравнений, содержащих переменную в основании логарифма.
2. Активизация знаний учащихся.
Устная работа:
- Найдите область определения функций:
(- 4; — 3) U (- 3; — 1) U (1;∞)
- Каким способом решается уравнение:
. Ответ: по определению логарифма. Решений нет!!
- При каком значении параметра а функция определена на множестве (1; ∞); если изменить основание, значение параметра изменится?
Ответ: а ≥ 1
Ответ: а ≥ 1
Ответ: а > 1
3. Основная часть урока.
Слайд 2. Виды уравнений и методы решения
На области определения по определению логарифма
Или
Пример Решение: x=6. Ответ: 6.
слайд 5.
На области определения по определению логарифма
Пример:
Решение: 7x-14=3-2x; 9x=17; x=17/9; НО. промежутки не пересекаются, значит, решений нет!! Ответ: решений нет.
Пример:Каким способом решается уравнение?
предполагаемый ответ учащихся: решаем, применяя определение логарифма (решение учеником письменно на доске и в тетрадях)
Решение:
при х= 6 верно. Ответ: 6
Слайд 8
Слайд 10. На найденной области определения
решим уравнение: , , х = 0 или х = 1,5
Ответ: 1,5
Слайд 11 Следующий вид уравнения:
Одна и та же функция в основании логарифма
Вопрос: Каким способом решать?
Один из вариантов ответов: область определения достаточно объёмная, поэтому переходим к следствию
Найдём корни этого уравнения и подстановкой в первоначальное логарифмическое, проверим.
Слайд 12. Одна и та же функция является подлогарифмическим выражением
Вопрос: Каким способом решать? Один из вариантов ответов: область определения достаточно объёмная, поэтому переходим к совокупности уравнений
Найдём корни этого уравнения и подстановкой в первоначальное логарифмическое, проверим.
Слайд 14. На промежутке решаем совокупность уравнений:
Слайд 15. Проверяем на принадлежность этих чисел области определения, делаем вывод: решением уравнения являются числа: ; . Ответ: ;.
Слайд 16 Следующий вид уравнений:
Область определения достаточно объёмная
Найдём корни этого уравнения и подстановкой в первоначальное логарифмическое, проверим.
Слайд 17. Как вы думаете, каким способом лучше решать это уравнение?
Один из вариантов ответов: переход к новому основанию (числовому)
Слайд 18. или к буквенному
Слайд 19. Пример:
(решение с подробным комментарием письменно на доске и в тетрадях).
Решение: Очевидно . Выполним преобразования основания и подлогарифмического выражения правой части уравнения
,
Перейдём в правой части уравнения к новому основанию х, применяя свойство: логарифм произведения равен сумме логарифмов множителей по такому же основанию
,
Выполним замену переменных
Получим уравнение , ,
Выполнив обратную замену, получим
Х= — 1.
Очевидно – 1 не входит в область определения заданного уравнения.
Или , , .
По свойству: если коэффициенты квадратного уравнения таковы, что
a + c – b =0, то Х= — 1, Х= ½. Ответ: ½
Слайд 20
Следующий тип уравнений
Слайд 21. Пример
Ответ: 5,5.
Слайд 22 «Комбинированные» виды уравнений
Пример
Решение: очевидно
Слайд 23 , ,
(очевидно, последнее уравнение решений не имеет)
Слайд 24 , . Ответ:
Слайд 25 Уравнения, левая часть которых – сумма взаимно обратных слагаемых
Пример: (*)
Очевидно, каждое слагаемое равно 1.
Получим систему, равносильную уравнению (*)
x = 2. Ответ: 2
Слайд 27. В чём отличие в решении следующего уравнения?
(*)
Равенство взаимно обратных слагаемых верно при условии х > 0,5, х ≠ 1,5.
На рассматриваемом промежутке уравнение (*) равносильно совокупности
Слайд 28
с учётом области определения: Ответ: 1
Подведение итогов урока
4. Домашнее задание.
Слайд 30. Решите уравнения: ,
P. S. Урок проведён в 10 классе физико-химического профиля. Уложились за урок за счёт экономии времени: на партах лежали у каждого ученика листы с напечатанными типами уравнений, учащиеся записывали только метод решения (без области определения и решения). Эти листы ученики забрали с собой и вклеили в тетрадь.
В слабом классе лучше потратить на эту тему сдвоенный урок.
P. S. S. В кабинете один компьютер с выходом на экран телевизора. В связи с этим, на слайдах текст печатается очень крупно.
Решение логарифмических уравнений — примеры с решениями
Решение простейших логарифмических уравнений
Как известно, решение простейшего логарифмического уравнения logax=b — это x=a b . Другими словами, простейшее логарифмическое уравнение logax=b имеет единственный корень, которым является степень a b .
Первый пример. Проще некуда.
Решите уравнение log5x=2
Все понятно без слов:
log5x=2
x=5 2
x=25
При решении простейших логарифмических уравнений переход от logax=b к x=a b , обычно, не представляет сложности. Часто, куда сложнее вычислить значение степени a b или упростить ее вид. Следующие примеры иллюстрируют сказанное.
Второй пример. А вычислить значение?
Решите логарифмическое уравнение
Это простейшее логарифмическое уравнение. Оно имеет единственный корень . Очевидно, полученная степень нуждается в доработке.
Сначала заменим квадратный корень из семи степенью: .
Остается вспомнить, как определяется степень с отрицательным показателем, и закончить вычисления:
На этом решение простейшего логарифмического уравнения завершено.
Третий пример. Извольте упростить.
Начинаем со стандартного при решении простейших логарифмических уравнений перехода:
Надо бы упростить полученную степень.
Возвести дробь в минус первую степень – это кувыркнуть ее вверх ногами:
Теперь глаза мозолит иррациональность в знаменателе, исправим эту ситуацию:
Таким образом, — искомое решение простейшего логарифмического уравнения.
Решение логарифмических уравнений разными методами
Сейчас пройдемся по всем основным методам решения логарифмических уравнений, и рассмотрим решения наиболее характерных и интересных, по нашему мнению, логарифмических уравнений.
по определению логарифма
По определению логарифма в первую очередь проводится решение логарифмических уравнений logaf(x)=b , где a и b — числа, причем a>0 , a≠1 , а f(x) – выражение с переменной x , таких как log2(x 2 +4·x+3)=3 , и др. Решение состоит в переходе от уравнения logaf(x)=b к уравнению f(x)=a b . Например, решение логарифмического уравнения log2(x 2 +4·x+3)=3 с опорой на определение логарифма заменяется решением уравнения x 2 +4·x+3=2 3 .
На определение логарифма можно опираться и при решении логарифмических уравнений logh(x)f(x)=g(x) , таких как logx(x 2 −3·x+6)=2 , log2(9−2 x )=3−x , logx(3·x lgx +4)=2·lgx и др. Решение уравнения logh(x)f(x)=g(x) заключается в решении уравнения f(x)=(h(x)) g(x) на области допустимых значений (ОДЗ) для исходного уравнения. Например, чтобы решать логарифмическое уравнение logx(x 2 −3·x+6)=2 по определению логарифма, надо решить уравнение x 2 −3·x+6=x 2 , и взять все корни, принадлежащие ОДЗ для исходного уравнения.
- Чтобы решить логарифмическое уравнение logaf(x)=b по определению логарифма, надо перейти к уравнению f(x)=a b и найти его решение.
- А чтобы решить по определению логарифма уравнение logh(x)f(x)=g(x) , надо перейти к уравнению f(x)=(h(x)) g(x) , решить его, и взять корни, принадлежащие ОДЗ для исходного логарифмического уравнения.
Рассмотрим примеры решения логарифмических уравнений.
Обычно решение оформляется кратко:
А теперь поясним, какие рассуждения за всем этим скрываются.
Заданное логарифмическое уравнение имеет вид logaf(x)=b , где f(x)=2·x−4 , a=1/2 , b=−2 . Такое логарифмическое уравнение можно решать по определению логарифма, то есть, заменять решение уравнения logaf(x)=b решением уравнения f(x)=a b .
Итак, переходим от исходного уравнения к уравнению . Это рациональное уравнение, решаем его:
Так получено решение исходного логарифмического уравнения.
Пример. Не забыть про проверку.
Решите логарифмическое уравнение logx(−x 2 +5·x+3)=2
Заданное уравнение можно рассматривать как уравнение logh(x)f(x)=g(x) , где f(x)=−x 2 +5·x+3 , h(x)=x , g(x)=2 , и мы знаем, что такие уравнения можно решать по определению логарифма. Решение этим методом на первом этапе предполагает переход от уравнения logh(x)f(x)=g(x) к уравнению f(x)=(h(x)) g(x) . Имеем −x 2 +5·x+3=x 2 .
Теперь нам надо решить полученное уравнение −x 2 +5·x+3=x 2 . Оно сводится к квадратному уравнению 2·x 2 −5·x−3=0 . Решаем его:
Остается пройти последний шаг решения логарифмического уравнения по определению логарифма – выяснить, какие из корней принадлежат ОДЗ для исходного уравнения. ОДЗ для исходного логарифмического уравнения logx(−x 2 +5·x+3)=2 определяется системой .
Очевидно, не удовлетворяет второму условию, значит, это посторонний корень для исходного уравнения. А корень x2=3 удовлетворяет всем условиям: . Значит, x2=3 – это корень уравнения logx(−x 2 +5·x+3)=2 .
На этом решение завершено. Уравнение имеет единственный корень 3 .
Естественно, так подробно решение не описывают. Обычно его оформляют кратко, но без ущерба для логики действий, например, так:
методом потенцирования
Метод потенцирования применяется для решения логарифмических уравнений, части которых являются логарифмами с одинаковыми основаниями, например, log5(x−1)=log57 , и др. Решение логарифмических уравнений методом потенцирования состоит в переходе от уравнения logh(x)f(x)=logh(x)g(x) к уравнению f(x)=g(x) на ОДЗ для исходного уравнения. Так решение уравнения можно заменить решением уравнения x+1=x 2 −1 на ОДЗ для исходного уравнения.
Название метода становится понятным, если вспомнить, что потенцирование – это восстановление выражения по его логарифму.
Обосновать метод можно, сославшись на свойства логарифмов. Из них мы знаем, что логарифмы двух положительных чисел с одинаковыми положительными и отличными от единицы основаниями равны тогда и только тогда, когда равны сами числа, то есть, , a>0 , a≠1 , b1>0 , b2>0 . Так вот переход от логарифмического уравнения logh(x)f(x)=logh(x)g(x) к уравнению f(x)=g(x) — это аналог замены logab1=logab2 на b1=b2 , а нахождение в рамках ОДЗ для исходного уравнения – это аналог выполнения условий a>0 , a≠1 , b1>0 , b2>0 .
Итак, чтобы решить логарифмическое уравнение logh(x)f(x)=logh(x)g(x) методом потенцирования, надо
- Перейти к уравнению f(x)=g(x) .
- Решить полученное уравнение.
- И взять корни, принадлежащие ОДЗ для исходного уравнения, остальные отбросить как посторонние. Другими словами, провести отсеивание посторонних корней.
Остается рассмотреть пример с решением.
Мы видим, что части уравнения являются логарифмами с одинаковыми основаниями. Подобные логарифмические уравнения удобно решать методом потенцирования.
Согласно выбранному методу, переходим от исходного уравнения к уравнению x+1=x 2 −1 .
Теперь нам надо решить полученное уравнение x+1=x 2 −1 . Перенос слагаемых из одной части уравнения в другую с противоположным знаком и приведение подобных слагаемых дает квадратное уравнение x 2 −x−2=0 , которое можно решить, например, через дискриминант:
Остается проверить принадлежность найденных корней области допустимых значений переменной x для исходного уравнения. Для нашего логарифмического уравнения ОДЗ определяют два условия x+1>0 и x 2 −1>0 . Очевидно, x1=−1 не удовлетворяет первому условию ( −1+1>0 — неверное), значит, это посторонний корень для решаемого уравнения. А корень x2=2 удовлетворяет обоим условиям ( 2+1>0 – верное, 2 2 −1>0 — верное). Значит, он является корнем уравнения .
На этом решение логарифмического уравнения методом потенцирования завершено. Уравнение имеет единственный корень, им является число 2 .
методом разложения на множители
Пример. Все как всегда.
Решение логарифмического уравнения можно провести методом разложения на множители, так как в левой части уравнения находится произведение двух выражений с переменной, а в правой – нуль.
Первый шаг – переход к совокупности уравнений:
Второй шаг – решение полученных логарифмических уравнений.
Первое уравнение можно решить по определению логарифма, а второе — методом потенцирования, после предварительного переноса второго логарифма в правую часть со знаком «плюс»:
На последнем шаге остается выяснить, принадлежат ли найденные корни 2 и 5 ОДЗ для решаемого логарифмического уравнения :
На этом решение логарифмического уравнения методом разложения на множители завершено.
путем введения новой переменной (замены переменной)
Решение логарифмических уравнений методом введения новой переменной, как правило, проводится в следующих типичных ситуациях:
- Когда переменная находится в составе некоторой сложной функции, как, например, в уравнении
- Когда переменная фигурирует в нескольких одинаковых выражениях и нигде более. Вот примеры логарифмических уравнений, соответствующие сказанному:
(часто, одинаковые выражение с переменной прячут за свойствами степеней, и приведенное выше в пример логарифмическое уравнение, скорее, будет выглядеть так или так )
Пример №1. Вводить или не вводить?
Решите логарифмическое уравнение
Введение новой переменной 2−log2x=t позволяет перейти от логарифмического уравнения к сравнительно простому уравнению t 4 =16 с понятной структурой и очевидным решением:
Возврат к старой переменной дает два логарифмических уравнения 2−log2x=2 и 2−log2x=−2 , решив которые находим интересующее нас решение исходного уравнения:
Итак, логарифмическое уравнение имеет два корня 1 и 16 .
В заключение заметим: введение новой переменной в подобных и, прямо скажем, простых ситуациях настолько прозрачно, что его проводят «в уме», и не отражают в решении:
Пример №2. Оказывается, оно квадратное.
Выражения 2 2·(log5x) 2 и 2 (log5x) 2 , в которых содержится переменная в заданном логарифмическом уравнении, почти одинаковые. Различие вносит лишь число 2 в показателе первой степени. Здесь несложно догадаться, что по свойству степени в степени, выражение 2 2·(log5x) 2 можно переписать как (2 (log5x) 2 ) 2 , что открывает дорогу к замене переменной 2 (log5x) 2 =t и переходу к квадратному уравнению t 2 −15·t−16=0 с новой переменной t .
Итак, проведем решение логарифмического уравнения через замену переменной:
Пример. Взаимно обратные логарифмы.
Решите логарифмическое уравнение
Здесь полезно вспомнить следствие из формулы перехода к новому основанию логарифма, которому отвечает формула logab=1/logba , a>0 , a≠1 , b>0 , b≠1 . Так возникает идея обозначить один из логарифмов в заданном логарифмическом уравнении за t , тогда другой логарифм будет выражаться через новую переменную t как 1/t .
Остается вернуться к старой переменной x , и закончить решение. Мы принимали logx+3(3·x+13)=t и нашли t=2 , поэтому
Итак, логарифмическое уравнение имеет единственное решение 1 .
дробь равна нулю
Решите логарифмическое уравнение
Решение логарифмических уравнений, в левых частях которых находится дроби, а в правых – нули, проводится в соответствии с методом решения уравнений «дробь равна нулю». При этом надо приравнять числитель дроби к нулю, и решить это уравнение на ОДЗ для исходного уравнения.
Итак, решение начинаем с приравнивания к нулю числителя дроби из левой части заданного уравнения. Это дает уравнение log3(x−3) 2 −4=0 , которое равносильно уравнению log3(x−3) 2 =4 . Решение полученного логарифмического уравнения можно провести по определению логарифма:
Остается проверить, принадлежат ли найденные корни области допустимых значений переменной x для исходного логарифмического уравнения. В нашем случае условий, которые определяют ОДЗ, довольно много, поэтому, кажется, рациональнее действовать через непосредственную подстановку. Подставим найденные корни в исходное уравнение и посмотрим, что при этом получается.
Подстановка x1=12 дает верное числовое равенство
Поэтому, 12 является корнем.
При подстановке x2=−6 получается не имеющее смысла выражение , так как под знаками логарифмов в знаменателе – отрицательные числа. Значит, −6 – посторонний корень.
методом логарифмирования
Решение логарифмических уравнений в определенных случаях приходится проводить через логарифмирование обеих частей уравнения. Обычно, к логарифмированию прибегают тогда, когда в одной части уравнения находится показательно степенное выражение, а в другой – положительное число, как в следующих уравнениях , и т.п.
Давайте решим одно из них, чтобы стало понятно, что дает логарифмирование уравнения.
Пример. Дожили, лог уравнения логарифмируем
Данное уравнение – это типичный представитель уравнений, для решения которых используется метод логарифмирования. В левой части уравнения – степень, на ОДЗ для уравнения эта степень принимает только положительные значения. Это открывает возможность прологарифмировать обе части заданного уравнения. В нашем случае логарифмирование целесообразно проводить по основанию 2 , так как в исходном уравнении присутствует логарифм с таким основанием. Так и поступим:
Для нашего уравнения ОДЗ определяется условием x>0 . Поэтому, мы спокойно можем вынести степень из-под знака логарифма, оперевшись на соответствующее свойство логарифмов (подробнее про решение логарифмических уравнений через преобразования поговорим в одном из следующих пунктов):
И это, собственно, то, ради чего логарифмирование затевалось – привести логарифмическое уравнение к более простому и привычному виду. Дальнейшие преобразования не требуют комментирования:
Полученное логарифмическое уравнение, очевидно, можно решить методом замены переменной:
графическим методом
К решению логарифмических уравнений графическим методом обычно прибегают тогда, когда, во-первых, функции, отвечающие частям заданного логарифмического уравнения, довольно простые в плане построения их графиков, и, во-вторых, не видно других более простых вариантов получить решение.
Пример. Графически так графически.
Сколько корней имеет уравнение
Сама формулировка задания подсказывает, что, скорее всего, решить уравнение, что называется, в лоб, и указать не только количеств корней, но и сами эти корни, не выйдет. Иначе бы вопрос стоял «решить уравнение». Действительно, путей решения этого уравнения не видно.
Однако, количество корней удобно определять по графикам функций, соответствующих частям уравнения. Более того, в данном случае построить графики этих функций довольно просто. Нам хорошо известны функции и y=log2x и их графики. Графики интересующих нас функций и y=log2(x−2) будут иметь схожую геометрию с точностью до преобразований растяжения и симметрии. Поэтому, нам достаточно взять несколько опорных точек, чтобы изобразить нужные кривые. Давайте получим их, учитывая, что область определения функции — это x≤15/4 , а область определения функции y=log2(x−2) — это x>2 .
Отмечаем эти точки на плоскости в прямоугольной системе координат, соединяем их плавными линиями, и чертеж готов:
Видно, что графики имеют одну точку пересечения на отрезке от трех до пятнадцати четвертых. Больше их быть не может, так как функция убывает на указанном отрезке от до нуля, а функция y=log2(x−2) возрастает на этом отрезке от нуля до log2(7/4) .
Это позволяет нам утверждать, что уравнение имеет один корень.
через подбор корня и возрастание-убывание функций
Решение логарифмических уравнений иногда приходится проводить, основываясь на возрастании и убывании функций, соответствующих частям уравнения. Это касается ситуаций, когда простые и привычные пути решения не просматриваются, но зато очевиден или легко подбирается корень логарифмического уравнения, а также легко обосновывается возрастание и убывание соответствующих функций. Приведем пример.
Пример. Подбор и единственность.
Для заданного уравнения не видно других подходов к решению, кроме как обращаться к функциям и их свойствам. Можно строить графики, но делать это для функции, отвечающей правой части уравнения, не очень приятно из-за довольно «большого» числа 11 и довольно «высокой» степени 5 . Попробуем обойтись без чертежа.
Вместо этого обопремся на возрастание логарифмической функции, отвечающей левой части уравнения, и убывание функции, отвечающей правой части уравнения (она убывает, как возрастающая от убывающей). Это позволяет утверждать, что если уравнение имеет корень, то он единственный. А найти корень позволяет подбор по рекомендациям, данным в статье, посвященной методу решения уравнений через возрастание-убывание, – им является число 10 .
На этом решение логарифмического уравнения завершено.
методом оценки
Пример. Оценить и дорешать.
Своего рода оценочная классика: логарифм, синус, косинус, корень – все в одном уравнении. Итак, пробуем провести решение уравнения методом оценки. Но сначала, все же, квадратный корень из квадрата заменим модулем:
Теперь к оценкам.
Косинус принимает значения из отрезка −1 до 1 , а его модуль – [0, 1] . Следовательно, . С другой стороны, как четная степень, откуда . Таким образом, значения выражения из левой части уравнения не превосходят 1 , а значения выражения из правой части уравнения не меньше 1 . Это позволяет нам заменить решение исходного уравнения решением следующей системы
Что делать с первым уравнением системы — сразу не понятно, зато вполне реально получить решение второго логарифмического уравнения:
Теперь путем подстановки выясним, удовлетворяют ли найденные корни логарифмического уравнения 2 и 3 первому уравнению системы, а значит, системе в целом, и исходному уравнению.
Давайте начнем с числа 3 , с ним все просто:
Это верное равенство, следовательно, 3 – решение системы и корень исходного уравнения.
А вот с числом 2 придется повозиться.
Это равенство неверное (обоснуем чуть ниже), следовательно, 2 – не является решением системы, и не является корнем исходного уравнения.
Таким образом, уравнение имеет один единственный корень 3 .
А вот обещанное обоснование.
Модуль косинуса равен единице, если аргумент косинуса равен . А не равно sin10 ни при каком целом k . Действительно, при k=0 , очевидно, sin10≠0 . При любом другом целом k равенство неверное, так как значения синуса находятся в отрезке от −1 до 1 .
через ОДЗ
Решение логарифмических уравнений часто требует нахождения ОДЗ: когда для проведения преобразований, когда для проверки. А порою ОДЗ позволяет даже получить решение.
Пример. ОДЗ от безысходности.
Беглый анализ уравнения, можно сказать, ставит в тупик относительно способа его решения. И почти единственным и, так или иначе, адекватным мероприятием выглядит нахождение ОДЗ. Что называется, в любом случае пригодится.
Вот как все обернулось: ОДЗ есть пустое множество. Следовательно, уравнение не имеет корней.
методом освобождения от внешней функции
Признаемся, почти никогда для решения логарифмических уравнений не приходилось прибегать к методу освобождения от внешней функции. Однако для полноты картины не помешает привести решение соответствующего примера.
Пример. Попробуй разгляди.
Найдите решение уравнения
Как тут действовать? Непонятно, что здесь можно предложить в альтернативу методу освобождения от внешней функции.
А так заданное логарифмическое уравнение можно рассматривать как уравнение , где функция f такая, что . Очевидно, f – возрастающая функция как сумма двух возрастающих. Это позволяет освободиться от внешней функции f в уравнении , то есть, на ОДЗ перейти к уравнению .
Здесь заметим, что область допустимых значений переменной для полученного уравнения совпадает с ОДЗ для исходного уравнения (она такова ). Значит, решение полученного уравнения является решением исходного уравнения.
Остается решить логарифмическое уравнение , что можно сделать через потенцирование:
Решение логарифмических уравнений через преобразование
Редкий раз решение логарифмических уравнений обходится без проведения преобразований. Характерными для логарифмических уравнений являются преобразования, проводящиеся на базе свойств корней и степеней. Все они по отдельности разобраны в статье «Преобразование логарифмических уравнений». Здесь мы рассмотрим примеры решения логарифмических уравнений со сравнительно сложными последовательностями преобразований.
Для начала напомним о необходимости использования модулей при вынесении четных показателей степеней из-под знаков логарифмов, а также при переходе от логарифмов произведений (частных) к суммам (разностям) логарифмов.
Пример. Про модуль не забыть.
Решите логарифмическое уравнение
Просматривается возможность прийти к одинаковым логарифмам в левой части уравнения. Для начала вынесем показатель 2 из-под знака логарифма, и так как он есть четное число, то не забудем про модуль:
Для раскрытия модуля нам потребуется ОДЗ для исходного уравнения:
С учетом этого, имеем
Дальше все просто:
Теперь еще раз обратим внимание на преобразование квадратов, кубов и других степеней логарифмов. Уж очень часто приходится видеть неверные преобразования, типа , вместо , или , вместо и т.п.
Пример. Квадраты логарифмов.
Просматривается возможность упростить вид заданного логарифмического уравнения. Для начала перепишем его как , чтобы не наделать ошибок при преобразовании квадратов логарифмов. Дальше все довольно прозрачно:
Теперь пора ввести новую переменную:
Остается вернуться к старой переменной:
Наконец, рассмотрим пример решения довольно сложного логарифмического уравнения, где сильно переплетены степени и логарифмы.
Просматриваются черты основного логарифмического тождества. Сейчас поработаем в этом направлении. Но сначала давайте найдем область допустимых значений переменной x – она бывает нужна при проведении преобразований и при проведении проверки. Тем более, в нашем случае ОДЗ находится легко:
Теперь приступаем к преобразованию:
А дальше все легко:
При найденных значениях переменной знаменатели дробей в уравнении в нуль не обращаются, а также 0 и 2 принадлежат ОДЗ для исходного уравнения, следовательно, являются его корнями.
Решение однородных логарифмических уравнений
В задачниках встречаются логарифмические уравнения, которые являются однородными уравнениями относительно некоторых логарифмов. Например, lg 2 (x+1)−lg(x+1)·lg(x−1)−2·lg 2 (x−1)=0 – это логарифмическое уравнение, однородное относительно логарифмов lg(x+1) и lg(x−1) .
Решение однородных логарифмических уравнений завязано на преобразовании, заключающемся в делении обеих частей уравнения на «старшую» степень одного из логарифмов, что в дальнейшем позволяет ввести новую переменную. При этом необходимо отдельно проверять, не являются ли корнями уравнения те значения переменной, при которых обращается в нуль логарифм, на который планируется проводить деление. Давайте обратимся к конкретному примеру.
Возьмем наше уравнение lg 2 (x+1)−lg(x+1)·lg(x−1)−2·lg 2 (x−1)=0 . Оно, как мы отметили, является однородным относительно логарифмов lg(x+1) и lg(x−1) . Давайте разделим обе части этого уравнения на старшую степень второго из этих логарифмов, то есть, на lg 2 (x−1) . Но, как известно, делить обе части уравнения мы имеем право только на выражение, не обращающееся в нуль, в противном случае можно потерять корни. Поэтому, стоит отдельно проверить, не являются ли корнями уравнения значения переменной, при которых lg 2 (x−1)=0 , а уже после этого спокойно проводить задуманное деление, не опасаясь потерять корни. В нашем случае lg 2 (x−1)=0 только при x=2 . Но x=2 не является решением исходного уравнения, так как его подстановка в исходное уравнение дает неверное числовое равенство. Теперь можно переходить к делению, считая lg 2 (x−1)≠0 . Имеем:
Дальше напрашиваются следующие преобразования
Остается закончить решение, воспользовавшись методом введения новой переменной. Приняв , имеем
http://urok.1sept.ru/articles/532964
http://www.cleverstudents.ru/equations/solving_logarithmic_equations.html
На этой странице вы узнаете
- Что значит расти по экспоненте?
- Как быстро избавиться от логарифмов с одинаковым основанием?
- Как не попасть в аварию в погоне за результатом?
Математики иногда скучают. Иначе как объяснить то, что для понимания этой пугающей многих учеников темы, нужно запомнить единственный факт: «Степень числа и логарифм — разная запись одного и того же математического события». В этой статье мы ближе познакомимся с логарифмами и увидим, что ничего экстремально сложного в них на самом деле нет.
Понятие логарифма
Математика очень интересная наука, действия в которой можно повернуть в обе стороны. Например, возведение в степень и извлечение корня — одно и то же действие, но совершаемое «в разные направления». Это как шарик-маятник, который качается туда-сюда.
Однако помимо извлечения корня степень числа имеет еще одно противодействие: это логарифм. Разберемся, чем же они отличаются.
Итак, извлекая корень, мы находим первоначальное число, которое возвели в степень. Например, если мы вычислим, чему равно (4^3), то получим 64. А если извлечем (sqrt[3]{64}), то получим число, которое возводили в степень. Иными словами, извлекая корень, мы находим основание степени.
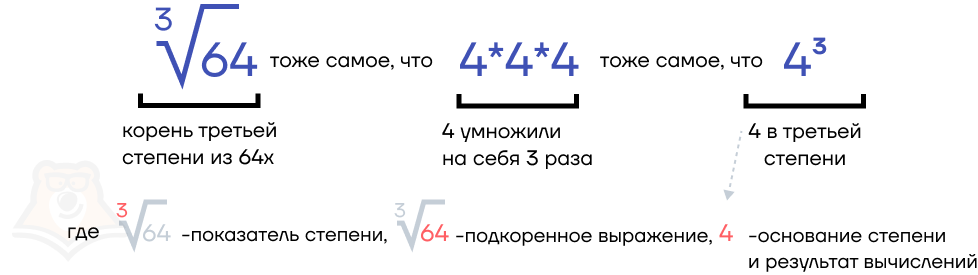
Но что, если мы знаем основание степени и число, полученное при возведении, но при этом не знаем показатель степени? Можем ли мы как-нибудь найти, в какую именно степень возвели то или иное число?
Ответ: да! Для этого и существуют логарифмы. Логарифм отвечает на вопрос: «В какую степень возвести число a, чтобы получилось число b?»
Например, мы возвели двойку в неизвестную степень и получили 4:
(2^x=4)
Зададим вопрос: в какую степень нужно возвести 2, чтобы получился такой результат? Ответ приходит сразу — это 2:
(2^2=4)
Эту же операцию можно записать значительно короче, если использовать логарифм. Запись будет выглядеть так:
(log_24=2)
Вот и всё!
Если понятие «степень» все еще звучит устрашающе, мы написали для вас статью «Действия с натуральными числами».
А теперь внедрим в нашу статью немного научности. Что такое логарифм во вселенной математики?
Логарифм — это число, в которое нужно возвести основание a, чтобы получить число b.
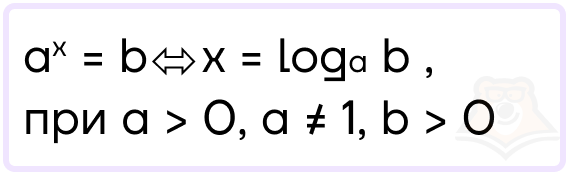
У каждого элемента любой математической функции есть название. Как называются элементы логарифма?
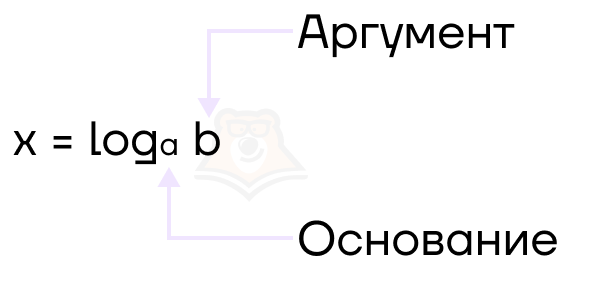
Снова вспомним корни. Корень степени 2 мы записываем без показателя степени, например, (sqrt{25}). Это связано с его распространенностью и «особенностью». Так и в логарифмах существуют свои «краткие записи», применяемые для «особенных» логарифмов. Такими логарифмами являются десятичный и натуральный. Рассмотрим их чуть подробнее.

Десятичный логарифм — это логарифм числа по основанию 10.
Например, нам нужно узнать, в какую степень нужно возвести 10, чтобы получить 100. То есть мы находим (log_{10}100=2). Аналогично (log_{10}1000=3) или (log_{10}100000=5).
Для сокращения записи мы не пишем основание, а само название логарифма немного меняем. Выглядит запись десятичного логарифма следующим образом:
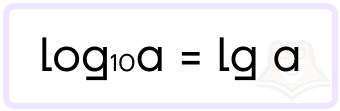
Запись такого логарифма нужно просто запомнить. Но не будет и ошибкой, если записать обычным способом.
Что же с натуральным логарифмом? Аналогично десятичному, в его основании стоит особое число — экспонента.
Экспонента — это такая математическая константа, постоянная (как, например, ускорение свободного падения в физике), которая примерно равна 2,72.
Натуральный логарифм — это логарифм по основанию е (e ≈ 2,72).
Такой логарифм тоже имеет «свою» запись, которую нужно запомнить:
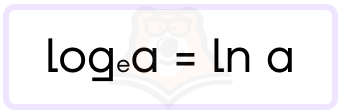
У натурального логарифма в основании стоит число e, которое называется числом Эйлера. На самом деле, это иррациональное число, которое имеет бесконечное количество знаков после запятой, но мы ограничиваемся краткой записью 2,72. Число e играет важную роль во многих разделах математики.

Экспонента — это показательная функция (y=e^x), где (e) — число Эйлера, равное примерно 2,72.
Особенность такой функции в том, что число Эйлера многократно умножается на само себя, а значит, неравномерно увеличивается. Примером такого увеличения может быть падение камушка: чем дольше он летит, тем выше его скорость. Другим примером может быть сложный процент, когда сумма вклада или долга увеличивается каждый год на определенное число процентов (про сложные проценты можно узнать в статье «Финансовые задачи. Проценты»). Такой рост называют ростом по экспоненте.
На самом деле, экспонента имеет множество интересных свойств, например, ее производная равна ей самой.
График экспоненты будет выглядеть как непрерывно и «неравномерно» возрастающая кривая.
Нельзя обходить такую важную тему, как логарифмы, стороной. Они часто встречаются в заданиях 5, 12 и 14 профильного ЕГЭ по математике или в №17 ЕГЭ по базовой математике. При умелом использовании их свойств можно упростить выражение или заменить запись логарифма на более удобную.
Рассмотрим пример задания из номера 5 первой части ЕГЭ по профильной математике.
Найдите корень уравнения (log_5(x+121)=4).
Решение. Немного изменим запись: если возвести 5 в степень 4, то мы получим (x+121). Значит, мы можем составить и решить уравнение:
(x+121=5^4)
(x+121=625)
(x=504)
Ответ: 504
Может возникнуть вопрос: неужели при решении каждого логарифмического уравнения или неравенства придется прибегать к «переформулировке»? На самом деле, нет, ведь для упрощения решений существуют свои правила, а главное, свойства логарифмов. Рассмотрим их чуть подробнее.
Основное логарифмическое тождество
Итак, какими свойствами обладает логарифм? Начнем с одного из самых важных, а именно — основного логарифмического тождества.
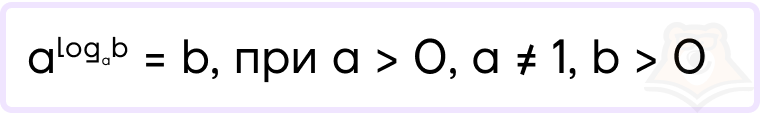
Возможно, вас смутило, что логарифм стоит в степени числа. На самом деле, логарифм — это тоже какое-то число, просто в другой записи. Так, (3^2) и (3^{log_24}=32) — одно и то же число, но в разных записях.
Разберемся чуть подробнее, как работает тождество. Путь (a=2, b=4). Тогда получаем запись:
(2^{log_24}=4)
Решим отдельно левую часть:
(2^{log_24}=2^2=4)
Получаем, что тождество верно. Но почему это так работает?
Заметим, что при вычислении логарифма мы получаем значение степени x, в которую должны возвести основание а, чтобы получить аргумент b.
(log_ab=x), тогда (a^x=b)
После этого мы снова возводим то же основание а в ту же степень, и снова получаем аргумент b. То есть делаем одно и то же действие дважды.
(a^{log_ab}=a^x=b)
Следовательно, это тождество позволяет сократить вычисление на несколько шагов. Важно: оно будет работать только в случае, когда основания степени и логарифма будут совпадать. Тогда совпадут и аргумент с ответом.
Рассмотрим, почему это не работает при несовпадающих основаниях. Для этого найдем значение выражения (3^{log_24}). Итак, (log_24=2), значит, мы получаем выражение (3^2=9). Очевидно, что (9neq4), соответственно, применить основное тождество логарифмов мы здесь не можем (поскольку (3neq2)).
Данное тождество часто используется для преобразований.
Свойства логарифмов
Логарифмы, как и числа, можно складывать, умножать и делать множество действий с ними. Как не запутаться в них, не производить лишних вычислений и не ошибиться? Для этого нужно хорошо знать все свойства, которые представлены в таблице ниже. Каждое из рассмотренных в таблице свойств можно использовать для преобразований.

Рассмотрим каждое свойство чуть подробнее.
Свойство 1. (log_ab^m=m*log_ab).
Попробуем найти значение выражения (log_28^2) без применения свойства. Тогда возведем аргумент в степень и получим:
(log_28^2=log_264)
Воспользовавшись определение логарифма, заметим, что (log_264=6).
Но что делать, если числа окажутся большими, или, более того, у логарифма не будет точного значения — примером такого логарифма может служить (log_57). Да и вычисление в несколько действий с большими числами может занять много времени.
Именно поэтому мы применяем это свойство!
(log_28^2=2*log_28=2*3=6)
Свойство 2. (log_{a^n}b=frac{1}{n}*log_ab)
Рассмотрим на примере логарифма (log_{2^2}4). Посчитаем без свойства:
(log_{2^2}4=log_44=1)
Заметим, что:
- в первом свойстве мы увеличивали аргумент логарифма (то есть конечный результат, который получается при возведении числа в степень);
- в этот раз мы увеличиваем уже число, которое возводим в степень.
Сравните:
(2^2=4) или (3^2=9)
Следовательно, когда мы будем производить «обратные» действия, то есть считать логарифм, то при увеличении основания степени (и сохранении результата возведения в степень), у нас должна уменьшиться сама степень, в которую мы возводим.
Например:
(2^4=16) и (4^2=16)
Именно поэтому у нас появляется дробь: она уменьшает степень во столько раз, во сколько мы увеличили первоначальное число:
(log_{2^2}4=frac{1}{2}log_24=frac{1}{2}*2=1)
Свойство 3. (log_{a^n}b^m=frac{m}{n}*log_ab)
Это свойство вытекает из двух предыдущих, просто их соединили вместе. Иначе пришлось бы отдельно выносить степень из аргумента и отдельно из основания логарифма. Сравните:
(log_{2^3}5^7=7*log_{2^3}5=7*frac{1}{3}*log_25=frac{7}{3}log_25)
или
(log_{2^3}5^7=frac{7}{3}log_25)
Свойство 4. (log_ab+log_ac=log_a(b*c))
Найдем значение выражения (log_24+log_28):
(log_24+log_28=2+3=5)
Но в случае, когда числа не будут так легко считаться (или вовсе не будут считаться), на помощь придет это свойство:
(log_512,5+log_52=log_525=2)
Свойство 5. (log_ab-log_ac=log_afrac{b}{c})
Аналогично с предыдущим свойством это нужно для упрощения вычислений.
Например:
(log_318-log_32=log_3frac{18}{2}=log_39=2)
Свойства 6 и 7. (log_aa=1) и (log_a1=0)
Эти свойства напрямую связаны с возведением числа в степень. Достаточно лишь ответить на два вопроса:
- В какую степень нужно возвести число, чтобы получилось такое же число?
- В какую степень нужно возвести любое число, чтобы получить 1?
Ответы на эти вопросы будут 1 и 0. Отсюда и эти свойства:
- Число в степени 1 будет равно само себе: (log_aa=1).
- Число в степени 0 будет равно 1: (log_a1=0).
Свойство 8. (log_ab=frac{log_cb}{log_ca})
Это свойство используется в случаях, когда нам нужно представить логарифм с любым другим основанием.
Например:
(log_25=frac{log_35}{log_25})
Это свойство может пригодиться в решении уравнений и неравенств для упрощения выражений.
Свойство 9. (log_ab=frac{1}{log_ba})
Что делать, если нам нужно представить логарифм с определенным основанием, которое равно аргументу этого логарифма? Все просто: мы можем поменять основание и аргумент местами, если воспользуемся свойством (log_ab=frac{1}{log_ba}).
Например:
(log_{27}3=frac{1}{log_327}=frac{1}{3})
Заметим, что это же выражение можно было решить немного по-другому:
(log_{27}3=log_{3^3}3=frac{1}{3}*log_33=frac{1}{3}).
В этом случае мы воспользовались свойствами 2 и 6.
Свойство 10. (a^{log_cb}=b^{log_ca})
Еще одно свойство, которое позволяет изменить аргумент логарифма, и при этом не менять значение выражения.
Рассмотрим на примере (2^{log_24}):
(2^{log_24}=2^2=4)
(2^{log_24}=4^{log_22}=4^1=4)
Для более простого запоминания свойств логарифмов предлагаем вам воспользоваться нашими забавными ассоциациями.

Теперь, когда мы знаем свойства логарифмов, мы можем перейти к более сложным преобразованиям — к решениям уравнений и неравенств.
Простейшие логарифмические уравнения
В других статьях мы уже рассматривали разные виды уравнений: линейные, квадратные, показательные и т.п. Настало время узнать про логарифмические уравнения.
Логарифмическое уравнение — это уравнение, в котором неизвестная стоит в аргументе или основании логарифмов.
Иными словами, если в уравнении мы видим логарифм с неизвестной — это логарифмическое уравнение.
Например, (log_2x=4) — логарифмическое уравнение.
А вот (log_25+x=x^2) не будет логарифмическим уравнением, поскольку неизвестная не стоит ни в аргументе, ни в основании логарифма.
Как решать логарифмические уравнения?
Логарифмическое уравнение нужно привести к такому виду:
(log_af(x)=log_ag(x)).
При решении таких уравнений нужно обязательно учитывать, что по определению аргумент логарифма всегда должен быть больше нуля, а основание больше нуля и не должно равняться единице. Эти ограничения называются областью допустимых значений или ОДЗ логарифма.
Область допустимых значений — это те значения, которые может принимать переменная x (или другая буква латинского алфавита) в выражении.
(log_ab)
ОДЗ логарифма: a > 0, a ≠ 0, b> 0.
Это можно сделать, приравняв аргументы. Почему мы можем так сделать? Представим, что мы возводим некоторое число в степень, это число будет стоять в основании логарифма. Если два логарифма равны, то и степени, в которые мы возвели число, равны. Следовательно, будет равен и результат возведения в степень, то есть аргумент логарифма!
(a^x=b)
(log_ab=x)
Тогда пусть (log_ab=log_ac)
(x=log_ac)
(a^x=c => b=c)
При этом проверить ОДЗ можно только у одного из логарифмов, поскольку если один из них положителен, а второй равен первому, то и второй будет положительным.
Например, если b=2, то из равенства b=c получаем c=b=2.
В логарифмических уравнениях встречаются более сложные выражения, которые в дальнейшем мы будем выражать в виде функций — например, f(x) или g(x).
Например:
Алгоритм решения логарифмического уравнения:
1. Написать ОДЗ.
2. Упростить выражения слева и справа от знака равенства, используя свойства логарифмов, если это возможно.
3. Если основания логарифмов одинаковые, избавиться от логарифмов. В противном случае — используя свойства логарифмов, привести к одинаковому основанию, а уже потом совершить эти действия.
4. Решить уравнение и сравнить с ОДЗ, выписать в ответ корни.
Рассмотрим на примере:
(log_2(5x-4)=log_2(x+8))
- В первую очередь найдем ОДЗ. Для этого вспомним, что аргумент логарифма всегда строго положителен:
(5x-4>0) и (x+8>0)
Найдем возможные значения х:
(5x>4) и (x>-8)
(x>frac{4}{5}) и (x>-8)
Нанесем найденные промежутки на числовую прямую и определим, какие значения может принимать х. Для этого нам нужно будет найти промежутки, которые удовлетворяют обоим неравенствам:
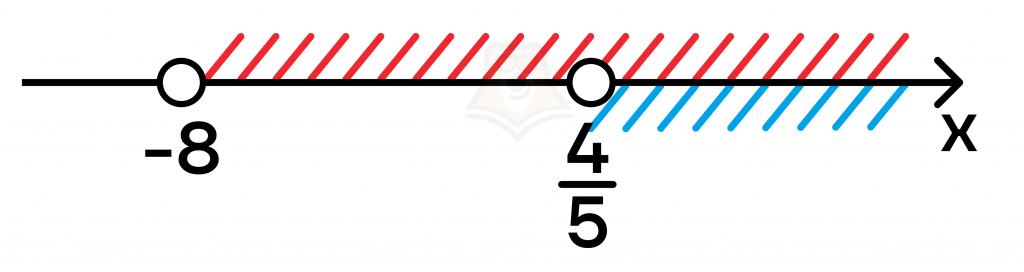
Теперь мы можем определить ОДЗ: (x in(frac{4}{5};+{infty}))
- Если в обеих частях уравнения находится логарифм по одинаковому основанию, то можно «скинуть» логарифмы и записать равенство аргументов. Поскольку и у первого, и у второго логарифма основания равны 2, то мы можем приравнять их аргументы:
(5x-4=x+8)
- Решим полученное уравнение:
(5x-x=8+4)
(4x=12)
(x=3)
- Подставим в ОДЗ и проверим, подходит ли корень. Поскольку (3>frac{4}{5}), то корень нам подходит.
Ответ: 3.
А теперь немного усложним задачу. Допустим, переменная будет стоять и в основании, и в аргументе логарифма.
Рассмотрим еще одно уравнение:
(log_2(x-4)=log_{4x}4+log_{4x}x)
- Найдем ОДЗ. Аргумент логарифма всегда строго больше 0, а основание больше 0 и не равно 1. Тогда получаем следующие неравенства для аргументов логарифмов:
(x>0)
(x-4>0)
И для оснований логарифмов:
(4x>0)
(4xneq1)
Решим неравенства:
(x>0)
(x>4)
(x>0)
(xneqfrac{1}{4})
Теперь отметим все ограничения на числовой прямой и найдем, чему равна ОДЗ:
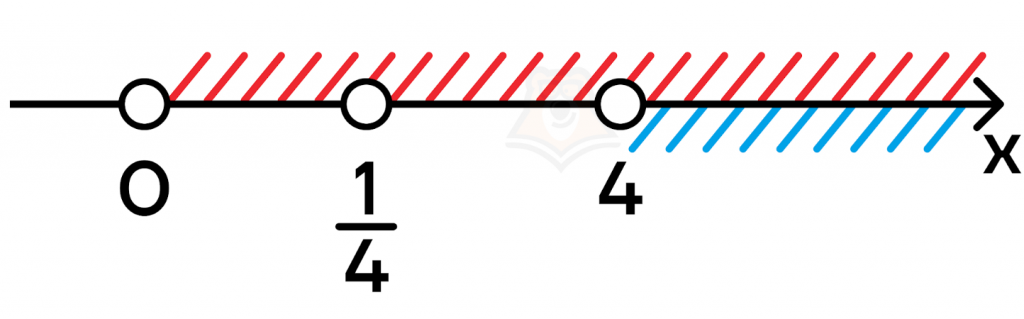
Поскольку нам нужно, чтобы ограничение удовлетворяло всем полученным неравенствам и уравнениям, то (xin(4;+{infty})).
- Теперь перейдем к решению самого уравнения. По свойствам логарифма (свойства 4 и 6) преобразуем правую часть уравнения:
(log_2(x-4)=log_{4x}4x)
(log_2(x-4)=1)
- Чтобы отбросить логарифмы и перейти к уравнению с аргументами, необходимо, чтобы их основания были равны. Поскольку основание левого логарифма равно 2, то представим правую часть в виде логарифма с таким же основанием 2:
(log_2(x-4)=log_22)
- Отбросим логарифмы и перейдем к уравнению с ними:
(x-4=2)
(x=6)
Поскольку (6>4), то корень принадлежит ОДЗ, а значит, его можно записать в ответ.
Ответ: 6.
Мы разобрали уравнения с логарифмами. Остался вопрос: а как решать неравенства с ними?
Простейшие логарифмические неравенства
Логарифмическое неравенство — это неравенство, в котором переменная стоит в аргументе или основании логарифма.
Для решения логарифмических неравенств тоже можно избавляться от логарифмов.
Делается это уже известным способом — если основания равны, то можно перейти к неравенству с аргументами. При этом нужно обращать внимание на основание логарифма.
Важно!
Если (0<a<1), тогда знак неравенства меняется на противоположный.
Если (a>1), тогда знак неравенства не меняется.
Разберемся, почему это так работает. Рассмотрим два примера:
(log_24=2)
(log_{frac{1}{2}}4=log_{2^{-1}}4=-1*log_24=-2)
Как можно увидеть, если основание логарифма меньше 1, то результат вычислений отрицательный (в случае, если аргумент больше 1). Это связано с тем, что при возведении дробного числа в степень, большую 1, это число только уменьшается, например:
((frac{1}{3})^2=frac{1}{9})
Но если мы возведем такое число в отрицательную степень, то получим больший результат:
((frac{1}{3})^{-2}=3^2=9)
Именно поэтому ради избежания путаницы со знаками, при отбрасывании логарифмов с основанием (0<a<1) мы меняем знак на противоположный: тем самым мы сразу избавляемся от минуса.
Например:
(log_{frac{1}{3}}9>0)
(log_{3^{-1}}9>0)
(-log_39>0 |*(-1))
(log_39<0)
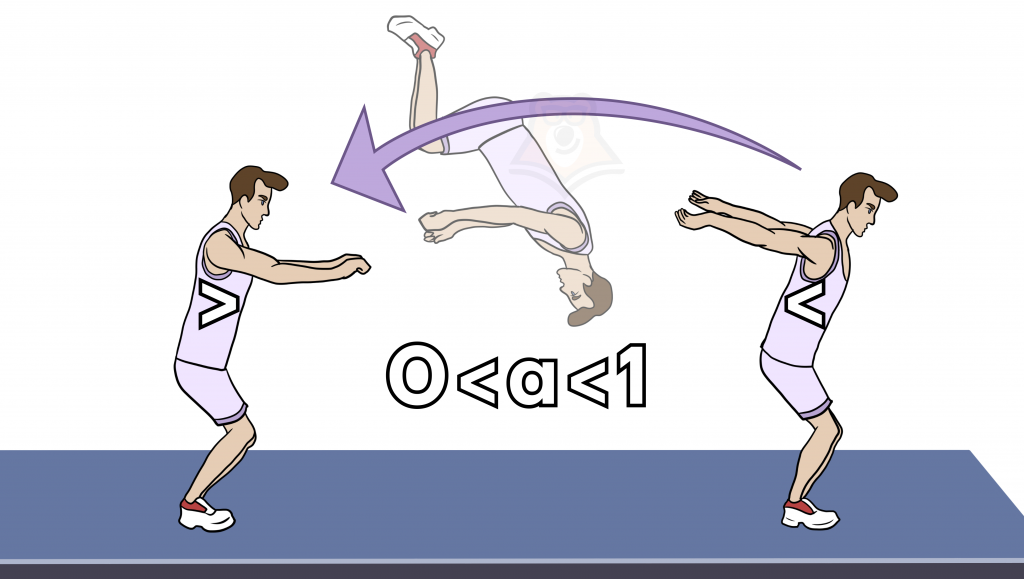
А теперь чуть подробнее рассмотрим, как действовать с логарифмическими неравенствами:

Алгоритм решения логарифмического неравенства:
1. Написать ОДЗ.
2. Упростить выражения слева и справа от знака неравенства, используя свойства логарифмов, если это возможно.
3. Если основания логарифмов одинаковые, избавиться от логарифмов по схеме выше. В противном случае — используя свойства логарифмов, привести к одинаковому основанию, а уже потом совершить эти действия.
4. Решить неравенство, пересечь с ОДЗ, записать ответ.
Обратим ваше внимание еще раз. Решая как логарифмические уравнения, так и неравенства, можно разогнаться слишком сильно и вылететь с дороги…
Чтобы такого не случилось, есть специальный ограничитель неправильных ответов — ОДЗ.
Работая с логарифмами и избавляясь от них, всегда следите за показаниями ОДЗ, иначе в ответ попадут лишние корни.
Логарифмические неравенства могут встретиться в номере 14 ЕГЭ по профильной математике. Рассмотрим один из их примеров:
Решите неравенство: (log_3^2x-10log_3xgeq-21)
Решение. Первым делом, найдем ОДЗ. Поскольку переменная стоит только в аргументе логарифма, то и ограничения вводим лишь на аргумент:
(x>0)
Перейдем к решению. Заметим, что (log_3x) — повторяющееся выражение, а значит, мы можем сделать замену.
Обратим внимание, что у первого логарифма степень стоит именно у логарифма, а не у аргумента.
Пусть (log_3x=t), тогда:
(t^2-10tgeq-21)
(t^2-10t+21geq0)
Теперь слева у нас получилось квадратное неравенство. Для его решения найдем нули функции, приравняв левую часть к 0:
(t^2-10t+21=0)
Найдем корни уравнения с помощью дискриминанта:
(D=b^2-4ac=10^2-4*1*21=100-84=16)
(t_1=frac{-b+sqrt{D}}{2a}=frac{10+4}{2}=7)
(t_2=frac{-b-sqrt{D}}{2a}=frac{10-4}{2}=3)
Воспользуемся методом интервалов (подробнее об этом методе можно прочитать в одноименной статье). Отметим корни на числовой прямой, расставим знаки и найдем промежутки:
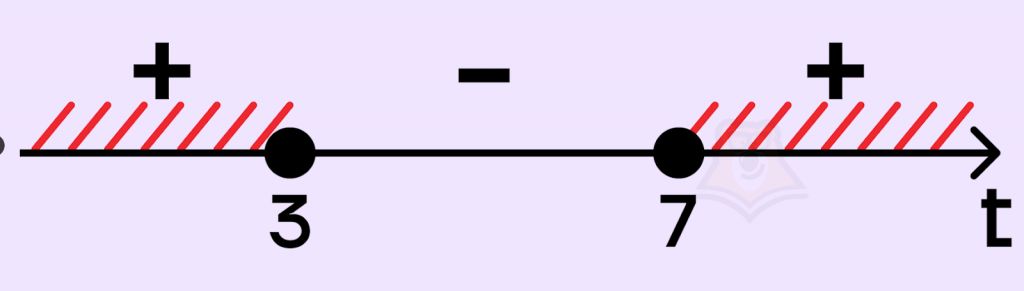
Получаем промежутки:

Сделаем обратную замену:
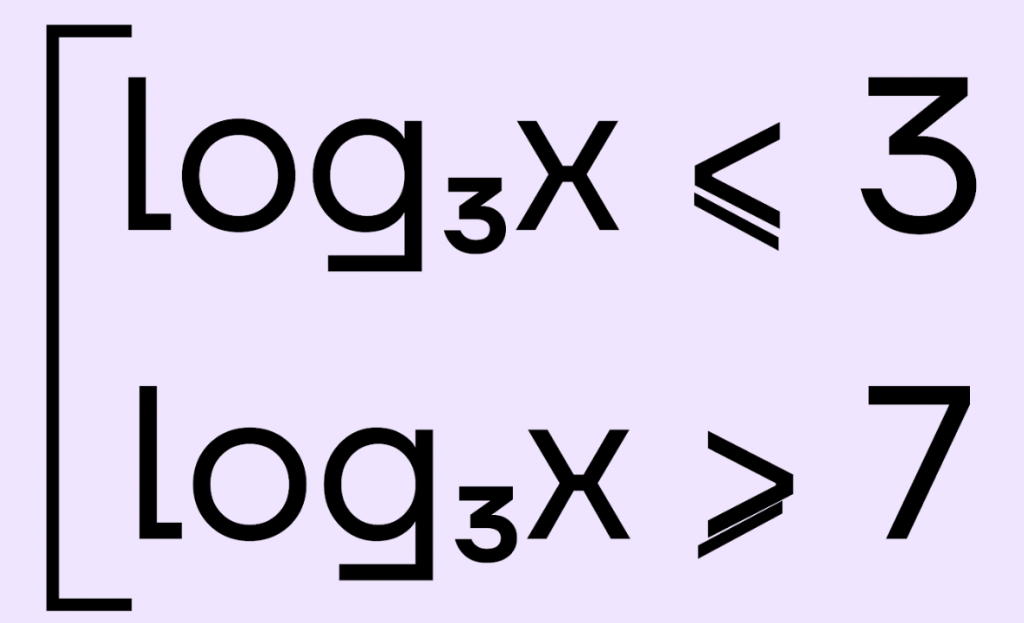
Представим правые части неравенства в виде логарифмов с основанием 3:
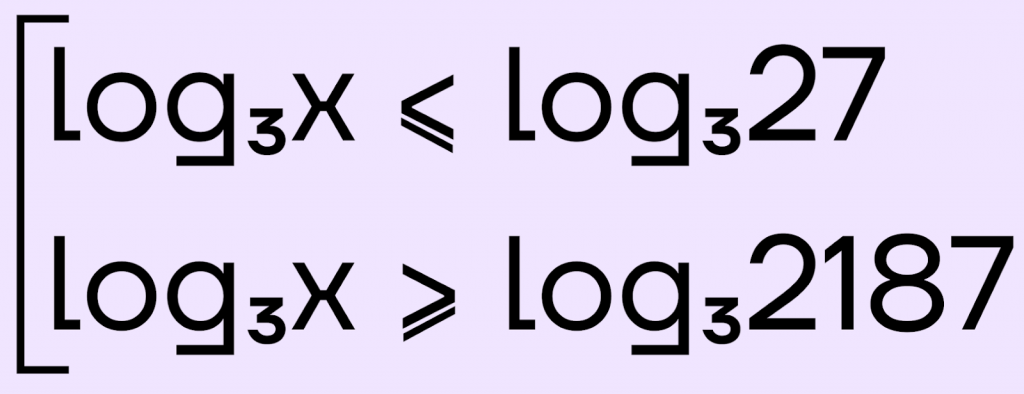
Теперь у нас справа и слева логарифмы с одинаковым основанием, соответственно, мы можем отбросить логарифмы и перейти к неравенствам с аргументами. Поскольку 3>1, то знаки неравенства менять не нужно:
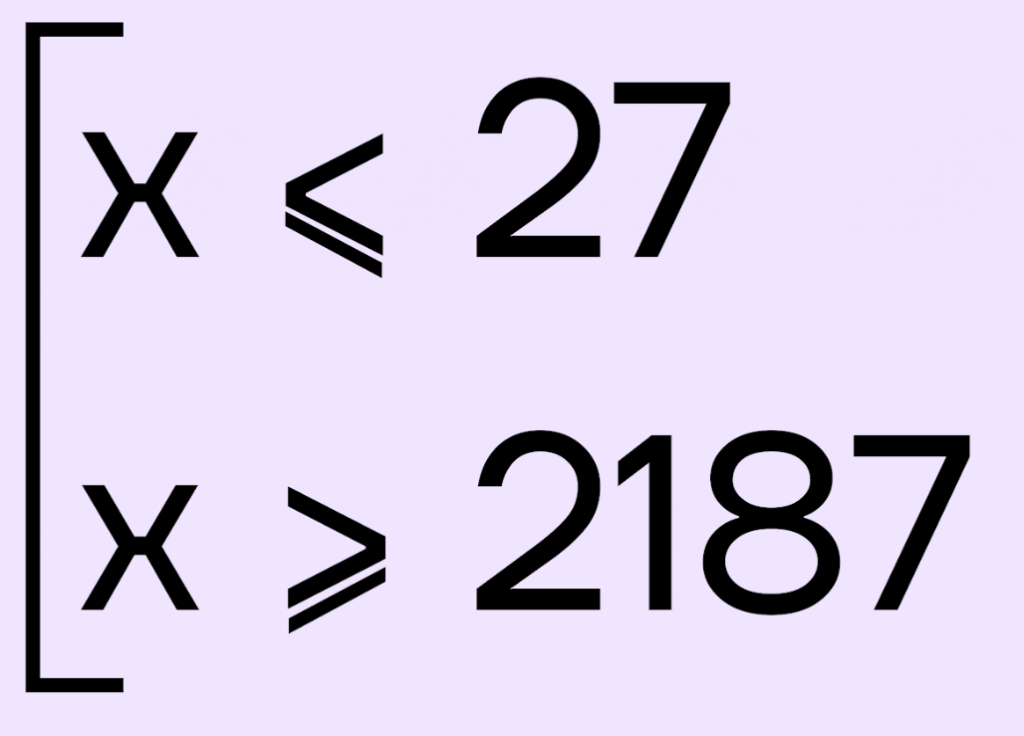
Отметим на числовой прямой полученные промежутки, а также нанесем ОДЗ:
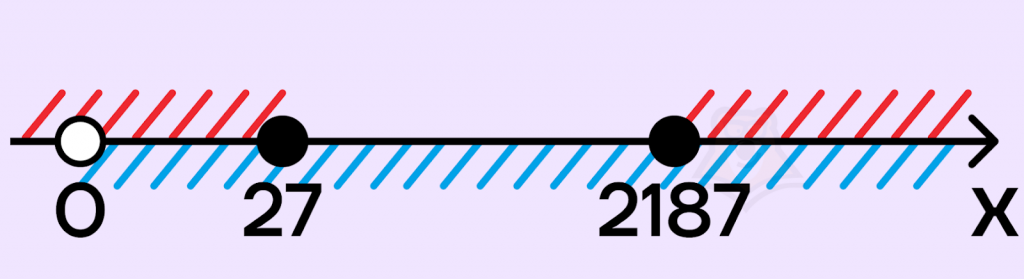
С учетом ОДЗ получаем промежутки: ((0;27]bigcup[2187;+{infty})). Это и будет ответ.
Ответ: ((0;27]bigcup[2187;+{infty}))
Теперь давайте рассмотрим решение неравенства с основанием, которое меньше 1.
(log_{frac{1}{5}}x^2geq log_{frac{1}{5}}x+2)
Шаг 1. Напишем ОДЗ. Аргумент логарифма должен быть строго больше 0, поэтому получаем два неравенства:
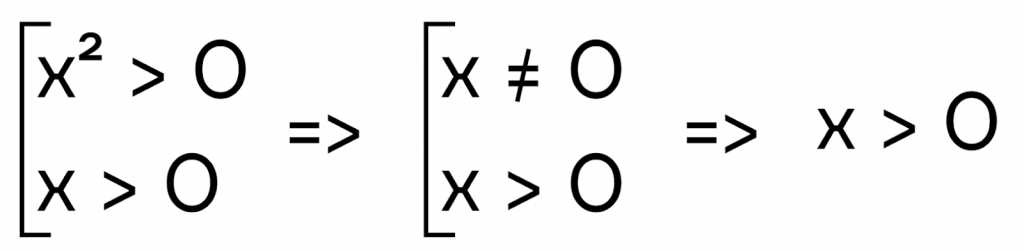
Шаг 2. Преобразуем правую часть. Для этого воспользуемся свойством логарифмов и вынесем степень аргумента перед логарифмом.
Поскольку степень положительная, то мы должны поставить аргумент в модуль, чтобы не потерять отрицательные значения:
(2*log_{frac{1}{5}}|x|geq log_{frac{1}{5}}x+2)
Шаг 3. Раскроем модуль. По ОДЗ мы получили, что x>0, а значит, мы можем убрать модуль, поскольку под ним всегда будет стоять положительное число:
(2*log_{frac{1}{5}}xgeq log_{frac{1}{5}}x+2)
Шаг 4. Перенесем одно слагаемое влево и упростим:
(2*log_{frac{1}{5}}x-log_{frac{1}{5}}xgeq 2)
(log_{frac{1}{5}}xgeq 2)
Представим правую часть в виде логарифма с основанием (frac{1}{5}):
(log_{frac{1}{5}}xgeq log_{frac{1}{5}}frac{1}{25})
Шаг 5. Отбросим логарифмы. Поскольку (frac{1}{5}<1), то знак неравенства меняется на противоположный:
(xgeq 125)
Шаг 6. Отметим полученный промежуток на числовой прямой и нанесем ОДЗ:
С учетом ОДЗ получаем промежуток ((0;frac{1}{25}]).
Ответ: ((0;frac{1}{25}])
Мы рассмотрели логарифмы, уравнения и неравенства с ними. Научиться решать их не так сложно. Практикуйтесь побольше, тогда все обязательно получится. А чтобы продолжить освоение математической науки, рекомендуем вам познакомиться со статьей «Тригонометрическая окружность и графики функций».
Термины
Дискриминант в квадратном уравнении — это выражение, которое ищется по формуле (D=b^2-4⋅a⋅c), где а, b и с берутся из уравнения. Подробнее о нем рассказано в статье «Линейные, квадратные и кубические уравнения».
Иррациональные числа — это числа, которые нельзя представить в виде обыкновенной дроби, то есть они не имеют точного значения.
Квадратное неравенство — это такое неравенство, которое можно привести к виду (ax^2+bx+c ⋁ 0), где a, b и с — любые числа (причем a ≠ 0), x — неизвестная переменная, а ⋁ — любой из знаков сравнения (> , < , ≤ , ≥ ). Решение таких неравенств мы обсуждаем в статье «Метод интервалов».
Модуль числа — это его абсолютная величина. При взятии модуля мы не учитываем знак этого числа — положительное оно или отрицательное. Модуль числа всегда неотрицателен и обозначается с помощью модульных скобок: |a| ≥ 0. Этому математическому понятию посвящена отдельная статья Учебника.
Нули функции — это значения аргумента, при которых функция равна нулю.
Показательная функция — это функция, у которой неизвестная находится в показателе степени. Например, (y = 2^x). Подробнее о ней мы рассказываем в одноименной статье.
Производная функции — это математическое понятие, показывающее скорость изменения функции в определенной точке. Подробнее про производные можно прочесть в статье «Исследование функции с помощью производной».
Фактчек
- Логарифм — это степень, в которую возводится основание логарифма, чтобы получить аргумент.
- Десятичный логарифм — это логарифм числа по основанию 10. Записывается так: lg a.
- Натуральный логарифм — это логарифм по основанию е (e ≈ 2,72). Записывается как ln a.
- Основное логарифмическое тождество: (a^{log_ab}=b), при (a >0, a ≠ 1, b>0).
- Существуют специальные свойства логарифмов, благодаря которым можно совершать преобразования.
- При решении уравнений и неравенств нельзя забывать про ОДЗ на аргумент и основание логарифма: основание больше нуля и не равно единице, аргумент больше нуля.
- В логарифмических неравенствах при переходе к неравенству аргументов логарифмов знак меняется на противоположный, если значение основания логарифма находится на промежутке от 0 до 1.
Проверь себя
Задание 1.
Решите уравнение (log_3(x^2+4)=log_3(4x)).
- 1 и -1
- 2 и -2
- 2
- -1
Задание 2.
Решите уравнение (log_28=log_{16}(x)+2).
- 16
- 12
- 1
- 8
Задание 3.
Решите уравнение (log_2(2x^2)-5=log_2(x) +log_2(x-5)).
- 0 и (frac{16}{3})
- 0 и (frac{32}{3})
- 32
- (frac{16}{3})
Задание 4.
Решите неравенство (log_9(x+4)geq log_9(2x)^2).
- ([-frac{4}{3};0)bigcup(0;4])
- ((0;4])
- ([-frac{4}{3};0))
- ([-frac{4}{3};4])
Задание 5.
Решите неравенство (log_{500}500geq log_2(1+3x)).
- ((0;frac{1}{3}])
- ((-frac{1}{3};frac{1}{3}])
- ([-frac{1}{3};frac{1}{3}])
- ((-frac{1}{3};0)
Ответы:1. — 3; 2. — 1; 3. — 4; 4. — 1; 5. — 2.
Решение
логарифмических уравнений-1
Логарифмическим
уравнением
называется уравнение, в котором
неизвестное содержится под знаком
логарифма ( в частности, в основании
логарифма).
Простейшее логарифмическое
уравение
имеет вид:
Решение
любого логарифмического уравнения
предполагает переход от логарифмов к
выражениям, стоящим под знаком логарифмов.
Однако это действие расширяет область
допустимых значений уравнения и может
привести к появлению посторонних корней.
Чтобы
избежать появления посторонних корней,
можно поступить одним из трех способов:
1.
Сделать
равносильный переход
от исходного уравнения к системе,
включающей область
допустимых значений уравнения:
или
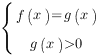
в
зависимости от того, какое неравенство
или
проще.
Если
уравнение содержит неизвестное в
основании логарифма:
,
то
мы переходим к системе:
2.
Отдельно
найти область допустимых значений
уравнения,
затем решить уравнение и проверить,
удовлетворяют ли найденные решения ОДЗ
уравнения.
3.
Решить уравнение, и потом сделать
проверку: подставить
найденные решения в исходное уравнение,
и проверить, получим ли мы верное
равенство.
Логарифмическое
уравнение любого уровня сложности в
конечном итоге всегда сводится к
простейшему логарифмическому уравнению.
Все
логарифмические уравнения можно
условно разделить на четыре типа:
1.
Уравнения, которые содержат логарифмы
только в первой степени. Они с помощью
преобразований и использования
свойств
логарифмов
приводятся к виду
или
Пример.
Решим уравнение:
Решение.
Выпишем
ОДЗ
уравнения:
Внимание!
Мы всегда ищем ОДЗ исходного
уравнения, а не того, которое получится
в процессе преобразований. То есть ОДЗ
записываем перед тем, как переходим к
решению уравнения.
Для
упрощения вычислений давайте перенесем
логарифмы с отрицательными коэффициентами
в противоположную часть уравнения –
из соображений, что умножать проще, чем
делить:
Представим
число 2 в виде логарифма по основанию
4:
Получим
уравнение:
Воспользуемся
свойствами
логарифмов:
Приравняем
выражения, стоящие под знаком логарифма:
Проверим,
удовлетворяет ли наш корень ОДЗ
уравнения:
Да,
удовлетворяет.
Ответ:
х=5
2.
Уравнения, которые содержат логарифмы
в степени, отличной от 1 (в частности, в
знаменателе дроби). Такие уравнения
решаются с помощью введения
замены переменной.
Пример.
Решим уравнение:
Решение.
Найдем
ОДЗ уравнения:
Уравнение
содержит логарифмы в квадрате, поэтому
решается с помощью замены переменной.
Важно!
Прежде чем вводить замену, нужно
«растащить» логарифмы, входящие в состав
уравнения на «кирпичики», используя
свойства логарифмов.
При
«растаскивании» логарифмов важно очень
аккуратно применять свойства логарифмов:
Кроме
того, здесь есть еще одно тонкое место,
и, чтобы избежать распространенной
ошибки, воспользуемся промежуточным
равенством: запишем степень логарифма
в таком виде:
Аналогично,
.
Подставим
полученные выражения в исходное
уравнение. Получим:
Теперь
мы видим, что неизвестное
содержится
в уравнении в составе .
Введем
замену: .
Так как
может
принимать любое действительное значение,
на переменную
мы никаких ограничений не накладываем.
Получили
уравнение:
Раскроем
скобки, приведем подобные члены и решим
квадратное уравнение:
,
Вернемся
к исходной переменной:
,
Отсюда:
,
Ответ: ,
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #