Элементарные функции комплексного переменного
Показательная функция комплексного переменного
В действительной области показательная функция вводится обычно в связи с обобщением понятия степени
. В комплексной области функцию требуется определить так, чтобы при
ее свойства совпадали с известными свойствами функции
. Одно из важнейших свойств функции
— представление ее рядом Тейлора: она является суммой сходящегося на всей числовой прямой ряда
.
Учитывая это, рассматриваем ряд и убеждаемся, что он абсолютно сходится при любом
, т.е. во всей комплексной плоскости
определена некоторая функция — сумма этого ряда. Так как при
имеем
, то вводим следующее определение: показательной функцией
в комплексной области называется функция, которая является суммой сходящегося во всей комплексной плоскости ряда
(2.3)
Из определения следует, что показательная функция определена во всей комплексной плоскости. В частности, при , где
— действительное число, имеем
. Используя свойства абсолютно сходящихся рядов (возможность перестановки и группировки членов ряда), ряд можно записать в виде алгебраической суммы двух рядов с действительными членами отделить действительную и мнимую части ряда:
Полученные ряды являются рядами Тейлора для функций и
. В результате имеем равенство
, или, обозначив
через
(2.4)
Формула (2.4) — формула Эйлера была использована для записи комплексного числа в показательной форме.
Функция обладает, очевидно, рядом свойств, справедливость которых установлена в действительной области, т.е. для
.
С другой стороны, в силу расширения множества, следует ожидать, что имеют место и другие свойства, аналога которых в действительной области нет.
К свойствам первой группы нужно отнести прежде всего формулу сложения:
(2.5)
Доказательство формулы сводится, согласно определению показательной функции, к доказательству справедливости при любых и
равенства
которое устанавливается путем перемножения абсолютно сходящихся рядов, записанных слева (см. пример 1.44).
Если в равенстве (2.5) положить — любое комплексное число, то, учитывая тождество
, можно записать
. Это равенство, справедливое при любых значениях
, означает, что функция
является периодической и ее период — чисто мнимое число
. Аналога этому свойству в действительной области нет, функция
— непериодическая.
Так же, как и в действительной области, показательная функция не обращается в нуль ни при каком значении аргумента. Действительно, если предположить противное, что существует
, при котором
, то из тождества
, где
— любое комплексное число, получили бы,
при любом
, что неверно. Однако это единственное исключение, т.е. нуль — единственное значение, которое не может принимать функция
. В отличие от
значение функции в комплексной области может быть отрицательным, например
. Вообще
может принимать любые значения в
, за исключением нуля. Это свойство доказывается просто, если в формуле (2.5) положить
и сравнить равенство
с показательной формой записи комплексного числа. В результате получим, что при фиксированном z , т.е. при фиксированных
и
, модуль числа
равен
, а аргумент равен
, т.е.
(2.6)
Отсюда получаем, что может принимать любые значения
, так как
— любое число.
Пример 2.13. Найти для чисел: а)
; б)
.
Решение
а) Находим модуль числа и аргумент
. После этого можно записать
, то есть
.
Можно записать решение иначе, используя формулу сложения (2.5) и формулу Эйлера (2.4):
Полому , а из показательной формы записи числа
находим
.
б) Представим число в виде произведения , а множитель
в показательной форме:
. Тогда
Поэтому имеем , или
, так как для
данного значения аргумента имеет место ограничение . После этого записываем
.
Пример 2.14. Найти , если
.
Решение
Применяя последовательно формулы (2.5),(2.6), находим
, то есть
.
Поэтому .
Пример 2.15. Показать, что функция является периодической и ее период — действительное число.
Решение
Нужно показать, что существует число такое, что
для любого
. Но из формулы (2.5) имеем
, поэтому число
должно быть таким, чтобы выполнялось равенство
, а это верно при
. Следовательно, период функции
— действительное число
.
Пример 2.16. Доказать, что функция является неоднолистной на множестве
. Найти область однолистности.
Решение
Неоднолистность функции следует из определения, так как существуют не равные значения аргумента, такие, что в них совпадают значения функции. Например, для и
получается
.
Чтобы определить область однолистности, запишем разность
или
.
Значения функции совпадают для тех и
, для которых выполняется равенство
, то есть
.
Однолистным отображение будет в любой области, принадлежащей горизонтальной полосе ширины , в частности полосе
или
(рис. 2.9).
Любая прямая , параллельная действительной оси отображается в луч
, так как из
получаем
. В частности, действительная ось
, то есть
, переходит в луч
— действительную положительную полуось, а прямая
, то есть
, — в луч
, геометрически это — та же действительная полуось
Для однозначности отображения на границе проведем разрез по лучу. При этом точкам прямой будут соответствовать точки нижнего «берега» оси
, а точкам прямой
точки верхнего «берега».
Такой же результат получим и для следующей полосы . Она отображается также в плоскость с разрезом
.
Вообще любая полоса с помощью функции
переходит в плоскость с разрезом по действительной положительной полуоси.
Нарушенную разрезом непрерывность отображения можно восстановить, построением римановой поверхности функции по такому же принципу как сделано для
.
Полученный результат (см. решение примера 2.16) запишем в виде утверждения: функция взаимно однозначно отображает:
1) любую полосу — в плоскость с разрезом по лучу
;
2) полосу в плоскость с разрезом по действительной отрицательной полуоси;
3) полосу во всю комплексную плоскость с разрезом по действительной положительной полуоси.
Тригонометрические и гиперболические комплексные функции
Функции вводятся аналогично показательной функции — как суммы соответствующих абсолютно сходящихся во всей комплексной плоскости рядов:
(2.7)
(2.8)
На основе этих функций определяются и другие тригонометрические и гиперболические:
Из определений следует, что функции являются четными, а остальные — нечетными.
Сравнивая формулы (2.7) и (2.8) с формулой (2.3) — определением функции , получаем следующие формулы, справедливые при любом
(2.9)
(2.10)
Формулы (2.9) и (2.10) — формулы Эйлера; они связывают тригонометрические и гиперболические функции с показательной. Формула (2.9) при , где
— действительная переменная, рассмотрена выше (см. формулу (2.4)).
Так как формулы (2.9) и (2.10) верны при любых значениях , то, заменяя
на
и учитывая, что
и
— нечетные, a
и
— четные функции, можем записать
Комбинируя эти формулы с (2.9) и (2.10), получаем представление тригонометрических и гиперболических функций через показательную:
(2.11)
(2.12)
Эти формулы позволяют использовать при исследовании гиперболических и тригонометрических функций в комплексной области свойства показательной функции и не обращаться к определениям (2.7),(2.8), т.е. не рассматривать более сложные операции — действия с рядами.
Так, с помощью (2.11) и (2.12) устанавливается справедливость таких формул сложения, как
и других формул, в частности формул тригонометрии.
Кроме того, что тригонометрические и гиперболические функции выражаются через , они еще и связаны между собой. Соответствующие формулы получаются из (2.11) и (2.12):
(2.13)
Отсюда, в частности, получаются такие формулы, как
Как и в действительной области, тригонометрические функции и
являются периодическими и их период равен
. Это следует из формул (2.11) (см. пример 2.15). А гиперболические функции, не будучи периодическими в действительной области, в комплексной области являются периодическими, их период, как и у функции
, — мнимое число
(это следует из рассмотрения равенств (2.12)).
Замечательным свойством, не имеющим аналога в действительной области, является свойство неограниченности (по модулю) функций и
. Эти функции могут принимать любые значения, в частности большие единицы. Например, для числа
по формуле (2.11) имеем:
.
Можно показать и в общем виде, что для любого числа найдется такое число
, что для всех
, удовлетворяющих условию
, выполняется неравенство
. Для доказательства следует использовать формулы (2.11).
Пример 2.17. Найти и
для чисел: а)
; б)
.
Решение
а) Используем формулу (2.13): , поэтому
, а так как
, то
и, следовательно,
.
б) Учитывая равенство , используем, как и выше, формулу (2.13):
Поэтому и, следовательно,
.
Пример 2.18. Найти , если a)
; б)
.
Решение
Для решения используем формулу сложения, обозначая , а также формулу (2.13).
а) Решим первый пример:
поэтому .
б) Решим второй пример:
поэтому .
Для решения можно использовать формулу сложения непосредственно для гиперболической функции:
Пример 2.19. Найти модуль и аргумент числа , если a)
; 6)
.
Решение
а) Используем определение функции и формулу (2.13):
поэтому .
б) Представим число в виде произведения двух чисел:
и найдем модуль и аргумент каждого. Для числа имеем
. Число
является действительным, причем отрицательным, так как
Поэтому . Окончательно, используя правило умножения комплексных чисел в тригонометрической форме, получаем
Пример 2.20. Найти мнимую часть числа , где
— тот корень уравнения
, который расположен в третьей четверти.
Решение
Корнями уравнения , или
, являются четыре комплексных числа, которые могут быть найдены по правилу извлечения корня из комплексного числа:
Для того чтобы отобрать корень, которому соответствует точка в третьей четверти, нужно взять . Искомым корнем будет число
, или в алгебраической форме
.
Вычислим теперь или, что то же,
. Можно перейти к показательной функции по формуле (2.12) или использовать формулу сложения для гиперболической функции и формулу (2.13):
Получаем ответ: .
Комплексный логарифм
Понятие функции, обратной показательной функции, как и в действительной области, связано с понятием логарифма числа.
Логарифмом комплексного числа называется число
такое, что справедливо равенство
; обозначается
. Таким образом,
.
Для нахождения логарифма числа , т.е. для нахождения действительной и мнимой частей числа
, запишем число
в показательной форме, и число
будем искать в алгебраической форме:
.
Тогда равенство или
есть равенство чисел, записанных в показательной форме, и из него находим
и
, а именно
, то есть
. Для искомого числа
получаем выражение:
, где
.
Из этого следует, что логарифм комплексного числа определяется неоднозначно; полученное выражение определяет множество значений логарифма данного числа ; обозначается
(2.14)
Для каждого фиксированного значения получаем определенное число — значение логарифма числа
; при
оно называется главным значением логарифма:
(2.15)
Пример 2.21. Найти — главные значения и
для следующих чисел:
а) ; б)
; в)
.
Решение
а) Находим модуль и аргумент числа . По формулам (2.14) и (2.15) получаем:
б) Для числа находим модуль и аргумент:
. Поэтому имеем результат:
в) Находим модуль и аргумент числа . Получаем ответ:
Пример 2.22. Найти модуль, аргумент, действительную и мнимую части числа .
Решение
Находим модуль и аргумент числа . По формуле (2.14) получаем
. Поэтому:
Точка расположена в первой четверти, так как
и
. Поэтому
Замечание 2.4. Введение понятия логарифма числа позволяет определить в комплексной области степень с любым комплексным показателем и показательную функцию с любым комплексным основанием
.
При и
, где
— натуральное число, степени
и
рассмотрены выше; при
и
, где
— целое число
, определение к также очевидно.
В общем случае при любом комплексном степень определяется формулой
(2.16)
Аналогично вводится функция с любым комплексным основанием
(2.17)
В силу бесконечной значности логарифма, каждому числу соответствует бесконечное множество значений степени
, определяемой по формуле (2.16), и бесконечное множество чисел, определяемых по формуле (2.17) при
. Среди этих множеств выделяются главные значения, которые соответствуют главным значениям логарифмов.
Пример 2.23. Показать, что выражение принимает только действительные значения.
Решение
Пример 2.24. Найти , где
— корень уравнения
, удовлетворяющий условию
.
Решение
Замечание 2.5. Введение понятия логарифма комплексного числа позволяет решать в комплексной области показательные уравнения. Простейшим таким уравнением является уравнение вида . Решение этого уравнения сводится к нахождению значений выражения
, то есть
.
Пример 2.25. Решить уравнения: a) ; б)
; в)
.
Решение
а) Из равенства по определению логарифма получаем
. Далее, учитывая равенства
, по формуле (2.14) находим
. Уравнение имеет бесчисленное множество решений, которые геометрически изображаются точками, расположенными на расстоянии
друг от друга на прямой
, параллельной мнимой оси. Среди решений есть действительное число
— точка на оси
.
б) Все решения уравнения получаются, как значения выражения , то есть
.
в) Из равенства получаем
. Находим модуль и аргумент числа
. Множество решений уравнения описывается равенством
В случаях «б» и «в» уравнения не имеют действительных решений, так как ни при каких значениях среди полученных множеств нет действительных чисел. Геометрически же соответствующие точки расположены на той же прямой
, что и в случае «а», на расстоянии
друг от друга; начальными значениями (при
) для них являются
и
. Решения уравнений «б» и «в» изображены на рис. 2.10 (по осям масштабы разные).
Пример 2.26. Найти из уравнения
.
Решение
Используя формулу (2.12), сведем задачу к решению показательного уравнения . Получим квадратное уравнение относительно функции
, корнями которого являются числа
. Далее нужно найти значения выражений
. Для этого используем формулу (2.14):
Получили два множества решений исходного уравнения:
Геометрически — это точки, лежащие на прямых
параллельных мнимой оси; расстояние между любыми соседними точками на каждой прямой равны ; начальные значения (при
):
или
и
(рис. 2.11).
Логарифмическая функция комплексного переменного
Логарифмическая функция вводится, как функция, обратная к показательной, т.е. как решение уравнения , значения функции при любом
определяются по формуле (2.14).
Функция, очевидно, многозначная и отображает плоскость на каждую из полос:
, или
.
В плоскости с разрезом по лучу возможно выделение однозначных ветвей, каждая из которых однозначно отображает эту плоскость на одну из полос
, в частности функция
— главное значение логарифмической функции отображает плоскость на полосу
(см. рис. 2.9). В плоскости с разрезом
также возможно выделение однозначных ветвей, каждая из которых однозначно отображает эту плоскость на одну из полос
, в частности функция
— главное значение логарифмической функции отображает плоскость на полосу
. Выделение ветви определяется заданием значения функции в одной из точек области.
Пример 2.27. Найти решение уравнения при условии
.
Решение
Обратные тригонометрические и гиперболические комплексные функции
Функции, обратные к тригонометрическим и гиперболическим функциям, определяются, как и в действительной области.
Например, обратным тригонометрическим синусом числа называется число
такое, что выполняется равенство
. Отображение обозначается, как и в действительной области,
.
Аналогично определяются и другие тригонометрические функции комплексного аргумента:
Из определений могут быть получены формулы для нахождения числа по заданному числу
.
Рассмотрим эту задачу на примере нахождения . По определению имеем
. Заменим
по формуле Эйлера (2.11), и из соотношения
или
, т.е. квадратного уравнения относительно
, находим
. Перед радикалом записан только знак плюс, так как в комплексной области
— двузначное выражение. Далее, используя определение логарифма, находим
Для каждого числа получаем бесконечное множество значений для
в силу двузначности
и бесконечной значности логарифма. Все это множество значений
обозначается
. Окончательный результат:
(2.18)
Формулы, аналогичные (2.18), могут быть получены и для других функций:
Все эти формулы, как и (2.18), дают бесконечнозначные выражения — определяют многозначные функции. Выделяя однозначную ветвь выражения , можно получить однозначные функции в каждом случае.
Большого практического значения эти формулы, как и (2.18), не имеют. Для нахождения значений обратных тригонометрических и обратных гиперболических функций можно использовать их определения и формулы связи тригонометрических и гиперболических функций с показательной функцией (формулы Эйлера (2.11)-(2.12)), т.е. применять метод, с помощью которого выведена формула (2.18). Этим методом решен пример 2.26, где найдено значение .
Замечание 2.6. Рассмотрим уравнения, содержащие тригонометрические и гиперболические функции. Простейшими из них являются уравнения:
Решение их, согласно определению, сводится к нахождению обратных тригонометрических и обратных гиперболических функций.
Пример 2.28. Решить уравнение .
Решение
Множество решений уравнения определяется выражением , или с помощью формулы (2.18):
. Выражение в скобках, в силу двузначности корня, записывается в виде
и
. Для каждого из этих чисел по сформулированному выше правилу находим логарифм:
а) для числа имеем
, поэтому
б) для числа имеем
, поэтому
Получаем два множества решений уравнения:
Геометрически — это множество точек, расположенных на расстоянии друг от друга на прямых, параллельных мнимой оси (рис. 2.12):
и
,
Действительных решений уравнение не имеет, так как ни при каком значении среди чисел
нет действительных. Это соответствует известному свойству функции
в действительной области
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Привет, сегодня поговорим про комплексный логарифм, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
комплексный логарифм , настоятельно рекомендую прочитать все из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного).
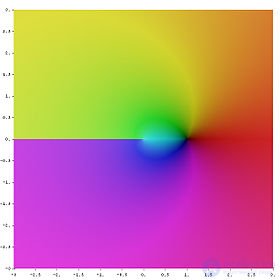
Наглядное представление функции натурального комплексного логарифма (главная ветвь). Аргумент значения функции обозначается цветом, а модуль — яркостью.
комплексный логарифм — аналитическая функция , получаемая распространением вещественного логарифма на всюкомплексную плоскость (кроме нуля). Существует несколько эквивалентных способов такого распространения. Данная функция имеет широкое применение в комплексном анализе. В отличие от вещественного случая, функция комплексного логарифма многозначна.
Содержание
- 1 Определение и свойства
- 2 Примеры значений комплексного логарифма
- 3 Комплексная логарифмическая функция и риманова поверхность
- 4 Аналитическое продолжение
- 5 Связь с обратными тригонометрическими и гиперболическими функциями
- 6 Исторический очерк
- 7 Литература
- 8 Примечания
Определение и свойства[править ]
Для комплексных чисел логарифм можно определить так же, как для вещественных, то есть как обращениепоказательной функции. На практике используется практически только натуральный комплексный логарифм, основание которого — число Эйлера 
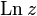
Другие, эквивалентные данному, варианты определения приведены ниже.
В поле комплексных чисел решение этого уравнения, в отличие от вещественного случая, не определено однозначно. Например, согласно тождеству Эйлера, 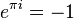
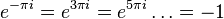
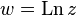
Комплексный нуль не имеет логарифма, поскольку комплексная экспонента не принимает нулевого значения. Ненулевое 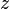
где
— произвольное целое число
Тогда 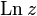
Здесь 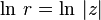
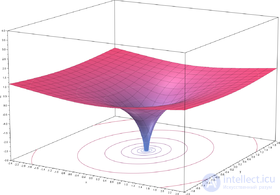
Вещественная часть комплексного логарифма
Из формулы видно, что у одного и только одного из значений мнимая часть находится в интервале 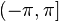
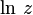
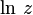
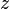
Из приведенной формулы также следует, что вещественная часть логарифма определяется следующим образом через компоненты аргумента:
На рисунке показано, что вещественная часть как функция компонентов центрально-симметрична и зависит только от расстояния до начала координат. Она получается вращением графика вещественного логарифма вокруг вертикальной оси. С приближением к нулю функция стремится к
Логарифм отрицательного числа находится по формуле[3]:
Примеры значений комплексного логарифма[править ]
Приведем главное значение логарифма (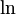
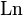
Следует быть осторожным при преобразованиях комплексных логарифмов, принимая во внимание, что они многозначны, и поэтому из равенства логарифмов каких-либо выражений не следует равенство этих выражений. Пример ошибочного рассуждения:
— явная ошибка.
Отметим, что слева стоит главное значение логарифма, а справа — значение из нижележащей ветви (
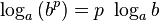
Комплексная логарифмическая функция и риманова поверхность[править ]
Риманова поверхность для комплексного логарифма
В комплексном анализе вместо рассмотрения многозначных функций на комплексной плоскости принято иное решение: рассматривать функцию как однозначную, но определенную не на плоскости, а на более сложном многообразии, которое называется римановой поверхностью[4]. Комплексная логарифмическая функция также относится к этой категории: ее образ (см. рисунок) состоит из бесконечного числа ветвей, закрученных в виде спирали. Эта поверхность непрерывна и односвязна. Единственный нуль у функции (первого порядка) получается при 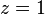
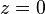
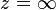
В силу односвязности риманова поверхность логарифма является универсальной накрывающей[6] для комплексной плоскости без точки 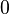
Аналитическое продолжение[править ]
Логарифм комплексного числа также может быть определен как аналитическое продолжение вещественного логарифма на всюкомплексную плоскость. Пусть кривая 
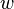
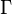
Если 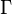
Главная ветвь логарифмической функции непрерывна и дифференцируема на всей комплексной плоскости, кроме отрицательной части вещественной оси, на которой мнимая часть скачком меняется на 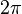
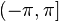
Из формулы аналитического продолжения следует, что на любой ветви логарифма[2]:
Для любой окружности 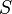
Интеграл берется в положительном направлении (против часовой стрелки). Это тождество лежит в основе теории вычетов.
Можно также определить аналитическое продолжение комплексного логарифма с помощью рядов, известных для вещественного случая:
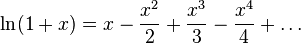 |
(Ряд 1) |
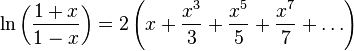 |
(Ряд 2) |
Однако из вида этих рядов следует, что в единице сумма ряда равна нулю, то есть ряд относится только к главной ветви многозначной функции комплексного логарифма. Радиус сходимости обоих рядов равен 1.
Связь с обратными тригонометрическими и гиперболическими функциями[править ]
Поскольку комплексные тригонометрические функции связаны с экспонентой (формула Эйлера), то комплексный логарифм как обратная к экспоненте функция связан собратными тригонометрическими функциями[7] [8]:
Гиперболические функции на комплексной плоскости можно рассматривать как тригонометрические функции мнимого аргумента, поэтому и здесь имеет место связь с логарифмом [8]:
— обратный гиперболический синус
— обратный гиперболический косинус
— обратный гиперболический тангенс
— обратный гиперболический котангенс
Исторический очерк[править ]
Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда еще не было ясно определено само понятие логарифма[9]. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Д’Аламбером и Эйлером. Бернулли и Д’Аламбер считали, что следует определить 
В XIX веке, с развитием комплексного анализа, исследование комплексного логарифма стимулировало новые открытия. Гаусс в 1811 году разработал полную теорию многозначности логарифмической функции[11], определяемой как интеграл от 
Разработка теории конформных отображений показала, что меркаторская проекция в картографии, возникшая еще до открытия логарифмов (1550), может быть описана как комплексный логарифм[12].
Литература[править ]
- Теория логарифмов
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.
- Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — 304 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — 680 с.
- История логарифмов
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трех томах. — М.: Наука, 1972. — Т. III.
- Колмогоров А. Н., Юшкевич А. П. (ред.). Математика XIX века. Геометрия. Теория аналитических функций. — М.: Наука, 1981. — Т. II.
Напиши свое отношение про комплексный логарифм. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое комплексный логарифм
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Комплексный анализ и операционное исчисление (теория функций комплексного переменного)
Комплексный логарифм по любому основанию
| Основание логарифма |
| Число |
| Логарифм комплексного числа по комплексному основанию |
Прежде, чем мы начнем речь непосредственно о логарифмах, хотелось бы поговорить о степенях чисел и их свойствах.
Действия над степенями осуществляются по следующим правилам и они Вам должны быть хорошо известны
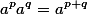
(cfrac{a^p}{a^q}=a^{p-q})
((cfrac{a}{b})^p=cfrac{a^p}{b^p})
где a,b,p и q —произвольные числа.
В 16 веке когда возникла насущная потребность рассчитывать многозначные числа, чаще всего для астрономии и мореплавания, возник вопрос «А можно ли заменить умножение и деление многозначных чисел на более легкие операции сложения и вычитания?»
Взглянув на выше приведенные формулы , мы замечаем что то похожее в двух формулах
(a^pa^q=a^{p+q}) и (cfrac{a^p}{a^q}=a^{p-q})
Осталось теперь превратить произвольное многозначное число в число вида
Для некоторых чисел это известно 

число a — называется основание степени, p-степень числа
Итак у нас все готово для того что бы мы могли «заменить» умножение сложением, а деление — вычитанием.
Для этого придуман логарифм, обладающим таким свойством что

a — основание логарифма, которое равно численно основанию степени.
Так вот, с 16-ого века, для решения задач, стали применять предварительно рассчитанные таблицы логарифов, для определенных чисел. В мои школьные годы мы использовали таблицы Брадиса.
Сейчас, при тотальной информатизации населения и товаров, наверное только наручные часы не умеют автоматически рассчитывать логарифмы.
Логарифмы обладают следующими свойствами
({log_a(uv)}=log_au+log_av)
({log_a(cfrac{u}{v})}=log_au-log_av)
({log_a(u)}^k=k*log_au)
({log_a(u)}^k=k*log_au)
(log_a(u)=cfrac{log_bu}{log_ba})
Последняя формула примечательна тем, что с помощью можно рассчитывать логарифм любого числа (кроме нуля) и любого основания, в том числе и комплексных чисел
b— это основание логарифма и оно может быть любым. Поэтому мы можем взять за основу число e=2.718… и получим что
(log_a(u)=cfrac{ln(u)}{ln(a)})
Натуральные логарифы комплексных чисел мы считать уже умеем, поэтому рассчитать логарифм любого числа по любому основанию не вызовет никаких затруднений.
В основании можно кроме цифровых значений можно ввести две тестовых константы e(2.718281828459) и pi(3.1415926535898)
Если введет e — то получите значение натурального логарифма
Чему равен натуральный логарифм мнимой единицы?
| Логарифм комплексного числа по комплексному основанию |
|
Логарифм числа 0+1i |
Таким образом бот помогает считать любые значения и выражения по любому основанию.
Где используются комплексные логарифмы?
Удачи в расчетах!
Элементарные функции комплексного переменного.
Рассмотрим некоторые
элементарные функции комплексного
переменного, а именно, показательную
функцию
,
логарифмическую функцию
,
тригонометрические —
,
,
,
и,
обратные тригонометрические функции
,
,
,
,а
также гиперболические функции
,
,
,
и обратные к ним функции
,
,
,
).
1. Показательная функция комплексного переменного.
Показательная
функция
определяется как
или
(12)
Очевидны следующие
свойства функции
.
1)
;
2)
.
Так как
,
то показательная функция
— периодическая функция периода
.
Пример 24.
Найти значение функции
в точке
и указать координаты точки комплексной
плоскости, соответствующей найденному
значению.
Решение.
,
откуда координаты искомой точки
.●
2. Логарифмическая функция комплексного переменного.
Логарифмическая
функция
определяется как обратная к показательной.
Определение.
Натуральным логарифмом
(
)
комплексного числа
называется показатель степени
,
в которую необходимо возвести число
,
чтобы получить число
.
Пусть
,
,
где
.
Тогда
,
откуда
,
,
,
,
.
,
где
(13)
Определение.
Выражение
называется главным
значением натурального логарифма числа
.
Из формулы (13)
следует, что действительная часть
натурального логарифма определяется
однозначно, а мнимая часть содержит
неопределенное слагаемое, кратное
,
т. е. существует бесконечное множество
значений натурального логарифма любого
числа
,
отличного от нуля.
Логарифм нуля не
существует.
Пример 25.
Вычислить
и
.
Решение.
Найдем модуль и аргумент числа
.
.
Так
как действительная и мнимая части числа
отрицательны, то главное значение
аргумента равно
.
Тогда
—
главное
значение логарифма данного числа и
.●
Пример 26.
Вычислить
и
.
Решение.
Модуль числа
равен
,
а главное значение аргумента равно
,
следовательно,
,
.●
С помощью логарифма
может быть определена любая степень
комплексного числа.
Пример 27.
Вычислить
.
Решение.
,
где
.
Обратите внимание,
что
-действительные числа.●
3. Тригонометрические функции комплексного переменного.
Тригонометрические
функции синус и косинус определены
ранее (см. формулы (6)).
Определение.
Тригонометрическая функция синус
комплексного переменного определяется
как
,
где
,
(14)
функция косинус
как
,
где
, (15)
функция тангенс
как
,
где
, (16)
функция котангенс
как
,
где
. (17)
Пример 28.
Вычислить
.
Решение.
.●
Пример 29.
Вычислить
.
Пример
28.
Вычислить
.
Решение.
●
Пример 30.
Доказать, что
.
Решение.
.●
Замечание.
Для тригонометрических функций
комплексной переменной имеют место и
другие тождества, справедливые для
тригонометрических функций действительного
аргумента
(см. пример 31).
Пример 31.
Доказать, что
.
Решение.
.
Пример 32.
Решить уравнение
.
Решение.
,
откуда
,
и
.
Решая квадратное
относительно
,
имеем
или
,
откуда
и
.
Ответ:
Замечание.
Числа
при
имеют одинаковые мнимые части, поэтому
они лежат на прямой, параллельной
действительной оси и отстоящей от нее
на расстоянии
.●
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ТФКП логарифм комплексного числа [0:41]
Логарифм комплексного числа (комплексный логарифм) — это решение уравнения вида ez = c относительно комплексной переменной z. В теории функций комплексного переменного рассматривается как многозначная аналитическая функция.
Обозначения[править]
Введём обозначения:
x — действительная часть (абсцисса) числа;
y — мнимая часть (ордината) числа;
r — модуль комплексного числа;
φ — аргумент комплексного числа;
x + iy — комплексное число;
ln x — натуральный логарифм вещественного числа;
Ln(x + iy) — комплексный натуральный логарифм.
Формула[править]
Примеры:[править]
См. также[править]
- Выражение гиперболических функций через тригонометрические
- Выражение тригонометрических функций через гиперболические
Другие операции:[править]
- сложение чисел;
- вычитание чисел;
- умножение чисел;
- деление чисел;
- обращение числа;
- возведение в степень;
- извлечение квадратного корня;
- извлечение кубического корня;
- извлечение корня n-ой степени;
- логарифмирование числа;
- возведение в комплексную степень;
- взятие комплексно сопряжённого числа;
- сложение комплексно сопряжённых чисел;
- вычитание комплексно сопряжённых чисел;
- умножение комплексно сопряжённых чисел;
- деление комплексно сопряжённых чисел;
- обращение комплексно сопряжённого числа.
Литература[править]
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970, стр.623.

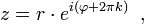 где
где  — произвольное целое число
— произвольное целое число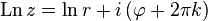
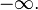

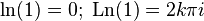

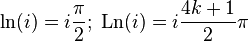
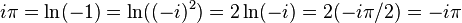 — явная ошибка.
— явная ошибка.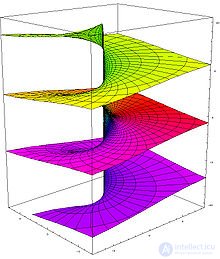
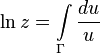
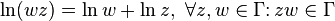

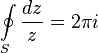
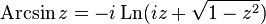
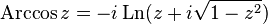
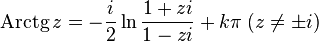

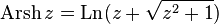 — обратный гиперболический синус
— обратный гиперболический синус 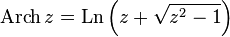 — обратный гиперболический косинус
— обратный гиперболический косинус 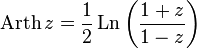 — обратный гиперболический тангенс
— обратный гиперболический тангенс 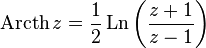 — обратный гиперболический котангенс
— обратный гиперболический котангенс ^p=a^pb^p)
^q=a^{pq})
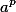
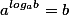


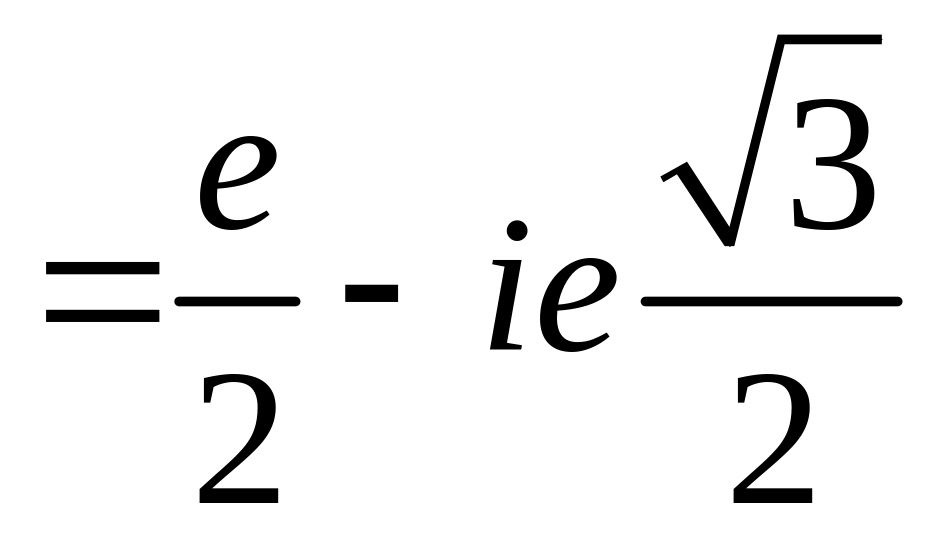
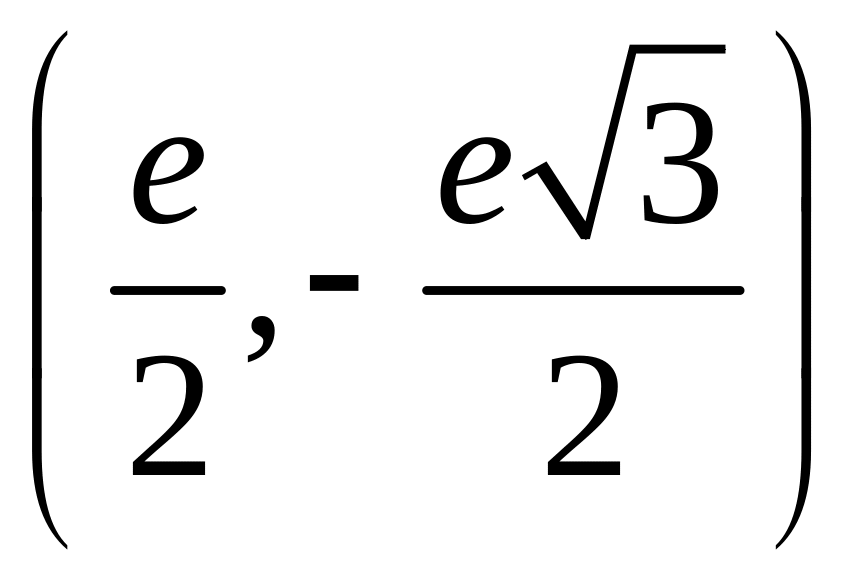
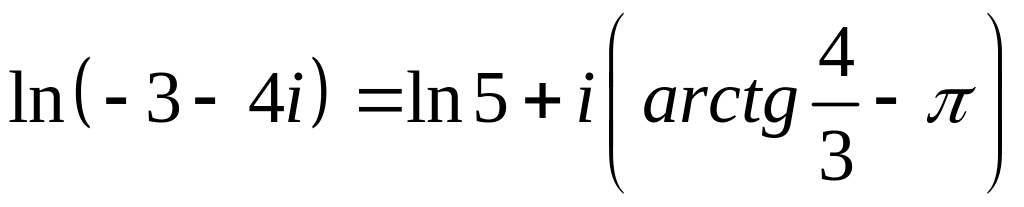
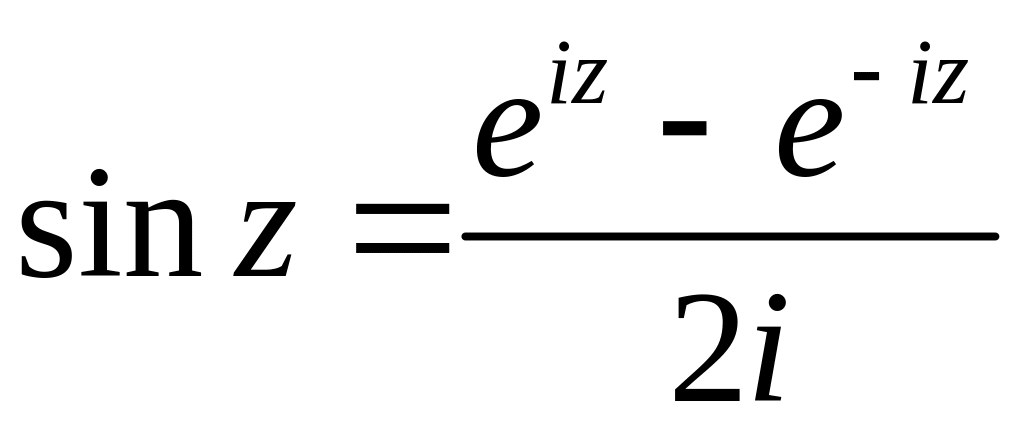
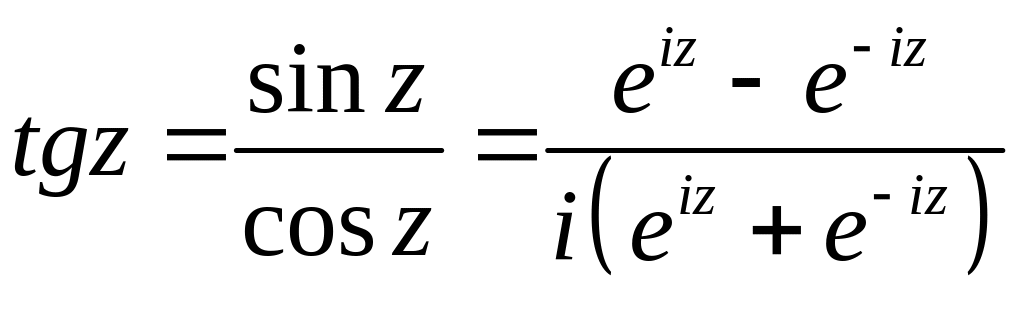
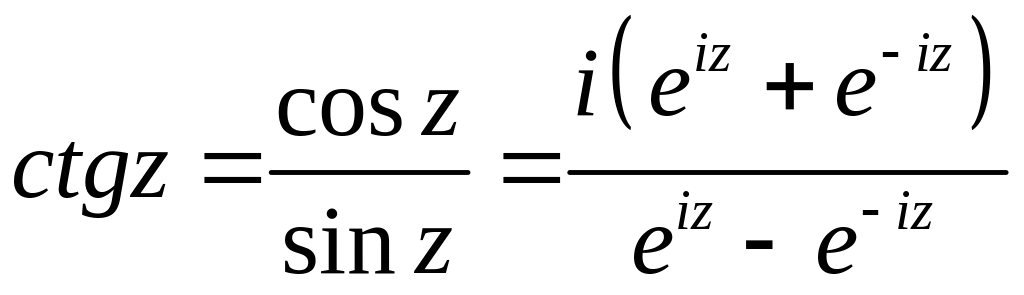
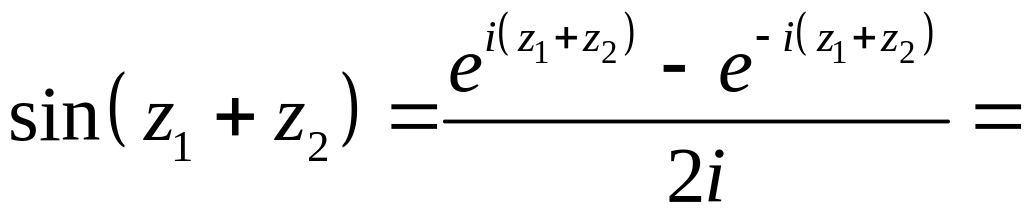
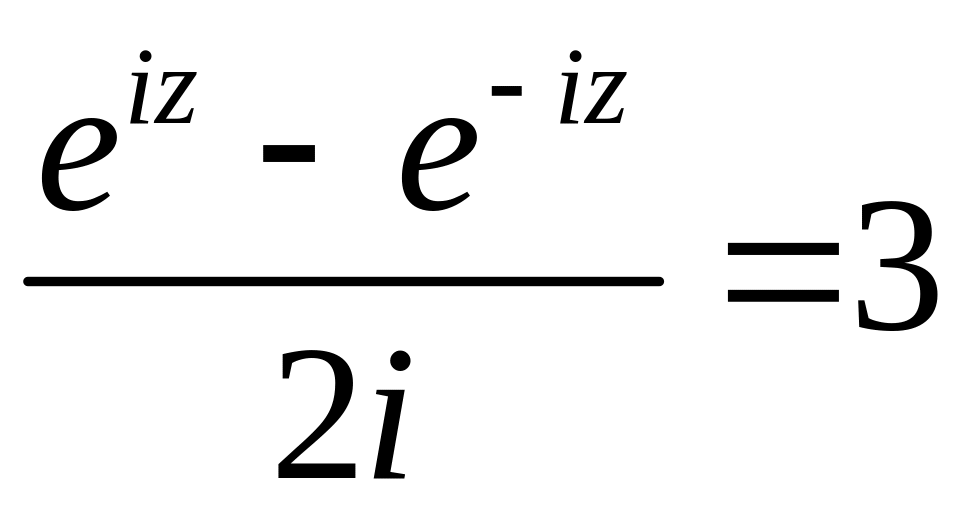



![{displaystyle Lnleft[r(cos varphi +isin varphi )right]=ln r+i(varphi +2pi n), r={sqrt {x^{2}+y^{2}}}, varphi =arctg{frac {y}{x}}, nin mathbb {Z} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/856e88750ecd92c2a8ce3b02852eb7d3a3a0dbcf)






