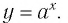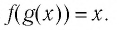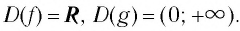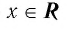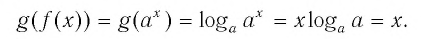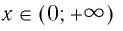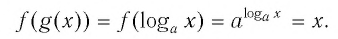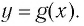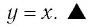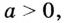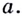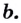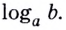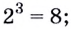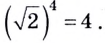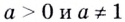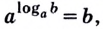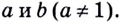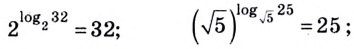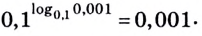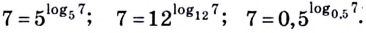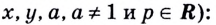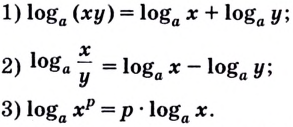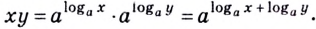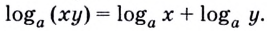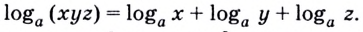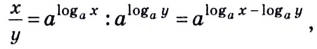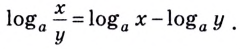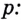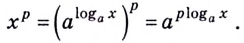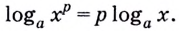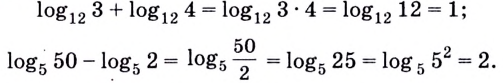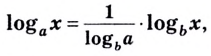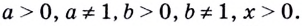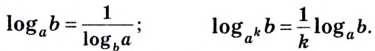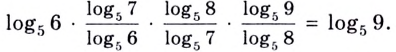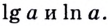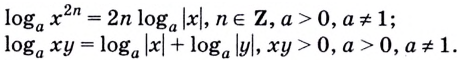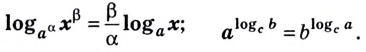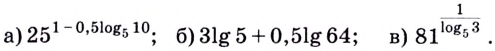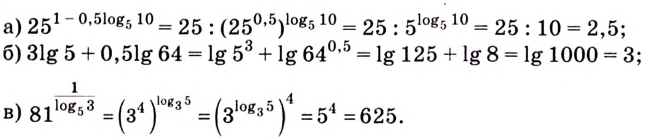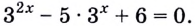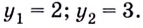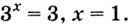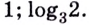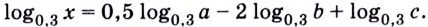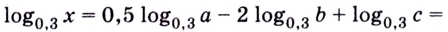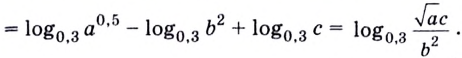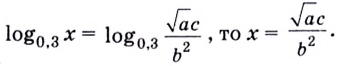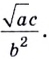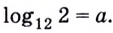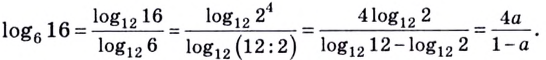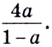1.11. Определение логарифма
10.
Логарифмом
числа b
по основанию b
называется показатель степени, в которую
нужно возвести число a,
чтобы получить b,
обозначается
и
20.
Десятичный логарифм — это логарифм по
основанию 10:
.
30.
Натуральный логарифм — это логарифм
по основанию
:
.
1.12. Основное
логарифмическое тождество:
Например,
1.13. Свойства логарифмов
-
Сумма логарифмов
есть логарифм произведения
-
Разность
логарифмов есть логарифм дроби
-
Число, стоящее
перед логарифмом ставим в показатель
степени выражения, стоящего после знака
логарифма
-
Переход к новому
основанию
Следствия:
|
5. |
6. |
7. |
8. |
-
Любое число
представимо в виде логарифма -
Любое число k>0
представимо в виде степени
Пример. Вычислить
a)
если
;
б)
►а) перейдём в
к основанию 2. Воспользуемся свойством
4:
.
б) заменим корни
степенями и воспользуемся свойством
6:
.◄
1.14. Логарифмирование и потенцирование
Если некоторое
выражение
составлено из положительных чисел с
помощью операций умножения, деления и
возведение в степень, то, используя
свойства логарифмов, можно выразить
через логарифмы входящих в выражение
чисел. Такое преобразование называется
логарифмированием.
Обратная задача: нахождение выражения
по его логарифму, называется потенцированием.
Пример 1.
Прологарифмировать по основанию
выражение
.
►
◄
Пример 2. Найти
,
если
►
◄
1.15. Теория многочленов
Многочленом степени
называется целая рациональная функция
|
(3) |
|
Многочлен |
|
|
Многочлен |
|
|
Многочлен |
|
|
Многочлен |
|
|
Многочлен |
Например,
есть многочлен
—
степени, 2 есть многочлен
—
степени.
Деление
многочленов:
1.16. Выделение целой части из дроби
Дробь называется
неправильной, если в числителе стоит
многочлен степени не ниже степени
многочлена знаменателя.
Тогда дробь можно
представить в виде:
,
где
— частное от деления
на
(целая
часть),
— полученный при этом остаток.
Пример. Выделить
целую часть из дроби
.
►Дробь неправильная,
делим числитель на знаменатель столбиком:
Целая
часть
(под уголком), а остаток
(в конце деления). Поэтому дробь будет
иметь вид:
◄
2. Алгебраические уравнения
Элементарная математика
|
Сканави М. Книга представляет собой повторительный курс элементарной математики и рассчитана на тех, кто хочет пополнить, укрепить и систематизировать свои знания. Как и в первом издании, содержание ориентировано на программы вступительных экзаменов в технические вузы и, в особенности, на программы подготовительных отделений при высших учебных заведениях, для учащихся которых, как мы надеемся, книга окажется полезной. (Книга включает в себя Ч1 — Арифметика, алгебра и элементарные функции и Ч2 — Геометрия. Каждый раздел включает в себя теоретическую часть и большое количество задач с решениями.) |
|
Оглавление
ВВЕДЕНИЕ
Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА
2. Простые и составные числа. Признаки делимости.
3. Наибольший общий делитель и наименьшее общее кратное.
4. Целые числа. Рациональные числа.
5. Десятичные дроби. Представление рациональных чисел десятичными дробями.
6. Иррациональные числа. Действительные числа.
7. Действия с приближенными числами.
8. Числовая ось. Координаты точки на плоскости.
§ 2. Степени и корни
9. Степени с натуральными показателями.
10. Степени с целыми показателями.
11. Корни.
12. Степени с рациональными показателями. Степени с действительными показателями.
13. Алгоритм извлечения квадратного корня.
§ 3. Комплексные числа
14. Основные понятия и определения.
15. Рациональные действия с комплексными числами.
16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа.
17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра.
18. Извлечение корня из комплексного числа.
Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
19. Алгебраические выражения. Одночлены и многочлены.
20. Формулы сокращенного умножения.
41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени.
42. Показательная функция.
43. Логарифмическая функция.
§ 3. Преобразование графиков
44. Параллельный сдвиг графика.
45. График квадратного трех члена.
46. График дробно-линейной функции.
47. Преобразование симметрии. Сжатие и растяжение графика.
48. Построение графиков функций.
49. Сложение графиков.
§ 4. Некоторые сведения о рациональных функциях
50. Целые и дробные рациональные функции. Деление многочленов.
51. Схема Горнера. Теорема Безу.
52. Нули многочлена. Разложение многочлена на множители.
Глава V. УРАВНЕНИЯ
53. Уравнение. Корни уравнения.
54. Равносильные уравнения.
55. Системы уравнений.
56. Графическое решение уравнений.
§. 2. Алгебраические уравнения с одной неизвестной
57. Число и кратность корней.
58. Уравнения первой степени (линейные уравнения).
59. Уравнения второй степени (квадратные уравнения).
60. Формулы Виета. Разложение квадратного трехчлена на множители.
61. Исследование квадратного уравнения.
62. Уравнения высших степеней. Целые корни.
63. Двучленные уравнения.
64. Уравнения, сводящиеся к квадратным.
65. Возвратные уравнения.
§ 3. Системы алгебраических уравнений
66. Линейные системы.
67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными.
68. Системы, состоящие из уравнения второй степени и линейного уравнения.
69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней.
§ 4. Иррациональные, показательные и логарифмические уравнения
70. Иррациональные уравнения.
71. Показательные уравнения.
72. Логарифмические уравнения.
73. Разные уравнения. Системы уравнений.
Глава VI. НЕРАВЕНСТВА
74. Свойства неравенств. Действия над неравенствами.
75. Алгебраические неравенства.
§ 2. Решение неравенств
76. Множество решений неравенства.
77. Графическое решение неравенств.
79. Квадратные неравенства.
80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х.
81. Иррациональные, показательные и логарифмические неравенства.
82. Неравенства с двумя неизвестными.
Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ
83. Числовая последовательность.
84. Предел числовой последовательности.
85. Бесконечно малые. Правила предельного перехода.
§ 2. Арифметическая прогрессия
86. Арифметическая прогрессия. Формула общего члена.
87. Свойства арифметической прогрессии.
88. Формула для суммы n членов арифметической прогрессии.
§ 3. Геометрическая прогрессия
89. Геометрическая прогрессия. Формула общего члена.
90. Свойства геометрической прогрессии.
91. Формулы для суммы n членов геометрической прогрессии.
92. Бесконечно убывающая геометрическая прогрессия.
Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ)
93. Вектор, проекция вектора.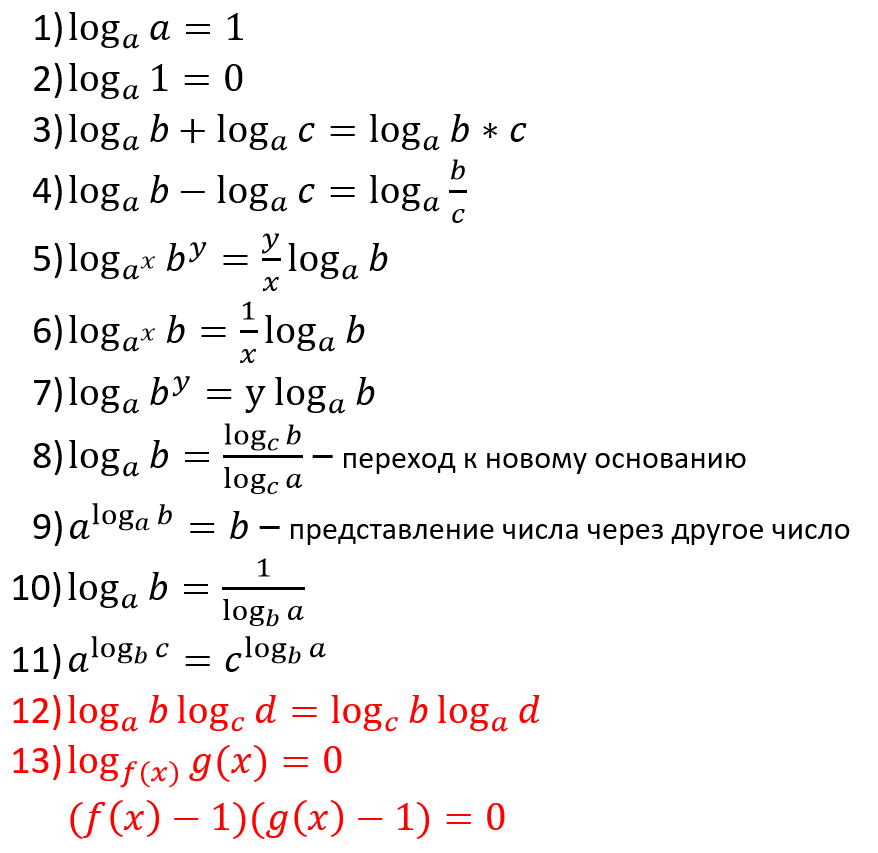
94. Положительные углы и дуги, меньшие 360°.
95. Углы и дуги, большие 360°.
96. Отрицательные углы. Сложение и вычитание углов.
§ 2. Тригонометрические функции произвольного угла
97. Определение основных тригонометрических функций.
98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi.
§ 3. Соотношения между тригонометрическими функциями одного и того же угла
99. Основные тригонометрические тождества.
100. Вычисление значений тригонометрических функций по значению одной из них.
101. Значения тригонометрических функций некоторых углов.
§ 4. Четность, нечетность и периодичность тригонометрических функций
102. Четность и нечетность.
103. Понятие периодической функции.
104. Периодичность тригонометрических функций.
§ 5. Формулы приведения
105. Зависимость между тригонометрическими функциями дополнительных углов.
106. Формулы приведения.
Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ
§ 1.
108. Области определения и области изменения значений тригонометрических функций.
109. Некоторые неравенства и их следствия.
§ 2. Графики тригонометрических функций
110. Первоначальные сведения о таблицах тригонометрических функций.
111. Основные графики.
112. Примеры построения графиков некоторых других тригонометрических функций.
113. Дальнейшие примеры построения графиков функций.
Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
114. Расстояние между двумя точками на плоскости.
115. Косинус суммы и разности двух аргументов.
116. Синус суммы и разности двух аргументов.
117. Тангенс суммы и разности двух аргументов.
118. О формулах сложения для нескольких аргументов.
§ 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a
119. Тригонометрические функции двойного аргумента.
120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n.
121. Тригонометрические функции половинного аргумента.
122. Выражение основных тригонометрических функций аргумента а через tg(a/2).
§ 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb
§ 4. Преобразование в произведение сумм вида
§ 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента
127. Преобразование в произведение выражения a•sina + b•cosa.
128. Преобразование в произведение выражений a•sina+b и a•cosa+b
129. Преобразование в произведение выражения a•tga+b.
Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ
130. Функция у = arcsin x (арксинус).
131. Функция y = arccos x (арккосинус).
132. Функция y = arctg x (арктангенс).
133. Функция y = arcctg x (арккотангенс).
134. Пример.
§ 2. Операции над обратными тригонометрическими функциями
135. Тригонометрические операции.
136. Операции сложения (вычитания).
§ 3. Обратные тригонометрические операции над тригонометрическими функциями
137.
138. Функция y = arctg (tg x).
Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
139. Уравнение sin х = а.
140. Уравнение cos х = a.
141. Уравнение tg x = a.
142. Уравнение ctg x = a.
143. Некоторые дополнения.
§ 2. Способ приведения к одной функции одного и того же аргумента
145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента.
146. Способ разложения на множители.
147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t.
§ 3. Некоторые частные приемы решения тригонометрических уравнений и систем
148. Введение вспомогательного аргумента.
149. Преобразование произведения в сумму или разность.
150. Переход к функциям удвоенного аргумента.
151. Решение уравнения типа…
152. Применение подстановок sinx ± соsx = y.
§ 4. Решение тригонометрических неравенств
154. Простейшие тригонометрические неравенства.
155. Примеры тригонометрических неравенств, сводящихся к простейшим.
Часть вторая. ГЕОМЕТРИЯ
156. Точка. Прямая. Луч. Отрезок.
157. Плоскость. Фигуры и тела.
160. Равенство фигур. Движение.
161. Равенство тел.
§ 2. Измерение геометрических величин
162. Сложение отрезков. Длина отрезка.
163. Общая мера двух отрезков.
164. Сравнительная длина отрезков и ломаных.
165. Измерение углов.
166. Радианная мера угла.
167. Измерение площадей.
168. Площадь прямоугольника. Объем прямоугольного параллелепипеда.
Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ
169. Перпендикуляр и наклонные.
170. Свойство перпендикуляра, проведенного к отрезку в его середине.
171. Параллельные прямые.
172. Углы, образованные двумя параллельными прямыми и секущей.
173. Углы с параллельными или перпендикулярными сторонами.
§ 2. Геометрические места точек. Окружность
174. Геометрическое место точек.
175. Свойство биссектрисы угла.
176. Окружность.
177. Взаимное расположение прямой и окружности. Касательная и секущая.
178. Хорда и диаметр. Сектор и сегмент.
179. Взаимное расположение двух окружностей.
§ 3. Основные задачи на построение
181. Деление отрезка пополам. Построение перпендикуляров.
182. Построение углов.
183. Другие задачи на построение.
Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ
184. Стороны и углы треугольника.
185. Биссектрисы треугольника. Вписанная окружность.
186. Оси симметрии сторон треугольника. Описанная окружность.
187. Медианы и выcоты треугольника.
188. Равенство треугольников.
189. Построение треугольников.
190. Равнобедренные треугольники.
191. Прямоугольные треугольники.
§ 2. Параллелограммы
192. Четырехугольники.
193. Параллелограмм и его свойства.
194. Прямоугольник.
§ 3. Трапеция
196. Трапеция.
197. Средняя линия треугольника.
198. Средняя линия трапеции.
199. Деление отрезка на равные части.
§ 4. Площади треугольников и четырехугольников
200. Площадь параллелограмма.
201. Площадь треугольника.
202. Площадь трапеции.
Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР
203. Пропорциональные отрезки.
204. Свойства биссектрис внутреннего и внешнего углов треугольника.
§ 2. Подобное преобразование фигур (гомотетия)
205. Определение гомотетичных фигур.
206. Свойства преобразования подобия.
§ 3. Общее подобное соответствие фигур
207. Подобные фигуры.
208. Периметры и площади подобных треугольников.
209. Применение подобия к решению задач на построение.
Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ
210. Углы с вершиной на окружности.
211. Углы с вершиной внутри и вне круга.
212. Угол, под которым виден данный отрезок.
213. Четырехугольники, вписанные в окружность.
214. Пропорциональные отрезки в круге.
215. Задачи на построение.
§ 2. Метрические соотношения в треугольнике
216. Пропорциональные отрезки в прямоугольном треугольнике.
218. Теорема синусов. Формула Герона.
217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов.
218. Теорема синусов. Формула Герона.
219. Радиусы вписанной и описанной окружностей.
§ 3. Решение треугольников
220. Таблицы функций.
221. Решение треугольников. Сводка основных формул.
222. Решение прямоугольных треугольников.
223. Решение косоугольных треугольников.
Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА
224. Выпуклые многоугольники.
225. Правильные многоугольники.
226. Соотношения между стороной, радиусом и апофемой.
227. Периметр и площадь правильного n-угольника.
228. Удвоение числа сторон правильного многоугольника.
§ 2. Длина окружности. Площадь круга и его частей
229. Длина окружности.
230. Площадь круга и его частей.
Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ
231. Взаимное расположение двух прямых в пространстве.
232. Взаимное расположение прямой линии и плоскости.
233. Взаимное расположение двух плоскостей.
234. Свойства параллельных прямых и плоскостей.
235. Построения в стереометрии.
§ 2. Перпендикулярность прямых и плоскостей
236. Перпендикуляр к плоскости.
237. Перпендикуляр и наклонные.
238. Угол между прямой и плоскостью.
239. Связь между перпендикулярностью и параллельностью прямых и плоскостей.
240. Общий перпендикуляр двух скрещивающихся прямых.
§ 3. Двугранные и многогранные углы
241. Двугранный угол.
242. Взаимно перпендикулярные плоскости.
243. Трехгранные углы.
244. Многогранные углы.
§ 4. Многогранники
245. Многогранники.
246. Правильные многогранники.
Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА
247. Цилиндры и призмы.
248. Параллелепипеды.
249. Объемы призм и цилиндров.
250. Площадь боковой поверхности призмы.
251. Площадь поверхности цилиндра.
§ 2. Пирамида. Конус
252. Свойства пирамиды и конуса.
253. Объем пирамиды и конуса.
254. Площадь боковой поверхности правильной пирамиды и конуса.
255. Усеченный конус и усеченная пирамида.
§ 3. Шаровая поверхность. Шар
256. Шар и шаровая поверхность.
257. Объем шара и его частей.
258. Площадь поверхности шара и ее частей.
259. Понятие телесного угла.
Ответы к упражнениям
Приложения
логарифмов | nool
Перейти к основному содержанию
Домашняя страница Технологического института Онтарио
nool
Функция f(x) = 2 x называется экспоненциальной функцией, потому что переменная x является показателем степени. В общем случае показательные функции имеют вид f(x) = a x , где a — положительная константа.
В науке важно уметь оценивать логарифмические функции, поскольку они встречаются во многих приложениях. Чтобы вычислить логарифм (по основанию 10) числа, введите число в свой калькулятор, затем нажмите клавишу [log]. Некоторые калькуляторы немного отличаются; поэтому важно, чтобы учащиеся были знакомы с собственным калькулятором. Также во многих ситуациях важно уметь определять антилогарифмическое значение логарифмического значения. Чтобы вычислить антилогарифм числа, введите число в калькулятор и нажмите [10 x ].
Пример: Найдите x в каждом из следующих уравнений: x = log 10 3,6 и log 10 x = 6,75.
Решение:
x = log 10 3,6
x = 0,556 x= 5,62×10 6
Пример: 90]10 .0009 -3 М до pH.
Решение :
PH = -LOG [H + ]
PH = -LOG [3,5 x 10 -3 ]
PH = 2,4
Пример: . Какое значение [H +] соответствует рН 4,3?
Решение :
PH = -LOG [H+]
4,3 = -LOG [H+]
-4,3 = log [H+]
[H+] = 10 -4,3
[H+] = = = = 10 -4,3
[H+] = = = 5,0 x 10 -5 M
Пример:
Объяснение и примеры, показатели, доказательства
Законы логарифмов — это правила, которые можно применять для упрощения и решения сложных логарифмических уравнений.
Основные законы бревен
Формула изменения закона находится в буклете с формулами, который вам дадут на экзамене.
Доказательство закона логарифмов
Не обязательно уметь доказывать каждый закон логарифма для экзамена, но важно понимать каждый шаг и почему он происходит.
Закон произведения (сложения)
1. Если и , то можно переписать логарифмы в виде экспоненциальной функции.
Для , основание равно x, показатель степени равен c , ответ на показатель степени равен a .
Следовательно, это можно записать как
Для , основание равно x, показатель степени равен d , а ответ на показатель степени равен b.
Следовательно, это можно записать как
2. Таким образом, используя наше экспоненциальное (индексное) правило,
3.
4. Поскольку включает как экспоненту с основанием x , так и логарифм с основанием x (), они компенсируют друг друга, чтобы стать просто c + d.
Этот шаг связан с тем, что логарифмы и экспоненты являются обратными функциями друг друга. Подумайте о том, когда мы компенсируем +4 и -4 в x +4 -4 = 10 — это тот же принцип.
5. Мы определили c и d в части 1. и
Следовательно,
Правило частных
1. Если и , то можно переписать логарифмы в виде экспоненциальной функции.
Ибо, основание равно x, показатель степени равен c, и ответ на показатель степени равен a .
Следовательно, это можно записать как
Для , основание равно x, показатель степени равен d, и ответ на показатель степени равен б.
Следовательно, это можно записать как
2.
3. Возьмем журнал обеих сторон.
4. Поскольку включает экспоненту с основанием x и логарифм с основанием x , они компенсируют друг друга и становятся просто c — d .
5. Мы определили c и d в части 1 где и :
Изменение основания
1. Пусть, где основание a , показатель степени равен k, и x экспоненциальный ответ на x .
Следовательно, его можно переписать в экспоненциальном виде:
2. Возьмите логарифм обеих сторон
3. Используйте степенное правило для упрощения
, которое затем можно подставить обратно в уравнение
4. Перестроить, чтобы получить k самостоятельно путем деления на
5. Поскольку k уже определено, его можно подставить в уравнение как использование наших экспоненциальных правил с негативами.
Журнал базы
- Набор, где база а, 9Показатель степени 0012 равен x, , а ответ на экспоненту равен a . Поэтому его можно записать как.
- В соответствии с экспоненциальными правилами, если ответ экспоненты равен основанию, то показатель степени должен быть равен 1.
Логарифм 1
- Набор, где основание равно a, показатель степени равен x, и ответ на экспоненту равен 1. Следовательно, это можно записать как.
- В соответствии с экспоненциальными правилами, если ответ экспоненты равен 1, то показатель степени должен быть равен 0.
Упрощение и решение с использованием законов бревен
Здесь мы рассмотрим несколько примеров упрощения ряда законов бревен.
Упрощение и решение с использованием 1 логарифмического закона
Показать логарифм (6) + логарифм (4) = логарифм (24)
логарифм (6) + логарифм (4) = логарифм (6 x 4) = логарифм (24)
Лог решения (14) — Лог (7)
Лог (14) — Лог (7) = Лог (14/7) = Лог (2) = 0,301 (3 ст.
Упростить 2логарифм (9), сохранить точная форма
Решить
Упрощение и решение с использованием законов множественных журналов
Возможно, будет полезно использовать правила, которые упрощают отдельные журналы, перед выполнением законов упрощения множественных журналов.
Решить
Упростить
Доказать, где
1. Используя правило степени, .
Следовательно,
2. Используя правило отношения,
3. Когда вы хотите удалить логарифм, вам нужно преобразовать его в экспоненту. Это работает так же, как обычно — просто убедитесь, что вы пометили каждую часть.
Основание равно 2; показатель степени равен 3; ответ на экспоненциальный
4. Решите как обычное уравнение являются законом продукта, частным законом, изменением основного закона и правилом силы.

Логарифмическое уравнение: решение на примерах
Как решить логарифмическое уравнение? Этим вопросом задаются многие школьники, особенно в преддверии сдачи ЕГЭ по математике. Ведь в задании С1 профильного ЕГЭ могут встретиться именно логарифмические уравнения.
Уравнение, в котором неизвестное находится внутри логарифмов, называется логарифмическим. Причем неизвестное может находится как в аргументе логарифма, так и в его основании.
Способов решения таких уравнений существует несколько. В этой статье мы разберем способ, который легко понять и запомнить.
Как решать уравнения с логарифмами: 2 способа с примерами
Решить логарифмическое уравнение можно разными способами. Чаще всего в школе учат решать логарифмическое уравнение с помощью определения логарифма. То есть мы имеем уравнение вида:Вспоминаем определение логарифма и получаем следующее:Таким образом мы получаем простое уравнение, которое сможем легко решить.
При решении логарифмических уравнений важно помнить об области определения логарифма, т.к. аргумент f(x) должен быть больше ноля. Поэтому после решения логарифмического уравнения мы всегда делаем проверку!
Давайте посмотрим, как это работает на примере:
Воспользуемся определением логарифма и получим:
Теперь перед нами простейшее уравнение, решить которое не составит труда:
Сделаем проверку. Подставим найденный Х в исходное уравнение:Так как 3 2 = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
Основной минус данного метода решения логарифмических уравнений в том, что многие ребята путают, что именно нужно возводить в степень. То есть при преобразовании logaf(x) = b, многие возводят не a в степень b, а наоборот b в степень a. Такая досадная ошибка может лишить вас драгоценных баллов на ЕГЭ.
Поэтому мы покажем еще один способ решения логарифмических уравнений.
Чтобы решить логарифмическое уравнение, нам нужно привести его к такому виду, когда и в правой, и в левой части уравнения будут стоять логарифмы с одинаковыми основаниями. Это выглядит вот так:
Когда уравнение приведено к такому виду, то мы можем «зачеркнуть» логарифмы и решить простое уравнение. Давайте разбираться на примере.
Решим еще раз то же самое уравнение, но теперь этим способом:В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2.
Для этого вспоминаем свойства логарифмов. Первое свойство, которое нам здесь понадобится – это логарифмическая единица. Напомним его:То есть в нашем случае:Возьмем правую часть нашего уравнения и начнем ее преобразовывать:Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:
Воспользуемся этим свойством в нашем случае, получим:Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили:Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение:
Да, действий в этом способе больше, чем при решении с помощью определения логарифма. Но все действия логичны и последовательны, в результате чего шансов ошибиться меньше. К тому же данный способ дает больше возможностей для решения более сложных логарифмических уравнений.
Разберем другой пример:Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:После преобразования правой части наше уравнение принимает следующий вид:Теперь можно зачеркнуть логарифмы и тогда получим:Вспоминаем свойства степеней:
Теперь делаем проверку:то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
Еще один пример решения логарифмического уравнения:Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:Теперь преобразуем правую часть уравнения:Выполнив преобразования правой и левой частей уравнения, мы получили:Теперь мы можем зачеркнуть логарифмы:
Решим данное квадратное уравнение, найдем дискриминант:
Сделаем проверку, подставим х1 = 1 в исходное уравнение:Верно, следовательно, х1 = 1 является корнем уравнения.
Теперь подставим х2 = -5 в исходное уравнение:Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х2 = -5 – посторонний корень.
Пример решения логарифмического уравнения с разными основаниями
Выше мы решали логарифмические уравнения, в которых участвовали логарифмы с одинаковыми основаниями. А что же делать, если основания у логарифмов разные? Например,
Правильно, нужно привести логарифмы в правой и левой части к одному основанию!
Итак, разберем наш пример:Преобразуем правую часть нашего уравнения:
Мы знаем, что 1/3 = 3 -1 . Еще мы знаем свойство логарифма, а именно вынесение показателя степени из логарифма:Применяем эти знания и получаем:Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:
Тогда получим:Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:Делаем проверку:Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим:Верно, следовательно, х = 4 является корнем уравнения.
Пример решения логарифмического уравнения с переменными основаниями
Выше мы разобрали примеры решения логарифмических уравнений, основания которых были постоянными, т.е. определенным значением – 2, 3, ½ … Но в основании логарифма может содержаться Х, тогда такое основание будет называться переменным. Например, logx+1(х 2 +5х-5) = 2. Мы видим, что основание логарифма в данном уравнении – х+1. Как же решать уравнение такого вида? Решать мы его будем по тому же принципу, что и предыдущие. Т.е. мы будем преобразовывать наше уравнение таким образом, чтобы слева и справа были логарифмы с одинаковым основанием.Преобразуем правую часть уравнения:Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:Теперь мы можем зачеркнуть логарифмы:Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:
1. Аргумент логарифма должен быть больше ноля, следовательно:
2. Основание логарифма должно быть больше 0 и не должно равняться единице, следовательно:
Сведем все требования в систему:
Данную систему требований мы можем упростить. Смотрите х 2 +5х-5 больше ноля, при этом оно приравнивается к (х + 1) 2 , которую в свою очередь так же больше ноля. Следовательно, требование х 2 +5х-5 > 0 выполняется автоматически и мы можем его не решать. Тогда наша система будет сведена к следующему:Перепишем нашу систему:Следовательно, наша система примет следующий вид:Теперь решаем наше уравнение:Справа у нас квадрат суммы:Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.
Для полной уверенности можем выполнить проверку, подставим х = 2 в исходное уравнение:
Т.к. 3 2 =9, то последнее выражение верно.
Как сделать проверку
Еще раз обращаем ваше внимание, что при решении логарифмических уравнений необходимо учитывать область допустимых значений. Так, основание логарифма должно быть больше ноля и не должно равняться единице. А его аргумент должен быть положительным, т.е. больше ноля.
Если наше уравнение имеет вид loga (f(x)) = loga (g(x)), то должны выполняться следующие ограничения:
После решения логарифмического уравнения нужно обязательно сделать проверку. Для этого вам необходимо подставить получившееся значения в исходное уравнение и посчитать его. Времени это займет немного, зато позволит не записать в ответ посторонние корни. Ведь так обидно правильно решить уравнение и при этом неправильно записать ответ!
Итак, теперь вы знаете, как решить логарифмическое уравнение с помощью определения логарифма и с помощью преобразования уравнения, когда в обеих его частях стоят логарифмы с одинаковыми основаниями, которые мы можем «зачеркнуть». Отличное знание свойств логарифма, учет области определения, выполнение проверки – залог успеха при решении логарифмических уравнений.
Алгебра
План урока:
Задание. Укажите корень логарифмического уравнения
Задание. Решите урав-ние
В чуть более сложных случаях под знаком логарифма может стоять не сама переменная х, а выражение с переменной. То есть урав-ние имеет вид
Задание. Найдите решение логарифмического уравнения
Задание. Решите урав-ние
Задание. Решите урав-ние
Получили показательное уравнение. Показатели степеней можно приравнять, если равны их основания:
Уравнения вида logaf(x) = logag(x)
Порою логарифм стоит в обеих частях равенства, то есть и слева, и справа от знака «равно». Если основания логарифмов совпадают, то должны совпадать и аргументы логарифмов.
Задание. Решите урав-ние
Задание. Найдите корень урав-ния
Ситуация несколько усложняется в том случае, когда, под знаком логарифма в обоих частях равенства стоят выражения с переменными, то есть оно имеет вид
С одной стороны, очевидно, что должно выполняться равенство f(x) = g(x). Но этого мало, ведь под знаком логарифма не должно стоять отрицательное число. Поэтому после получения корней следует подставить их в урав-ние и убедиться, что они не являются посторонними корнями.
Задание. Решите урав-ние
Получили квадратное уравнение, которое решаем с помощью дискриминанта:
Получили два корня, (– 3) и 4. Однако теперь подставим их в исходное урав-ние и посмотрим, что у нас получится. При х = – 3 имеем:
Это верное равенство, поэтому х = – 3 действительно является корнем урав-ния. Теперь проверяем х = 4:
Хотя выражения и справа, и слева одинаковы, равенство верным считать нельзя, ведь выражение log3 (– 1) не имеет смысла! Действительно, нельзя вычислять логарифм от отрицательного числа. Поэтому корень х = 4 оказывается посторонним, и у нас остается только один настоящий корень – число (– 3).
Уравнения, требующие предварительных преобразований
Естественно, не всегда в обоих частях логарифмических уравнений и неравенств стоят только логарифмы с совпадающими основаниями. Часто требуется выполнить некоторые предварительные преобразования, чтобы привести урав-ние к виду logaf(x) = logag(x).
Задание. Решите урав-ние
с помощью которой любой множитель можно внести под знак логарифма. Сделаем это и в нашем случае:
Теперь в обеих частях равенства не стоит ничего, кроме логарифмов с одинаковыми основаниями. Поэтому мы можем приравнять их аргументы:
Задание. Решите урав-ние
Снова проверяем каждый из корней, подставляя его в исходное ур-ние. Прих = –1 получаем
Задание. Решите урав-ние
Решение. В правой части снова стоит сумма, но на этот раз не логарифмов. Однако число 1 можно представить как log5 5. Тогда урав-ние можно преобразовать:
Задание. Решите урав-ние
Решение. Данный пример похож на простейшее логарифмическое уравнение, однако переменная находится в основании логарифма, а не в аргументе. По определению логарифма мы можем записать, что
Первый вариант придется отбросить, так как основание логарифма, (а в данном случае это выражение х – 5) не может быть отрицательным числом. Получается, что
Задание. Решите урав-ние
Решение. Здесь ситуация осложняется тем, что основания логарифмов разные. Поэтому один из них необходимо привести к новому основанию. Попробуем привести log25x 4 к основанию 5, используя известную нам формулу
Мы добились того, что у логарифмов одинаковые основания, а потому мы можем приравнять их аргументы:
Логарифмические уравнения с заменой переменных
Иногда приходится делать некоторые замены, чтобы уравнение приняло более привычный вид.
Задание. Решите уравнение методом замены переменной
Задание. Найдите решение уравнения методом замены переменной
Решение. Для начала напомним, что символ lg означает десятичный логарифм. Отдельно знаменатель дроби в правой части:
Логарифмирование уравнений
Ясно, что если от равных величин взять логарифмы по одному и тому же основанию, то тогда эти логарифмы окажутся также равными. Если подобный прием применяют при решении урав-ния, то, говорят, что производится логарифмирование уравнения. Иногда оно позволяет решить некоторые особо сложные примеры.
Задание. Укажите корни урав-ния
Здесь переменная величина находится одновременно и в основании степени, и в ее показателе. Возьмем от правой и левой части урав-ния логарифм по основанию 5:
Возвращаемся от переменной t к переменной х:
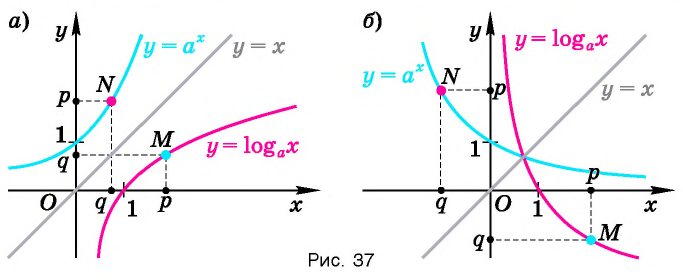
Переход от логарифмических неравенств к нелогарифмическим
Рассмотрим график логарифмической функции у = logax при условии а > 1. Она является возрастающей функцией. Если на оси Ох отложить два числа tи s так, чтобы t располагалось левее s (то есть t 1). Но это не совсем так. Дело в том, что надо учесть ещё и тот факт, что под знаком логарифма может стоять исключительно положительное число. Получается, что от простейшего логарифмического неравенства
Естественно, вместо величин t и s могут стоять как числа, так и выражения с переменными.
Задание. Найдите решение логарифмического неравенства
Ответ можно оставить и в такой форме, однако всё же принято записывать его в виде промежутка. Очевидно, что нерав-во 0 logas:
Но, снова-таки, мы должны учесть, числа t может быть лишь положительным (тогда s, которое больше t, автоматически также окажется положительным). Получается, что при 0 loga s можно перейти к двойному нерав-ву 0 2 – 45х + 200 имеет решение
Однако в системе (5) есть ещё два неравенства, х > 0 и 45 >x. Их решениями являются промежутки (0; + ∞) и (– ∞; 45). Чтобы определить решение всей системы, отметим на одной прямой решения каждого отдельного нерав-ва и найдем область их пересечения:
Видно, что решениями нерав-ва будут являться промежутки (0; 5) и (40; 45), на которых справедливы все три нерав-ва, входящих в систему (5).
Логарифмические уравнения
Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы.
Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.
При этом 0,;a> 0,;aneq 1′ alt=’b> 0,;a> 0,;aneq 1′ />.
Обратим внимание на область допустимых значений логарифма:
Основное логарифмическое тождество:
Основные формулы для логарифмов:
(Логарифм произведения равен сумме логарифмов)
(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)
Формула перехода к новому основанию:
Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.
Все это пригодится нам в решении логарифмических уравнений.
Простейшие логарифмические уравнения
Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.
Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение определено при 0,;a> 0,;aneq 1′ alt=’b> 0,;a> 0,;aneq 1′ />.
Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.
2. Решите уравнение:
В левой части уравнения – логарифм, в правой – число 7. Применив основное логарифмическое тождество, представим число 7 в виде . Дальше все просто.
3. Решите уравнение:
Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.
4. Решите уравнение:
Область допустимых значений: 0.’ alt=’4+x> 0.’ /> Значит, -4.’ alt=’x> -4.’ />
Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом -4′ alt=’x> -4′ />.
5. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:
0\ x^<2>-4> 0\ x^<2>+x=x^<2>-4 endright.Leftrightarrow left <beginx^<2>+x> 0\ x^<2>-4> 0\ x=-4 endright.Leftrightarrow x=-4′ alt=’log _<8>left ( x^<2>+x right )=log _<8>left ( x^<2>-4 right )Leftrightarrow left <beginx^<2>+x> 0\ x^<2>-4> 0\ x^<2>+x=x^<2>-4 endright.Leftrightarrow left <beginx^<2>+x> 0\ x^<2>-4> 0\ x=-4 endright.Leftrightarrow x=-4′ />
Ответ: –4.
Заметим, что решения логарифмических уравнений лучше всего записывать в виде цепочки равносильных переходов. Это поможет нам не забыть про область допустимых значений.
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Запишем решение как цепочку равносильных переходов.
0 endright.Leftrightarrow left <beginleft (2^<log _<2>left ( 4x+5 right )> right )^<frac<1><2>>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <beginleft ( 4x+5 right )^<frac<1><2>>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <beginsqrt<4x+5>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <begin4x+5=81\ x> -1frac<1> <4>endright.Leftrightarrow left <beginx=19\ x> -1frac<1> <4>endright.’ alt=’2^<log _<4>left ( 4x+5 right )>=9Leftrightarrow left <begin2^frac<<log _<2>left ( 4x+5 right )>><2>=9\ 4x+5> 0 endright.Leftrightarrow left <beginleft (2^<log _<2>left ( 4x+5 right )> right )^<frac<1><2>>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <beginleft ( 4x+5 right )^<frac<1><2>>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <beginsqrt<4x+5>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <begin4x+5=81\ x> -1frac<1> <4>endright.Leftrightarrow left <beginx=19\ x> -1frac<1> <4>endright.’ />
Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.
ОДЗ:
0\ x> 0\ xneq 1 endright.’ alt=’left <begin12-x> 0\ x> 0\ xneq 1 endright.’ />
Теперь можно «убрать» логарифмы.
— посторонний корень, поскольку должно выполняться условие 0′ alt=’x> 0′ />.
8. Решите уравнение .
ОДЗ уравнения: 0′ alt=’x> 0′ />
Сделаем замену . Как и в алгебраических уравнениях, мы делаем замену переменной всегда, когда только возможно.
Вернемся к переменной х:
Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25. Выражение под корнем в правой части также положительно. Значит, х может быть любым действительным числом.
Представим сумму логарифмов в левой части как логарифм произведения. В правой части – перейдем к логарифму по основанию 3. И используем формулу логарифма степени.
Такое уравнение называется биквадратным. В него входят выражения и . Сделаем замену
Вернемся к переменной х. Получим:
. Мы нашли все корни исходного уравнения.
Логарифмические уравнения могут встретиться вам и в задании №1 Профильного ЕГЭ по математике, и в задании №12. И если в задании №1 нужно решить простейшее уравнение, то в задаче 12 решение состоит из двух пунктов. Второй пункт – отбор корней на заданном отрезке или интервале.
http://100urokov.ru/predmety/urok-9-uravneniya-logarifmicheskie
В данном уроке мы будем учиться работать с логарифмом на уже весьма и весьма приличном уровне. Поэтому для успешного решения примеров этого урока рекомендую погулять по ссылкам:
Что такое логарифм?
Действия с логарифмами. Постигаем азы!
Почитайте, пока не поздно.) Почитали? Всё понятно! Отлично! Тогда движемся дальше.)
Теперь настал черёд завязывания более крепкой дружбы с логарифмами и, соответственно, решения серьёзных (в том числе сложных и нестандартных) примеров.
Чтобы не скакать из темы в тему, прежде всего я ещё разочек выпишу все основные свойства и формулы логарифмов. Вот они:
Это основной набор формул, необходимых для успешной работы с логарифмами практически на любом уровне сложности. Иногда в школе (и в некоторых продвинутых учебниках) дают больше формул, но в целом приведённого перечня для решения большей части примеров оказывается вполне достаточно. Эти формулы надо помнить! Но, ещё раз повторяю, не просто помнить, а уметь применять! Причём в обоих направлениях — как слева направо, так и справа налево. Вроде бы это всё и так понятно и очевидно, но… дальше всё поймёте.) Как надо помнить формулы, я вам вряд ли смогу подсказать, а вот как уметь применять — подробно расскажу и покажу в этом уроке.
Итак, продолжаем наши игры!
Все формулы. Все степени. Много дробей! Двоюродные и троюродные братья.
Ну что ж, теперь приступаем к работе со всеми формулами (кроме последней формулы перехода к новому основанию). Используем все свойства степеней и активно включаем в работу степени с отрицательными и дробными показателями. Поди сообрази, что, например,
0,04 = 5-2.
Или
Это уже не родные, а двоюродные и троюродные братья по степени получаются…)
Посему, если есть пробелы в степенях, то для начала милости прошу сюда:
Что такое степень. Свойства степеней.
Ну, а для тех, кто со степенями давно на «ты» — продолжаем.)
Пример 1
За что зацепиться? Хорошо, если сразу догадались, а если нет? Если нет, значит, перечитываем первый практический совет прошлого урока — переходим к обыкновенным дробям!
У нас в одну кучу намешаны десятичная дробь и смешанное число. Вот и перейдём к единообразию — к обычным дробям. А там, глядишь, и забрезжит свет в конце тоннеля…
Пишем:
Так, уже кое-чего проясняется: 49 с семёркой родня, а 100 — с десяткой:
49 = 72
100 = 102
Стало быть, по свойствам степеней можно записать:
Ну, вот и спасительный лучик света! Выносим двойку за логарифм и получаем:
Уже всё стало выглядеть гораздо симпатичнее. Всё бы ничего, только основание 7/10 и аргумент 10/7 у нас записаны кверху ногами. Что делать? Да свойства степеней вспомнить! На этот раз — с отрицательным показателем:
И снова выносим показатель степени (минус единицу) за знак логарифма, переворачиваем аргумент и получаем:
Ответ: -2
Готово дело.) Теперь пробуем самостоятельно:
Ответ: -1
А теперь вовлекаем в наш увлекательный процесс корни. То есть, не что иное, как… степени с дробными показателями. Да-да!
Пример 2
Надеюсь, вы не забыли, что lg — это просто логарифм по основанию 10? Или десятичный логарифм? Пример достаточно простой, без заморочек. Надо всего лишь вспомнить, что корень кубический из 7000 — это 70001/3. С семёркой — аналогично. А дальше по формуле разности логарифмов да по формуле деления степеней. Получим:
Ответ: 1
Вот так вот. Здесь мы снова перешли к обычным дробям. Но не от десятичных дробей или смешанных чисел, а от корней. В этом безобидном примере вполне можно было бы и без дробей обойтись, работать напрямую с корнями, но в более сложных примерах корни могут вконец запутать. Как, например, вот в таком примерчике:
Пример 3
С чего начать? И тройка есть, и девятка. Правда, три в квадрате — это и будет девятка… Но в примере ещё и корни разных степеней смешались в кучу — квадратный и кубический! Ужас… Но паниковать и сдаваться рано. Перейдём-ка от корней к степеням с дробными показателями! Распишем девятку как 32. А там, того гляди, всё и наладится.)
Верные мысли! Итак, по свойствам степеней для основания и для аргумента мы можем записать:
Вот всё и прояснилось.) Оба числа — и основание, и аргумент — оказались… родственниками! По тройке.) Только совсем уж дальними. Даже не троюродными, а десятиюродными братьями: основание — это три в степени 3/2, а аргумент — та же тройка, но в степени 7/3… Тем не менее факт остаётся фактом — родство по степени (хоть и очень дальнее) установлено. Вот и все формулы и свойства заработали! Выносим наши дробные показатели из за знак логарифма и аккуратно считаем:
Вот так. Здесь уже, конечно, немножко повозиться со степенями пришлось. А что делать… Так что не стесняемся переходить от корней к дробям! И всё получится. Обязательно.)
Вот вам и очередные практические советы:
При наличии дробей в примере, переходим от дробей к степеням с отрицательными показателями.
При наличии корней переходим от корней к степеням с дробными показателями.
Что ж, пришла пора разгрызть и какой-нибудь особо крепкий орешек. Как, например, вот такой примерчик:
Пример 4
Вычислить:
Опять же, с чего начинать? Если имеете хоть малейшее представление — флаг вам в руки. Вперёд и с песнями, как говорится.) Если понятия не имеете — подключаем зелёные практические советы и размышляем синим цветом. Примерно так:
«Ух, наворотили… Кошмар! Напролом явно не решается, надо сначала как-то преобразовывать пример. Но — как? Будем вспоминать практические советы.
1. Если в одном примере смешались в кучу разные типы дробей, то переходим к обыкновенным дробям.
Где здесь дроби? Дробей не видно. Ладно, этот пункт пока пропустим. Что там у нас ещё есть? Вот это:
2. Степени популярных чисел надо знать. В лицо! При наличии в примере разных чисел пытаемся найти «братьев по степени».
Так, кое-какая зацепочка уже появилась… 121 — это 11 в квадрате. Ещё можно расписать 125 как 5 в кубе и 9 как 3 в квадрате, но 5 и 3 — никакие не братья и не сёстры по степени. Пригодится или нет — пока непонятно, но к сведению примем. Поехали дальше.)
3. Любую степень можно записать множителем перед логарифмом. И наоборот — любой числовой коэффициент можно спрятать внутрь логарифма. Если он мешает, конечно.
Коэффициентов в нашем примере нет, логарифмы и так чистые. Отметаем этот совет. Что у нас там ещё припасено?
4. Всегда прикидываем, нельзя исходное выражение преобразовать под какую-нибудь готовую формулу?
Вот и прикидываем: на что похож внешний вид нашего примера? Ну же? Ну, конечно! На самую первую формулу — основное логарифмическое тождество! Единственная формула, где логарифм тусуется в показателе степени.
С ним мы пока что ни разу не работали. Что ж, поработаем! Попробуем преобразовать наш пример под эту формулу: других вариантов как-то выкрутиться у нас просто нет!
Но в формуле в показателе стоит один логарифм! А у нас — сумма. Что нам мешает сложить логарифмы по соответствующей формуле суммы? Основания мешают! Они… они — разные! Ну-ка, может, ещё не все практические советы у нас использованы? Вспоминаем:
5. При наличии дробей в примере, переходим от дробей к степеням с отрицательными показателями. При наличии корней переходим от корней к степеням с дробными показателями.
Так, ну дробей в нашем примере нету, это видно. А вот корень в основании — преобразуем. Вот так:
А во втором логарифме в основании тоже стоит 11, только в квадрате… Уже кое-какие проблески! Выпишу-ка я показатель отдельно, дабы не запутаться… С учётом наших размышлений.)
Уже лучше. Теперь выносим показатели степеней из оснований перед логарифмами (не забыть бы перевернуть…):
Великолепно! Основания логарифмов выровнялись! Только вот новая беда… Коэффициенты появились… Хотелось бы сложить логарифмы, ан нет, не канает… Так стоп! Чего же я туплю-то! Можно же их по другой формуле спрятать вовнутрь!
Ну вот. Уже идеально для формулы сложения! Только внутри логарифмов что-то несусветное стало твориться. Не беда, перейдём к маленьким числам: зря, что ли, мы 125 и 9 в виде степеней пятёрки и тройки расписывали?
Пока всё чин-чинарём. Теперь, по правилам действий со степенями, можно записать:
Вот, практически, и всё. Досчитываем наш показатель по формуле сложения логарифмов:
Пример становится всё лучше и лучше! Возвращаемся к нашему исходному примеру, вставляем в него наш преобразованный показатель и получаем ответ!
Йес!!! Ничего себе, примерчик, однако ж…»
Ответ: 75
Вот такой пример. Запутанный, да, я не спорю. И зачем я так детально его разобрал? С практическими советами, мыслями… Мог бы и в пару строк уложиться… Дело в том, что разбор одного конкретного примера — занятие бесполезное. Не попадётся он. А вот разъяснить на конкретном примере, как именно надо выкручиваться в любом (да-да, любом!) задании — совсем другое дело!
Главное в этом разборе — подход. Мы применяем весь наш арсенал инструментов к конкретному примеру. Пробуем поочерёдно все инструменты, как ключики к замку. Что-то срабатывает, а что-то нет. Это не страшно и не смертельно. Не подошло — пробуем что-то другое! Что-то обязательно подойдёт! Сложные и запутанные задания именно так и решаются. И никак иначе.)
Конечно, с опытом всё будет делаться гораздо короче и какие-то шаги будут в уме делаться и вообще пропускаться. За ненадобностью. Тут практика рулит. Тренироваться и решать надо. Используя изложенный здесь подход. И тогда всё получится. Обязательно!
Формула перехода к новому основанию. Немного приколов… И немного формул сокращённого умножения.
Поднимаемся ещё на ступень повыше. Запускаем теперь в дело самую последнюю формулу из нашего списка — это формула перехода к новому основанию. Вот она:
В чём суть этой формулы, когда она применяется и как именно она работает? Объясняю по пунктам.
Формула эта применяется, когда основания логарифмов — разные. Но не просто разные, а ещё и не родственные по степени! Которые друг в друга через простую степень не превращаются. Скажем, 2 и 3. Или 5 и 7. Заметьте, что нам уже встречались разные основания у логарифмов в одном и том же примере, но там или всё и так славненько срасталось, или переход был через степени. Например, если основания логарифмов 1/125 и 25, то можно догадаться, что это родня! По пятёрке. Ибо 1/125 = 5-3, а 25 = 52. Не так очевидно, конечно, но и мы уже всё-таки на серьёзном уровне с вами. А дальше дело техники: выносим показатели за логарифмы и — вперёд.
Но если основания не родственные, а без выравнивания оснований в примере никак, то выход только один — работать по этой формуле.
Запомнить её очень легко. По шагам:
1) Слева пишем логарифм, основание которого нам не нравится. Справа рисуем черту дроби.
2) В числитель пишем логарифм числа b, но уже по новому основанию k. Какому именно основанию? А какому угодно! В том-то весь и фокус! Естественно, тому, которое нам удобнее. Кроме единицы, разумеется.)
3) В знаменатель пишем логарифм старого основания a по тому же новому основанию k.
Обратите внимание на саму структуру формулы: слева в основании буквы k вообще нет! В этом-то и вся фишка! Это означает, что новому логарифму мы можем выбрать какое угодно основание. Обычно выбирают то, которое нам удобно в конкретном примере. Если, скажем, в примере куча логарифмов по основанию 3 и затесался один по основанию 7, то его и менять будем. На тройку.
А в знаменатель пишем логарифм старого основания. Так уже математика требует. В результате логарифм со старым основанием исчезает из примера. Вот и всё. Вот и вся суть формулы перехода. Ну что, посмотрим на формулу перехода в действии?
Пример 5
Вычислить:
Что тут можно увидеть? Ну, во-первых, разные основания. Причём не родственные: из четвёрки пятёрку простым возведением в степень никак не получить. Во-вторых, наблюдаем произведение логарифмов. Такой формулы в наших свойствах нету. Не путаем с логарифмом произведения! Или с суммой логарифмов… Что же делать? Первым делом перейдём к одному основанию. Что-то же делать всё равно надо! К какому основанию пойдём? Ну, ясное дело, что не к 30 или 1,234. У нас на выбор два варианта — либо к четвёрке, либо к пятёрке. В данном примере абсолютно без разницы, к чему переходить. Давайте к четвёрке пойдём: всё-таки число поменьше.) Итак, первый логарифм не трогаем (у него и так основание четыре), а вот второй логарифм превращаем по формуле перехода в дробь:
Всё. Логарифм по основанию 5 из примера благополучно исчез, и в основаниях остались только четвёрки. Вставляем полученную дробь в наш пример, упрощаем и считаем:
Ответ: 2
Вот так. Откуда же я узнал, что надо переходить к другому основанию? Ведь я мог и что-то ещё замутить. Скажем, log516 расписать как
log516 = log524 = 4log52
и дальше как-то ещё выкручиваться. Да. Можно. Но с богатым опытом приходит уже так называемое математическое чутьё на формулы и преобразования.) Когда в уме наперёд уже умеешь просчитывать, к чему может привести тот или иной манёвр и не идёшь по заведомо негодному пути.
Вот вам очередной практический совет на данную тему.
Если перед вами сложное логарифмическое выражение, в котором основания логарифмов разные, то первым делом пробуем сделать их одинаковыми. Или через степени или по формуле перехода. Очень часто этот манёвр срабатывает проясняет дальнейшую ситуацию.
А теперь рассмотрим один фокус на формулу перехода, который частенько любят проделывать составители примеров. По-другому эту фишку даже и не назовёшь. Настолько элементарна, а в тупик может поставить даже отличника!
Пример 6
Вычислить:
Основания уже одинаковые, но формулы деления логарифмов не существует, да… Можно, конечно, сообразить, что 125 = 53 и старым добрым способом, но что делать, если внутри логарифмов сидит что-нибудь более навороченное? Вот и впадают в ступор…
Здесь же достаточно всего лишь разглядеть формулу перехода к новому основанию. Вернее, не просто формулу, а её правую часть! И, если запустить эту формулу справа налево, то сразу получим:
И все дела! Да-да! Это ответ.)
Ответ: 3
Частенько эту фишку применяют с какими-нибудь совершенно дикими основаниями. На испуг берут, типа.) Как, например, вот такое задание:
Пример 7
Вычислить:
В основании число «пи», как тут не испугаться… Однако, если догадаться, что наша ужасная дробь — всего лишь правая часть формулы перехода к новому основанию и сработать справа налево, то получим всего-навсего:
Вот и всё. И нету больше никакого «пи».) А уж сложить парочку логарифмов с одинаковыми основаниями — пустяшное дело. Не пример, а одно удовольствие:
log1236 + log124 = log12144 = 2
Ответ: 2
Вот такой вот приёмчик. Теперь, надеюсь, не растеряетесь, в случае чего.)
Рассмотрим ещё одну распространённую фишку с формулой перехода. Вернее, её частный случай.
Что произойдёт, если за новое основание мы возьмём аргумент логарифма? Давайте посмотрим!
Во как! Оказывается, если поменять местами a и b, то наш новый логарифм станет всего лишь обратным к старому! Весьма и весьма полезная формулка. Имеет смысл запомнить.) Решим примерчик и на эту тему:
Пример 8
Вычислить:
Что делать будем? Скобки раскрывать? Можно, конечно, но пример явно намекает на более элегантное преобразование. Перейдём в логарифме по основанию 40 к основанию 2. Двойка чем-то привлекательнее, чем сорок, не находите?) Поскольку в аргументе логарифма стоит также двойка, то при переходе к основанию 2 достаточно просто перевернуть этот логарифм. И все дела.)
Получим:
И что дальше? Куда пристегнуть тройку? А дальше новый фокус! Дело всё в том, что мы не можем напрямую сложить логарифм и число. Но зато логарифмы между собой — запросто! Как выкрутимся? А сделаем-ка из тройки… логарифм! Да-да! Для этого сначала выберем ему основание. Вариантов выбора много, но я предлагаю выбрать 2. Думаю, возражений не будет?)
А дальше пишем вот такое простое равенство:
3 = log223
Всё легко и просто: тройка уходит показателем в степень нашего выбранного основания. Сама цепочка превращений выглядит вот так:
По этапам:
1) Вместо тройки пишем степень с выбранным основанием 2 и показателем, равным этой самой тройке.
2) Берём логарифм от этой степени по тому же самому основанию 2.
3) Всё!
Конечно, можно было бы и сразу тройку на логарифм заменить, благо здесь числа совсем простые, но лучше запомнить эту простую цепочку. А то придётся где-нибудь, к примеру, превращать в логарифм по основанию 11 число 1/7… А по цепочке всё совсем элементарно:
Просекли фишку? Тогда возвращаемся к нашим баранам и дорешиваем:
Ответ: 1
Да… Кто бы мог подумать.)
Конечно, в числовых выражениях этот приёмчик с превращением числа в логарифм достаточно экзотичен. Но вот в логарифмических уравнениях и неравенствах он применяется на полную катушку! Имейте его в виду.)
Заметьте, что обычно мы стараемся поступать наоборот — упрощать всякие ужасы типа дробей, корней, синусов да логарифмов. Доводить их, по возможности, до конечного числа. А тут — наоборот, из числа делаем логарифм. Что хотим, то и творим! Так что математика — на самом деле весьма и весьма творческая наука! Во многом даже искусство.)
Запоминаем:
При необходимости любое число можно превратить в логарифм по любому основанию (кроме единицы, конечно).
Осталось разобраться с совсем уж хардкорными примерами. Где и так пробуешь и сяк, но не упрощается он никак! На такие примеры есть своё особое секретное оружие.) Срабатывает безотказно. Если уметь грамотно им пользоваться, конечно. Как вам такой примерчик!
Пример 9
Вычислить:
За что зацепиться? Все основания уже одинаковые (семёрка), но это особо не спасает. Кстати, обращаю ваше внимание на весьма и весьма частый косяк. В числителе стоят квадраты логарифмов. Именно самих логарифмов, а не их аргументов! Это означает, что вынести двойки из логарифмов наружу мы не имеем права! Не там двойки стоят… Стало быть, уже привычных нам логарифмических формул, готовых к употреблению, нету. Что же делать?
Спокойно! Без паники! Никто и никогда не может гарантировать, что сразу влёт всё решится.) К сожалению…
Чтобы расправиться с этим злым примером, забудем на минутку про логарифмы и плавненько переместимся в седьмой класс. Формулы сокращённого умножения не забыли, надеюсь? А теперь внимательно присматриваемся к нашему примеру. Что ещё, кроме логарифмов, в нём можно увидеть? Разность… Разность ква… Ну, конечно! Разность квадратов! Такая родная и до боли знакомая формула:
a2–b2 = (a—b)(a+b)
Правда, в применении к логарифмам. Ну и что из этого? Ведь в формуле под буковками a и b может скрываться всё что угодно — и логарифмы, и синусы, и степени — любые выражения! Формула всё равно сработает!
Итак, заменяем наш числитель на произведение скобок по формуле разности квадратов:
Вот и всё встало на свои места! И все формулы заработали! Решать пример стало одно удовольствие.)
В первых скобках (разность) получается:
Во вторых скобках (сумма) будет:
Вставляем в пример наши промежуточные результаты, сокращаем и получаем:
Ответ: 1
Простенько и со вкусом.) Здесь-то всё ясно. Но в тревожной боевой обстановке ЕГЭ подобный пример может и в ступор вогнать. Дело всё в том, что большинство учеников подсознательно пытаются решить пример в том формате, в котором он задан. Например, если задан пример на логарифмы, то мы с головой погружены в логарифмы и варимся только в них, а вынырнуть на поверхность да оглядеться вокруг — не можем. С тригонометрией аналогично — решаем пример только в рамках тригонометрии. И, в случае чего, не можем напрячься и выскочить из этих жёстких рамок… А надо уметь! Хотя бы иногда.)
Посему очередной по счёту практический совет:
Замороченные примеры проверяем на алгебру седьмого класса — разложение на множители, формулы сокращённого умножения и т.п.
Ещё из той же оперы для самостоятельного решения:
lg24 + lg16·lg25 + lg225 =
Ответ: 4
Ну что, поздравляю! Вот мы и набрались достаточного количества знаний для уверенной работы с логарифмами практически на любом уровне сложности! Дальше путь только один — решать примеры! Как можно больше.) И особо рекомендую не пренебрегать зелёными советами. Они не зря даются в материале.) Их надо помнить и им надо следовать.) И тогда не логарифмы будут командовать вами, а вы — логарифмами.)
До встречи!
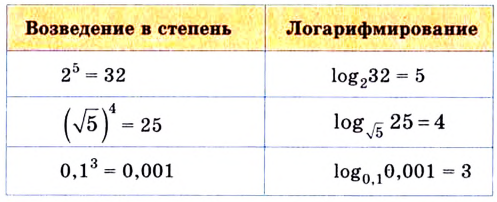
Все знакомы, что такое степень числа (если нет, то вам сюда). В таблице приведены различные степени числа 2. Глядя на таблицу, ясно, что, например, число 32 – это 2 в пятой степени, то есть двойка, умноженная на саму себя пять раз.
Теперь при помощи этой таблицы введем понятие логарифма.
Логарифм от числа 32 по основанию 2 ((log_{2}(32))) – это в какую степень нужно возвести двойку, чтобы получить 32. Из таблицы видно, что 2 нужно возвести в пятую степень. Значит наш логарифм равен 5:
$$ log_{2}(32)=5;$$
Аналогично, глядя в таблицу получим, что:
$$log_{2}(4)=2;$$
$$log_{2}(8)=3;$$
$$log_{2}(16)=4;$$
$$log_{2}(64)=6;$$
$$log_{2}(128)=7.$$
Естественно, логарифм бывает не только по основанию 2, а по любым основаниям больших 0 и неравных 1. Можете так же создавать таблицы для разных чисел. Но, конечно, со временем вы это будете делать в уме.
Теперь дадим определение логарифма в общем виде:
Логарифмом положительного числа (b) по основанию положительно числа (a) называется степень (c), в которую нужно возвести число (a), чтобы получить (b)
$$log_{a}(b)=c;$$
$$a^{c}=b.$$
Будьте внимательны! В первое время обычно путают, что такое основание и то, что стоит под логарифмом (аргумент). Логарифм — это всегда функция, зависящая от двух переменных. Чтобы их не путать, помните определение логарифма – это степень, в которую нужно возвести основание, чтобы получить аргумент.
Но, конечно, вы часто будете сталкиваться не с такими простыми логарифмами, как в примерах с двойкой, а очень часто будет, что логарифм нельзя в уме посчитать. Действительно, что скажете про логарифм пяти по основанию два:
$$log_{2}(5)=???$$
Как его посчитать? При помощи калькулятора. Он нам покажет, что такой логарифм равен иррациональному числу:
$$log_{2}(5)=2,32192809…$$
Или логарифм шести по основанию 4:
$$log_{4}(6)= 1.2924812…$$
На уроках математики пользоваться калькулятором нельзя, поэтому на экзаменах и контрольных принято оставлять такие логарифмы в виде логарифма – не считая его, это не будет ошибкой!
Но иногда можно столкнуться с заданием, где нужно примерно оценить значение логарифма – это очень просто! Давайте для примера оценим логарифм (log_{4}(6)). Необходимо подобрать слева и справа от 6 такие ближайшие числа, логарифм от которых мы сможем посчитать, другими словами, надо найти степени 4-ки ближайшие к 6-ке:
$$ log_{4}(4) lt log_{4}(6) lt log_{4}(16);$$
$$ 1 lt log_{4}(6) lt 2. $$
Значит (log_{4}(6)) принадлежите промежутку от 1 до 2:
$$ log_{4}(6) in (1;2). $$
Как посчитать логарифм
Перед тем, как научиться считать логарифмы, нужно ввести несколько ограничений. Дело в том, что функция логарифма (log_{a}(b)) существует только при положительных значениях основания (a) и аргумента (b). И кроме этого на основание накладывается условие, что оно не должно быть равно (1).
$$ log_{a}(b) quad существует,;при quad a gt 0; ;b gt 0 ;a neq 1.$$
Почему так? Это следует из определения показательной функций. Показательная функция не может быть (0). А основание не равно (1), потому что тогда логарифм теряет смысл – ведь (1) в любой степени это будет (1).
При этих ограничениях логарифм существует.
В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.
Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д.
$$log_{3}(frac{1}{3})=-1;$$
Так как (вспоминайте определение отрицательной степени)
$$3^{-1}=frac{1}{3};$$
Теперь давайте разберем общий алгоритм вычисления логарифмов:
- Во-первых, постарайтесь представить основание и аргумент (то, что стоит под логарифмом) в виде степеней с одинаковым основанием. Параллельно с этим избавляемся от всех десятичных дробей – переводим их в обыкновенные.
- Разобраться в какую степень (x) нужно возвести основание, чтобы получить аргумент. Когда у вас там и там степени с одинаковым основанием, это сделать довольно просто.
- (x) и будет искомым значением логарифма.
Давайте разберем на примерах.
Пример 1. Посчитать логарифм (9) по основанию (3): (log_{3}(9))
- Сначала представим аргумент и основание в виде степени тройки:
$$ 3=3^1, qquad 9=3^2;$$ - Теперь надо разобраться в какую степень (x) нужно возвести (3^1), чтобы получить (3^2)
$$ (3^1)^x=3^2, $$
$$ 3^{1*x}=3^2, $$
$$ 1*x=2,$$
$$ x=2.$$ - Вот мы и решили:
$$log_{3}(9)=2.$$
Пример 2. Вычислить логарифм (frac{1}{125}) по основанию (5): (log_{5}(frac{1}{125}))
- Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1, qquad frac{1}{125}=frac{1}{5^3}=5^{-3};$$ - В какую степень (x) надо возвести (5^1), чтобы получить (5^{-3}):
$$ (5^1)^x=5^{-3}, $$
$$ 5^{1*x}=5^{-3},$$
$$1*x=-3,$$
$$x=-3.$$ - Получили ответ:
$$ log_{5}(frac{1}{125})=-3.$$
Пример 3. Вычислить логарифм (4) по основанию (64): (log_{64}(4))
- Представим аргумент и основание в виде степени двойки:
$$ 64=2^6, qquad 4=2^2;$$ - В какую степень (x) надо возвести (2^6), чтобы получить (2^{2}):
$$ (2^6)^x=2^{2}, $$
$$ 2^{6*x}=2^{2},$$
$$6*x=2,$$
$$x=frac{2}{6}=frac{1}{3}.$$ - Получили ответ:
$$ log_{64}(4)=frac{1}{3}.$$
Пример 4. Вычислить логарифм (1) по основанию (8): (log_{8}(1))
- Представим аргумент и основание в виде степени двойки:
$$ 8=2^3 qquad 1=2^0;$$ - В какую степень (x) надо возвести (2^3), чтобы получить (2^{0}):
$$ (2^3)^x=2^{0}, $$
$$ 2^{3*x}=2^{0},$$
$$3*x=0,$$
$$x=frac{0}{3}=0.$$ - Получили ответ:
$$ log_{8}(1)=0.$$
Пример 5. Вычислить логарифм (15) по основанию (5): (log_{5}(15))
- Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1 qquad 15= ???;$$
(15) в виде степени пятерки не представляется, поэтому этот логарифм мы не можем посчитать. У него значение будет иррациональное. Оставляем так, как есть:
$$ log_{5}(15).$$
Внимание!
Как понять, что некоторое число (a) не будет являться степенью другого числа (b). Это довольно просто – нужно разложить (a) на простые множители.
$$16=2*2*2*2=2^4,$$
(16) разложили, как произведение четырех двоек, значит (16) будет степенью двойки.
$$ 48=6*8=3*2*2*2*2,$$
Разложив (48) на простые множители, видно, что у нас есть два множителя (2) и (3), значит (48) не будет степенью.
Теперь поговорим о наиболее часто встречающихся логарифмах. Для них даже придумали специально названия – десятичный логарифм и натуральный логарифм. Давайте разбираться.
Десятичный логарифм
На самом деле, все просто. Десятичный логарифм – это любой обыкновенный логарифм, но с основанием 10. Обозначается — (lg(a)).
Пример 6
$$ log_{10}(100)= lg(100)=2;$$
$$log_{10}(1000)=lg(1000)=3;$$
$$log_{10}(10)=lg(10)=1.$$
Натуральный логарифм
Натуральным логарифмом называется логарифм по основанию (e). Обозначение — (ln(x)). Что такое (e)? Так обозначают экспоненту, число-константу, равную, примерно, (2,718281828459…). Это число известно тем, что используется в многих математических законах. Просто запомните, что логарифмы с основанием (e) часто встречаются, и поэтому им придумали специальное название – натуральный логарифм.
Пример 7
$$ log_{e}(e^2)=ln(e^2)=2;$$
$$ log_{e}(e)=ln(e)=1;$$
$$ log_{e}(e^5)=ln(e^5)=5.$$
Натуральные и десятичные логарифмы подчиняются тем же самым свойствам и правилам, что и обыкновенные логарифмы.
У логарифмов есть несколько свойств, по которым можно проводить преобразования и вычисления. Кроме этих свойств, никаких операций с логарифмами делать нельзя.
Свойства логарифмов
$$1. ; log_{a}(1)=0;$$
$$2. ; log_{a}(a)=1;$$
$$3. ; log_{a}(b*c)=log_{a}(b)+ log_{a}(c);$$
$$4. ; log_{a}(frac{b}{c})= log_{a}(b)- log_{a}(c);$$
$$5. ; log_{a}(b^m)= m*log_{a}(b);$$
$$6. ; log_{a^m}(b)=frac{1}{m}* log_{a}(b);$$
$$ 7. ; log_{a}(b)=frac{ log_{c}(b)}{ log_{c}(a)}, ; b gt 0; ; c gt 0; ; c neq 1; $$
$$ 8. ; log_{a}(b)=frac{1}{log_{b}(a)};$$
$$ 9. ; a^{ log_{a}(b)}=b.$$
Давайте разберем несколько примеров на свойства логарифмов.
Пример 8. Воспользоваться формулой (3). Логарифм от произведения – это сумма логарифмов.
$$log_{a}(b*c)=log_{a}(b)+ log_{a}(c);$$
$$ log_{3}(12)=log_{3}(3*4)=log_{3}(3)+log_{3}(4)=1+log_{3}(4);$$
$$ log_{3}(2.7)+log_{3}(10)=log_{3}(2.7*10)=log_{3}(27)=3;$$
Пример 9. Воспользоваться формулой (4). Логарифм от частного – это разность логарифмов.
$$ log_{a}(frac{b}{c})= log_{a}(b)- log_{a}(c);$$
$$ log_{7}(98)-log_{7}(2)=log_{7}(frac{98}{2})=log_{7}(49)=2;$$
Пример 10. Формула (5,6). Свойства степени.
$$log_{a}(b^m)= m*log_{a}(b);$$
$$log_{a^m}(b)=frac{1}{m}* log_{a}(b);$$
Логично, что будет выполняться и такое соотношение:
$$log_{a^m}(b^n)=frac{n}{m}* log_{a}(b);$$
И если (m=n), то:
$$log_{a^m}(b^m)=frac{m}{m}* log_{a}(b);=log_{a}(b)$$
$$log_{4}(9)=log_{2^2}(3^2)=log_{2}(3);$$
Пример 11. Формулы (7,8). Переход к другому основанию.
$$ log_{a}(b)=frac{ log_{c}(b)}{ log_{c}(a)}, ; b gt 0;c gt 0;c neq 1; $$
$$ log_{a}(b)=frac{1}{log_{b}(a)};$$
$$log_{4}(5)=frac{1}{log_{5}(4)};$$
$$log_{4}(5)=frac{log_{7}(5)}{log_{7}(4)};$$
Содержание:
Множеством (областью) значений показательной функции
Такое значение аргумента единственное, так как если 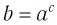
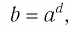
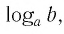
Таким образом, равенство 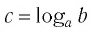
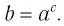
Определение:
Пусть 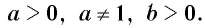
Приведем несколько примеров:
Нахождение логарифма числа называется логарифмированием.
Обозначим 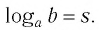
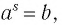
Это равенство называется основным логарифмическим тождеством.
Согласно этому тождеству, например, имеем: 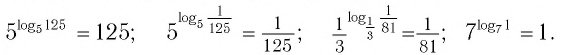
Например:
История логарифма
Логарифмы были изобретены в 1614 г. шотландским математиком Д. Непером (1550—1617) и независимо от него на 6 лет позднее швейцарским механиком и математиком И. Бюрги (1552—1632).
Оба исследователя хотели найти новое удобное средство арифметических вычислений, но их определения логарифма различны и у обоих не похожи на современные. Понимание логарифма как показателя степени с данным основанием впервые появилось в XVIII в. в работах английского математика В. Гардинера (1742). Широкому распространению этого определения логарифма более других содействовал Jl. Эйлер, который впервые применил в этой связи и термин «основание».
Термин «логарифм» принадлежит Неперу. Он возник из сочетания греческих слов логос — отношение и аритмос — число. Слово «логарифм», таким образом, означало «число отношения».
Пример:
а) Записать число 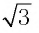
б) Записать число -5 в виде логарифмов по основанию 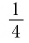
Решение:
а) По определению логарифма имеем:
б) По определению логарифма имеем:
Пример:
Между какими целыми числами находится число
Решение:
Пусть 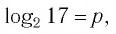
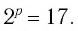
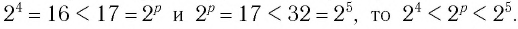
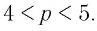
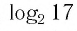
Ответ:
Пример:
Решить уравнение:
Решение:
а) Поскольку 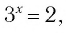
б)
Ответ:
Логарифмы по основанию 10 имеют особое название — десятичные логарифмы. Десятичный логарифм числа b обозначается 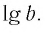
▲ Особое обозначение и название имеют не только десятичные логарифмы, но и логарифмы, основанием которых является число е:
Такие логарифмы называются натуральными.
Логарифмы по основанию е позволяют выражать математическую зависимость, которая характеризует многие биологические, химические, физические, социальные и другие процессы. По-видимому, этим объясняется и название «натуральные логарифмы», т. е. естественные (этот термин ввел в 1659 г. итальянский математик П. Менголи). Натуральные и десятичные логарифмы имели большое значение для облегчения вычислений в XVII—XX вв. до создания мощных современных вычислительных средств. Натуральные логарифмы имеют и большое теоретическое значение.▲
Основные свойства логарифмов
Теорема:
При любых положительных значениях b и с верно равенство:
Доказательство:
Докажем утверждение (1).
По основному логарифмическому тождеству
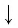
Таким образом, имеем:
Отсюда по следствию из п. 2.3 получаем равенство (1).
Докажем утверждение (2). Преобразуем левую часть равенства (2):
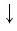
Заметим, что равенство (2) можно доказать тем же способом, что и равенство (1), — сделайте это самостоятельно.
Равенство (1) означает, что логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел.
Равенство (2) означает, что логарифм дроби с положительными. числителем и знаменателем равен разности логарифмов числителя и знаменателя.
Замечание. Равенства, доказанные в теореме 1 (как и другие равенства этого пункта), являются тождествами. Действительно, каждое из них превращается в верное числовое равенство при любых значениях a, b и с, для которых входящие в равенство выражения имеют смысл.
Теорема:
При любых значениях s и положительных значениях b верно равенство
Доказательство:
По основному логарифмическому тождеству
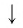
Таким образом, имеем
Отсюда по следствию из п. 2.3 получаем равенство (3).
Следствие 1. Если числа 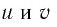
Следствие 2. При любом целом 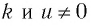
Пример №1
Найти значение выражения:
Решение:
Ответ:
Теорема:
При любых значениях 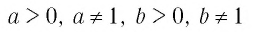
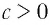
Доказательство:
Способ 1. По основному логарифмическому тождеству имеем
Прологарифмировав левую и правую части этого тождества по основанию а, получим
Применив тождество (3), имеем
Так как 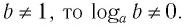
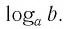
Способ 2. Пусть 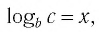
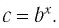
Откуда имеем
Итак,
Тождество (6) называется формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Обычно в таблицах, калькуляторах даются значения логарифмов по основанию 10, а когда нужно найти значение логарифма по другому основанию, пользуются формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Следствием из тождества (6) при основании а = с является формула
(убедитесь в этом самостоятельно).
Пример №2
Найти значение выражения, если
Решение:




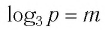
6)


Ответ:
Следствие 3. Имеют место тождества:
Тождества (8) и (9) можно доказать, используя уже доказанные тождества из этого пункта.
Пример №3
Упростить выражение
Решение:
Используя определение логарифма, представим числа 1 и 3 в виде логарифмов по основанию 2:
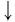
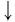
Ответ:
Развитие науки, прежде всего астрономии, уже в XVI в. привело к необходимости громоздких вычислений при умножении и делении многозначных чисел. Эти вычислительные проблемы были в некоторой степени решены с открытием логарифмов и созданием таблиц логарифмов.
Логарифмическая функция
Рассмотрим выражение 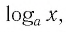
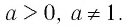
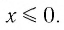
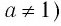
Определение:
Логарифмической функцией называется функция вида 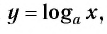
Область определения логарифмической функции — это естественная область определения выражения 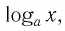
Графики некоторых логарифмических функций изображены на рисунке 34. Эти изображения (как и для графиков других функций) можно было получить, строя их по точкам. Отметим некоторые особенности изображенных графиков.
График функции 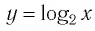
Когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» опускается вниз. А когда значения аргумента х увеличиваются, то график «медленно» поднимается вверх (ем. рис. 34). Аналогично для любой функции 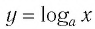
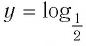
Заметим, что когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» поднимается вверх. А когда значения аргумента х увеличиваются, то график «медленно» опускается вниз. Аналогично для любой функции 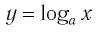
Теорема (о свойствах логарифмической функции 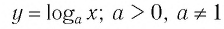
- Областью определения логарифмической функции является интервал
- Множеством (областью) значений логарифмической функции является множество R всех действительных чисел.
- Логарифмическая функция не имеет ни наименьшего, ни наибольшего значений.
- График логарифмической функции пересекается с осью абсцисс в точке (1; 0) и не пересекается с осью ординат.
- Значение аргумента х = 1 является нулем логарифмической функции.
- 6. При а > 1 логарифмическая функция принимает отрицательные значения на интервале (0; 1) и принимает положительные значения на интервале
И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале
и принимает положительные значения на интервале (0; 1).
- Логарифмическая функция не является ни четной, ни нечетной.
- При а > 1 логарифмическая функция возрастает на всей области определения. При 0 < а < 1 логарифмическая функция убывает на всей области определения.
- Логарифмическая функция не является периодической.
Изображение графика логарифмической функции позволяет наглядно представить эти свойства.
Множество (область) значений логарифмической функции — проекция ее графика на ось Оу, а на рисунках 35 и 36 видно, что эта проекция есть ось Оу. Это значит, что для любой точки 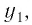
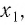
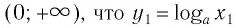
Множество (область) значений логарифмической функции — это множество всех действительных чисел, а в нем нет ни наименьшего числа, ни наибольшего (свойство 3).
График логарифмической функции проходит через точку (1; 0) и лежит в правой полуплоскости (свойства 4, 5).
При а > 1 график логарифмической функции лежит в IV координатном угле, когда 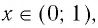
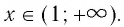
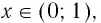
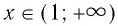
Область определения логарифмической функции — интервал 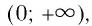
На рисунке 35 видно, что при а > 1 логарифмическая функция возрастает на области определения, а на рисунке 36 видно, что при 0 < а < 1 логарифмическая функция убывает на области определения (свойство 8).
Пусть точка 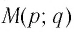
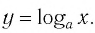
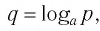
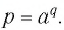
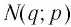
Заметим, что точки 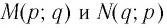
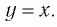
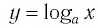
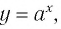
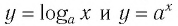
Последнее утверждение дает возможность, зная график функции 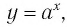
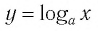
▲ Симметричность графиков функций 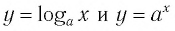
Функции 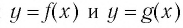
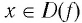
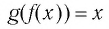
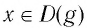
Покажем, что показательная и логарифмическая функции с одним, и тем же основанием а взаимно обратны.
Пусть 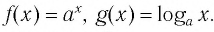
Для любого
Для любого
Покажем, что графики взаимно обратных функций 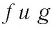
Пусть точка 
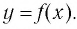
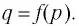
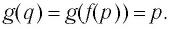
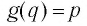
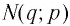
Таким образом, каждой точке М на графике функции 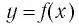
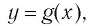
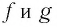
- Заказать решение задач по высшей математике
Логарифмы и их свойства
В предыдущем параграфе вы находили корни уравнения вида 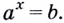
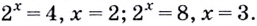
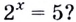
Для записи корней показательного уравнения используют понятие «логарифм» и соответствующий символ. Корнем уравнения 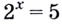
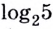
Рассмотрим общий случай-.
Пусть 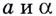
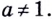
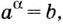
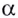
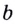
Логарифмом числа 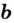
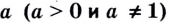
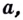
Логарифм числа 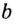
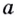
Примеры:
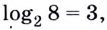
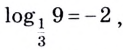
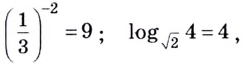
Основанием логарифма может быть произвольное положительное число, кроме единицы. Как известно, если 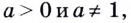
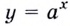
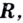
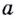
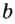
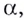
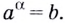
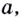
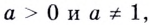
Полезно помнить, что для каждого
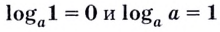
Нахождение логарифма числа называют логарифмированием. Эта операция обратная к операции возведения в степень с соответствующим основанием.
Согласно определению логарифма, если 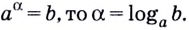
которое называют основным логарифмическим тождеством. Оно правильное для любых положительных
Например:
С помощью основного логарифмического тождества любое положительное число можно представить в виде степени, имеющей заданное основание.
Например:
Докажем ещё несколько важных свойств логарифмов (для положительных
1) По основному логарифмическому тождеству и основному свойству степени
Итак, 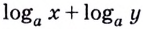
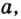
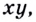
Эту формулу можно обобщить на три и более множителя:
Кратко говорят: логарифм произведения равен сумме логарифмов множителей.
2) Доказательство аналогичное предыдущему:
отсюда
Кратко говорят: логарифм частного равен разности логарифмов делимого и делителя.
3) Возведём обе части тождества 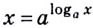
Итак,
Доказанные формулы можно использовать и справа налево, например:
В логарифмах переходить от одного основания к другому можно при помощи формулы перехода
где
Докажем эту формулу. Поскольку положительные числа 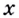
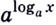
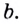
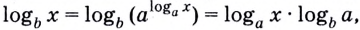
Обратите внимание! Как следствия из формулы перехода можно получить следующие формулы:
Докажите их самостоятельно.
Пример №4
Упростите выражение 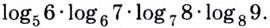
Решение:
Сведём все логарифмы к основанию 5. Имеем:
Особенно часто используют логарифмы по основаниям 10 и 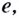
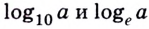
Рассмотренные в параграфе свойства логарифмов правиль-1 ные при условии, что переменные принимают положительные значения. С помощью модуля можно расширить использование некоторых формул. Например:
Для преобразования выражений, решения уравнений и неравенств используют и другие формулы, содержащие логарифмы:
Докажите их самостоятельно.
Пример №5
Вычислите:
Решение:
Пример №6
Решите уравнение:
Решение:
Пусть 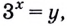
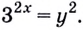
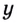
Получим: 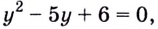
Поскольку 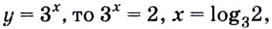
Ответ.
Пример №7
Найдите 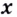
Решение:
Поскольку
Ответ.
Пример №8
Вычислите 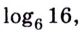
Решение:
Ответ.
- Корень из числа — нахождение и вычисление
- Теория множеств — виды, операции и примеры
- Числовые множества
- Вектор — определение и основные понятия
- Бесконечно убывающая геометрическая прогрессия
- Периодические дроби
- Степень с рациональным показателем
- Степень с действительным показателем


 И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с.
И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с.
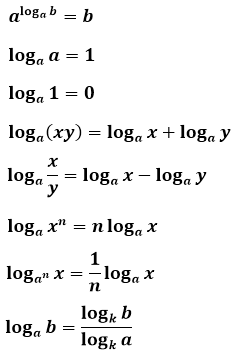
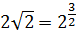
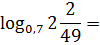
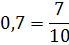
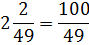
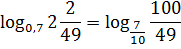
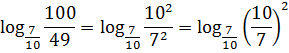
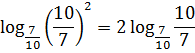
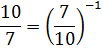
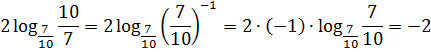
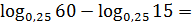
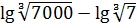
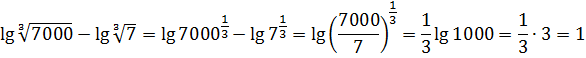
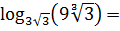
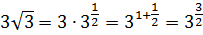
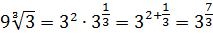
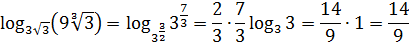
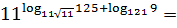
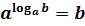
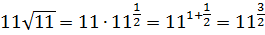
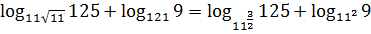
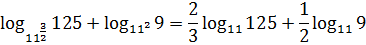
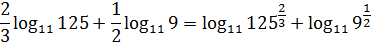
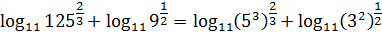
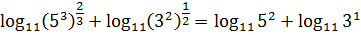
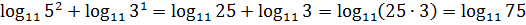

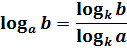
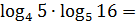
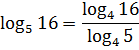
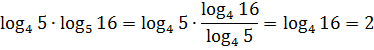
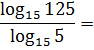
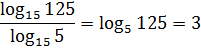
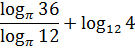
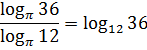
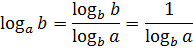
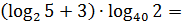
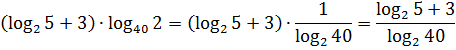
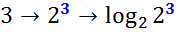
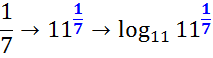
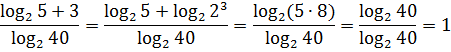
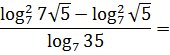
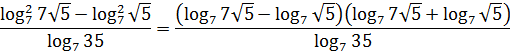
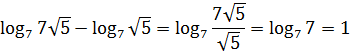
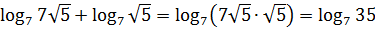
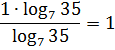
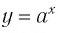
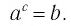
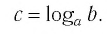
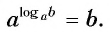
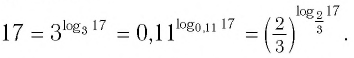
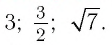
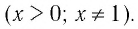
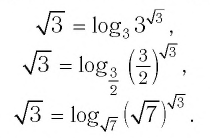
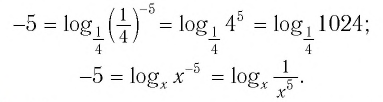
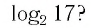
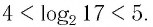
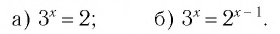
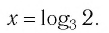
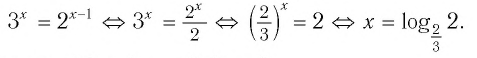
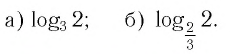
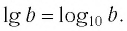
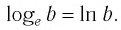
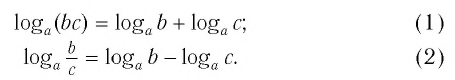
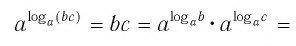
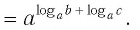
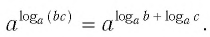
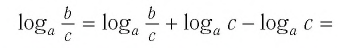
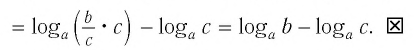

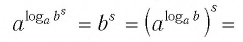
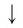
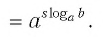
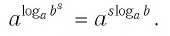

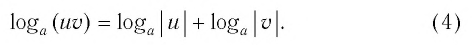
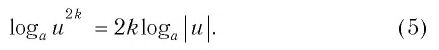
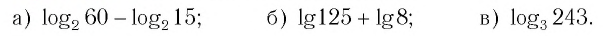
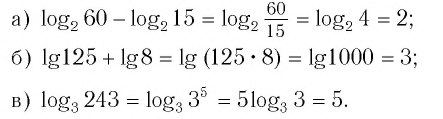
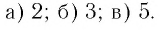

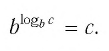
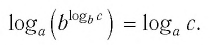
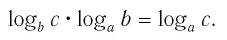

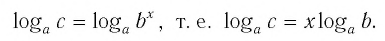
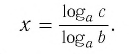
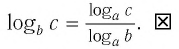

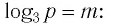
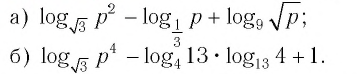
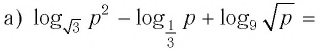
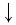
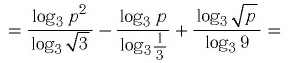
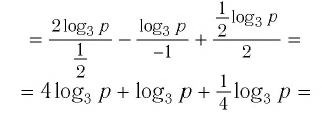
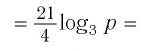
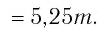
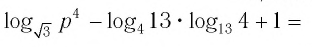
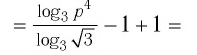
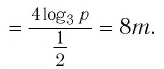
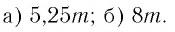

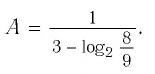
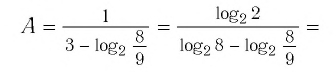
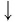
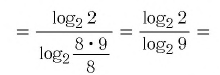
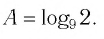
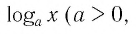
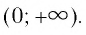
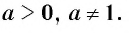
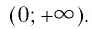
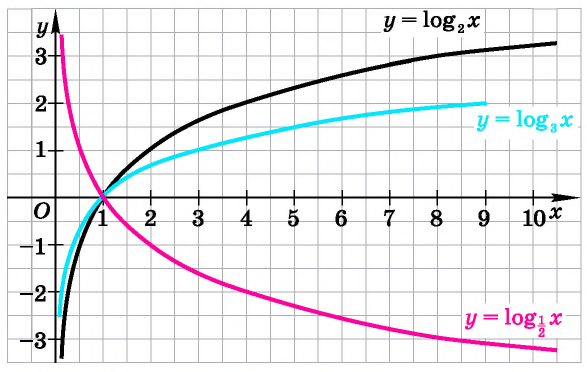
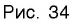
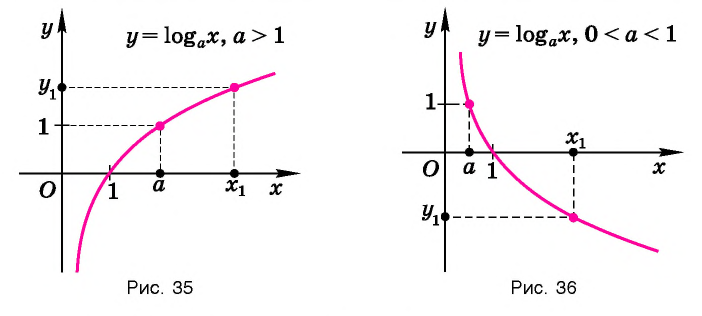
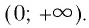
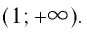 И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале
И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале 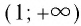 и принимает положительные значения на интервале (0; 1).
и принимает положительные значения на интервале (0; 1).