Рассмотрим две важные характеристики колебательных систем в механике и теории электричества и магнетизма: коэффициент затухания и логарифмический декремент затухания. Мы остановимся на так называемых затухающих колебаниях – таких колебаниях, амплитуда которых со временем уменьшается из-за потери энергии.
Чаще всего затухание происходит из-за трения — об воздух или поверхность, любую жидкую или газообразную среду, в которую помещено тело. Тело, проплывая в газе или жидкости или скользя по поверхности, передает этой среде внутреннюю энергию из за трения. Собственная суммарная кинетическая и потенциальная энергия при этом уменьшается. Соответственно уменьшается и скорость, а с ней — амплитуда.
Затухающие колебания можно поделить на свободные затухающие колебания и колебания, происходящие под действием внешних сил.
Как определить коэффициент затухания свободных затухающих механических колебаний
md2xdt2=−kx−rvmfrac{d^2x}{dt^2}=-kx-rv
mm — масса колеблющегося тела,
xx — его координата (смещение относительно точки равновесия x=0x=0),
−kx-kx — сила упругости, даваемая законом Гука для небольших смещений,
kk — коэффициент упругости,
−rv-rv — сила трения,
rr — коэффициент трения,
vv — скорость тела.
Это уравнение имеет решение:
x(t)=A0e−βtcos(ωt+φ)x(t)=A_0e^{-beta t}cos(omega t+varphi)
A0A_0 — амплитуда,
ωomega— циклическая частота,
φvarphi — начальная фаза,
βbeta — коэффициент затухания.
ω=ω02−β2omega=sqrt{omega_0^2-beta^2}
ω02=kmomega_0^2=frac{k}{m}
ω0omega_0 — собственная частота.
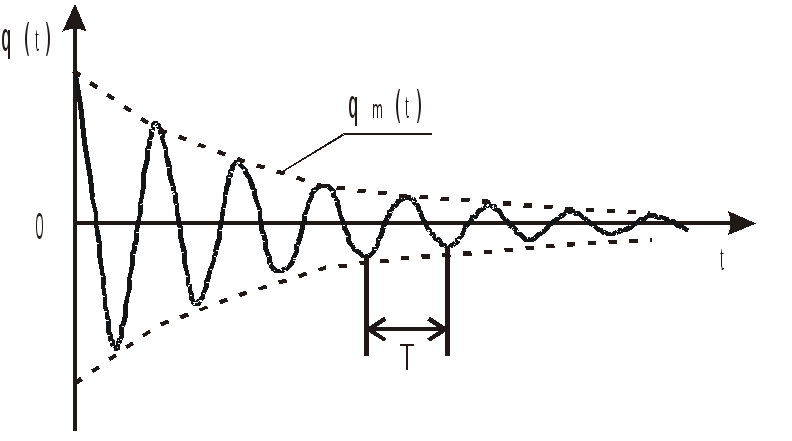
Коэффициент затухания βbeta – это величина, обратная времени, за которое амплитуда колебания уменьшилась в ee раз, где ee — основание натуральных логарифмов.
β=1NTbeta=frac{1}{NT}
NN — число колебаний после которых амплитуда уменьшилась в ee раз,
TT — период колебаний,
T=2πωT=frac{2pi}{omega}
Логарифмический декремент затухания свободных затухающих колебаний маятника
Маятник трется об воздух. И, казалось бы, как понять, какую он энергию отдает воздуху? Наверное, тут не обойтись без температуры, давления, плотности газообразной среды, и это долго, сложно, нудно… Может, и так. Но все это укладывается в коэффициент затухания ββ.
Определить логарифмический декремент затухания можно двумя способами — с помощью замеров амплитуды и с коэффициентом затухания. Для первого нужно лишь замерить две последовательные амплитуды. Тогда формула проста:
λ=lnA0e−βtA0e−β(t+T)lambda=lnfrac{A_0e^{-beta t}}{A_0e^{-beta (t+T)}}
Если же известен коэффициент затухания, амплитуда не нужна. Логарифмический декремент затухания будет равен его произведению на период колебаний:
λ=βTlambda=βT
Логарифмический декремент затухания электрического колебательного контура
Колебания в электрическом контуре возникают при отсутствии активного сопротивления в цепи, содержащей катушку индуктивности и конденсатор. Ток колеблется туда-сюда. Затухание этих колебаний удивительно похоже на затухание механических колебаний, потому, проведя несколько опытов, ученые пришли к выводу, что у электрического контура есть свой коэффициент затухания, и, соответственно, формула такая же, как для механических колебаний:
λ=βTlambda=βT
T=2πLCT=2πsqrt{LC}
LL — индуктивность катушки,
CC — емкость конденсатора.
Коэффициент затухания вынужденных механических колебаний
Конечно, в вынужденных колебаниях тоже существует затухание. Разница свободных и вынужденных колебаний в существовании добавочной силы, которая возвращает амплитуду к ее начальному значению, не давая маятнику остановиться, т.е. нивелирует работу силы трения.
Уравнение движения такой системы:
md2xdt2=−kx−rv+Fmfrac{d^2x}{dt^2}=-kx-rv+F.
Здесь все величины те же самые, что и в свободных колебаниях, но появляется внешняя сила FF:
F=mF0cos(ωt)F=mF_0cos(omega t).
F0F_0 имеет размерность силы, деленной на массу.
x=Asin(ωt+φ)x=Asin(omega t+varphi)
AA — амплитуда колебаний.
A=F0m(ω02−ω2)2+4β2ω2A=frac{F_0}{msqrt{{(omega_0^2-omega^2)^2}+4beta^2omega^2}{}}.
В случае затухающих вынужденных колебаний коэффициентом затухания снова является величина βbeta.
Тест по теме «Коэффициент и логарифмический декремент затухания»
10
Министерство Российской Федерации
по
связи и информатизации
Сибирский
государственный университет
телекоммуникаций
и информатики
Кафедра
физики
Методические указания
к лабораторной
работе по теме
«Исследование
свободных затухающих колебаний в
электрическом контуре»
Разработчик:
ст. преподаватель Стрельцов А. И.
Новосибирск
2005
Лабораторная
работа 5.1
Исследование
свободных затухающих колебаний в
электрическом контуре
Цель работы:
-
Ознакомиться с физическими процессами,
происходящими в электрическом контуре -
Исследовать влияние величин ёмкости
конденсатора и индуктивности катушки
на период колебаний в контуре с малым
сопротивлением -
Установить характер зависимости
логарифмического декремента затухания
колебаний от сопротивления контура.
Теоретическое введение
Процессы периодическогоизменения
какой-либо физической величины с течением
времени называютсяколебательными
процессамиили просто –колебаниями.
Устройство или совокупность физических
тел, в которых может происходить
колебательный процесс, называют
колебательной системой. Каждая
колебательная система обладает
единственным состоянием, в котором она
может находиться бесконечно долго, не
совершая колебаний. Такое состояние
колебательной системы называетсясостоянием равновесия. Следовательно,
чтобы в системе возникли колебания, её
необходимохотя бы один развывести
из состояния равновесия.
Классифицировать колебательные процессы
можно по нескольким основаниям:
-
По физической природе колебания бывают
механическимииэлектромагнитными, -
По наличию внешних сил в колебательной
системе колебания делятся на свободныеивынужденные. -
По характеру зависимости амплитуды от
времени различают незатухающиеизатухающие. Незатухающие колебания,
происходящие по закону синуса или
косинуса, часто называютгармоническими.
Свободныминазываются колебания в
системе в отсутствие внешних воздействий
на эту систему. Если же на колебательную
систему действует внешняя (периодически
изменяющаяся) сила, такие колебания
будутвынужденными.
В идеальной колебательной системе, в
которой отсутствуют диссипативные силы
(силы трения, сопротивления и т. п.),
колебания будут продолжаться вечно.
Такие процессы получили название
незатухающих колебаний. Поскольку
в реальных колебательных системах
всегда присутствуют силы сопротивления,
то однажды возникшие в системе колебания
не будут продолжаться вечно. С течением
времени их амплитуда будет все меньше
и меньше, в конце концов, она станет
равной нулю и колебания прекратятся.Колебания, амплитуда которых
уменьшается с течением времени, называются
затухающими.Именно этот вид
колебаний мы и будем исследовать в
данной работе.
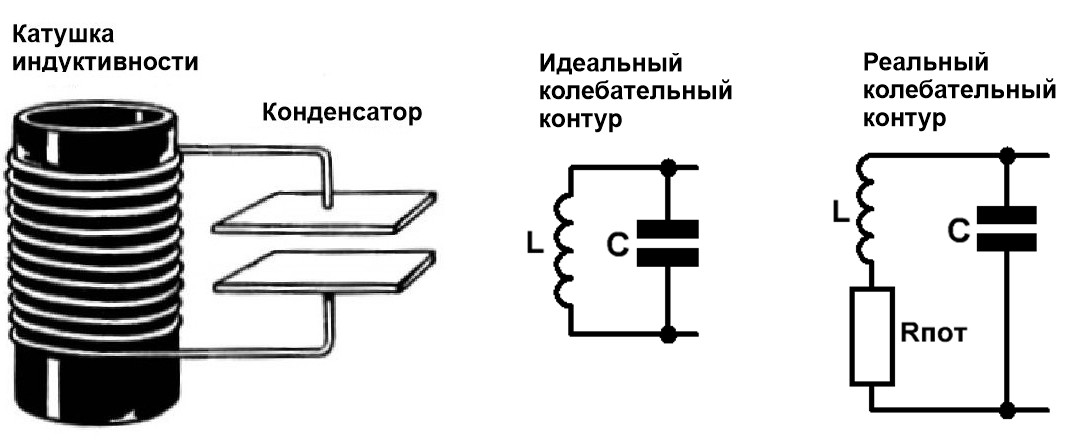
Устройство, в котором могут существовать
электромагнитные колебания, называется
электрическим колебательным контуром.Существует два вида колебательных
контуров:
-
Контур без активного сопротивления
(идеальный контур). В таком
колебательном контуре однажды начавшиеся
электромагнитные колебания будут
продолжаться вечно. Схема идеального
колебательного контура изображена на
рисунке 1. -
Контур с активным сопротивлением
(реальный контур). В реальном контуре
амплитуда колебаний будет уменьшаться
с течением времени за счет потерь
энергии на нагревание сопротивления,
то есть, колебания будут затухающими.
Схема реального колебательного контура
изображена на рисунке 2.
Рисунок 1 Рисунок 2
В данной работе нас будет интересовать
реальный колебательный контур (рисунок
2). Для математического описания процессов
в реальном контуре используем второе
правило Кирхгофа:алгебраическая
сумма падений напряжения в контуре
равна алгебраической сумме действующих
в нем ЭДС.
(1)
Падение напряжения:
-
На активном сопротивлении
(2)
где
— сила тока в контуре,
— активное сопротивление,
-
На конденсаторе
(3)
где
— заряд конденсатора,
— его ёмкость. Формула (3) следует из
определения электрической ёмкости.
(4)
ЭДС, развиваемая в контуре – это ЭДС
индукции, возникающая в катушке
индуктивности при изменении силы тока
в ней, а, следовательно, и магнитного
потока сквозь её сечение. Величина ЭДС
индукции определяется согласно закону
электромагнитной индукции Фарадея:
ЭДС индукции в замкнутом контуре
пропорциональна скорости изменения
магнитного потока через сечение контура:
(5)
где
— магнитный поток через площадь сечения
катушки. Формула (5) может быть записана
в другом виде:
(6)
где
— индуктивность катушки.
Второе правило Кирхгофа (1) для нашего
контура запишется в виде
(7)
Подставим выражения (2), (3) и (6) в формулу
(7):
(8)
По определению, сила тока – это первая
производная заряда по времени:
(9)
Тогда, подставив (9) в (8) и выполнив деление
каждого слагаемого на
,
перейдем в нем к единственной переменной
– заряду:
(10)
Это и есть дифференциальное уравнение
затухающих колебаний электрического
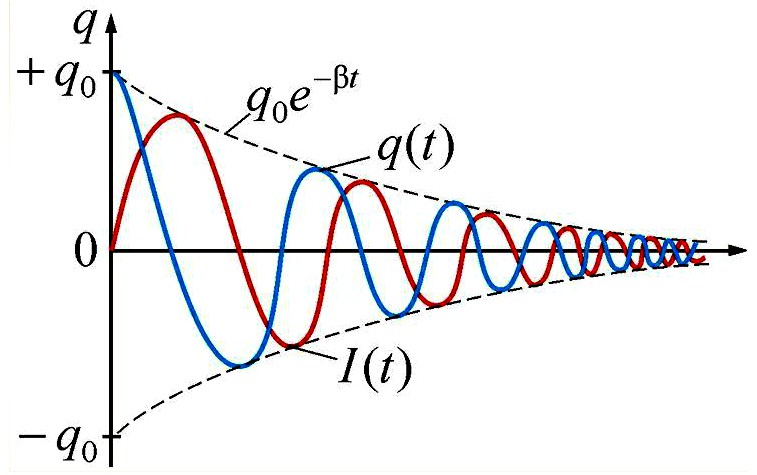
заряда в реальном колебательном контуре.Егорешениямиявляются функции
(11)
и
(11’)
где
(12)
— амплитуда затухающих колебанийзаряда, а
(13)
— коэффициент затухания, показывающий
интенсивность убывания амплитуды
колебаний. График затухающих колебаний,
соответствующий выражению (11), приведен
на рисунке 3.
Рисунок 3. График затухающих колебаний
заряда на обкладках конденсатора.
Величина
(14)
получила название собственной частотыколебательного контура. Подставляя
решение (11) в уравнение (10) и выполнив
необходимые тригонометрические
преобразования, получив выражение для
вычислениячастоты затухающих колебанийв контуре:
(15)
Изменение амплитуды затухающих колебаний,
согласно (12), происходит по экспоненциальному
закону. Пусть за время
амплитуда колебаний уменьшится в
раз (
— основание натуральных логарифмов).
Тогда, с одной стороны,
(16)
с другой стороны,
(17)
Из этих соотношений следует, что
,
откуда
(18)
Величина
,
определяемая формулой (18), получила
названиевремени релаксации. Таким
образом,время релаксации – это
промежуток времени, за который амплитуда
затухающих колебаний уменьшается в
раз. Из (18) и (13) можно выразить время
релаксации через параметры контура:
(19)
Кроме перечисленных выше величин,
затухание колебаний в реальном контуре
характеризуется еще двумя параметрами:
логарифмическим декрементом затуханияидобротностью колебательного контура.
Логарифмический декремент затухания
– физическая величина, равная натуральному
логарифму отношения двух последовательных
амплитуд, отстоящих по времени на период:
(20)
Упростив (20), получив еще одно выражение
для логарифмического декремента
затухания
(21)
Добротность колебательной системы
– это физическая величина, равная
произведению
на
отношение энергии системы в произвольный
момент времени к убыли этой энергии за
один период затухающих колебаний:
(22)
Так как энергия пропорциональна квадрату
амплитуды, то

При малых значениях логарифмического
декремента затухания добротность
колебательной системы равна
(24)
Из (13), (15) и (21) следует выражение добротности
системы через параметры контура:
(25)
Чем больше добротность колебательной
системы, тем меньше затухание и тем
дольше будут длиться колебания в ней.
Параллельный и последовательный колебательный контур
Что такое колебательный LC-контур? Принцип работы, формулы расчёта основных
параметров. Онлайн калькулятор резонансной
частоты колебательного контура,
добротности и коэффициента затухания в зависимости от величин индуктивности,
ёмкости и сопротивления потерь
Колебательный контур – это пассивная электрическая цепь, состоящая из конденсатора и катушки индуктивности, в которой
возможно возбудить свободные электромагнитные колебания.
Если конденсатор и катушка соединены параллельно, то контур называется параллельным, при последовательном соединении элементов колебательный
контур называется последовательным.
Для начала рассмотрим параллельный колебательный контур, который в радиотехнике используется как основа частотно-избирательных цепей и встречается намного
чаще последовательного.
Рис.1 Параллельный колебательный контур, его изображение на схеме (идеальный
колебательный контур), реальный колебательный контур
При анализе цепи колебательного контура обычно используется реалистичная модель (Рис.1 справа), состоящая из идеальных пассивных элементов и активного
сопротивления потерь катушки – Rпот.
Сопротивление потерь катушки Rпот складывается из потерь в проводах, диэлектрике, сердечнике и экране (если он есть).
Поскольку потери в контурном конденсаторе на порядки меньше, чем потери в катушке, то его сопротивление потерь при расчётах обычно не учитывается.
Так, за счёт чего в колебательном контуре возникают свободные колебания? Для того чтобы ответить на этот вопрос, давайте соберём простейшую схему (Рис.2)
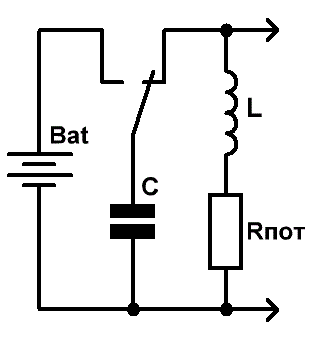
Рис.2 Колебательный процесс в параллельном колебательном контуре
Для возбуждения в контуре колебаний конденсатор следует предварительно зарядить, сообщая его обкладкам заряд
qmax от внешнего источника Bat напряжением
Umax.
После того как конденсатор будет заряжен, переводим переключатель в правое по схеме положение, отключая контур от источника, и наблюдаем возникшие в цепи затухающие
электромагнитные колебания, при которых происходит превращение энергии электрического поля в энергию магнитного поля и наоборот (Рис.2 справа).
Из-за потерь, возникающих в элементах контура, электромагнитные колебания в цепи всегда будут затухающими. Скорость их затухания зависит от величины этих потерь,
суммарное значение которых характеризуются параметром, называемым добротностью колебательного контура Q. Численно добротность равна числу
колебаний от момента возбуждения свободных колебаний до момента, когда их амплитуда уменьшится в
еπ = 23,14 раз. Для желающих поподробнее познакомиться с тем, что такое добротность и как её
измерить, имеет смысл посетить страницу – ссылка на страницу.
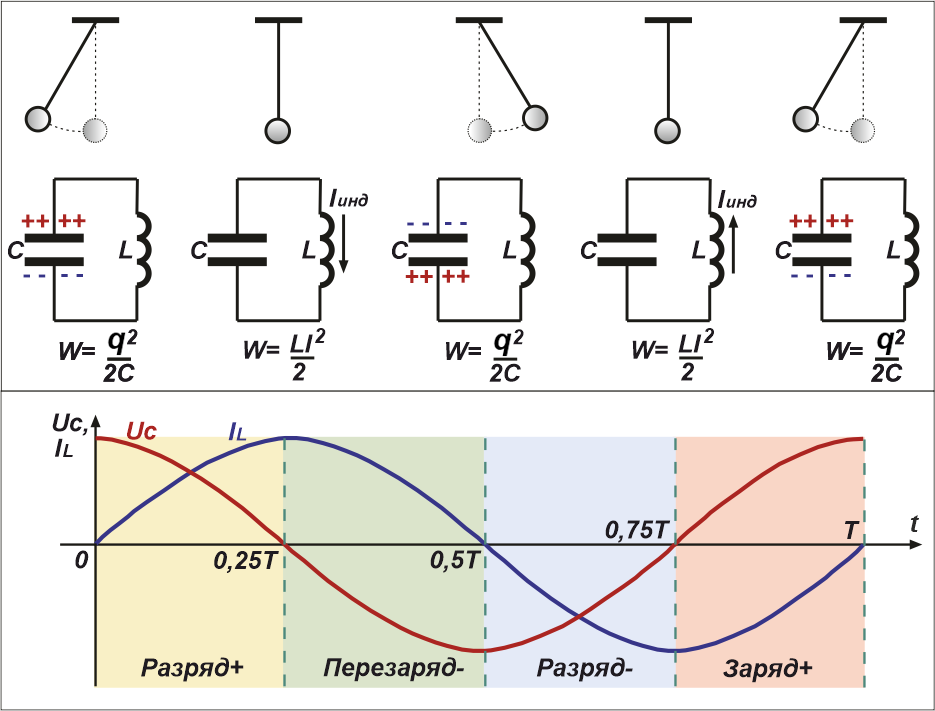
А мы тем временем рассмотрим последовательные фазы колебаний, происходящие в контуре после зарядки конденсатора.
Рис.3 Фазы колебаний, происходящих в колебательном контуре за полный период
Электромагнитные колебания, а также описывающие их уравнения во многом подобны механическим колебаниям.
Опишем стадии колебательного процесса за полный период колебаний:
1. t = 0 – начало разрядки конденсатора (энергия электрического поля, запасённая в конденсаторе, равна
W = q2/2C ).
Через катушку начинает течь ток. При этом катушка оказывает сопротивление моментальному росту тока, поскольку в ней присутствует ЭДС
самоиндукции, препятствующая этому росту.
2. t = 0,25Т – конденсатор полностью разряжен.
Ток через катушку максимален, так как вся энергия из конденсатора перешла в энергию магнитного электрического поля катушки
W = L*I2/2.
Начиная с этого момента, эта энергия начинает опять перетекать в конденсатор, перезаряжая его потенциалом обратной полярности.
3. t = 0,5Т – конденсатор опять полностью заряжен, но потенциалом противоположной полярности. Ток через
катушку индуктивности равен нулю. Начинается фаза, описанная в п.1, но с током, текущем в обратном направлении.
4. t = 0,75Т – конденсатор вновь полностью разряжен, ток через катушку максимален и направлен
в противоположную (по отношению к п.2) сторону.
5. t = Т – всё начинается сначала, т. е. аналогично 1п.
А теперь – формулы, которые могут понадобиться при расчёте колебательного LC контура:
Период колебаний: T0 = 2π√LC ;
Частота: F0 = 1/T0 ;
Круговая (циклическая) частота: ω0 = 2π/T0 =
2πF0 ;
Максимальный заряд конденсатора: qmax = UmaxC ;
Максимальная сила тока через катушку: Imax = ωqmax .
Добротность колебательного контура:
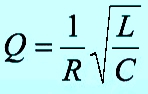
Мгновенные значения напряжения, силы тока и энергии можно рассчитать по формулам:
Заряд: q(t) = qmax cos(ωt) ;
Напряжение: U(t) = Umax cos(ωt) ;
Сила тока: I(t) = Imax sin(ωt) ;
Энергия: W(t) = I(t)2L/2 + q(t)2/(2C) .
Все приведённые формулы хороши для идеального колебательного контура, в котором нет потерь, а соответственно, и нет затухания колебаний. Для реальных же контуров
(с потерями) вводятся дополнительные параметры, характеризующие скорость затухания колебаний. Одними из таких параметров являются коэффициент затухания
β и логарифмический декремент колебаний λ.
Коэффициент затухания β – это величина, характеризующая скорость затухания колебаний и обратно
пропорциональная времени τ, по истечении которого амплитуда колебаний убывает в
е раз.
Для колебательного контура данная величина вычисляется по формуле:
β = Rпотерь /(2L).
Логарифмическим декрементом затухания λ называется величина, равная натуральному логарифму отношения
двух последовательных амплитуд, отстоящих друг от друга на период колебаний. Численно логарифмический декремент колебаний равен коэффициенту затухания,
умноженному на период колебаний:
λ = βT.
С учётом коэффициента затухания наши формулы приобретают следующий вид:
Заряд: q(t) = qmax cos(ωt) e(-βt) ;
Напряжение: U(t) = Umax cos(ωt) e(-βt) ;
Сила тока: I(t) = Imax sin(ωt) e(-βt) ;
Энергия: W(t) = I(t)2L/2 + q(t)2/(2C) ;
Период:
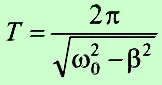
Круговая (циклическая) частота:
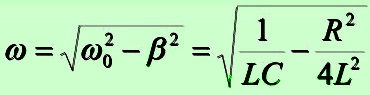
Добротность: Q = Lω/R .
При относительно высокой добротности цепи, то есть когда колебания затухают не слишком быстро и выполняется условие
β2 << ω02, круговая частота контура равна
ω ≈ ω0 ,
а формулы по расчёту резонансной частоты и добротности принимают привычный вид, приведённый выше на синем фоне.
Для проверки знаний, полученных в рамках данной статьи, приведём онлайн калькулятор для расчёта основных параметров колебательного контура.
РАСЧЁТ РЕЗОНАНСНОЙ ЧАСТОТЫ, ДОБРОТНОСТИ И КОЭФФИЦИЕНТА ЗАТУХАНИЯ КОНТУРА
Ёмкость конденсатора контура |
||
Индуктивность катушки контура L |
||
Сопротивление потерь Rпот |
||
Резонансная частота |
||
Добротность = кол-во колебаний |
||
Коэффициент затухания β (сек-1) |
Для последовательного колебательного контура резонансная частота (период и круговая частота) не зависит от сопротивления потерь, однако остальные приведённые
выше параметры описываются теми же формулами, что и для параллельного. При этом в составе частотно-избирательных цепей эти контуры ведут себя по-разному и
имеют значительно отличающиеся друг от друга передаточные характеристики. Какие это характеристики? – рассмотрим в рамках отдельной статьи.
А на следующей странице рассмотрим, как на добротность LC-контура влияют сопротивления нагрузки и источника сигнала.