Как найти логическое выражение по таблице истинности

План урока:

Способы решению задач по логике

Табличный способ – этапы, особенности

Сравнение методов решения

Построение таблиц истинности для различных типов задач

Построение электрических схем, реализующих логические операции

Способы решения задач по логике

Многие задачи можно решить, используя инструменты алгебры логики. Чтобы получить результат, можно пойти 3 путями:

• рассуждая над условием;
• решая логические операции;
• используя таблицы истинности.

Логический подход подразумевает перевод условия из естественного языка на язык символов, схем и формул. Для такой формализации высказываний нужно выполнить ряд шагов.

Этапы решения логических задач:

• Разобраться с условием на естественном языке, выделив простые высказывания, и дать им символьные обозначения (латиница).
• Записать условие в виде формулы. Решить ее поэтапно, упрощая, учитывая приоритеты (( ), ¬, &, V).
• Просчитать формулы строчно или при помощи таблиц истинности, учитывая законы алгебры логики.
• Проверить, соответствует ли полученный результат условию задачи.

Табличный способ – этапы, особенности

Таблица истинности – табличное выражение результата логических операций для каждого отдельного набора значений переменных.

Такие таблицы позволяют абстрагироваться от маловажной информации, сосредоточиться только на связях между исходными данными, над происходящими процессами. Таким образом, человек может абстрагироваться от непонятной для него информации, решать неспецифические задачи.

Метод таблиц

Чтобы использовать таблицы истинности, необходимо формализовать условие, то есть отойти от деталей задачи, обозначая первоначальную информацию при помощи букв и цифр 0 и 1.

Существует общий алгоритм построения таблиц:

• Определить число логических значений/переменных (n) в примере.
• Установить вид, число и тип операций. Важно заранее определить очередность действий, выразить это при помощи скобок.
• Полученные данные позволяют рассчитать сколько нужно столбцов – это сумма числа переменных и операций.
• Нарисовать таблицу, заполнить шапку, записав обозначение переменных и выбранные действия.
• Определить, сколько существует наборов логических переменных (т.е. число строчек) по формуле m = 2ⁿ+ 1 (шапка).
• Заполнить столбцы, вписав наборы значений логических переменных (0 или 1).
• Записать результаты логических операций, указанных в шапке для каждой совокупности значений.
• Сделать выводы на основании полученных результатов.

Если необходимо перебрать все значения простых выражений, то для задач:

• с 2-мя переменными может быть только 4 набора логических переменных;

Если словесно описывать все эти комбинаций, на каждый из примеров понадобится десятки строк текста.

 Обязательно учитывают приоритет операций:

• Указанные в скобках.
• Отрицание.
• Логическая конъюнкция чисел.
• Дизъюнкция.
• Строгая дизъюнкция.
• Импликация.
• Эквивалентность.

Обозначение логических операций:

Сравнение методов решения

Метод рассуждений

Он заключается в пошаговом анализе условий с промежуточными выводами на каждом этапе. Выполняется анализ таблицы истинности каждого логического выражения.

Пример №1.

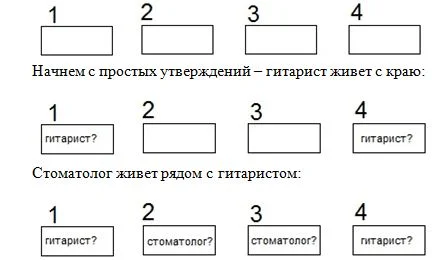
Андрей, Владимир, Георгий и Дмитрий живут на одной улице, они соседи. Они работают по таким специальностям: гитарист, плотник, егерь и стоматолог.

Известно, что:

• дом плотника правее егеря;
• стоматолог проживает левее егеря;
• дом гитариста с самого краю;
• стоматолог живет рядом с гитаристом;
• Владимир не гитарист, и его дом не соседствует с гитаристом;
• дома Дмитрия и егеря соседние;
• здание, в котором прописан Андрей, правее стоматолога;
• между домами Андрея и Дмитрия один дом.

Чтобы рассуждать было проще, добавим изображение зданий, присвоим им номера:

Но стоматолог живет левее егеря, а правее егеря – плотник. Получается, что дом гитариста не может быть последним, а дом стоматолога не может быть предпоследними. То есть, егерь живет в предпоследнем доме:

Между домами Андрея и Дмитрия стоит один дом, значит, дом Андрея не может быть предпоследним, получается номер – 4, что автоматом исключает проживание там Дмитрия и Владимира.

Условие задачи заняло 2 предложения, а рассуждений получилось на 2 страницы.

Такой подход лучше не использовать, если условие сложное или много данных.

Табличный метод

Более удачным подходом к решению задач с большим количеством данных (несколько множеств), считается табличный, или графический (диаграммы).

Чтобы построить таблицу истинности логических выражений, следует:

• Разбить задачу на простейшие утверждения, которые обозначить символами (большие буквы латинского алфавита).
• Записать условие задачи, как составное выражение из символов логических операций.
• Нарисовать таблицу истинности для полученных данных.
• Выбрать такой вариант, при котором полученные значения подходят под условие.
• Проверить соответствие выбранного варианта и условия задачи.

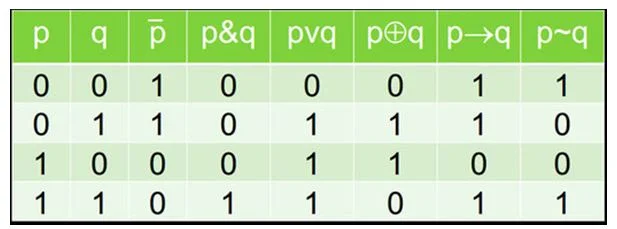
Чтобы преобразовывать условие задачи в логические выражения и операции, удобно пользоваться такой сводной таблицей истинности логических операций:

Рассмотрим тот же пример.

Определяем, что только гитарист может жить в первом доме, далее смотрим на заметки и условия и получаем таких жителей:

Метод компактнее, для некоторых задач нагляднее.

Построение таблиц истинности для различных типов задач

Несмотря на многообразие задач, многие условия повторяются, если оставить сухие формулы, не вникая в имена, места, профессии. Разобравшись с примером один раз, можно решать аналогичные задачи без труда. Рассмотрим несколько любопытных заданий, решив при помощи логически.

Пример 2.

Известно, что если первый студент летал в Англию на стажировку, то и второй тоже летал, но неправда, что если летал третий, то и второй.

Разобьём условие на 3 простые высказывания, присвоим им буквенные обозначения:

А — «Первый студент летал в Англию»;

В — «Второй студент летал в Англию»;

С — «Третий студент летал в Англию».

Запишем выясненные данные при помощи логических операций:

Пример 3.

Есть три 8-ых класса (А, В, С), которые соревнуются между собой за средний бал. Учителя в начале года сделали такие предположения:

• Если А получит максимальный бал, то максимальный бал получат Ви С.
• А и С получат или не получат максимальный бал одновременно.
• Необходимым условием получения высшего бала С класса является получение высшего бала В классом.

По завершении года оказалось, что 2 предсказания оказались верными, а одно – ошибочным.

Выясним, какие же классы добились высшего бала.

Разбиваем условие задачи на элементарные высказывания:

А – «А добьется высшего бала»;

В – «В добьется высшего бала»;

С – «С добьется высшего бала».

Запишем логические операции, описанные в примере:

Мы заполнили таблицу истинности для всех возможных значений исходных данных. В примере говорилось, что только 2 утверждения в конце года казались истинными, а 1- ложным. Такому условию отвечает 3-я строка в таблице.

Пример 4.

Во время знакомства девушка, любительница загадок, сказала, что ее имя узнать легко:

• последняя – гласная (Х1);
• или первая буква согласная (Х2)
• вторая – согласная (Х3).

¬(Х1→Х2)VХ3

Предложенные имена: Арина, Артур, Кэтрин, София.

Решим задачу, используя таблицу.

Сначала решим пошагово, выполняя операции по приоритету:

Указанному условию соответствует первое имя.

Пример 5.

Попробуем решать задачи, в которые нет четких высказываний, истинных или ложных. В них половина информации, правда, половина – ложь, при этом неизвестно, какая именно. Под такой тип задач можно подставить любое условие, но научившись решать его, можно разобраться со всеми аналогичными.

Известно, что в олимпиаде по химии участвовали 4 ученицы 8 класса: Марина, Света, Саша и Галя. Они заняли первые 4 места. Какое место заняла каждая из девочек, если есть их высказывания о победителях, но в них лишь половина информации правдива – первая или вторая половина предложения.

Маша Марина: «Саша заняла второе место, а Света – первое».

Полина Света: «Нет, это не так, Саша – победительница, а Галя, – на втором месте».

Ольга Саша: «Зачем вы всех путаете? Третье место за Мариной, а Света – на четвертом месте».

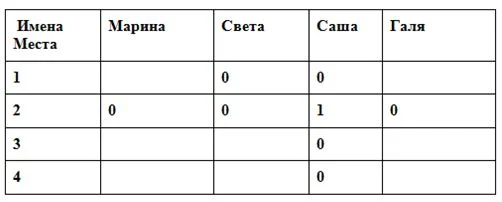
Составляем таблица для перебора вариантов. Правду обозначаем «1», ложь – «0».

Берем любое (Марины) утверждение и принимаем его первую часть за правду. Значит, Саша – 2 место, тогда Света не 1-ое (вторая половина фразы – ложь), остальных девочек на 2 место ставим «0».

Берем утверждение второй девочки. Так как Саша не может быть победительницей, то в этой фразе первая часть – ложь, а вторая должна быть истинной. Но в нем и вторая часть – неверна (второе место за Сашей, мы так приняли в начале).Уже на второй фразе получается противоречие всему.

Итог: Победительницей олимпиады стала Светлана, на втором месте – Галина, на третьем – Марина, на последнем из четырех – Александра.

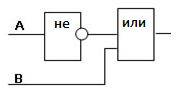
 Построение электронных схем, реализующих логические операции

Если рассмотреть электросхемы с точки зрения логики, особенно компьютерные, то их также можно описать при помощи «1» и «0» – электричество идет или не идет по проводам.

Попробуем нарисовать логические элементы схемы питания лампочки для нескольких простых операций.

Электросхема с конъюнктором

 Рассмотрим все варианты:

• Все контакты включены, тогда источник света горит.
• Первый контакт в положении «выключено» – свет не горит.
• Второй контакт выключен – лампа не светит.
• Все контакты отключены – свет не горит.

Заключение – эта электрическая цепь реализует операцию «И».

Дизъюнктор, схема электропитания

Рассмотрим этот вид электрической цепочки:

• Все контакты включены – лампа горит.
• Первый контакт включен, второй выключен – свет горит.
• Обратная ситуация – выключен первый, включен второй – лампа светится.
• Все контакты выключены – света нет.

Заключение – такой вид электросхем соответствует логической операции «ИЛИ».

Инвертор в электросхемах

В этой схеме переключатель не ручной, а автоматический. Здесь процесс обратный – когда ток не идет, контакты замыкаются, горит свет. Если же в сеть подается электричество, пластинка размыкается вследствие электромагнитной индукции, и сеть разъединяется – света нет.

Заключение: схема соответствует логической операции «НЕ».

Умение читать и решать логические операции, строить соответствующие электросхемы, позволяет создавать иерархически более сложные конструкции, которые используются для реализации процессов в современных ПК.

Обозначение логических элементов

Удобно создавать электросхемы в ПО SmartNotebook, которое используется с интерактивной доской.

Построение логического выражения

по заданной таблице истинности

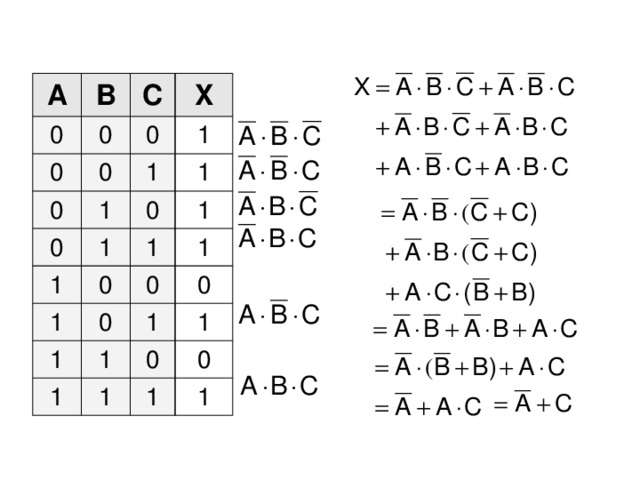
Пусть задана таблица истинности. Определить F(x, y, z).

1). В заданной таблице выбираются строки, в которых значение F = 1 .

x

y

0

0

z

0

F(x, y, z)

0

0

0

1

1

0

1

0

1

1

1

0

1

1

1

0

0

0

1

0

1

1

1

1

0

1

1

1

0

2). Для каждой строки, где F=1 записать конъюнкцию входных переменных. При этом те переменные, которые имеют значение 0 , записываются с отрицанием .

Например:

x*y*z

1-я строка:

3). Все полученные конъюнкции объединяются знаками дизъюнкции .

x

0

y

0

0

z

0

F(x, y, z)

0

0

1

1

0

1

1

1

1

0

1

0

1

1

1

0

0

0

1

1

0

1

1

0

1

1

1

0

x*y*z

1-я строка:

x*y*z

2-я строка:

x*y*z

3-я строка:

x*y*z

6-я строка:

x*y*z

7-я строка:

F(x,y,z) = x*y*z + x*y*z + x*y*z + x*y*z + x*y*z

F(x,y,z) = x*y*z + x*y*z + x*y*z + x*y*z + x*y*z=

= x*y*(z + z) + x*y*z + x*z*(y +y)=

= x*y*1 + x*y*z + x*z*1=

y*(x + x*z) + x*z=

= x*y + x*y*z + x*z=

x + z

=y*x + y*z + x*z

A

B

0

0

0

C

0

0

0

X

1

1

1

0

1

1

0

1

1

0

1

1

1

0

0

1

0

1

1

1

1

1

0

0

1

1

Что такое логический элемент?

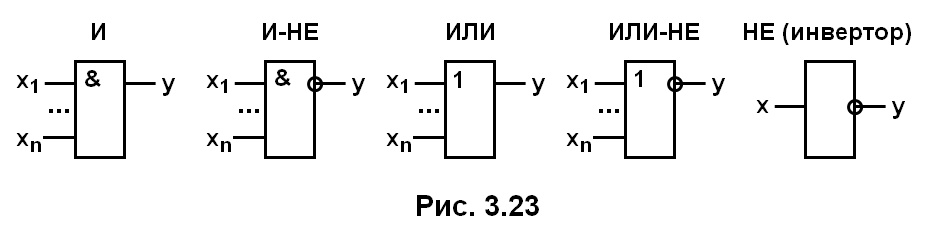
Логический элемент (логический вентиль) — это электронная схема, выполняющая некоторую простейшую логическую операцию. На рис. 3.23 приведены примеры условных графических обозначений некоторых логических элементов.

Логический элемент может быть реализован в виде отдельной интегральной схемы. Часто интегральная схема содержит несколько логических элементов.

Логические элементы используются в устройствах цифровой электроники (логических устройствах) для выполнения простого преобразования логических сигналов.

Рассмотрим наиболее широко используемую исторически сложившуюся классификацию. Она построена и с учетом того, какие электронные приборы являются основными в соответствующих интегральных схемах, и с учетом особенностей использованных схемотехнических решений.

Классы логических элементов

Выделяются следующие классы логических элементов (так называемые логики):

• резисторно-транзисторная логика (РТЛ);
• диодно-транзисторная логика (ДТЛ);
• транзисторно-транзисторная логика (ТТЛ);
• эмиттерно-связанная логика (ЭСЛ);
• транзисторно-транзисторная логика с диодами Шоттки (ТТЛШ);
• логика на основе МОП-транзисторов с каналами типа p(p-МДП);
• логика на основе МОП-транзисторов с каналами типа n(n-МДП);
• логика на основе комплементарных ключей на МДП-транзисторах (КМДП, КМОП);
• интегральная инжекционная логика И2Л;
• логика на основе полупроводника из арсенида галлия GaAs;

В настоящее время наиболее широко используются следующие логики: ТТЛ, ТТЛШ, КМОП, ЭСЛ. Устарела и практически не используется РТЛ. Для разрабатываемых в настоящее время устройств можно рекомендовать использовать КМОП-логику, а также логику на основе GaAs.

Логические элементы и другие цифровые электронные устройства выпускаются в составе серий микросхем. Серия микросхем — это совокупность микросхем, характеризуемых общими технологическими и схемотехнически­ми решениями, а также уровнями электрических сигналов и напряжения питания.

Приведенная классификация охватывает не только собственно логические элементы, но и другие цифровые устройства, в том числе микропроцессорные. Однако здесь следует учитывать, что при производстве сложных цифровых устройств некоторые логики не использовались и не используются.

Промышленные серии логики

Примеры серии микросхем:ТТЛ − К155, КМ155, К133, КМ133;ТТЛШ − 530, КР531, КМ531, КР1531, 533, К555, КМ555, 1533, КР1533;ЭСЛ − 100, К500, К1500;КМОП — 564, К561, 1564, КР1554;GaAs-К6500;

Каждая серия микросхем, несмотря на то, что она обычно содержит самые разнообразные цифровые устройства, характеризуется некоторым набором параметров, дающих достаточно подробное представление об этой серии. При определении этих параметров ориентируются именно на логические элементы — простейшие устройства серии микросхем. В соответствии с этим говорят о параметрах не серии микросхем, а о параметрах логических элементов данной серии.

Параметры логических элементов

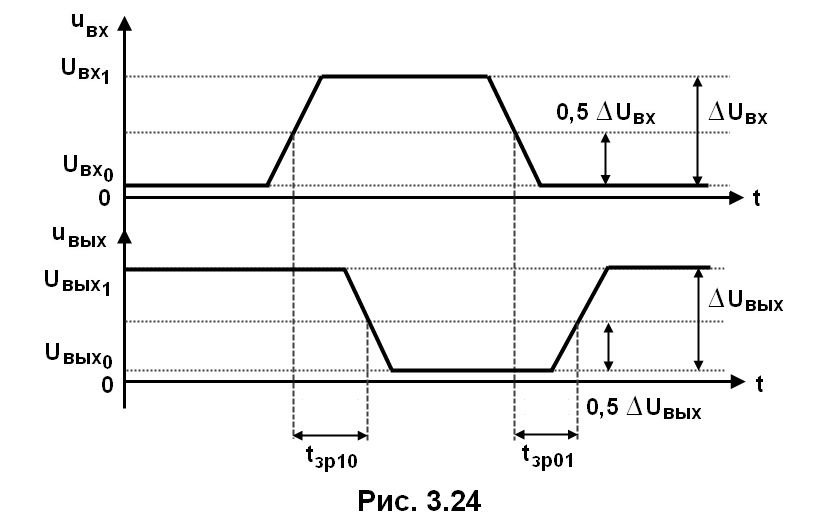
Быстродействие характеризуют временем задержки распространения сигнала tзр и максимальной рабочей частотой Fмaкс. Обратимся к идеализированным временным диаграммам, соответствующим элементу НЕ (инвертору) (рис. 3.24).

Через Uвхl и Uвыxl обозначены уровни входного и выходного напряжений, соответствующие логической единице, а через Uвх0 и Uвыx0 — соответствующие логическому нулю. Различают время задержки tзр10 распространения при переключении из состояния 1 в состояние 0 и при переключении из состояния 0 в состояние 1 — tзр01, а также среднее время задержки распространения tзр , причем

tзр = 0,5 · ( tзр10 + tзр01)

Васильев Дмитрий Петрович Профессор электротехники СПбГПУ

Время задержки принято определять по перепадам уровней 0,5∆Uвх и 0,5∆Uвыx. Максимальная рабочая частота Fмaкс — это частота, при которой сохраняется работоспособность схемы.

Нагрузочная способность характеризуется коэффициентом объединения по входу K оби коэффициентом разветвления по выходу Kраз (иногда используют термин «коэффициент объединения по выходу»). Величина K об — это число логических входов, величина K раз — максимальное число однотипных логических элементов, которые могут быть подключены к выходу данного логического элемента. Типичные значения их таковы:

Kоб= 2…8, K раз = 4…10. Для элементов с повышенной нагрузочной способностью K раз = 20…30.

Помехоустойчивость в статическом режиме характеризуют напряжением Uпст, которое называют статической помехоустойчивостью. Это такое максимально допустимое напряжение статической помехи на входе, при котором еще не происходит изменение выходных уровней логического элемента.

Важным параметром является мощность, потребляемая микросхемой от источника питания. Если эта мощность различна для двух логических состояний, то часто указывают среднюю потребляемую мощность для этих состояний.

Важными являются также следующие параметры:

• напряжение питания;
• входные пороговые напряжения высокого и низкого уровня Uвх1.порог и Uвх.0порог, соответствующие изменению состояния логического элемента;
• выходные напряжения высокого и низкого уровней Uвых1 и Uвых0.

Используются и другие параметры.

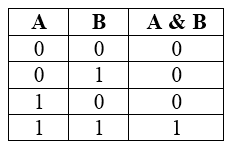
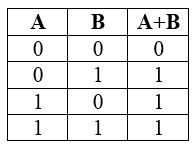
Конъюнкция или логическое умножение (в теории множеств – это пересечение)

Конъюнкция является сложным логическим выражением, которое истинно в том и только том случае, когда оба простых выражения являются истинными. Такая ситуация возможно лишь в единственном случае, во всех остальных случаях конъюнкция ложна.

Обозначение: &, $wedge$, $cdot$.

Таблица истинности для конъюнкции

Рисунок 1.

Свойства конъюнкции:

1. Если хотя бы одно из подвыражений конъюнкции ложно на некотором наборе значений переменных, то и вся конъюнкция будет ложной для этого набора значений.
2. Если все выражения конъюнкции истинны на некотором наборе значений переменных, то и вся конъюнкция тоже будет истинна.
3. Значение всей конъюнкции сложного выражения не зависит от порядка записи подвыражений, к которым она применяется (как в математике умножение).

Готовые работы на аналогичную тему

• 410 руб.Логические операции и их свойстваКурсовая работа
• 260 руб.Логические операции и их свойстваРеферат
• 220 руб.Логические операции и их свойстваКонтрольная работа

Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость

Дизъюнкция или логическое сложение (в теории множеств это объединение)

Дизъюнкция является сложным логическим выражением, которое истинно практически всегда, за исключением, когда все выражения ложны.

Обозначение: +, $vee$.

Таблица истинности для дизъюнкции

Рисунок 2.

Свойства дизъюнкции:

1. Если хотя бы одно из подвыражений дизъюнкции истинно на некотором наборе значений переменных, то и вся дизъюнкция принимает истинное значение для данного набора подвыражений.
2. Если все выражения из некоторого списка дизъюнкции ложны на некотором наборе значений переменных, то и вся дизъюнкция этих выражений тоже ложна.
3. Значение всей дизъюнкции не зависит от порядка записи подвыражений (как в математике – сложение).

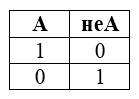
Отрицание, логическое отрицание или инверсия (в теории множеств это отрицание)

Отрицание — означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО и в итоге получаем, что если исходное выражение истинно, то отрицание исходного – будет ложно и наоборот, если исходное выражение ложно, то его отрицание будет истинно.

Обозначения: не $A$, $bar{A}$, $¬A$.

Таблица истинности для инверсии

Рисунок 3.

Свойства отрицания:

«Двойное отрицание» $¬¬A$ является следствием суждения $A$, то есть имеет место тавтология в формальной логике и равно самому значению в булевой логике.

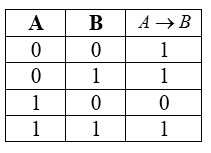
Импликация или логическое следование

Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть, данная логическая операция связывает два простых логических выражения, из которых первое является условием ($A$), а второе ($A$) является следствием условия ($A$).

Обозначения: $to$, $Rightarrow$.

Таблица истинности для импликации

Рисунок 4.

Свойства импликации:

1. $A to B = ¬A vee B$.
2. Импликация $A to B$ ложна, если $A=1$ и $B=0$.
3. Если $A=0$, то импликация $A to B$ истинна при любом значении $B$, (из лжи может следовать истинна).

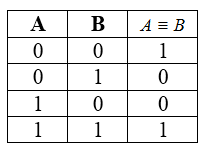
Эквивалентность или логическая равнозначность

Эквивалентность — это сложное логическое выражение, которое истинно на равных значениях переменных $A$ и $B$.

Обозначения: $leftrightarrow$, $Leftrightarrow$, $equiv$.

Таблица истинности для эквивалентности

Рисунок 5.

Свойства эквивалентности:

1. Эквивалентность истинна на равных наборах значений переменных $A$ и $B$.
2. КНФ $A equiv B = (bar{A} vee B) cdot (A cdot bar{B})$
3. ДНФ $A equiv B = bar{A} cdot bar{B} vee A cdot B$

Задача анализа логических схем

Задача анализа заключается в определении функции f, реализуемой заданной логической схемой. При решении такой задачи удобно придерживаться следующей последовательности действий.

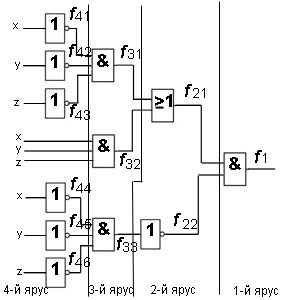
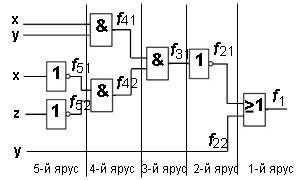
1. Логическая схема разбивается на ярусы. Ярусам присваиваются последовательные номера.
2. Выводы каждого логического элемента обозначаются названием искомой функции, снабжённым цифровым индексом, где первая цифра — номер яруса, а остальные цифры — порядковый номер элемента в ярусе.
3. Для каждого элемента записывается аналитическое выражение, связывающее его выходную функцию с входными переменными. Выражение определяется логической функцией, реализуемой данным логическим элементом.
4. Производится подстановка одних выходных функций через другие, пока не получится булева функция, выраженная через входные переменные.

Пример 1. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Решение. Разбиваем логическую схему на ярусы, что уже показано на рисунке. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z:

В итоге получим функцию, которую реализует на выходе логическая схема:

Таблица истинности для данной логической схемы:

x	y	z					f
1	1	1	0	1	1	1	1
1	1	0	0	0	0	1	0
1	0	1	0	0	0	1	0
1	0	0	0	0	0	1	0
0	1	1	0	0	0	1	0
0	1	0	0	0	0	1	0
0	0	1	0	0	0	1	0
0	0	0	1	0	1	0	0

Найти булеву функцию логической схемы самостоятельно, а затем посмотреть решение

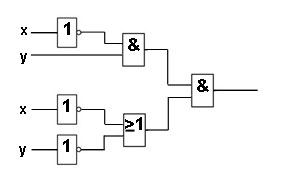
Пример 2. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Правильное решение и ответ .

Пример 3. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Продолжаем искать булеву функцию логической схемы вместе

Пример 4. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

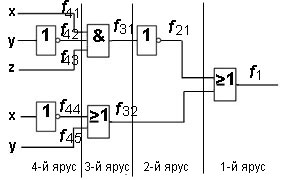
Решение. Разбиваем логическую схему на ярусы. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z:

В итоге получим функцию, которую реализует на выходе логическая схема:

Таблица истинности для данной логической схемы:

x	y	z			f
1	1	1	0	1	1
1	1	0	0	1	1
1	0	1	1	0	1
1	0	0	0	0	0
0	1	1	0	1	1
0	1	0	0	1	1
0	0	1	0	1	1
0	0	0	0	1	1

Пример 5. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

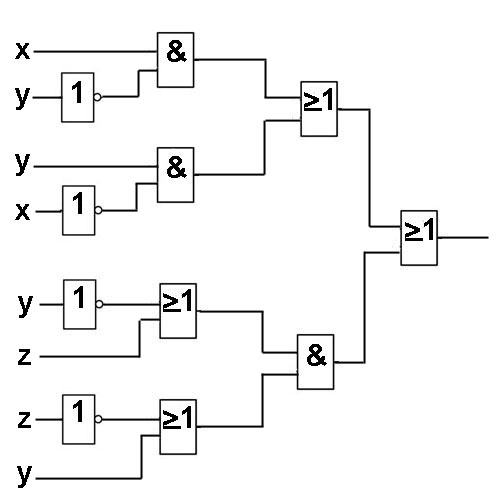
Решение. Разбиваем логическую схему на ярусы. Структура данной логической схемы, в отличие от предыдущих примеров, имеет 5 ярусов, а не 4. Но одна входная переменная — самая нижняя — пробегает все ярусы и напрямую входит в логический элемент в первом ярусе. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z:

В итоге получим функцию, которую реализует на выходе логическая схема:

Таблица истинности для данной логической схемы:

x	y	z			f
1	1	1	1	1	1
1	1	0	1	1	1
1	0	1	1	0	1
1	0	0	1	0	1
0	1	1	1	1	1
0	1	0	1	1	1
0	0	1	1	0	1
0	0	0	1	0	1

Задача синтеза логических схем в булевом базисе

Разработка логической схемы по её аналитическому описанию имеет название задачи синтеза логической схемы.

Каждой дизъюнкции (логической сумме) соответствует элемент «ИЛИ», число входов которого определяется количеством переменных в дизъюнкции. Каждой конъюнкции (логическому произведению) соответствует элемент «И», число входов которого определяется количеством переменных в конъюнкции. Каждому отрицанию (инверсии) соответствует элемент «НЕ».

Часто разработка логической схемы начинается с определения логической функции, которую должна реализовать логическая схемы. В этом случае дана только таблица истинности логической схемы. Мы разберём именно такой пример, то есть, решим задачу, полностью обратную рассмотренной выше задаче анализа логических схем.

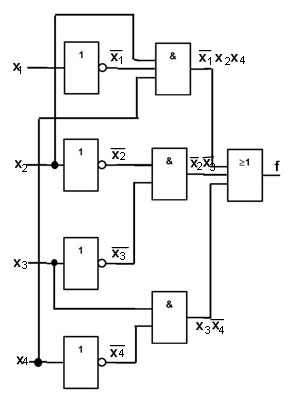
Пример 6. Построить логическую схему, реализующую функцию с данной таблицей истинности:

x	y	f
1	1	0
1	0	0
0	1	1
0	0	0

Решение. Разбираем таблицу истинности для логической схемы. Определяем функцию, которая получится на выходе схемы и промежуточные функции, которые на входе принимают аргументы x и y. В первой строке результатом реализации выходной функции при том, что значения входных переменных равны единицам, должен быть логический «0», во второй строке — при разных значениях входных переменных на выходе тоже должен быть логический «0». Поэтому нужно, чтобы выходная функция была конъюнкцией (логическим произведением).

Теперь подбираем промежуточные функции. Получаем следующую таблицу для промежуточных функций и выходной функции — конъюнкции промежуточных функций:

0	0	0
0	1	0
1	1	1
0	1	0

Для построения логической схемы необходимо элементы, реализующие логические операции, указанные в выходной функции, располагать в порядке, заданной этой функцией. Из выражения видно, что понадобятся 3 схемы «НЕ», две двухвходовых схемы «И» и одна двухвходовая схема «ИЛИ». В соответствии с выходной функцией получаем следующую логическую схему:

А теперь очередь дошла до функций алгебры логики четырёх переменных. Сначала выполним синтез логической схемы в булевом базисе.

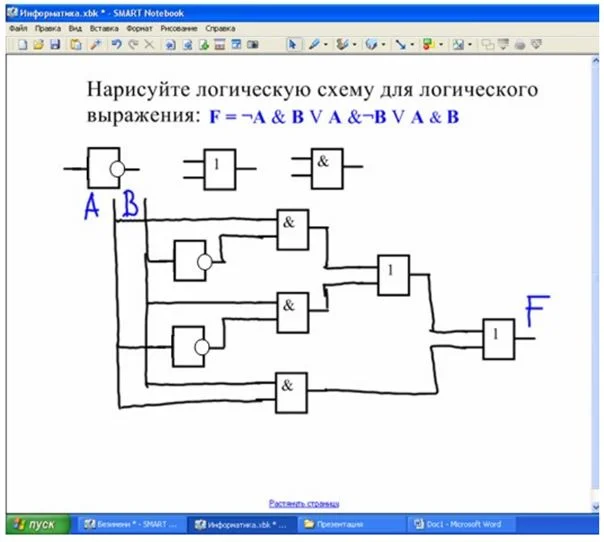
Пример 7. Построить в булевом базисе логическую схему, реализующую функцию алгебры логики

Решение. Для построения логической схемы потребуются 4 схемы «НЕ», одна трёхвходовая схема «И», 2 двухвходовые схемы «И» и одна трёхвходовая схема «ИЛИ». В соответствии с этим получаем следующую логическую схему:

Примеры решения задач «Логические основы работы компьютера»

Теория по этой теме по этой теме Пройти тестирование по этой теме Контрольная по этой теме

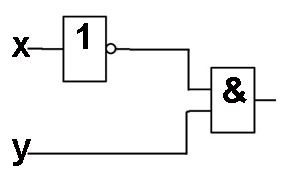
№1.

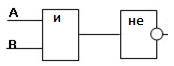
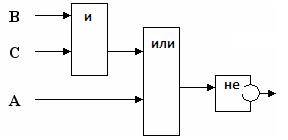
Дана логическая функция: F(А,В) = ¬ (А / В). Постройте соответствующую ей функциональную схему.

Решение:

Функциональная схема будет содержать 2 входа А и В. Рассмотрим логическое выражение и определим порядок действий в нем:

• первым  выполняется логическое умножение А / В, следовательно, сигналы с входов А и В подаются на конъюнктор;
• далее выполняется логическое отрицание ¬(А / В), следовательно, сигнал, полученный на выходе из конъюнктора должен быть инвертирован, т.е. подан на инвертор.

Выход инвертора является выходом функциональной схемы.

Изобразим схему, следуя данным действиям:

№2.

Определите логическую функцию, соответствующую заданной функциональной схеме:

Решение:

Функциональная схема содержит 2 входа А и В. Вход А инвертирован и его выход является входом дизъюнктора. Вход В подает сигнал на дизъюнктор. Выход дизъюнктора является выходом функциональной схемы.

Итак, последовательность действий:

• ¬A — сигнал входа А инвертирован;
• ¬A / B — на дизъюнктор подают инвертированный сигнал входа А и нормальный входа В.

Выход дизъюнктора является выходом функциональной схемы. Следовательно, логическая функция F –это функция двух переменных А и В и имеет вид:

F(A, B) = ¬A / B

Ответ: F(A, B) = ¬A / B

№3.

Постройте логическую схему, соответствующую логическому выражению и найдите значение логического выражения: F=A/B/ ¬C, если А=1, В=1, С=1.

Решение:

Значение логического выражения  — 1

№4.

Постройте логическую схему, соответствующую логическому выражению и найдите значение логического выражения: F= ¬(A/B/C),если А=0, В=1, С=1.

Решение:

Значение логического выражения  — 1

Примеры

Для закрепления материала можно попробовать составить таблицу истинности для ранее упомянутых логических выражений. Рассмотрим три примера:

• Штрих Шеффера.
• Стрелка Пирса.
• Определение эквивалентности.

Штрих Шеффера

Штрих Шеффера — это логическое выражение, которое можно записать в виде «не (А и Б)». Здесь две переменные, и два действия. Конъюнкция в скобках, значит, она выполняется первой. В таблице будет шапка и четыре строки со значениями переменных, а также четыре столбца. Заполним таблицу:

А	Б	А и Б	не (А и Б)
Л	Л	Л	И
Л	И	Л	И
И	Л	Л	И
И	И	И	Л

Отрицание конъюнкции выглядит как дизъюнкция отрицаний. Это можно проверить, если составить таблицу истинности для выражения «не А или не Б». Проделайте это самостоятельно и обратите внимание, что здесь будет уже три операции.

Стрелка Пирса

Рассматривая Стрелку Пирса, которая представляет собой отрицание дизъюнкции «не (А или Б)», сравним её с конъюнкцией отрицаний «не А и не Б». Заполним две таблицы:

А	Б	А или Б	не (А или Б)
Л	Л	Л	И
Л	И	И	Л
И	Л	И	И
И	И	И	Л

А	Б	не А	не Б	не А и не Б
Л	Л	И	И	И
Л	И	И	Л	Л
И	Л	Л	И	И
И	И	Л	Л	Л

Значения выражений совпали. Изучив два эти примера, можно прийти к выводу, как раскрывать скобки после отрицания: отрицание применяется ко всем переменным в скобках, конъюнкция меняется на дизъюнкцию, а дизъюнкция — на конъюнкцию.

Определение эквивалентности

Про утверждения А и Б можно сказать, что они эквивалентны, тогда и только тогда, когда из А следует Б и из Б следует А. Запишем это как логическое выражение и построим для него таблицу истинности. «(А эквивалентно Б) эквивалентно (из А следует Б) и (из Б следует А)».

Здесь две переменных и пять действий. Строим таблицу:

А	Б	В = (из А следует Б)	Г = (из Б следует А)	Д = А эквивалентно Б	Е = В и Г	Д эквивалентно Е
Л	Л	И	И	И	И	И
Л	И	И	Л	Л	Л	И
И	Л	Л	И	Л	Л	И
И	И	И	И	И	И	И

В последнем столбце все значения истинные. Это значит, что приведенное определение эквивалентности верно при любых значениях А и Б. Значит, оно всегда истинно. Именно так с помощью таблицы истинности можно проверить корректность любых определений и логических построений.

0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Выбираем строки, где
и
выписываем конъюнкции всех переменных,
при чем, если переменная в этом наборе
равна 1, то записываем ее саму, а если
переменная = 0, то ее отрицание.

Для данного примера

коньюнкция этих дизъюнкций и будет
искомой формулой:

Определение:Конъюнкция
называетсяэлементарной, если
все переменные, входящие в нее, различны.
Количество букв, входящих в элементарную
конъюнкцию или элементарную дизъюнкцию,
называетсярангом.

Число 1 считается элементарной конъюнкцией
ранга 0. Переменная считается элементарной
конъюнкцией или элементарной дизъюнкцией
ранга 1. Число 0 считается элементарной
дизъюнкцией ранга 0. Любую конъюнкцию
переменных, не являющуюся тождественно
ложной, можно привести к виду элементарной,
а любую дизъюнкцию букв, не являющуюся
тождественно истинной, также можно
привести к виду элементарной. Для этого
надо применить свойства коммутативности,
идемпотентности и ассоциативности
конъюнкции и дизъюнкции.

Строго доказано, что любую формулу
булевой алгебры можно выразить с помощью
операций , &,.
Интуитивно этот факт очевиден, вспомним
алгоритм составления формулы по таблице
истинности. При этом мы используем
только эти операции. Такая форма записи
называетсядизъюнктивной нормальной
формой(ДНФ). Это своеобразный механизм
нормализации формул алгебры логики.

Определение:ДНФ– это
дизъюнкция различных элементарных
конъюнкций (т.е. каждая конъюнкция
состоит из элементарных высказываний
или их отрицаний).

Аналогично определяется КНФ – коньюктивная
нормальная форма.

Определение:Если в ДНФ все
элементарные конъюнкции имеют один и
тот же ранг, равный числу переменных,
от которых зависит ДНФ, то она называетсясовершенной (СДНФ).

Теорема. Для любой функции, не
являющейся тождественно ложной,
существует и притом единственная СДНФ.

Следствие. Любую булеву функцию,
не являющуюся тождественно ложной можно
представить в виде суперпозиции&,,,
причем отрицание относится только к
переменным.

Определение:Система логических
операций называется функционально
полной, если с помощью этих операций и
констант этой системы можно представить
любую функцию булевой алгебры.

Системы {&,,};
{,};
{&,},{/}
– являются функционально полными

{&,}
– функционально неполная.

Мы примем эти факты без доказательства,
и решая задачи, будем стараться любую
формулу представить с помощью {&,,}.
Позже мы более подробно обсудим вопрос
функциональной полноты и неполноты
системы операций.

Тема 1.7. Методы упрощения логических выражений. Методы решения логических задач.

Рассмотрим пример решения логической
задачи.

Пример:

После обсуждения состава участников
экспедиции решено, что должны выполняться
два условия.

1. Если поедет Арбузов, то должны ехать
   Брюквин или Вишневский

2. Если поедут Арбузов и Вишневский то
   поедет Брюквин

Составить логическую формулу принятия
решения в символической форме, упростить
полученную формулу и сформулировать
по ней новое условие формирования
экспедиции.

Введём переменные и соответствующие
им элементарные высказывания.

— поедет Арбузов

— поедет Брюквин

— поедет Вишневский

Тогда выработанные условия формирования
экспедиции будут выглядеть следующим
образом:

1. 

2. 

Составим общую формулу и упростим
выражение

т.е. если поедет Арбузов, то поедет
Брюквин.

Пример:

Если завтра будет хорошая погода, то мы
пойдем на пляж или поедем в лес. Составим
формулу нашего поведения на завтра.

–
хорошая погода

– мы пойдем на пляж

– мы поедем в лес

Теперь построим отрицание этой фразы

т.о. получим высказывание «Завтра
будет хорошая погода, и мы не пойдем в
лес и на пляж.

Желающие могут построить таблицу
истинности и проверить это утверждение.

Пример:

По подозрению в совершенном преступлении,
задержаны Браун, Джон и Смит. Один из
них уважаемый в городе старик, второй
чиновник, а третий известный мошенник.
В ходе следствия старик говорил правду,
мошенник лгал, а третий задержанный в
одном случае говорил правду, а в другом
лгал.

Вот что они говорили:

Браун: Я совершил это. Джон не виноват.
(Б&Д)

Джон: Браун не виноват. Преступник Смит.
(Б&С)

Смит: Я не виноват. Виноват Браун (С&Б)

Опишем эти высказывания формально:

— преступление совершил Браун

— преступление совершил Джон

— преступление совершил Смит

Тогда их слова описываются следующими
выражениями:

Браун:

Джон:

Смит:

Т.к. по условиям задачи две из этих &ложны и одна истинна, то

Составим таблицу истинности

NN
1	0	0	0	0	0	0	0
2	0	0	1	0	1	0	1
3	0	1	0	0	0	0	0
4	0	1	1	0	1	0	1
5	1	0	0	1	0	1	1
6	1	0	1	1	0	0	1
7	1	1	0	0	0	1	1
8	1	1	1	0	0	0	0

1. Исключим из рассмотрения те наборы, на
   которых
   (по условию задачи одна из&- истинна, следовательно,)
   1, 3, 8

2. Исключим случай 5, т.к. в нем две &истинны, что противоречит условию
   задачи.

3. В случаях 4, 6, 7 у нас в начальном наборе
   две 1 , т.е. 2 преступника, а по условию
   задачи он один.

Остается только случай 2 , т.е. преступник
Смит, и оба его высказывания ложны.

следовательно–
ложно и—
истинно

=
1 – Джон уважаемый старик

Остается, что Браун чиновник, и поскольку
– ложно , то– истинно.

Пользуясь законами и тождествами булевой
алгебры можно упрощать логические
выражения.

Пример:

Упражнение:

(X&Y&Z)(X&Y&Z)X&Y

Соседние файлы в папке Коспект лекций

• #

  16.03.2016266 б10desktop.ini

• #

  16.03.201611.67 Кб10Folder.htt

• #
• #
• #
• #
• #
• #

Для любой логической формулы можно построить бесконечное количество равносильных ей формул. Для этого потребуется произвести некоторое количество тождественных преобразований. Одной из главных задач в алгебре логики является нахождение канонических форм формул. Проще говоря таких, которые построены по одному канону (правилу).

Форма представления какой-либо логической функции будет считаться нормальной, если она выражена через конъюнкцию, дизъюнкцию, а также отрицание переменных. Среди всех нормальных форм можно выделить совершенно нормальные. Это тот случай, когда функция может быть записана только одним единственным способом.

Классы СКНФ и СДНФ

В при решении задач в алгебре логики особая роль отводится классам конъюнктивных и дизъюнктивных совершенно нормальных форм. Они основаны на стандартных понятиях элементарной конъюнкции и дизъюнкции.

СКНФ

Форма любой логической формулы нормального типа не может содержать знаки эквивалентности, импликации, а также отрицания неэлементарных формул. Она может существовать только в двух видах:

• КНФ – конъюнктивная нормальная форма, представляющая собой конъюнкцию нескольких дизъюнкций. К примеру, [(A vee bar{B} vee C) wedge(A vee C)];
• ДНФ – дизъюнктивная нормальная форма, которая является дизъюнкцией нескольких конъюнкций. К примеру, [(A wedge bar{B} wedge C) vee(A wedge C)].

Правила построения СКНФ

В алгебре логики для любого набора переменных, при котором конечное значение функции становится нулевым, можно записать сумму. При этом переменные, имеющие числовые значение больше единицы, должны браться с отрицательным знаком.

Построение должно осуществляться по следующему алгоритму:

1. В таблице нужно отметить такие наборы переменных, при которых [f=1].
2. Для каждого выбранного набора переменных записываем КНФ, при этом если значение какой-либо из них равно 1, то она включается в неизменном виде, иначе – ее отрицание.
3. На последнем этапе все полученные конъюнкции следует связать операциями дизъюнкции.

СНДФ

Любую булеву формулу в алгебре логики, не являющуюся тождественно ложной, можно представить в виде СНДФ, но только в одном единственном виде.

Правила построения СДНФ

Если существует определённый набор переменных, при котором значение функции равно единице, то можно записать произведения, учитывая, что переменные, значение которых больше нуля, нужно брать с отрицанием.

Алгоритм построения будет следующим:

1. В таблице отмечаются все те наборы переменных, при которых [f=0]
2. Для каждого отмеченного набора всех переменных записывается ДНФ, при этом если значение какой-либо из них равно нулю, то включается сама переменная, в любом другом случае ее нужно инвертировать.
3. В конце все полученные дизъюнкции связываются друг с другом операциями конъюнкции.

Примеры нахождения СКНФ и СДНФ

Рассмотрим несколько примеров нахождения СКНФ и СДНФ с помощью данных таблицы истинности.