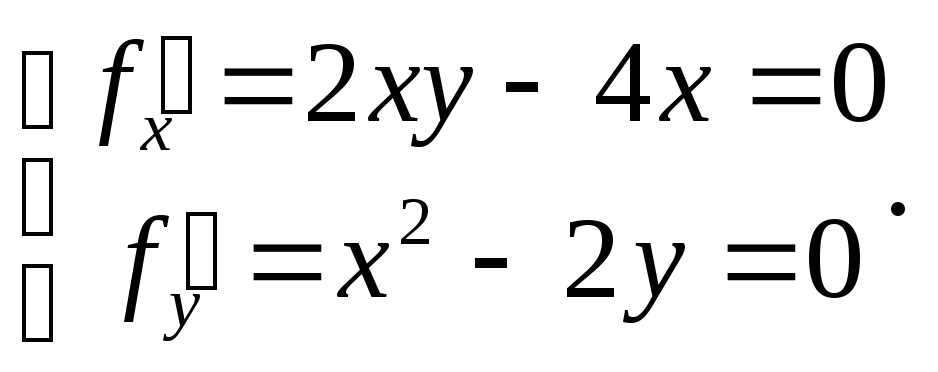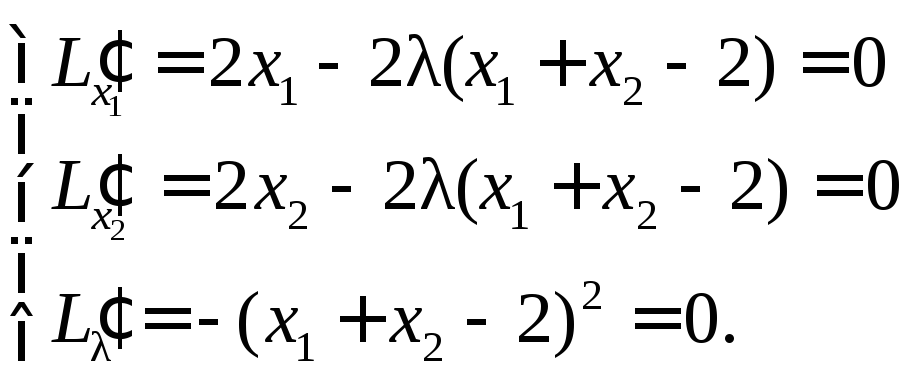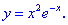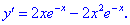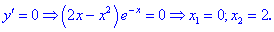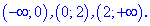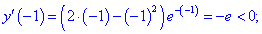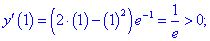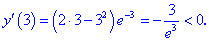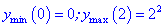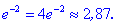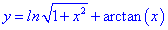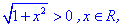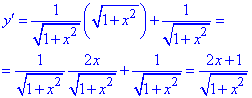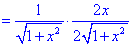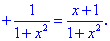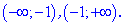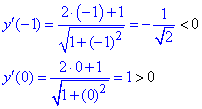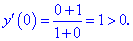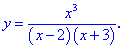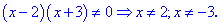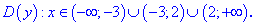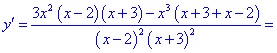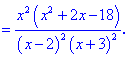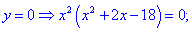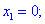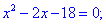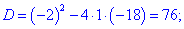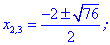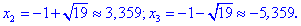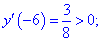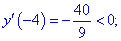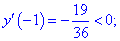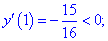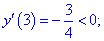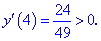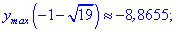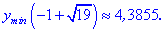Исследовать квадратичную форму
на
знакоопределенность.
Решение Матрица квадратичной формы имеет вид: .
Так
как один из угловых миноров равен нулю
и правило знаков (случай чередования
знаков) «мягко» нарушается, необходимо
исследовать знаки главных миноров:
В соответствии с критерием Сильвестра
квадратичная форма квазиотрицательна.
3.4. Схема отыскания локального экстремума
На основании
теоремы о признаках локального экстремума
можно предложить следующую схему
отыскания точек локального экстремума
дважды непрерывно дифференцируемой
функции:
10 Составляется система уравнений.
20Путем решения этой системы
находятся стационарные точкифункции
.
30Составляется матрица Гессе.
40Для каждой стационарной точкивычисляется
,
устанавливается ее знакоопределенность
(например, с помощью критерия Сильвестра)
и делается вывод относительно наличия
и квалификации экстремума (максимум
это или минимум).
50Вычисляются значения функциив точках экстремума.
Замечание
На практике иногда целесообразно
совмещать пункты 30и 40, а
именно начинать процедуру установления
знакоопределенности (вычислять угловые
миноры с помощью критерия Сильвестра)
в общем виде (не подставляя конкретных
значений).
Это может сократить объем вычислений
и сэкономить время.
Пример
Исследовать на экстремум функцию
.
Решение
10 Составим систему уравнений:
20Решим систему и найдем стационарные
точки функции:
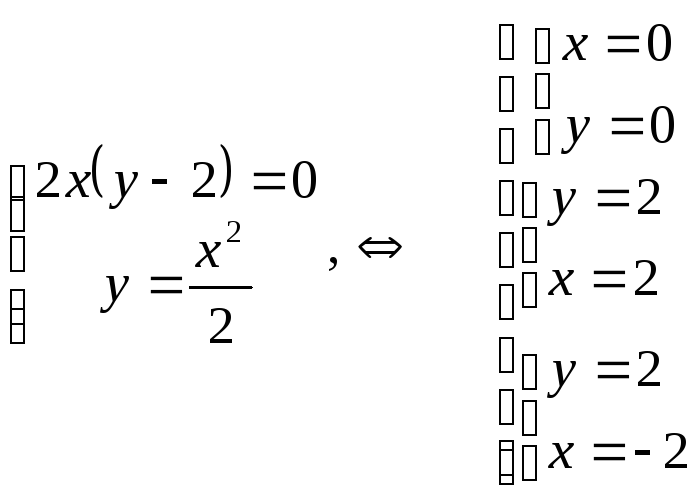
Таким образом, имеем три стационарные
точки: М1(0 ;0);М2(2 ;2)
иМ3(-2 ;2) –.
Рис. 3. График функции
;
указаны точки графика, соответствующие
стационарным точкам
30Составим матрицу Гессе:
.
40Для каждой стационарной точки
вычисляем значение матрицы Гессе,
устанавливаем ее знакоопределенность
и делаем вывод относительно наличия и
квалификации экстремума (максимум это
или минимум):
Нет экстремума, так как в случае максимума и в случае минимума угловой минор второго порядка должен быть неотрицательным. Нет экстремума.
50Вычисляем значения функциив точке экстремума:
В точке локального максимума М1(0;0):.
Посмотрим, является ли найденная точка
точкой глобального максимума. Чтобы
удостовериться в обратном, достаточно
найти значения переменных хиу,
при которых значение функции будет
больше, чем в точке локального максимума.
Покажем большее, а именно, что данная
функция вообще не имеет глобального
максимума. Положим,
ахустремим к.
Тогда, очевидно,.
А это означает, что функция не ограничена,
а значит не может иметь глобального
максимума.
-
Классические задачи математического
программирования
4.1. Постановка задачи
Так называется задача
отыскания
глобального экстремума целевой функции
нескольких (n) переменных
приmусловиях связи
(1m
<n), накладываемых
на эти переменные:


В этом случае допустимое множество
задачи имеет вид
.
Так же, как и при рассмотрении задач
безусловной оптимизации, будем считать,
что область определения функций
и
совпадает со всем пространством
.
Если же в области определения функцийили
появляются граничные точки, будем
относить эти задачи к задачам нелинейного
программирования. А причины возникновения
границ будем искать в существе
рассматриваемой экономической задачи,
что в математической модели должно
выражаться в виде наличия соответствующих
ограничений.
Всюду далее будем предполагать, что
и
–
дважды непрерывно дифференцируемые
функции в своей области определения.
Наглядное представление об условном
экстремуме и его отличии от безусловного
может дать следующий наглядный пример.
Предположим, что мы идем по тропинке на
склоне горы в направлении, указанном
стрелкой ( Рис. 4). Проекция
тропинки на горизонтальную плоскость
представляет собой некоторую линию
.
Когда мы идем по тропинке, проекция
нашего положения на ней перемещается
вдоль этой линии. Слева от тропинки
поверхность горы поднимается вверх,
справа – опускается вниз. Целевая
функция– высота нашего положения над уровнем
моря. Сама тропинка идет то вниз, то
вверх в зависимости от рельефа горы.
Вершина горы находится в точке– это наивысшая точка. На горизонтальной
плоскости ей соответствует точкабезусловного экстремума функции
.
Но нас интересует только тропинка. Если
мы спускаемся вниз по ней, а затем
поднимаемся вверх, то в точкахи
,
где спуск сменяется подъемом (точкии
на тропинке), располагается точка
условного минимума. А в точке,
в которой подъем сменяется спуском
(точкана тропинке), располагается точка
условного максимума. Условного – потому
что нашим условием является рассмотрение
только точек, находящихся на линии,
т.е. когда мы находимся на тропинке. Нас
совершенно не интересует, что находится
слева и справа от нее, хотя слева всегда
есть точки и повыше, а справа – пониже,
чем на тропинке.
Рис. 4. Наглядная иллюстрация
понятия условного экстремума
Замечание 1.В классической задаче
математического программирования
рассматривается случай, когда число
связей меньшеn,
поскольку, как правило, введение каждой
новой связи ведет к уменьшению размерности
задачи на единицу. Таким образом, уже
приnсвязях размерность
задачи (допустимого множества), как
правило, была бы равна нулю (отдельные
точки), а при большем числе связей
допустимое множество вообще будет
пустым. Хотя возможны исключения и в
ту, и в другую стороны: приразмерность допустимого множества
может оказаться положительной, а придопустимое множество может оказаться
пустым.
Замечание 2.Рассматриваемые далее
методы решения классической задачи
математического программирования
предполагают поиск локальных экстремумов
во внутренних точках общей области
определения целевой функции
и всех функций связи
.
Разумеется, что при этом рассматриваемые
точки должны удовлетворять условиям
связи
Глобальный экстремум (если он существует)
следует искать среди точек локального
экстремума. Однако напомним, что
глобальный максимум (наибольшее значение)
и глобальный минимум (наименьшее
значение) могут не существовать, несмотря
на наличие локальных экстремумов. Из
этого следует, что прежде, чем искать
глобальный экстремум, нужно убедиться
в его существовании.
В простейших
случаях задача отыскания точек локального
условного экстремума может быть решена
методом исключения переменных: часть
переменных выражается из условий связи
(решается система ) и полученные
выражения подставляются в целевую
функцию – см. примеры 1 – 3. Данный метод
наиболее прост для использования, когда
условия связи представляют собой
линейные уравнения (системы).
Пример
Найти
точки условного экстремума и экстремальные
значения функции
при условии
.
-
Признаки
условного локального экстремума
В более сложных случаях (когда решение
системы затруднено) отыскание точек
локального условного экстремума может
быть осуществлено методом Лагранжа.
Метод Лагранжа основывается на
использовании вспомогательной функции,
называемой функцией Лагранжа, или
лагранжианом:
,
или в скалярной записи:
.
Компоненты вектора
называются
множителями Лагранжа.
Очевидно, при выполнении условия связи
(т.е. всюду на допустимом множестве)
значения функции Лагранжа не зависят
оти
совпадают со значениями целевой функции:.
Таким образом, задача нахождения
условного максимума (минимума) функцииэквивалентна задаче нахождения (условного
же!) максимума (минимума) функциипри том же условии связи
на переменные
.
Выведем
необходимые, а также достаточные условия
существования условного локального
экстремума. При этом будем предполагать.
Что мы имеем дело с внутренней точкой
общей области определения функций
и
.
Вначале на примере функции двух переменных
при одном условии связи будет
продемонстрирована идея вывода, а затем
сформулирована соответствующая теорема.
4.2.1.Идея вывода необходимого условия I
порядка.Продемонстрируем идею вывода
необходимого условия I порядка для
функции двух переменных и одного
уравнения связи:,
поскольку этот случай допускает
наглядную графическую иллюстрацию.
Тогда задача примет вид: найти локальные
экстремумы функциипри условии связи
.
В
типичном случае условие связи представляет
собой некоторую кривую на плоскости
(линию уровня функции
)
– Рис. 5. Градиент функции(если
он не нулевой!) направлен, как известно,
перпендикулярно к линии уровня (в одну
из двух сторон). Посмотрим, какое
направление может иметь градиент целевой
функциив точке экстремума.
Рис. 5. Соотношение возможных и
невозможных (приведены в скобках)
направлений градиентов целевой функции
и функции, описывающей условие связи,
в точке экстремума
Нетрудно
видеть, что если
направлен под углом к
(не
равным нулю и 1800), то ни максимума,
ни минимума в рассматриваемой точке
быть не может, поскольку в этом случае
в одном из направлений вдоль линии
уровняцелевая функция будет возрастать, а в
противоположном – убывать. Таким
образом,обязан быть коллинеарным с
.
А это означает, что существует некоторое
(положительное, отрицательное или даже
нулевое – если=0) число
такое, что
.
Последнее
равенство можно представить в виде:
,
или,
где
обозначает градиент функции по переменным
и
(
считается параметром, т.е. константой).
Очевидно, условие
коллинеарности градиентов:
может выполняться не только на линии
уровня,
но и на других линиях уровня вида.
Поэтому, чтобы исключить такие лишние
решения уравнения , к нему целесообразно
добавить условие принадлежности точки
допустимому множеству:.
Это условие, очевидно, можно записать
как,
или как
.
Это
также является одним из необходимых
условий. Собирая вместе условия и ,
получим новое необходимое условие –
систему уравнений для нахождения точек,
подозрительных на условный локальный
экстремум:
.
При
решении системы (4) мы находим не только
«подозрительные» точки
,
но и множители Лагранжа,
которые, вообще говоря, не имеют отношения
к конечной цели решения математической
задачи – нахождения точек условного
экстремума. Однако, как мы увидим в
дальнейшем, множители Лагранжа играют
важную роль в экономических задачах.
Обратим
внимание на то, что в левой части
уравнения стоит градиент функции
Лагранжа от трех переменных, причем
формально никаких условий связи на
переменные хиу не накладывается.
Это означает, что при вычислении этого
градиента не нужно решать уравнениеотносительно,уили
,
т.е. находить функцию
или
и подставлять ее в
.
Таким образом, решение уравнения дает
нам множество безусловных стационарных
точек функции Лагранжа. В этом и состоит
главное достоинство и смысл метода
Лагранжа.
Безусловность стационарных точек
означает, что они ищутся в пространстве
без учета (в явном виде) условия связи
переменных,
т.е. при вычислении частных производных
все переменные считаются независимыми.
Условия связи,
как уже отмечалось, учитывается при
решении системы (4), в которую входит, в
частности, уравнение,
что равносильно этому условию связи.
Тем самым гарантируется, что при решении
системы (4) мы получим только точки из
допустимого множества.
4.2.2. Условие Якоби.Единственным
ограничением, которое мы наложили при
выводе данного необходимого условия,
является неравенство нулю градиента
функции.
Это ограничение называетсяусловием
Якоби. Очевидно, если условие Якоби
не выполняется, то не удастся подобрать
такого,
чтобы выполнялось равенство(за исключением случая
).
Для случая большего числа ограничений
условие Якоби выглядит как линейная
независимость градиентов.
Покажем, что требование выполнения
условия Якобисущественно, т.е. при
его нарушении условие первого порядка
(4) не является необходимым.
Пример
Пусть требуется отыскать условный
экстремум функции
при условии связи
(рис.5).
а)
б)
Рис. 6. Иллюстрация к примеру 1: а)
функция, задающая условие связи; жирной
прямой линией показано допустимое
множество; б) целевая функция: жирной
кривой линией показан график целевой
функции в пределах допустимого множества
Решая эту задачу методом исключения
переменной:
,
получим:
.
Эта функция, очевидно, имеет минимум в
точке
,
а значит, функцияf
при указанном условии связи имеет
минимум в точке (1;1). Значение целевой
функции в точке минимума.
Попробуем решить эту задачу методом
Лагранжа.
Составим функцию Лагранжа:
.
Выпишем необходимые условия первого
порядка:
Из последнего равенства получаем
.
С учетом этого, из первого равенства
имеем,
а из второго:.
Возвращаясь к третьему, получим: 4 = 0,
т.е. система несовместна. Таким образом,
в данном случае метод Лагранжа не выявил
точку условного минимума.
В чем причина? А причина, оказывается,
в том, что в этой точке (как, впрочем, и
на всем допустимом множестве
)
градиент функцииgравен нулю, т.е. условие Якоби не
выполняется:
.
Как быть в таком случае?
В данном случае видно, что, не изменяя
существа задачи (допустимого множества),
можно упростить условие связи, т.е.
вместо заданного взять эквивалентное
ему:
.
В этом случае градиент
не обращается в нуль нигде, и метод
Лагранжа дает:
откуда
,
т.е. в этом случае потери стационарной
точки не происходит.
В данном случае указанное выше упрощение
условия связи очевидно. Однако так
обстоит дело далеко не всегда. Даже в
этом примере, если в условии связи
раскрыть скобки, не сразу видно, как
упростить выражение
.
Как уже говорилось, в общем случае
ограничений
выполнение
условия Якоби в точке
означает, что градиенты функций
линейно независимы, т.е. не существует
нетривиальной линейной комбинации.
Это равносильно
тому, что матрица частных производных
этих функций имеет в точке
ранг
(т.е. матрица полного ранга):

4.2.3. Идея вывода условий II
порядка. Проиллюстрируем вывод
необходимого условияIIпорядка и достаточного условия. Будем
при этом считать, что необходимое условие
I порядка уже обосновано. Оно войдет,
естественно, и в общее необходимое
условие, и в достаточное условие.
Воспользуемся тем же приемом, которым
мы доказывали необходимое и достаточное
условия для безусловного экстремума –
разложением по формуле Тейлора. Однако
в данном случае мы будем раскладывать
не целевую функцию, а функцию Лагранжа
(которая на допустимом множестве
совпадает с целевой функцией) и учитывать,
что ее максимум рассматривается не во
всей окрестности, а лишь на допустимом
множестве
.
Доказательство будем проводить для
условного локального максимума. Для
доказательства теоремы о минимуме
достаточно рассмотреть функцию
,
применить к ней теорему о максимуме и
затем «пересчитать» полученные
соотношения для.
Будем предполагать, что
и
– дважды непрерывно дифференцируемые
функции в некоторой окрестности точкиОчевидно, таким же свойством обладает
и функция.
Таким образом, в некоторой (полной)
окрестности,
т.е. для,
можно написать разложение по формуле
Тейлора до членов второго порядка
включительно:
,
или, так как
:
.
В соответствии с определением условного
локального максимума необходимо и
достаточно, чтобы в некоторой окрестности
рассматриваемой точки
для любого
,
для которого,
выполнялось условие:,
т.е.
(для строгого
максимума – знак неравенства строгий:
«<» при
).
Итак, наличие условного локального
максимума в точке
эквивалентно выполнению условия .
Применяя рассуждения, аналогичные тем,
что использовались для безусловного
экстремума, можно показать, что из
вытекает–для
необходимости и– для достаточности.
Более тонкий анализ показывает, что
условие
может быть заменено на более удобное
для использования линейное условие.
Проиллюстрируем существо отличия
векторов
в условиях
и
.
В первом случае берутся такие векторы,
что точкипринадлежат допустимому множеству. Во
втором случае векторнаправлен по касательной к поверхности
уровня(он перпендикулярен ко всем градиентам
)
– Рис. 7. Ясно, что когда,
векториз условия
будет стремиться к вектору
из условия
.
Рис. 7. Иллюстрация различия между
векторамив условиях
(а)
и
(б)
4.2.4. Теорема о
признаках условного локального
экстремума.Приведенные рассуждения
приводят к следующей теореме.
Соседние файлы в папке МОРы хсехелп
- #
- #
- #
- #
- #
- #
12. Исследование функций с помощью производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Поиск точек экстремума локального минимума и максимума функций
(blacktriangleright) Если функция задана как частное двух других функций, то [{Large{left(dfrac fgright)’=dfrac{f’cdot
g-fcdot g’}{g^2}}}]
(blacktriangleright) Для того, чтобы найти точки экстремума, необходимо схематично изобразить график функции.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).
[begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]
Задание
1
#881
Уровень задания: Равен ЕГЭ
Найдите точку локального минимума функции
(y = -dfrac{x^2 + 2016^2}{x}).
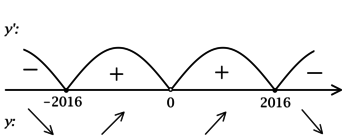
ОДЗ: (x neq 0). Решим на ОДЗ:
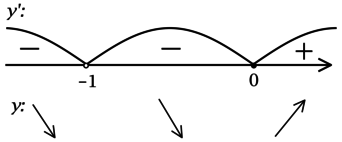
1) [y’ = -dfrac{2x^2 — (x^2 + 2016^2)}{x^2} = dfrac{2016^2 — x^2}{x^2}.]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует):
[dfrac{2016^2 — x^2}{x^2} = 0qquadLeftrightarrowqquad x^2 = 2016^2] – на ОДЗ, откуда находим корни (x_1 = -2016, x_2 = 2016). Производная функции (y) не существует при (x = 0), но (x = 0) не входит в ОДЗ. Таким образом, [y’ = dfrac{(2016-x)(2016+x)}{x^2}.] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
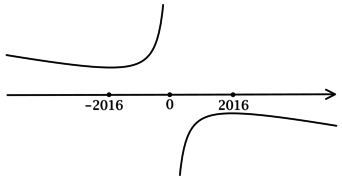
3) Эскиз графика (y):
Таким образом, (x = -2016) – точка локального минимума функции (y).
Ответ: -2016
Задание
2
#882
Уровень задания: Равен ЕГЭ
Найдите точку локального максимума функции
(y = dfrac{3,2}{x} + 5x + 1024).
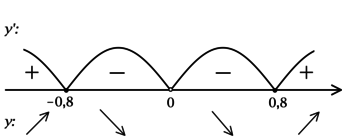
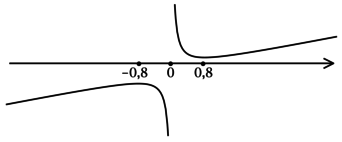
ОДЗ: (x neq 0). Решим на ОДЗ:
1) [y’ = -dfrac{3,2}{x^2} + 5 = dfrac{5x^2-3,2}{x^2} = 5dfrac{x^2 — 0,64}{x^2}.]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [5dfrac{x^2 — 0,64}{x^2} = 0qquadLeftrightarrowqquad x^2 — 0,64] – на ОДЗ, откуда находим корни (x_1 = -0,8, x_2 = 0,8). Производная функции (y) не существует при (x = 0), но (x = 0) не входит в ОДЗ. Таким образом, [y’ = 5dfrac{(x — 0,8)(x + 0,8)}{x^2}.] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = -0,8) – точка локального максимума функции (y).
Ответ: -0,8
Задание
3
#6920
Уровень задания: Равен ЕГЭ
Найдите точку локального максимума функции
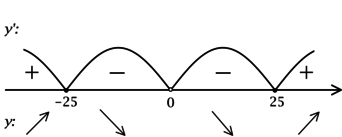
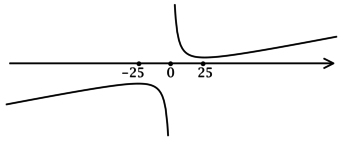
(y = dfrac{3x^2 + 1875}{x}).
ОДЗ: (x neq 0). Решим на ОДЗ:
1) [y’ = dfrac{6x^2 — (3x^2 + 1875)}{x^2} = dfrac{3x^2 —
1875}{x^2} = 3cdot dfrac{x^2 — 625}{x^2}.]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [3cdot dfrac{x^2 — 625}{x^2} = 0qquadLeftrightarrowqquad x^2-625=0, xne 0] – на ОДЗ, откуда находим корни (x_1 = 25, x_2 = -25). Производная функции (y) не существует при (x = 0), но (x = 0) не входит в ОДЗ. Таким образом, [y’ = 3cdot dfrac{(x — 25)(x + 25)}{x^2}.] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = -25) – точка локального максимума функции (y).
Ответ:
-25
Задание
4
#884
Уровень задания: Равен ЕГЭ
Найдите точку локального минимума функции
(y = dfrac{e^x}{x + 1}).
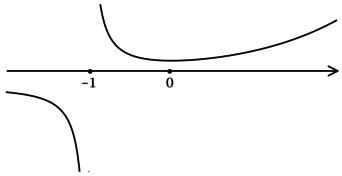
ОДЗ: (x neq -1). Решим на ОДЗ:
1) [y’ = e^xleft(dfrac{1}{x + 1} — dfrac{1}{(x + 1)^2}right) = dfrac{e^x}{(x + 1)^2}x.]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{e^x}{(x + 1)^2}x = 0qquadLeftrightarrowqquad x = 0] – на ОДЗ (так как (e^{x} > 0) при любом (x)). Производная функции (y) не существует при (x = -1), но (x = -1) не входит в ОДЗ. Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = 0) – точка локального минимума функции (y).
Ответ: 0
Задание
5
#2359
Уровень задания: Равен ЕГЭ
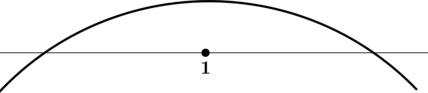
Найдите точку максимума функции (y = dfrac{x}{e^x}).
ОДЗ: (x) – произвольный.
1) [y’ = dfrac{1cdot e^x — e^xcdot x}{e^{2x}} = dfrac{1 — x}{e^x}]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{1 — x}{e^x} = 0qquadLeftrightarrowqquad x = 1,.] Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика:
Таким образом, (x = 1) – точка максимума функции (y).
Ответ: 1
Задание
6
#2360
Уровень задания: Равен ЕГЭ
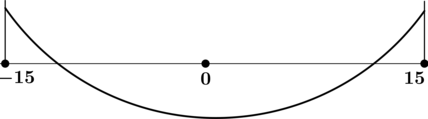
Найдите точку минимума функции (y = dfrac{x^2 — 1}{x^2 + 1}) на отрезке ([-15; 15]).
ОДЗ: (x) – произвольный.
1) [y’ = dfrac{2xcdot (x^2 + 1) — 2xcdot(x^2 — 1)}{(x^2 + 1)^2} = dfrac{4x}{(x^2 + 1)^2}]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{4x}{(x^2 + 1)^2} = 0qquadLeftrightarrowqquad x = 0,.] Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-15; 15]):
4) Эскиз графика на отрезке ([-15; 15]):
Таким образом, (x = 0) – точка минимума функции (y) на отрезке ([-15; 15]).
Ответ: 0
Задание
7
#2361
Уровень задания: Равен ЕГЭ
Найдите точку минимума функции (y = dfrac{x^2}{x^3 + 1}) на промежутке ((-1; 1]).
ОДЗ: (xneq -1).
1) [y’ = dfrac{2x(x^3 + 1) — 3x^2cdot x^2}{(x^3 + 1)^2} = dfrac{-x^4 + 2x}{(x^3 + 1)^2}]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{-x^4 + 2x}{(x^3 + 1)^2} = 0qquadLeftrightarrowqquad
left[
begin{gathered}
x = 0\
x = sqrt[3]{2}
end{gathered}
right.] Производная не существует при (x = — 1).
2) Найдём промежутки знакопостоянства (y’):
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом промежутке ((-1; 1]):
4) Эскиз графика на промежутке ((-1; 1]):
Таким образом, (x = 0) – точка минимума функции (y) на промежутке ((-1; 1]).
Ответ: 0

УСТАЛ? Просто отдохни
Отыскание локальных максимумов и минимумов не обходится без дифференцирования и является необходимым при исследовании функции и построении ее графика.
Точка 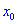
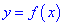
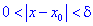
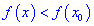
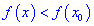
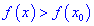
Точки максимума и минимума называются точками экстремума функции, а значения функции в экстремальных точках — ее экстремальными значениями.
НЕОБХОДИМОЕ УСЛОВИЕ ЛОКАЛЬНОГО ЭКСТРЕМУМА:
Если функция имеет в точке 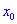
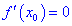
Точки которые удовлетворяют выписанным выше требованиям называют критическими точками.
Однако в каждой критической точке функция имеет экстремум. Ответ на вопрос: будет критическая точка точкой экстремума дает следующая теорема.
ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА ФУНКЦИИ
Теорема І. Пусть функция 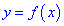
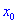
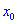
Тогда для точки 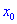
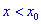
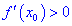
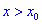
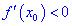
Если же для 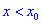
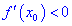
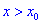
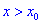
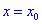
Теорема ІІ. Пусть функция дважды дифференцируема в окрестности точки 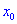
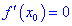
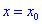
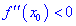
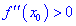
Если же вторая производная равна нулю 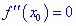
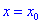
При исследовании функций на экстремумы используют обе теоремы. Первая на практике проще, поскольку не требует нахождения второй производной.
ПРАВИЛА НАХОЖДЕНИЯ ЕКСТРЕМУМОВ (МАКСИМУМОВ И МИНИМУМОВ) С ПОМОЩЬЮ ПЕРВОЙ ПРОИЗВОДНОЙ
1) найти область определения 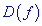
2) найти первую производную 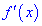
3) найти критические точки;
4) исследовать знак производной 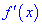
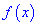
При этом критическая точка 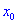
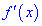
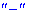

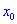
Вместо данного правила можно определять вторую производную 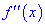
5) вычислить значения функции в точках экстремума.
Рассмотрим теперь исследование функции на экстремумы на конкретных примерах.
————————————
Примеры.
Сборник В.Ю. Клепко, В.Л. Голец «Высшая математика в примерах и задачах»
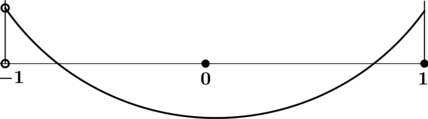
1. (4.53.7)
1) Областью определения будет множество действительных чисел
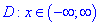
2) Находим производную
3) Вычисляем критические точки
Они разбивают область определения на следующие интервалы
4) Исследуем знак производной на найденных интервалах методом подстановки значений
Таким образом первая точка 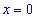
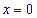
5) Вычисляем значение функции
——————————
2. (4.53.9)
1) Областью определения будет множество действительных чисел 
и функция арктангенс определена на всей действительной оси.
2) Находим производную
3) С условия равенства производной нулю находим критическую точку
Она разбивает область определения на два интервала
4) Определим знак производной в каждой из областей
Таким образом находим, что в критической точке 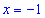
5) Вычислим экстремум функции
——————————
3. (4.53.13)
1) Функция определена когда знаменатель не превращается в ноль
Из этого следует, что область определения состоит из трех интервалов
2) Вычисляем производную
3) Приравниваем производную к нулю и находим критические точки.
4) Устанавливаем знак производной в каждой из областей, подстановкой соответствующих значений.
Таким образом точка 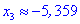
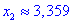
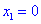
5) Находим значение в критических точках
Несмотря на то, что значение функции 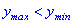
———————————————-
Посмотреть материалы:
- Исследования функции и построения графика
- Интервалы монотонности функции
- Наибольшее и наименьшее значение функции на отрезке
- Выпуклость и вогнутисть графика функции
- Асимптоты функции
- Область определения функции