Как найти ломаную квадрата

а) Даже вычисление площади самого квадрата кажется неприступной задачей. Но заметим, что ломаная змейкой «вертится» вокруг диагонали (АС). Может, попробовать «распрямить» ее? Для этого рассмотрим прямоугольный треугольник (AEC), гипотенуза которого равна диагонали (АС) квадрата (ABCD), а катеты параллельны звеньям ломаной (рис. 2). Тогда катеты легко найти: (АЕ=1+3+5+7+9+11=36), (ЕС=2+4+6+8+10=30), и по теореме Пифагора (AC^2=36^2+30^2=2196). Значит, гипотенуза (AC=sqrt{2196}).

Зная диагональ квадрата, можно вычислить его сторону: она в (sqrt2) раз меньше диагонали и равна (sqrt{2196}/sqrt2=sqrt{1098}). Заметим, что (sqrt{1098}=sqrt{9+1089}=sqrt{3^2+33^2}). Это означает, что сторона (AB) равна гипотенузе прямоугольного треугольника с катетами 3 и 33 или утроенной гипотенузе прямоугольного треугольника с катетами 1 и 11. А из этого следует, что вершины квадрата (ABCD) лежат в узлах квадратной сетки.

Как говорилось в подсказке, палеточный метод вычисления площадей заключается в том, что фигуру, площадь которой требуется найти, можно накрыть палеткой — прозрачной пленкой, которая расчерчена на единичные квадратики, — и посчитать число клеток, попавших в фигуру. Обычно с помощью палетки вычисляют приближенное значение площади. В нашем же случае вершины квадрата попали в узлы палетки, поэтому звенья ломаной 1-2-3-…-11 будут идти по линиям сетки, и мы вычислим точные значения площадей (рис. 3).

Естественно, не обязательно использовать реальную палетку — можно воспользоваться каким-либо графическим редактором. Для этого надо нарисовать квадрат с ломаной и отдельно квадратную сетку, после чего наложить сетку на наши фигуры и определить площади желтой и зеленой частей квадрата.

Удобнее всего найти площадь зеленой части, если разбить ее на два прямоугольных треугольника и пять прямоугольников (см. рис. 3): (S_{text зел} = 2cdotleft(frac12cdot3cdot33right) +3cdot2+5cdot6+7cdot12+9cdot20+8cdot30=639).

Учитывая, что площадь квадрата равна 1098, находим площадь его желтой части: (S_{text жел}=1098-639=459), поэтому отношение площадей равно 459/639. После сокращения получим 51/71.

б) Решение пункта а) обобщается и на задачу в общем виде для произвольного нечетного числа (n=2k-1).

Диагональ (АС) можно найти с помощью теоремы Пифагора как гипотенузу прямоугольного треугольника (АСЕ), в котором катет (AE=1+3+5+ldots+(2k-1)), то есть равен сумме первых (k) нечетных чисел.

Напомню, что эта сумма легко вычисляется с помощью геометрической интерпретации (рис. 4). Очевидно, что в квадрате со стороной (k), разбитом на единичные квадратики, общее число квадратиков равно (k^2), но если их считать группами, образующими синие и белые уголки, то легко видеть, что эта сумма равна искомой (1+3+5+ldots+(2k-1)).

Итак, (AE=k^2), а если число (k) выразить через (n), то получим (AE=left(frac{n+1}{2}right)^2).

Катет (CE) равен сумме четных чисел от 2 до (n-1), то есть (2+4+6+…+(n-1)). Эту сумму можно найти, используя формулу суммы первых членов арифметической прогрессии, поэтому (CE=frac{n^2-1}{4}) (рис. 5).

Значит, (AC^2=AE^2+CE^2=left(frac{n+1}{2}right)^4 + left(frac{n^2-1}{4}right)^2), после упрощения получим (AC^2=frac18(n+1)^2(n^2+1)). Пользуясь тем, что площадь квадрата в два раза меньше квадрата его диагонали, находим, что она равна (S_{text кв}=frac1{16}(n+1)^2(n^2+1)).

Продолжая действовать по аналогии с пунктом а), найдем теперь площадь большей части (на рис. 3 она была затонирована зеленым цветом). Эта часть состоит из двух равных прямоугольных треугольников и нескольких прямоугольников. Катеты прямоугольных треугольников равны (frac{n(n+1)}{4}) и (frac{n+1}{4}), поэтому сумма площадей этих треугольников равна (frac{n(n+1)^2}{16}).

Сумму площадей прямоугольников, образующих ступени найдем так:

[begin{gather}2cdot3+(2+4)cdot5+(2+4+6)cdot7+(2+ldots+8)cdot9+ldotsqquadqquad\ qquadqquadldots+(2+4+ldots+(n-1))cdot n-frac{n+1}{4}cdotfrac{n^2-1}{4}.end{gather}]

Здесь основанием каждого прямоугольника является нечетное звено данной ломаной, а его высота равна сумме первых четных чисел. Пусть (n=2k+1), где (k) — номер прямоугольника, тогда площадь (k)-го прямоугольника равна ((2k+1)cdot(2+4+6+…+2k)). Учитывая, что сумма (2+4+ldots+2k=2(1+ldots+k)=k(k+1)), получим, что площадь (k)-го прямоугольника равна (k(k+1)(2k+1)) или (2k^3+3k^2+k). Поэтому площадь (S_{text ступ}) ступенчатого многоугольника равна (sumlimits_{k=1}^{frac{n-1}2}(2k^3+3k^2+k)) или (2sumlimits_{k=1}^{frac{n-1}2}k^3+3sumlimits_{k=1}^{frac{n-1}2}k^2+sumlimits_{k=1}^{frac{n-1}2}k).

Способов суммирования степеней разработано много, см., например, задачу Суммы квадратов, суммы кубов…. Используя их, получим:

[begin{gather}S_{text ступ}=2cdotfrac14cdotleft(frac{n-1}2right)^2 left(frac{n-1}2+1right)^2 +qquadqquadqquadqquadqquad\ qquad + 3cdotfrac16cdot left(frac{n-1}2right) left(frac{n-1}2+1right)left(2cdotfrac{n-1}2+1right) +qquad\ qquadqquadqquadqquadqquad+frac12cdotleft(frac{n-1}2right)left(frac{n-1}2+1right).end{gather}]

После упрощения получим (S_{text ступ}=frac{1}{32}cdot(n-1)(n+1)^2(n+3)). Осталось из этой площади вычесть площадь (frac{n+1}{4}cdotfrac{n^2-1}{4}) (последний прямоугольник ступенчатой фигуры не полностью входит в зеленую часть квадрата) и добавить площадь (frac{n(n+1)^2}{16}) двух прямоугольных треугольников. Проделав это, получим площадь зеленой части квадрата: (S_{text зел}=frac1{32}cdot(n+1)^2(n^2+2n-1)).

Теперь вычисляем площадь желтой части квадрата:

[S_{text жел}=S_{text кв}-S_{text зел}=frac{1}{16}(n+1)^2(n^2+1)-frac{1}{32}(n+1)^2(n^2+2n-1)=qquad\ qquadqquadqquad=frac{1}{32}(n+1)^2(n^2-2n+3).]

Тогда искомое отношение площадей:

[frac{S_{text жел}}{S_{text зел}}=frac{n^2-2n+3}{n^2+2n-1}.]

Дотошный читатель может заметить, что в предложенном решении есть скользкое место. Дело в том, что нечетные числа бывают двух видов в зависимости от остатка при делении на 4 — (4m+1) и (4m+3). Рассмотренное решение полностью подходит для всех нечетных чисел вида (4m+3), поскольку именно в этом случае все вершины квадрата попадают в узлы квадратной сетки. В случае, когда (n=4m+1), две вершины квадрата попадают в узлы сетки, а две другие попадают в центры единичных квадратов. Проанализировав эту ситуацию, нетрудно убедиться в том, что и в этом случае все формулы работают, и несмотря, что некоторые площади становятся дробными, на окончательное отношение это никак не влияет (это можно показать, если масштаб квадратной сетки взять в два раза меньше).

Ломаная линия

• Замкнутая и незамкнутая ломаная
• Самопересекающаяся ломаная
• Длина ломаной

Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.

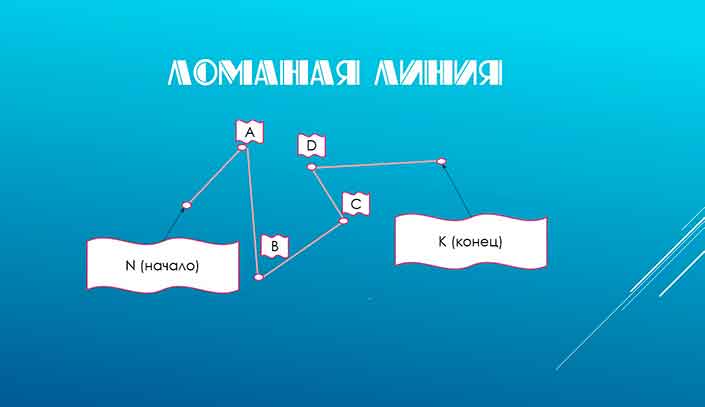
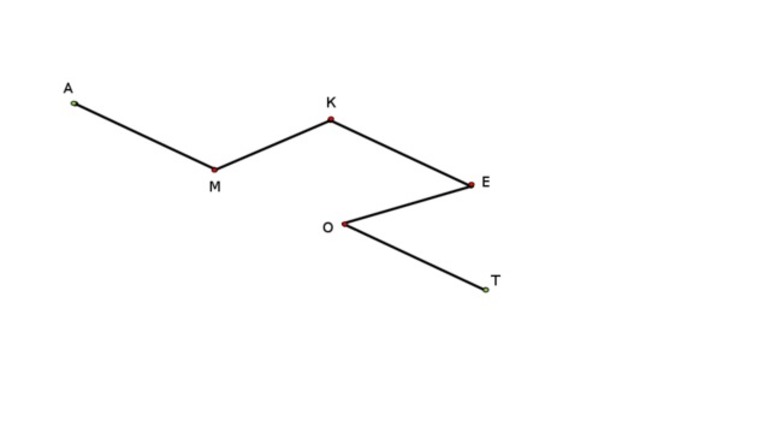
Построим ломаную из четырёх отрезков:

Отрезки  AB,  BC,  CD  и  DE  — это звенья ломаной. Точки  A,  B,  C,  D  и  E  — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная  ABCDE  или ломаная  EDCBA.

Замкнутая и незамкнутая ломаная

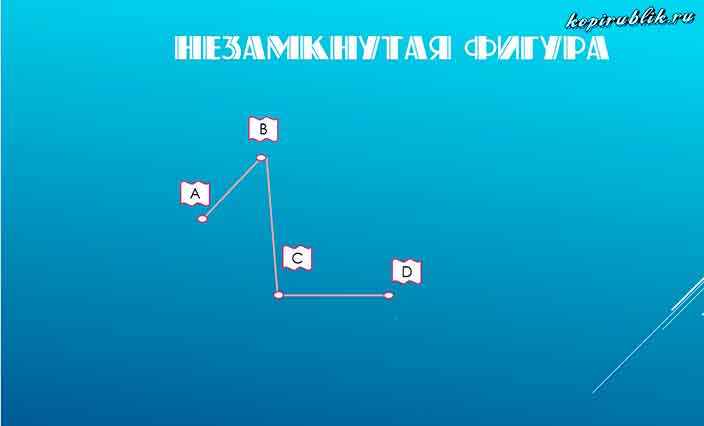
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:

незамкнутая ломаная  ABCD.

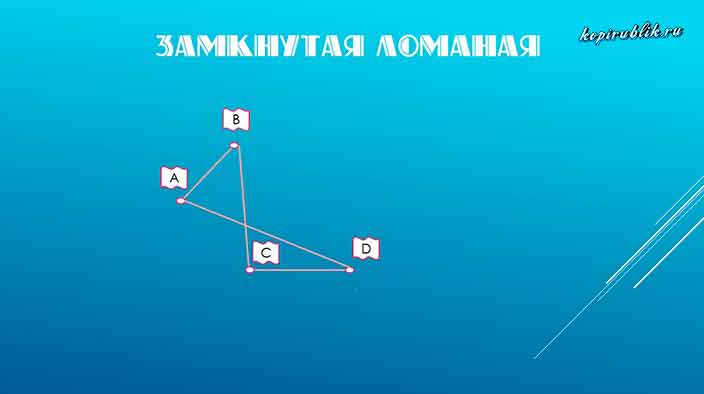
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:

замкнутая ломаная  ABC.

Самопересекающаяся ломаная

Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:

точки  F,  T,  K  — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.

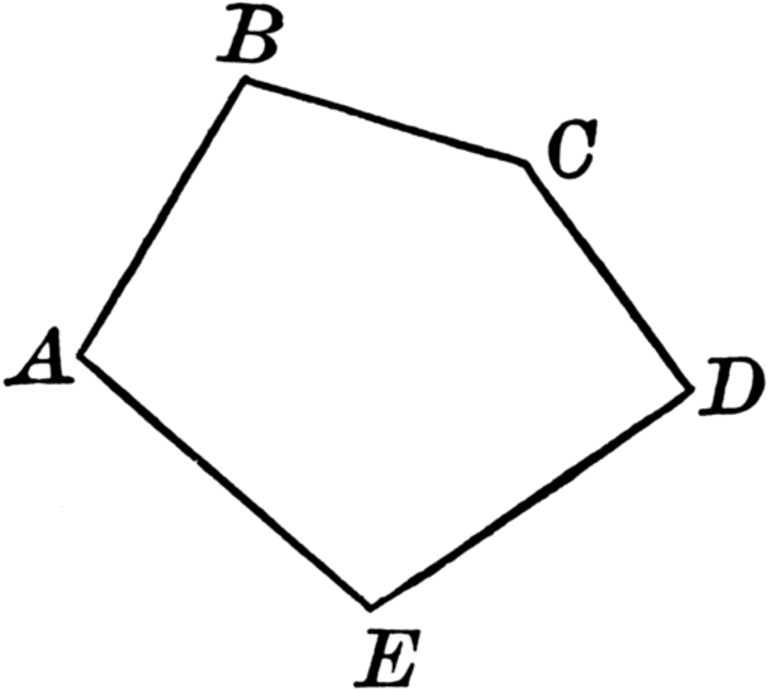
Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником:

многоугольник  ABCDE.

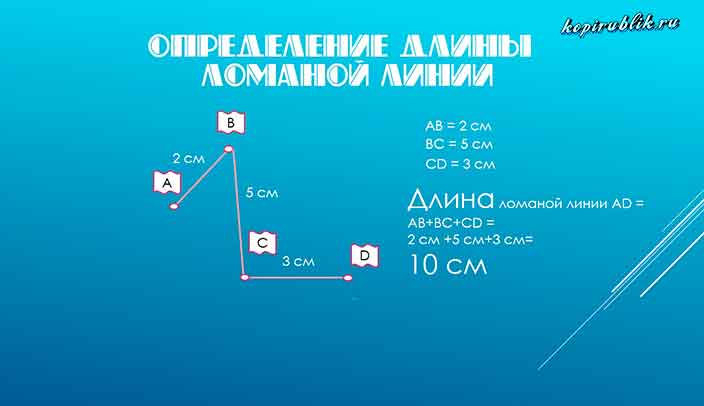
Длина ломаной

Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.

Математика, 2 класс. Урок №13.

Длина ломаной. Закрепление

Перечень вопросов, рассматриваемых в теме:

— Как найти длину ломаной?

Глоссарий по теме:

Ломаная — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего.

Звенья — отрезки, из которых состоит ломаная.

Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.

Длина ломаной – это сумма длин всех её звеньев.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.32-35

2. Математика. Проверочные работы. 2 кл.: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017 — с.20, 21

3. Математика. Тесты. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017 — с.20, 21, 25

Теоретический материал для самостоятельного изучения

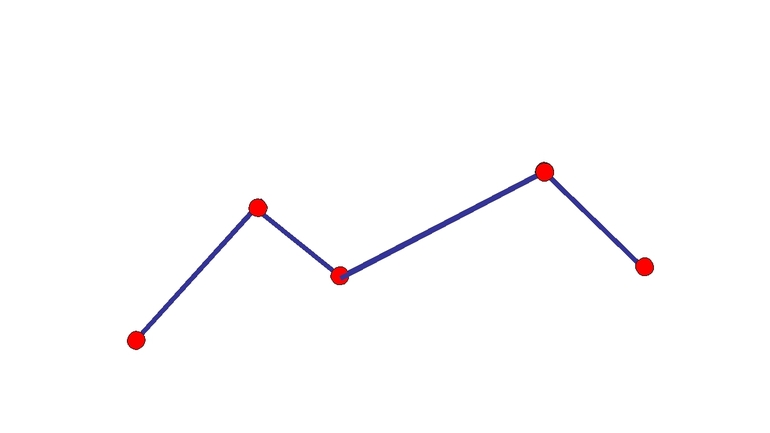
На рисунке мы видим ломаную линию, состоящую из трёх звеньев.

Как найти длину ломаной линии? Это можно сделать двумя способами.

Первый способ. Сначала узнаем длину каждого звена с помощью линейки

Длина первого звена 4 см.

Длина второго звена 6 см.

Длина третьего звена 5 см.

Найдем сумму этих длин.

4+6+5=15 (см)

Найдем длину ломаной вторым способом.

Отложим на прямой один за другим отрезки, равные по длине звеньям ломаной. Это можно сделать с помощью циркуля. Накладываем циркуль на первый отрезок, переносим его на прямую.

Накладываем циркуль на второй отрезок, переносим его на прямую.

Накладываем циркуль на третий отрезок, переносим его на прямую.

Теперь узнаем длину ломаной. Длина ломаной 15 см. В этом случае узнавать длину каждого звена ломаной не надо.

Выводы: длину ломаной можно находить двумя способами.

Первый способ: узнаем длину каждого звена с помощью линейки и найдем сумму этих длин.

Второй способ: с помощью циркуля откладываем на прямой один за другим отрезки, равные по длине звеньям ломаной. Затем измеряем длину всего отрезка. Это и будет длина всей ломаной.

Тренировочные задания.

1. Подчеркните длину ломаной, составленной из трёх звеньев такой длины: 2 см, 3 см и 5 см

Варианты ответов:

10 см 8 см 7 см

Правильный вариант:

10 см 8 см 7 см

2. Расположите ломаные линии по порядку: от самой короткой до самой длинной

Правильный вариант: Найдем длину каждой ломаной

6 + 2 + 2 = 10 см

7 + 5 = 12 см

2 + 1 + 3 +2 = 8 см

3 + 1 + 5 = 9 см

Расставим в порядке возрастания:

2 + 1 + 3 + 2 = 8 см

3 + 1 + 5 = 9 см

6 + 2 + 2 = 10 см

7 + 5 = 12 см

Ломаная линия — определение

Одним из наиболее простых и понятных геометрических терминов считают прямую линию. Есть в математике похожая фигура, но с некоторыми характерными чертами. Давайте попробуем разобраться, что такое ломаная линия и каковы её особенности.

Ломаная линия — математическая фигура, включающая в себя несколько отрезков, которые меняют направление.

Если выражаться более чётко, то это черта, которая не является прямой по всей длине, но может не иметь изгибов на отдельном отрезке.

Таким образом, фигура в обязательном порядке отвечает нескольким признакам:

• состоит из отрезков, которые являются её звеньями;
• конец каждого звена является началом следующего (кроме последнего);
• находящиеся рядом отрезки не могут располагаться на прямой, то есть угол между ними не равен 180 градусам.

Обозначение ломаной линии

Чтобы отметить ломаную линию на чертеже вам необходимо указать наименования точек стыка, в которых она меняет направление, латинскими буквами.

Из чего состоит ломаная линия

Как вы уже успели заметить, на рисунках присутствуют звенья — отрезки, составляющие ломаную линию. А вот начальные и конечные точки этих составных частей — вершины. На картинке вершины ломаной ABCD — позиции A, B, C, D.

Признак замкнутости ломаной линии

Классификация ломаных линий прежде всего осуществляется по свойству замыкания.

Замкнутая ломаная линия — фигура, у которой конечная позиция совпадает с начальной. Иначе говоря, когда она заканчивается в том же месте, где начиналась.

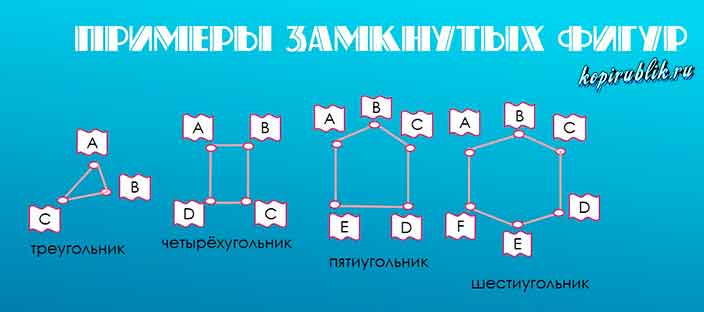
Яркие представители — треугольник и квадрат, а также остальные виды многоугольников:

Незамкнутая ломаная линия — фигура, которая приходит в позицию, отличающуюся от начальной.

Время от времени, у учащихся возникает вопрос: «Как определить, замкнутая фигура или нет?». Ответ будет весьма прост:»Когда число отрезков равно количеству вершин — она замкнутая, а при наблюдающемся неравенстве — незамкнутая».

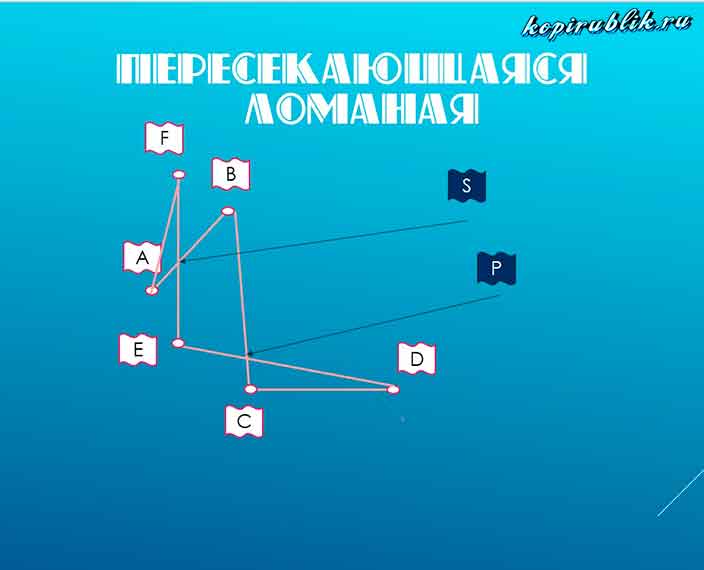
В качестве дополнительного вида рассматривают понятие самопересекающаяся ломаная линия — та, которая скрещивается на пути своего следования. Для данного термина не имеет значения сколько раз произошло пересечение.

На рисунке отмечены точки пересечения — S, P, а также вершины — A,B,C,D,E,F.

Иногда люди спрашивают — «Могут ли вершины являться точками пересечения?». Чтобы найти ответ, обратите внимание на рисунок с пересекающейся и одновременно замыкающейся — ломаной линией:

Изображение отличается от предыдущего: отрезок EB перемещён, поэтому вершина A приобрела статус точки пересечения.

Как измерить длину ломаной линии

Ломаная линия, имеющая начало и конец, имеет распространённую стандартную характеристику — длину. Имея цель сделать замер её длины, необходимо суммировать длины всех её составных частей — отрезков.

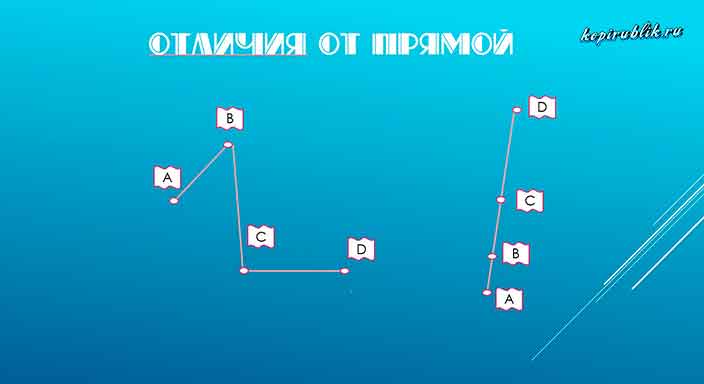
Чем ломаная линия отличается от прямой

При взгляде на рисунок очевидно: уникальный признак ломаной линии — отсутствие углов, равных 180 градусам. В остальном, фигуры одинаковые и обладают схожими свойствами, например, длиной.

Примеры ломаных линий в быту

В целях наилучшего усвоения теории, разумно на практике ознакомиться с примерами ломаных линий из жизни.

Ломаная линия— график фондового рынка. Так как отрезки графика очень маленькие, поэтому может показаться, что это кривая, но при ближайшем рассмотрении оказывается, что это не так.

Фасад дома при переводе на «язык геометрии» выглядит как замкнутая ломаная линия.

Пирамиды древнего Египта обладали формой треугольника — одной из самых популярных ломаных линий.

Краткое описание

Специалисты называют ломаной ту геометрическую фигуру, которая представляет собой непрямую линию, состоящую исключительно из многочисленных соединённых отрезков. Учащимся нужно запомнить, что все эти фрагменты могут сходиться под абсолютно разными углами. Проще говоря, если есть даже самый маленький угол между двумя соединёнными отрезками, то это линия своеобразного ломаного типа.

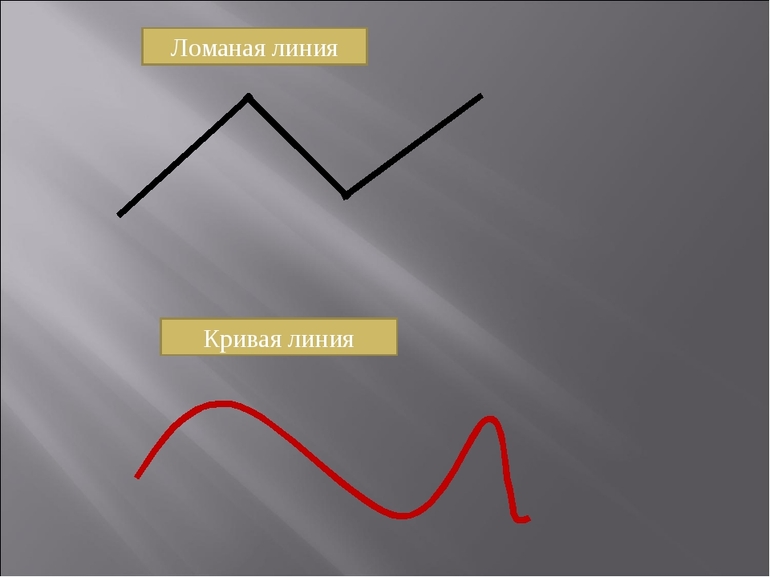
Прямая тоже может состоять сразу из нескольких геометрических фрагментов, но угол их соединения приравнивается к нулю. Для избежания грубых математических ошибок нужно помнить, что ломаная линия отличается от кривой, так как отдельные отрезки представляют собой прямую линию, чего нельзя сказать о кривой.

В некоторых случаях пространственная ломаная может образовывать замкнутую фигуру. Но такая ситуация возможна только тогда, когда концы крайних отрезков совпадают, а также пересекают самих себя. Рассматриваемая в математике фигура состоит из вершин и отрезков, которые и соединяют эти вершины. Но в этом случае действует правило — два последних отрезка не должны лежать на одной прямой.

Сторонами или звеньями изогнутой линии принято называть составные отрезки. Минимальное количество звеньев — два. Специалисты привыкли называть чёрными точками конечные вершины ломаной линии. Чтобы графически всё выглядело правильно, необходимо использовать обозначения в соответствии с названиями задействованных вершин.

Если конечные вершины совпадают, тогда речь касается изогнутой замкнутой линии. В качестве примера можно рассмотреть многоугольник. Эта фигура представляет собой плоскую замкнутую ломаную, которая лишена каких-либо самопересечений. Вершины ломаной линии и её звенья относятся к многоугольнику. Если речь касается фигуры с тремя сторонами и вершинами, то это треугольник.

Немного сложнее разобраться с замкнутой ломаной и её четырьмя сторонами, так как это может быть прямоугольник, квадрат, параллелограмм, ромб и даже трапеция. Если фигура имеет пять или более сторон, то она называется n-угольником. Символ n указывает на точное число вершин.

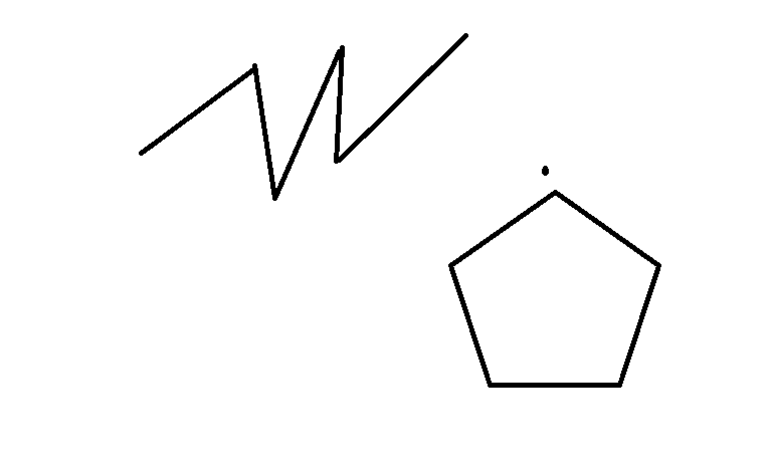
Некоторые математические примеры касаются изогнутой линии с самопересечениями (пятиконечная звезда). К этой категории также можно отнести зигзаг, в котором каждый второй отрезок параллелен другому, а последние формируют одинаковый угол.

Математическое определение

Ломанной принято называть ту геометрическую фигуру, которая состоит из обычных отрезков (R1, R2, R3 и R4, Rn-1 Rn). Вершинами изогнутой принято называть точки R1…Rn, а вот все остальные отрезки — это неотъемлемые звенья. Если для любого w действует формула {1, 2, n — 2}, а отрезки не расположены на одной прямой, то такая ломанная будет называться невырожденной. В противном случае придётся иметь дело с вырожденным примером.

Для лучшего усвоения этой темы следует рассмотреть несколько примеров. Изогнутая может иметь самопересечение, но это возможно только в том случае, если минимум два отрезка обладают общей точкой (за исключением вершины).

В математике часто можно встретить фигуру, которая является обычной ломаной линией. В этом случае практикуется применение следующей записи: R1R2R3R4R5R6. Если ученику предстоит разобраться со всеми нюансами построения замкнутой ломаной из трёх звеньев и более, тогда ему понадобятся вспомогательные отрезки (к примеру: R1, R2, а также Rn -1 Rn, которые не должны лежать на одной прямой).

Замкнутую плоскую ломаную линию принято называть многоугольником. Если рассматривать многогранники, то все стороны фигуры будут называться рёбрами. Учителя России предпочитают создавать краткосрочное планирование по этой теме, так как в этом случае можно донести больше полезной информации до учеников.

Гораздо проще разобраться с изгибами зигзага, так как они используются в швейном деле, в распространённом декоративном оформлении предметов обихода в качестве орнамента. Стоит отметить, что изогнутая линия нашла широкое применение в различных отраслях:

1. Архитектура. Изогнутые линии позволяют сооружать интересные номера.
2. Картография (тщательное проектирование маршрутов и подробное схематическое изображение всех улиц).
3. Химическая отрасль (различные соединения и своеобразные молекулярные структуры).
4. Востребованный дизайн ландшафтов (утончённое оформление, расположение дорожек).
5. Медицина (мониторы для наблюдения за сердечным ритмом).
6. Метод освоения каллиграфических навыков в китайском языке.

Изучение этой темы в математике является обязательным, так как от этого зависит качество усвоения материала учеником.

Основные разновидности ломаных

Геометрическая фигура может быть построена совершенно по любому из действующих методов. Специалисты выделяют замкнутую, а также незамкнутую ломанную. Повышенное внимание уделяют самопересекающимся, непересекающимся линиям. Классическая замкнутая ломаная является многоугольником. В математике самопересекающейся принято называть ту линию, отрезки которой имеют минимум одно пересечение. По своей структуре ломаная может быть весьма разнообразной, из-за чего нужно внимательно относиться ко всем аспектам.

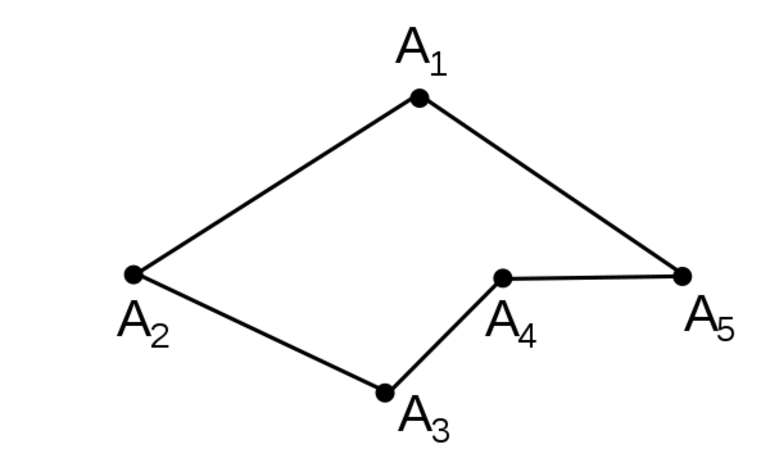
В начальных классах школы принято рассматривать следующий пример: ломаная включает в себя сразу пять звеньев либо сторон: ZX, XC, CV, VB, BN. Та точка, где неизбежно соединяются два звена, называется вершиной. В этом случае имеется сразу четыре вершины: X, С, V, B.

Повышенное внимание нужно уделить изучению звена ломаной. Звеньями эксперты привыкли называть стороны либо отрезки, из которых образована линия. Всего одно такое звено может быть рассмотрено только в качестве отрезка. А вот для построения ломаной необходимо задействовать как минимум два звена. Вершины — это классические точки, которые представляют собой концы одних отрезков ломаной. Обозначить точки можно только латинскими буквами.

Пример замкнутой, а также традиционной незамкнутой ломаной линии, которую часто можно встретить в геометрии и алгебре:

Если необходимо определить точную длину ломаной, то для этого следует поочерёдно сложить все известные данные задействованных звеньев (ZX + XC + CV + VB + BN).

Базовые понятия

Чтобы гарантировано освоить все правила, которые касаются использования изогнутой линии в математике, необходимо разобраться со звеньями. Существует ряд нюансов, которые можно сопоставить с элементарной геометрической конструкцией. Линию формируют отдельные отрезки, которые в математике называются звеньями. Если все концы ломаной соединяются в одной точке, то такая фигура будет называться замкнутой.

Все задействованные звенья могут обладать взаимными пересечениями. Вершинами специалисты привыкли называть точки соединения отрезков. О многоугольнике можно говорить только в том случае, если звенья не пересекаются между собой. Звено обозначают сразу двумя латинскими буквами. Каждая вершина изогнутой линии может обозначаться только одной буквой. Только тщательное изучение всех правил и нюансов позволит правильно решать математические задачи.

Особенности построения многоугольников

В этом случае речь касается геометрической фигуры, отличающейся итоговым количеством звеньев, углов. Последние могут быть сформированы только несколькими звеньями замкнутой ломаной, которые сходятся в одной точке. Задействованные звенья также могут носить логическое название сторон многоугольника. Общие точки двух отрезков называются вершинами. Стоит учесть, что количество сторон либо звеньев в каждой такой фигуре в точности соответствует количеству углов. Если задействовать замкнутую ломаную из трёх отрезков, то в итоге получится треугольник.

Абсолютно все многоугольники обладают одинаковыми свойствами. Самая маленькая фигура включает в себя всего три стороны. Но расположенные в непосредственной близости треугольники могут формировать совершенно новые фигуры. Если имеющиеся вершины изучаемого многоугольника являются своеобразным дополнением одной стороны, то их всегда называют соседними.

Когда многоугольник был расположен относительно одной прямой в любой плоскости, то она называется выпуклой. А вот прямая может содержать в себе одну сторону фигуры и принадлежать полуплоскости. Если отрезок соединяет не соседние вершины, то он называется диагональю. Смежный внутренний угол при некоторой вершине называется внешним.

Следует отметить тот факт, что когда все имеющиеся углы и стороны многоугольника равны между собой, то речь касается правильных отрезков. Каждая геометрическая фигура обладает определёнными параметрами. Треугольниками в алгебре принято называть обычную плоскую фигуру, которая состоит из трёх точек, не расположенных на одной прямой. Для соединения используются обычные отрезки. Точки выступают в роли вершин треугольника. Такая фигура имеет всего три угла. Специалисты различают 6 разновидностей треугольников:

1. Элементарные разносторонние. В этом случае каждая следующая сторона отличается своей длиной.
2. Равносторонние. Абсолютно все стороны обладают идентичной длиной.
3. Специфические остроугольные. Сформированные углы имеют острую форму.
4. Универсальные равнобедренные. Сразу две стороны из трёх существующих обладают одинаковой длиной.
5. Тупоугольные. Фигура обладает одним тупым углом.
6. Традиционные прямоугольные. Нарисованная фигура должна иметь минимум один прямой угол.

Четырёхугольником называют ту конструкцию, которая обладает четырьмя сторонами и четырьмя сторонами. Использование таких геометрических фигур обладает определёнными нюансами.

Ключевые нюансы

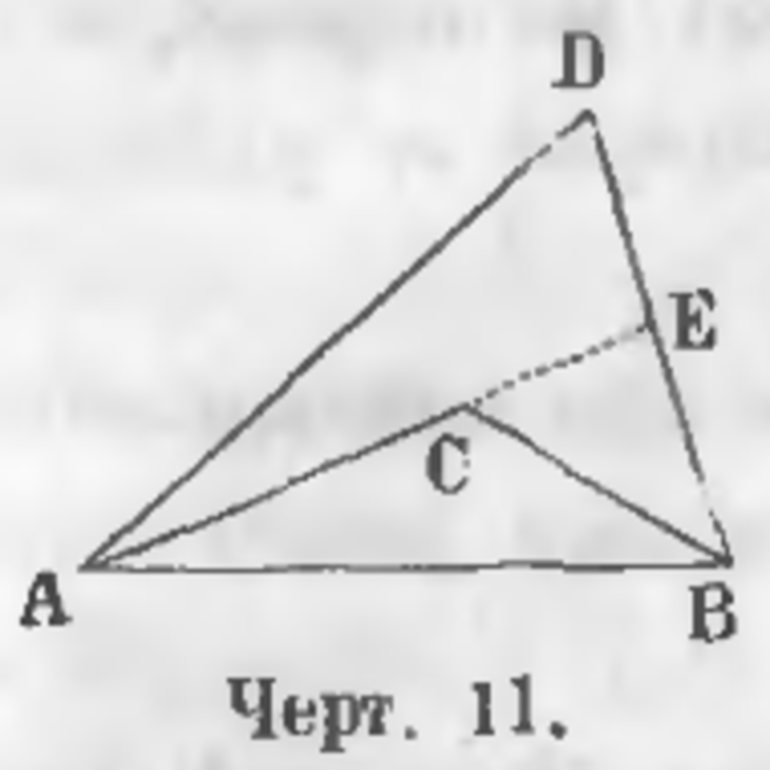
Существует две линии SWT и SFT одинаковой толщины, которые соединяют свободные концы одной прямой ST. В итоге образуется ломаная. Изогнутая SFT именуется внутренней ломаной, а вот SWT внешней. В качестве примера лучше всего рассмотреть фигуру, которая соответствует математической теореме, что внешняя изогнутая превышает внутреннюю.

По условиям задачи были даны две ломаные: внутренняя SFT и внешняя SWT. Необходимо доказать, что SWT больше SFT. Для решения этой задачи нужно продолжить линию SF до пересечения с отрезком WT в точке Е. Линия SWE как ломаная гораздо больше прямой SE. Ломанная FET больше имеющейся прямой FT. Если сложить между собой все эти неравенства, то в итоге можно получить: SW+ WE + FE + ET > SF + FE + FT.

Для получения достоверного результата нужно вычесть из обеих частей неравенства по СЕ:

• SW+ WE + ET > SF + FT.
• WE + ET = WT.

Необходимо рассмотреть и вторую теорему, в соответствии с которой итоговая сумма пересекающихся изогнутых линий больше не пересекающихся. По условиям задачи были даны обычные пересекающиеся ломаные HLK и HRK, а также HR, LK и пересекающиеся части. Решение выглядит следующим образом: неравенства отрезков вытекают из того, что ломаная HEL гораздо больше прямой HL, а вот координаты KER превышают KR.

Нелишним также будет научиться находить общую меру сразу двух линий при помощи линейки. Это правило обязательно осваивают в начальных классах. Для поиска неизвестной общей меры обязательно нужно на большую линию наложить меньшую, потом первый остаток на меньший отрезок, а второй остаток на первый. Все эти манипуляции повторяют ровно до тех пор, пока самый последний остаток максимально не уложится в предпоследнем выполненном действии. Измерение линий всегда означает то, что учащемуся необходимо отыскать её отношение к другим отрезкам, принятым за единицу. Полученное значение называют длиной этой линии, которая может выражаться исключительно в каких-нибудь единицах.

Изучение ломаных линий очень важно, так как они окружают человека повсюду. Речь касается прямых линий, которые меняют своё первоначальное направление, замыкаются, а также пересекаются.