Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.
Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.
Виды треугольников по углам
Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.
Виды треугольников по сторонам
Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.
Медиана, биссектриса, высота, средняя линия треугольника
Медиана
Определение
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.
По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.
Биссектриса
Определение
Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.
В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD1, EE1 и CC1.
По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.
Высота
Определение
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.
На рисунке показаны высоты треугольника АВС: АН1, ВН2 и СН3.
По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.
Средняя линия
Определение
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.
Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.
Задание 25OM21R
В треугольнике АВС известны длины сторон АВ=36, АС=54, точка О – центр окружности, описанной около треугольника АВС. Прямая ВD, перпендикулярная прямой АО, пересекает сторону АС в точке D. Найдите СD.
Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.
При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 900.
Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.
Составим отношение сторон:
AEAB=ABAF откуда по свойству пропорции АВ2=АЕ∙АF
Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.
Составим отношение сторон:
AEAD=ACAF ; откуда выразим AD=AE∙AFАC=AE∙AFAC
Теперь рассмотрим наши два полученных равенства: АВ2=АЕ∙АF и AD=AE∙AFAC
Видим, что 362=АЕ∙АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD=AE∙AFAC=36254=24
Теперь найдем CD=AC-AD=54-24=30
Ответ: 30
pазбирался: Даниил Романович | обсудить разбор
Задание 18OM21R
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.
Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор
Задание 15OM21R
В треугольнике АВС известно, что угол ВАС равен 840, АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.
Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 840:2=420
Ответ: 42
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 7.8k
Перпендикуляр от точки к прямой
Отрезок (AC) называется перпендикуляром, проведённым из точки (A) прямой (a), если прямые (AC) и (a) перпендикулярны.
Точка (C) называется основанием перпендикуляра.
От точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

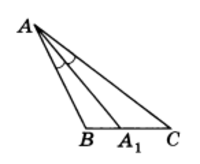
Докажем, что от точки (A), не лежащей на прямой (BC), можно провести перпендикуляр к этой прямой.
Допустим, что дан угол
∠ABC
.
Отложим от луча (BC) угол, равный данному, и совместим эти углы накладыванием (представим, что сложим лист бумаги с равными углами по стороне (BC)).
Сторона (BA) совместится со стороной
BA1
.
При этом точка (A) наложится на некоторую точку
A1
.
Следовательно, совмещается угол
∠ACB
с
∠A1CB
.
Но углы
∠ACB
и
∠A1CB
— смежные, значит, каждый из них прямой.
Прямая
AA1
перпендикулярна прямой (BC), а отрезок (AC) является перпендикуляром от точки (A) к прямой (BC).
Если допустить, что через точку (A) можно провести ещё один перпендикуляр к прямой (BC), то он бы находился на прямой, пересекающейся с
AA1
. Но две к одной и той же прямой перпендикулярные прямые должны быть параллельны и не могут пересекаться.
Это противоречие, что означает: через данную точку к прямой можно провести только один перпендикуляр.
Медианы, биссектрисы и высоты треугольника
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Поэтому для построения медианы необходимо выполнить следующие действия:
1) найти середину стороны;
2) соединить точку, являющуюся серединой стороны треугольника, с противолежащей вершиной отрезком — это и будет медиана.
У треугольника три стороны, следовательно, можно построить три медианы.
Все медианы пересекаются в одной точке.
Биссектриса треугольника — это отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне.
Поэтому для построения биссектрисы необходимо выполнить следующие действия:
1) построить биссектрису какого-либо угла треугольника (биссектриса угла — это луч, выходящий из вершины угла и делящий его на две равные части);
2) найти точку пересечения биссектрисы угла треугольника с противоположной стороной;
3) соединить вершину треугольника с точкой пересечения на противоположной стороне отрезком — это и будет биссектриса треугольника.
У треугольника три угла и три биссектрисы.
Все биссектрисы пересекаются в одной точке.
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противоположную сторону.
Поэтому для построения высоты необходимо выполнить следующие действия:
1) провести прямую, содержащую одну из сторон треугольника (в случае, если проводится высота из вершины острого угла в тупоугольном треугольнике);
2) из вершины, лежащей напротив проведённой прямой, опустить перпендикуляр к ней (перпендикуляр — это отрезок, проведённый из точки к прямой, составляющей с ней угол 90°) — это и будет высота.
Так же как медианы и биссектрисы, треугольник имеет три высоты.
Высоты треугольника пересекаются в одной точке.
Но, как выше упомянуто, для некоторых видов треугольников построение высот и точки их пересечения отличаются.
Если треугольник с прямым углом, то стороны, образующие прямой угол, можно назвать высотами, так как они перпендикулярны одна к другой. Точкой пересечения высот является общая вершина перпендикулярных сторон.
Если треугольник с тупым углом, то высоты, опущенные с вершин острых углов, выходят вне треугольника к продолжениям сторон. Прямые, на которых расположены высоты, пересекаются вне треугольника.
Обрати внимание!
Если из одной и той же вершины провести медиану, биссектрису и высоту, то медиана окажется самым длинным отрезком, а высота — самым коротким отрезком.
Равнобедренный треугольник
Если у треугольника две стороны равны, то такой треугольник называют равнобедренным.
Равные стороны называют боковыми, а третью сторону — основанием.
(AB = BC) — боковые стороны , (AC) — основание.
Если у треугольника все три стороны равны, то такой треугольник является равносторонним.
Равнобедренный треугольник имеет некоторые свойства, которые не имеют треугольники с разными сторонами.
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
3. В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой.
4. В равнобедренном треугольнике высота, проведённая к основанию, является биссектрисой и медианой.
Первое и второе свойство можно доказать, если докажем равенство двух треугольников, которые образуются, если из угла напротив основания провести биссектрису (BD).
Рассмотрим равнобедренный треугольник (ABC) с основанием (AC) и докажем, что
ΔABD=ΔCBD
.
Пусть (BD) — биссектриса треугольника (ABC).
ΔABD=ΔCBD
по первому признаку равенства треугольников ((AB = BC) по условию, (BD) — общая сторона,
∠ABD=∠CBD
, так как (BD) — биссектриса).
У равных треугольников равны все соответствующие элементы:
1.
∠A=∠C
— доказано, что прилежащие основанию углы равны.
2. (AD = DC) — доказано, что биссектриса является медианой.
3.
∠ADB=∠CDB
— так как смежные углы, сумма которых
180°
, равны, то каждый из них равен
90°
, то есть медиана является высотой.
Можно очень легко самостоятельно доказать и третье, и четвёртое свойства.
- Точка
- Линия
- Прямая линия
- Луч
- Отрезок
- Ломанная линия
- Многоугольник
- Как научить складывать и вычитать числа
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
A
B
C
точка 1, точка 2, точка 3
1
2
3
Можно нарисовать на листке бумаги три точки "А" и предложить ребёнку провести линию через две точки "А". Но как понять через какие? A A A
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
a
b
c
Линия может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
a
прямая линия AB
B
A
Прямые могут быть
- пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча
A
A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
a
луч AB
B
A
Лучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
C
B
A
Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
B
A
прямая линия AB
B
A
От прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками.
✂
B
A
✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
B
A
Задача: где прямая, луч, отрезок, кривая?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
A
B
C
D
E
64
62
127
52
Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее, а у какой больше вершин? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
A
B
C
D
E
F
120
60
58
122
98
141
Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т.д.
треугольники
четырёхугольники: квадрат, прямоугольник, дельтоид, ромб, параллелограмм, трапеция
пятиугольники
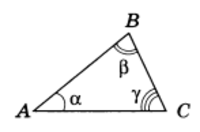
Рис.1
Пусть А, В, С — три произвольные точки, не лежащие на одной прямой. Фигура, состоящая из трех отрезков АВ, ВС, АС (рис.1), называется треугольником
ABC (обозначается: Л ABC). Треугольником также называют часть плоскости, ограниченную отрезками АВ, ВС, АС (плоский треугольник).
Точки А, В, С — вершины, отрезки АВ, ВС, АС — стороны треугольника. Сумма длин трех сторон треугольника называется его периметром.
Углом (или внутренним углом) треугольника ABC при вершине А называется угол, образованный лучами АВ и АС. Так же определяются углы треугольника при вершинах В и С.
Углы CAB, ABC у ВСА треугольника ABC часто обозначают одной буквой (А, В, С соответственно) или греческими буквами α, β, γ (при этом внутри углов рисуют дуги, см. рис. 1). Говорят, что угол А противолежит стороне ВС или сторона ВС противолежит углу А; так же угол В и сторона АС, угол С и сторона АВ противолежат (друг другу).
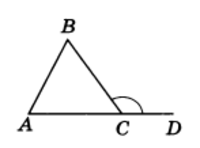
Рис.2
Угол, смежный с каким-нибудь углом треугольника, называется внешним углом этого треугольника. Таков, например, угол BCD (рис.2). При каждом угле треугольника можно построить по два внешних угла (продолжив одну или другую сторону угла). Эти два угла равны как углы вертикальные.
Рис.3
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны, называется биссектрисой треугольника (рис.3).
Любой треугольник имеет три биссектрисы.
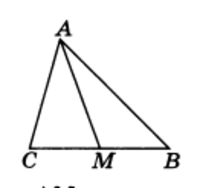
Рис.4
Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называется медианой треугольника (рис.4).
Любой треугольник имеет три медианы.
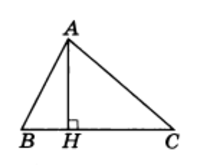
Рис.5
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону, называется высотой треугольника (рис. 5).
Любой треугольник имеет три высоты.
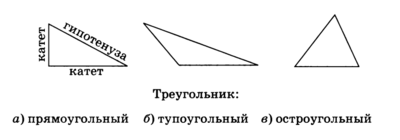
Рис.6
Если один из углов треугольника прямой, то треугольник прямоугольный (рис.6, а); если один из углов тупой — тупоугольный (рис.6, б); если все три угла острые — остроугольный (рис.6, в).
В прямоугольном треугольнике сторона, лежащая против прямого угла, называется гипотенузой, две другие стороны — катетами.
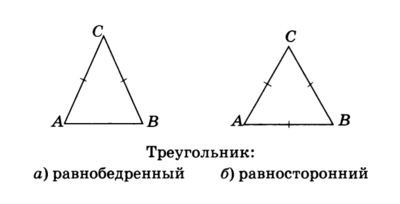
Рис.7
Треугольник, две стороны которого равны, называется равнобедренным (АС = ВС на рис.7, а). Третья сторона — основание, равные стороны — боковые стороны.
Треугольник, три стороны которого равны (АС = ВС = АВ на рис.7, б), называется равносторонним.
Пример 1. Периметр равнобедренного треугольника равен 50 м, боковая сторона — 15 м. Найти основание.
Решение. Обозначим основание через х. Тогда периметр треугольника составит x + 15 + 15. По условию эта сумма равна 50 м, т. е. х + 30 = 50, откуда х = 20. Итак, основание равно 20 м.
Пример 2. Периметр равнобедренного треугольника равен 70 м. Боковая сторона больше основания на 5 м. Найти стороны треугольника.
Решение. Воспользуемся рисунком 7, а. Обозначим АВ через х, тогда ВС = АС через х + 5.

Рис.7
Тогда периметр треугольника составит (х + 5) + (х + 5) + х.
По условию эта сумма равна 70, т. е. Зх + 10 = 70, или х = 20.
Следовательно, стороны треугольника 20 см, 25 см и 25 см.
Пример 3. Треугольник, периметр которого равен 24 см, делится высотой на два треугольника, периметры которых равны 12 см и 20 см. Найти высоту треугольника.
Решение. Пусть условию задачи отвечает рисунок 5.
АН — высота треугольника ABC
Рис.5
Обозначим периметры треугольников АВС, АВН и АСН соответственно через Р, Р1 и Р2. Из рисунка 5 видно, что Р1 + Р2 = Р + 2АН, или 12 + 20 = 24 + 2AH, откуда АН = 4.
Пример 4. Укажите номера верных утверждений.
-
Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
-
Треугольник со сторонами 1, 2, 4 существует.
-
Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
Видео-решение.
Укажите номера верных утверждений
Хочу разобраться с 3D-моделированием, соответственно, реализация на готовых движках на данный момент совершенно не интересует.
Действую по стандартной стратегии: выпустить луч от камеры в направлении пикселя на экране, затем найти точку пересечения луча и плоскости, в которой лежит полигон (треугольник). Для нахождения уравнения плоскости полигона хочу использовать метод Гаусса, луч задаю пересечением двух плоскостей (2 коэффициента назначаю сам, остальные 2 ищу тем же методом Гаусса — нахожу уравнение плоскости, в которой лежит луч, повторяю операцию с другими начальными коэффициентами — получаю уравнение другой плоскости). Далее просто подставляю в матрицу 3х3 коэффициенты трех плоскостей и нахожу точку их пересечения.
Проблема заключается в поиске уравнения плоскости полигона в случае, когда эта плоскость проходит через точку (0, 0, 0), так как я изначально выбираю коэффициент D = 1 (для такой плоскости он всегда будет равен 0). Не знаете ли вы, как обычно решают эту проблему?
UPDATE: Вот решение, которое получилось у меня:
Вместо поиска уравнений плоскостей, действительно проще работать сразу с векторами.
Пусть плоскость задается тремя точками: A, B, C. А прямая двумя: D, E. Точка T — пересечение прямой с плоскостью. Можно воспользоваться двумя свойствами векторов:
- Смешанное произведение компланарных векторов = 0
- Векторное произведение коллинеарных векторов = нулевому вектору
Вот так получается матрица координат точки T:
Дальше можно решать тем же методом Гаусса.
При таком подходе матрица не будет иметь решения методом Гаусса только в двух случаях: когда прямая лежит в плоскости и когда они параллельны