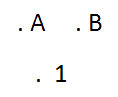- Луч — геометрическое понятие
- Отличия луча от прямой и от отрезка
- Взаимное расположение лучей
- Можно ли сравнить два луча?
- Луч — альтернативные значения слова
Не секрет, что знания, которые вы получили в школьные годы не всегда остаются с вами впоследствии Иногда бывает полезно изучить новое или освежить в памяти то, что вы давно забыли. Сегодня вы вспомните такое понятие как луч.
Луч — геометрическое понятие
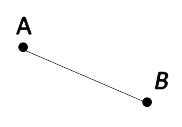
Луч — это такая прямая линия, один из концов которой ограничен точкой, а другой продолжается до бесконечности. Таким образом, фигура тянется вперёд без ограничений. но только с одной стороны. Вторая сторона не может тянуться дальше точки, которая является началом фигуры.
На картинке вы можете посмотреть, что такое луч и как он выглядит:
Луч отмечается посредством строчной латинской буквы или двух таких точек, которые обозначены заглавными буквами латинского алфавита.
Если вы увидите отрезок с двумя точками и продолжите его в одну из сторон, как показано на рисунке, то получится луч.
Отличия луча от прямой и от отрезка
В геометрии есть три схожих понятия, которые подразумевают под собой черту — это луч, отрезок, прямая. Эти фигуры всегда изображаются без изгибов и имеют ряд особенностей.
В рамках курса математики луч — это полупрямая. Дело в том, что с одного конца он обладает признаком бесконечности, который присущ прямой линии.
В начальной точке луч имеет сходство с отрезком, так как он так же ограничен точкой.
Обратите внимание — быстро отличить фигуры друг от друга вы можете по наличию у них начала и конца:
- отрезок имеет начальную и конечную точки;
- луч — только начало;
- прямая — не располагает начальной и конечной точками.
Взаимное расположение лучей
Если на прямой линии вы поставите точку, то на ней сформируются два таких луча, начало которых находится в одной точке.
На рисунке начало для лучей — общая точка A.
По взаимному расположению лучи делятся на пересекающиеся и непересекающиеся.
Параллельный луч — это фигура, у которой любая точка находится на одинаковом расстоянии от соответствующей точки другого луча. Параллельные лучи не могут пересекаться.
Дополнительные лучи — это фигуры, которые обладают такими признаками, как:
- имеют совпадающее начало в одной точке;
- располагаются на одной прямой линии;
- направляются в разные стороны, то есть угол между ними составляет 180 градусов.
Можно ли сравнить два луча?
Луч — это такая фигура, которую нельзя измерить. Он продолжается без ограничений, поэтому не обладает характеристикой длины.
Так как невозможно измерить несколько лучей, сравнить их вы тоже не сможете.
Луч — альтернативные значения слова
Русский язык достаточно сложен и необычайно многообразен, поэтому многие слова имеют несколько разных значений, а разнообразные сочетания способны радикально менять смысл слов, которые являются их составными частями.
Сможете ли вы сходу ответить на вопрос: «Что такое луч света?». Это словосочетание употребляется нами с детства, но не так легко выразить, что оно означает.
Такая фраза описывает прямую линию, по которой направляется световая энергия. Эта энергия исходит от разных источников:
- Солнце;
- звёзды;
- лампочка.
В быту вы можете услышать словосочетание «луч света в тёмном царстве». Такие слова означают — среди негативных явлений присутствует что-то хорошее. Короткое слово всегда ассоциируется с чем-то светлым, добрым и положительным.
Фраза «луч надежды» указывает, что среди множества нежелательных последствий существует не высокая вероятность благополучного исхода.
Также рекомендуем прочитать:
Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства.
Познакомимся с основными геометрическими понятиями, изучаемыми в начальной школе.
Точка
Запомните!
Точка — это основная и самая простая геометрическая фигура.
В геометрии точка обозначается заглавной латинской буквой или цифрой.
Многие латинские буквы по написанию похожи на английские буквы.
В тексте точку обозначают следующим символом: «(·) A» — точка «А».
Прямая
Запомните!
Прямая — это самая простая геометрическая фигура, которая не имеет ни начала, ни конца.
Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.
- Через две точки можно провести единственную прямую.
- Две прямые могут пересекаться только в одной точке.
- Через одну точку можно провести бесконечное множество прямых.
Способы обозначения прямых
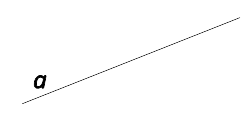
- Строчной латинской буквой:
Прямая «a».
- Двумя заглавными латинскими буквами в том случае, если этими буквами обозначены
точки, расположенные на прямой.
Прямая «АB».
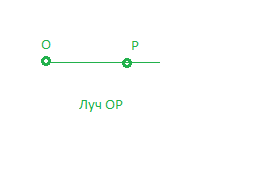
Луч
Запомните!
Луч — это часть прямой линии, которая расположена по одну сторону от какой-либо точки.
У луча есть начало, но нет конца.
Способы обозначения лучей
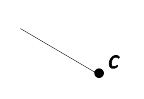
- Строчной латинской буквой:
Луч «c».
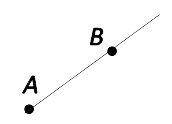
- Двумя заглавными латинскими буквами в том случае, когда первая точка — начало луча, а
вторая точка лежит на луче.
Луч «AB».
Отрезок
Запомните!
Отрезок — это часть прямой линии, которая ограничена двумя точками (концами отрезка).
У отрезка есть и начало, и конец.
Основное свойство отрезка — это его длина.
Длина отрезка — это расстояние между его концами.
В математике отрезок обозначается заглавными латинскими буквами.
Отрезок «AB».
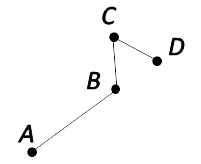
Ломаная
Запомните!
Ломаная — это геометрическая фигура, состоящая из точек, которые соединены отрезками.
Вершины ломаной — это точки, в которых соединяются отрезки, образующие ломаную.
Звенья ломаной — это отрезки ломаной.
В математике ломаная обозначается заглавными латинскими
буквами.
Ломаная «ABCD».
Вершины ломаной — A, B, C, D.
Звенья ломаной — AB, BC, CD.
Запомните!
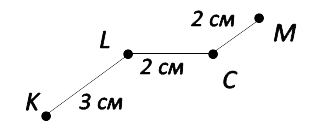
Чтобы найти длину ломаной, необходимо сложить длины всех её звеньев (отрезков), из
которых она состоит.
KLCM = KL + LC + CM = 3 см + 2 см + 2 см = 7 см
Вот мы и познакомились с основами геометрии. Теперь мы готовы рассмотреть не менее важную
геометрическую фигуру — угол.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
25 февраля 2017 в 9:40
Ильназ Хуснутдинов
Профиль
Благодарили: 0
Сообщений: 2
Ильназ Хуснутдинов
Профиль
Благодарили: 0
Сообщений: 2
6. (4 балла) Дан отрезок MP длиной 39 см. На нем отмечены точки G и H таким образом, что длины отрезков GP = 26 см, MH = 23 см. Найти длину отрезка GH в дециметрах.
0
Спасибо
Ответить
25 февраля 2017 в 9:37
Ильназ Хуснутдинов
Профиль
Благодарили: 0
Сообщений: 2
Ильназ Хуснутдинов
Профиль
Благодарили: 0
Сообщений: 2
Дан отрезок MP длиной 39 см. На нем отмечены точки G и H таким образом, что длины отрезков GP = 26 см, MH = 23 см. Найти длину отрезка GH в дециметрах.
0
Спасибо
Ответить
13 сентября 2016 в 8:06
Serega Pavlichenko
Профиль
Благодарили: 0
Сообщений: 1
Serega Pavlichenko
Профиль
Благодарили: 0
Сообщений: 1
найдите длину единичного отрезка координатного луча.Отметьте на координатном луче точки Е(2) и Д(5)
0
Спасибо
Ответить
19 сентября 2016 в 14:44
Ответ для Serega Pavlichenko
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Единичный отрезок- это отрезок равный 1делению. Точка E — на расстоянии 2 деления от начала луча, а точка Д — на расстоянии 5 делений от начала луча.
0
Спасибо
Ответить
10 июня 2016 в 9:50
Дарья Бондарь
Профиль
Благодарили: 0
Сообщений: 4
Дарья Бондарь
Профиль
Благодарили: 0
Сообщений: 4
Объясните, какой отрезок называется перпендикуляром, проведенным из данной точки к данной прямой.
0
Спасибо
Ответить
24 июня 2016 в 12:39
Ответ для Дарья Бондарь
Павел Асафов
Профиль
Благодарили: 0
Сообщений: 2
Павел Асафов
Профиль
Благодарили: 0
Сообщений: 2
отрезок, образующий с данной прямой угол 90 градусов
0
Спасибо
Ответить
9 июня 2016 в 10:28
Дарья Бондарь
Профиль
Благодарили: 0
Сообщений: 4
Дарья Бондарь
Профиль
Благодарили: 0
Сообщений: 4
Какими инструментами пользуются для измерения расстояний?
0
Спасибо
Ответить
9 июня 2016 в 10:53
Ответ для Дарья Бондарь
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Линейка, рулетка. Расстояние можно измерить по карте, зная масштаб и имея линейку.
0
Спасибо
Ответить
19 марта 2016 в 17:01
Настюшка Петрухова
Профиль
Благодарили: 0
Сообщений: 1
Настюшка Петрухова
Профиль
Благодарили: 0
Сообщений: 1
Дается отрезок, единичный отрезок равен 10 клеточкам. Как на нем указать 0,75 и 2,15???
0
Спасибо
Ответить
25 марта 2016 в 19:21
Ответ для Настюшка Петрухова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Если я правильно понимаю задание, то необходимо нарисовать соответствующие отрезки. Если единичный отрезок равен 10 клеточек, то 0,75 от него =10*0,75=7,5 клеток. А 2,15 = 2,15*10=21,5 клетка.
0
Спасибо
Ответить
3 октября 2015 в 11:37
Ольга Сырая
Профиль
Благодарили: 0
Сообщений: 1
Ольга Сырая
Профиль
Благодарили: 0
Сообщений: 1
На прямой поставили 3 точки. Сколько получилось отрезков? Мы решили, что 2. Но это олимпиадная задача и ответ пришел -3. Неужели АС это тоже отрезок?
0
Спасибо
Ответить
6 октября 2015 в 17:56
Ответ для Ольга Сырая
Альбина Серб
Профиль
Благодарили: 0
Сообщений: 2
Альбина Серб
Профиль
Благодарили: 0
Сообщений: 2
да
0
Спасибо
Ответить
25 сентября 2015 в 19:16
Снежана Бабюк
Профиль
Благодарили: 0
Сообщений: 1
Снежана Бабюк
Профиль
Благодарили: 0
Сообщений: 1
выберите геометрические фигуры понятие которых не определяется:
прямая, квадрат, плоскость, треугольник, окружность, точка, полупрямая, отрезок.
0
Спасибо
Ответить
12 сентября 2016 в 11:39
Ответ для Снежана Бабюк
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Прямая, плоскость и точка.
0
Спасибо
Ответить
15 сентября 2015 в 13:19
Марьям Туманова
Профиль
Благодарили: 0
Сообщений: 1
Марьям Туманова
Профиль
Благодарили: 0
Сообщений: 1
начерти отрезок мн длиной 4 см.начерти отрезок, каторий длиннееотрезкамн: а)на 3см; б)в3раза.какой длиныполулся каждый отрезок?
0
Спасибо
Ответить
17 сентября 2015 в 21:23
Ответ для Марьям Туманова
Ега Превосходный
Профиль
Благодарили: 0
Сообщений: 2
Ега Превосходный
Профиль
Благодарили: 0
Сообщений: 2
1 отрезок 4 см., второй 7 см., третий в трираза больше когого? если первого то полусится12см если вророго то получится 21см записать так( 4+3)* 3=21 см
0
Спасибо
Ответить
Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.
Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.
Запомните
Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.
Плоскость нельзя измерять, потому что она бесконечная.
Плоскость нельзя согнуть, в каком бы положении она ни находилась.
Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.
Прямая линия
Запомните
Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.
Даже когда мы рисуем на листе бумаги небольшой кусок прямой линии, то мы предполагаем, что этот лист бумаги – это бесконечная плоскость, и мы можем мысленно раздвинуть видимые границы бумаги и продлить прямую бесконечно долго.
Обозначение прямой
В основном прямую, как и любую другую линию, обозначают при помощи строчной (маленькой) буквы латинского алфавита.
Иногда обозначение прямой линии происходит при помощи двух точек, которые принадлежат (часто говорят просто – лежат на) этой прямой. В этом случае ее обозначают названием этих двух точек.
Например, на рисунке 1 обозначены такие прямые:
- c
- KL
Рис. 1 Обозначение прямой линии
Если на одной прямой лежат три и более известных нам точек, то обозначить эту линию можно любой из комбинаций имен любых двух точек.
Рис. 2 Обозначение прямой с несколькими точками
На рисунке 2 видно, что на одной прямой b лежат четыре точки: D, G, H, O. Поэтому данную прямую мы можем назвать любым из этих семи имен: b, DG, DH, DO, GH, GO или HO.
Некоторые свойства прямой
Две точки, лежащие на одной прямой, создают отрезок этой прямой.
Через две любые точки на плоскости можно провести единственную прямую.
Рис. 3 Отрезок на прямой
Две разные прямые могут пересекаться или не пересекаться.
Две прямые пересекаются в том случае, если у них есть общая точка.
И наоборот, если у двух разных прямых нет общей точки, тогда эти прямые не пересекаются.
Рис. 5 Пересечение прямых
На рисунке 5 можно видеть, что прямые l и q пересекаются в точке O, а прямые q и g не пересекаются.
Обозначение пересечения письменно записывается при помощи символа ∩: l ∩ q — прямая l пересекается с прямой q.
Как вам уже известно из этого урока, на рисунках мы можем отображать только часть прямых (поскольку они бесконечные), и что их можно мысленно увеличивать, делать более протяженными. Поэтому, если мысленно продлить прямые l и g, то станет понятно, что они тоже пересекаются.
Взаимное расположение точек и прямой, а также их обозначение, точно такое же, как и у всех линий вообще.
Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.
Луч
Определение
Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.
Рис. 6 Деление прямой линии точкой
На рисунке 1 точка O делит прямую a на две части, то есть, на два луча. Один из них, как вы видите, длится бесконечно вправо, а другой – бесконечно влево. Оба они начинаются в одной и той же точке O, которую называют началом луча.
У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.
Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.
Обозначение луча
Луч, как и прямую, обозначают двумя способами.
Рис. 7 Обозначение луча
На рисунке 2 приведены примеры обозначения луча:
- a – строчной (маленькая) буква латинского алфавита;
- OF – точками, расположенными на луче. При этом на первом месте всегда пишут точку начала луча, а на втором – любую точку, которая принадлежит лучу.
Луч имеет второе название – полупрямая.
Два луча, которые лежат на одной прямой, начинаются в одной точке и направлены в разные стороны, называются дополнительными друг другу лучами, поскольку в соединенном виде они формируют одну прямую линию в точке их начала.
Если лучи лежат на одной прямой, начинаются в одной точке и направлены в одну сторону, их называют совпадающие, или говорят, что эти лучи совпадают.
Рис. 8 Дополнительные друг другу и совпадающие лучи
На рисунке 8 видно, что:
- CB и CH – дополнительные друг другу лучи,
- BC и BH – совпадающие лучи,
- HC и HB – совпадающие лучи.
Математика
5 класс
Урок №21
Прямая, луч, отрезок
Перечень рассматриваемых вопросов:
— понятия «прямая», «луч», «отрезок»;
— отличия прямой, луча, отрезка;
— прямая, луч, отрезок на чертежах, рисунках и моделях.
Тезаурус
Отрезок – часть прямой, ограниченный двумя точками.
Концы отрезка – точки, ограничивающие отрезок.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф.Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009.–142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин.– М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Основными геометрическими фигурами принято считать плоскость, прямую и точку, все остальные фигуры образуются из них или их частей, поясним сказанное на примерах. Начнём с того, что различные геометрические фигуры располагаются на плоскости. Представление о плоскости даёт нам, например, поверхность стола или школьной доски. Стоит отметить, что эти поверхности имеют края. У плоскости нет краёв. Она безгранично простирается во всех направлениях.
Введём ещё одно понятие – прямая. Её обозначают малой латинской буквой (например, а) или двумя заглавными буквами (например, АВ, если на прямой отмечены соответствующие точки).
Стоит заметить, что прямая линия не имеет ни начала, ни конца, поэтому её изображение можно продолжить в обе стороны. Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.
Две различные прямые на плоскости могут и не пересекаться, сколько бы их не продолжали, такие прямые называют параллельными.
Параллельные прямые можно легко построить с помощью линейки и угольника, передвигая его вдоль линейки так, как показано на рисунке.
Через любые две точки можно провести только одну прямую.
Выполним построение. Для этого отметим две точки А и В и проведём через эти точки прямую b.
Провести через точки А и В другую прямую, отличную от прямой b, нельзя.
Используя прямую и точку в виде деталей геометрического конструктора, можно создавать новые геометрические объекты.
Например, начертим прямую с и отметим на ней точку А. Точка А разделила прямую на две части.
Каждую из этих частей называют лучом, исходящим из точки А.
Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.
Луч следует обозначать двумя заглавными буквами латинского алфавита, при этом на первое место надо ставить обозначение начала луча. Например, АВ, как в нашем случае, где точка А – начало луча.
Переставлять буквы в названии луча нельзя.
Теперь рассмотрим ещё одно важное геометрическое понятие – отрезок.
Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ.
В отличие от луча, в названии отрезка переставлять буквы допустимо, поэтому его можно обозначить как АВ, так и ВА.
Заметим, что два отрезка называются равными, если они совмещаются при наложении.
Итак, сегодня мы познакомились с понятиями прямая, луч, отрезок, как одними из основополагающих понятий в геометрии.
Это интересно
Помимо геометрии, мы можем встретить слово «луч» и в других научных областях.
- Космические лучи – это элементарные частицы и ядра атомов, движущиеся с высокими энергиями в космическом пространстве.
- Противосумеречные лучи (англ. anticrepuscular rays) – расходящиеся веером лучи, наблюдающиеся на закате дня со стороны, противоположной Солнцу (то есть, на востоке).
- Белохохлый солнечный луч (лат. Aglaeactis castelnaudii) – вид птиц из семейства колибри (Trochilidae).
- Луч света в темном царстве – крылатое выражение, вошедшее в речь после публикации в 1860 году статьи публициста-демократа Николая Александровича Добролюбова, посвящённой драме А. Н. Островского «Гроза».
Разбор решения заданий тренировочного модуля
№ 1. Тип задания: добавление подписей к изображениям.
Разместите нужные подписи к изображениям.
Для выполнения задания обратитесь к теоретическому материалу урока.
Правильные ответы:
1) а – это прямая.
2) АВ – это отрезок.
3) А – это луч.
№ 2. Тип задания: подстановка элементов в пропуски в тексте.
Вставьте в текст нужные слова.
Через__________ две____________ можно провести только одну _________.
Слова: любые; точки; прямую; ломаную.
Правильный ответ: через любые две точки можно провести только одну прямую.

4.4
Средняя оценка: 4.4
Всего получено оценок: 398.
4.4
Средняя оценка: 4.4
Всего получено оценок: 398.
Луч – это одно из основных базовых построений наравне с точкой и прямой. Изучение луча в курсе математики 5 класса дает начало другим важным темам: системам координат и углам на плоскости.
Определение
Луч это прямая, ограниченная с одной стороны. Это определение лучше усвоится, если выучить свойства луча:
- Имеет начало, но не имеет конца
- Имеет направление
- Бесконечен, т.е. не имеет размера.
Правильное обозначение луча спорный вопрос. Наиболее правильный вариант это две точки, например ОА. Причем первой точкой обозначают начало луча. Но также обозначают отрезки и прямые, поэтому чаще пишут луч с началом в точке О.
Углы
Углы – это единственные фигуры, состоящие из лучей. Что такое угол? Это геометрическая фигура, состоящая из двух лучей, начало которых лежит в одной точке. В фигурах углы состоят из отрезков, а не из лучей.
Может случиться ситуация, когда оде стороны угла будут совпадать, тогда говорят, что величина угла равна 0 градусов. Может получиться и так, что обе стороны угла образуют прямую, тогда говорят, что угол равен 180 градусам. Такой угол называют развернутым, а лучи основным и дополнительным.
Величина угла отражает поворот одного луча относительно другого.
Координатные лучи
Еще одно применение лучей это различные системы координат. В математике 5 класса первой темой идет изучение координатной прямой. Это два луча с углом поворота в 180 градусов. Начало лучей обозначается за нулевую точку или начало отчета. Влево от начала отчета откладываются отрицательные координаты, в право-положительные. Другое название координатной прямой: числовой луч.
С помощью координатного луча удобно сравнивать дроби и таким образом решать неравенство.
С помощью координатных лучей создается и координатная плоскость. Так называемая декартова система координат состоит из двух координатных прямых или 4 лучей. Подобная система позволяет определять положение точки на плоскости, вычерчивать графики функций и графически решать разного рода уравнения.
Помимо декартовой системы существует полярная система координат. В полярной системе используются понятия угла и координатной прямой. Координатная прямая определяет положение точки, а угол степень ее подъема над осью.
Полярная система координат одна из самых древних в истории человечества. Так сложилось, что именно пользуясь этой системой, древние мореплаватели покоряли неизвестные просторы нашего мира. Декартова система появилась гораздо позднее. Но она более удобна для ориентации на местности. Декартову систему проще использовать как в разделах математики, так и других дисциплинах: физике, теплотехнике, гидравлике и программировании.
Декартовая система четырьмя лучами делиться на 4 четверти, положение точки в каждой из которых определяется знаком координат. Координаты подразделяют на абсциссы и ординаты. Проще говоря на х и у. Например точка (3, 4) имеет две положительные координаты, а значит она будет находиться в первой четверти. Обе отрицательные координаты соответствуют третьей четверти, положительный у при отрицательном х это вторая четверть, а отрицательный у при положительном х – четвертая.
Чтобы построить точку в декартовых системах координат необходимо от деления числового луча, соответствующего координате, поднять перпендикуляр. Координаты две, значит и перпендикуляров будет два. Точка их пересечения и будет искомой точкой.
Числовая прямая
Числовая прямая – это луч, с нанесенными на него числами или интервалами чисел. Числовую прямую используют для сравнения дробей, рисунков к задаче и нахождения ОДЗ функции. Последнее встречается чаще всего.
Фигурной скобкой на прямой обозначается область, в которую не могут попадать корни. После решения уравнения, найденные корни наносятся на числовую прямую. Попавшие в фигурную скобку недопустимых значений корни исключаются из решения.
Что мы узнали?
Мы узнали, что такое луч и числовая прямая. Поговорили о фигурах, составленных из лучей и системах координат, где применяются числовые прямые. Проработали вопрос наглядности изображения нужных точек и разобрались с тем, как правильно проставлять координаты на координатном луче.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Артём Закутний
8/10
-
Антон Кабашный
8/10
-
Дария Петроченко
9/10
-
Валик-Ти Кукурузов
7/10
-
Виктор Финякин
7/10
-
Александр Барсов
10/10
-
Юля Александрова
8/10
-
Вова Свистельников
7/10
-
Наталия Левина
8/10
-
Марина Молодцова
6/10
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 398.
А какая ваша оценка?